中考数学压轴题专项汇编专题30函数与面积

2023年中考数学专题复习：二次函数的面积问题压轴训练1．综合与探究如图，在平面直角坐标系中，二次函数y ＝x 2＋bx ＋c 的图象与x 轴交于A 、B 两点，A 点在原点的左侧，B 点的坐标为（3，0），与y 轴交于C （0，﹣3）点，点P 是直线BC 下方的抛物线上一动点．(1)求这个二次函数的表达式．(2)当点P 运动到什么位置时，四边形ABPC 的面积最大？求出此时P 点的坐标和四边形ABPC 的最大面积．(3)连接PO 、PC ，并把△POC 沿CO 翻折，得到四边形POP ′C ，那么是否存在点P ，使四边形POP ′C 为菱形？若存在，请求出此时点P 的坐标；若不存在，请说明理由．2．如图，抛物线2y x bx c =++经过()1,0A -、()4,5B 两点，点E 是线段AB 上一动点，过点E 作x 轴的垂线，交抛物线于点F ．(1)求抛物线的解析式；(2)求线段EF 的最大值；(3)抛物线与x 轴的另一个交点为点C ，在抛物线上是否存在一个动点P ，使得25ACP ABC S S ∆∆=？若存在，求出点P 的坐标；若不存在，请说明理由．3．如图，二次函数23y ax bx =++的图像与x 正半轴相交于点B ，负半轴相交于点A ，其中A 点坐标是（－1，0），B 点坐标是（3，0）．(1)求此二次函数的解析式；(2)如图1，点P 在第一象限的抛物线上运动，过点P 作PD x ⊥轴于点D ，交线段BC 于点E ，线段BC 把△CPD 分割成两个三角形的面积比为1△2，求P 点坐标；(3)如图2，若点H 在抛物线上，点F 在x 轴上，当以B 、C 、H 、F 为顶点的四边形是平行四边形时，请直接写出点F 的坐标．4．如图，抛物线2y x bx c =-++与x 轴交于A ，B 两点，与y 轴交于C 点，直线BC 方程为3y x =-．(1)求抛物线的解析式；(2)点P 为抛物线上一点，若12PBC ABC S S =，请直接写出点P 的坐标；(3)点Q 是抛物线上一点，若45ACQ ∠=︒，求点Q 的坐标．5．如图，已知直线y ＝43x +4与x 轴交于点A ，与y 轴交于点C ，抛物线y ＝ax 2+bx +c 经过A ，C 两点，且与x 轴的另一个交点为B ，对称轴为直线x ＝﹣1．(1)求抛物线的表达式；(2)D 是第二象限内抛物线上的动点，设点D 的横坐标为m ，求四边形ABCD 面积S 的最大值及此时D 点的坐标；(3)若点P 在抛物线对称轴上，是否存在点P ，Q ，使以点A ，C ，P ，Q 为顶点的四边形是以AC 为对角线的菱形？若存在，请求出P ，Q 两点的坐标；若不存在，请说明理由．6．综合与探究：如图，抛物线26y ax bx =+-与x 轴相交于A ，B 两点，与y 轴相交于点C ，2OA =，4OB =，直线l 是抛物线的对称轴，在直线l 右侧的抛物线上有一动点D ，连接AD ，BD ，BC ，CD ．(1)求抛物线的函数表达式；(2)若点D 在x 轴的下方，当BCD △的面积是92时，求ABD △的面积； (3)在（2）的条件下，点M 是x 轴上一点，点N 是抛物线上一动点，是否存在点N ，使得以点B ，D ，M ，N 为顶点，以BD 为一边的四边形是平行四边形，若存在，请直接写出点N 的坐标；若不存在，请说明理由．7．如图，在平面直角坐标系中，直线y ＝2x ＋4与x 轴，y 轴分别交于A ，B 两点，抛物线()20y ax x c a =++≠经过A ，B 两点与x 轴相交于点C 点．(1)求抛物线的解析式；(2)点P 在抛物线上，连接PB ，当△PBC ＋△OBA ＝45°时，求点P 的坐标；(3)点M 为抛物线上任意一点，当13ABM ABC S S =△△::时，请直接写出点M 的坐标．8．如图，抛物线2y x bx c =++与x 轴交于,(4,0)A B 两点（A 在B 的左侧），与y 轴交于点(0,4)C -，点P 在抛物线上，连接,BC BP ．(1)求抛物线的解析式；(2)如图1，若点P 在第四象限，点D 在线段BC 上，连接PD 并延长交x 轴于点E ，连接CE ，记DCE 的面积为1S ，DBP 的面积为2S ，当12S S 时，求点P 的坐标；(3)如图2，若点P 在第二象限，点F 为抛物线的顶点，抛物线的对称轴l 与线段BC 交于点G ，当90PBC CFG ∠+∠=︒时，求点P 的横坐标．9．如图，抛物线y ＝ax 2+bx +4与x 轴相交于点A （0），B 0），与y 轴相交于点C ，抛物线的对称轴与x 轴相交于点D ，点P 是x 轴上的一个动点，连接CP ，并把线段CP 绕着点C 按逆时针方向旋转60°，得到CQ ，连接PQ ，OQ ．(1)求抛物线的解析式；(2)当点P 运动到点D 时，求Q 点坐标，并判断点Q 是否在抛物线上；(3)当△OPQ P 的坐标．10．如图，在平面直角坐标系中，抛物线2y ax x m =++（a ≠0）的图象与x 轴交于A 、C 两点，与y 轴交于点B ，其中点B 坐标为（0，－4），点C 坐标为（2，0）．(1)求此抛物线的函数解析式．(2)点D 是直线AB 下方抛物线上一个动点，连接AD 、BD ，探究是否存在点D ，使得△ABD 的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由．(3)点P 为该抛物线对称轴上的动点，使得△P AB 为直角三角形，请求出点P 的坐标．11．如图，在平面直角坐标系中，抛物线22y ax bx =+-与x 轴交于(1,0)A -，B 两点，其对称轴1x =与x 轴交于点D ．图1 图2(1)求该抛物线的函数表达式；(2)如图1，点P 为第四象限内的抛物线上一动点，连接PB ，PC ，CD ，求四边形PBDC 面积的最大值和此时点P 的坐标；(3)将该抛物线向左平移3个单位长度得到抛物线y'，平移后的抛物线与原抛物线的对称轴相交于点E ，点F 为抛物线y'对称轴上的一点，M 是原抛物线上的动点，直接写出所有使得以点A ，E ，F ，M 为顶点的四边形是平行四边形的点M 的坐标，并把求其中一个点M 的坐标的过程写出来．12．如图，抛物线22y ax bx =++经过点()()1040，，，A B -，与y 轴交于点C ．(1)求抛物线的解析式；(2)点D 为y 轴右侧抛物线上一点，是否存在点D ，使23ABC ABD S S =△△若存在，求出点D 的坐标；若不存在，请说明理由；(3)将直线BC 绕点B 顺时针旋转45°，与直线AC 交于点F ，直接写出BF 的长．13．如图，在平面直角坐标系中，抛物线2(0)y ax c a =+≠与x 轴交于A ，B 两点，点B 的坐标是(2,0)，顶点C 的坐标是(0,4)，M 是抛物线上一动点，且位于第一象限，直线AM 与y 轴交于点G ．(1)求该抛物线的解析式；(2)如图1，N 是抛物线上一点，且位于第二象限，连接OM ，记AOG MOG ，的面积分别为12,S S ．当122S S =，且直线CN AM ∥时，求证：点N 与点M 关于y 轴对称；(3)如图2，直线BM 与y 轴交于点H ，是否存在点M ，使得27OH OG -=．若存在，求出点M 的坐标；若不存在，请说明理由．14．如图，已知在平面直角坐标系xOy 中，抛物线y =-12x 2+bx +c 经过点A （-2，0）．与点C （0，4）．与x 轴的正半轴交于点B ．(1)求抛物线的表达式；(2)如果D 是抛物线上一点，AD 与线段BC 相交于点E ，且AD 将四边形ABDC 分成面积相等的两部分，求DE AE的值； (3)如果P 是x 轴上一点，△PCB =△ACO ，求△PCO 的正切值．15．如图，抛物线23y ax bx =+-交x 轴于()30A -,，()10B ,两点，与y 轴交于点.C 连接AC ，BC ．(1)求抛物线的解析式；(2)如图1，点P 为抛物线在第三象限的一个动点，PM x ⊥轴于点M ，交AC 于点G ，PE AC ⊥于点E ，当PGE 的面积为1时，求点P 的坐标；(3)如图2，若Q 为抛物线上一点，直线OQ 与线段AC 交于点N ，是否存在这样的点Q ，使得以A ，O ，N 为顶点的三角形与ABC 相似．若存在，请求出此时点Q 的坐标；若不存在，请说明理由．16．在平面直角坐标系中，已知抛物线经过A （－4，0），B （0，－4），C （2，0）三点．(1)求抛物线的解析式；(2)若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S ．求S 关于m 的函数关系式，并求出S 的最大值．(3)若点P 是抛物线上的动点，点Q 是直线y ＝－x 上的动点，判断有几个位置能够使得点P 、Q 、B 、 O 为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标．17．如图，直线y ＝x +2与抛物线y ＝ax 2-8x +6（a ≠0）相交于A （4，6）和B （12，52），点P 是线段AB 上异于A 、B 的动点，过点P 作PD △x 轴于点E ，交抛物线于点D ．(1)求抛物线的解析式；(2)当D 为抛物线顶点的时候，求△ADC 的面积；(3)是否存在这样的点P ，使△ADC 的面积有最大值，若存在，求出这个最大值，若不存在，请说明理由．18．如图，已经抛物线经过点(0,0)O ，(5,5)A ，且它的对称轴为2x =．(1)求此抛物线的解析式；(2)若点B 是抛物线对称轴上的一点，且点B 在第一象限，当OAB 的面积为15时，求B 的坐标；(3)在（2）的条件下，P 是抛物线上的动点，当PA PB -的值最大时，求P 的坐标以及PA PB -的最大值19．如图：已知关于x 的二次函数y =x 2+bx +c 的图像与x 轴交于点A （1，0）和点B ，与y 轴交于点C （0，3）．(1)求二次函数的解析式；(2)在抛物线的对称轴上是否存在一点P，使△PBC为等腰三角形，若存在，请求出点P的坐标；(3)有一个点M在线段CB上运动，作MN△x轴交抛物线于点N，问当M、N点位于何处时，△BCN的面积最大，求最大面积.20．如图，抛物线y＝ax2+bx﹣3与x轴交于点A（﹣1，0）和点B（9，0），与y轴交于点C，连接AC．BC．(1)求抛物线的解析式；(2)将△AOC以每秒一个单位的速度沿x轴向右平移，平移的时间为t秒，平移后的△A1O1C1与△ABC重叠部分的面积为S．当A1与B重合时，停止平移，求S与t的函数关系式；(3)点M在抛物线上，当△MAB＝2△ACO时，请直接写出点M的横坐标．答案1．(1)223y x x =--(2)P 点坐标为315,24⎛⎫- ⎪⎝⎭，四边形ABPC 的最大面积为758(3)存在，P 点坐标为32⎫-⎪⎪⎝⎭2．(1)223y x x =-- (2)254(3)存在，点P 的坐标为(12) 或(12)或()12-或(12)-3．(1)2y x 2x 3=-++(2)P 点坐标115(,)24或(2,3)(3)F 点坐标为：(1,0)、(5,0)、)2,0、()2-4．(1)y =-x 2+4x -3或352,）或) (3)(72,54-)5．(1)y ＝﹣43x 2﹣83x +4 (2)S 最大＝252，D （﹣32，5） (3)存在，Q （﹣2，198） 6．(1)233642y x x =-- (2)454(3)存在，151,4N ⎛⎫-- ⎪⎝⎭或1514N ⎛⎫ ⎪⎝⎭或1514N ⎛⎫ ⎪⎝⎭ 7．(1)2142y x x =-++(2)()6,8-和53,2⎛⎫ ⎪⎝⎭(3)()12,4M ，()24,8M --8．(1)234y x x =--(2)()34P -，(3)点P 的横坐标为65-9．(1)2144y x =-+(2)Q ，4），点Q 在抛物线上(3)符合条件的点P 0），，0），（0），（0）10．(1)2142y x x =+- (2)（-2，-4）(3)P 点坐标为：（-1，3），（-1，-5），(12--，，(12--，11．(1)224233y x x =--； (2)PBDC S 四边形的最大值为174，此时点P 的坐标为3(2，5)2-； (3)点M 的坐标为(4,14)-或(0,2)M -或(2,2)-．12．(1)213222y x x =-++ (2)存在，点D 的坐标为：（1，3）或（2，3）或（5，-3）(3)13．(1)24y x =-+(3)存在，115,24M ⎛⎫ ⎪⎝⎭14．(1)抛物线解析式为y =-12x 2+x +4； (2)14DE AE =；(3)△PCO 的正切值13或3．15．(1)223y x x =+-(2)()14P --，或()23--， (3)存在，坐标为⎝⎭或⎝⎭或或(-16．(1)2142y x x =+- (2)24=--S m m ，4(3)()4,4Q -或(2-+-或(2--+或()4,4-17．(1)抛物线的表达式为：y ＝2x 2﹣8x +6(2)18(3)当x ＝94时，S △ADC 最大值为：147818．(1)24.yx x (2)()2,8B(3)2,12,PPA PB -的最大值为19．(1)243y x x =-+(2)存在，P （2，2） （2，（2，3，（2（2，(3)当3322M ⎛⎫ ⎪⎝⎭，，3324N ⎛⎫- ⎪⎝⎭，时，△BCN 的面积最大，最大面积为27820．(1)218333y x x =-- (2)()()()222236012012719602331591020t t t S t t t t t ⎧-+<≤⎪⎪⎪=-+<≤⎨⎪⎪-+<≤⎪⎩(3)274或454．。

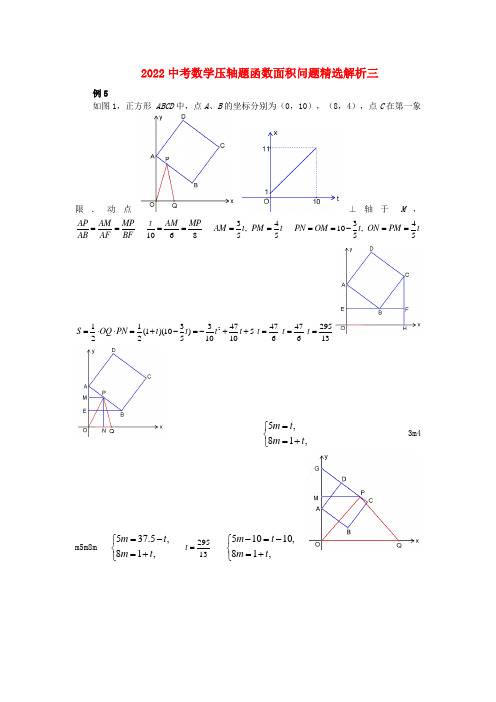
2022中考数学压轴题函数面积问题精选解析三例5如图1，正方形 ABCD 中，点A 、B 的坐标分别为（0，10），（8，4），点C 在第一象限．动点⊥轴于M ，AP AM MPAB AF BF==1068t AM MP ==34,55AM t PM t==3410,55PN OM t ON PM t==-==2113347(1)(10)52251010S OQ PN t t t t =⋅⋅=+-=-++476t =476t =29513t =5,81,m t m t =⎧⎨=+⎩3m4m5m8m537.5,81,m t m t =-⎧⎨=+⎩29513t =51010,81,m t m t -=-⎧⎨=+⎩c bx x y ++=2（2）如图1，在边长一定的矩形ABCD 中，CD ＝1，点C 在轴右侧沿抛物线c bx x y ++=2 滑动，在滑动过程中CD ∥轴，轴上时，AB 落在轴上①求边BC 的长②当矩形ABCD 在滑动过程中被轴分成两部分的面积比为1:4时，求点C 的坐标图1解析（1）因为抛物线c bx x y ++=2经过点（0，10）和点（4，2），所以10,164 2.c b c =⎧⎨++=⎩解得6b =-，10c =．因此抛物线的解析式为＝2－6＋10．（2）①因为CD ＝1，点D 在 轴上，所以点C 的横坐标为1．在＝2－6＋10中，当＝1时，＝5．所以边BC 的长为5．②因为矩形边长一定，所以BC ＝5．如图2，当矩形ABCD 在轴上方部分的面积与这个矩形面积的比为1:5时，点C 的纵坐标为1．解方程2－6＋10＝1，得123x x ==．此时点C的坐标为3，1．如图3，当矩形ABCD 在轴上方部分的面积与这个矩形面积的比为5:1时，点C 的纵坐标为4．解方程2－6＋10＝4，得133x =233x =C 的坐标为3＋，4或3－，4．图2 图3考点伸展在本题情景下，以CD 为半径的⊙C 如果与坐标轴相切，那么符合条件的点C 有哪些 解：由于CD ＝1，抛物线的顶点为（3，1），因此与坐标轴相切的⊙C 有三个，点C 的坐标分别为（1，5），（－1，17），（3，1）．在本题情景下，以CB 为半径的⊙C 如果与坐标轴相切，那么符合条件的点C 有哪些 解：由于点（5，5）恰好在抛物线上，因此与坐标轴相切的⊙C 有两个，点C 的坐标分别为（5，5），（－5，65）．。

2022年中考数学二次函数--图形面积与最值问题压轴题专项训练1．如图，抛物线y＝x2＋bx＋c与x轴交于点A（﹣1，0），与y轴交于点C（0，﹣3）．(1)求该抛物线的解析式及顶点坐标；(2)若P是线段OB上一动点，过P作y轴的平行线交抛物线于点H，交BC于点N，设OP＝t时，△BCH的面积为S．求S关于t的函数关系式；若S有最大值，请求出S的最大值，若没有，请说明理由．(3)若P是x轴上一个动点，过P作射线PQ∥AC交抛物线于点Q，在抛物线上是否存在这样的点Q，使以A，P，Q，C为顶点的四边形为平行四边形？若存在，请直接写出P点的坐标；若不存在，请说明理由．2．已知抛物线y＝ax2＋bx＋3与x轴交于A、B两点（点A在点B的左侧）．与y轴交于点C．其中OC＝OB，tan∠CAO＝3(1)求抛物线的解析式；(2)P是第一象限内的抛物线上一动点，Q为线段PB的中点，求△CPQ面积的最大值时P点坐标：(3)将抛物线沿射线CB方向平移个单位得新抛物线y′．M为新抛物线y′的顶点．D为新抛物线y′上任意一点，N为x轴上一点．当以M、N、C、D为顶点的四边形是平行四边形时，直接写出所有符合条件的点N 的坐标．并选择一个你喜欢的N点．写出求解过程．3．如图，抛物线223=-++与x轴交于,A B两点（A点在B点的左侧），与y轴交于点C，连接AC，y ax axBC，A点的坐标是（1-，0），点P是抛物线上的一个动点，其横坐标为m，且m>0．(1)求此抛物线的解析式；(2)若点Q是直线AC上的一个动点，且位于x轴的上方，当PQ∥y轴时，作PM⊥PQ，交抛物线于点M（点M在点P的右侧），以PQ，PM为邻边构造矩形PQNM，求该矩形周长的最小值；(3)设抛物线在点C与点P之间的部分（含点C和P）最高点与最低点的纵坐标之差为h．①求h关于m的函数解析式，并写出自变量m的取值范围；②当h=16时，直接写出△BCP的面积．4．在一个三角形中，如果其中某两边的长度之和等于第三边长度的两倍，则称该三角形为“调和三角形”例如我们学过的等边三角形就是“调和三角形”．(1)已知一个“调和三角形”三条边的长度分别为4，6，m﹣1，求m的值．(2)已知Rt△ABC是“调和三角形”，它的三边长分别为a，b，c，且a＜b＜c．①求a：b：c的值；②若△ABC周长的数值与面积的数值相等，求a，b，c的值．(3)在（2）的条件下，动点P从点A出发以每秒2个单位长度的速度沿路线A→B→C运动，动点Q从点C 出发以每秒1个单位长度的速度向点A运动，当其中一点到达终点时，另一点也随之停止运动，设运动时间为t秒，设y＝PQ2．①求y关于t的函数关系式；②求y的最小值．5．如图1，抛物线C1：y＝ax2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，且顶点为C，直线y＝kx+2经过A，C两点．(1)求直线AC的表达式与抛物线C1的表达式；(2)如图2，将抛物线C1沿射线AC方向平移一定距离后，得到抛物线为C2，其顶点为D，抛物线C2与直线y＝kx+2的另一交点为E，与x轴交于M，N两点（M点在N点右边），若S△MDE＝23S△MAE，求点D的坐标；(3)如图3，若抛物线C1向上平移4个单位得到抛物线C3，正方形GHST的顶点G，H在x轴上，顶点S，T 在x轴上方的抛物线C3上，P（m，0）是射线GH上一动点，则正方形GHST的边长为，当m＝时，PSPT有最小值．6．如图，已知抛物线212y x bx c =++经过()4,0A -，()0,4B -，()2,0C 三点．(1)求抛物线的解析式；(2)若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，AMB 的面积为S ．求S 关于m 的函数关系式，并求出S 的最大值．7．如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +c 的图象与轴交于A (﹣1，0)，B (4，0)，与y 轴交于点C (0，﹣3)，连接AC 、BC ．(1)求抛物线的函数表达式；(2)如图1，点D 是抛物线上位于第四象限内的一点，连接AD ，点E 是AD 的中点，连接BE 、CE ，求△BCE 面积的最小值；(3)如图2，点P 是抛物线上位于第四象限内的一点，点Q 在y 轴上，∠PBQ ＝∠OBC ，是否存在这样的点P 、Q 使BP ＝BQ ，若存在，求出点P 的坐标；若不存在，请说明理由．8．如图，抛物线y＝ax2＋bx＋4交x轴于点A（﹣1，0）、B（4，0），交y轴于点C，点P是直线BC上方抛物线上的一点．(1)求抛物线的解析式；(2)求△PBC的面积的最大值以及此时点P的坐标；(3)在（2）的条件下，将直线BC向右平移74个单位得到直线l，直线l交对称轴右侧的抛物线于点Q，连接PQ，点R为直线BC上的一动点，请问在在平面直角坐标系内是否存在一点T，使得四边形PQTR为菱形，若存在，请直接写出点T的坐标；若不存在，请说明理由．9．如图1，在平面直角坐标系中，已知矩形ABCD的三个顶点A（﹣3，4）、B（﹣3，0）、C（﹣1，0）．以D为顶点的抛物线y＝ax2＋bx＋c过点B．动点P以每秒1个单位的速度从点D出发，沿DC边向点C运动，运动的时间为t秒．过点P作PE⊥CD交BD于点E，过点E作EF⊥AD于点F，交抛物线于点G．(1)求该抛物线的解析式；(2)连接BG ，求△BGD 的面积最大值；(3)如图2，在点P 运动的同时，点Q 从点B 出发，沿BA 边以每秒1个单位的速度向点A 运动．动点P 、Q 运动的过程中，在矩形ABCD 内（包括其边界）是否存在点H ，使以B ，Q ，E ，H 为顶点的四边形是菱形？若不存在，请说明理由；若存在，请直接写出t 的值：t ＝ ．10．如图，抛物线26y ax bx =++与直线2y x =+相交于15,22A ⎛⎫ ⎪⎝⎭、()4,6B 两点，点P 是线段AB 上的动点（不与A 、B 两点重合），过点P 作PC x ⊥轴于点D ，交抛物线于点C ，点E 是直线AB 与x 轴的交点．(1)求抛物线的解析式；(2)当点C 是抛物线的顶点时，求BCE 的面积；(3)是否存在点P ，使得BCE 的面积最大？若存在，求出这个最大值：若不存在，请说明理由．11．综合与探究：如图，在平面直角坐标系中，直线y ＝﹣3x ﹣3与x 轴交于点A ，与y 轴交于点C ．抛物线y ＝x 2＋bx ＋c 经过A 、C 两点，且与x 轴交于另一点B （点B 在点A 右侧）．(1)求抛物线的解析式及点B 坐标；(2)设该抛物线的顶点为点H ，则S △BCH ＝ ；(3)若点M 是线段BC 上一动点，过点M 的直线ED 平行y 轴交x 轴于点D ，交抛物线于点E ，求ME 长的最大值及点M 的坐标；(4)在（3）的条件下：当ME 取得最大值时，在x 轴上是否存在这样的点P ，使得以点M 、点B 、点P 为顶点的三角形是等腰三角形？若存在，请直接写出所有点P 的坐标；若不存在，请说明理由．12．如图，抛物线y ＝243x bx c -++经过点A （3，0），B （0，2），连接AB ，点P 是第一象限内抛物线上一动点．(1)求抛物线的表达式；(2)过点P 作x 轴的垂线，交AB 于点Q ，判断是否存在点P ，使得以P 、Q 、B 为顶点的三角形是直角三角形，若存在，请求出点P 的坐标，若不存在，请说明理由；(3)点C与点B关于x轴对称，连接AC，AP，PC，当点P运动到什么位置时，△ACP的面积最大？求△ACP 面积的最大值及此时点P的坐标．13．已知抛物线y＝ax2＋bx＋c（a≠0）与x轴交于A、B两点（点A在点B的左边），与y轴交于点C（0，﹣3），顶点D的坐标为（1，﹣4）．(1)求抛物线的解析式；(2)如图1，抛物线在第四象限的图象上有一点M，求四边形ABMC面积的最大值及此时点M的坐标；(3)如图2，直线CD交x轴于点E，若点P是线段EC上的一个动点，是否存在以点P、E、O为顶点的三角形与△ABC相似．若存在，请直接写出点P的坐标；若不存在，请说明理由．14．如图，在平面直角坐标系xOy中，直线y＝﹣x＋3与两坐标轴交于A、B两点，抛物线y＝x2＋bx＋c过点A和点B，并与x轴交于另一点C，顶点为D．点E在对称轴右侧的抛物线上．(1)求抛物线的函数表达式和顶点D的坐标；(2)若点F 在抛物线的对称轴上，且EF ∥x 轴，若以点D ，E ，F 为顶点的三角形与△ABD 相似，求出此时点E 的坐标；(3)若点P 为坐标平面内一动点，满足tan ∠APB ＝3，请直接写出△P AB 面积最大时点P 的坐标及该三角形面积的最大值．15．如图，抛物线23y ax bx =++与x 轴交于(2,0)A -、(6,0)B 两点，与y 轴交于点C ．直线l 与抛物线交于A 、D 两点，与y 轴交于点E ，点D 的横坐标为4．(1)求抛物线的解析式与直线l 的解析式；(2)若点P 是抛物线上的点且在直线l 上方，连接PA 、PD ，求当PAD ∆面积最大时点P 的坐标及该面积的最大值；(3)若点Q 是抛物线上的点，且45ADQ ∠=︒，请直接写出点Q 的坐标．16．如图，抛物线y ＝ax 2＋bx ＋2交x 轴于点A （﹣3，0）和点B （1，0），交y 轴于点C ．已知点D 的坐标为（﹣1，0），点P 为第二象限内抛物线上的一个动点，连接AP 、PC 、CD ．(1)求这个抛物线的表达式．(2)点P 为第二象限内抛物线上的一个动点，求四边形ADCP 面积的最大值．(3)①点M 在平面内，当△CDM 是以CM 为斜边的等腰直角三角形时，求出满足条件的所有点M 的坐标； ②在①的条件下，点N 在抛物线对称轴上，当∠MNC ＝45°时，求出满足条件的所有点N 的坐标．17．如图，已知抛物线212y x bx c =-++的顶点C 的坐标为()3,2-，此抛物线交x 轴于点A ，B 两点，点P 为直线AD 上方抛物线上一点，过点P 作PE x ⊥轴垂足为E ，连接AP ，PD ．(1)求抛物线和直线AD 的解析式；(2)求线段PN 的最大值；(3)当APD △的面积是ABC 的面积的54时，求点P 的坐标．18．如图，直线y 12=x +2与x 轴，y 轴分别交于点A ，C ，抛物线y 12=-x 2+bx +c 经过A ，C 两点，与x 轴的另一交点为B ，点D 是抛物线上一动点．(1)求抛物线的解析式；(2)当点D 在直线AC 上方时，连接BC ，CD ，BD ，BD 交AC 于点E ，令△CDE 的面积为S 1，△BCE 的面积为S 2，求12S S 的最大值； (3)点F 是该抛物线对称轴上一动点，是否存在以点B ，C ，D ，F 为顶点的平行四边形？若存在，请直接写出点D 的坐标；若不存在，请说明理由．19．如图所示，在平面直角坐标系中，抛物线y ＝ax 2+bx +c （a ≠0）的顶点坐标为C （3，6），并与y 轴交于点B （0，3），点A 是对称轴与x 轴的交点．(1)求抛物线的解析式；(2)如图①所示，P 是抛物线上的一个动点，且位于第一象限，连接BP ，AP ，求△ABP 的面积的最大值；(3)如图②所示，在对称轴AC 的右侧作∠ACD ＝30°交抛物线于点D ，求出D 点的坐标；并探究：在y 轴上是否存在点Q ，使∠CQD ＝60°？若存在，求点Q 的坐标；若不存在，请说明理由．20．如图，抛物线2y x bx c =-++与x 轴交于A （-1，0），B （3，0）两点，与y 轴交于点C ，直线3y x =-+经过B，C两点，连接AC．(1)求抛物线的表达式；(2)点E为直线BC上方的抛物线上的一动点（点E不与点B，C重合），连接BE，CE，设四边形BECA的面积为S，求S的最大值；(3)若点Q在x轴上，则在抛物线上是否存在一点P，使得以B，C，P，Q四点为顶点的四边形是平行四边形？若存在，请直接写出P点的坐标；若不存在，请说明理由．参考答案：1．解：把点A （﹣1，0），点C （0，﹣3）代入抛物线的解析式为y ＝x 2+bx +c 中得：103b c c -+=⎧⎨=-⎩解得：23b c =-⎧⎨=-⎩∴抛物线的解析式为y ＝x 2﹣2x ﹣3∵y ＝x 2﹣2x ﹣3＝（x ﹣1）2﹣4∴顶点的坐标为（1，﹣4）(2)如图1，设直线BC 的解析式为y ＝kx +d （k ≠0）当y ＝0时，x 2﹣2x ﹣3＝0解得：x 1＝3，x 2＝﹣1∴B （3，0）将B （3，0），C （0，﹣3）代入y ＝kx +d 中得：303k d d +=⎧⎨=-⎩，解得：13k d =⎧⎨=-⎩ ∴直线BC 的解析式为y ＝x ﹣3∵OP ＝t设点P 的坐标为（t ，0），则点N 的坐标为（t ，t ﹣3），H （t ，t 2﹣2t ﹣3） ∴NH ＝t ﹣3﹣（t 2﹣2t ﹣3）＝﹣t 2+3t ∴223327()22813(3)22BCH S t t S NH OB t ===-+=--+△∵0≤t≤3，32-＜，∴当t32=时，S取最大值，最大值为278；(3)分两种情况：①当Q在x轴的上方时，如图2和图4，四边形ACPQ是平行四边形根据A（﹣1，0）和C（0，﹣3）可知：点Q的纵坐标为3当y＝3时，x2﹣2x﹣3＝3解得：x1＝1x2＝1∴P（20）或（20）②当Q在x轴的下方时，如图3，四边形ACQP是平行四边形，当y＝﹣3时，由对称得：Q（2，﹣3）∴P （1，0）综上，P 点的坐标为（2，0）或（20）或（1，0）2．∵抛物线解析式为23y ax bx =++，令x ＝0，得y ＝3，∴点C 坐标为（0，3），∴OC=OB ＝3，∴B 坐标为（3，0）．∵tan ∠CAO ＝3，即3OC OA=， ∴OA ＝1，∴点A 坐标为（-1，0），∴可设抛物线解析式为y ＝a （x +1）（x ﹣3），代入C 点坐标得：y ＝a （0+1）（0﹣3）解得：a ＝-1，∴22(1)(3)23(1)4y x x x x x =-+-=-++=--+，∴抛物线解析式为：2y x 2x 3=-++；(2)∵Q 为线段PB 中点，∴S △CPQ ＝12S △CPB ，当S △CPB 面积最大时，△CPQ 面积最大．设P 坐标（a ，223a a -++），如图，过点P 作//PH y 轴交BC 于点H ，∴H 坐标为（a ，-a +3），∴223(23)(3)PH a a a a a =-++-=-+-+ ∴22113327()(3)3()22228PB B C C PH x x a S a a =⋅-=-+⨯=--+， ∴当32a =时，即P 坐标为(32，154)时，CPB S 面积最大，最大值为278， ∴127216CPQ CPB S S ==； (3)沿CB 方向平移2个单位，向下2个单位，∴新抛物线解析式为2(3)2y x =--+，∴M （3，2），C 坐标为（0，3），设N 点坐标为（n ，0），根据平行四边形的性质，分类讨论①当22C N M D y y y y ++=时，即23022D y ++=， 解得：1=D y ．∴21(3)2x =--+解得：1242x x ==，∴xD ＝4或xD ＝2，当xD ＝4时，22C N M D x x x x ++=，即03422N x ++=， 解得：7N x =；当xD ＝2时，22C N M D x x x x ++=，即03222N x ++=， 解得：5N x =；∴N 坐标为（7，0）或（5，0）；①当 22C D M N y y y y ++=时，即32022D y ++=， 解得：1D y =-．∴21(3)2x -=--+解得：1233x x ==∴3D x =3D x =当3D x =22C D M N x x x x ++=32N x +=，解得：N x当3D x =22C D M N x x x x ++=32N x +=，解得：N x =∴N 0）或（0）；综上，可知N 点坐标为（7，0）或（5，00）或（0）； 3．解：∵抛物线223y ax ax =-++与x 轴交于,A B 两点（A 点在B 点的左侧），与y 轴交于点C ，连接AC ，BC ，A 点的坐标是（1-，0），∴令0x =，则3y =，()0,3C ∴将点()1,0A -代入得023a a =--+解得1a =则抛物线的解析式为2y x 2x 3=-++ (2)点P 是抛物线上的一个动点，其横坐标为m ，且m >0．点Q 是直线AC 上的一个动点，且位于x 轴的上方，PQ ∥y 轴Q ∴点在P 点上方，()1,0A -,()0,3C ，设直线AC 的解析式为y kx b =+30b k b =⎧⎨-+=⎩解得33k b =⎧⎨=⎩∴直线AC 的解析式为33y x =+设()2,23P m m m -++，则(),33Q m m +()223323PQ m m m m m ∴=+--++=+抛物线的解析式为2y x 2x 3=-++()214x =--+对称轴为1x =，顶点坐标为()1,4， PM PQ ⊥P M y y ∴= 根据对称性可得21P PM x =-21m =-设矩形PQNM 的周长为l ，①当1m =时，0PM =，不能构成矩形，②当01m <<时， 22PM m =-则()22222224l m m m m m =++-=-+ 当21222x -=-=⨯时，2min 1117224142222l ⎛⎫=⨯-⨯+=-+= ⎪⎝⎭ ③当1m 时，22PM m =-则()22222264l m m m m m =++-=+- 对称轴为63222x =-=-⨯ 则当1m 时，不存在最小值综上所述，矩形PQNM 的周长的最小值为72(3)当0＜0m≤1时，h=-m 2+2m+3-3=-m 2+2m ；当1＜m≤2时，h=4-3=1；当m ＞2时，h=4-（-m 2+2m+3）=m 2-2m+1；②当h=16时，m 2-2m+1=16，解得m=5或m=-3（舍），∴P （5，-12），过点P 作PQ ⊥x 轴交直线BC 与点Q ，令y=0，则-x 2+2x+3=0，解得x=-1或x=3，∴B （3，0），设直线BC 的解析式为y=k'x+b'，3,30b k b =⎧∴⎨+=''⎩' 3,1b k =⎧∴⎨=-'⎩' ∴y=-x+3，∴Q （5，-2），∴PQ=10，∴S △PCB =S △CPQ -S △BPQ =12×5×10-12×10×2=25-10=15． 4． 解：“调和三角形”某两边的长度之和等于第三边长度的两倍， ∴①当462(1)m +=-时， 解得6m =，②当1426m -+=⨯时，解得9m =，③当6124m +-=⨯时，解得3m =（不合题意舍去），综上，m 的值为6或9；(2)解：①Rt ABC 是“调和三角形”，且a b c <<， 222a b c ∴+=，①2a c b +=，②由②，得2a c b +=，代入①， 得222()2a c a c ++=， 整理得(53)()0a c a c -+=， a ，b ，c 为三角形三边，0a b c ∴<<<，530a c ∴-=，故:3:5a c =，同理可得，:3:4a b =，::3:4:5a b c ∴=；②若ABC ∆周长的数值与面积的数值相等， 即12a b c ab ++=， ::3:4:5a b c =，43b a ∴=，53c a =， 12a b c ab ∴++=， 即45143323a a a a a ++=⨯，解得6a =或0a =（舍去）， 6a ∴=，8b =，10c =；(3)解：①（Ⅰ）当P 点在AB 上时，即05t 时， 过P 作PD AC ⊥于D ，则有2AP t =，CQ t =，A A ∠=∠，90PDA BCA ∠=∠=︒，APD ABC ∴∆∆∽，::3:4:5PD AD AP ∴=，65PD t ∴=，85AD t =， 8138855DQ t t t ∴=--=-， 222PQ PD DQ =+，222261341208()(8)645555PQ t t t t ∴=+-=-+； （Ⅱ）当P 在BC 上时，即58t <时，此时，6102162PC t t =+-=-，CQ t =，222222(162)564256PQ PD DQ t t t t ∴=+=-+=-+，综上，y 关于t 的函数关系式：()22412086405{55564256(58)t t t y t t t -+=-+<；②由y 关于t 的函数关系式可知当P 在AB 上时有最小值， 224120841104230464()55541205y t t t =-+=-+， ∴当10441t =，y 有最小值为2304205．5．解：如图1，∵直线y＝kx+2经过A（﹣1，0），∴﹣k+2＝0，解得k＝2，∴直线AC的表达式为y＝2x+2；由抛物线与x轴交于A（﹣1，0），B（3，0）两点，得抛物线的对称轴为直线x＝1，当x＝1时，y＝2×1+2＝4，∴抛物线的顶点C的坐标为（1，4）；设抛物线的表达式为y＝a（x﹣1）2+4，则4a+4＝0，解得a＝﹣1，∴抛物线C1的表达式为y＝﹣（x﹣1）2+4，即y＝﹣x2+2x+3．(2)解：如图2，作DQ⊥x轴于点Q，EF⊥DQ于点F，设抛物线C2的顶点D的横坐标为t.∵抛物线C 2由抛物线C 1沿射线AC 方向平移得到，∴D （t ，2t +2），∴抛物线C 2的表达式可表示为y ＝﹣（x ﹣t ）2+2t +2，由222()22y x y x t t =+⎧⎨=--++⎩，得2x +2＝﹣（x ﹣t ）2+2t +2， 解关于x 的方程，得x 1＝t ﹣2，x 2＝t ，则点E 、F 的横坐标分别为t ﹣2、t ，∴EF ＝t ﹣（t ﹣2）＝2，∵S △MDE ＝23S △MAE ， ∴DE AE ＝23 ， ∴DE DA ＝25； ∵EF ∥AQ ，∴△DEF ∽△DAQ ， ∴25EF DE AQ DA ==， ∴2＝25AQ ， ∴AQ ＝5，∴OQ ＝5﹣1＝4；当x ＝4时，y ＝2×4+2＝10， ∴D （4，10）．(3)解：由（1）得，抛物线C 1的表达式为y ＝﹣（x ﹣1）2+4，将抛物线y ＝﹣（x ﹣1）2+4向上平移4个单位得到的抛物线为y ＝﹣（x ﹣1）2+8，即y ＝﹣x 2+2x +7，∴抛物线C 3的表达式为y ＝﹣x 2+2x +7．由题意可知，正方形GHST 与抛物线C 3有相同的对称轴直线x ＝1，如图3，设H （t ，0），则S （t ，2t ﹣2），∴﹣t 2+2t +7＝2t ﹣2，解得t 1＝3，t 2＝﹣3（不符合题意，舍去），∴H （3，0）．∴SH ＝2（t ﹣1）＝2×（3﹣1）＝4，∴正方形的边长为4；将△PSH 绕点S 顺时针90°得到△KST ，取SK 的中点R ，连结TR 、PR ，则点K 在GT 上， 设PS ＝KS ＝t （t ＞0），则TR ＝SR ＝12KS ＝12t ，由旋转得，∠PSR ＝90°，∴PR t ， ∵PR +TR ≥PT ，t +12t ≥PT ， ∴t PT ≥即PS PT ≥∴PS PT ； 如图4，当PS PT时，则点R 落在PT 上. 设PT 交SH 于点L ．∵∠PSL ＝∠TSR ＝∠PTS ，∠SPL ＝∠TPS （公共角），∴△PLS ∽△PST ， ∴SL PS TS PT =， ∴SL ＝＝2； ∵∠KTS ＝∠LST ＝90°，ST ＝TS （公共边），∠TSK ＝∠STL ，∴△KST ≌△LTS （ASA ），∴PH ＝KT ＝SL ＝2，∴OP ＝2＝，∴P （，0），∴m ＝．故答案为：4，． 6．解：把A （-4，0），C （2，0）代入y =12x 2+bx +c 得， 11640214202b c b c ⎧⨯-+=⎪⎪⎨⎪⨯++=⎪⎩，解得14b c =⎧⎨=-⎩，∴抛物线的解析式为y=12x2+x-4；(2)解：如图，过点M作MN⊥AC，垂足为N，抛物线y=12x2+x-4与y轴的交点B坐标为（0，-4），即OB=4，又∵M（m，12m2+m-4），∴ON=-m，MN=-12m2-m+4，AN=4-（-m）=4+m，∴S△ABM=S△ANM+S梯形MNOB-S△AOB=12（4+m）（-12m2-m+4）+12（-12m2-m+4+4）（-m）-12×4×4=-m2-4m=-（m+2）2+4，∴当m=-2时，S最大=4，答：S与m的函数关系式为S=-m2-4m，S的最大值为4．7．解：∵抛物线y＝ax2+bx+c的图象与轴交于A（﹣1，0），B（4，0），∴设该抛物线的函数表达式为y＝a(x+1)(x﹣4)，将C（0，﹣3）代入，得：﹣4a＝﹣3，解得：a＝34，∴y＝34(x+1)(x﹣4)＝34x2﹣94x﹣3，∴该抛物线的函数表达式为y＝34x2﹣94x﹣3；(2)（2）设直线BC 的解析式为y ＝kx +n ，∵B （4，0），C （0，﹣3），∴403k n n +=⎧⎨=-⎩， 解得：343k n ⎧=⎪⎨⎪=-⎩， ∴直线BC 的解析式为y ＝34x ﹣3， 过点E 作EM ∥y 轴，交BC 于M ，设D (t ，34t 2﹣94t ﹣3)， ∵点E 是AD 的中点，∴E (12t -，38t 2﹣98x ﹣32)， ∴M (12t -，3278t -)， ∴EM ＝38t 2﹣98x ﹣32﹣3278t -＝38t 2﹣32x +158， ∴S △BCE ＝12EM •OB ＝2(38t 2﹣32x +158)＝34 (t ﹣2)2+34， ∵34＞0， ∴当t ＝2时，S △BCE 取得最小值34；(3)解：存在，P 20116927⎛⎫- ⎪⎝⎭，，Q (0，-6427)． 如图2，在BC 上截取BE ＝BO ＝4，过点E 作EG ∥OC 交x 轴于G ，作EF ⊥BC 交y 轴于F，交抛物线于P ，∵B （4，0），C （0，﹣3），∴OB ＝4，OC ＝3，CE ＝BC ﹣BE ＝1，∵∠BOC ＝90°，∴BC5=，∵EG ∥OC ，∴△BEG ∽△BCO ， ∴EG BG BE OC OB BC ==， ∴4345EG BG ==， ∴EG ＝125，BG ＝165， ∴OG ＝OB ﹣BG ＝4﹣16455=， ∴E (45，﹣125)， ∵EF ⊥BC ，∴∠CEF ＝∠COB ＝90°，∵∠ECF ＝∠OCB ，∴△ECF ∽△OCB ， ∴CE OC CF BC =，即135CF =， ∴CF ＝53， OF ＝OC ﹣CF ＝3﹣5433=， ∴F (0，﹣43)， 设直线EF 的解析式为y ＝k 1x +n 1，∵E (45，﹣125)，F (0，﹣43)， ∴1114125543k n n ⎧+=-⎪⎪⎨⎪=-⎪⎩，解得：114343k n ⎧=-⎪⎪⎨⎪=-⎪⎩， ∴直线EF 的解析式为y ＝43-x 43-， 联立方程组，得：2443349334y x y x x ⎧=--⎪⎪⎨⎪=--⎪⎩， 解得：1110x y =-⎧⎨=⎩（舍去），2220911627x y ⎧=⎪⎪⎨⎪=-⎪⎩， ∴P 20116927⎛⎫- ⎪⎝⎭，， 在Rt △BPE 中，PE6427=， ∵∠PBQ ＝∠OBC ，∴∠PBE +∠CBQ ＝∠CBQ +∠QBO ，∴∠PBE ＝∠QBO ，在△PEB 和△QOB 中，PBE QBO BE BOPEB QOB ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△PEB ≌△QOB （ASA ），∴BP ＝BQ ，OQ ＝PE ＝6427， ∴Q (0，-6427)， ∴存在，P 20116927⎛⎫- ⎪⎝⎭，，Q (0，-6427)．8．解：将A （﹣1，0）、B （4，0）代入抛物线公式，如下：0401644a b a b =-+⎧⎨=++⎩， 求得13a b =-⎧⎨=⎩． 抛物线解析式为：y ＝﹣x 2+3x +4．(2)解：设P 到直线BC 的距离为d ，P 点坐标为（x ，﹣x 2+3x +4）（0＜x ＜4），∵y ＝﹣x 2+3x +4交y 轴于点C ，令x ＝0，∴y ＝4，∴C （0，4），由B （4，0），C （0，4）两点求得直线BC 的解析式为：y +x ﹣4＝0．做直线BC 的平行线K ：y ＝﹣x +m ，因为K 与BC 平行，我们将K 平移，根据题意，点P 是直线BC 上方抛物线上的一点，∴随着K 平行移动，以BC 为底的△PBC 的高d 在逐渐增大，当K 与抛物线y ＝﹣x 2+3x +4恰有一个交点时，此时以BC 为底的△PBC 的高d 最大，即此时△PBC 面积最大． ∵此时K ：y ＝﹣x +m 与抛物线y ＝﹣x 2+3x +4相交，且仅有一个交点，∴﹣x +m ＝﹣x 2+3x +4，m ＝8．∴直线K ：y ＝﹣x +8．此时求K 和抛物线的交点为：﹣x +8＝﹣x 2+3x +4，解得x ＝2，将x ＝2代入直线K ：y ＝﹣x +8，解得y ＝6．因此P （2，6）．现在我们来求P 到直线BC 的距离，即△PBC 的高d ：过P 作垂直于BC 的直线k ：y ＝x +m ．∵P 在直线k 上，∴6＝2+m ，∴m ＝4，直线k ＝x +4．直线K 与直线k 的交点为：44y x y x =-+⎧⎨=+⎩， 解得交点坐标（0，4），即交点为C 点．因此的△PBC 的高d 即为B 点和C 点两点之间的距离，∴d ＝|BC|=在△PBC 中，∵|BC |＝△PBC 的面积的最大值S △PBC 12=|BC |•d 12=⨯=8． (3) 解：存在．直线BC 向右平移74个单位得到直线l ， ∴l ：y ＝﹣（x 74-）+4＝﹣x 234+． 223434y x y x x ⎧=-+⎪⎨⎪=-++⎩，解得127212x x ⎧=⎪⎪⎨⎪=⎪⎩． 二次函数y ＝﹣x 2+3x +4对称轴为x 32=， ∵直线l 交对称轴右侧的抛物线于点Q ，∴x 72=，代入y ＝﹣x 23944+=． ∴Q （7924，）． 设T （a ，b ）．∵R 为直线BC 上的一动点，∴设R（x，﹣x+4）．（Ⅰ）假设T在Q点左侧：∴72a<．此时P（2，6），T（a，b）为菱形对称顶点，Q（7924，），R（x，﹣x+4）为菱形对称定点．在菱形中PTQR中，|PR|＝|QT|，=①又∵对角线互相垂直平分，且对称顶点横纵坐标的中点相等，即：72222946422xaxb⎧+⎪+=⎪⎪⎨⎪-++⎪=⎪⎩，②由①，②解得113.53871.7887ab=⎧⎨=-⎩，220.53872.2887ab=-⎧⎨=⎩，又∵a72＜，∴此时T点坐标为：T（﹣0.5387，2.2887）．（Ⅱ）假设T在Q点右侧：∴a72＞．此时P（2，6），Q（7924，）为菱形对称顶点，T（a，b），R（x，﹣x+4）为菱形对称定点．在菱形PTQR中，|PR|＝|PT|，③又∵对角线互相垂直平分，且对称顶点横纵坐标的中点相等，即：96442722b xa x⎧+⎪=-+⎪⎨⎪+=+⎪⎩，④由③，④解得a2697562=＞，符号题意．此时b27756=．此时T点坐标为：T（26956，27756）．综上所述：T存在两点，分别为：T（﹣0.5387，2.2887）和T（26956，27756）．9．（1）∵矩形ABCD的三个顶点的坐标分别为A（﹣3，4）、B（﹣3，0）、C（﹣1，0），∴D（﹣1，4），由抛物线的顶点为D（﹣1，4），设抛物线的解析式为y＝a（x+1）2+4，∵抛物线经过点B（﹣3，0），∴4a+4＝0，解得a＝﹣1，∴该抛物线的解析式为y＝﹣（x+1）2+4，即y＝﹣x2﹣2x+3；(2)如图1，设直线BD的解析式为y＝kx+d，则304k dk d-+=⎧⎨-+=⎩，解得，∴y＝2x+6，设G（x，﹣x2﹣2x+3）（﹣3＜x＜﹣1），则E（x，2x+6），∴GE＝﹣x2﹣2x+3﹣（2x+6）＝﹣x2﹣4x﹣3，∵AD＝﹣1﹣（﹣3）＝2，∴S△BGD＝12GE•AF+12GE•DF＝12GE•AD＝12×2（﹣x2﹣4x﹣3）＝﹣（x+2）2+1，∴当x＝﹣2时，S△BGD最大＝1，∴△BGD面积的最大值为1．(3)存在．理由如下：如图2，菱形BQHE 以BE 为一边.由题意，得BQ ＝PD ＝EF ＝t ，∵PQ ∥EF ，∴四边形BQFE 是平行四边形，∴当BQ ＝QF ＝t 时，四边形BQFE 是菱形，此时点H 与点F 重合．∵QF ∥BD ，∴∠AQF ＝∠QBD ，∵AD ＝2，AB ＝4，∠A ＝90°，∴BD =∴AQ AB QF BD ===，∴AQ BQ =，∴4t +=，解得20t =-如图3，菱形BQEH 以BE 为对角线，连结QH 交BE 于点R ，则QH ⊥BE ，BR ＝ER ， ∴∠BRQ ＝90°，∴BR AB BQ BD ==∴BR =， 同理，PD CD DE BD ===∴DE ==，∴2= 解得2013t =，综上所述，20t =-2013t =，故答案为：20-2013．10．解：把15,22A ⎛⎫ ⎪⎝⎭、()4,6B 代入抛物线26y ax bx =++中得：115642216466a b a b ⎧++=⎪⎨⎪++=⎩ 解得：28a b =⎧⎨=-⎩∴抛物线的解析式为：2286y x x =-+．(2)解：如图1，∵()22286222y x x x =-+=--∴顶点()2,2C -对于直线2y x =+，当2x =时，224y =+=∴()426PC =--=当0y =时，20x +=，解得2x =-∴()2,0E -∴PC BCE B E P C S S S =+△△()1122B D PC ED PC x x =⨯+⨯- ()()1122D E B D PC x x PC x x =⨯-+⨯- ()12B E PC x x =⨯- ()16422=⨯⨯+ 18=∴△BCE 的面积为18．(3)解：存在设点P 的坐标为(),2m m +，则()2,286C m m m -+∴()222286294PC m m m m =+--+=-+-∴BCE S ()12B E PC x x =⨯- ()()21294422m m =⨯-+-⨯+ 29147648m ⎛⎫=--+ ⎪⎝⎭ ∵60-<∴当94m =时，BCE S 最大，这个最大值是1478． 11．解：∵直线y ＝﹣3x ﹣3与x 轴、y 轴分别交于点A 、C ， ∴A （﹣1，0），C （0，﹣3），∵抛物线y ＝x 2+bx +c 经过点A （﹣1，0），C （0，﹣3）， ∴ 103b c c -+=⎧⎨=-⎩， 解得 23b c =-⎧⎨=-⎩ ， ∴抛物线的解析式为y ＝x 2﹣2x ﹣3．当y ＝0时，由x 2﹣2x ﹣3＝0，得x 1＝﹣1，x 2＝3， ∴B （3，0）．(2)解：如图1，设抛物线的对称轴交BC 于点F ，交x 轴于点G ．设直线BC的解析式为y＝kx﹣3，把B（3，0）代入得3k﹣3＝0，解得k＝1，∴y＝x﹣3；∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴抛物线的顶点H（1，﹣4），当x＝1时，y＝x﹣3=1﹣3＝﹣2，∴F（1，﹣2），∴FH＝﹣2﹣（﹣4）＝2，∴S△BCH＝12FH•OG+12FH•BG＝12FH•OB＝12×2×3＝3．故答案为：3．(3)解：设E（x，x2﹣2x﹣3）（0＜x＜3），则M（x，x﹣3），∴ME＝x﹣3﹣（x2﹣2x﹣3）＝﹣x2+3x＝﹣（x﹣32）2+94，∴当x＝32时，ME最大＝94，此时M（32，-32）．(4)解：存在．如图2，由（3）得，当ME 最大时，则D （32，0），M （32，-32）， ∴DO ＝DB ＝DM ＝32； ∵∠BDM ＝90°，∴DE 垂直平分OB∴OM =BM∵OM 2=BM 2= DB 2 +DM 2 =(32)2+(32)2=92∴OM ＝BM ＝ 当点P 与原点O 重合时，则PM ＝BM ， △PBM 是等腰三角形，此时点P 的坐标是（0，0）,即P 1（0，0）；当BP ＝BM P 在点B 的左侧时， △PBM 是等腰三角形，则OP ＝3∴点P 0），即P 20）； 当点P 与点D 重合时，则PM ＝PB ＝32， 此时△PBM 是等腰三角形，∴点P 的坐标为（32，0），即P 3（32，0）；当BP ＝BM P 在点B 的右侧时， △PBM 是等腰三角形，则OP ＝∴点P 0），即P 40）．综上所述，P 1（0，0），P 2，0），P 3（32，0），P 40）． 12．解：∵抛物线y ＝﹣43x 2+bx +c 经过点A （3，0），B （0，2）， 把点A （3，0），B （0，2）代入解析式得：493032b c c ⎧-⨯++=⎪⎨⎪=⎩， 解得1032b c ⎧=⎪⎨⎪=⎩， ∴二次函数的解析式为：241033y x =-+x +2； (2)解：设P （m ，﹣43m 2+103m +2）， 当∠BPQ ＝90°时，则有BP ∥x 轴，如图，∴点P 的纵坐标为2，∴﹣43x 2+103x +2＝2， 解得：x 1＝0（舍去）或x 2＝52， ∴P 1（52，2）； 当∠PBQ ＝90°时，过点P 作PM ⊥y 轴，垂足为M ，如图，则∠PBM +∠BPM ＝90°，PM ＝m ，BM ＝﹣43m 2+103m +2﹣2=﹣43m 2+103m ， ∵∠PBQ ＝90°，∴∠PBM +∠OBA ＝90°，∴∠OBA ＝∠BPM ，∴△PMB ∽△BOA ， ∴PM BO ＝MB OA ， 即2m ＝2410333m m +， 解得：m ＝0（舍）或m ＝118， ∴P 2（118，6516）， 综上所述，当以PQB 为顶点的三角形是直角三角形时，点P 的坐标为（52，2）或（1165,816）；(3)解：设PQ 的延长线交AC 与点N ，∵B （0，2），点C 与点B 关于x 轴对称，∴C （0，﹣2），设直线AC 的表达式为：y ＝k 1x +a 1，把A ，C 代入得：111302k a a +=⎧⎨=-⎩，解得11232k a ⎧=⎪⎨⎪=-⎩， ∴直线AC 的表达式为：223y x =-， 设点P （n ，241033n -+n +2），则N （n ，223n -）， ∴PN ＝241033n -+n +2﹣（223n -）＝24833n -+n +4， ∴S △APC ＝12PN ×OA ＝12（24833n -+n +4）×3＝﹣2n 2+4n +6＝﹣2（n ﹣1）2+8， ∵a ＝﹣2＜0，S △APC 有最大值，且0＜n ＜3，∴当n ＝1时，△APC 的面积最大，最大面积是8，此时，P （1，4），综上所述，△APC 面积的最大值是8，点P 的坐标是（1，4）．13．设抛物线的表达式为y ＝a （x ﹣1）2﹣4，将点C （0，﹣3）代入得：4a ﹣4＝0，解得a ＝1，∴抛物线表达式为：y ＝（x ﹣1）2﹣4；(2)连接BC ，作MN ∥y 轴交BC 于点N ，交AB 于点E ，作CF ⊥MN 于点F ，如图，由（1）知，抛物线表达式为y ＝（x ﹣1）2﹣4＝x 2﹣2x ﹣3，令y ＝0，可解得x 1＝﹣1，x 2＝3，∴点A 坐标（﹣1，0），点B 坐标（3，0），设直线BC 的表达式为y ＝kx +b ，将点B （3，0），C （0，﹣3）代入得：303k b b +=⎧⎨=-⎩， ∴13k b =⎧⎨=-⎩， ∴直线BC 表达式为y ＝x ﹣3，设M 点（m ，m 2﹣2m ﹣3），则点N （m ，m ﹣3），222393(23)3()24M N MN y y m m m m m m =-=----=-+=--+ ∴S 四边形ABMC ＝S △ABC +S △BCM＝S △ABC +S △CMN +S △BMN ＝1122AB OC MN CF ⨯⨯+⨯⨯+12MN BE ⨯⨯ ＝1143()22MN CF BE ⨯⨯+⨯⨯+ ＝6+132MN ⨯⨯ ＝23375()228m --+ 当32m =时，即点M 坐标315(,)24-时，四边形ABMC 面积的最大值758； (3) 如图，作PQ 垂直x 轴，设直线CD ：y ＝px +q ，将点C ，D 分别代入得，43p q q +=-⎧⎨=-⎩，解得13p q =-⎧⎨=-⎩， ∴直线BC ：y ＝﹣x ﹣3，当y ＝0时，解得x ＝﹣3，∴点E 坐标为（﹣3，0），∵OE ＝OC ＝OB ＝3，∴∠OEC ＝∠OBC ＝45°，在Rt △OBC 中，BC①当△BAC ∽△EPO 时，AB EPBC EO =3EP =，解得EP ＝在Rt △EPQ 中，∠OEC ＝45°，∴sin 45°＝PQ EP， 解得PQ ＝2，∴EQ ＝PQ ＝2，此时点P 坐标（﹣1，﹣2）；②当△BAC ∽△EOP 时，BA EOBC EP =3EP=，解得EP 在Rt △EPQ 中，∠OEC ＝45°，∴sin 45°＝PQ EP ， 解得94PQ = ∴94EQ PQ ==，此时点P 坐标39(,)44--； 综上所述，当点P 坐标为（﹣1，﹣2）或39(,)44--时，点P 、E 、O 为顶点的三角形与△ABC相似．14．∵直线y＝﹣x+3与y轴、x轴分别交于A、B两点、∴A（0，3），B（3，0），将A（0，3）、B（3，0）代入y＝x2+bx+c，得：3093cb c=⎧⎨=++⎩，解得：43bc=-⎧⎨=⎩，∴抛物线的函数表达式为y＝x2﹣4x+3，∵y＝x2﹣4x+3＝（x﹣2）2﹣1∴抛物线的顶点D的坐标为（2，﹣1）．(2)∵A（0，3），B（3，0），D（2，﹣1），∴AB2＝32+32＝18，AD2＝（2﹣0）2+（3+1）2＝20，BD2＝（3﹣2）2+（0+1）2＝2，∴AB2+BD2＝AD2，∴△ABD为直角三角形，且∠ABD＝90°，设点E（m，m2﹣4m+3）（m＞2）．∵EF∥x轴，∴DF＝m2﹣4m+3+1＝m2﹣4m+4，FE＝m﹣2，∠DFE＝90°，∴∠DFE＝∠ABD＝90°，∴如图1，以点D，E，F为顶点的三角形与△ABD相似，且∠FDE＝∠BAD，则DF FE AB BD=，由AB2＝32+32＝18，BD2＝（3﹣2）2+（0+1）2＝2，得AB＝，BD= 2=解得m1＝5，m2＝2（不符合题意，舍去）．∴E（5，8）；如图2，以点D，E，F为顶点的三角形与△ABD相似，且∠FDE＝∠BDA，则DF FE BD AB=，2=解得m173=，m2＝2（不符合题意，舍去），∴E（73，89-）．综上所述，点E的坐标为（5，8）或（73，89-）．(3)由（2）得，tan∠ADB==3，∵tan∠APB＝3，∴∠APB＝∠ADB，∴点P在过A、B、D三点，即以AD为直径的圆上．如图3，取AD的中点Q，以点Q为圆心，以QA为半径作圆，连接QB，∵QB12=AD＝QA，∴点B在⊙Q上；连接并延长OQ、QO分别交AB于点G、⊙Q于点H，作PR⊥AB于点R，连接PG、PQ．∵QB＝P A，OB＝OA，∴HG垂直平分AB，由PG≤QG+PQ，得PG≤GH，∵PR≤PG，∴PR≤GH；∵S △P AB 12=AB •PR ， ∴当点P 与点H 重合时，△P AB 的面积最大，此时S △P AB 12=AB •GH ．由AD 2＝（2﹣0）2+（3+1）2＝20，得AD ＝∵∠ABQ ＝90°，AQ 12=AD =AG 12=AB =，∴QG =∵HQ ＝AQ =∴GH =∴S △P AB 最大12=⨯= 过点H 作HL ⊥x 轴于点L ，∵∠OHL ＝90°﹣∠HOL ＝90°﹣∠BOG ＝∠OBA ＝45°，∴OL ＝OH •tan45°=；∵OG 12=AB =，∴OH ＝GH ﹣OG ==，∴HL ＝OL ==∴H ． ∵此时点P 与点H 重合，∴P ．综上所述，△P AB P ）． 15． 解：抛物线23y ax bx =++与x 轴交于(2,0)A -、(6,0)B 两点， ∴设抛物线的解析式为2(2)(6)412y a x x ax ax a =+-=--， ∴123a -=， 解得14a =-，∴抛物线的解析式为211(2)(6)344y x x x x =-+-=-++， ∵点D 在抛物线上，当x =4时2144334y =-⨯++=，∴点D （4，3），直线l 经过(2,0)A -、(4,3)D ，设直线l 的解析式为(0)y kx m k =+≠，代入坐标得： 2043k m k m -+=⎧⎨+=⎩， 解得，121k b ⎧=⎪⎨⎪=⎩， ∴直线l 的解析式为112y x =+； (2)解：如图1中，过点P 作//PF y 轴交AD 于点F ．设点P 的横坐标为m ， ∴21(,3)4P m m m -++，则112，F m m ⎛⎫+ ⎪⎝⎭．()132PAD D A S x x PF PF ∆=⋅-⋅=， ()2221111193121424244PF m m m m m m =-++--=-++=--+， ∴()2Δ3273144PAD S PF m ==--+， 304-<，抛物线开口向下，函数有最大值， 1m ∴=时， PAD S ∆最大=274，当m =1, 211151134444y =-⨯++=-+=， ∴15(1,)4P ． (3) （3）如图2中，将线段AD 绕点A 逆时针旋转90︒得到AT ， ∴y =4-(-2)=6，-2-x =3-0,解得x =-5 则(5,6)T -，设DT 交抛物线于点Q ，则45ADQ ∠=︒， (4,3)D ，∴直线DT 的解析式为11333y x =-+， ∴213411333y x x y x ⎧=-++⎪⎪⎨⎪=-+⎪⎩， 43359x y ⎧=⎪⎪⎨⎪=⎪⎩或43x y =⎧⎨=⎩， 4(,9)335Q ∴， 作点T 关于AD 的对称点(),T x y '，。

挑战2023年中考数学解答题压轴真题汇编专题03二次函数中面积问题压轴真题训练1．（2022•连云港）已知二次函数y＝x2+（m﹣2）x+m﹣4，其中m＞2．（1）当该函数的图象经过原点O（0，0），求此时函数图象的顶点A的坐标；（2）求证：二次函数y＝x2+（m﹣2）x+m﹣4的顶点在第三象限；（3）如图，在（1）的条件下，若平移该二次函数的图象，使其顶点在直线y ＝﹣x﹣2上运动，平移后所得函数的图象与y轴的负半轴的交点为B，求△AOB面积的最大值．【解答】（1）解：把O（0，0）代入y＝x2+（m﹣2）x+m﹣4得：m﹣4＝0，解得m＝4，∴y＝x2+2x＝（x+1）2﹣1，∴函数图像的顶点A的坐标为（﹣1，﹣1）；（2）证明：由抛物线顶点坐标公式得y＝x2+（m﹣2）x+m﹣4的顶点为（，），∵m＞2，∴2﹣m＜0，∴＜0，∵＝﹣（m﹣4）2﹣1≤﹣1＜0，∴二次函数y＝x2+（m﹣2）x+m﹣4的顶点在第三象限；（3）解：设平移后图像对应的二次函数表达式为y＝x2+bx+c，其顶点为（﹣，），当x＝0时，B（0，c），将（﹣，）代入y＝﹣x﹣2得：＝﹣2，∴c＝，∵B（0，c）在y轴的负半轴，∴c＜0，∴OB＝﹣c＝﹣，过点A作AH⊥OB于H，如图：∵A（﹣1，﹣1），∴AH＝1，在△AOB中，S△AOB＝OB•AH＝×（﹣）×1＝﹣b2﹣b+1＝﹣（b+1）2+，∵﹣＜0，取最大值，最大值为，∴当b＝﹣1时，此时c＜0，S△AOB答：△AOB面积的最大值是．2．（2022•成都）如图，在平面直角坐标系xOy中，直线y＝kx﹣3（k≠0）与抛物线y＝﹣x2相交于A，B两点（点A在点B的左侧），点B关于y轴的对称点为B'．（1）当k＝2时，求A，B两点的坐标；（2）连接OA，OB，AB'，BB'，若△B'AB的面积与△OAB的面积相等，求k 的值；（3）试探究直线AB'是否经过某一定点．若是，请求出该定点的坐标；若不是，请说明理由．【解答】解：（1）当k＝2时，直线为y＝2x﹣3，由得：或，∴A（﹣3，﹣9），B（1，﹣1）；（2）当k＞0时，如图：∵△B'AB的面积与△OAB的面积相等，∴OB'∥AB，∴∠OB'B＝∠B'BC，∵B、B'关于y轴对称，∴OB＝OB'，∠ODB＝∠ODB'＝90°，∴∠OB'B＝∠OBB'，∴∠OBB'＝∠B'BC，∵∠ODB＝90°＝∠CDB，BD＝BD，∴△BOD≌△BCD（ASA），∴OD＝CD，在y＝kx﹣3中，令x＝0得y＝﹣3，∴C（0，﹣3），OC＝3，∴OD＝OC＝，D（0，﹣），在y＝﹣x2中，令y＝﹣得﹣＝﹣x2，解得x＝或x＝﹣，∴B（，﹣），把B（，﹣）代入y＝kx﹣3得：﹣＝k﹣3，解得k＝；当k＜0时，过B'作B'F∥AB交y轴于F，如图：在y＝kx﹣3中，令x＝0得y＝﹣3，∴E（0，﹣3），OE＝3，∵△B'AB的面积与△OAB的面积相等，∴OE＝EF＝3，∵B、B'关于y轴对称，∴FB＝FB'，∠FGB＝∠FGB'＝90°，∴∠FB'B＝∠FBB'，∵B'F∥AB，∴∠EBB'＝∠FB'B，∴∠EBB'＝∠FBB'，∵∠BGE＝90°＝∠BGF，BG＝BG，∴△BGF≌△BGE（ASA），∴GE＝GF＝EF＝，∴OG＝OE+GE＝，G（0，﹣），在y＝﹣x2中，令y＝﹣得﹣＝﹣x2，解得x＝或x＝﹣，∴B（，﹣），把B（，﹣）代入y＝kx﹣3得：﹣＝k﹣3，解得k＝﹣，综上所述，k的值为或﹣；（3）直线AB'经过定点（0，3），理由如下：由得：x2+kx﹣3＝0，设x2+kx﹣3＝0二根为a，b，∴a+b＝﹣k，ab＝﹣3，A（a，﹣a2），B（b，﹣b2），∵B、B'关于y轴对称，∴B'（﹣b，﹣b2），设直线AB'解析式为y＝mx+n，将A（a，﹣a2），B'（﹣b，﹣b2）代入得：，解得：，∵a+b＝﹣k，ab＝﹣3，∴m＝﹣（a﹣b）＝b﹣a＝＝，n＝﹣ab＝﹣（﹣3）＝3，∴直线AB'解析式为y＝•x+3，令x＝0得y＝3，∴直线AB'经过定点（0，3）．3．（2022•巴中）如图1，抛物线y＝ax2+2x+c，交x轴于A、B两点，交y轴于点C，F为抛物线顶点，直线EF垂直于x轴于点E，当y≥0时，﹣1≤x≤3．（1）求抛物线的表达式；（2）点P是线段BE上的动点（除B、E外），过点P作x轴的垂线交抛物线于点D．①当点P的横坐标为2时，求四边形ACFD的面积；②如图2，直线AD，BD分别与抛物线对称轴交于M、N两点．试问，EM+EN是否为定值？如果是，请求出这个定值；如果不是，请说明理由．【解答】解：（1）∵当y≥0时，﹣1≤x≤3，∴x1＝﹣1，x2＝3是ax2+2x+c＝0的两根，A（﹣1，0），B（3，0），∴，解得：，∴抛物线的表达式为：y＝﹣x2+2x+3；（2）①把x＝2代入y＝﹣x2+2x+3得：y＝3，∴D（2，3）．又当x＝0，y＝3，∴C（0，3），∴线段CD∥x轴．∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴F（1，4），；②设D（m，﹣m2+2m+3）（1＜m＜3），直线AD：y＝k1x+b1，BD：y＝k2x+b2，因此可得：或，解得：或，∴直线AD：y＝（3﹣m）x+（3﹣m），BD：y＝﹣（m+1）x+3（m+1）．令x＝1得y M＝6﹣2m，y N＝2m+2，∴ME＝6﹣2m，NE＝2m+2，∴NE+ME＝8．4．（2022•阜新）如图，已知二次函数y＝﹣x2+bx+c的图象交x轴于点A（﹣1，0），B（5，0），交y轴于点C．（1）求这个二次函数的表达式；（2）如图1，点M从点B出发，以每秒个单位长度的速度沿线段BC向点C运动，点N从点O出发，以每秒1个单位长度的速度沿线段OB向点B运动，点M，N同时出发．设运动时间为t秒（0＜t＜5）．当t为何值时，△BMN 的面积最大？最大面积是多少？（3）已知P是抛物线上一点，在直线BC上是否存在点Q，使以A，C，P，Q为顶点的四边形是平行四边形？若存在，直接写出点Q坐标；若不存在，请说明理由．【解答】解：（1）将点A（﹣1，0），B（5，0）代入y＝﹣x2+bx+c中，得，解这个方程组得，∴二次函数的表达式为y＝﹣x2+4x+5；（2）过点M作ME⊥x轴于点E，如图：设△BMN面积为S，根据题意得：ON＝t，BM＝．∵B（5，0），∴BN＝5﹣t，在y＝﹣x2+4x+5中，令x＝0得y＝5，∴C（0，5），∴OC＝OB＝5，∴∠OBC＝45°．∴ME＝BM sin45°＝，∴S＝BN•ME＝（5﹣t）•t＝﹣t2+t＝﹣（t﹣）2+，∵0＜t＜5，∴当时，△BMN的面积最大，最大面积是；（3）存在点Q，使以A，C，P，Q为顶点的四边形是平行四边形，理由如下：由B（5，0），C（0，5）得直线BC解析式为y＝﹣x+5，设Q（m，﹣m+5），P（n，﹣n2+4n+5），又A（﹣1，0），C（0，5），①当PQ，AC是对角线，则PQ，AC的中点重合，∴，解得m＝0（与C重合，舍去）或m＝﹣7，∴Q（﹣7，12）；②当QA，PC为对角线，则QA，PC的中点重合，∴，解得m＝0（舍去）或m＝7，∴Q（7，﹣2）；③当QC，PA为对角线，则QC，PA的中点重合，∴，解得m＝1或m＝2，∴Q（1，4）或（2，3），综上所述，Q的坐标为（﹣7，12）或（7，﹣2）或（1，4）或（2，3）．5．（2022•鞍山）如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B两点，与y轴交于点C（0，2），连接BC．（1）求抛物线的解析式．（2）点P是第三象限抛物线上一点，直线PB与y轴交于点D，△BCD的面积为12，求点P的坐标．（3）在（2）的条件下，若点E是线段BC上点，连接OE，将△OEB沿直线OE翻折得到△OEB'，当直线EB'与直线BP相交所成锐角为45°，时，求点B'的坐标．【解答】解：（1）将A（﹣1，0），C（0，2）代入y＝﹣x2+bx+c，∴，解得，∴y＝﹣x2+x+2；（2）令y＝0，则﹣x2+x+2＝0，解得x＝﹣1或x＝4，∴B（4，0），∴OB＝4，＝×4×（2+OD）＝12，∴S△BCD∴OD＝4，∴D（0，﹣4），设直线BD的解析式为y＝kx+b，∴，解得，∴y＝x﹣4，联立方程组，解得或，∴P（﹣3，﹣7）；（3）如图1，当B'在第一象限时，设直线BC的解析式为y＝k'x+b'，∴，解得，∴y＝﹣x+2，设E（t，﹣t+2），∴OH＝t，EH＝﹣t+2，∵D（0，﹣4），B（4，0），∴OB＝OD，∴∠ODB＝45°，∵直线EB'与直线BP相交所成锐角为45°，∴EB'∥CD，由折叠可知，OB'＝BO＝4，BE＝B'E，在Rt△OHB'中，B'H＝，∴B'E＝﹣（﹣t+2）＝+t﹣2，∴BE＝+t﹣2，在Rt△BHE中，（+t﹣2）2＝（4﹣t）2+（﹣t+2）2，解得t＝，∵0≤t≤4，∴t＝，∴B'（，）；如图2，当B'在第二象限，∠BGB'＝45°时，∵∠ABP＝45°，∴B'G∥x轴，∵将△OEB沿直线OE翻折得到△OEB'，∴BE＝B'E，OB＝OB'，∠BOE＝∠B'OE，∴∠BOE＝∠B'EO，∴B'E∥B'O，∵B'E＝BO，∴四边形B'OBE是平行四边形，∴B'E＝4，∴B'（t﹣4，﹣t+2），由折叠可知OB＝OB'＝4，∴平行四边形OBEB'是菱形，∴BE＝OB，∴＝4，解得t＝4+或t＝4﹣，∵0≤t≤4，∴t＝4﹣，∴B'（﹣，）；综上所述：B'的坐标为（，）或（﹣，）．方法2：在Rt△BCO中，BC＝2，CO：OB：BC＝1：2：，∵BP与x轴和y轴的夹角都是45°，BP与B'E的夹角为45°，∴B'E∥x轴或B'E∥y轴，当B'E∥y轴时，延长B'E交x轴于F，∴B'F⊥OB，∵∠CBA＝∠OB'E，∴△OB'F∽△CBO，∴OF：FB'：B'O＝1：2：，∵OB＝OB'＝4，∴FO＝，B'F＝，∴B'（，）；当B'E∥x轴时，过B'作B'F⊥x中交于F，∴B'F⊥OF，B'E∥OB，∵B'E和BE关于OE对称，OB和OB'关于OE对称，∴BE∥OB'，∵∠FOB'＝∠OBC，∴△OB'F∽△BCO，∴B'F：FO：OB'＝1：2：，∵OB＝OB'＝4，∴B'F＝，OF＝，∴B'（﹣，）；综上所述：B'坐标为（，）或（﹣，）．6．（2022•菏泽）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于A（﹣2，0）、B（8，0）两点，与y轴交于点C（0，4），连接AC、BC．（1）求抛物线的表达式；（2）将△ABC沿AC所在直线折叠，得到△ADC，点B的对应点为D，直接写出点D的坐标，并求出四边形OADC的面积；（3）点P是抛物线上的一动点，当∠PCB＝∠ABC时，求点P的坐标．【解答】解：（1）∵抛物线y＝ax2+bx+c（a≠0）与x轴交于A（﹣2，0）、B（8，0）两点，与y轴交于点C（0，4），∴，解得：．∴抛物线的表达式为y＝﹣+x+4；（2）点D的坐标为（﹣8，8），理由：将△ABC沿AC所在直线折叠，得到△ADC，点B的对应点为D，如图，过点D作DE⊥x轴于点E，∵A（﹣2，0）、B（8，0），C（0，4），∴OA＝2，OB＝8，OC＝4．∵，，∴．∵∠AOC＝∠COB＝90°，∴△AOC∽△COB，∴∠ACO＝∠CBO．∵∠CBO+∠OCB＝90°，∴∠ACO+∠OCB＝90°，∴∠ACB＝90°，∵将△ABC沿AC所在直线折叠，得到△ADC，点B的对应点为D，∴点D，C，B三点在一条直线上．由轴对称的性质得：BC＝CD，AB＝AD．∵OC⊥AB，DE⊥AB，∴DE∥OC，∴OC为△BDE的中位线，∴OE＝OB＝8，DE＝2OC＝8，∴D（﹣8，8）；＝S△ABC，由题意得：S△ACD+S△ADC ∴四边形OADC的面积＝S△OAC+S△ABC＝S△OAC＝OC•OA+AB•OC＝4×2+10×4＝4+20＝24；（3）①当点P在BC上方时，如图，∵∠PCB＝∠ABC，∴PC∥AB，∴点C，P的纵坐标相等，∴点P的纵坐标为4，令y＝4，则﹣+x+4＝4，解得：x＝0或x＝6，∴P（6，4）；②当点P在BC下方时，如图，设PC交x轴于点H，∵∠PCB＝∠ABC，∴HC＝HB．设HB＝HC＝m，∴OH＝OB﹣HB＝8﹣m，在Rt△COH中，∵OC2+OH2＝CH2，∴42+（8﹣m）2＝m2，解得：m＝5，∴OH＝3，∴H（3，0）．设直线PC的解析式为y＝kx+n，∴，解得：．∴y＝﹣x+4．∴，解得：，．∴P（，﹣）．综上，点P的坐标为（6，4）或（，﹣）．7．（2022•沈阳）如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣3经过点B （6，0）和点D（4，﹣3），与x轴的另一个交点为A，与y轴交于点C，作直线AD．（1）①求抛物线的函数表达式；②直接写出直线AD的函数表达式；（2）点E是直线AD下方的抛物线上一点，连接BE交AD于点F，连接BD，DE，△BDF的面积记为S1，△DEF的面积记为S2，当S1＝2S2时，求点E的坐标；（3）点G为抛物线的顶点，将抛物线图象中x轴下方的部分沿x轴向上翻折，与抛物线剩下的部分组成新的曲线记为C1，点C的对应点为C′，点G的对应点为G′，将曲线C1沿y轴向下平移n个单位长度（0＜n＜6）．曲线C1与直线BC的公共点中，选两个公共点记作点P和点Q，若四边形C′G′QP 是平行四边形，直接写出点P的坐标．【解答】解：（1）①∵抛物线y＝ax2+bx﹣3经过点B（6，0）和点D（4，﹣3），∴，解得：，∴抛物线的函数表达式为y＝x2﹣x﹣3；②由①得y＝x2﹣x﹣3，当y＝0时，x2﹣x﹣3＝0，解得：x1＝6，x2＝﹣2，∴A（﹣2，0），设直线AD的函数表达式为y＝kx+d，则，解得：，∴直线AD的函数表达式为y＝x﹣1；（2）如图1，过点B作BG∥y轴交直线AD于G，过点E作EH∥y轴交直线AD于H，∵S1＝2S2，即＝2，∴＝2，∵BG∥y轴，EH∥y轴，∴BG∥EH，∴△BFG∽△EFH，∴＝＝2，即BG＝2EH，∵点G在直线y＝x﹣1上，BG∥y轴，∴G（6，﹣4），∴BG＝4，∴EH＝2，设E（x，x2﹣x﹣3），则H（x，x﹣1），∴EH＝x﹣1﹣（x2﹣x﹣3）＝﹣x2+x+2，∴﹣x2+x+2＝2，解得：x1＝0，x2＝2，∴E（0，﹣3）或（2，﹣4）；（3）∵y＝x2﹣x﹣3＝（x﹣2）2﹣4，∴顶点坐标为G（2，﹣4），当x＝0时，y＝3，即点C（0，﹣3），∴点C′（0，3），G′（2，4），∴向上翻折部分的图象解析式为y＝﹣（x﹣2）2+4，∴向上翻折部分平移后的函数解析式为y＝﹣（x﹣2）2+4﹣n，平移后抛物线剩下部分的解析式为y＝（x﹣2）2﹣4﹣n，设直线BC的解析式为y＝k′x+d′（k′≠0），把点B（6，0），C（0，﹣3）代入得：，解得：，∴直线BC的解析式为y＝x﹣3，同理直线C′G′的解析式为y＝x+3，∴BC∥C′G′，设点P的坐标为（s，s﹣3），∵点C′（0，3），G′（2，4），∴点C′向右平移2个单位，再向上平移1个单位得到点G′，∵四边形C′G′QP是平行四边形，∴点Q（s+2，s﹣2），当点P，Q均在向上翻折部分平移后的图象上时，则，解得：，∵0＜n＜6，∴s＝0，n＝6不符合题意，舍去；当点P在向上翻折部分平移后的图象上，点Q在平移后抛物线剩下部分的图象上时，则，解得：或（不合题意，舍去），当点P在平移后抛物线剩下部分的图象上，点Q在向上翻折部分平移后的图象上时，则，解得：或（不合题意，舍去），综上所述，点P的坐标为（1+，）或（1﹣，）．8．（2022•西藏）在平面直角坐标系中，抛物线y＝﹣x2+（m﹣1）x+2m与x 轴交于A，B（4，0）两点，与y轴交于点C，点P是抛物线在第一象限内的一个动点．（1）求抛物线的解析式，并直接写出点A，C的坐标；（2）如图甲，点M是直线BC上的一个动点，连接AM，OM，是否存在点M 使AM+OM最小，若存在，请求出点M的坐标，若不存在，请说明理由；（3）如图乙，过点P作PF⊥BC，垂足为F，过点C作CD⊥BC，交x轴于点D，连接DP交BC于点E，连接CP．设△PEF的面积为S1，△PEC的面积为S2，是否存在点P，使得最大，若存在，请求出点P的坐标，若不存在，请说明理由．【解答】解：（1）将B（4，0）代入y＝﹣x2+（m﹣1）x+2m，∴﹣8+4（m﹣1）+2m＝0，解得m＝2，∴y＝﹣x2+x+4，令x＝0，则y＝4，∴C（0，4），令y＝0，则﹣x2+x+4＝0，解得x＝4或x＝﹣2，∴A（﹣2，0）；（2）存在点M使AM+OM最小，理由如下：作O点关于BC的对称点O'，连接AO'交BC于点M，连接BO'，由对称性可知，OM＝O'M，∴AM+OM＝AM+O'M≥AO'，当A、M、O'三点共线时，AM+OM有最小值，∵B（4，0），C（0，4），∴OB＝OC，∴∠CBO＝45°，由对称性可知∠O'BM＝45°，∴BO'⊥BO，∴O'（4，4），设直线AO'的解析式为y＝kx+b，∴，解得，∴y＝x+，设直线BC的解析式为y＝k'x+4，∴4k'+4＝0，∴k'＝﹣1，∴y＝﹣x+4，联立方程组，解得，∴M（，）；（3）存在点P，使得最大，理由如下：连接PB，过P点作PG∥y轴交CB于点G，设P（t，﹣t2+t+4），则G（t，﹣t+4），∴PG＝﹣t2+2t，∵OB＝OC＝4，∴BC＝4，＝×4×（﹣t2+2t）＝﹣t2+4t＝×4×PF，∴S△BCP∴PF＝﹣t2+t，∵CD⊥BC，PF⊥BC，∴PF∥CD，∴＝，∵＝，∴＝，∵B、D两点关于y轴对称，∴CD＝4，∴＝﹣（t2﹣4t）＝﹣（t﹣2）2+，∵P点在第一象限内，∴0＜t＜4，∴当t＝2时，有最大值，此时P（2，4）．9．（2022•青海）如图1，抛物线y＝x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）求该抛物线的解析式；（2）若点E是抛物线的对称轴与直线BC的交点，点F是抛物线的顶点，求EF的长；＝6的点P？（3）设点P是（1）中抛物线上的一个动点，是否存在满足S△P AB 如果存在，请求出点P的坐标；若不存在，请说明理由．（请在图2中探讨）【解答】解：（1）将A（﹣1，0），B（3，0）代入y＝x2+bx+c，得：，解得：，∴该抛物线的解析式为y＝x2﹣2x﹣3．（2）∵抛物线的解析式为y＝x2﹣2x﹣3，∴抛物线的顶点F的坐标为（1，﹣4），抛物线的对称轴为直线x＝1．当x＝0时，y＝02﹣2×0﹣3＝﹣3，∴点C的坐标为（0，﹣3）．设直线BC的解析式为y＝mx+n（m≠0），将B（3，0），C（0，﹣3）代入y＝mx+n，得：，解得：，∴直线BC的解析式为y＝x﹣3．当x＝1时，y＝1﹣3＝﹣2，∴点E的坐标为（1，﹣2），∴EF＝|﹣2﹣（﹣4）|＝2．（3）∵点A的坐标为（﹣1，0），点B的坐标为（3，0），∴AB＝|3﹣（﹣1）|＝4．设点P的坐标为（t，t2﹣2t﹣3）．＝6，∵S△P AB∴×4×|t2﹣2t﹣3|＝6，即t2﹣2t﹣3＝3或t2﹣2t﹣3＝﹣3，解得：t1＝1﹣，t2＝1+，t3＝0，t4＝2，＝6的点P，点P的坐标为（1﹣，3）或（1+，3）或∴存在满足S△P AB（0，﹣3）或（2，﹣3）．10．（2022•上海）在平面直角坐标系xOy中，抛物线y＝x2+bx+c过点A（﹣2，﹣1），B（0，﹣3）．（1）求抛物线的解析式；（2）平移抛物线，平移后的顶点为P（m，n）（m＞0）．＝3，设直线x＝k，在这条直线的右侧原抛物线和新抛物线均ⅰ．如果S△OBP呈上升趋势，求k的取值范围；ⅱ．点P在原抛物线上，新抛物线交y轴于点Q，且∠BPQ＝120°，求点P 的坐标．【解答】解：（1）将A（﹣2，﹣1），B（0，﹣3）代入y＝x2+bx+c，得：，解得：，∴抛物线的解析式为y＝x2﹣3．（2）i．∵y＝x2﹣3，∴抛物线的顶点坐标为（0，﹣3），即点B是原抛物线的顶点，∵平移后的抛物线顶点为P（m，n），∴抛物线平移了|m|个单位，＝×3|m|＝3，∴S△OPB∵m＞0，∴m＝2，即平移后的抛物线的对称轴为直线x＝2，∵在x＝k的右侧，两抛物线都上升，原抛物线的对称轴为y轴，开口向上，∴k≥2；ii．把P（m，n）代入y＝x2﹣3，∴n＝﹣3，∴P（m，﹣3），由题意得，新抛物线的解析式为y＝+n＝﹣3，∴Q（0，m2﹣3），∵B（0，﹣3），∴BQ＝m2，+，PQ2＝，∴BP＝PQ，如图，过点P作PC⊥y轴于C，则PC＝|m|，∵PB＝PQ，PC⊥BQ，∴BC＝BQ＝m2，∠BPC＝∠BPQ＝×120°＝60°，∴tan∠BPC＝tan60°＝＝，∴m＝2或m＝﹣2（舍），∴n＝﹣3＝3，∴P点的坐标为（2，3）．轴交于A，B两点，A（1，0），AB＝4，点P为线段AB上的动点，过P作PQ∥BC交AC于点Q．（1）求该抛物线的解析式；（2）求△CPQ面积的最大值，并求此时P点坐标．【解答】（1）∵抛物线y＝x2+bx+c（b，c是常数）的顶点为C，与x轴交于A，B两点，A（1，0），AB＝4，∴B（﹣3，0），∴，解得，∴抛物线的解析式为y＝x2+2x﹣3；（2）过Q作QE⊥x轴于E，过C作CF⊥x轴于F，设P（m，0），则P A＝1﹣m，∵y＝x2+2x﹣3＝（x+1）2﹣4，∴C（﹣1，﹣4），∴CF＝4，∵PQ∥BC，∴△PQA∽△BCA，∴，即，∴QE＝1﹣m，＝S△PCA﹣S△PQA∴S△CPQ＝PA•CF﹣PA•QE＝（1﹣m）×4﹣（1﹣m）（1﹣m）＝﹣（m+1）2+2，∵﹣3≤m≤1，有最大值2，∴当m＝﹣1时S△CPQ∴△CPQ面积的最大值为2，此时P点坐标为（﹣1，0）．11．（2022•福建）在平面直角坐标系xOy中，已知抛物线y＝ax2+bx经过A（4，0），B（1，4）两点．P是抛物线上一点，且在直线AB的上方．（1）求抛物线的解析式；（2）若△OAB面积是△PAB面积的2倍，求点P的坐标；（3）如图，OP交AB于点C，PD∥BO交AB于点D．记△CDP，△CPB，△CBO的面积分别为S1，S2，S3．判断+是否存在最大值．若存在，求出最大值；若不存在，请说明理由．【解答】解：（1）将A（4，0），B（1，4）代入y＝ax2+bx，∴，解得．∴抛物线的解析式为：y＝﹣x2+x．（2）设直线AB的解析式为：y＝kx+t，将A（4，0），B（1，4）代入y＝kx+t，∴，解得．∵A（4，0），B（1，4），＝×4×4＝8，∴S△OAB＝2S△P AB＝8，即S△P AB＝4，∴S△OAB过点P作PM⊥x轴于点M，PM与AB交于点N，过点B作BE⊥PM于点E，如图，＝S△PNB+S△PNA＝PN×BE+PN×AM＝PN＝4，∴S△P AB∴PN＝．设点P的横坐标为m，∴P（m，﹣m2+m）（1＜m＜4），N（m，﹣m+），∴PN＝﹣m2+m﹣（﹣m+）＝．解得m＝2或m＝3；∴P（2，）或（3，4）．（3）∵PD∥OB，∴∠DPC＝∠BOC，∠PDC＝∠OBC，∴△DPC∽△BOC，∴CP：CO＝CD：CB＝PD：OB，∵＝＝，＝＝，∴+＝．设直线AB交y轴于点F．则F（0，），过点P作PH⊥x轴，垂足为H，PH交AB于点G，如图，∵∠PDC＝∠OBC，∴∠PDG＝∠OBF，∵PG∥OF，∴∠PGD＝∠OFB，∴△PDG∽△OBF，∴PD：OB＝PG：OF，设P（n，﹣n2+n）（1＜n＜4），由（2）可知，PG＝﹣n2+n﹣，∴+＝＝＝PG＝﹣（n﹣）2+．∵1＜n＜4，∴当n＝时，+的最大值为．12．（2022•岳阳）如图1，在平面直角坐标系xOy中，抛物线F1：y＝x2+bx+c 经过点A（﹣3，0）和点B（1，0）．（1）求抛物线F1的解析式；（2）如图2，作抛物线F2，使它与抛物线F1关于原点O成中心对称，请直接写出抛物线F2的解析式；（3）如图3，将（2）中抛物线F2向上平移2个单位，得到抛物线F3，抛物线F1与抛物线F3相交于C，D两点（点C在点D的左侧）．①求点C和点D的坐标；②若点M，N分别为抛物线F1和抛物线F3上C，D之间的动点（点M，N与点C，D不重合），试求四边形CMDN面积的最大值．【解答】解：（1）将点A（﹣3，0）和点B（1，0）代入y＝x2+bx+c，∴，解得，∴y＝x2+2x﹣3；（2）∵y＝x2+2x﹣3＝（x+1）2﹣4，∴抛物线的顶点（﹣1，﹣4），∵顶点（﹣1，﹣4）关于原点的对称点为（1，4），∴抛物线F2的解析式为y＝﹣（x﹣1）2+4，∴y＝﹣x2+2x+3；（3）由题意可得，抛物线F3的解析式为y＝﹣（x﹣1）2+6＝﹣x2+2x+5，①联立方程组，解得x＝2或x＝﹣2，∴C（﹣2，﹣3）或D（2，5）；②设直线CD的解析式为y＝kx+b，∴，解得，∴y＝2x+1，过点M作MF∥y轴交CD于点F，过点N作NE∥y轴交CD于点E，设M（m，m2+2m﹣3），N（n，﹣n2+2n+5），则F（m，2m+1），E（n，2n+1），∴MF＝2m+1﹣（m2+2m﹣3）＝﹣m2+4，NE＝﹣n2+2n+5﹣2n﹣1＝﹣n2+4，∵﹣2＜m＜2，﹣2＜n＜2，∴当m＝0时，MF有最大值4，当n＝0时，NE有最大值4，＝S△CDN+S△CDM＝×4×（MF+NE）＝2（MF+NE），∵S四边形CMDN∴当MF+NE最大时，四边形CMDN面积的最大值为16．13．（2023•沛县模拟）如图，已知抛物线y＝﹣x2+ax经过点A（4，0）和B（1，m）点，其对称轴交x轴于点H，点C是抛物线在直线AB上方的一个动点（不含A，B两点）．（1）求a、m的值．（2）连接AB、OB，若△AOB的面积是△ABC的面积的2倍，求点C的坐标．（3）若直线AC、OC分别交该抛物线的对称轴于点E、F，试问EH+FH是否为定值，若是，请求出该定值；若不是，请说明理由．【解答】解：（1）将点A的坐标代入抛物线表达式得：0＝﹣16+4a，解得：a＝4，即抛物线的表达式为：y＝﹣x2+4x，当x＝1时，y＝﹣x2+4x＝3，即点B（1，3），即m＝3，故a＝4，m＝3；（2）延长AB交y轴于点N，过点C作CM∥AB交y轴于点M，设直线AB的表达式为：y＝kx+b，则，解得：，即点N（0，4），即ON＝4，∵△AOB的面积是△ABC的面积的2倍，∴MN＝ON＝2，即点M（0，6），∵CM∥AB，故直线CM的表达式为：y＝﹣x+6，联立上式和抛物线的表达式得：﹣x2+4x＝﹣x+6，解得：x＝2或3，即点C（2，4）或（3，3）；（3）是定值，理由：设点C（t，﹣t2+4t），由点A、C的坐标得：直线AC的表达式为：y＝﹣t（x﹣4），当x＝2时，y＝2t，即点E（2，2t），则EH＝2t，由点C的坐标得，直线CO的表达式为：y＝（﹣t+4）x，当x＝2时，y＝（﹣t+4）x＝﹣2t+8，即点F（2，﹣2t+8），则FH＝﹣2t+8，则EH+FH＝2t﹣2t+8＝8，为定值．14．（2023•柳南区一模）如图，已知抛物线的图象经过点C（0，3），与x轴交于A，B两点，顶点坐标D（1，4），连接BC交对称轴于点E．（1）求抛物线的解析式；（2）若点P是抛物线上的一个动点，位于直线BC的上方（点P与B，C不重合），过P作y轴的平行线交BC于F点；①设点P的横坐标为m，当四边形DEFP是平行四边形时，求m的值；②在①的条件下，抛物线上是否存在点Q，使得△QBC的面积与△PBC的面积相等，若存在，请求出点Q坐标；若不存在，请说明理由．【解答】解：（1）∵顶点坐标D（1，4），∴设二次函数解析式y＝a（x﹣1）2+4，把C（3，0）代入y＝a（x﹣1）2+4，解得a＝﹣1，∴抛物线解析式为y＝﹣x2+2x+3；（2）①当y＝0时，则﹣x2+2x+3＝0，∴x1＝1，x2＝3，∴点B（3，0），∵点C（0，3），设直线BC的解析式为y＝kx+b（k≠0），把B（3，0），C（0，3）代入直线y＝kx+b（k≠0）得，解得，∴BC解析式为y＝﹣x+3，∵点D（1，4），∴点E（1，2），∴DE＝2，设点P（m，﹣m2+2m+3），则点F（m，﹣m+3），∴PF＝（﹣m2+2m+3）﹣（m+3）＝﹣m2+3m，∵四边形DEFP是平行四边形，∴PF＝DE，∴﹣2+4＝﹣m2+3m，解得m1＝1（不合题意舍去），m2＝2，∴m＝2；②当点Q、点P在直线BC的同侧时，如图所示：∵四边形DEFP是平行四边形，∴PD∥BC，＝S△DBC，∴S△BPC＝S△QBC，∴当点Q与点D重合时，S△BPC∴点Q（1，4）；当点P与点Q在直线BC的异侧时，延长PD交y轴于H，在OC上截取CN ＝CH＝2，则N（0，1），过点N作BC的平行线交抛物线于点Q，如图所示：∵DP∥BC，∴设直线DP的解析式为y＝﹣x+d，将D（1，4）代入y＝﹣x+d得到4＝﹣1+d，解得d＝5，∴直线DP的解析式为y＝﹣x+5，∴点H（0，5），∵C（0，3），∴CH＝2，∵BC∥QN，NC＝CH，∴QN与BC的距离与DP与BC的距离相等，＝S△BCP，∴S△BCQ∵QN∥BC，点N（0，1），∴直线QN的解析式为y＝﹣x+1，联立方程组得，解得或，综上所述，满足题意的点，点，点Q3（1，4）．15．（2022•淄博）如图，抛物线y＝﹣x2+bx+c与x轴相交于A，B两点（点A 在点B的左侧），顶点D（1，4）在直线l：y＝x+t上，动点P（m，n）在x轴上方的抛物线上．（1）求这条抛物线对应的函数表达式；（2）过点P作PM⊥x轴于点M，PN⊥l于点N，当1＜m＜3时，求PM+PN 的最大值；（3）设直线AP，BP与抛物线的对称轴分别相交于点E，F，请探索以A，F，B，G（G是点E关于x轴的对称点）为顶点的四边形面积是否随着P点的运动而发生变化，若不变，求出这个四边形的面积；若变化，说明理由．【解答】解：（1）∵抛物线的顶点D（1，4），∴可以假设抛物线的解析式为y＝﹣（x﹣1）2+4＝﹣x2+2x+3；（2）如图，设直线l交x轴于点T，连接PT，BD，BD交PM于点J．设P （m，﹣m2+2m+3）．点D（1，4）在直线l：y＝x+t上，∴4＝+t，∴t＝，∴直线DT的解析式为y＝x+，令y＝0，得到x＝﹣2，∴T（﹣2，0），∴OT＝2，∵B（3，0），∴OB＝3，∴BT＝5，∵DT＝＝5，∴TD＝TB，∵PM⊥BT，PN⊥DT，∴四边形DTBP的面积＝△PDT的面积+△PBT的面积＝×DT×PN+×TB×PM＝（PM+PN），∴四边形DTBP的面积最大时，PM+PN的值最大，∵D（1，4），B（3，0），∴直线BD的解析式为y＝﹣2x+6，∴J（m，﹣2m+6），∴PJ＝﹣m2+4m﹣3，∵四边形DTBP的面积＝△DTB的面积+△BDP的面积＝×5×4+×（﹣m2+4m﹣3）×2＝﹣m2+4m+7＝﹣（m﹣2）2+11∵﹣1＜0，∴m＝2时，四边形DTBP的面积最大，最大值为11，∴PM+PN的最大值＝×11＝；解法二：延长MP交直线l与点H，易得直线l：y＝x+，∴H（m，m+）设直线l交x轴于点C，交y轴于点L，∴C（﹣2，0），L（0，），∴CL＝，∴sin∠CLO＝，由LO∥HM，∴∠NHM＝∠CLO，∴sin∠NHM＝，∴PH＝m++m2﹣2m﹣3＝m2﹣m﹣，∴PN＝PH，∴PM+PN＝﹣m2+2m+3+（m2﹣m﹣）＝﹣（m﹣2）2+，∵﹣＜0，∴m＝2时，PM+PN的值最小，最小值为；（3）四边形AFBG的面积不变．理由：如图，设P（m，﹣m2+2m+3），∵A（﹣1，0），B（3，0），∴直线AP的解析式为y＝﹣（m﹣3）x﹣m+3，∴E（1，﹣2m+6），∵E，G关于x轴对称，∴G（1，2m﹣6），∴直线PB的解析式y＝﹣（m+1）x+3（m+1），∴F（1，2m+2），∴GF＝2m+2﹣（2m﹣6）＝8，∴四边形AFBG的面积＝×AB×FG＝×4×8＝16．∴四边形AFBG的面积是定值．16．（2022•烟台）如图，已知直线y＝x+4与x轴交于点A，与y轴交于点C，抛物线y＝ax2+bx+c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x＝﹣1．（1）求抛物线的表达式；（2）D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD 面积S的最大值及此时D点的坐标；（3）若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．【解答】解：（1）当x＝0时，y＝4，∴C（0，4），当y＝0时，x+4＝0，∴x＝﹣3，∴A（﹣3，0），∵对称轴为直线x＝﹣1，∴B（1，0），∴设抛物线的表达式：y＝a（x﹣1）•（x+3），∴4＝﹣3a，∴a＝﹣，∴抛物线的表达式为：y＝﹣（x﹣1）•（x+3）＝﹣x2﹣x+4；（2）如图1，作DF⊥AB于F，交AC于E，∴D（m，﹣﹣m+4），E（m，m+4），∴DE＝﹣﹣m+4﹣（m+4）＝﹣m2﹣4m，＝OA＝•（﹣m2﹣4m）＝﹣2m2﹣6m，∴S△ADC＝＝＝8，∵S△ABC∴S＝﹣2m2﹣6m+8＝﹣2（m+）2+，∴当m＝﹣时，S＝，最大当m＝﹣时，y＝﹣＝5，∴D（﹣，5）；（3）存在点P和点Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形，理由如下：设P（﹣1，n），∵以A，C，P，Q为顶点的四边形是以AC为对角线的菱形，∴P A＝PC，即：P A2＝PC2，∴（﹣1+3）2+n2＝1+（n﹣4）2，∴n＝，∴P（﹣1，），∵x P+x Q＝x A+x C，y P+y Q＝y A+y C∴x Q＝﹣3﹣（﹣1）＝﹣2，y Q＝4﹣＝，∴Q（﹣2，）．17．（2022•内江）如图，抛物线y＝ax2+bx+c与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．（1）求这条抛物线所对应的函数的表达式；（2）若点D为该抛物线上的一个动点，且在直线AC上方，求点D到直线AC的距离的最大值及此时点D的坐标；（3）点P为抛物线上一点，连接CP，直线CP把四边形CBP A的面积分为1：5两部分，求点P的坐标．【解答】解：（1）∵抛物线y＝ax2+bx+c与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．∴，解得：，∴抛物线的解析式为y＝﹣x2﹣x+2；（2）过点D作DH⊥AB于H，交直线AC于点G，过点D作DE⊥AC于E，如图．设直线AC的解析式为y＝kx+t，则，解得：，∴直线AC的解析式为y＝x+2．设点D的横坐标为m，则点G的横坐标也为m，∴DH＝﹣m2﹣m+2，GH＝m+2∴DG＝﹣m2﹣m+2﹣m﹣2＝﹣m2﹣m，∵DE⊥AC，DH⊥AB，∴∠EDG+∠DGE＝∠AGH+∠CAO＝90°，∵∠DGE＝∠AGH，∴∠EDG＝∠CAO，∴cos∠EDG＝cos∠CAO＝＝，∴，∴DE＝DG＝（﹣m2﹣m）＝﹣（m2+4m）＝﹣（m+2）2+，∴当m＝﹣2时，点D到直线AC的距离取得最大值．此时y D＝﹣×（﹣2）2﹣×（﹣2）+2＝2，即点D的坐标为（﹣2，2）；（3）如图，设直线CP交x轴于点E，直线CP把四边形CBP A的面积分为1：5两部分，：S△PCA＝EB×（y C﹣y P）：AE×（y C﹣y P）＝BE：AE，又∵S△PCB则BE：AE＝1：5或5：1则AE＝5或1，即点E的坐标为（1，0）或（﹣3，0），将点E的坐标代入直线CP的表达式：y＝nx+2，解得：n＝﹣2或，故直线CP的表达式为：y＝﹣2x+2或y＝x+2，联立方程组或，解得：x＝6或﹣，故点P的坐标为（6，﹣10）或（﹣，﹣）．18．（2021•西宁）如图，在平面直角坐标系xOy中，一次函数y＝﹣x+3的图象与x轴交于点A，与y轴交于点B，点C的坐标为（﹣2，0），抛物线经过A，B，C三点．（1）求抛物线的解析式；（2）直线AD与y轴负半轴交于点D，且∠BAO＝∠DAO，求证：OB＝OD；（3）在（2）的条件下，若直线AD与抛物线的对称轴l交于点E，连接BE，在第一象限内的抛物线上是否存在一点P，使四边形BEAP的面积最大？若存在，请求出点P的坐标及四边形BEAP面积的最大值；若不存在，请说明理由．【解答】解：（1）令y＝0，则﹣x+3＝0，解得x＝6，令x＝0，则y＝3，∴A（6，0），B（0，3），设抛物线的解析式为y＝ax2+bx+c，把A，B，C三点坐标代入解析式，得：，解得：，∴抛物线的解析式为y＝x2+x+3；（2）证明：∵在平面直角坐标系xOy中，∴∠BOA＝∠DOA＝90°，在△BOA和△DOA中，。

初中数学函数面积问题题型解析函数中的面积问题是函数中的一个重点，对这一问题，不少同学解题时，不知如何入手。

本文就这类问题的题型剖析如下：一、已知函数解析式求面积［例1］已知函数8x 4y -=，求该图像与x 轴、y 轴围成三角形的面积。

解：函数8x 4y -=当x=0时，8y -=当x=2时，y=0∴函数8x 4y -=与两坐标轴的交点坐标为（0，－8）和（2，0） ∴82821|2||8|21=⨯⨯=⨯-⨯点评：求三角形的面积时，应先确定三角形的底和高，那么三角形的底和高分别是什么，又怎样表示呢？作出函数8x 4y -=的图像，直线与坐标轴围成的三角形便一目了然了。

相似练习1. 求直线y=x+4与直线4x y +-=与x 轴围成三角形的面积；2. 直线a x 2y +=与b x y +-=的图像都过点A （－2，0）且与y 轴交于B 、C 两点，求ΔABC 的面积。

二、已知面积求解析式［例2］直线y=3x+k 与两坐标轴围成三角形的面积为24，求k 的值。

解：y=3x+k 与两坐标轴的交点为（0，k ）和（3k -，0） ∴2421|3k |k =⨯-⨯ 12k 144k 2±==，点评：已知三角形的面积，相当于直线与坐标轴交点到原点的距离的乘积可知，由此可转化成求交点坐标，即可得答案。

［例3］已知直线l 和直线l'：x+y=20交于点P ，与x 轴交于点A （8，0），且ΔPAO的面积为16，求直线l 的解析式。

解：∵直线l 与x 轴交于点A （8，0）∴AO=8∵ΔPAO 的面积为16∴三角形的高为4∴P 点的纵坐标为4或－4∵直线l 与直线l'：20y x =+交于点P ，∴P 点坐标为（16，4）或（24，－4）∴直线l 过点A （8，0）和（16，4）或A （8，0）和P （24，－4）∴设直线l ：b kx y +=则⎩⎨⎧=+=+4b k 160b k 8 或⎩⎨⎧=+=+-4b 24k 0b 8k 解得21k =，b=4或41k -=，b=2 ∴2x 41y 4x 21y +-=-=或点评：由已知三角形的面积，可想到以寻找底和高为突破口。

2023年九年级数学中考专题：二次函数综合压轴题（面积问题）一、解答题1．如图，在平面直角坐标系中，抛物线2y x bx c =-++与x 轴交于A ，B 两点．与y 轴交于点C ．且点A 的坐标为(10)-，，点C 的坐标为(05)，．(1)求该抛物线的表达式；(2)若点P 是第一象限内抛物线上一动点，连接PC PB BC 、、，设点P 的横坐标为t ． ①当t 为何值时，PBC 的面积最大，并求出最大面积；①当t 为何值时，PBC 是直角三角形．(3)若点M 是抛物线上一点，点N 是抛物线对称轴上一点，存在点M 使得以B ，C ，M ，N 为顶点的四边形是平行四边形，请直接写出点M 的坐标．2．如图，直线112y x =-+交y 轴于点A ，交x 轴于点C ，抛物线212y x bx c =-++经过点A ，点C ，且交x 轴于另一点B ．(1)直接写出点A ，点B ，点C 的坐标及抛物线的解析式；(2)在直线AC 上方的抛物线上有一点M ，求四边形ABCM 面积的最大值及此时点M 的坐标；(3)将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90︒得到线段''O A ，若线段''O A 与抛物线只有一个公共点，请结合函数图象，求m 的取值范围．3．如图，已知抛物线2y x bx c =++经过()1,0A -、()3,0B 两点．(1)求抛物线的解析式和顶点坐标；(2)当03x <<时，求y 的取值范围；(3)点P 为抛物线上一点，若10PAB S =，求出此时点P 的坐标．4．如图，抛物线25y ax bx =+-的图象与x 轴交于()10A -，，()50B ，两点，与y 轴交于点C ，顶点为D ．(1)求此抛物线的解析式及顶点坐标；(2)在抛物线的对称轴上是否存在点Q ，使得QAC △的周长最小？若存在，求出Q 点的坐标并计算QAC △的周长；若不存在，请说明理由；(3)设点M 在第四象限，且在抛物线上，当MBC 的面积最大，求此时点M 的坐标．（直接写出结果）5．如图，已知二次函数24y ax x c =-+的图象与坐标轴交于点()1,0A -和()05C -，．(1)求该二次函数的解析式和它与x 轴的另一个交点B 的坐标；(2)设抛物线的顶点为D ，求四边形ACDB 的面积；(3)点P ()22-，是二次函数的对称轴上一点，连接OP ，找出x 轴上所有点M ，使得OPM 是等腰三角形，并直接写出所有点M 的坐标．6．已知，如图，抛物线22y ax ax c =++与y 轴负半轴交于点C ，与x 轴交于A ，B 两点，点A 在点B 左侧．点B 的坐标为()1,0，3OC OB =．(1)求抛物线的解析式；(2)若点D 是第三象限抛物线上的动点，当四边形ABCD 面积最大时，求出此时面积的最大值和点D 的坐标．(3)将抛物线22y ax ax c =++向右平移2个单位，平移后的抛物线与原抛物线相交于点M ，N 在原抛物线的对称轴上，H 为平移后的抛物线上一点，当以A 、M 、H 、N 为顶点的四边形是平行四边形时，直接写出点H 的坐标．7．如图，已知抛物线2y x bx c =-++经过(30)A ，，(03)B ，两点．(1)求此抛物线的解析式和直线AB 的解析式；(2)如图①，动点E 从O 点出发，沿着OA 方向以1个单位/秒的速度向终点A 匀速运动，同时，动点F 从A 点出发，沿着AB 个单位/秒的速度向终点B 匀速运动，当E ，F 中任意一点到达终点时另一点也随之停止运动，连接EF ，设运动时间为t 秒，当t 为何值时，AEF △与ABO 相似．(3)如图①，动点P 在直线AB 上方，且在抛物线上，求出PAB 的最大面积，并指出此时点P 的坐标．8．如图，抛物线212y x bx c =-++与x 轴交于点()6,0A -和点()10B ，，交y 轴于点C ，连接AC ．(1)求抛物线的解析式；(2)点P 是直线AC 上方抛物线上一动点，过点P 作PQ y ∥轴，交直线AC 于点Q ． ①当点P 在何位置时，PAC △面积S 最大？最大面积是多少？①抛物线上是否存在点P ，使以P ，Q ，O ，C 为顶点的四边形是平行四边形？若存在，求出点P 的坐标，若不存在，请说明理由．9．如图，已知抛物线2y x bx c =--+经过()()1030A B -，，，两点(1)求抛物线的解析式和顶点坐标；(2)当1x -<<3时，直接写出y 的取值范围；(3)点P 为抛物线上的一点，若10PAB S =，求出此时点P 的坐标．10．如图，在平面直角坐标系中，点O 为坐标原点，抛物线23y ax x c =++与一次函数4y x =-+分别交y 轴于点A ，交x 轴于点C ．(1)求抛物线的解析式；(2)第一象限内一动点P 在抛物线上，过点P 作x 轴的垂线交AC 于点Q ，垂足为D ，设点P 的横坐标为t ，APC △的面积为S ，求S 与t 的函数解析式（不要求写出自变量t 的取值范围）；(3)在（2）的条件下，当线段PQ 最大时，点E 是抛物线第二象限上一动点，点F 为直线EF 与抛物线另一交点，且EF 交直线PQ 于点R ，若90ER FR EQF =∠=︒，，求点R 的坐标．11．如图，抛物线22y x x k =-+与x 轴交于A 、B 两点，与y 轴交于点()0,3C -．(1)求抛物线的解析式和点A 和点B 的坐标；(2)在x 轴下方的抛物线上是否存在一点D ，使四边形ABDC 的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由；(3)在抛物线22y x x k =-+上求点Q ，使BCQ △是以BC 为直角边的直角三角形． 12．如图，已知抛物线过点()0,0O ，()3,3A ，且它的对称轴为1x =，点B 是抛物线对称轴上的一点，且点B 在第一象限．(1)求此抛物线的解析式；(2)当OAB 的面积为92时，求B 的坐标； (3)在（2）的条件下，P 是抛物线上的动点，当PA PB -的值最大时，求P 的坐标以及PA PB -的最大值．13．如图，已知抛物线235y x bx c =-++交x 轴于()50A ，，()10B -，两点，交y 轴于点C ．点P 是线段AC 上一动点．(1)求该抛物线解析式；(2)连接OP 并延长交抛物线于点D ，连接AD ，是否存在点P ，使AOP APD S S =△△．若存在，请求出点P 坐标；若不存在，请说明理由；(3)连接BC ，过点P 作PE CB ∥交x 轴于点E ．将CEP △沿CE 翻折，当点P 的对应点P '恰好落在x 轴上时，则E 的坐标为 ．14．如图，抛物线()20y ax bx c a =++≠与y 轴交于点()04C ，，与x 轴交于点A 和点B ，其中点A 的坐标为()20-，，抛物线的对称轴1x =与抛物线交于点D ，与直线BC 交于点E ．(1)求抛物线的解析式；(2)若点F 是直线BC 上方的抛物线上的一个动点，是否存在点F 使四边形ABFC 的面积为17，若存在，求出点F 的坐标；若不存在，请说明理由；(3)平行于DE 的一条动直线l 与直线BC 相交于点P ，与抛物线相交于点Q ，若以D 、E 、P 、Q 为顶点的四边形是平行四边形，求点P 的坐标．15．如图，直线y kx =与抛物线2y x c =+交于A ，B 两点，其中点B 的坐标是()2,2(1)求直线AB 及抛物线的解析式；(2)C 为抛物线上的一点，ABC 的面积为3，求点C 的坐标；(3)P 在抛物线上，Q 在直线AB 上，M 在坐标平面内，当以A ，P ，Q ，M 为顶点的四边形为正方形时，直接写出点M 的坐标．16．如图1，抛物线2y x bx c =++与x 轴交于A 、B 两（点A 在点B 左侧），与y 轴交于点C ，直线3y x =-+经过B 、C 两点．(1)求抛物线的解析式；(2)点D 在抛物线上，连接BD 、CD ，若BCD △的面积为15，求点D 的坐标；(3)如图2，连接AC ，点E 在抛物线上，连接AE ，若2BAE ACB ∠=∠，求点E 的坐标． 17．如图，在平面直角坐标系中，直线3y x =-+与y 轴交于点A ，与x 轴交于点B ，抛物线2y x bx c =-++过A 、B 两点．(1)求抛物线的解析式；(2)过点A 作AC 平行于x 轴，抛物线于点C ，点F 为抛物线上一动点（点F 在AC 上方），作FD 平行于y 轴交AB 于点D ．问当点F 在何位置时，四边形AFCD 的面积最大？并求出最大面积．(3)当3t x t +≤≤时，函数2y x bx c =-++的最大值为4，求t 的值．18．如图，抛物线2y ax bx c =++的顶点为()2,4M --，与x 轴交于A 、B 两点，且()6,0A -，与y 轴交于点C ．(1)求抛物线的函数解析式；(2)求ABC 的面积；(3)能否在抛物线第三象限的图象上找到一点P ，使APC △的面积最大？若能，请求出点P 的坐标；若不能，请说明理由．参考答案：1．(1)245y x x =-++(2)①当52t =时，ABC S ∆=最大①t 为3或22 (3)(38)，或(316)--，或(716)-，2．(1)()0,1A ；()1,0B -；()2,0C ；211122y x x =-++ (2)最大值为2，此时M 的坐标为()1,12m ≤≤-1m ≤≤3．(1)抛物线的解析式为2=23y x x --；顶点坐标为()1,4-(2)当03x <<时，40x -≤<(3)P 点坐标为()2,5-或()4,54．(1)245y x x =--；顶点坐标为()29-，(2)存在，()23Q -，，QAC △(3)()2.58.75M -，5．(1)()2455,0y x x B =--，(2)30(3)()()()()12344,02,0M M M M -、、、6．(1)223y x x =+-(2)最大值758，点315,24D ⎛⎫-- ⎪⎝⎭(3)()2,3-或()2,5-或()4,21-7．(1)抛物线的解析式为223y x x =-++，直线AB 的解析式为3y x =-+(2)1或32(3)ABP 的面积的最大值为278，此时点P 的坐标为31524⎛⎫ ⎪⎝⎭，8．(1)215322y x x =--+(2)①当()3,6P -时，S 最大值为272；①存在， 当3P ⎛-+ ⎝⎭或3⎛- ⎝⎭时，以P ，Q ，O ，C 为顶点的四边形是平行四边形9．(1)223y x x =-++，顶点坐标为()14， (2)04y <≤(3)点P 的坐标为()()5524---，，，10．(1)234y x x =-++(2)228S t t =-+(3)()2,2-11．(1)()214y x =--；()1,0A -，()3,0B (2)存在点315,24D ⎛⎫- ⎪⎝⎭，使四边形ABDC 的面积最大为758 (3)存在，点()12,5Q -、()21,4Q -，使1BCQ 、2BCQ 是以BC 为直角边的直角三角形12．(1)22y x x =-(2)点B 的坐标为()1,4(3)321(,),24-P13．(1)2312355y x x =-++；(2)存在，P ⎝⎭或⎝⎭(3)()1-14．(1)2142y x x =-++ (2)不存在，理由见解析(3)()131P ，，(22P ，(32P15．(1)直线AB 的解析式为y x =，抛物线的解析式是22y x =-(2)12C C ⎝⎭⎝⎭,，()()340,2,1,1C C -- (3)()()()()23411,1021113M M M M -,,-,-,,-,-16．(1)243y x x =-+(2)点D 的坐标为(5,8)或(2,11)-时，BCD △的面积为15(3)点E 的坐标为13()3409，或58()39，-17．(1)223y x x =-++ (2)31524F ⎛⎫ ⎪⎝⎭，，面积最大为94 (3)21t -≤≤18．(1)2134y x x =+- (2)12 (3)能，点P 的坐标为153,4⎛⎫-- ⎪⎝⎭。