2012-2013第一学期阿阳实验学校九年级数学期末

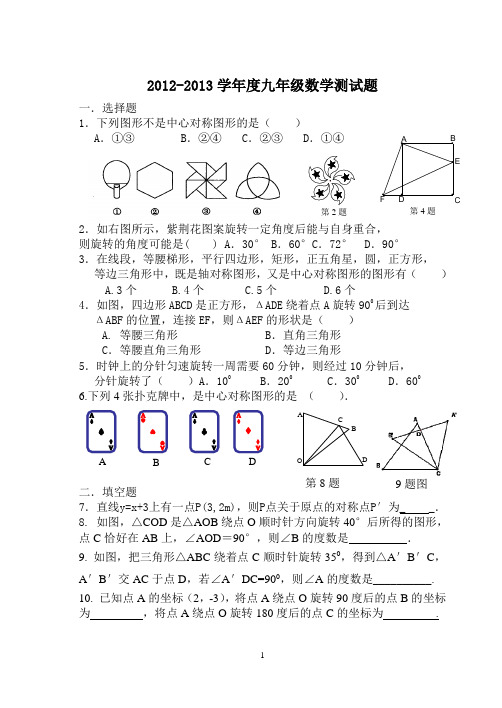
2012-2013学年度九年级数学测试题一．选择题1．下列图形不是中心对称图形的是（ ）A ．①③B ．②④C ．②③D ．①④2．如右图所示，紫荆花图案旋转一定角度后能与自身重合， 则旋转的角度可能是( ) A ．30° B ．60°C ．72° D ．90°3．在线段，等腰梯形，平行四边形，矩形，正五角星，圆，正方形， 等边三角形中，既是轴对称图形，又是中心对称图形的图形有（ ）A.3个B.4个C.5个D.6个4．如图，四边形ABCD 是正方形，ΔADE 绕着点A 旋转900后到达 ΔABF 的位置，连接EF ，则ΔAEF 的形状是（ ）A. 等腰三角形 B ．直角三角形C ．等腰直角三角形D ．等边三角形5．时钟上的分针匀速旋转一周需要60分钟，则经过10分钟后， 分针旋转了（ ）A ．100 B ．200 C ．300 D ．6006.下列4张扑克牌中，是中心对称图形的是 （ ）．二．填空题7．直线y=x+3上有一点P(3,2m)，则P 点关于原点的对称点P ′为_ _．8. 如图，△COD 是△AOB 绕点O 顺时针方向旋转40°后所得的图形，点C 恰好在AB 上，∠AOD ＝90°，则∠B 的度数是 ．9. 如图，把三角形△ABC 绕着点C 顺时针旋转350，得到△A ＇B ＇C ，A ＇B ＇交AC 于点D ，若∠A ＇DC=900，则∠A 的度数是__________.10. 已知点A 的坐标（2，-3），将点A 绕点O 旋转90度后的点B 的坐标为 ，将点A 绕点O 旋转180度后的点C 的坐标为 .第2题 第4题 O DC BA 第8题 ABCD 9题图三．解答题11.如图所示的正方形网格中，△ABC 的顶点均在格点上，在所给直角坐标系中解答下列问题：（1）分别写出点A 、B 两点的坐标；（2）作出△ABC 关于坐标原点成中心对称的△A 1B 1C 1；12.已知PA=5,PB=4,PC=3,点P 是等边三角形ABC 内一点，则∠BPC 是多少度？13. 正方形ABCD 和正方形AEFG 有一公共点A ，点G ．E 分别在线段AD 、AB 上（如图（1）所示），连接DF 、BF ．（1）求证：DF=BF ，（2）若将正方形AEFG 绕点A 按顺时针方向旋转，连接DG 、BE （如图（2）所示），在旋转过程中，请猜想线段DG 、BE 始终有什么数量关系和位置关系并证明你的猜想．图9。

北京市西城区2012—2013学年度第一学期期末试卷（北区）九年级数学 2013.1一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1．二次函数2)1(2+-=x y 的最小值是 A ．1- B ．1 C ．2- D ．22．如图，⊙O 是△ABC 的外接圆，若∠ABC ＝40°，则∠AOC的度数为A ．20°B ．40°C ．60°D ．80° 3．两圆的半径分别为2和3，若圆心距为5，则这两圆的位置关系是 A ．相交 B ．外离 C ．外切 D ．内切 4．三角尺在灯泡O 的照射下在墙上形成的影子如图所示. 若20cm 50cm OA OA '==，，则这个三角尺的周长 与它在墙上形成的影子的周长的比是 A ．5：2 B ．2：5 C ．4：25 D ．25：45．如图，正方形ABCD 的内切圆和外接圆的圆心为O ， EF 与GH 是此外接圆的直径，EF =4，AD ⊥GH ， EF ⊥GH ，则图中阴影部分的面积是 A ．π B ．2π C ．3π D ．4π6．某学校组织艺术摄影展，上交的作品要求如下：七寸照片 （长7英寸，宽5英寸）；将照片贴在一张矩形衬纸的正中央， 照片四周外露衬纸的宽度相同；矩形衬纸的面积为照片面积的 3倍．设照片四周外露衬纸的宽度为x 英寸（如图），下面所列 方程正确的是A ．(7)(5)375x x ++⨯=⨯B ．(7)(5)375x x ++=⨯⨯C ．(72)(52)375x x ++⨯=⨯ D ．(72)(52)375x x ++=⨯⨯E7．如图，直线443y x =-+与x 轴、y 轴分别交于A 、B 两点，△AOB 绕点A 顺时针旋转90°后得到△AO B ''，则点B 的对应点B '坐标为 A ．（3，4） B ．（7，4）C ．（7，3）D ．（3，7）8．如图，△ABC 中，∠B =60°，∠ACB =75°，点D 是BC 边上一动点，以AD 为直径作⊙O ，分别交AB 、AC 于E 、F ，若弦EF 的最小值 为1，则AB 的长为A. 22B. 632C. 1.5D.二、填空题（本题共16分，每小题4分）9．扇形的半径为9，且圆心角为120°，则它的弧长为_______.10．已知抛物线23y x x =--经过点)2(1y A ，、)3(2y B ，， 则1y 与2y 的大小关系是_______．11．如图，P A 、PB 分别与⊙O 相切于A 、B 两点，且OP =2，∠APB =60°.若点C 在⊙O 上，且AC ∠CAB 的度数为_______．12．已知二次函数c bx ax y ++=2的图象与x 轴交于(1,0)和(1x ,0)，其中121x -<<-，与y 轴交于正半轴上一点．下列结论：①0>b ；②241b ac <；③a b >；④a c a 2-<<-．其中所有正确结论的序号是_______．三、解答题（本题共30分，每小题5分）132604cos 30+sin 45tan 60-⋅．14．已知抛物线241y x x =-+．（1）用配方法将241y x x =-+化成2()y a x h k =-+的形式；（2）将此抛物线向右平移1个单位，再向上平移2个单位，求平移后所得抛物线的解析式．15．如图，在Rt △ABC 中，∠C =90°，点D 在AC 边上．若AD =12CD ，sin ∠CBD =23，求AD 的长和tan A 的值．16．如图，AB 是⊙O 的直径，CD 是⊙O 的一条弦，且CD ⊥AB于点E ．（1）求证：∠BCO =∠D ；（2）若CD =AE =2，求⊙O 的半径．17．如图，在□ABCD 中，点E 在BC 边上，点F 在DC 的延长线上，且∠DAE =∠F ． （1）求证：△ABE ∽△ECF ；（2）若AB =5，AD =8，BE =2，求FC 的长．18．如图，一艘海轮位于灯塔P 的南偏东45°方向，距离灯塔100海里的A 处，它计划沿正北方向航行，去往位于灯塔 P 的北偏东30°方向上的B 处. （1）B 处距离灯塔P 有多远？（2）圆形暗礁区域的圆心位于PB 的延长线上，距离灯塔200海里的O 处.已知圆形暗礁区域的半径为50海里， 进入圆形暗礁区域就有触礁的危险.请判断若海轮到达 B 处是否有触礁的危险，并说明理由．四、解答题（本题共20分，每小题5分） 19．已知抛物线322--=x x y .（1）它与x 轴的交点的坐标为_______； （2）在坐标系中利用描点法画出它的图象；（3）将该抛物线在x 轴下方的部分(不包含与x 轴的交点)记为G ，若直线b x y +=与G只有一个公共点，则b 的取值范围是_______．20．如图，AB 是⊙O 的直径，点C 在⊙O 上，过点C 与AB 的延长线交于点P ，∠COB =2∠PCB . （1）求证：PC 是⊙O 的切线；（2）点M 是弧AB 的中点，CM 交AB 于点N ， 若MN · MC =8，求⊙O 的直径.21．平面直角坐标系xOy 中，原点O 是正三角形ABC 外接圆的圆心，点A 在y 轴的正半轴上，△ABC 的边长为6．以原点O 为旋转中心将△ABC 沿逆时针方向旋转α角，得到△A B C '''，点A '、B '、C '分别为点A 、B 、C 的对应点． （1）当α=60°时，①请在图1中画出△A B C '''；②若AB 分别与C A ''、B A ''交于点D 、E ，则DE 的长为_______；（2）如图2，当C A ''⊥AB 时，B A ''分别与AB 、BC 交于点F 、G ，则点A '的坐标为_______，△FBG 的周长为_______，△ABC 与△A B C '''重叠部分的面积为 _______．22．阅读下面的材料：小明在学习中遇到这样一个问题：若1≤x ≤m ，求二次函数267y x x =-+的最大值．他画图研究后发现，1x =和5x =时的函数值相等，于是他认为需要对m 进行分类讨论．他的解答过程如下：∵二次函数267y x x =-+的对称轴为直线3x =∴由对称性可知，1x =和5x =时的函数值相等∴若1≤m ＜5，则1x =时，y 的最大值为2； 若m ≥5，则m x =时，y 的最大值为26m -请你参考小明的思路，解答下列问题：（1）当2-≤x ≤4时，二次函数422++=x x y （2）若p ≤x ≤2，求二次函数1422++=x x y （3）若t ≤x ≤t +2时，二次函数1422++=x x y五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23．已知抛物线212(1)y x m x n =+-+经过点（1-，132m +）． （1）求n m -的值；（2）若此抛物线的顶点为（p ，q ），用含m 的式子分别表示p 和q ，并求q 与p 之间 的函数关系式； （3）若一次函数2128y mx =--，且对于任意的实数x ，都有1y ≥22y ，直接写出m 的取值范围.24．以平面上一点O 为直角顶点，分别画出两个直角三角形，记作△AOB 和△COD ，其中∠ABO =∠DCO =30°．（1）点E 、F 、M 分别是AC 、CD 、DB 的中点，连接FM 、EM ．①如图1，当点D 、C 分别在AO 、BO 的延长线上时，FM EM=_______；②如图2，将图1中的△AOB 绕点O 沿顺时针方向旋转α角（060α<< ），其 他条件不变，判断FM EM的值是否发生变化，并对你的结论进行证明；（2）如图3，若BO=，点N 在线段OD 上，且NO =2.点P 是线段AB 上的一个动点，在将△AOB 绕点O 旋转的过程中，线段PN 长度的最小值为_______，最大值为_______．图2CDBOMEF ADMBOFCEA图125．如图1，平面直角坐标系xOy 中，抛物线212y x bx c =++与x 轴交于A 、B 两点，点C 是AB 的中点，CD ⊥AB 且CD =AB .直线BE 与y 轴平行，点F 是射线BE 上的一个动点，连接AD 、AF 、DF .（1）若点F 的坐标为（92，1），AF ①求此抛物线的解析式；②点P 是此抛物线上一个动点，点Q 在此抛物线的对称轴上，以点A 、F 、P 、Q为顶点构成的四边形是平行四边形，请直接写出点Q 的坐标；（2）若22b c +=-，2b t =--，且AB 的长为kt ，其中0t >.如图2，当∠DAF =45°时，求k 的值和∠DF A 的正切值.。

九年级数学（A 卷） 第1页（共6页）2012—2013学年度第一学期海口市九年级数学科期末检测题（A 卷）时间：100分钟 满分：120分 得分：一、选择题（每小题3分，共42分）在下列各题的四个备选答案中，只有一个是正确的，请把你认为正确的答案的字母代号填写在下表相应题号的方格内.1．计算2)32(的结果是A ．6 B. 12 C. 18 D. 36 2. 下列计算正确的是A ．3+2=5 B. 3×2=6 C. 12-3=3 D. 12÷3=4 3. 函数y =x 1中自变量x 的取值范围是A. x ≠1B. x ＜1C. x ≥1D. x ≤14．若x =1+2，y =1-2, 则xy 的值为A. -1B. 1C. 3D. 22 5．一元二次方程x 2-9x=0的解是A. x=0B. x=9C. x 1=-3，x 2=3D. x 1=0，x 2=9 6. 用配方法解方程x 2-6x -7=0，下列配方正确的是A ．(x -3)2=16B ．(x +3)2=16C ．(x -3)2=7D ．(x -3)2=27. 关于x 的方程x 2+bx+c=0的两个实数根分别为 -2和3，则分解因式x 2+bx+c 等于A. (x -2)(x -3)B. (x -2)( x +3)C. (x +2)( x -3)D. (x +2)(x +3) 8. 掷一枚普通的硬币3次，落地后出现两个正面一个反面朝上的概率是A ．81B ．83C ．41D ．61九年级数学（A 卷） 第2页（共6页）9. 生物兴趣小组的学生，将自己收集的标本向本组其他成员各赠送一件，全组共互赠送110件, 若设全组有x 名同学，则可列方程为A. x (x +1)=110B. x (x -1)=110C. x (x +1)=220D. x (x -1)=220 10．如图1，将△ABC 沿DE 翻折，折痕DE ∥BC ，DB =2AD ，DE =4，则BC 等于A ．6B ．8C ．10D ．12 11. 在图2所示的直角坐标系中，P 是第一象限的点，其坐标为(3,4)，则sin α等于A ．53B ．54C ．43D ．3412. 如图3，△ABC 中，∠BAC =90°，D 、E 分别是边BC 、AC 的中点，AD 、BE 交于点F ，若BC =1，则AF 等于 A ．21 B ．31 C ．32 D ．4113. 如图4，一斜坡上栽树，相邻在坡面上的距离AB =13m ，水平距离为12m ，则该斜坡坡度i 为A ．5:12B ．12:13C ．12:5D ．1:314．如图5，在□ABCD 中，AB =6，BC =10，E 为AD 上一点，且BE =BC ，CE =CD ，则DE 等于A ．5B ．4C ．3.6D ．312m图4ABD图5EABCD E图1 A 图3DEF图2九年级数学（A 卷） 第3页（共6页）二、填空题（每小题4分，共16分） 15. 当a 时，2)3(-a + a -3=0．16. 如图6，点P 把线段AB 分成两条线段AP 和BP ，如果ABAP AP PB =，那么称线段AB 被点P 黄金分割，AP 与AB 的比叫做黄金比. 这个黄金比为 . 17. 如图7，∠AOB 是放置在正方形网格中的一个角，则cos ∠AOB 的值为 .18. 如图8，在□ABCD 中，E 是CD 的延长线上一点，BE 与AD 交于点F ，CD =2DE ．若△DEF 的面积为a ，则□ABCD 的面积为 （用含a 的代数式表示）． 三、解答题（共62分）19．计算(第（1）、（2）小题每题4分，第（3）小题5分，共13分) （1）6318⨯ ； （2） 515420--；（3） (1-2cos30°)2+︒60tan 3.ABDC图8E FOAB图7ABP图6九年级数学（A 卷） 第4页（共6页）20．（8分）把一张边长为10cm ，宽为8cm 的矩形硬纸板的四周各剪去一个同样大小的正方形，再折合成一个无盖的长方体盒子（如图9）. 如果这个无盖的长方体底面积为48cm 2，那么该长方体盒子体积是多少？21．（8分）一个不透明的盒子中，装有2个白球和1个红球，这些球除颜色外其余都相同. （1）你同意下列说法吗？请说明理由.① 搅匀后从中任意摸出一个．．．．球，不是白球就是红球，因此摸出白球和摸出红球这两个事件是等可能的.② 如果将摸出的第一个球放回搅匀再摸出第二个球，两次摸球就可能出现3种结果，即“都是红球”、“都是白球”、“一红一白”. 这三个事件发生的概率相等.（2）搅匀后从中任意摸．出一个．．．球，要使摸出红球的概率为43，应如何添加红球？图23.3.1图9九年级数学（A 卷） 第5页（共6页）22．（9分）如图10，在△ABC 中，∠C =90°，∠B =30°，AD 是∠BAC 的角平分线.若AD =4,求△ABC 的周长.23．(11分)在图11的方格纸中，△OAB 的顶点坐标分别为O (0,0)、A (-2,-1)、B (-1,-3)，P (a ,b )是△AOB 的边AB 上一点.（1）以原点O 为位似中心，在y 轴的左侧画出△OAB 的一个位似△OA 1B 1，使它与△OAB 的相似比为2:1，并分别写出点A 、P 的对应点A 1、P 1的坐标； （2）画出将△OA 1B 1 向右平移5个单位后的△O 2A 2B 2, 并写出点A 2、P 2的坐标； （3）判断△OAB 与△O 2A 2B 2,能否是关于某一点M 为位似中心的位似图形，若是，请在图11中标出位似中心M ，并写出点M 的坐标.D AB图10图11九年级数学（A 卷） 第6页（共6页）24.（13分）在矩形ABCD 中，AB =4，AD =5，P 是射线BC 上的一个动点，作PE ⊥AP ，PE 交射线DC 于点E ，射线AE 交射线BC 于点F ．（1）如图12，当点P 在边BC 上时（点P 与点B 、C 都不重合），设BP =x .① 用含x 的代数式表示CE 的长；② 当CF =3时，求x 的值；（2）当tan ∠P AE =21时，求BP 的长．（提示：分两种情况讨论，即点P 在BC 边上和点P 在BC 的延长线上.)备用图九年级数学（A 卷） 第7页（共6页）2012—2013学年度第一学期海口市九年级数学科期末检测题(A 卷)参考答案及评分标准一、BCDAD ACBBD BBAC 二、15．≤3 16. 251+- 17. 22 18．12a三、19．（1）原式=61831⨯ …（2分） （2）原式=2-551554- …（2分）=23 …（4分） =2-5 …（4分）（3）原式=(1-3)2+33…（2分）=1-23+3+3 …（4分） =4-3 …（5分）20. 设剪去的小正方形边长为x cm ， …………………（1分）根据题意，得 (10-2x )(8-2x )=48. …………………（5分） 解这个方程，得x 1=1，x 2=8 . …………………（6分） 当x 2=8时，2x =16cm ＞8cm ，所以x 2=8不合题意舍去，只取x =1 .长方体盒子体积=48×1=48cm 3. 答：该长方体盒子体积是48cm 3. …（8分） 21．（1）① 不同意． …………………（1分）因为摸出白球的概率是32，摸出红球的概率是31， 所以摸出白球和摸出红球不是等可能的． …………………（2分）②不同意．所有等可能的结果，用树状图分析如下： …………………（3分）由图可知共有9种等可能的结果.P (两红)=91，P (两白)=94，P (一红一白)=94. …………………（6分）（2）解法1：设应添加x 个红球，由题意，得 4331=++x x .解得x =5（经检验是原方程的解） 答：应添加5个红球． …………（8分） 解法2：∵ 添加后P （摸出红球）=43, ∴ 添加后P（摸出白球）41431=-=. ∴ 添加后球的总个数8412=÷=． ∴ 应添加8-3=5个红球． …………………（8分）红白1 白2红 白1 白2 红 白1 白2 红 白1 白2九年级数学（A 卷） 第8页（共6页）22. ∵ △ABC 中，∠C =90º，∠B =30º，∴ ∠BAC =60º，∵ AD 是∠BAC 的角平分线，∴ ∠CAD =∠BAD =30º， …（1分）∴ 在Rt △ADC 中，AC =AD •cos ∠CAD =4×cos30º=4×23=23.…（3分） ∴ 在Rt △ACB 中，BC =AC •t a n ∠BAC =23×tan60º=23×3=6.（5分）AB =2AC =43. …（7分）∴ △ABC 的周长=AB +BC +AC =43+6+23=6+63. …（9分） (注：用其它方法求解参照以上标准给分.)23．（1）A 1(-4,-2)，P 1(2a ,2b ) ； …（4分） （2）A 2(1,-2)，P 2(2a +5,2b )； …（8分）（3）△OAB 与△O 2A 2B 2是关于点M (-5,0) 为位似中心的位似图形. …（11分）24．（1）①在矩形ABCD 中， ∵ PE ⊥AP ，∴ ∠CPE +∠APB =90°． 又∵ ∠BAP +∠APB =90°，∴ ∠CPE =∠BAP ． ∵ ∠ECP =∠B =90°， ∴ △PCE ∽△ABP ． ……（2分）∴ ABBPPCCE =，即45x x CE =-． ∴ CE =x x 45412+-． ……（4分）② ∵ CE ∥AB ，∴ △ECF ∽△ABF ．……（5分）∴ AB CEBF CF =，即483CE =． ……（6分） ∴ CE =23． ……（7分）∴ 23=x x 45412+-. ……（8分） 解这个方程，得x 1=2，x 2=3. ……（9分）（2）（i ）当点P 在边BC 上时，∵ tan ∠P AE =21，∴ 21=AP EP ． ∵ △PCE ∽△ABP ，∴ 21==AP EP AB CP ．（10分）∵ AB =4，∴ CP =2．∴ BP =3． ……（11（ii ）当点P 在边BC 的延长线上时，同理可得21=AB CP ． ……（12分） ∵ AB =4，∴ CP =2．∴ BP =7． ……（13分） (注：用其它方法求解参照以上标准给分.)图1 图3。

东城区2012-2013学年第一学期期末统一检测初三数学试题参考答案及评分标准 2013.1三、解答题（本题共30分，每小题5分） 13. 解方程：2316x x -= ． 解：移项，得2361x x -= ． ………………..1分 二次项系数化为1，得 2123x x -= ． ………………..2分 配方 24(1)3x -= ． ………………..4分 由此可得11x =21x = ………………..5分 14. 解：根据题意，由勾股定理可知222BC BO CO =+.∴ 5BC =cm. ………………..2分∴ 圆锥形漏斗的侧面积=15OB BC ππ⋅⋅= cm 2 ． ………………..5分 15．解：△ABC 和△DEF 相似． ………………..1分由勾股定理，得AB =AC =BC =5，DE =4，DF =2，EF = ………………..3分22AB AC BC DE DF EF ==== ………………..4分∴△ABC ∽△DEF ． ………………..5分 16．（1）………………..3分（2）………………..5分17．解：(1) ∵ 关于x 的一元二次方程(m -2)x 2 + 2mx + m +3 = 0 有两个不相等的实数根， ∴ 20m -≠，即2m ≠. ………………..1分 又 ∵ 2(2)4(2)(3)4(6)m m m m ∆=--+=--， ∴ 0∆>即4(6)0m -->．解得 6m <．∴ m 的取值范围是6m <且m ≠ -2． ………………..2分(2)在6m <且m ≠ -2的范围内，最大整数m 为5． ………………..3分 此时，方程化为231080x x ++=．∴ 方程的根为 12x =-， 243x =- ． ………………..5分18．解： ∵ 四边形ABCD 是圆内接四边形，∴ ∠B +∠D =180°． ………………..1分 ∵ 四边形OABC 为平行四边形，∴ ∠AOC =∠B ． ………………..2分 又由题意可知 ∠AOC =2∠D ．∴可求∠D=60°．………………..3分连结OD，可得AO=OD，CO=OD．∴∠OAD=∠ODA，∠OCD=∠ODC．………………..4分∴∠OAD+∠OCD=∠ODA+∠ODC=∠D=60°．………………..5分四、解答题（本题共20分，每小题5分）20．解：（1）证明：如图，连接OB．∵PB是⊙O的切线，∴∠PBO＝90°．∵ OA＝OB，BA⊥PO于D，∴AD＝BD，∠POA＝∠POB．又∵PO＝PO，∴△P AO≌△PBO．∴∠P AO＝∠PBO＝90°．∴直线P A为⊙O的切线．………………..2分（2）∵OA＝OC，AD＝BD，BC＝6，∴OD＝12BC＝3．设AD＝x．∵AD∶FD=1∶2，∴FD＝2x，OA＝OF＝2x－3．在Rt△AOD中，由勾股定理，得(2x－3)2＝x2＋32．解之得，x1＝4，x2＝0（不合题意，舍去）．∴AD＝4，OA＝2x－3＝5．即⊙O的半径的长5．………………..5分21. 解：（1）三类垃圾随机投入三类垃圾箱的树状图如下：………………..2分由树状图可知垃圾投放正确的概率为3193=；………………..3分 （2）“厨余垃圾”投放正确的概率为40024001001003=++. ………………..5分 22. 解：（1）当280≤<x 时，80=V . ………………..1分当18828≤<x 时，设b kx V +=，由图象可知，⎩⎨⎧+=+=.1880,2880b k b k解得：⎪⎩⎪⎨⎧=-=.94,21b k∴ 当18828≤<x 时，9421+-=x V . ………………..3分 （2）根据题意，得211-+94-9422P Vx x x x x ⎛⎫===+ ⎪⎝⎭=()21--9444182x +.答：当车流密度x 为94辆/千米时，车流量P 最大，为4418辆/时. …………..5分 23. 解：（1） 二次函数的对称轴方程为1x =，由二次函数的图象可知二次函数的顶点坐标为（1,-3），二次函数与x 轴的交点坐标为(0,0),(2,0)，于是得到方程组3,420.a b a b +=-⎧⎨+=⎩ ……………………………………..2分解方程得3,6.a b =⎧⎨=-⎩二次函数的解析式为 236y x =-. ……………………………………..3分 （2）由（1）得二次函数解析式为236y x =-．依题意并结合图象可知，一次函数的图象与二次函数的图象交点的横坐标分别为1和53，由此可得交点坐标为(1,3)-和55(,)33-． …………………………..4分将交点坐标分别代入一次函数解析式y kx n =+中，得 355 .33k n k n +=-⎧⎪⎨+=-⎪⎩，解得 2 5k n =⎧⎨=-⎩，．∴ 一次函数的解析式为25y x =-． ……………………………..6分 （3）3. ……………………………………………..7分 24．解：（1）∵ ∠BAC =90°，AB =AC =2，∴ ∠B =∠C，BC =又∵FEB FED DEB EQC C ∠=∠+∠=∠+∠,DEF C ∠=∠, ∴ ∠DEB =∠EQC . ∴ △BPE ∽△CEQ ． ∴BP CE BE CQ=． 设BP 为x ，CQ 为y ， ∴y =． ∴ 2y x=． 自变量x 的取值范围是0＜x ＜1． ……………………………..3分（2）解：∵ ∠AEF =∠B =∠C ,且∠AQE ＞∠C ,∴ ∠AQE ＞∠AEF . ∴ AE ≠AQ .当AE =EQ 时，可证△ABE ≌ECQ . ∴ CE =AB =2 .∴ BE =BC -EC=2.当AQ =EQ 时，可知∠QAE =∠QEA =45°. ∴ AE ⊥BC .∴ 点E 是BC 的中点.∴ BE综上，在∠DEF 运动过程中，△AEQ 能成等腰三角形，此时BE 的长为2 或……………………………..7分25．解：（1） 抛物线22(1)6y x m x m =---+-与y 轴交于点B （0 , 3），∴ 26 3.m -= ∴ 3.m =±抛物线的顶点在第二象限，∴ 3.m =∴ 抛物线的解析式为223y x x =--+. ………2分（2）猜想：CD AC ⊥. ………3分证明如下：A （-3 , 0），B （0 , 3），C （-1 , 4），∴ AB AC BC ===∴ 222AB BC AC +=. ∴ 90ABC ∠=︒.∴ 90CAB ACB ∠+∠=︒.又CAB DCB ∠=∠ , ∴ 90DCB ACB ∠+∠=︒. ∴ CD AC ⊥. ………4分 （3）当0＜t ≤32时，如图， EF 交AB于点Q ，GF 交AC 于点N ，过N 做MP //F E 交x 轴于P 点，交BF 的延长线点M ， BF 的延长线交AC 于点K ． 由△AGN ∽△KFN ，得AG PNKF MN=，即332t PNPNt =--. 解得PN ＝2t ．∴231113=33(3)232222FGE QAE AGN S S S S t t t t t ∆∆∆--=⨯⨯---⨯=-+阴影.当32＜t ≤3时，如图， EF 交AB 于点N ，交AC 于点M ,BF 交AC 于点P ． 由△AME ∽△PMF ，得AE MEPF MF =． 即3332t ME ME t -=--． 解得ME ＝2(3－t )．∴221119=(3)2(3)(3)32222MAE NAE S S S t t t t t ∆∆-=⨯-⨯---=-+阴影. 综上所述：S ＝22333 0),221933 (3).222t t t t t t ⎧-+<⎪⎪⎨⎪-+<⎪⎩≤≤( ………………………………………….8分。

2012-2013学年广东省广州市从化市九年级（上）期末数学试卷一、选择题：（本大题10个小题，每题3分，共30分，在每小题给出的四个选择项中，只有一项是符合题目要求的，请将答案填在下列表格中）1．（3分）一元二次方程x2=1的解是（）A．x=1 B．x=﹣1 C．x=±1 D．x=02．（3分）下面计算正确的是（）A．3+√3=3√3B．√27÷√3=3 C．√2•√3=√5D．√4=±23．（3分）下列图形中，既是中心对称又是轴对称的图形是（）A．B．C．D．4．（3分）下列事件：①明天会出太阳；②掷一枚硬币，正面向上；③地球绕着太阳转；④打开电视机，正在播足球赛．其中随机事件是（）A．①②B．①③C．①④D．①②④5．（3分）如图，已知AB为⊙O的直径，点C在⊙O上，∠C=15°，则∠BOC的度数为（）A．15°B．30°C．45°D．60°6．（3分）下列对抛物线y=﹣2（x+3）2﹣1描述不正确的是（）A．开口向下B．y有最大值C．对称轴是x=﹣3 D．顶点坐标为（3，﹣1）7．（3分）一元二次方程x（x﹣2）=0根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．只有一个实数根D．没有实数根8．（3分）如图，两个同心圆的半径分别为3cm和5cm，弦AB与小圆相切于点C，则AB 的长为（）A．4cm B．5cm C．6cm D．8cm9．（3分）如图，正方形OABC的边长为2，则该正方形绕点O逆时针旋转45°后，B点的坐标为（）A．（2，2）B．（0，2√2）C．（2√2，0）D．（0，2）10．（3分）如图为二次函数y=ax2+bx+c（a≠0）的图象，则下列说法：①a＞0 ②2a+b=0 ③a+b+c＞0 ④当﹣1＜x＜3时，y＞0其中正确的个数为（）A．1 B．2 C．3 D．4二、填空题（本题共6小题，每小题3分，共18分，请把正确答案填在试卷的空格上）11．（3分）函数y=√x−3中，自变量x的取值范围是．12．（3分）若x1，x2是一元二次方程x2﹣5x+6=0的两个根，则x1+x2的值是；13．（3分）有长度分别为2cm，3cm，4cm，7cm的四条线段，任取其中三条能组成三角形的概率是．14．（3分）如图所示的五角星绕中心点旋转一定的角度后能与自身完全重合，则其旋转的角度至少为度．15．（3分）将抛物线y=2x2的图象先向上平移3个单位，再向右平移4个单位所得的解析式为．16．（3分）如图，Rt△ABC中AC=4，BC=3，绕其中一条线段旋转一周，所得图形的最小表面积是．三、解答题（本题有9个小题，共102分．解答应写出文字说明、证明过程或演算步骤）17．（10分）解方程：x2=3x．18．（10分）如图，方格纸中的每个小方格都是正方形，△ABC的顶点均在格点上，建立平面直角坐标系（1）以原点O为对称中心，画出与△ABC关于原点O对称的△A1B1C1，并写出A1的坐标．（2）将原来的△ABC绕着点B顺时针旋转90°得到△A2B2C2，试在图上画出△A2B2C2的图形．19．（10分）现有形状、大小、颜色完全一样的三张卡片，上面分别标有数字“1”、“2”、“3”，第一次从这三张卡片中随机抽取一张，记下数字后放回；第二次在从这三张卡片中随机抽取一张并记下数字．请用列表或画树状图的方法表示出上述试验所有可能的结果，并求第二次抽取的数字大于第一次抽取的数字的概率．20．（10分）已知一元二次方程x2﹣4x+k=0（1）若这个方程有实数根，求k的取值范围；（2）若此方程有一个根是1，求√k(√27−1)的值．21．（12分）如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，交⊙O于点F．（1）求证：AB=AC；（2）当∠ABC满足什么条件时，AC是⊙O的切线？说明理由．22．（12分）已知二次函数y=x2﹣4x+3的图象交x轴于A，B两点，交y轴于点C．（1）求二次函数的顶点坐标与函数的最值；（2）求△ABC的面积．23．（12分）某市为进一步创建宜居城市，2009年市政府对市区绿化工程投入的资金是2000万元，2011年投入的资金是2420万元，设两年间每年投入资金的年平均增长率相同．（1）求该市对市区绿化工程投入资金的年平均增长率；（2）若该市对市区绿化工程投入资金的年平均增长率保持不变，预计2012年市政府对市区绿化工程投入的资金是多少万元？24．（12分）如图，已知PA、PB切⊙O于A、B两点，连AB，且PA，PB的长是方程x2﹣2mx+3=0的两根，AB=m．试求：（1）⊙O的半径；̂围成图形（即阴影部分）的面积．（2）由PA，PB，AB2012-2013学年广东省广州市从化市九年级（上）期末数学试卷参考答案与试题解析一、选择题：（本大题10个小题，每题3分，共30分，在每小题给出的四个选择项中，只有一项是符合题目要求的，请将答案填在下列表格中）1．（3分）一元二次方程x2=1的解是（）A．x=1 B．x=﹣1 C．x=±1 D．x=0【解答】解：x2=1，开方得：x=±1．故选：C．2．（3分）下面计算正确的是（）A．3+√3=3√3B．√27÷√3=3 C．√2•√3=√5D．√4=±2【解答】解：A、不能合并，故选项错误；B、√27÷√3=√9=3，故选项正确；C、√2⋅√3=√6，故选项错误；D、√4=2，故选项错误．故选：B．3．（3分）下列图形中，既是中心对称又是轴对称的图形是（）A．B．C．D．【解答】解：A、不是轴对称图形，也不是中心对称图形；B、是轴对称图形，不是中心对称图形；C、是轴对称图形，也是中心对称图形；D、是轴对称图形，不是中心对称图形．故选：C．4．（3分）下列事件：①明天会出太阳；②掷一枚硬币，正面向上；③地球绕着太阳转；④打开电视机，正在播足球赛．其中随机事件是（）A．①②B．①③C．①④D．①②④【解答】解：①是随机事件；②是随机事件；③是必然事件；④是随机事件．故选：D．5．（3分）如图，已知AB为⊙O的直径，点C在⊙O上，∠C=15°，则∠BOC的度数为（）A．15°B．30°C．45°D．60°【解答】解：∵OA=OC，∴∠A=∠C=15°；∴∠BOC=2∠A=30°；故选：B．6．（3分）下列对抛物线y=﹣2（x+3）2﹣1描述不正确的是（）A．开口向下B．y有最大值C．对称轴是x=﹣3 D．顶点坐标为（3，﹣1）【解答】解：∵抛物线y=﹣2（x+3）2﹣1中a=﹣2＜0，∴抛物线开口向下，y有最大值，故A、B正确；∵抛物线的解析式为；y=﹣2（x+3）2﹣1，∴抛物线的对称轴是x=﹣3，顶点坐标为（﹣3，﹣1），故C正确，D错误．故选：D．7．（3分）一元二次方程x（x﹣2）=0根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．只有一个实数根D．没有实数根【解答】解：原方程变形为：x2﹣2x=0，∵△=（﹣2）2﹣4×1×0=4＞0，∴原方程有两个不相等的实数根．故选：A．8．（3分）如图，两个同心圆的半径分别为3cm和5cm，弦AB与小圆相切于点C，则AB 的长为（）A．4cm B．5cm C．6cm D．8cm【解答】解：连接OC和OB，∵弦AB与小圆相切，∴OC⊥AB，在Rt△OBC中，BC=√OB2−OC2=√52−32=4，∴AB=2BC=8cm．故选：D．9．（3分）如图，正方形OABC的边长为2，则该正方形绕点O逆时针旋转45°后，B点的坐标为（）A．（2，2）B．（0，2√2）C．（2√2，0）D．（0，2）【解答】解：如图，连接OB，则OB=√OA2+AB2=2√2，绕点O逆时针旋转45°后，B点在y轴正半轴上，坐标为（0，2√2）．故选：B ．10．（3分）如图为二次函数y=ax 2+bx+c （a ≠0）的图象，则下列说法：①a ＞0 ②2a+b=0 ③a+b+c ＞0 ④当﹣1＜x ＜3时，y ＞0其中正确的个数为（ ）A ．1B ．2C ．3D ．4【解答】解：①图象开口向下，能得到a ＜0；②对称轴在y 轴右侧，x=−1+32=1，则有﹣b 2a =1，即2a+b=0； ③当x=1时，y ＞0，则a+b+c ＞0；④由图可知，当﹣1＜x ＜3时，y ＞0．故选：C ．二、填空题（本题共6小题，每小题3分，共18分，请把正确答案填在试卷的空格上）11．（3分）函数y =√x −3中，自变量x 的取值范围是 x ≥3 ．【解答】解：根据题意得：x ﹣3≥0，解得：x ≥3．故答案是：x ≥3．12．（3分）若x 1，x 2是一元二次方程x 2﹣5x+6=0的两个根，则x 1+x 2的值是 5 ；【解答】解：x 1，x 2是一元二次方程x 2﹣5x+6=0的两个根，∴x1+x2=﹣−5=5．113．（3分）有长度分别为2cm，3cm，4cm，7cm的四条线段，任取其中三条能组成三角形的概率是1．4【解答】解：∵长度为2cm、3cm、4cm、7cm的四条线段，从中任取三条线段共有2.3.4，2.3.7，3.4.7，2.4.7四种情况，而能组成三角形的有2、3、4；共有1种情况，所以能组成三角形的概率是1．4．故答案为：1414．（3分）如图所示的五角星绕中心点旋转一定的角度后能与自身完全重合，则其旋转的角度至少为72度．【解答】解：五角星绕中心点旋转一定的角度后能与自身完全重合，则其旋转的角度至少为360=72度．515．（3分）将抛物线y=2x2的图象先向上平移3个单位，再向右平移4个单位所得的解析式为y=2（x﹣4）2+3．【解答】解：依题意可知，原抛物线顶点坐标为（0，0），平移后抛物线顶点坐标为（4，3），又因为平移不改变二次项系数，所以所得抛物线解析式为：y=2（x﹣4）2+3．故答案为：y=2（x﹣4）2+3．16．（3分）如图，Rt△ABC中AC=4，BC=3，绕其中一条线段旋转一周，所得图形的最小π．表面积是845【解答】解：当以AB为轴，则由AC=4，BC=3，由勾股定理得，AB=5，斜边上的高=12，5由几何体是由两个圆锥组成，∴几何体的表面积=12×2×125π×（3+4）=845π， 当以BC 为轴，几何体的表面积=π×4×5+π×42=36π，当以AC 为轴，几何体的表面积=π×3×5+π×32=24π，∴绕其中AB 旋转一周，所得图形的最小表面积是：845π． 故答案为：845π．三、解答题（本题有9个小题，共102分．解答应写出文字说明、证明过程或演算步骤）17．（10分）解方程：x 2=3x ．【解答】解：移项得：x 2﹣3x=0，x （x ﹣3）=0，x=0，x ﹣3=0，解得：x 1=0，x 2=3．18．（10分）如图，方格纸中的每个小方格都是正方形，△ABC 的顶点均在格点上，建立平面直角坐标系（1）以原点O 为对称中心，画出与△ABC 关于原点O 对称的△A 1B 1C 1，并写出A 1的坐标．（2）将原来的△ABC 绕着点B 顺时针旋转90°得到△A 2B 2C 2，试在图上画出△A 2B 2C 2的图形．【解答】解：（1）如图所示，△A 1B 1C 1即为所求三角形，点A 1的坐标是A 1（6，﹣1）；（2）△A 2B 2C 2即为所求作的三角形．19．（10分）现有形状、大小、颜色完全一样的三张卡片，上面分别标有数字“1”、“2”、“3”，第一次从这三张卡片中随机抽取一张，记下数字后放回；第二次在从这三张卡片中随机抽取一张并记下数字．请用列表或画树状图的方法表示出上述试验所有可能的结果，并求第二次抽取的数字大于第一次抽取的数字的概率．【解答】解：画树状图得：∵共有9种等可能的结果，第二次抽取的数字大于第一次抽取的数字的有3种情况， ∴第二次抽取的数字大于第一次抽取的数字的概率为：39=13．20．（10分）已知一元二次方程x 2﹣4x+k=0（1）若这个方程有实数根，求k 的取值范围；（2）若此方程有一个根是1，求 √k(√27−1)的值．【解答】解：（1）这里a=1，b=﹣4，c=k ，由方程有实数根，得到b 2﹣4ac ≥0，即16﹣4k ≥0，解得：k ≤4；（2）将x=1代入方程得：1﹣4+k=0，即k=3，则√k （√27﹣1）=√3×（3√3﹣1）=9﹣√3．21．（12分）如图，AB 是⊙O 的直径，BD 是⊙O 的弦，延长BD 到点C ，使DC=BD ，连接AC ，交⊙O 于点F ．（1）求证：AB=AC ；（2）当∠ABC 满足什么条件时，AC 是⊙O 的切线？说明理由．【解答】（1）证明：连接AD．∵AB是⊙O的直径，∴∠ADB=90°．∵DC=BD，∴AB=AC．（2）解：当∠ABC=45°时，AC是⊙O的切线．理由如下：∵AB=AC，∴∠C=∠ABC=45°，∴∠BAC=90°，又∵AB是⊙O的直径，∴AC是⊙O的切线，故当∠ABC=45°时，AC是⊙O的切线．22．（12分）已知二次函数y=x2﹣4x+3的图象交x轴于A，B两点，交y轴于点C．（1）求二次函数的顶点坐标与函数的最值；（2）求△ABC的面积．【解答】解：（1）配方得：y=x2﹣4x+3=x2﹣4x+4﹣1=（x﹣2）2﹣1，故顶点的坐标是（2，﹣1），故函数的最值为：﹣1；（2）∵二次函数y=x2﹣4x+3的图象交x轴于A，B两点，交y轴于点C．∴0=（x﹣2）2﹣1，解得：x=1或3，则图象与x轴交点为：A（1，0），B（3，0），则图象与y轴交点为：C（0，3），故△ABC的面积为：S=1×2×3=3．223．（12分）某市为进一步创建宜居城市，2009年市政府对市区绿化工程投入的资金是2000万元，2011年投入的资金是2420万元，设两年间每年投入资金的年平均增长率相同．（1）求该市对市区绿化工程投入资金的年平均增长率；（2）若该市对市区绿化工程投入资金的年平均增长率保持不变，预计2012年市政府对市区绿化工程投入的资金是多少万元？【解答】解：（1）设该市对市区绿化工程投入资金的年平均增长率为x，（1分）根据题意得，2000（1+x）2=2420（6分）得x1=0.1=10%，x2=﹣2.1（舍去）（8分）答：该市对市区绿化工程投入资金的年平均增长率为10%．（2）预计2012年投入资金：2420（1+10%）=2662（万元）（12分）答：2012年需投入资金2662万元．24．（12分）如图，已知PA、PB切⊙O于A、B两点，连AB，且PA，PB的长是方程x2﹣2mx+3=0的两根，AB=m．试求：（1）⊙O的半径；̂围成图形（即阴影部分）的面积．（2）由PA，PB，AB【解答】解：（1）连OA，OB，∵PA=PB，（1分）∴△=（﹣2m）2﹣4×3=0，∴m 2=3，m ＞0，∴m=√3，∴x 2﹣2√3x+3=0，∴x 1=x 2=√3，∴PA=PB=AB=√3，∴△ABP 等边三角形，∴∠APB=60°，（3分）∴∠APO=30°，∵PA=√3，∴OA=1；（4分）（2）∵∠AOP=60°，∴∠AOB=120°，S 阴=S 四边形OAPB ﹣S 扇形OAB=2S △AOP ﹣S 扇形OAB=2×12×1×√3﹣120⋅π⋅12360， =√3﹣13π．（8分）25．（14分）如图，已知二次函数图象的顶点坐标为C （1，0），直线y=x+m 与该二次函数的图象交于A 、B 两点，其中A 点的坐标为（3，4），B 点在y 轴上．（1）求m 的值及这个二次函数的关系式；（2）P 为线段AB 上的一个动点（点P 与A 、B 不重合），过P 作x 轴的垂线与这个二次函数的图象交于点E ，设线段PE 的长为h ，点P 的横坐标为x ，求h 与x 之间的函数关系式，并写出自变量x 的取值范围；（3）D 为直线AB 与这个二次函数图象对称轴的交点，在线段AB 上是否存在一点P ，使得四边形DCEP 是平行四边形？若存在，请求出此时P 点的坐标；若不存在，请说明理由．【解答】解：（1）∵点A（3，4）在直线y=x+m上，∴4=3+m．∴m=1．设所求二次函数的关系式为y=a（x﹣1）2．∵点A（3，4）在二次函数y=a（x﹣1）2的图象上，∴4=a（3﹣1）2，∴a=1．∴所求二次函数的关系式为y=（x﹣1）2．即y=x2﹣2x+1．（2）设P、E两点的纵坐标分别为y P和y E．∴PE=h=y P﹣y E=（x+1）﹣（x2﹣2x+1）=﹣x2+3x．即h=﹣x2+3x（0＜x＜3）．（3）存在．解法1：要使四边形DCEP是平行四边形，必需有PE=DC．∵点D在直线y=x+1上，∴点D的坐标为（1，2），∴﹣x2+3x=2．即x2﹣3x+2=0．解之，得x1=2，x2=1（不合题意，舍去）∴当P点的坐标为（2，3）时，四边形DCEP是平行四边形．解法2：要使四边形DCEP是平行四边形，必需有BP∥CE．设直线CE的函数关系式为y=x+b．∵直线CE经过点C（1，0），∴0=1+b，∴b=﹣1．∴直线CE的函数关系式为y=x﹣1．∴{y=x−1y=x2−2x+1得x2﹣3x+2=0．解之，得x1=2，x2=1（不合题意，舍去）∴当P点的坐标为（2，3）时，四边形DCEP是平行四边形．。

2012-2013安阳市九年级上期数学期末测试一、精心选一选（每题3分，共21分）1.下列各图中既是轴对称又是中心对称图形的是【】A B C D2.下列说法正确的是【】A.“明天降雨的概率是80%”表示明天有80%的时间降雨；B.“一批铅笔的废品率为0.1%”表示如果从中抽出一只铅笔肯定不是废品。

C. “彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖。

D．在同一年出生的367名学生中，至少有两人的生日是同一天。

3.两个半径分别是1和3的圆，圆心距离为3，那么两圆的位置关系是【】A.相切B.外离C.内含D.外切4.如图，AB是⊙O的直径，弧BD＝弧BC，∠A＝25°. 则∠BOD的度数为【】A.12.5°B.30°C.40°D.50°5.若方程x2－2x＋m＝0有两个相等的实数根.则m的值为【】A.大于1B.大于等于1C.等于1；D.小于等于16.一个不透明的袋子中装有6个白球，4个黄球和5个红球，则任意摸出一个球是红球的概率是【】A. B. C. D.7.如果有意义，那么x【】A、x≥1B、x≤1C、x＝1 D. 不能确定二、填空题（每小题3分，共21分）10、如图，圆柱形水管内积水的水面宽度AB＝8cm、C为弧AB的中点，圆柱形水管的截面内半径为5 cm，则此时水深CD的值为______________。

11、某商品原价200元，连续两次降价a%后售价为148元，根据题意，可列方程_______________________________。

16、（5分）解方程：(x＋2)2＝5(x＋2)18、（9分）一个不透明的口袋里装有红、黄、绿三种颜色的球（除以颜色不同外，其余都相同）其中红球有2个，黄球有1个，从中里摸出一个球是红球的概率为。

⑴试求袋中绿球的个数；⑵第1次从袋中任意摸出1个球（不放回）。

第2次再任意摸出1个球，请你用画树状图或列表格的方法，求两次都摸到红球的概率。