9.3.3历年真题近十年(尖子生题库)打印版

【拔尖特训】2023-2024学年九年级数学上册尖子生培优必刷题（人教版）专题24.1圆（限时满分培优训练）班级：___________________ 姓名：_________________ 得分：_______________注意事项：本试卷满分100分，试题共23题，其中选择10道、填空6道、解答7道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2022秋•大荔县期末）已知⊙O的半径是3cm，则⊙O中最长的弦长是（）A．3cm B．6cm C．1.5cm D．√3cm2．（2022秋•郯城县校级期末）有下列四种说法：①半径确定了，圆就确定了；②直径是弦；③弦是直径；④半圆是弧，但弧不一定是半圆．其中，错误的说法有（）A．1种B．2种C．3种D．4种3．（2023•怀宁县一模）如图，⊙O的直径AB与弦CD的延长线交于点E，若DE＝OB，∠AOC＝87°，则∠E等于（）A．42°B．29°C．21°D．20°4．（2022秋•郧西县期末）由所有到已知点O的距离大于或等于2，并且小于或等于3的点组成的图形的面积为（）A．4πB．9πC．5πD．13π5．（2022秋•广水市期中）下列说法正确的是（）A．直径是弦，弦是直径B．半圆是弧C．无论过圆内哪一点，只能作一条直径D．直径的长度是半径的2倍6．（2022春•莘县期末）下列说法：①直径是弦；②弦是直径；③半径相等的两个半圆是等弧；④长度相等的两条弧是等弧；⑤半圆是弧，但弧不一定是半圆．正确的说法有（）A．1个B．2个C．3个D．4个7．（2021春•阳谷县期末）已知AB是⊙O的弦，⊙O的半径为r，下列关系式一定成立的是（）A．AB＞r B．AB＜r C．AB＜2r D．AB≤2r̂上的点，连接AD并延长与OB的延长线交于点C，8．（2022•广陵区二模）如图，在扇形AOB中，D为AB若CD＝OA，∠O＝72°，则∠A的度数为（）A．35°B．52.5°C．70°D．72°9．（2021秋•莱阳市期末）东汉初年，我国的《周髀算经》里就有“径一周三”的古率，提出了圆的直径与̂）向右水平拉直（保持M端不动），根据该周长之间存在一定的比例关系．将图中的半圆弧形铁丝（MN古率，与拉直后铁丝N端的位置最接近的是（）A．点A B．点B C．点C D．点D10．（2022秋•南岗区校级月考）如图，在⊙O中，AB为直径，CD⊥AB于C，四边形CDEF是正方形，连接BD，若CO＝3，OF＝1，则BD＝（）A．3√5B．4√5C．13D．2√10二、填空题（本大题共6小题，每小题3分，共18分）请把答案直接填写在横线上11．（2022秋•夏邑县期中）下列说法中正确的有（填序号）．①直径是圆中最大的弦；②长度相等的两条弧一定是等弧；③半径相等的两个圆是等圆；④面积相等的两个圆是等圆．12．（2022秋•新罗区校级期中）如图，⊙O的半径为4cm，∠AOB＝60°，则弦AB的长为cm．13．（2022秋•通榆县期中）如图，在⊙O中，点A在圆内，点B在圆上，点C在圆外，若OA＝3，OC＝5，则OB的长度可能为（写出一个即可）．14．（2022秋•通榆县期中）如图，点B，E在半圆O上，四边形OABC，四边形ODEF均为矩形．若AB＝3，BC＝4，则DF的长为．15．（2021秋•延平区校级月考）如图，点A、D、G、M在半圆上，四边形ABOC、DEOF、HMNO均为矩形，设BC＝a，EF＝b，HN＝c，则a、b、c三者间的大小关系为．16．（2022•望花区模拟）如图，数学知识在生产和生活中被广泛应用．下列实例所应用的最主要的几何知识为：①射击时，瞄准具的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”；②车轮做成圆形，应用了“圆上各点到圆心的距离相等”；③学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的对角线互相垂直平分”；④地板砖可以做成矩形，应用了“矩形对边相等”．上述说法正确的是．（填序号）三、解答题（本大题共7小题，共52分．解答时应写出文字说明、证明过程或演算步骤）17．设AB＝4cm，作出满足下列要求的图形（1）到点A的距离等于3cm，且到点B的距离等于2cm的所有点组成的图形；（2）到点A的距离小于3cm，且到点B的距离小于2cm的所有点组成的图形；（3）到点A的距离大于3cm，且到点B的距离小于2cm的所有点组成的图形．18．（2021秋•崆峒区期末）如图，CD是⊙O的直径，点A在DC的延长线上，∠A＝20°，AE交⊙O于点B，且AB＝OC．（1）求∠AOB的度数．（2）求∠EOD的度数．19．（2022秋•邗江区期中）如图，半圆O的直径AB＝8，半径OC⊥AB，D为弧AC上一点，DE⊥OC，DF⊥OA，垂足分别为E、F，求EF的长．20．（2022秋•朝阳区校级月考）如图，在△ABC中，∠C＝90°，以点C为圆心，BC为半径的圆交AB于点D，交AC于点E．若∠A＝25°，求∠DCE的度数．21．（2021秋•东台市月考）如图，⊙O的半径OC⊥AB，D为BĈ上一点，DE⊥OC，DF⊥AB，垂足分别为E、F，EF＝3，求直径AB的长．22．（2021秋•赣榆区校级月考）已知：如图，BD、CE是△ABC的高，M为BC的中点．试说明点B、C、D、E在以点M为圆心的同一个圆上．23．如图，AB是⊙O的直径，把AB分成几条相等的线段，以每条线段为直径分别画小圆，设AB＝a，那么⊙O的周长L＝πa．（1）计算：①把AB分成两条相等的线段，每个小圆的周长；②把AB分成三条相等的线段，每个小圆的周长L3＝；③把AB分成四条相等的线段，每个小圆的周长L4＝；…④把AB分成n条相等的线段，每个小圆的周长L n＝；（2）请仿照上面的探索方法和步骤，计算并导出：当把大圆直径平均分成n等分时，以每条线段为直径画小圆，那么每个小圆的面积S n与大圆的面积S的关系是：S n＝S．。

初中尖子生试题及答案一、选择题（每题2分，共20分）1. 下列哪个选项是正确的？A. 地球是太阳系中最大的行星B. 地球是太阳系中唯一存在生命的星球C. 月球是地球的卫星D. 火星是太阳系中最大的行星答案：C2. 以下哪种物质不是人体所需的微量元素？A. 铁B. 钙C. 锌D. 钠答案：B3. 以下哪个选项是牛顿第二定律的表达式？A. F=maB. F=G*(m1*m2)/r^2C. p=mvD. E=mc^2答案：A4. 以下哪个选项是光合作用的产物？A. 氧气和水B. 二氧化碳和水C. 氧气和葡萄糖D. 二氧化碳和葡萄糖答案：C5. 以下哪个选项是正确的？A. 所有金属都能导电B. 所有金属都是固体C. 所有金属都有磁性D. 所有金属都是稀有金属答案：A6. 以下哪个选项是正确的？A. 酸雨是由于大气中的二氧化碳造成的B. 酸雨是由于大气中的二氧化硫造成的C. 酸雨是由于大气中的氮气造成的D. 酸雨是由于大气中的氧气造成的答案：B7. 以下哪个选项是正确的？A. 细胞是所有生物体的基本单位B. 病毒不是生物体C. 细胞是所有生物体的最小单位D. 病毒是所有生物体的基本单位答案：A8. 以下哪个选项是正确的？A. 地球的自转周期是24小时B. 地球的公转周期是365天C. 地球的自转周期是365天D. 地球的公转周期是24小时答案：A9. 以下哪个选项是正确的？A. 光年是时间单位B. 光年是长度单位C. 光年是速度单位D. 光年是质量单位答案：B10. 以下哪个选项是正确的？A. 所有植物都能进行光合作用B. 所有动物都能进行光合作用C. 所有植物都不能进行光合作用D. 所有动物都不能进行光合作用答案：D二、填空题（每题2分，共20分）1. 地球的大气层中最外层是________。

答案：散逸层2. 人体最大的器官是________。

答案：皮肤3. 牛顿第三定律表明，作用力和反作用力大小相等，方向________。

九年级数学尖子生题库一、代数部分1. 一元二次方程题目：已知方程公式有两个相等的实数根，求公式的值。

解析：对于一元二次方程公式，判别式公式。

当公式时，方程有两个相等的实数根。

在方程公式中，公式，公式，公式，则公式，即公式，解得公式。

2. 二次函数题目：二次函数公式的图象经过点公式，公式，公式，求这个二次函数的解析式。

解析：把点公式，公式，公式分别代入二次函数公式中，得到方程组公式。

将公式代入后两个方程得公式，两式相加得公式，即公式（不符合公式，舍去）。

重新计算，两式相减得公式，解得公式，把公式，公式代入公式得公式，解得公式（错误）。

重新检查，将公式代入公式，由公式得公式，代入公式得公式，公式，公式，则公式（错误），应该是公式不符合题意，重新计算，将点公式代入公式得公式，把公式和公式代入得公式，把公式和公式代入得公式，两式相加得公式，公式（舍去），两式相减得公式，公式，把公式代入公式得公式（舍去），发现错误，重新开始，将公式代入得公式，把公式代入得公式，把公式代入得公式，两式相加得公式，公式（舍去），重新思考，将公式代入公式得公式，把公式代入公式得公式，把公式代入公式得公式，两式相加得公式，公式（舍去），再次检查，由公式，两式相加公式，公式（错误），应该是两式相加公式，公式不符合题意，重新计算，由公式得公式，代入公式得公式，公式，公式，则公式（错误），正确的是把公式代入公式得公式，把公式代入公式得公式，把公式代入公式得公式，两式相加得公式，公式（舍去），重新开始，把公式代入公式得公式，把公式代入公式得公式，把公式代入公式得公式，两式相加得公式，公式（舍去），重新计算，把公式代入公式得公式，把公式代入公式得公式，把公式代入公式得公式，两式相加得公式，公式（舍去），最后发现，把公式代入公式得公式，把公式代入公式得公式，把公式代入公式得公式，两式相加得公式，公式（舍去），重新思考，将公式代入公式得公式，把公式代入公式得公式，把公式代入公式得公式，两式相加得公式，公式（舍去），重新计算，将公式代入公式得公式，把公式代入公式得公式，把公式代入公式得公式，两式相加得公式，公式（舍去），正确的是：把公式代入公式得公式，把公式代入公式得公式，把公式代入公式得公式，两式相加得公式，公式（舍去），重新计算，将公式代入公式得公式，把公式代入公式得公式，把公式代入公式得公式，两式相加得公式，公式（舍去），重新开始，把公式代入公式得公式，把公式代入公式得公式，把公式代入公式得公式，两式相减得公式，公式，把公式代入公式得公式（错误），重新计算，把公式代入公式得公式，把公式代入公式得公式，把公式代入公式得公式，两式相减得公式，公式，把公式代入公式得公式（错误），正确的是把公式代入公式得公式，把公式代入公式得公式，把公式代入公式得公式，两式相减得公式，公式，把公式代入公式得公式（错误），最后得出公式。

九年级英语中考英语介词专项尖子生必刷卷含答案一、选择题1．—I want to visit Liaoning History Museum. Is it open today?—No. It opens every day ________ Monday.A．except B．till C．between D．after2．— Maybe you should call her up.—But I don’t want to talk with her ________ the phone.A．at B．in C．on D．with3．She was forced to marry ________ her mind to receive the following painful life. A．against B．with C．by D．in4．It is believed that ________ December 21, 1891, the first basketball game in history was played.A．in B．on C．at D．for5．—Why can’t we drive in the emergency lane (应急车道) on expressway?—Because the lane makes it possible to race ________ the clock to save people’s lives. A．beyond B．over C．against D．through 6．Don’t be afraid of difficulties. Remember: kites rise highest ________ the wind, not with it. A．over B．against C．across D．along7．—Hi, Mom directed by Jia ling is a hit ________ this year.—It really is. It shows us the deep love between a mother and a daughter.A．/ B．in C．on D．at8．Some of the technology we’ve seen on sc reen is ________ our ability to create. But that might not be true for long.A．against B．during C．beyond D．through 9．Everyone was touched ________ words after they watched the film Hi, MOM 《你好，李焕英》directed by Jia Ling.A．under B．across C．beyond D．against 10．New York City, also known ________ Big Apple, becomes one of the world’s greatest business and cultural centers.A．as B．by C．for D．to11．— Would you like to visit the zoo with me now?—Sorry, it’s _______ the visiting hours. Let’s go there tomorrow.A．beyond B．through C．during D．on12．If your temperature is_______37.3°, you should go to the doctor instead of going to school. A．above B．against C．under D．below 13．Peter is clever enough to read and write __________ the age of 4.A．between B．at C．to D．during 14．Switzerland lies ________ France, Germany, Austria and Italy.A．between B．among C．against D．beyond 15．—How long have you lived in the new building?—_____2010.A．After B．In C．Since D．Before 16．—How was your trip to Sanya, Aunt Anne?—Fantastic. My baby and I were taken good care of the flight.A．along B．over C．past D．during 17．During the online learning, some parents were too impatient________ their children to solve the problem ________ a proper way.A．in; with B．with; in C．for; in D．to; with18．The blue planet is so far from the earth that radio signals, travel ________ the speed of light, take 16 hours to reach the spacecraft.A．for B．in C．on D．at19．—A serious study of physics is impossible ________ some knowledge of maths.—I couldn’t agree more. So we should also learn maths well.A．among B．between C．against D．without20．—Do you really want to refuse this offer?—I have to. I’m afraid the job is ________ my ability.A．beyond B．beside C．behind D．between21．A study shows that rude languages spoken to children may have bad results that go________ those of beating them.A．against B．beyond C．except D．with22．—My aunt’s 3-year-old daughter can eat a meal with chopsticks.— Really? Most children ________ her age still use spoons.A．of B．in C．on D．for23．—It's reported that Stanley Ho Hung-sun passed away on May 26th at the age of 98.—The whole country felt sad about that. As a successful businessman, his contribution to society and love for the motherland went far ________ his wealth.A．beside B．over C．beyond D．above24．My mum searched ________ the messy books and found my pencil was under a Harry Potter. A．as B．across C．through D．for25．The chopsticks are ________ wood.A．made of B．made from C．made in D．made with 26．The girl is ________ a singer ________ everyone in her hometown.A．well known as; for B．well-know as; toC．well known as; to D．best known for; for27．The girl is _____ a singer _____ everyone in her hometown.A．well known as; for B．well known as; to C．well-know as; to D．best known for; for 28．If success is a gate, the road ________ this gate must be full of difficulties.A．beyond B．opposite C．towards D．across29．My family is always ___________ me no matter what I decide to do. That makes me very pleased.A．above B．behind C．against D．through 30．Because of COVID-19, this summer holiday will begin ________ July 18.A．on B．in C．for D．at31．To our joy, Tom pleased everybody by making his dog walk ________ two legs.A．by B．over C．from D．on32．Bees and butterflies play _______ flowers. Then they hide _______ the April showers. A．among; from B．among; in C．with; in D．with; on 33．Family is always _________ me, so I can follow my dreams with great courage.A．beyond B．forward C．past D．behind34．— What do you think of those smart kids in the game show?— There is no doubt that many of them have a gift ________ maths.A．for B．in C．on D．at35．In the end， Mr Song came up____a good method to solve the problem．A．for B．at C．in D．with36．—We must study hard to enter our ideal high school.—Exactly! Just as President Xi says,“Happiness is achieved ________ hard work.”A．through B．across C．along D．with37．Almost everyone was touched ________ words after they saw Jia Ling’s moving film Hi Mom. A．beyond B．under C．of D．in38．There is a stone bridge ________ the river in front of my house.A．over B．under C．above D．below39．The 20th China Jiangning Hengxi Watermelon Festival was held ________ May this year. A．at B．on C．in D．from40．The rain is beating ________ the windows and Cindy is listening to the rain quietly. A．above B．across C．around D．against 41．—You look frightened, what’s up?— A terrible accident happened this morning. A truck was running fast when an old man was about to cross the road. I bet he will not live ________ the night.A．along B．away C．through D．in42．The ending of the film Diary of Dinosaurs was so surprising and fully went ________ my imagination.A．across B．over C．through D．beyond 43．—How did you get to the zoo, Helen?—I went to the bus station ________ my bike, and took the No. l bus to the zoo.A．on B．by C．in D．with44．— When will Mr. Smith arrive?— ________ September 6th.A．At B．In C．On D．For45．Last week, Oprah Winfrey had an interview ________ Harry and Meghan.A．with B．to C．about D．on46．Sometimes I feel stressed because what my parents want me to do has gone ________ my ability.A．through B．against C．above D．beyond47．I like reading. I often fill my bookshelf ________ all kinds of books, like novels, detective stories, and so on.A．on B．in C．with D．of48．Don’t be afraid of difficulti es. Remember: kites rise highest ________ the wind, not with it. A．against B．above C．across D．along 49．—Thanks for looking after me ________ my illness, Millie.—Don’t mention it. That’s what friends are for.A．beyond B．through C．across D．with50．The story The Ugly Duckling ________ Hans Christian Andersen has remained popular among children for centuries.A．in B．on C．by D．with二、选择题51．—The Civil Code (民法典) ________ to be a big success and it is a milestone in our country legal science.—I can’t agree mor e.A．turns out B．puts out C．takes out D．breaks out52．A survey about why teenagers like bilibili so much was ________ here last week. A．taken out B．carried out C．turned out D．worked out 53．—Dad，would you please____a brighter light in my bedroom？—Certainly．A．put in B．hand out C．hand in D．put out54．A big fire ________ in a factory last month. It is important for us to be careful with fire. A．put out B．turned out C．got out D．broke out55．A forest fire ________ in September in Australia last year and many rare animals lost their lives in it.A．turned out B．broke out C．put out D．worked out 56．—Amy, how many of your classmates have brothers or sisters?—Believe it or not, it ________ to be one quarter.A．takes out B．breaks out C．turns out D．finds out 57．Sometimes results will just ________ opposite of our wish. We need to accept them anyway. A．carry out B．break out C．run out D．turn out 58．This bus doesn’t go to the train station. I am afraid you will have to ________ at the next stop and take BRT Line 1.A．get out B．get off C．get through D．get down 59．—What happened, Martin?—Last night, someone ________ my house and stole many valuable things.A．broke into B．broke down C．turned into D．turned down 60．The workers ________ a sign to warn people of the danger here.A．put out B．put in C．put up D．put on61．It’s rude and impolite to ________ before others while everyone is queuing to buy tickets. A．take in B．cut in C．put in D．break in62．A society cannot be successful if it ________ tradition, but it cannot be successful either if we do something to stop progress.A．takes away B．throws away C．gets away D．puts away 63．Scientists need to ________ several surveys before making a conclusion.A．give up B．carry out C．hear of D．look for 64．—What can I do for you, Linda?—I hope you can help me ________ the useless words in my article.A．make up B．cut out C．turn off D．put up65．—I ________ reading English every morning.—Yes, English is very important and it ________ the first language in England and some other countries.A．used to; is used by B．used to; is used asC．am used to; is used as D．am used to; is used by66．Judy waited a long time for her mom, but she didn't ________.A．show up B．get up C．wake up D．stay up 67．There’s no doubt the Belt and Road will successfully ________ cooperation and development between China and other countries along the line.A．push for B．care for C．look for D．hope for 68．—Hello, this is Taicang Middle School.—I want to talk to Mr. Chen. Can you ________ me ________?A．put…in B．put…out C．put…through D．put…up 69．—Who’s going to ________ the children while you are away?—Don’t worry. My mum will come.A．look at B．look around C．look after D．look like 70．Most boys ________ toy guns while girls ________ have dolls.A．would rather; prefer B．prefer; would ratherC．would rather; would rather D．prefer; prefer71．The director of Up series passed away, and the workmates are thinking about whether the documentary can ________ without him.A．carry on B．carry out C．take on D．take out 72．My sister seldom spends time on TV or computer at weekends because reading ________ most of her free time.A．takes on B．takes up C．takes away D．takes off 73．There is no doubt that the United Nations will continue to ________ building a community with a shared future for mankind.A．look for B．care for C．hope for D．push for 74．When you are given a difficult task, try to ________ it and finish it.A．join in B．stick with C．search for D．think of 75．—I’m sorry to ________ on you, but there is something I don’t understand.—It doesn’t mat ter.A．cut down B．cut out C．cut in D．cut off76．—In order to improve my English, I have already made a detailed plan.—Great! I think all you need to do next is _________.A．pick it out B．carry it out C．find it out D．point it out 77．Much to everyone’s surp rise, Hi, Mom ________ to be a biggest hit.A．turns out B．puts out C．carries out D．breaks out 78．The job ________ to be harder than they thought.A．found out B．turned out C．ran out D．worked out 79．Andrew once tried to ________ a brighter light in his bedroom, but he failed in the end. A．put on B．put in C．put out D．put up 80．—Oh, my God! I have ________ 5 pounds!—No worries. It’s normal for a growing teenager.A．put up B．put down C．put on D．put off81．－Oh,my God! I have ________ five pounds!－No worries. It’s normal for a growing teenage girl.A．put up B．put down C．put on D．put off82．Do you think it is necessary to ________ a special home for the elderly with life difficulties. A．set out B．set up C．set down D．set off 83．—Many students don’t know how to ________ stress and become worried.—I think they’d better ask their teachers for help.A．argue with B．come up with C．deal with84．Such lovely weather! Let's _________ the tent near the lake.A．build up B．put up C．put in D．build in 85．—________ at these three years in junior high, which teacher will you miss most?—Mr. Zhang. His classes are always interesting and lively.A．Looking back B．Looking around C．Looking up D．Looking for86．I really shouldn't have shouted at my parents like that, but .A．it was none of your business B．I just couldn't help itC．I didn't care about it D．I couldn't agree more87．I know how busy you must be and naturally I wouldn’t want to ________ too much of your time.A．take on B．take away C．take up D．take off88．My brother often _________ his spare time to help me with my spoken English.A．puts up B．gives up C．opens up D．tidies up89．Jane is such a confident girl that she believes she can ________ the hard task alone. A．carry out B．turn out C．pick out D．give out 90．Every time a serious disease ________, city planners will come up with new ideas to fight it. A．breaks down B．breaks out C．breaks into D．breaks up 91．Daniel, stop playing computer games, please! It has ________ your free time too much. A．turned up B．picked up C．put up D．taken up92．I know how busy you must be and naturally I wouldn’t want to ________ too much of your time.A．put up B．take up C．give up D．make up93．Life is full of ups and downs. When your friends are unhappy, tell them something funny and encourage them to ________.A．put up B．cheer up C．stay up D．give up94．A new high-speed railway station ________ Taixing ________ Shanghai will be built soon. A．connecting; to B．connected; to C．connects; with D．connected; and 95．—Your spoken English is very good. How do you improve it?—Thanks. Mrs. Wang always asks us to ________ dialogues in our English classes and practice speaking English as often as possible.A．take up B．make up C．put up D．mop up 96．—Who is the best basketball player in your class?—Daniel. And he takes any chance to ________ his sports skills to girls.A．take off B．turn off C．fall off D．show off97．I know how busy you must be and I wouldn’t want to ________ too much of your time. A．put up B．take up C．set up D．make up 98．—Have you made a plan to raise money to protect the animals in danger?—Yes. Now we are thinking about how to ________.A．pick it out B．carry it out C．find it out D．put it out 99．The baby is sleeping. Would you please ________?A．turned the radio on B．turn the radio downC．turned the radio off D．turn the radio up100．Based on local cultures and museums, schools should develop local courses ________ art, history, geography, and biology.A．led to B．taken on C．chosen from D．connected with 【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【详解】句意：——我想去参观辽宁历史博物馆。

小学尖子生测试卷及答案数学卷（包括三道大题，14道小题，时间60分钟，满分80分．）一、填空题Ⅰ（本道大题包含5道小题，每道小题4分）1. 计算：111111+12222323333434491010++++⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=________。

2. 有30个数：1.64, 1.64+130，1.64+230，……1.64+2930。

如果取每个数的整数部分，并将这些整数相加，那么，这些整数之和是_______。

3. 某次数学竞赛原定一等奖10人，二等奖20人，现在将一等奖中最后4人调整为二等奖，这样，得二等奖的学生平均分提高了1分，得一等奖的学生的平均分提高了3分。

那么，原来一等奖平均分比二等奖平均分多______分。

4. 在一条公路上，甲、乙两个地点相距600米，张明每小时行走4千米，李强每小时行走5千米。

8点整，他们两人从甲、乙两地同时出发相向而行，1分钟后他们都调头反向而行，再过3分钟，他们又调头相向而行，依次按照1、3、5、7……（连续奇数）分钟数调头行走。

那么，张、李两个人相遇时是8点_________分。

5. 某班在一学年中组织了三次郊游活动，有70％的学生参加了第一次郊游，80％的同学参加了第二次郊游，90％的同学参加了第三次郊游，有l2人这三次郊游都参加了，全班每人至少参加两次。

这个班有_________学生。

二、填空题Ⅱ（本道大题包含7道小题，前面每道小题6分，第12题8分）6. 在自然数中恰有4个因数的所有两位数的个数是 个。

7. 甲、乙两个盒子共装了400多个球，如果甲给乙x 个，则甲比乙少196；如果乙给甲x 个，则乙比甲少176；则x =____________。

8. 一方有难，八方支援，武汉市红十字会决定由甲、乙两个服装厂生产同一规格的成衣送往灾区。

现知每个厂的人员和设备都能全力进行上衣和裤子的生产。

但是各厂的特点不同，甲厂每月用53的时间生产上衣，52的时间生产裤子，每月生产900套成衣；乙厂每月用74的时间生产上衣，73的时间生产裤子，每月生产1200套成衣。

【拔尖特训】2023-2024学年九年级数学上册尖子生培优必刷题（人教版）专题24.4圆周角（限时满分培优训练）班级：___________________ 姓名：_________________ 得分：_______________注意事项：本试卷满分100分，试题共23题，其中选择10道、填空6道、解答7道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2022秋•普兰店区期末）如图，AB是⊙O的直径，AC、BC是⊙O的弦，若∠A＝30°，则∠B的度数为（）A．70°B．90°C．40°D．60°2．（2022秋•从化区期末）如图，AB是⊙O的直径，若AC＝4，∠D＝60°，则BC的长等于（）A．8B．10C．2√3D．4√33．（2022秋•新乡期末）下列语句中不正确的有（）①平分弦的直径垂直于弦；②相等的圆心角所对的弧相等；③长度相等的两条弧是等弧；④圆是轴对称图形，任何一条直径都是它的对称轴；⑤圆内接四边形的对角互补；⑥在同圆或等圆中，如果两条弦相等，那么他们所对的圆周角相等．A．5个B．4个C．3个D．2个4．（2023•新疆一模）如图，AB是⊙O的直径，AC为弦，∠BAC＝25°，在⊙O上任取一点D，且点D与点C位于直径AB的两侧，连接AD和DC，则∠D的度数是（）A．50°B．60°C．65°D．75°5．（2023•南关区校级模拟）如图，一块直角三角板的30°角的顶点P落在⊙O上，两边分别交⊙O于A，B两点，连结AO，BO，则∠AOB的度数是（）A．30°B．60°C．80°D．90°6．（2022秋•增城区校级期末）如图，∠DCE是⊙O内接四边形ABCD的一个外角，若∠DCE＝82°，那么∠BOD的度数为（）A．160°B．162°C．164°D．170°7．（易错题）（2023•岷县校级三模）如图，在⊙O中，AB是直径，弦AC＝5，∠BAC＝∠D．则AB的长为（）A．5B．10C．5√2D．10√2̂=AD̂，AD、BC的延长线相交8．（易错题）（2023•梁溪区模拟）如图，已知四边形ABCD内接于⊙O，AB于点E，AF为直径，连接BF．若∠BAF＝32°，∠E＝40°，则∠CBF的度数为（）A．16°B．24°C．12°D．14°9．（易错题）（2023•全椒县三模）如图是以O为圆心，AB为直径的圆形纸片，点C在⊙O上．将该纸片沿直线CO对折，点B落在⊙O上的点D处（不与点A重合），连接CB，CD，AD．设CD与直径AB交于点E，若AD＝ED，则∠B的度数为（）A．24°B．30°C．36°D．44°10．（易错题）（2021•武汉）如图，AB是⊙O的直径，BC是⊙O的弦，先将BĈ沿BC翻折交AB于点D，̂沿AB翻折交BC于点E．若BÊ=DÊ，设∠ABC＝α，则α所在的范围是（）再将BDA．21.9°＜α＜22.3°B．22.3°＜α＜22.7°C．22.7°＜α＜23.1°D．23.1°＜α＜23.5°二、填空题（本大题共6小题，每小题3分，共18分）请把答案直接填写在横线上11．（2023•武侯区校级模拟）如图，四边形ABCD是⊙O的内接四边形，对角线BD过点O，若∠ABD＝65°，则∠ACB的度数为°．12．（2022秋•西岗区校级期末）如图，在⊙O中，弦BC＝2，点A是圆上一点，且∠BAC＝30°，则⊙O 的半径是．13．（2023•武侯区模拟）半径为3cm的⊙O中有长为3√3的弦AB，则弦AB所对的圆周角为．14．（2023•宁夏）如图，四边形ABCD内接于⊙O，延长AD至点E，已知∠AOC＝140°那么∠CDE ＝°．15．（易错题）（2023•丹徒区二模）如图，菱形ABCD的顶点A、D都在⊙O上，且∠OAD＝12°，设AC 与⊙O交于点E，则∠AEB的度数是．16．（易错题）（2021秋•海陵区校级月考）如图，半径为3的⊙O中，弦AB∥CD，∠AOC＝90°，设AB ＝a，CD＝b，则a2+b2＝．三、解答题（本大题共7小题，共52分．解答时应写出文字说明、证明过程或演算步骤）17．（2022秋•淮阴区月考）如图，在⊙O的内接四边形ABCD中，∠BAD＝60°，∠ACB＝70°．求∠BCD 和∠ABD的度数．18．（2022秋•泗阳县期中）如图，AB是⊙O的直径，D是弦AC的延长线上一点，且CD＝AC，DB的延长线交⊙O于点E，CD与CE相等吗？为什么？19．（易错题）（2022秋•滨湖区校级期中）如图，在⊙O中，直径AB与弦CD相交于点P，∠CAB＝45°，∠APD＝75°．（1）求∠B的大小；（2）已知圆心O到BD的距离为3，求AD的长．20．（易错题）（2023•新会区二模）如图，点A、B、C在⊙O上，BC是直径，∠ABC的角平分线BD与⊙O 交于点D，与AC交于点M，且BM＝MD，连接OD，交AC于点N．（1）证明：OD⊥AC；（2）试猜想AB与OD之间的数量关系，并证明．21．（2023•浚县三模）如图，四边形ABCD是⊙O的内接四边形，且对角线BD经过⊙O的圆心O，过点A 作AE⊥CD，与CD的延长线交于点E，且DA平分∠BDE．（1）求证：∠ABO＝∠EAD；（2）若⊙O的半径为5，CD＝6，求AD的长．22．（易错题）（2023春•南岗区校级月考）在圆⊙O中，AB为弦（不是直径），K为弧AB的中点，C为优弧AB上一点，连接KC交AB于M（1）如图1，作直径CT，连接KT，求证：∠KTC＝∠KMB；（2）如图2，作直径AD交KC于N，若∠ADC＝45°，求证：AN＝AM．23．（培优题）（2021秋•东区期末）如图，四边形ABCD内接于⊙O，AC为直径，AC和BD交于点E，AB ＝BC．（1）求∠ADB的度数；（2）过B作AD的平行线，交AC于F，试判断线段EA，CF，EF之间满足的等量关系，并说明理由．。

一、选择题（每题3分，共30分）1. 下列各数中，绝对值最小的是（）A. -2B. 2C. 0D. -3答案：C2. 若a > b，则下列不等式中正确的是（）A. a + 1 > b + 1B. a - 1 > b - 1C. a + 2 > b + 2D. a - 2 > b - 2答案：A3. 已知函数f(x) = 2x - 3，则f(-1)的值为（）A. -1B. 1C. 2D. 3答案：A4. 在直角坐标系中，点P(2, 3)关于x轴的对称点坐标是（）A. (2, -3)B. (-2, 3)C. (2, 3)D. (-2, -3)答案：A5. 已知等腰三角形ABC中，AB = AC，且底边BC = 6cm，则腰AB的长度为（）A. 3cmB. 4cmC. 5cmD. 6cm答案：C6. 若等差数列{an}的首项为2，公差为3，则第10项an的值为（）A. 25B. 28C. 31D. 34答案：B7. 下列函数中，在定义域内单调递增的是（）A. y = x^2B. y = 2xC. y = -xD. y = x^3答案：B8. 已知圆的半径为r，则其直径的长度为（）A. rB. 2rC. r^2D. 4r答案：B9. 若a、b、c为等比数列，且a + b + c = 12，abc = 27，则b的值为（）A. 3B. 6C. 9D. 12答案：B10. 在平面直角坐标系中，直线y = 2x + 1与y轴的交点坐标为（）A. (0, 1)B. (1, 0)C. (0, -1)D. (-1, 0)答案：A二、填空题（每题3分，共30分）11. 若a > b，则a - b的符号为（）答案：正12. 函数f(x) = 3x^2 - 2x + 1的顶点坐标为（）答案：（1/3，-2/3）13. 已知等差数列{an}的前三项分别为1，4，7，则第10项an的值为（）答案：2914. 在直角三角形ABC中，∠C = 90°，AB = 5cm，BC = 3cm，则AC的长度为（）答案：4cm15. 若等比数列{an}的首项为3，公比为2，则第5项an的值为（）答案：9616. 已知函数f(x) = x^2 - 4x + 3，则f(2)的值为（）答案：-117. 在平面直角坐标系中，点P(3, 4)关于原点的对称点坐标是（）答案：（-3，-4）18. 若a、b、c为等差数列，且a + b + c = 18，abc = 27，则b的值为（）答案：319. 下列函数中，在定义域内单调递减的是（）答案：y = -x20. 已知圆的半径为r，则其周长的长度为（）答案：2πr三、解答题（每题10分，共40分）21. 解一元二次方程：x^2 - 5x + 6 = 0答案：x1 = 2，x2 = 322. 已知等差数列{an}的首项为3，公差为2，求前n项和Sn答案：Sn = n(3 + 2n - 1)/223. 已知函数f(x) = 2x + 1，求f(-3)的值答案：f(-3) = -524. 在平面直角坐标系中，直线y = 3x - 2与y轴的交点坐标是（），求该直线与x轴的交点坐标答案：交点坐标为（2/3，-2），与x轴的交点坐标为（2/3，0）。

20202021学年九年级数学下册尖子生同步培优题典【人教版】 专题27.6位似姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分100分，试题共24题，其中选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2020•河北模拟）如图，平面直角坐标系xOy 中，点A 、B 的坐标分别为（4，0）、（2，﹣3），△AB ′O ′是△ABO 关于点A 的位似图形，且O '的坐标为（﹣2，0），则点B '的坐标为（ ）A ．（1，﹣5）B ．（32，﹣5）C ．（1，−92）D ．（32，−92） 2．（2019秋•河北区期末）平面直角坐标系中，点E （﹣4，2），F （﹣1，﹣1），以原点O 为位似中心，把△EFO 缩小为△E ′F ′O ，且△E ′F ′O 与△EFO 的相似比为1：2，则点E 的对应点E ′的坐标为（ ）A ．（2，﹣1）B ．（8，﹣4）C ．（2，﹣1）或（﹣2，1）D ．（8，﹣4）或（﹣8，4）3．（2020•重庆）如图，在平面直角坐标系中，△ABC 的顶点坐标分别是A （1，2），B （1，1），C （3，1），以原点为位似中心，在原点的同侧画△DEF ，使△DEF 与△ABC 成位似图形，且相似比为2：1，则线段DF 的长度为（ ）A ．√5B ．2C ．4D ．2√54．（2019•无锡模拟）如图，在平面直角坐标系中，△ABC 与△A 1B 1C 1是以点P 为位似中心的位似图形，且顶点都在格点上，则点P 的坐标为（ ）A ．（﹣4，﹣3）B ．（﹣3，﹣4）C ．（﹣3，﹣3）D ．（﹣4，﹣4）5．（2018•潍坊）在平面直角坐标系中，点P （m ，n ）是线段AB 上一点，以原点O 为位似中心把△AOB 放大到原来的两倍，则点P 的对应点的坐标为（ ）A ．（2m ，2n ）B ．（2m ，2n ）或（﹣2m ，﹣2n ）C ．（12m ，12n ） D ．（12m ，12n ）或（−12m ，−12n ） 6．（2020春•永年区期末）在平面直角坐标系中，A （1，2），B （4，6），若把线段AB 扩大2倍得线段A 'B '，若A ′（2，4），则B ′的坐标可以是（ ）A ．（2，3）B ．（3，2）C ．（8，12）D ．（12，8）7．（2020•长葛市一模）如图，已知△ABC 与△DEF 位似，位似中心为点O ，且△ABC 的面积等于△DEF 面积的49，则AO ：AD 的值为（ ）A ．2：3B ．2：5C ．4：9D ．4：138．（2019•娄底模拟）如图，四边形ABCD 与四边形EFGH 位似，位似中心点是O ，OEEA =34，则FG BC 的值为（ ）A ．34B ．43C ．37D ．47 9．（2020•渝北区自主招生）如图，在平面直角坐标系中，已知点A （﹣2，1），B （﹣1，2），以原点O 为位似中心，相似比为2，把△ABO 放大，则点B 的对应点B ′的坐标是（ ）A ．（﹣4，2）B ．（﹣2，4）C ．（﹣4，2）或（﹣2，4）D ．（﹣2，4）或（2，﹣4）10．（2019春•招远市期末）如图，以某点为位似中心，将△OAB 进行位似变换得到△DFE ，若△OAB 与△DFE 的相似比为k ，则位似中心的坐标与k 的值分别为（ ）A ．（2，2），2B ．（0，0），2C ．（2，2），12D ．（0，0），12二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上11．（2019•滨州）在平面直角坐标系中，△ABO 三个顶点的坐标分别为A （﹣2，4），B （﹣4，0），O （0，0）．以原点O 为位似中心，把这个三角形缩小为原来的12，得到△CDO ，则点A 的对应点C 的坐标是 ．12．（2020•兰州）如图，四边形ABCD 与四边形A ′B ′C ′D ′位似，位似中心为点O ，OC ＝6，CC ′＝4，AB ＝3，则A ′B ′＝ ．13．（2020•苏家屯区一模）如图，△ABC 与△DEF 位似，位似中心为点O ，且BC ：EF ＝3：2，则S △ABC ：S △DEF ＝ ．14．（2019秋•沈河区期末）如图，在平面直角坐标系中，线段AB 两个端点的坐标分别为A （2.5，5），B （5，0），以坐标原点为位似中心，将线段AB 在第一象限内缩小得到线段CD ，其中点A 对应点C ，点B 对应点D ，若点C 的坐标为（1.25，2.5），则点D 的坐标为 ．15．（2019秋•铁西区期末）如图，在边长为1的正方形网格中，两个三角形的顶点都在小正方形的顶点，且两个三角形是位似图形，点O 和点P 也在小正方形的顶点，则这两个三角形的位似中心是点 ．16．（2020春•海淀区校级期末）如图，在直角坐标系中，矩形OABC 的顶点O 在坐标原点，边OA 在x 轴上，OC 在y 轴上，且OA ＝8，OC ＝6，点B 在第二象限，如果矩形OA ′B ′C ′与矩形OABC 关于点O 位似，且矩形OA ′B ′C ′的面积等于矩形OABC 面积的14．那么点B ′的坐标是 ．17．（2020秋•松江区月考）如果两个三角形不仅是相似三角形，而且每组对应点的连线交于一点，那么这两个三角形叫做位似三角形，这个点叫做位似中心．如图，△ABC 和△A 1B 1C 1是以点O 为位似中心的位似三角形，若C 1为OC 的中点，AB ＝4．则A 1B 1的长为 ．18．（2020•郴州）在平面直角坐标系中，将△AOB 以点O 为位似中心，23为位似比作位似变换，得到△A 1OB 1，已知A （2，3），则点A 1的坐标是 ．三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）19．（2019秋•来宾期末）如图，已知O 是坐标原点，AB 两点的坐标分别为（3，﹣1），（2，1）．（1）以点O 为位似中心，在y 轴的左侧将△OAB 放大2倍；（2）分别写出A ，B 两点的对应点A '，B '的坐标．20．（2019秋•西城区期末）如图，△ABO 三个顶点的坐标分别为A （﹣2，4），B （﹣4，0），O （0，0），以原点O 为位似中心，画出一个三角形，使它与△ABO 的相似比为12．21．（2018秋•苏州期末）如图，在正方形网格纸中，△ABC 的三个顶点都在格点上．以点O 为位似中心，把△ABC 按相似比2：1放大，得到对应的△A 'B 'C '．（1）请在第一象限内画出△A 'B 'C '；设D （a ，b ）为线段AC 上一点，则点D 经过上述变换后得到的对应点D '的坐标为 （用含a 、b 的式子表示）；（2）△A 'B 'C '的面积为 ．22．（2019秋•唐山期末）如图，BD，AC相交于点P，连结AB，BC，CD，DA，∠DAP＝∠CBP．（1）求证：△ADP∽△BCP；（2）直接回答△ADP与△BCP是不是位似图形？（3）若AB＝8，CD＝4，DP＝3，求AP的长．23．（2016•盐城）如果两个一次函数y＝k1x+b1和y＝k2x+b2满足k1＝k2，b1≠b2，那么称这两个一次函数为“平行一次函数”．如图，已知函数y＝﹣2x+4的图象与x轴、y轴分别交于A、B两点，一次函数y＝kx+b与y＝﹣2x+4是“平行一次函数”（1）若函数y＝kx+b的图象过点（3，1），求b的值；（2）若函数y＝kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形，位似中心为原点，位似比为1：2，求函数y＝kx+b的表达式．24．（2020•如皋市一模）如图，△ABC中，P′是边AB上一点，四边形P'Q'M'N'是正方形，点Q'，M在边BC上，点N′在△ABC内．连接BN′，并延长交AC于点N，过点N作NM⊥BC于点M，NP⊥MN交AB于点P，PQ⊥BC于点Q．（1）求证：四边形PQMN为正方形；（2）若∠A＝90°，AC＝1.5m，△ABC的面积＝1.5m2．求PN的长．。

六年级下学期第一单元尖子生检测题姓名一、填空欢乐谷（每空 2 分，共 32 分）1.一个圆柱形钢棒，底面直径为 6 厘米，高是10 厘米，它的侧面积是（）平方厘米，表面积是（）平方厘米，体积是（）立方厘米，与它等底等高的圆锥体体积是（）立方厘米。

2.把一张长 6 分米，宽 3 分米的长方形纸片卷成一个圆柱，并把圆柱直立在桌子上，它的最大容积是（）。

（π取 3）3.一个圆柱体沿着底面的一条直径竖直切开，表面积增加了40 平方厘米，已知这个圆柱体的高是 10 厘米，它的体积是（）立方厘米。

4.一个正方体棱长12 厘米，把它削成一个最大的圆柱，圆柱的体积是（）立方厘米，再把这个圆柱削成一个最大的圆锥，圆锥的体积是（）立方厘米。

5.把一个棱长为 a 的正方体木块削成一个最大的直圆柱，将削去原来的（） %。

6.某圆锥的体积是12.56 立方分米，高是 3 分米，底面积是（）平方分米。

7.把一个圆柱体削成一个最大的圆锥体，削去部分是这个圆锥体体积的（）倍。

8.把一个圆柱的侧面展开得到一个正方形，这个正方形的边长是12.56 厘米，圆柱的表面积是（）平方厘米。

9.一个圆柱体和一个圆锥体等底等高，圆柱体的体积和圆锥体的体积和32 立方厘米，圆锥体的体积是（）立方厘米。

10.用边长 5 分米的正方形围成一个圆柱，这个圆柱的侧面得是（）平方分米，它的底面周长是（）分米，它的体积用含有π的式子表示是（）。

二、判断快车（每题 2 分，共 14 分）1.圆柱的体积是圆锥体积的 3 倍。

-------------------------------------------------------------- （）2.圆柱的高有无数条，圆锥的高也有无数条。

----------------------------------------------- （）3.圆柱的底面半径扩大到原来的2 倍，高不变，它的侧面积就扩大到原来的 4 倍。

九年级尖子生选拔数学试题本试卷共13页，满分120分，考试时间120分钟，考生请将卷Ⅰ的答案转涂到答题卡上。

卷Ⅰ（选择题,共33分）一、精心选一选，慧眼识金!（每小题3分，共33分)1。

如图，下列图形都是由面积为1的正方形按一定的规律组成，其中，第(1）个图形中的正方形有2个,第(2）个图形中面积为1的正方形有5个,第（3）个图形中面积为1的正方形有9个，……，按此规律，则第(6）个图形中面积为1的正方形的个数为( ）A.20 B。

27 C。

35 D.402。

观察下列一组图形中点的个数，其中第1个图片共有4个点，第2个图中共有10个点，第3个图中共有19个点，…按此规律第5个图中共有点的个数是（)A.31 B。

46 C.51 D.66 3。

下列图形都是按照一定规律组成，第一个图形中共有2个三角形,第二个图形中共有8个三角形,第三个图形中共有14个三角形，……，依此规律，第五个图形中三角形的个数是( )A。

22 B.24 C。

26 D。

28 4。

如图,将n个边长都为2的正方形按照如图所示摆放，点A1，A2，…，A n分别是正方形的中心，则这n个正方形重叠部分的面积之和是（）A。

n B。

n—1 C。

（14）n-1 D。

14n5. 如图，四边形ABCD中，AC=a,BD=b，且AC⊥BD，顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2,如此进行下去，得到四边形A n B n C n D n。

下列结论正确的是（)①四边形A4B4C4D4是菱形；②四边形A3B3C3D3是矩形；③四边形A7B7C7D7周长为8a b+；④四边形A nB nC nD n面积为·2na b.A。

①②③ B.②③④ C.①③④ D.①②③④6. 如图，已知A1、A2、……、A n、A n＋1是x轴上的点，且OA1＝A1A2＝A2A3＝……＝A n A n＋1＝1，分别过点A1、A2、……、A n、A n＋1作x轴的垂线交直线y＝2x于点B1、B2、……、B n、B n＋1,连接A1B2、B1A2、A2B3、B2A3、……、A n B n＋1、B n A n＋1，依次相交于点P1、P2、P3、……、P n，△A1B1P1、△A2B2P2、……、△A n B n P n的面积依次为S1、S2、……、S n，则S n为（)A.121nn++B.231nn-C。

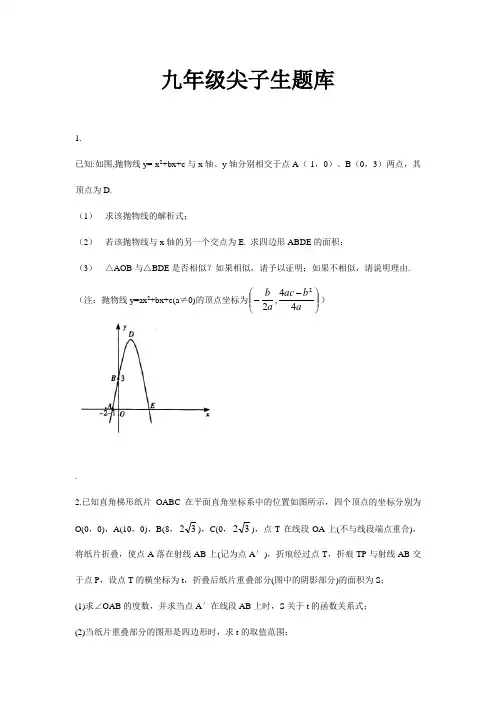
九年级尖子生题库1.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D.（1） 求该抛物线的解析式；（2） 若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积；（3） △AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a bac a b 44,22）.2.已知直角梯形纸片OABC 在平面直角坐标系中的位置如图所示，四个顶点的坐标分别为O(0，0)，A(10，0)，B(8，32)，C(0，32)，点T 在线段OA 上(不与线段端点重合)，将纸片折叠，使点A 落在射线AB 上(记为点A ′)，折痕经过点T ，折痕TP 与射线AB 交于点P ，设点T 的横坐标为t ，折叠后纸片重叠部分(图中的阴影部分)的面积为S ； (1)求∠OAB 的度数，并求当点A ′在线段AB 上时，S 关于t 的函数关系式； (2)当纸片重叠部分的图形是四边形时，求t 的取值范围；(3)S 存在最大值吗？若存在，求出这个最大值，并求此时t 的值；若不存在，请说明理由.3. （08浙江温州）如图，在Rt ABC △中，90A ∠=，6AB =，8AC =，D E ，分别是边AB AC ，的中点，点P 从点D 出发沿DE 方向运动，过点P 作PQ BC ⊥于Q ，过点Q 作QR BA ∥交AC 于 R ，当点Q 与点C 重合时，点P 停止运动．设BQ x =，QR y =．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）；（3）是否存在点P ，使PQR △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．xOATxOAT4.在△ABC 中，∠A ＝90°，AB ＝4，AC ＝3，M 是AB 上的动点（不与A ，B 重合），过M 点作MN ∥BC 交AC 于点N ．以MN 为直径作⊙O ，并在⊙O 内作内接矩形AMPN ．令AM ＝x ．（1）用含x 的代数式表示△ＭNP 的面积S ； （2）当x 为何值时，⊙O 与直线BC 相切？（3）在动点M 的运动过程中，记△ＭNP 与梯形BCNM 重合的面积为y ，试求y 关于x 的函数表达式，并求x 为何值时，y 的值最大，最大值是多少？5、如图1，已知双曲线y=xk(k>0)与直线y=k ′x 交于A ，B 两点，点A 在第一象限.试解答下列问题：(1)若点A 的坐标为(4，2).则点B 的坐标为 ；若点A 的横坐标为m ，则点B 的坐标可表示为 ；（2）如图2，过原点O 作另一条直线l ，交双曲线y=xk(k>0)于P ，Q 两点，点P 在第一象限.①说明四边形APBQ 一定是平行四边形；②设点A.P 的横坐标分别为m ，n ，四边形APBQ 可能是矩形吗?可能是正方形吗?若可能，直接写出mn 应满足的条件；若不可能，请说明理由.A BC D ER P H QB图 1BD 图 2P图 36.如图1，在平面直角坐标系中，己知ΔAOB 是等边三角形，点A 的坐标是(0，4)，点B 在第一象限，点P 是x 轴上的一个动点，连结AP ，并把ΔAOP 绕着点A 按逆时针方向旋转.使边AO 与AB 重合.得到ΔABD.（1）求直线AB 的解析式；（2）当点P 运动到点（3，0）时，求此时DP 的长及点D 的坐标；（3）是否存在点P ，使ΔOPD 的面积等于43，若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由.7.如图1，四边形ABCD 是正方形，G 是CD 边上的一个动点(点G 与C 、D 不重合)，以CG 为一边在正方形ABCD 外作正方形CEFG ，连结BG ，DE ．我们探究下列图中线段BG 、线段DE 的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG 、线段DE 的长度关系及所在直线的位置关系；②将图1中的正方形CEFG 绕着点C 按顺时针(或逆时针)方向旋转任意角度 ，得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断．（2）将原题中正方形改为矩形（如图4—6），且AB=a，BC=b，CE=ka，CG=kb (a≠b，k>0)，第(1)题①中得到的结论哪些成立，哪些不成立？若成立，以图5为例简要说明理由．（3）在第(2)题图5中，连结DG、BE，且a=3，b=2，k=12，求22BE DG+的值．8.如图1所示，直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C 作直线l．将直线l平移，平移后的直线l与x轴交于点D，与y轴交于点E．（1）将直线l向右平移，设平移距离CD为t(t≥0)，直角梯形OABC被直线l扫过的面积（图中阴影部份）为s，s关于t的函数图象如图2所示，OM为线段，MN为抛物线的一部分，NQ 为射线，N 点横坐标为4． ①求梯形上底AB 的长及直角梯形OABC 的面积； ②当42<<t 时，求S 关于t 的函数解析式；（2）在第（1）题的条件下，当直线l 向左或向右平移时（包括l 与直线BC 重合），在直线．．AB ．．上是否存在点P ，使PDE ∆为等腰直角三角形?若存在，请直接写出所有满足条件的点P 的坐标;若不存在，请说明理由．9.如图，菱形ABCD 的边长为2，BD=2，E 、F 分别是边AD ，CD 上的两个动点，且满足AE+CF=2.（1）求证：△BDE ≌△BCF ； （2）判断△BEF 的形状，并说明理由； （3）设△BEF 的面积为S ，求S 的取值范围.10.如图，抛物线21:23L y x x =--+交x 轴于A 、B 两点，交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ，2L 交x 轴于C 、D 两点. （1）求抛物线2L 对应的函数表达式；（2）抛物线1L 或2L 在x 轴上方的部分是否存在点N ，使以A ，C ，M ，N 为顶点的四边形是平行四边形.若存在，求出点N 的坐标；若不存在，请说明理由；（3）若点P 是抛物线1L 上的一个动点（P 不与点A 、B 重合），那么点P 关于原点的对称点Q 是否在抛物线2L 上，请说明理由.11. 2008年5月1日，目前世界上最长的跨海大桥——杭州湾跨海大桥通车了．通车后，苏南A 地到宁波港的路程比原来缩短了120千米．已知运输车速度不变时，行驶时间将从原来的3时20分缩短到2时．（1）求A 地经杭州湾跨海大桥到宁波港的路程．（2）若货物运输费用包括运输成本和时间成本，已知某车货物从A 地到宁波港的运输成本是每千米1.8元，时间成本是每时28元，那么该车货物从A 地经杭州湾跨海大桥到宁波港的运输费用是多少元？（3）A 地准备开辟宁波方向的外运路线，即货物从A 地经杭州湾跨海大桥到宁波港，再从宁波港运到B 地．若有一批货物（不超过10车）从A 地按外运路线运到B 地的运费需8320元，其中从A 地经杭州湾跨海大桥到宁波港的每车运输费用与（2）中相同，从宁波港到B 地的海上运费对一批不超过10车的货物计费方式是：一车800元，当货物每增加1车时，每车的海上运费就减少20元，问这批货物有几车？12.如图1，把一张标准纸一次又一次对开，得到“2开”纸、“4开”纸、“8开”纸、“16开”纸…．已知标准纸．．．的短边长为a ． （1）如图2，把这张标准纸对开得到的“16开”张纸按如下步骤折叠：第一步 将矩形的短边AB 与长边AD 对齐折叠，点B 落在AD 上的点B '处，铺平后得折痕AE ；第二步 将长边AD 与折痕AE 对齐折叠，点D 正好与点E 重合，铺平后得折痕AF ． 则:AD AB 的值是 ，AD AB ，的长分别是 ， ．（2）“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等？若相等，直接写出这个比值；若不相等，请分别计算它们的比值．（3）如图3，由8个大小相等的小正方形构成“L ”型图案，它的四个顶点E F G H ，，，分别在“16开”纸的边AB BC CD DA ，，，上，求DG 的长．（4）已知梯形MNPQ 中，MN PQ ∥，90M =∠，2MN MQ PQ ==，且四个顶点M N P Q ，，，都在“4开”纸的边上，请直接写出2个符合条件且大小不同的直角梯形的面积．13.如图，在梯形ABCD 中，AB ∥CD ，AB ＝7，CD ＝1，AD ＝BC ＝5．点M ，N 分别在边AD ，BC 上运动，并保持MN ∥AB ，ME ⊥AB ，NF ⊥AB ，垂足分别为E ，F ．（1）求梯形ABCD 的面积； （2）求四边形MEFN 面积的最大值．（3）试判断四边形MEFN 能否为正方形，若能， 求出正方形MEFN 的面积；若不能，请说明理由．14．如图，点A （m ，m ＋1），B （m ＋3，m －1）都在反比例函数xky =的图象上． （1）求m ，k 的值；（2）如果M 为x 轴上一点，N 为y 轴上一点，C D A BE F NMABCD BCA D EGHF FE B '4开2开8开16开 图1图2 图3a以点A ，B ，M ，N 为顶点的四边形是平行四边形， 试求直线MN 的函数表达式．（3）选做题：在平面直角坐标系中，点P 的坐标 为（5，0），点Q 的坐标为（0，3），把线段PQ 向右平 移4个单位，然后再向上平移2个单位，得到线段P 1Q 1， 则点P 1的坐标为 ，点Q 1的坐标为．15．我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线.如图12，点A 、B 、C 、D 分别是“蛋圆”与坐标轴的交点，已知点D 的坐标为(0，-3)，AB 为半圆的直径，半圆圆心M 的坐标为(1,0)，半圆半径为2.友情提示：本大题第（1）小题4分，第（2）小题7分．对完成第（2）小题有困难的同学可以做下面的（3）选做题．选做题2分，所得分数计入总分．但第（2）、（3）小题都做的，第（3）小题的得分不重复计入总分．(1)请你求出“蛋圆”抛物线部分的解析式，并写出自变量的取值范围；(2)你能求出经过点C的“蛋圆”切线的解析式吗？试试看；(3)开动脑筋想一想，相信你能求出经过点D的“蛋圆”切线的解析式.16.将一矩形纸片OABC 放在平面直角坐标系中，(00)O ，，(60)A ，，(03)C ，．动点Q 从点O 出发以每秒1个单位长的速度沿OC 向终点C 运动，运动23秒时，动点P 从点A 出发以相等的速度沿AO 向终点O 运动．当其中一点到达终点时，另一点也停止运动．设点P 的运动时间为t （秒）． （1）用含t 的代数式表示OP OQ ，；（2）当1t 时，如图1，将OPQ △沿PQ 翻折，点O 恰好落在CB 边上的点D 处，求点D 的坐标；（4） 连结AC ，将OPQ △沿PQ 翻折，得到EPQ △，如图2．问：PQ 与AC 能否平行？PE 与AC能否垂直？若能，求出相应的t 值；若不能，说明理由．图117.如图16，在平面直角坐标系中，直线y =-x 轴交于点A ，与y 轴交于点C ，抛物线2(0)y ax x c a =+≠经过A B C ，，三点． （1）求过A B C ，，三点抛物线的解析式并求出顶点F 的坐标；（2）在抛物线上是否存在点P ，使ABP △为直角三角形，若存在，直接写出P 点坐标；若不存在，请说明理由；（3）试探究在直线AC 上是否存在一点M ，使得MBF △的周长最小，若存在，求出M 点的坐标；若不存在，请说明理由．x18.如图所示，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴的负半轴上，边OC 在y 轴的正半轴上，且1AB =，OB =ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD ．点A 的对应点为点E ，点B 的对应点为点F ，点C 的对应点为点D ，抛物线2y ax bx c =++过点A E D ，，． （1）判断点E 是否在y 轴上，并说明理由； （2）求抛物线的函数表达式；（3）在x 轴的上方是否存在点P ，点Q ，使以点O B P Q ，，，为顶点的平行四边形的面积是矩形ABOC 面积的2倍，且点P 在抛物线上，若存在，请求出点P ，点Q 的坐标；若不存在，请说明理由．19. 已知：如图14，抛物线2334y x =-+与x 轴交于点A ，点B ，与直线34y x b =-+相交于点B ，点C ，直线34y x b =-+与y 轴交于点E ． （1）写出直线BC 的解析式． （2）求ABC △的面积．（3）若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动（不与A B ，重合），x同时，点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动．设运动时间为t 秒，请写出MNB △的面积S 与t 的函数关系式，并求出点M 运动多少时间时，MNB △的面积最大，最大面积是多少？20.如图，在平面直角坐标系xOy 中，△OAB 的顶点Ａ的坐标为（10，0），顶点B 在第一象限内，且AB 5sin ∠OAB=55. （1）若点C 是点B 关于x 轴的对称点，求经过O 、C 、A 三点的抛物线的函数表达式； （2）在(1)中，抛物线上是否存在一点P ，使以P 、O 、C 、A 为顶点的四边形为梯形？若存在，求出点P 的坐标；若不存在，请说明理由；（3）若将点O 、点A 分别变换为点Q （ -2k ,0）、点R （5k ，0）（k>1的常数），设过Q 、R 两点，且以QR 的垂直平分线为对称轴的抛物线与y 轴的交点为N ，其顶点为M ，记△QNM 的面积为QMN S ∆，△QNR 的面积QNR S ∆，求QMN S ∆∶QNR S ∆的值.21.在平面直角坐标系中△ABC 的边AB 在x 轴上，且OA>OB,以AB 为直径的圆过点C 若C 的坐标为(0,2),AB=5, A,B 两点的横坐标X A ,X B 是关于X 的方程2(2)10x m x n -++-=的两根:(1) 求m ，n 的值(2) 若∠ACB 的平分线所在的直线l 交x 轴于点D ，试求直线l 对应的一次函数的解析式 (3) 过点D 任作一直线`l 分别交射线CA ，CB （点C 除外）于点M ，N ，则11CM CN+的值是否为定值，若是，求出定值，若不是，请说明理由22.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D.(1)求该抛物线的解析式；(2)若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积；(3)△AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22）ACO BNDML`23.已知抛物线c bx ax y ++=232，（Ⅰ）若1==b a ，1-=c ，求该抛物线与x 轴公共点的坐标；（Ⅱ）若1==b a ，且当11<<-x 时，抛物线与x 轴有且只有一个公共点，求c 的取值范围；（Ⅲ）若0=++c b a ，且01=x 时，对应的01>y ；12=x 时，对应的02>y ，试判断当10<<x 时，抛物线与x 轴是否有公共点？若有，请证明你的结论；若没有，阐述理由． 24.如图①，四边形AEFG 和ABCD 都是正方形，它们的边长分别为a b ，（2b a ≥），且点F 在AD 上（以下问题的结果均可用a b ，的代数式表示）．（1）求DBF S △；（2）把正方形AEFG 绕点A 按逆时针方向旋转45°得图②，求图②中的DBF S △；（3）把正方形AEFG 绕点A 旋转一周，在旋转的过程中，DBF S △是否存在最大值、最小值？如果存在，直接写出最大值、最小值；如果不存在，请说明理由． .25.已知24AB AD ==，，90DAB ∠=，AD BC ∥（如图13）．E 是射线BC 上的动点（点E 与点B 不重合），M 是线段DE 的中点．（1）设BE x =，ABM △的面积为y ，求y 关于x 的函数解析式，并写出函数的定义域； （2）如果以线段AB 为直径的圆与以线段DE 为直径的圆外切，求线段BE 的长； （3）联结BD ，交线段AM 于点N ，如果以A N D ，，为顶点的三角形与BME △相似，求线段BE 的长．DCBAE FGGF EACD ①②BA DMEC图13 BADC备用图26.某县社会主义新农村建设办公室，为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题，想在这三个地方的其中一处建一所供水站．由供水站直接铺设管道到另外两处．如图，甲，乙两村坐落在夹角为30的两条公路的AB段和CD段（村子和公路的宽均不计），点M表示这所中学．点B在点M的北偏西30的3km处，点A在点M的正西方向，点D在点M的南偏西60的处．为使供水站铺设到另两处的管道长度之和最短，现有如下三种方案：方案一：供水站建在点M处，请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值；方案二：供水站建在乙村（线段CD某处），甲村要求管道建设到A处，请你在图①中，画出铺设到点A和点M处的管道长度之和最小的线路图，并求其最小值；方案三：供水站建在甲村（线段AB某处），请你在图②中，画出铺设到乙村某处和点M处的管道长度之和最小的线路图，并求其最小值．综上，你认为把供水站建在何处，所需铺设的管道最短？C C27.已知：如图①，在Rt △ACB 中，∠C ＝90°，AC ＝4cm ，BC ＝3cm ，点P 由B 出发沿BA 方向向点A 匀速运动，速度为1cm/s ；点Q 由A 出发沿AC 方向向点C 匀速运动，速度为2cm/s ；连接PQ ．若设运动的时间为t （s ）（0＜t ＜2），解答下列问题： （1）当t 为何值时，PQ ∥BC ？（2）设△AQP 的面积为y （2cm ），求y 与t 之间的函数关系式；（3）是否存在某一时刻t ，使线段PQ 恰好把Rt △ACB 的周长和面积同时平分？若存在，求出此时t 的值；若不存在，说明理由；（4）如图②，连接PC ，并把△PQC 沿QC 翻折，得到四边形PQP ′C ，那么是否存在某一时刻t ，使四边形PQP ′C 为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．28.已知双曲线k y x =与直线14y x =相交于A 、B 两点.第一象限上的点M （m ，n ）（在A 点左侧）是双曲线ky x=上的动点.过点B 作BD ∥y 轴于点D.过N （0，－n ）作NC ∥x 轴交双曲线ky x=于点E ，交BD 于点C.（1）若点D 坐标是（－8，0），求A 、B 两点坐标及k 的值.（2）若B 是CD 的中点，四边形OBCE 的面积为4，求直线CM 的解析式.（3）设直线AM 、BM 分别与y 轴相交于P 、Q 两点，且MA ＝pMP ，MB ＝qMQ ，求p －q 的值.P '图①D B CE NO A Myx29. 一种电讯信号转发装置的发射直径为31km ．现要求：在一边长为30km 的正方形城区选择若干个安装点，每个点安装一个这种转发装置，使这些装置转发的信号能完全覆盖这个城市．问：（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能达到预设的要求？ （2）至少需要选择多少个安装点，才能使这些点安装了这种转发装置后达到预设的要求？ 答题要求：请你在解答时，画出必要的示意图，并用必要的计算、推理和文字来说明你的理由．（下面给出了几个边长为30km 的正方形城区示意图，供解题时选用）图1 图2 图3 图4尖子生题库答案1. 解：（ 1）由已知得：310c b c =⎧⎨--+=⎩解得c=3,b =2∴抛物线的线的解析式为223y x x =-++(2)由顶点坐标公式得顶点坐标为（1，4） 所以对称轴为x=1,A,E 关于x=1对称，所以设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO BOFD S S S ∆++梯形=111()222AO BO BO DF OF EF DF ⋅++⋅+⋅=11113(34)124222⨯⨯++⨯+⨯⨯ =9 （3）相似如图，=====所以2220BD BE +=, 220DE =即： 222BD BE DE +=,所以BDE ∆是直角三角形 所以90AOB DBE ∠=∠=︒,且2AO BO BD BE ==, 所以AOBDBE ∆∆.2. (1) ∵A ，B 两点的坐标分别是A(10，0)和B(8，32)， ∴381032OAB tan =-=∠，∴︒=∠60OAB当点A ´在线段AB 上时，∵︒=∠60OAB ，TA=TA ´， ∴△A ´TA 是等边三角形，且A T TP '⊥，∴)t 10(2360sin )t 10(TP -=︒-=，)t 10(21AT 21AP P A -==='， ∴2TPA )t 10(83TP P A 21S S -=⋅'=='∆， 当A ´与B 重合时，AT=AB=460sin 32=︒， 所以此时10t 6<≤.(2)当点A ´在线段AB 的延长线，且点P 在线段AB(不与B 重合)上时， 纸片重叠部分的图形是四边形(如图(1)，其中E 是TA ´与CB 的交点)， 当点P 与B 重合时，AT=2AB=8，点T 的坐标是(2，又由(1)中求得当A ´与B 重合时，T 的坐标是(6，0) 所以当纸片重叠部分的图形是四边形时，6t 2<<. (3)S 存在最大值○1当10t 6<≤时，2)t 10(83S -=， 在对称轴t=10的左边，S 的值随着t 的增大而减小，∴当t=6时，S 的值最大是32.○2当6t 2<≤时，由图○1，重叠部分的面积EB A TP A S S S '∆'∆-= ∵△A ´EB 的高是︒'60sin B A ，∴23)4t 10(21)t 10(83S 22⨯----=34)2t (83)28t 4t (8322+--=++-=当t=2时，S 的值最大是34；○3当2t 0<<，即当点A ´和点P 都在线段AB 的延长线是(如图○2，其中E 是TA ´与CB 的交点，F 是TP 与CB 的交点)，∵ETF FTP EFT ∠=∠=∠，四边形ETAB 是等腰形，∴EF=ET=AB=4， ∴3432421OC EF 21S =⨯⨯=⋅=综上所述，S 的最大值是34，此时t 的值是2t 0≤<. 3. 解：（1）Rt A ∠=∠，6AB =，8AC =，10BC ∴=．点D 为AB 中点，132BD AB ∴==． 90DHB A ∠=∠=，B B ∠=∠．BHD BAC ∴△∽△， DH BD AC BC ∴=，3128105BD DH AC BC ∴==⨯=． （2）QR AB ∥，90QRC A ∴∠=∠=．C C ∠=∠，RQC ABC ∴△∽△， AT ORQ QC AB BC ∴=，10610y x-∴=， 即y 关于x 的函数关系式为：365y x =-+． （3）存在，分三种情况：①当PQ PR =时，过点P 作PM QR ⊥于M ，则QM RM =．1290∠+∠=，290C ∠+∠=，1C ∴∠=∠．84cos 1cos 105C ∴∠===，45QM QP ∴=， 1364251255x ⎛⎫-+ ⎪⎝⎭∴=，185x ∴=． ②当PQ RQ =时，312655x -+=， 6x ∴=．③当PR QR =时，则R 为PQ 中垂线上的点， 于是点R 为EC 的中点，11224CR CE AC ∴===．tan QR BAC CR CA ==， 366528x -+∴=，152x ∴=．综上所述，当x 为185或6或152时，PQR △为等腰三角形．4. 解：（1）∵MN ∥BC ，∴∠AMN =∠B ，∠ANM ＝∠C ． ∴ △AMN ∽ △ABC ．∴ AM AN AB AC=，即43x AN=．ABCD ERP H QM 21 HQA BCD E R PHQB图 1∴ AN ＝43x ． ……………2分 ∴ S =2133248MNP AMN S S x x x ∆∆==⋅⋅=．（0＜x ＜4） ……………3分 （2）如图2，设直线BC 与⊙O 相切于点D ，连结AO ，OD ，则AO =OD =21MN ． 在Rt △ABC 中，BC．由（1）知 △AMN ∽ △ABC ．∴ AM MN AB BC=，即45x MN=．∴ 54MN x =， ∴ 58OD x =． …………………5分过M 点作MQ ⊥BC 于Q ，则58MQ OD x ==． 在Rt △BMQ 与Rt △BCA 中，∠B 是公共角， ∴ △BMQ ∽△BCA ． ∴ BM QM BC AC=．∴ 55258324xBM x ⨯==，25424AB BM MA x x =+=+=． ∴ x ＝4996． ∴ 当x ＝4996时，⊙O 与直线BC 相切．…………………………………7分 （3）随点M 的运动，当P 点落在直线BC 上时，连结AP ，则O 点为AP 的中点．∵ MN ∥BC ，∴ ∠AMN =∠B ，∠AOM ＝∠APC∴ △AMO ∽ △ABP ．∴ 12AM AO AB AP ==． AM ＝MB ＝2．故以下分两种情况讨论：BD 图 2QBP 图 3① 当0＜x ≤2时，2Δ83x S y PMN ==．∴ 当x ＝2时，2332.82y =⨯=最大 ……………………………………8分 ② 当2＜x ＜4时，设PM ，PN 分别交BC 于E ，F ． ∵ 四边形AMPN 是矩形， ∴ PN ∥AM ，PN ＝AM ＝x ． 又∵ MN ∥BC ，∴ 四边形MBFN 是平行四边形． ∴ FN ＝BM ＝4－x ．∴ ()424PF x x x =--=-． 又△PEF ∽ △ACB ．∴ 2PEF ABCS PF AB S ∆∆⎛⎫= ⎪⎝⎭． ∴ ()2322PEF S x ∆=-． ……………………………………………… 9分 MNP PEF y S S ∆∆=-＝()222339266828x x x x --=-+-．……………………10分当2＜x ＜4时，29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭．∴ 当83x =时，满足2＜x ＜4，2y =最大． ……………………11分 综上所述，当83x =时，y 值最大，最大值是2． …………………………12分5. 解：（1）（-4，-2）；（-m,-km）(2) ①由于双曲线是关于原点成中心对称的，所以OP=OQ,OA=OB,所以四边形APBQ一定是平行四边形 ②可能是矩形，mn=k 即可不可能是正方形，因为Op 不能与OA 垂直.P 图 4解：（1）作BE ⊥OA ， ∴ΔAOB 是等边三角形 ∴BE=OB ·sin60o=∴B(∵A(0,4),设AB 的解析式为4y kx =+,所以42+=,解得3k =-,的以直线AB 的解析式为43y x =-+ （2）由旋转知，AP=AD, ∠PAD=60o, ∴ΔAPD 是等边三角形，=6. 解：（1）作BE ⊥OA ，∴ΔAOB 是等边三角形∴BE=OB ·sin60o=B(∵A(0,4),设AB 的解析式为4y kx =+,所以42+=,解得k =, 以直线AB的解析式为4y x =+ （2）由旋转知，AP=AD, ∠PAD=60o, ∴ΔAPD 是等边三角形，=如图，作B E ⊥AO,DH ⊥OA,GB ⊥DH,显然ΔGBD 中∠GBD=30°∴GD=12BD=2,DH=GH+GD=2+2, ∴32,OH=OE+HE=OE+BG=37222+=∴D(532,72) (3)设OP=x,则由（2）可得D(323,22x x ++)若ΔOPD 的面积为：133(2)224x x += 解得：23213x -±=所以P(23213-±,0)7. 解:(1)①,BG DE BG DE =⊥ ………………………………………………………………2分②,BG DE BG DE=⊥仍然成立 ……………………………………………………1分在图（2）中证明如下∵四边形ABCD 、四边形ABCD 都是正方形 ∴ BC CD =，CG CE =， 090BCD ECG ∠=∠= ∴BCG DCE ∠=∠…………………………………………………………………1分∴BCG DCE ∆≅∆ （SAS ）………………………………………………………1分∴BG DE = CBG CDE ∠=∠又∵BHC DHO ∠=∠ 090CBG BHC ∠+∠= ∴090CDE DHO ∠+∠= ∴090DOH ∠= ∴BG DE ⊥ …………………………………………………………………………1分（2）BG DE ⊥成立，BG DE =不成立 …………………………………………………2分简要说明如下∵四边形ABCD 、四边形CEFG 都是矩形，且AB a =，BC b =，CG kb =，CE ka =(a b ≠，0k >)∴BC CG bDC CE a==，090BCD ECG ∠=∠= ∴BCG DCE ∠=∠∴BCG DCE ∆∆………………………………………………………………………1分∴CBG CDE ∠=∠又∵BHC DHO ∠=∠ 090CBG BHC ∠+∠= ∴090CDE DHO ∠+∠= ∴090DOH ∠= ∴BG DE ⊥ ……………………………………………………………………………1分（3）∵BG DE ⊥ ∴22222222BE DG OB OE OG OD BD GE +=+++=+ 又∵3a =，2b =，k =12∴222222365231()24BD GE +=+++=………………………………………………1分 ∴22654BE DG +=………………………………………………………………………1分 8. 解：（1）①2AB = ……………………………………………………………………………842OA ==，4OC =，S 梯形OABC =12 ……………………………………………2分②当42<<t 时，直角梯形OABC 被直线l 扫过的面积=直角梯形OABC 面积－直角三角开DOE 面积2112(4)2(4)842S t t t t =--⨯-=-+-…………………………………………4分（2）存在 ……………………………………………………………………………………1分123458(12,4),(4,4),(,4),(4,4),(8,4)3P P P P P --- …（每个点对各得1分）……5分对于第（2）题我们提供如下详细解答（评分无此要求）.下面提供参考解法二：① 以点D 为直角顶点，作1PP x ⊥轴Rt ODE ∆在中，2OE OD =∴，设2OD b OE b ==，.1Rt ODE Rt PPD ∆≈∆，（图示4b∴=，28b=，在上面二图中分别可得到P点的生标为P（－12，4）、P（－4，4）E点在0点与A点之间不可能；②以点E为直角顶点同理在②二图中分别可得P点的生标为P（－83，4）、P（8，4）E点在0点下方不可能.以点P为直角顶点同理在③二图中分别可得P 点的生标为P （－4，4）（与①情形二重合舍去）、P （4，4）， E 点在A 点下方不可能.综上可得P 点的生标共5个解，分别为P （－12，4）、P （－4，4）、P （－83，4）、 P （8，4）、P （4，4）．下面提供参考解法二：以直角进行分类进行讨论（分三类）： 第一类如上解法⑴中所示图22P DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b)的中点坐标为b (-,b)2，直线DE 的中垂线方程：1()22by b x -=-+，令4y =得3(8,4)2bP -DE ==得2332640b b -+=解得 121883b b P P ==∴=3b，将之代入（-8，4）（4，4)、22(4,4)P -；第二类如上解法②中所示图22E DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b)，直线PE 的方程：122y x b =-+，令4y =得(48,4)P b -．由已知可得PE DE =即=22(28)b b =-解之得 ，123443b b P P ==∴=，将之代入（4b-8，4）（8，4)、48(,4)3P - 第三类如上解法③中所示图22D DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b)，直线PD 的方程：1()2y x b =-+，令4y =得(8,4)P b --．由已知可得PD DE =即=12544b b P P ==-∴=，将之代入（-b-8，4）（-12，4)、 6(4,4)P -（6(4,4)P -与2P 重合舍去）．综上可得P 点的生标共5个解，分别为P （－12，4）、P （－4，4）、P （－83，4）、 P （8，4）、P （4，4）．事实上，我们可以得到更一般的结论： 如果得出AB a OC b ==、、OA h =、设b ak h-=，则P 点的情形如下9.10.11. 解：（1）设A 地经杭州湾跨海大桥到宁波港的路程为x 千米， 由题意得1201023x x+=， ··················································································· 2分 解得180x =．A ∴地经杭州湾跨海大桥到宁波港的路程为180千米． ·········································· 4分 （2）1.8180282380⨯+⨯=（元），∴该车货物从A 地经杭州湾跨海大桥到宁波港的运输费用为380元．························ 6分（3）设这批货物有y 车，由题意得[80020(1)]3808320y y y -⨯-+=， ···················································· 8分 整理得2604160y y -+=，解得18y =，252y =（不合题意，舍去）， ······················································· 9分∴这批货物有8车． ····················································································· 10分12. 解：（1144a a ，，． ·········································································· 3分（2． ·············· 5分（无“相等”不扣分有“相等”，比值错给1分） （3）设DG x =，在矩形ABCD 中，90B C D ∠=∠=∠=，90HGF ∠=，90DHG CGF DGH ∴∠=∠=-∠，HDG GCF ∴△∽△， 12DG HG CF GF ∴==， 22CF DG x ∴==． ······················································································ 6分 同理BEF CFG ∠=∠．EF FG =， FBE GCF ∴△≌△，14BF CG a x ∴==-． ·················································································· 7分 CF BF BC +=，1244x a x a ∴+-=， ················································································· 8分解得x =．即14DG a =． ························································································ 9分 （4）2316a ， ······························································································ 10分2278-． 12分 13. 解：（1）分别过D ，C 两点作DG ⊥AB 于点G ，CH ⊥AB 于点H ． (1)分∵ AB ∥CD ，∴ DG ＝CH ，DG ∥CH ．∴ 四边形DGHC 为矩形，GH ＝CD ＝1． ∵ DG ＝CH ，AD ＝BC ，∠AGD ＝∠BHC ＝90°， ∴ △AGD ≌△BHC （HL ）． ∴ AG ＝BH ＝2172-=-GH AB ＝3． ………2分 ∵ 在Rt △AGD 中，AG ＝3，AD ＝5， ∴ DG ＝4．∴ ()174162ABCD S +⨯==梯形． ………………………………………………3分（2）∵ MN ∥AB ，ME ⊥AB ，NF ⊥AB ，∴ ME ＝NF ，ME ∥NF ． ∴ 四边形MEFN 为矩形．∵ AB ∥CD ，AD ＝BC ， ∴ ∠A ＝∠B ．∵ ME ＝NF ，∠MEA ＝∠NFB ＝90°， ∴ △MEA ≌△NFB （AAS ）．∴ AE ＝BF ． ……………………4分 设AE ＝x ，则EF ＝7－2x ． ……………5分 ∵ ∠A ＝∠A ，∠MEA ＝∠DGA ＝90°， ∴ △MEA ∽△DGA ． ∴DGME AG AE =．A BE F G HABE F G H∴ ME ＝x 34． …………………………………………………………6分∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形． ……………………8分 当x ＝47时，ME ＝37＜4，∴四边形MEFN 面积的最大值为649．……………9分 （3）能． ……………………………………………………………………10分 由（2）可知，设AE ＝x ，则EF ＝7－2x ，ME ＝x 34．若四边形MEFN 为正方形，则ME ＝EF ． 即=34x 7－2x ．解，得 1021=x ． ……………………………………………11分 ∴ EF ＝21147272105x -=-⨯=＜4． ∴ 四边形MEFN 能为正方形，其面积为251965142=⎪⎭⎫⎝⎛=MEFNS 正方形．14. 解：（1）由题意可知，()()()131-+=+m m m m ．解，得 m ＝3． ………………………………3分∴ A （3，4），B （6，2）；∴ k ＝4×3=12． ……………………………4分（2）存在两种情况，如图：①当M 点在x 轴的正半轴上，N 点在y 轴的正半轴 上时，设M 1点坐标为（x 1，0），N 1点坐标为（0，y 1）．∵ 四边形AN 1M 1B 为平行四边形，∴ 线段N 1M 1可看作由线段AB 向左平移3个单位，再向下平移2个单位得到的（也可看作向下平移2个单位，再向左平移3个单位得到的）．由（1）知A 点坐标为（3，4），B 点坐标为（6，2），∴ N 1点坐标为（0，4－2），即N 1（0，2）； ………………………………5分 M 1点坐标为（6－3，0），即M 1（3，0）． ………………………………6分 设直线M 1N 1的函数表达式为21+=x k y ，把x ＝3，y ＝0代入，解得321-=k ． ∴ 直线M 1N 1的函数表达式为232+-=x y ． ……………………………………8分②当M 点在x 轴的负半轴上，N 点在y 轴的负半轴上时，设M 2点坐标为（x 2，0），N 2点坐标为（0，y 2）．∵ AB ∥N 1M 1，AB ∥M 2N 2，AB ＝N 1M 1，AB ＝M 2N 2， ∴ N 1M 1∥M 2N 2，N 1M 1＝M 2N 2．∴ 线段M 2N 2与线段N 1M 1关于原点O 成中心对称．∴ M 2点坐标为（-3，0），N 2点坐标为（0，-2）． ………………………9分 设直线M 2N 2的函数表达式为22-=x k y ，把x ＝-3，y ＝0代入，解得322-=k ， ∴ 直线M 2N 2的函数表达式为232--=x y ．所以，直线MN 的函数表达式为232+-=x y 或232--=x y ． ………………11分（3）选做题：（9，2），（4，5）． ………………………………………………2分 15. 解：(1)解法1：根据题意可得：A (-1,0)，B (3,0)；则设抛物线的解析式为)3)(1(-+=x x a y (a ≠0)又点D (0，-3)在抛物线上，∴a (0+1)(0-3)=-3，解之得：a =1∴y =x 2-2x -3 ······················································································ 3分 自变量范围：-1≤x ≤3 ········································································· 4分解法2：设抛物线的解析式为c bx ax y ++=2(a ≠0)根据题意可知，A (-1,0)，B (3,0)，D (0，-3)三点都在抛物线上∴⎪⎩⎪⎨⎧-==++=+-30390c c b a c b a ，解之得：⎪⎩⎪⎨⎧-=-==321c b a∴y =x 2-2x -3 ···································································· 3分 自变量范围：-1≤x ≤3 ····················································· 4分(2)设经过点C “蛋圆”的切线CE 交x 轴于点E ，连结CM ， 在Rt △MOC 中，∵OM =1，CM =2，∴∠CMO =60°,OC =3 在Rt △MCE 中，∵OC =2，∠CMO =60°，∴ME =4∴点C 、E 的坐标分别为(0，3)，(-3,0) ··········································· 6分∴切线CE 的解析式为3x3y += ··················································· 8分(3)设过点D (0，-3)，“蛋圆”切线的解析式为：y =kx -3(k ≠0) ······················· 9分由题意可知方程组⎪⎩⎪⎨⎧--=-=3232x x y kx y 只有一组解 即3232--=-x x kx 有两个相等实根，∴k =-2······································· 11分 ∴过点D “蛋圆”切线的解析式y =-2x -3 ············································· 12分16.解：（1）6OP t =-，23OQ t =+．（2）当1t =时，过D 点作1DD OA ⊥，交OA 于1D ，如图1， 则53DQ QO ==，43QC =， 1CD ∴=，(13)D ∴，． （3）①PQ 能与AC 平行． 若PQ AC ∥，如图2，则OP OAOQ OC=， 即66233t t -=+，149t ∴=，而703t ≤≤， 149t ∴=．②PE 不能与AC 垂直．若PE AC ⊥，延长QE 交OA 于F ，如图3，则23335t QF OQ AC OC +==．图1。

【拔尖特训】2023-2024学年九年级数学上册尖子生培优必刷题（人教版）专题23.2中心对称（限时满分培优训练）班级：___________________ 姓名：_________________ 得分：_______________注意事项：本试卷满分100分，试题共23题，其中选择10道、填空6道、解答7道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2023•高台县开学）下列美丽的图案中，是中心对称图形的是（）A．B．C．D．2．（2023春•浦东新区校级期末）下列图形中，一定是中心对称但不一定是轴对称图形的是（）A．菱形B．矩形C．等腰梯形D．平行四边形3．（2023春•社旗县期末）如图，△ABC与△A′B′C′关于O成中心对称，下列结论中不成立的是（）A．OC＝OC′B．OA＝OA′C．BC＝B′C′D．∠ABC＝∠A′C′B′4．（2023•大兴区一模）如图，在正方形网格中，A，B，C，D，E，F，G，H，I，J是网格线交点，△ABC 与△DEF关于某点成中心对称，则其对称中心是（）A．点G B．点H C．点I D．点J5．（2023春•宽甸县期末）在平面直角坐标系中，将点P（3，2）向右平移2个单位长度，所得到的点关于原点中心对称后的点的坐标为（）A．（1，2）B．（﹣1，﹣2）C．（5，2）D．（﹣5，﹣2）6．（2021•镜湖区校级一模）已知点A关于x轴的对称点坐标为（﹣1，2），则点A关于原点的对称点的坐标为（）A．（1，2）B．（﹣1，﹣2）C．（2，﹣1）D．（1，﹣2）7．（2023•襄都区校级一模）如图，将△ABC绕点C顺时针旋转180°得到△DEC，连接AE，BD，添加下列条件后不一定使四边形ABDE既是中心对称图形又是轴对称图形的是（）A．AB＝BC B．AC＝BC C．AC=12BE D．AC⊥BC8．（2023春•沈丘县期末）如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB向点B运动，移动到点B停止，延长EO交CD于点F，则四边形AECF形状不可能是（）A．平行四边形B．菱形C．正方形D．矩形9．（2023春•翠屏区期末）如图，在平面直角坐标系中，四边形OABC是平行四边形，四边形ODEC为正方形，点C的坐标是（0，2），点A的坐标是（2，1），若直线l把▱OABC与正方形ODEC组成的图形分成面积相等的两部分，则直线l的解析式是（）A．y=14x+54B．y=12x+32C．y=−14x+34D．y=−14x+3210．（2023春•襄汾县期末）如图，点O为矩形ABCD的对称中心，AD＞AB，点E从点B出发（不含点B）沿BC向点C运动，移动到点C停止，延长EO交AD于点F，则四边形BEDF形状的变化依次为（）A．平行四边形→菱形→正方形→矩形B．平行四边形→正方形→菱形→矩形C．平行四边形→菱形→平行四边形→矩形D．平行四边形→正方形→平行四边形一矩形二、填空题（本大题共6小题，每小题3分，共18分）请把答案直接填写在横线上11．（2022秋•湖北期末）在平面直角坐标系中，与点P（2，﹣3）关于原点对称的点的坐标是．12．（2022秋•北辰区校级期末）如图是一个中心对称图形，A为对称中心，若∠C＝90°，∠B＝30°，AC ＝3，则BB′的长为．13．（2022秋•闵行区校级期末）在以下图形：线段、角、等腰三角形、平行四边形、长方形、圆中，既是轴对称图形又是中心对称图形是．14．（2023春•宛城区期末）图1和图2中所有的小正方形都全等，若将图1的正方形放在图2中①②③④的某一位置，使它与原来7个小正方形组成的图形是中心对称图形，则应该放到的这个位置的序号是．15．（2023春•沈河区校级月考）已知两个完全相同的直角三角形纸片△ABC、△DEF，如图放置，点B、D 重合，点F在BC上，AB与EF交于点G．∠C＝∠EFB＝90°，∠E＝∠ABC＝30°，∠A＝∠EBF＝60°，现将图中的△EFB绕点F按每秒12°的速度沿逆时针方向旋转180°，在旋转的过程中，△EFB恰有一边与AB平行的时间为秒．16．（2023春•泰州期末）如图，在矩形ABCD中，AB＝4，AD＝6，点P、M、N分别在边AB、AD、BC上运动，且线段MN始终经过矩形的对称中心，则△PMN周长的最小值为．三、解答题（本大题共7小题，共52分．解答时应写出文字说明、证明过程或演算步骤）17．（2023春•常德期中）如图所示，△ABC与△A′B′C′关于点O中心对称，但点O不慎被涂掉了．（1）请你找到对称中心O的位置；（2）连接线段BC′和线段B′C，试判断四边形BC′B′C的形状，并说明理由．18．（2023春•丹东期末）如图，在平面直角坐标系中，已知点A（2，﹣2），点P是x轴上的一个动点．（1）A1，A2分别是点A关于原点的对称点和关于y轴对称的点，直接写出点A1，A2的坐标，并在图中描出点A1，A2．（2）求使△APO为等腰三角形的点P的坐标．19．（2023•通榆县模拟）在棋盘中建立如图所示的直角坐标系，三颗棋子A，O，B的位置如图，它们的坐标分别是（﹣1，1），（0，0）和（1，0）．（1）在图①中添加一颗棋子C，使得以A，O，B，C四颗棋子为顶点的四边形为一个轴对称图形，但不是中心对称图形；（2）在图②中添加一颗棋子P，使得以A，O，B，P四颗棋子为顶点的四边形为中心对称图形，但不是轴对称图形，并直接写出棋子P的坐标．20．（2023春•渠县校级期中）在△ABC中，∠ABC＜90°，将△ABC在平面内绕点B顺时针旋转（旋转角不超过180°），得到△DBE，其中点A的对应点为点D，连接CE，CE∥AB．（1）如图1，试猜想∠ABC与∠BEC之间满足的等量关系，并给出证明；（2）如图2，若点D在边BC上，DC＝2，AC=√19，求AB的长．21．（2023春•海淀区校级月考）在Rt△ABC中，∠ABC＝90°，∠BAC＝30°，D为边BC延长线上一动点，点E在边AC延长线上，CE＝CD．点D关于点B的对称点为点F，连接AD，EF．（1）设CD＝a，BC＝b．判断AE与CF的数量关系，并证明；（2）取AD中点P，连接PE、PF，补全图形，判断PE与PF的数量关系与位置关系，并证明．22．（2022秋•西安期末）如图1，点E为正方形ABCD内一点，∠AEB＝90°，将△ABE绕点B顺时针方向旋转90°，得到△CBE'（点A的对应点为点C），延长AE交CE'于点F，连接DE．（1）试判断四边形BEFE'的形状，并说明理由；（2）若DA＝DE，如图2，请猜想线段CF与E'F的数量关系，并加以证明．23．（2022•黄冈模拟）（1）如图1，O是等边△ABC内一点，连接OA、OB、OC，且OA＝3，OB＝4，OC ＝5，将△BAO绕点B顺时针旋转后得到△BCD，连接OD．求：①旋转角的度数；②线段OD的长；③求∠BDC的度数．（2）如图2所示，O是等腰直角△ABC（∠ABC＝90°）内一点，连接OA、OB、OC，将△BAO绕点B 顺时针旋转后得到△BCD，连接OD．当OA、OB、OC满足什么条件时，∠ODC＝90°？请给出证明．。

初中尖子生试题及答案一、选择题（每题2分，共20分）1. 下列哪个选项是正确的？A. 地球自转的方向是自东向西B. 地球公转的方向是自东向西C. 地球自转的方向是自西向东D. 地球公转的方向是自西向东答案：C2. 以下哪种植物属于被子植物？A. 松树B. 蕨类C. 银杏D. 玉米答案：D3. 以下哪个历史事件标志着中国封建社会的开始？A. 秦始皇统一六国B. 陈胜吴广起义C. 黄巾起义D. 春秋五霸答案：A4. 以下哪个是光合作用的产物？A. 氧气B. 二氧化碳C. 氮气D. 甲烷5. 以下哪种元素是人体必需的微量元素？A. 钙B. 钠C. 铁D. 钾答案：C6. 以下哪个是牛顿三大定律之一？A. 能量守恒定律B. 万有引力定律C. 牛顿第一定律D. 牛顿第三定律答案：C7. 以下哪个是化学变化？A. 水的沸腾B. 铁的生锈C. 冰的融化D. 木头的燃烧答案：B8. 以下哪个是英语中的不规则动词？A. goB. runC. eatD. have答案：D9. 以下哪个是细胞的基本结构？B. 细胞膜C. 细胞质D. 细胞核答案：B10. 以下哪个是中国古代四大发明之一？A. 造纸术B. 指南针C. 火药D. 印刷术答案：A二、填空题（每题2分，共20分）1. 地球的五带包括热带、温带和______。

答案：寒带2. 人体最大的器官是______。

答案：皮肤3. 光合作用主要发生在植物的______。

答案：叶绿体4. 牛顿第一定律也被称为______。

答案：惯性定律5. 化学变化和物理变化的区别在于是否有______的生成。

答案：新物质6. 英语中的“不规则动词”是指其过去式和过去分词形式与______形式不同。

答案：原形7. 细胞膜的主要功能是控制物质的进出，保护______。

答案：细胞内部8. 四大文明古国包括古中国、古埃及、古印度和______。

答案：古巴比伦9. 造纸术的发明极大地促进了______的传播。

20191.解析 因为{}1234567234{}}23{567U A B ===，，，，，，，，，，，，，，，所以C 17{}6U A =，，， 则{67?}U B A =I ，ð. 故选C ．2.解析 (1,)A =-+∞，(,2)B =-∞，(1,2)AB =-.故选C. 3.解析 因为{}1,0,1,2A =-，2{|1}{|11}B x x x x ==-剟?， 所以{}1,0,1A B =-.故选A ．4.解析 由数轴可知，{}1A B x x =>.故选C.5.解析 设集合{}1,1,2,3,5A =-，{}13C x x =∈<R …， 则{}1,2AC =. 又{}2,3,4B =， 所以{}{}{}{}1,22,3,41,2,3,4A C B ==. 故选D.6.解析 因为{}1,0,1,6A =-，{}|0,B x x x =>∈R ，所以{}{}{}1,0,1,6|0,1,6A B x x x =->∈=R .7.解析 {1,3}U A =-ð，{1}U A B =-ð.故选A ． 2010-20181．A 【解析】由题意{0,2}A B =，故选A ．2．C 【解析】因为{1,2,3,4,5}U =，{1,3}A =，所以=U A ð{2，4，5}．故选C ．3．C 【解析】因为{}1,3,5,7A =，{}2,3,4,5B =，所以{3,5}A B =，故选C ．4．A 【解析】{|||2}(2,2)A x x =<=-，{2,0,1,2}B =-，∴{0,1}A B =，故选A ．5．C 【解析】由题意知，{|10}A x x =-≥，则{1,2}A B =．故选C ．6．C 【解析】由题意{1,0,1,2,3,4}A B =-，∴(){1,0,1}A B C =-，故选C ．7．A 【解析】∵3{|}2B x x =<，∴3{|}2A B x x =<， 选A ． 8．A 【解析】由并集的概念可知，{1,2,3,4}A B =，选A ．9．B 【解析】由集合交集的定义{2,4}A B =，选B ．10．B 【解析】∵{1,2,4,6}A B =，(){1,2,4}A B C =，选B ．11．C 【解析】{|02}M x x =<<，所以{|02}M N x x =<<，选C ．12．C 【解析】{|22}U A x x =-≤≤ð，选C ．13．A 【解析】由题意可知{|12}P Q x x =-<<，选A ．14．B 【解析】由题意得，{1,3,5,7}A =，{|25}B x x =剟，则{3,5}A B =．选B ．15．D 【解析】易知{|33}B x x =-<<，又{1,2,3}A =，所以{1,2}A B =故选D ．16．C 【解析】由补集的概念，得{0,2,6,10}A B =ð，故选C ．17．A 【解析】∵(1,2)A =-，(0,3)B =，∴(1,3)A B =-．18．D 【解析】集合{|32,}A x x n n N ==+∈，当0n =时，322n +=，当1n =时， 325n +=，当2n =时，328n +=，当3n =时，3211n +=，当4n =时，3214n +=，∵{6,8,10,12,14}B =，∴A B 中元素的个数为2，选D ．19．A 【解析】{|32}A B x x =-<<．20．B 【解析】{2,5}U B ð=，∴U A B =ð{2,5}．21【解析】考查集合的运算推理．3∈B ，23a +=，1a =．22．C 【解析】因为{|13}B x x =<<，所以(2,3)AB =，故选C ． 23．D 【解析】∵{0,1}MN =． 24．B 【解析】{1}M N =．25．{}6,8【解析】()U A B ð={6,8}{2,6,8}{6,8}=．26．A 【解析】{}|13A x x x =-≤或≥，故A B =[-2, -1]． 27．D 【解析】{}|12N x x =≤≤，∴M N =｛1，2｝．28．B 【解析】∵{}1,2B =-，∴A B ={}2．29. 30．C 【解析】∵(0,2)A =，[1,4]B =，所以AB =[1,2)． 31．C 【解析】{}{}{}1,0,10,1,21,0,1,2M N ⋃=-⋃=-，选C ．32．A 【解析】P Q =}{34x x ≤<．33．B 【解析】由题意知{|2}U x N x =∈≥，{|A x N x =∈，所以U A ð={|2x N x ∈<≤，选B ．34．C 【解析】∵{}{}2|200,2A x x x =-==．∴AB =={}0,2． 35．C 【解析】A B ={|23}x x <<．36．B 【解析】∵21x <，∴11x -<<，∴M N ={}|01x x <≤，故选B ．37．C 【解析】{}|3,3A x x =-<，{}|15R B x x x =->≤或ð，∴()R A B =ð{}|31x x --≤≤．38．D 【解析】由已知得，{=0A B x x ≤或}1x ≥，故()U A B =ð{|01}x x <<．39．A 【解析】{|12}A x x =-≤≤，Z B =，故AB ={1,0,1,2}-． 40．C 【解析】{}2,4,7U A =ð．41．C 【解析】“存在集合C 使得,U A C B C ⊆⊆ð”⇔“∅=B A ”，选C ． 42．B 【解析】A =(-∞,0)∪(2，+∞)，∴AB =R ，故选B ． 43．A 【解析】{}1,4,9,16B =，∴{}1,4AB =． 44．A 【解析】∵(1,3)M =-，∴{}0,1,2MN =． 45．C 【解析】因为{31}M x x =-<<，{3,2,1,0,1}N =---, 所以M N {2,1,0}=--，选C ．46．A 【解析】由题意{}1,2,3A B =，且{1,2}B =，所以A 中必有3，没有4，{}3,4U B =ð，故U A B =ð{}3． 47．C 【解析】0,0,1,2,0,1,2x y x y ==-=--；1,0,1,2,1,0,1x y x y ==-=-；2,0,1,2,2,1,0x y x y ==-=．∴B 中的元素为2,1,0,1,2--共5个．48．A 【解析】A ：1->x ，{|1}R A x x =-≤ð，(){1,2}R A B =--ð，所以答案选A49.50．B 【解析】集合B 中含-1，0，故{}1,0A B =-．51．A 【解析】∵{}2,0S =-，{}0,2T =，∴ST ={}0． 52．B 【解析】特殊值法,不妨令2,3,4x y z ===,1w =,则()(),,3,4,1y z w S =∈,()(),,2,3,1x y w S =∈,故选B ．如果利用直接法：因为(),,x y z S ∈，(),,z w x S ∈，所以x y z <<…①，y z x <<…②，z x y <<…③三个式子中恰有一个成立；z w x <<…④，w x z <<…⑤，x z w <<…⑥三个式子中恰有一个成立.配对后只有四种情况：第一种：①⑤成立，此时w x y z <<<，于是(),,y z w S ∈，(),,x y w S ∈；第二种：①⑥成立，此时x y z w <<<，于是(),,y z w S ∈，(),,x y w S ∈；第三种：②④成立，此时y z w x <<<，于是(),,y z w S ∈，(),,x y w S ∈；第四种：③④成立，此时z w x y <<<，于是(),,y z w S ∈，(),,x y w S ∈.综合上述四种情况，可得(),,y z w S ∈，(),,x y w S ∈.53．D 【解析】()f x 的定义域为M =[-1,1],故R M ð=(,1)(1,)-∞-⋃+∞,选D54．A 【解析】当0a =时，10=不合，当0a ≠时，0∆=，则4a =．55.{1，8}【解析】由集合的交运算可得A B ={1，8}．56．A 【解析】U M ð={,,}246．57．D 【解析】{}3,4,5Q =，∴U Q ð={}1,2,6，∴U P Q ð={}1,2．58．D 【解析】由M ={1，2，3，4}，N ={-2，2}，可知-2∈N ，但是-2∉M ，则N ⊄M ，故A 错误．∵MN ={1，2，3，4，-2}≠M ，故B 错误．M∩N ={2}≠N ，故C 错误，D 正确．故选D ．59．B 【解析】A =（-1,2），故B ⊂≠A ，故选B ．60.61．C 【解析】根据题意容易看出x y +只能取-1,1,3等3个数值．故共有3个元素．62．D 【解析】{|1}P x x =< ∴{|1}R P x x =≥ð，又∵{|1}Q x x =>，∴R Q P ⊆ð，故选D ．63．B 【解析】{1,3}P M N ==，故P 的子集有4个．64．C 【解析】因为P M P =，所以M P ⊆，即a P ∈，得21a ≤，解得11a -≤≤，所以a 的取值范围是[1,1]-．65．D 【解析】因为{1,2,3,4}MN =，所以()()U U M N 痧=()U M N ð={5,6}．66．B 【解析】因为U M N ⊂ð，所以()()()U U U U N NM N M ==痧痧 =[()]U U N M 痧={1,3,5}．67．C 【解析】由2211x y x y ⎧+=⎨+=⎩消去y ，得20x x -=，解得0x =或1x =，这时1y =或0y =，即{(0,1),(1,0)}A B =，有2个元素．68．A 【解析】集合{1,0,1}{0,1,2}={0,1}M N =-．69．D 【解析】{}{}|1,|12R R B x x A B x x ==痧≥≤≤70．A 【解析】根据题意可知，N 是M 的真子集，所以MN M =． 71．C 【解析】{}{}{}1,2,32,3,42,3M N ==故选C.72．5【解析】{1,2,3}{2,4,5}{1,2,3,4,5}A B ==，5个元素． 73．{1,2,3}【解析】{2}U B =ð，A(U B ð)={1,2,3}．所以R A ð=2(,0],2⎛⎫-∞+∞ ⎪ ⎪⎝⎭．74．1【解析】由题意1B ∈，显然1a =，此时234a +=，满足题意，故1a =．75．D 【解析】因为{3}AB =，所以3∈A ，又因为{9}U B A =ð，所以9∈A ，所以选D ．本题也可以用Venn 图的方法帮助理解．。

专题3.3垂径定理姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分100分，试题共24题，其中选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2019秋•金平区期末）下列语句，错误的是（）A．直径是弦B．相等的圆心角所对的弧相等C．弦的垂直平分线一定经过圆心D．平分弧的半径垂直于弧所对的弦2．（2019春•西湖区校级月考）如图，⊙O的直径CD＝10，AB是⊙O的弦，AB⊥CD于M，且DM：MC ＝4：1，则AB的长是（）A．2 B．8 C．16 D．3．（2019秋•兴国县期末）如图，⊙O的弦AB⊥OC，且OD＝2DC，AB＝2，则⊙O的半径为（）A．1 B．2 C．3 D．94．（2019秋•天津期末）如图，已知AB、AC都是⊙O的弦，OM⊥AB，ON⊥AC，垂足分别为M，N，若MN，那么BC等于（）A．5 B．C．2D．5．（2020•龙泉驿区模拟）如图，AB是⊙O的直径，弦CD⊥AB于点E，BE＝1cm，CD＝6cm，则AE为（）cm．A．4 B．9 C．5 D．86．（2019秋•通州区期末）如图，将⊙O沿着弦AB翻折，劣弧恰好经过圆心O．如果弦AB＝4，那么⊙O 的半径长度为（）A．2 B．4 C．2D．47．（2019秋•仪征市期末）如图，在⊙O中，分别将、沿两条互相平行的弦AB、CD折叠，折叠后的弧均过圆心，若⊙O的半径为4，则四边形ABCD的面积是（）A．8 B．16 C．32 D．328．（2019秋•连云港期中）如图，四边形ABCD内接于⊙O，AB＝AD，BC＝3．劣弧BC沿弦BC翻折，刚好经过圆心O．当对角线BD最大时，则弦AB的长是（）A．B．2C．D．29．（2020•浙江自主招生）如图，将半径为4cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长度为（）A．4cm B．cm C．cm D．（2）cm10．（2018•高邮市一模）如图，已知⊙O的半径为5，AB是⊙O的弦，AB＝8，Q为AB中点，P是圆上的一点（不与A、B重合），连接PQ，则PQ的最小值为（）A．1 B．2 C．3 D．8二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上11．（2019秋•黄岩区期末）如图，⊙O的直径CD长为6，点E是直径CD上一点，且CE＝1，过点E作弦AB⊥CD，则弦AB长为．12．（2020秋•梁溪区期中）把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF＝CD＝12cm，则球的半径为cm．13．（2020秋•西城区校级期中）筒车是我国古代发明的一种水利灌溉工具，彰显了我国古代劳动人民的智慧，如图1，点P表示筒车的一个盛水桶．如图2，当筒车工作时，盛水桶的运行路径是以轴心O为圆心，5m为半径的圆，且圆心在水面上方．若圆被水面截得的弦AB长为8m，则筒车工作时，盛水桶在水面以下的最大深度为m．14．（2019秋•顺义区期末）如图，⊙O的直径AB＝10，弦CD⊥AB于点E，若BE＝2，则CD的长为．15．（2019秋•瑞安市期中）一面墙上有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接于矩形，如图，若矩形的高为2m，宽为m，则要打掉墙体的面积为m2．16．（2020•常州模拟）石拱桥是中国传统桥梁四大基本形式之一，如图，已知一石拱桥的桥顶到水面的距离CD为8m，桥拱半径OC为5m，求水面宽AB＝m．17．（2019秋•瑞安市期末）某公路上有一隧道，顶部是圆弧形拱顶，圆心为O，隧道的水平宽AB为24m，AB离地面的高度AE＝10 m，拱顶最高处C离地面的高度CD为18m，在拱顶的M，N处安装照明灯，且M，N离地面的高度相等都等于17m，则MN＝m．18．（2019秋•宿豫区期中）如图，⊙O的半径为5，OP＝3，过点P画弦AB，则AB的取值范围是．三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）19．（2019秋•奉化区期末）如图，在一座圆弧形拱桥，它的跨度AB为60m，拱高PM为18m，当洪水泛滥到跨度只有30m时，就要采取紧急措施，若某次洪水中，拱顶离水面只有4m，即PN＝4m时，试通过计算说明是否需要采取紧急措施．20．（2019秋•东城区校级期中）如图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分，如图EM经过圆心交⊙O于点E，EM⊥CD，并且CD＝4cm，EM＝6cm，求⊙O的半径．21．如图，正方形ABCD内接于⊙O，M为的中点，连接BM，CM，求证：BM＝CM．22．（2019秋•海淀区期中）如图，一条公路的转弯处是一段圆弧（），点O是这段弧所在圆的圆心．AB ＝100m，C是上一点，OC⊥AB，垂足为D，CD＝10m，求这段弯路的半径．23．（2019秋•东台市期中）如图，在⊙O中，直径为MN，正方形ABCD的四个顶点分别在半径OM、OP 以及⊙O上，并且∠POM＝45°，若AB＝1．（1）求OD的长；（2）求⊙O的半径．24．（2017秋•农安县校级期中）如图，在平面直角坐标系中，点M在x轴的正半轴上，⊙M交x轴于A，B两点，交y轴于C，D两点，且C为弧AE的中点，连接CE、AE、CB、EB、AE与y轴交于点F，已知A（﹣2，0）、C（0，4）．（1）求证：AF＝CF；（2）求⊙M的半径及EB的长．。

20202021学年九年级数学下册尖子生同步培优题典【人教版】专题28.1锐角三角函数姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分100分，试题共24题，其中选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2020•河池）在Rt △ABC 中，∠C ＝90°，BC ＝5，AC ＝12，则sin B 的值是（ ） A ．512B ．125C ．513D ．12132．（2019秋•玉环市期末）Rt △ABC 中，∠C ＝90°，若AB ＝4，cos A =45，则AC 的长为（ ） A ．125B ．165C ．203D ．53．（2020•普陀区一模）已知在Rt △ABC 中，∠C ＝90°，sin A =13，那么下列说法中正确的是（ ） A ．cos B =13B ．cot A =13C ．tan A =2√23D ．cot B =2√234．（2018秋•枞阳县期末）在△ABC 中，∠C ＝90°，若cos A =13，则sin B 的值为（ ） A ．13B ．23C ．√33D ．15．（2018秋•市中区校级期中）已知α为锐角，且tan α=13，则sin α＝（ ） A ．23B ．√105C ．3√1010D ．√10106．（2020•岳麓区模拟）如图，在6×6的正方形网格中，△ABC 的顶点都在小正方形的顶点上，则tan ∠BAC 的值是（ ）A ．45B ．43C ．34D ．357．（2019秋•港南区期末）在Rt △ABC 中，AC ＝8，BC ＝6，则cos A 的值等于（ ） A ．35B ．√74C ．45或√74D ．45或2√778．（2019•崇川区二模）如图，在Rt △ABC 中，斜边AB 的长为m ，∠A ＝35°，则直角边BC 的长是（ ）A ．m sin35°B ．m cos35°C ．m sin35°D ．mcos35°9．（2017•费县模拟）如图，已知直线l 1∥l 2∥l 3∥l 4，相邻两条平行直线间的距离都是1，如果正方形ABCD 的四个顶点分别在四条直线上，则sin α＝（ ）A ．12B ．√55C ．√52D ．2√5510．（2009•黑河）如图，⊙O 是△ABC 的外接圆，AD 是⊙O 的直径，若⊙O 的半径为32，AC ＝2，则sin B 的值是（ ）A ．23B ．32C ．34D ．43二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上11．（2019•杭州模拟）在Rt △ABC 中，∠C ＝90°，若AB ＝4，sin A =35，则斜边AB 边上的高CD 的长为 12．（2018•闵行区一模）如图，在Rt △ABC 中，∠ACB ＝90°，CD 是高，如果∠A ＝α，AC ＝4，那么BD ＝ ．（用锐角α的三角比表示）13．（2020•铁东区三模）如图，将∠BAC 放置在5×5的正方形网格中，如果顶点A 、B 、C 均在格点上，那么∠BAC 的正切值为 ．14．（2017秋•蓝田县期末）如图，在Rt △ABC ，∠C ＝90°，sin B =45，AB ＝15，则AC 的值是 ．15．（2019•武侯区模拟）在Rt △ABC 中，若∠C ＝90°，sin A =23，则sin B ＝ ． 16．（2019•咸宁模拟）如图，P （12，a ）在反比例函数y =60x图象上，PH ⊥x 轴于H ，则tan ∠POH 的值为 ．17．（2018•云梦县一模）如图，在Rt △ABD 中，∠A ＝90°，点C 在AD 上，∠ACB ＝45°，tan ∠D =23，则CD CA= ．18．（2018•即墨区自主招生）已知三角函数的变换公式：（a ）cos （x +y ）＝cos x cos y ﹣sin x sin y ，（b ）sin （﹣x ）＝﹣sin x ，（c ）cos （﹣x ）＝cos x ，则下列说法正确的序号是 ． ①cos （﹣30°）=−√32； ②cos75°=√6−√24；③cos （x ﹣y ）＝cos x cos y +sin x sin y ；④cos2x＝cos2x﹣sin2x．三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）19．（2019秋•昌平区期末）如图，在Rt△ABC中，∠C＝90°，tan A=13，BC＝2，求AB的长．20．如图，在Rt△ABC中，∠ABC＝90°，BD⊥AC，BC＝1，AC=√5．（1）求sin A的值．（2）你能通过sin A的值求sin∠CBD的值吗？若能，请求出sin∠CBD的值，若不能，请说明理由．21．（2018秋•无锡月考）如图，在Rt△ABC中，∠C＝90°，AB＝15，sin∠A=35，求BC的长和tan∠B的值．22．（2017秋•宝山区期中）如图，△ABC中，AC＝13，BC＝21，tan C=125，求：边AB的长和∠A的正弦值．23．（2020秋•浦东新区期中）如图，在△ABC中，AB＝AC，AD⊥BC，垂足为点D，BC＝18，AD＝6．（1）求sin B的值；（2）点E在AB上，且BE＝2AE，过E作EF⊥BC，垂足为点F，求DE的长．24．（2020•福州模拟）已知△ABC ，AB ＝AC ，∠BAC ＝90°，D 是AB 边上一点，连接CD ，E 是CD 上一点，且∠AED ＝45°． （1）如图1，若AE ＝DE ， ①求证：CD 平分∠ACB ； ②求AD DB的值；（2）如图2，连接BE ，若AE ⊥BE ，求tan ∠ABE 的值．。

卜人入州八九几市潮王学校顺德一中德胜2021届九年级数学尖子生资料3北师大1、为庆贺“六一〞儿童节，某幼儿园举行用火柴棒摆“金鱼〞比赛．如下列图： 按照上面的规律，摆n 个“金鱼〞需用火柴棒的根数为〔〕 A ．26n +B ．86n +C ．44n +D ．8n2、如图，矩形ABCD 中，AB ＞AD ，AB =a ，AN 平分∠DAB ，DM ⊥AN 于点M ，CN ⊥AN 于点N ．那么DM +CN 的值是〔用含a 的代数式表示〕()A ．aB ．a 54C ．a 22D ．a 23D3某种加密规那么为：明文a 、b 对应的密文为a －2b 、2a ＋b ．例如，明文1、2对应的密文是－3、4．当接收方收到密文是1、7时，解密得到的明文是_____。

4、将4个数a b c d ，，，排成2行、2列，两边各加一条竖直线记成a bc d，定义a bc dad bc =-，上述记号就叫做2阶行列式．假设1111x x xx +--+6=，那么x =__________．5、填在下面三个田字格内的数有一样的规律，根据此规律，C=．请你根据这些数据估计上面问题之答案大约是.6、〔2021〕15．如图，假设正方形OABC 的顶点B 和正方形ADEF 的顶点E 都在函数1y x=〔0x >〕的图象上，那么点E 的坐标是 〔，〕.7假设由信纸折成的长方形纸条〔图１〕长AB 为27cm ，宽为xcm,分别答复以下问题：（1） 为了保证可以折成图4P 〕，试求x 的取值范围？（2） 假设不但要折成图4的形状，而且为了美观，希望纸条两端超出点P 的长度相等，即最终图形〔图4〕是轴对称图形。

那么当x=4cm 时，在图1中开场折叠时，点M 应该取在什么位置？8、〔09〕25．一般地，学习几何要从作图开场，再观察图形，根据图形的某一类一共同特征对图形进展分类〔即给一类图形下定义——定义概念便于归类、交流与表达〕，然后继续研究图形的其它特征、断定方法以及图形的组合、图形之间的关系、图形的计算等问题.课本里对四边形的研究即遵循着上面的思路．当然，在学习几何的不同阶段，可能研究的是几何的局部问题．比方有下面的问题，请你研究． ：四边形ABCD 中，AB DC =，且ACB DBC ∠=∠．〔1〕借助网格画出四边形ABCD 所有可能的形状；〔2〕简要说明在什么情况下四边形ABCD 具有所画的形状．参考答案：1、A 。

三中尖子生考试卷和答案一、单项选择题（每题3分，共30分）1. 下列关于中国历史的说法，错误的是：A. 秦始皇统一六国，建立了中国历史上第一个中央集权的封建国家。

B. 唐朝是中国历史上经济、文化、科技高度发展的时期。

C. 明朝时期，中国开始实行闭关锁国政策。

D. 清朝末年，中国开始进行洋务运动，以求自强。

答案：C2. 以下哪个不是中国四大发明之一？A. 造纸术B. 印刷术C. 指南针D. 望远镜答案：D3. 以下哪项不是中国古典文学的代表作？A. 《红楼梦》B. 《西游记》C. 《百年孤独》D. 《水浒传》答案：C4. 下列关于中国地理的描述，正确的是：A. 长江是中国最长的河流。

B. 珠穆朗玛峰是世界上最高的山峰。

C. 中国最大的沙漠是塔克拉玛干沙漠。

D. 中国位于亚洲的东部，太平洋的西岸。

答案：D5. 下列关于中国传统节日的描述，错误的是：A. 春节是中国最重要的传统节日之一，也称为农历新年。

B. 中秋节是农历八月十五，人们会赏月、吃月饼。

C. 端午节是为了纪念屈原，人们会吃粽子、赛龙舟。

D. 重阳节是农历五月初五，人们会登高、赏菊。

答案：D6. 下列关于中国现代史的描述，正确的是：A. 1911年辛亥革命成功，结束了清朝的统治。

B. 1949年中华人民共和国成立，标志着新中国的诞生。

C. 1978年中国开始实行改革开放政策。

D. 以上都是。

答案：D7. 下列关于中国科技成就的描述，错误的是：A. 中国古代四大发明对世界文明的发展产生了深远影响。

B. 中国是世界上第一个发明纸张的国家。

C. 中国古代的天文学和数学成就领先于世界。

D. 中国在现代科技领域没有取得任何重要成就。

答案：D8. 下列关于中国经济发展的描述，正确的是：A. 中国是世界上最大的发展中国家。

B. 中国经济总量位居世界第二。

C. 中国是全球最大的贸易国之一。

D. 以上都是。

答案：D9. 下列关于中国外交政策的描述，错误的是：A. 中国奉行独立自主的和平外交政策。