轮系及其传动比计算
- 格式:doc
- 大小:351.50 KB
- 文档页数:17





定轴轮系传动比的计算在机械传动系统中,传动比指的是输入轴和输出轴之间的转速或转矩比值。
定轴轮系是常见的传动形式之一,其传动比可在设计中给定或计算得到。
本文将介绍定轴轮系传动比的计算方法,并结合实例进行说明。
定轴轮系传动比计算是基于轮系的齿轮参数进行的。
对于一个定轴轮系,通常包含两个或多个齿轮,其中一个齿轮固定在输入轴上,称为主动齿轮;其他齿轮则固定在输出轴或其他齿轮上,称为从动齿轮。
传动比的计算主要依赖于齿轮的齿数和模数等参数。
传动比的计算公式如下:传动比=(主动齿轮齿数/从动齿轮齿数)*(从动齿轮模数/主动齿轮模数)首先,需要明确所需要计算的是速比还是力比。
速比是输出轴速度与输入轴速度之比,力比是输出轴扭矩与输入轴扭矩之比。
这两种比值在实际应用中有不同的需求和意义。
以速比为例,假设一个齿轮传动系统,主动齿轮齿数为N1,模数为M1;从动齿轮齿数为N2,模数为M2、传动比就可以根据上述公式计算得到。
举例来说,假设主动齿轮有20齿(N1=20),模数为2(M1=2),从动齿轮有60齿(N2=60),模数为5(M2=5)。
将这些参数代入传动比公式,计算得到传动比为:传动比=(20/60)*(5/2)=0.4167这意味着输入轴每转一圈,输出轴将转0.4167圈。
也就是说,输出轴的转速是输入轴转速的0.4167倍。
类似地,如果需要计算力比,则可以根据上述公式进行类似的计算。
但需要注意的是,力比与速比不同,它不仅取决于齿数,还与轴的半径和材料等因素有关。
在实际设计中,为了满足特定的工作要求,传动比往往需要进行合理的选择和优化。
可以通过修改主动齿轮和从动齿轮的参数,如齿数、模数等,来实现不同的传动比。
同时,还需要考虑齿轮的尺寸、轴距、强度等因素,以保证传动系统的可靠性和效率。
总而言之,定轴轮系传动比的计算依赖于齿轮的齿数和模数等参数。
通过应用传动比公式,可以计算出期望的速比或力比。
在实际应用中,还需要综合考虑其他因素,以确定最优的传动方案。
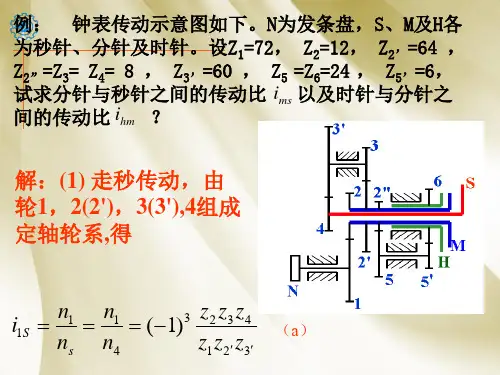

轮系的分类传动比及相关计算讲解轮系是车辆传动系统的重要组成部分,用于将发动机的动力传递给车轮以推动车辆行驶。
轮系可以根据不同的参数进行分类,传动比是轮系中的一个重要参数,而相关计算则可以用于设计和优化轮系。
1.按照传动方式分类:前驱轮系:是指发动机的动力通过传动轴传递给前轮驱动的轮系,常见于前置发动机的前驱车辆。
后驱轮系:是指发动机的动力通过传动轴传递给后轮驱动的轮系,常见于后置发动机的后驱车辆。
四驱轮系:是指发动机的动力通过传动轴同时传递给前轮和后轮驱动的轮系,常见于越野车和高性能跑车。
2.按照结构形式分类:直接驱动轮系:是指发动机的动力直接传递给车轮的轮系,其传动方式相对简单,但传动比较大,常见于低速载重车辆。
间接驱动轮系:是指发动机的动力通过变速器、传动轴等部件传递给车轮的轮系,可以灵活调整传动比以适应不同的驾驶需求。
传动比:传动比是轮系中的一个重要参数,用于描述发动机输出转速和车轮转速之间的比值。
传动比的大小决定了车辆的加速性能、终速以及燃油经济性等。
传动比=车轮转速/发动机转速传动比的计算:传动比的计算可以根据不同的传动方式和结构形式进行。
1.直接驱动轮系的传动比计算:由于直接驱动轮系没有其他传动部件,传动比等于1,即车轮转速等于发动机转速。
2.间接驱动轮系的传动比计算:传动比等于变速器的传动比乘以传动轴的传动比。
传动比计算实例:假设辆车的变速器传动比为2.5,传动轴传动比为3.2,发动机转速为3000转/分钟,求车轮转速。
传动比=2.5*3.2=8相关计算:在轮系设计和优化中,常常需要进行一些相关计算,以满足特定的性能要求。
1.功率计算:根据发动机的输出功率和传动效率,可以计算出轮系的输出功率。
输出功率=发动机输出功率*传动效率2.扭矩计算:根据发动机的输出扭矩和传动效率,可以计算出轮系的输出扭矩。
输出扭矩=发动机输出扭矩*传动效率3.速度计算:根据车轮转速和轮系的传动比,可以计算出车辆的行驶速度。

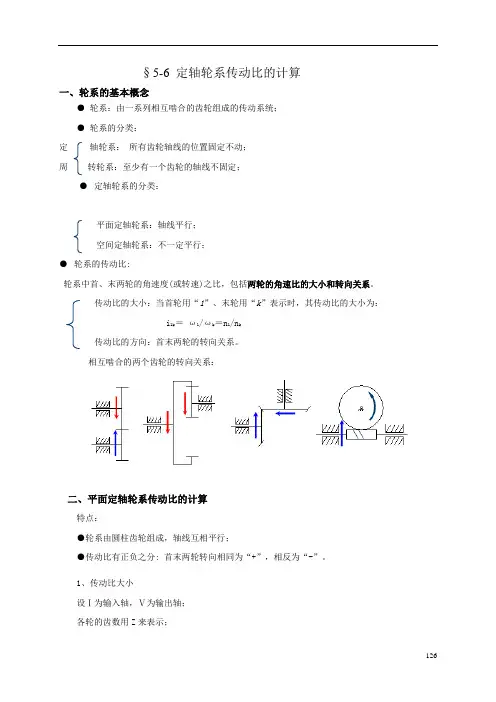
§5-6 定轴轮系传动比的计算一、轮系的基本概念●轮系:由一系列相互啮合的齿轮组成的传动系统;●轮系的分类:定轴轮系:所有齿轮轴线的位置固定不动;周转轮系:至少有一个齿轮的轴线不固定;●定轴轮系的分类:平面定轴轮系:轴线平行;空间定轴轮系:不一定平行;●轮系的传动比:轮系中首、末两轮的角速度(或转速)之比,包括两轮的角速比的大小和转向关系。
传动比的大小:当首轮用“1”、末轮用“k”表示时,其传动比的大小为:i1k=ω1/ωk=n1/n k传动比的方向:首末两轮的转向关系。
相互啮合的两个齿轮的转向关系:二、平面定轴轮系传动比的计算特点:●轮系由圆柱齿轮组成,轴线互相平行;●传动比有正负之分: 首末两轮转向相同为“+”,相反为“-”。
1、传动比大小设Ⅰ为输入轴,Ⅴ为输出轴;各轮的齿数用Z来表示;126127角速度用ω表示;首先计算各对齿轮的传动比:所以:结论: 定轴轮系的传动比等于各对齿轮传动比的连乘积,其值等于各对齿轮的从动轮齿数的乘积与主动轮齿数的乘积之比; 2、传动比方向在计算传动比时,应计入传动比的符号: 首末两轮转向相同为“+”,相反为“-”。
(1)公式法式中:m 为外啮合圆柱齿轮的对数 举例:(2)箭头标注法采用直接在图中标注箭头的方法来确定首末两轮的转向,转向相同为“+”,相反为“-”。
举例:122112z z i ==ωω32223332z i z ωωωω'''===33434443z i z ωωωω'''===455445z z i ==ωω11211)1(--==k km k k z z z z i K K ωω三、空间定轴轮系的传动比特点:●轮系中包含有空间齿轮(如锥齿轮、蜗轮蜗杆、螺旋齿轮等);●首末两轮的轴线不一定平行。
1 传动比的大小2 传动比的方向注意:只能采用箭头标注法,不能采用(-1)m法判断。
分两种情况讨论:情况1:首、末两轮轴线平行传动比计算式前应加“+”、“-”号,表示两轮的转向关系。

复合轮系的传动比计算举例复合轮系是一种广泛应用于机械传动系统中的传动装置,它通过将多个齿轮组合在一起来实现不同传动比的选择。
在计算复合轮系的传动比时,需要考虑到齿轮的模数、齿数、齿轮传动的组合方式以及齿轮轴的结构等因素。
下面将以一个具体的例子来说明复合轮系的传动比计算方法,并对齿轮的选型进行分析。
假设传动的输入轴为轴1,输出轴为轴3,而轴2为一个中间轴。
传动需要实现从轴1到轴3的传递,且需要通过轴2实现一个降速传递。
该传动的传动比为1:3首先,需要确定传动比为1:3,即轴1的转速是轴3转速的1/3假设齿轮1和齿轮2分别安装在轴1和轴2上,齿轮3和齿轮4分别安装在轴2和轴3上。
设齿轮1、齿轮2、齿轮3和齿轮4的模数分别为m1、m2、m3和m4,齿数分别为z1、z2、z3和z4齿轮的模数和齿数的关系为:m=z/n,其中,m为齿轮的模数,z为齿数,n为模数选择系数。
根据传动比的要求,可以得到以下关系:(1)z1/z2=(z3/z4)*(n3/n4),根据实际情况,可以对齿轮进行合理的选型。
一般选取齿数较大的齿轮作为主动齿轮,较小的齿轮作为从动齿轮,以保证齿轮的强度和寿命。
假设选择n1=1,n2=1,n3=1,n4=2,则可以得到以下方程:(1)z1/z2=(z3/z4)*(1/2),为了方便计算,我们假设齿数z1为30,则可以得到:(1)30/z2=(z3/z4)*(1/2),通过求解以上方程,可以得到齿轮的组合方式和齿数的选取。
例如,当z2=60,z3=40,z4=80时,满足以上方程的条件。
再通过计算得到各个轴的转速:n1=n2=1n3=n1*z1/z3=1*30/40=0.75n4=n2*z2/z4=1*60/80=0.75所以,传动比为:n=n1/n3=1/0.75=1.33即轴1的转速是轴3转速的1.33倍,满足1:3的要求。
以上是复合轮系传动比计算的一个例子。
对于实际的应用,根据具体的传动要求和条件,可以进行不同的选型和计算,以满足特定的传动比要求。
第八章 轮系及其传动比计算 第四十八讲 齿轮系及其分类 如图8—1所示,由一系列齿轮相互啮合而组成的传动系统简称轮系。根据轮系中各齿轮运动形式的不同,轮系分类如下: 图8—1 图8—2 图8—3 定轴轮系中所有齿轮的轴线全部固定,若所有齿轮的轴线全部在同一平面或相互平行的平
面内,则称为平面定轴轮系,如图8—1所示,若所有齿轮的轴线并不全部在同一平面或相互平行的平面内,则称为空间定轴轮系;若轮系中有一个或几个齿轮轴线的位置并不固定,而是绕着其它齿轮的固定轴线回转,如图8—2,8—3所示,则这种轮系称为周转轮系,其中绕着固定轴线回转的这种齿轮称为中心轮(或太阳轮),即绕自身轴线回转又绕着其它齿轮的固定轴线回转的齿轮称为行星轮,支撑行星轮的构 图8—4 件称为系杆(或转臂或行星架),在周转轮系中,一般都以中心轮或系杆作为运动的输入或输出构件,常称其为周转轮系的基本构件;周转轮系还可按其所具有的自由度数目作进一步的划分;若周转轮系的自由度为2,则称其为差动轮系如图8—2所示,为了确定这种轮系的运动,须给定两个构件以独立运动规律,若周转轮系的自由度为1,如图8—3所示,则称其为行星轮系,为了确定这种轮系的运动,只须给定轮系中一个构件以独立运动规律即可;在各种实际机械中所用的轮系,往往既包含定轴轮系部分,又包含周转轮系部分,或者由几部分周转轮系组成,这种复杂的轮系称为复合轮系如图8—4所示,该复合轮系可分为左边的周转轮系和右边的定轴轮系两部分。 第四十九讲 定轴轮系的传动比 1、传动比大小的计算 由前面齿轮机构的知识可知,一对齿轮:
i12 =ω1 /ω2 =z2 /z1
对于齿轮系,设输入轴的角速度为ω1,输出轴的角速度为ωm ,按定义有:
i1m=ω1 /ωm
当i1m>1时为减速, i1m<1时为增速。 因为轮系是由一对对齿轮相互啮合组成的,如图8—1所示,当轮系由m对啮合齿轮组成时,有: 2、首、末轮转向的确定 因为角速度是矢量,故传动比计算还有首末两轮的转向问题。对直齿轮表示方法有两种。 1)用“+”、“-”表示 适用于平面定轴轮系,由于所有齿轮轴线平行,故首末两轮转向不是相同就是相反,相同取“+”表示,相反取“-”表示,如图8—5所示,一对齿轮外啮合时两轮转向相反,用“-”表示;一对齿轮内啮合时两轮转向相同,用“+”表示。可用此法逐一对各对啮合齿轮进行分析,直至确定首末两轮的转向关
系。设轮系中有m对外啮合齿轮,则末轮转向为(-1)m,此时有:
积所有主动轮齿数的连乘积所有从动轮齿数的连乘m
mi)1(1
图8—5
2)画箭头 如图8—6所示,箭头所指方向为齿轮上离我们最近一点的速度方向。 外啮合时:两箭头同时指向(或远离)啮合点。头头相对或尾尾相对。 内啮合时:两箭头同向。 对于空间定轴轮系,只能用画箭头的方法来确定从动轮的转向。 (1)锥齿轮,如图8—7所示,可见一对相互啮合的锥齿轮其转向用箭头表示时箭头方向要么同时指向节点,要么同时背离节点。 (2)蜗轮蜗杆,由齿轮机构中蜗轮蜗杆一讲的知识可知,一对相互啮合的蜗轮蜗杆其转向可用左右手定则来判断,如图8—8所示。 (3)交错轴斜齿轮,用画速度多边形确定,如图8—9所示。 图8—6 图8—7 图8—8 图8—9 例一:已知如图8—10所示轮系中各轮齿数,
求传动比i15。 解:1.先确定各齿轮的转向,用画箭头的方法可确定首末两轮转向相反。 2. 计算传动比 其中齿轮2对传动比没有影响,但能改变从动轮的转向,称其为过轮或中介轮。 图8—10 第五十讲 周转轮系的传动比
周转轮系的分类除按自由度以外,还可根据其基本构件的不同来加以分类,如图所示,设轮系中的太阳轮以K表示,系杆以H表示,则图8—11所示为2K—H型轮系;图8—12为3K型轮系,因其基本构件为3个中心轮,而系杆只起支撑行星轮的作用。在实际机构中常用2K—H型轮系。 图8—11 图8—12 周转轮系由回转轴线固定的基本构件太阳轮(中心轮)、行星架(系杆或转臂)和回转轴线不固定的其它构件行星轮组成。由于有一个既有公转又有自转的行星轮,因此传动比计算时不能直接套用定轴轮系的传动比计算公式,因为定轴轮系中所有的齿轮轴线都是固定的。为了套用定轴轮系传动比计算公式,必须想办法将行星轮的回转轴线固定,同时由不能让基本构件的回转轴线发生变化。如图所示,我们发现在周转轮系中,基本构件的回转轴线相同,而行星轮即绕其自身轴线转动,有随系杆绕其回转轴线转动,因此,只要想办法让系杆固定,就可将行星轮的回转轴线固定,即把周转轮系变为定轴轮系,如图8—13所示。
反转原理:给周转轮系施以附加的公共转动-H后,不改变轮系中各构件之间的相对运动, 但原轮系将转化成为一新的定轴轮系,可按定轴轮系的公式计算该新轮系的传动比。转化后所得的定轴轮系称为原周转轮系轮系的“转化轮系”。将整个轮系机构按-H反转后,各构件的角速度的变化如下:
图8—13 构件 原角速度 转化后的角速度 1 ω1 ωH1=ω1-ωH
2 ω2 ωH2=ω2-ωH
3 ω3 ωH3=ω3-ωH
H ωH ωHH=ωH-ωH=0 由角速度变化可知机构转化后,系杆角速度为0,既系杆变成了机架,周转轮系演变成定轴轮系,因此可直接套用定轴轮系传动比的计算公式。上式“-”说明在转化轮系中ωH1与ωH3方向相反。 通用表达式: 特别注意: 1、齿轮m、n的轴线必须平行。 2、计算公式中的±不能去掉,它不仅表明转化轮系中两个 3、太阳轮m、n之间的转向关系,而且影响到ωm、ωn、ωH的计算结果。 如果周转轮系是行星轮系,则ωm、ωn中必有一个为0(不妨设ωn=0),此时上述通式可改写如下: 即: )(11ZfiiHmnHm
以上公式中的ωi可用转速ni代替: 用转速表示有:
)(zfnnnnnniHnHmHnHmHmn 图8—14 例二、如图8—14所示2K-H轮系中,Z1=Z 2=20,Z 3=60,轮3固定。 求:1)i1H 。
2)n1=1, n3=-1,求nH 及i1H 的值。 3)n1=1, n3=1,求nH及i1H 的值。
∴ i1H=4 , 齿轮1和系杆转向相同。
得: i1H = n1 / nH =-2,两者转向相反。 n1=1, n3=1,得: i1H = n1 / nH =1,两者转向相同。 结论:1、轮1转4圈,系杆H同向转1圈。 2、轮1逆时针转1圈,轮3顺时针转1圈,则系杆顺时针转2圈。 3、轮1轮3各逆时针转1圈,则系杆逆时针转1圈。
特别强调:1、i13≠ iH
13
2、i13≠- z3/z1
例三:如图8—15示圆锥齿轮组成的轮系中,已知:z1=33,z2=12,z2’=33,求i3H
解:判别转向:齿轮1、3方向相反 i3H =2
特别注意:转化轮系中两齿轮轴线不平行时,不能直接计算!
图8—15
不成立!ωH2 ≠ω2-ωH
事实上,因角速度ω2是一个向量,它与牵连角速度ωH和相对角速度ωH2之间的关系为:ω2 =ωH +ωH
2
∵P为绝对瞬心,故轮2中心速度为:V2o=r2ωH
2 又V2o=r1ωH
∴ωH2=ωH r1/ r2=ωH tg1=ωH ctgδ2 第五十一讲 复合轮系的传动比 复合轮系或者是由定轴部分与周转部分组成,或者是由几部分周转轮系组成,因此复合轮系传动比求解的思路是:先将复合轮系分解为基本轮系,分别计算各基本轮系的传动比,然后根据组合方式找出各轮系间的关系,联立求解。 根据上述方法,复合轮系分解的关键是将周转轮系分离出来。因为所有周转轮系分离完后复合轮系要么分离完了,要么只剩下定轴轮系了。周转轮系的分离步骤是先找回转轴线不固定的行星轮,找出后确定支撑行星轮的系杆,然后再找出与行星轮啮合的中心轮,至此,一个周转轮系就分离出来了;用上述方法一直寻找,混合轮系中可能有多个周转轮系,而一个基本周转轮系中至多只有三个中心轮。剩余的就是定轴轮系。 例四:如图8—16示为龙门刨床工作台的变速机构,J、K为电磁制动器,设已知各轮的齿数,
求J、K分别刹车时的传动比i1B。 解:1、刹住J时:1-2-3为定轴轮系,B-5-4-3’为周转轮系,3-3’将两者连接。 定轴部分:i13=ω1/ω3=-z3/ z1
周转部分:iB3’ 5=(ω3’-ωB)/(0-ωB) =-z5/z3’
连接条件:ω3=ω3’
联立解得:)1('351311zzzziBB 2、刹住K时:A-1-2-3为周转轮系,B-5-4-3’为周转轮系,5-A将两者连接。 周转轮系1:i A13=(ω1 -ωA ) /(0 -ωA )
=-z3/z1 图8—16 周转轮系2:iB3’5=(ω3’-ωB )/(ω5-ωB)=-z5/z3’
连接条件:ω5=ωA
联立解得:BABABBiizzzzi51515'31311)1)(1(
总传动比为两个串联周转轮系的传动比的乘积。 混合轮系的解题步骤: 1、找出所有的基本轮系。关键是找出周转轮系! 2、求各基本轮系的传动比。 3、根据各基本轮系之间的连接条件,联立基本轮系的传动比方程组求解。