(完整word版)一次函数图像的应用

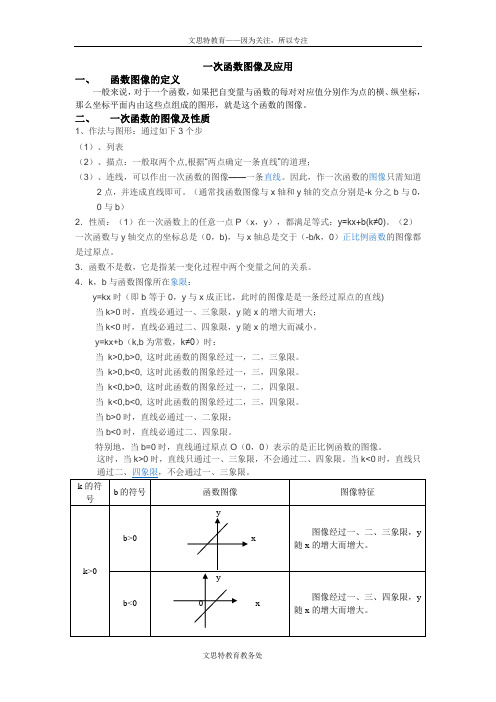
一次函数图像及应用一、函数图像的定义一般来说，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图像。

二、一次函数的图像及性质三、小试身手1、画出函数y=2x-1与y=-0.5x+1的图象2、直线y=2x-3与x轴交点坐标为_______，与y轴交点坐标为_________，•图象经过第________象限，y随x增大而_________．3、分别说出满足下列条件的一次函数的图象过哪几个象限？（1）k>0 b>0 （2）k>0 b<0（3）k<0 b>0 （4）k<0 b<04、在同一直角坐标系中画出下列函数图象，并归纳y=kx+b（k、b是常数，k≠0）中b对函数图象的影响．１．y=x-1 y=x y=x+1２．y=-2x+1 y=-2x y=-2x-1练习巩固1、例1 小芳以200米／分的速度起跑后，先匀加速跑5分钟，每分提高速度20米／分，又匀速跑10分钟．试写出这段时间里她跑步速度y（米／分）随跑步时间x（分）变化的函数关系式，并画出图象．2、Ａ城有肥料200吨，Ｂ城有肥料300吨，现要把这些肥料全部运往Ｃ、Ｄ两乡．从Ａ城往Ｃ、Ｄ两乡运肥料费用分别为每吨20元和25元；从Ｂ城往Ｃ、Ｄ两乡运肥料费用分别为每吨15元和24元．现Ｃ乡需要肥料240吨，Ｄ乡需要肥料260吨．怎样调运总运费最少？3、从Ａ、Ｂ两水库向甲、乙两地调水，其中甲地需水15万吨，乙地需水13万吨，Ａ、Ｂ两水库各可调出水14万吨．从Ａ地到甲地50千米，到乙地30千米；从Ｂ地到甲地60千米，到乙地45千米．设计一个调运方案使水的调运量（万吨·千米）最少．4、某单位急需用车，但又不准备买车，他们准备和一个体车主或一国有出租车公司其中一家签让合同．设汽车每月行驶x千米，应付给个体车主的月费用是y 1元，应付给出租车公司的月费用是y2元，y1、y2分别是x之间函数关系如下图所示．每月行驶的路程等于多少时，租两家车的费用相同，是多少元？四、课后习题1.当x <0时,函数y =-2x 的图象在A.第一象限B.第二象限C.第三象限D.第四象限2.直线x y 3-=过点(0,0)和点A.(1,-3)B.(1,3)C.(-1,-3)D.(3,-1)3.函数x y 2=与x y 3-=的共同特点是A.图象经过一､三象限B.图象经过二､四象限C.图象经过原点D.y 随着x 的增大而增大4.函数y =-x 21+1和y =x 21+1的图象交于一点,这点的坐标是A.(1,21) B.(-1,23) C.(1,0) D.(0,1)5.函数x m y )1(-=(1≠m ),y 随着x 的增大而增大,则A.m <0B.m >0C.m <1D.m >19.下面图象中,不可能是关于x 的一次函数y =mx -(m -3)的图象的是10.在同一个直角坐标系中,对于函数①y=-x-1,②y=x+1,③y=-x+1,④y=-2(x+1)的图象,下列说法正确的是A.通过点(-1,0)的是①和③B.交点在y轴上的②和④C.相互平行的是①和③D.关于x轴对称的是②和③32.某公司市场营业员销部的营销人员的个人收入与其每月的销售量成一次函数关系,其图象如图所示.由图中给出的信息可知,营销人员没有销售时的收入是A.310B.300C.290D.28033.如图,OA,BA分别表示甲､乙两名学生运动的一次函数图象,图中s和t分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快A.2.5米B.2米C.1.5米D.1米34.一游泳池长90米,甲､乙二人分别在游泳池相对两边同时朝另一边游泳,甲的速度是3米/秒,乙的速度是2米/秒,图中的实线和虚线分别为甲､乙与游泳池一边的距离随游泳时间的变化而变化图象.若不计转向时间,则从开始起到3分钟止他们相遇的次数为A.2次B.3次C.4次D.5次。

一次函数的函数图像与方程解析解的实际应用一次函数是数学中常见的一种函数类型，它可以表示为y = ax + b的形式，其中a和b为已知值，x和y为自变量和因变量。

在这篇文章中，我们将讨论一次函数的函数图像以及如何使用方程解析解来解决实际应用问题。

一、一次函数的函数图像一次函数的函数图像是一条直线，其斜率确定了直线的倾斜程度，截距则决定了直线与y轴的交点。

根据斜率的正负，可以判断直线是上升还是下降。

下面我们来看几个具体的例子。

1. 实例一：y = 2x + 1这个函数表示了一个斜率为2，截距为1的直线。

根据斜率的正值，我们知道这条直线上升。

当x增加1个单位时，y增加2个单位。

当x减小1个单位时，y减小2个单位。

通过这些关系，我们可以画出该函数的函数图像。

2. 实例二：y = -3x + 2这个函数表示了一个斜率为-3，截距为2的直线。

根据斜率的负值，我们知道这条直线下降。

当x增加1个单位时，y减小3个单位。

当x减小1个单位时，y增加3个单位。

同样地，我们可以通过这些关系画出该函数的函数图像。

通过观察这些例子，我们可以发现直线的倾斜程度（斜率）以及它与y轴的交点（截距）等信息可以从一次函数的解析解中推导出来。

这样，我们可以在解析解的基础上直观地了解一次函数的函数图像。

二、一次函数方程解析解的实际应用一次函数的解析解除了可以用来绘制函数图像之外，还可以应用于解决实际问题。

我们将通过以下两个实际应用问题来说明。

1. 实例一：销售收入问题假设一个公司以每件产品x销售价y的方式进行销售。

已知该公司每个月的固定成本是1000元，每件产品的可变成本是30元。

我们希望找到销售多少件产品时，公司能够实现盈亏平衡。

根据以上信息，我们可以写出一次函数的方程：总收入 = 总成本根据题意，总收入为yx，总成本为1000 + 30x。

将它们相等并整理方程，可得：yx = 1000 + 30x解这个一次方程，我们可以求得x的解析解。

最全一次函数图像专题(带解析)完整版.doc最全一次函数图像专题(带解析)完整版一次函数也称为一次方程或线性方程，是数学中的重要概念。

在本专题中，我们将详细讨论一次函数的图像及相关概念和性质。

一、一次函数的定义与性质一次函数是指形如y = kx + b的函数，其中k和b为常数，k 称为斜率，b称为截距。

一次函数的图像是一条直线，其斜率决定了直线的倾斜程度，截距决定了直线与y轴的交点位置。

二、一次函数的图像特征1. 斜率k的正负决定了直线的倾斜方向。

当k为正数时，直线向右上方倾斜；当k为负数时，直线向右下方倾斜。

2. 斜率k的绝对值决定了直线的倾斜程度。

绝对值越大，倾斜程度越大。

3. 当k为0时，直线为水平线；当k不存在时，直线为竖直线。

三、一次函数图像的基本形状1. 当k>0时，直线从左下方向右上方倾斜。

2. 当k=1时，直线为45°斜线。

3. 当k=-1时，直线为水平斜线。

4. 当k=0时，直线为水平线。

5. 当k不存在时，直线为竖直线。

四、一次函数的图像平移1. 沿x轴平移的结果：将y = kx + b中的b替换为b'，则得到的函数为y = kx + b'。

平移后的直线与原直线平行，斜率不变，但截距发生了变化。

2. 沿y轴平移的结果：将y = kx + b中的k替换为k'，则得到的函数为y = k'x + b。

平移后的直线与原直线平行，截距不变，但斜率发生了变化。

五、一次函数的图像伸缩1. 垂直伸缩的结果：将y = kx + b中的k替换为ak，其中a 为正数。

当a>1时，直线变得更陡峭；当0<a<1时，直线变得更平缓。

2. 水平伸缩的结果：将y = kx + b中的x替换为x/a，其中a为正数。

当a>1时，直线变得更平缓；当0<a<1时，直线变得更陡峭。

六、一次函数的解析法与图像的关系1. 斜率k的正负决定了图像的倾斜方向。