剔除异常数据的几种统计检验方法
- 格式:pdf
- 大小:494.81 KB
- 文档页数:9

异常值处理的四种方法异常值是数据分析中常见的问题,它们可能是由于测量误差、数据输入错误或其他原因导致的。
异常值对数据分析的结果有很大的影响。
因此,处理异常值是数据分析的一个重要环节。
本文将介绍四种常见的异常值处理方法。
一、删除异常值删除异常值是最常见的异常值处理方法之一。
该方法是将数据集中的异常值删除,然后重新计算统计指标。
这种方法的优点是简单易行,但也有一些缺点。
首先,删除异常值可能会导致数据集的大小减小,从而影响统计分析的准确性。
其次,删除异常值可能会导致数据集的偏差,从而影响数据分析的结果。
二、替换异常值替换异常值是另一种常见的异常值处理方法。
该方法是将异常值替换为数据集中的其他值,例如平均值、中位数或众数。
这种方法的优点是可以保留数据集的大小和形状,从而减少数据集的偏差。
但是,替换异常值可能会导致数据集的平均值、中位数或众数等统计指标发生变化,从而影响数据分析的结果。
三、离群值检测离群值检测是一种用于识别异常值的方法。
该方法是通过统计学方法或机器学习方法来识别数据集中的异常值。
常用的离群值检测方法包括箱线图、Z分数、Tukey方法和LOF方法等。
这种方法的优点是可以准确地识别异常值,从而提高数据分析的准确性。
但是,离群值检测可能会导致一些正常值被错误地标记为异常值,从而影响数据分析的结果。
四、分组处理分组处理是一种将数据集分组并分别处理的方法。
该方法是将数据集中的异常值分组,并对每个组进行单独的处理。
例如,可以将数据集按照年龄、性别、职业等因素分组,并对每个组进行单独的处理。
这种方法的优点是可以保留数据集的大小和形状,从而减少数据集的偏差。
但是,分组处理可能会导致数据集中的某些组大小太小,从而影响数据分析的结果。
综上所述,异常值处理是数据分析的一个重要环节。
不同的异常值处理方法有不同的优缺点,需要根据具体情况选择合适的方法。
在实际应用中,可以根据经验和领域知识来选择合适的方法,并结合多种方法进行处理,以提高数据分析的准确性和可靠性。

试验数据异常值的检验及剔除方法
摘要
异常值(outliers)指的是可能存在的测试数据点,其值大大偏离了
它们的数据集的中位数或平均值,如果未及时发现和处理这些异常值,将
会严重影响实验数据的准确性和有效性,因此,检验和剔除测试数据中的
异常值是必不可少的任务。
本文将介绍测试数据异常值检验和剔除的方法,旨在有效改善测试数据的准确性和有效性。
一、异常值的定义
异常值简单来说,指的是数据集中与其他所有值有明显差异的数据点。
它可能是由于实验环境的变化,实验设备的变化,数据获取的失误而产生的,或者错误的测量结果导致的。
二、异常值的检验
在检验数据中是否存在异常值之前,首先要明确测试数据的分布类型。
根据数据的分布,可采用不同的检验方法,通常按照如下步骤检验异常值:(1)可先将测试数据按照箱线图或四分位图等形式画出,看看数据
是否符合正态分布;
(2)可以计算数据的中位数、平均数、标准偏差等,来查看异常值
的程度;
(3)可以根据数据的中位数、平均数等,计算出数据的上下限,这
样便可以将数据划分为”正常“和”异常“;
(4)可以使用基于概率的检验方法,此方法可以给出异常值的检验
结果。

如何检测异常值并且剔除它们异常值(Outliers)是指与大多数数据样本显著不同或者离群的数据点。
异常值可能是由数据采集错误、数据录入错误、异常事件或者其他非统计因素引起的。
检测和剔除异常值在数据分析和模型建立中非常重要,因为异常值的存在可能会明显干扰分析结果和模型性能。
以下是一些常见的方法和技巧可以用来检测和剔除异常值:1. 箱线图(Box plot):箱线图是一种可视化工具,可以显示数据的五数概括(最小值、第一四分位数、中位数、第三四分位数、最大值),同时也可以检测潜在的异常值。
箱线图会将数据点超出上下限的点标记为异常值,并且可以根据不同的判断标准来确定。
2. 3σ原则(3-sigma rule):根据正态分布的性质,在正态分布中,约有99.7%的观测值落在距离均值±3倍标准差的范围内,因此可以将超出这个范围的观测值视为异常值。
可以通过计算数据的均值和标准差,然后筛选出超出均值±3倍标准差的数据点。
3. 置信区间(Confidence interval):可以使用置信区间来检查数据点是否在预期的范围内。
根据样本的大小和置信水平,可以计算置信区间的上限和下限,并将超出这个范围的数据视为异常值。
一般来说,95%的置信区间可以覆盖绝大多数正态分布数据。
4. Z-score:Z-score可以帮助我们判断一个数据点与均值之间的差异程度。
Z-score表示一个数据点距离均值的标准差数目。
一般来说,超过±3的Z-score值可以视为异常值。
5. Tukey方法:Tukey方法是一种基于四分位数的判断异常值的方法。
该方法通过计算第一四分位数(Q1)和第三四分位数(Q3),然后计算Q3 + 1.5 * IQR和Q1 - 1.5 * IQR,其中IQR表示四分位差(Q3 - Q1),超出这个范围的数据点可以被视为异常值。
6.检查数据的物理规律:在一些情况下,可以根据数据的物理规律来判断异常值。

浅谈计量检定中异常值的判别与剔除摘要:本文解释了异常值的定义及造成异常值的原因,说明了计量检定中剔除异常值的意义,列举了剔除异常值常用的三个统计判别方法,包括拉依达准则、格拉布斯准则和狄克逊准则。
同时,举例比较了统计判别方法的差异,及在计量检定中,怎样选择合适的统计判别法剔除异常值。
关键词:计量检定;异常值;判别;剔除;准则一、异常值的定义及计量检定中造成异常值的原因异常值又称离群值,指在对一个被测量重复观测所获的若干观测结果中,出现了与其他值偏离较远且不符合统计规律的个别值,他们可能属于来自不同的总体,或属于意外的、偶然的测量错误。
也称为存在着“粗大误差”。
造成异常值的原因:震动、冲击、电源变化、电磁干扰等意外的条件变化,人为的读数、记录或计算错误,仪器内部的偶发故障、操作不当等。
二、计量检定中剔除异常值的意义通过计量检定获得的数据中混有异常值,必然会歪曲测量结果,能将该值剔除不用,可使结果更符合客观情况,但若剔除了一些偏离较远但不属于异常值的数据,却适得其反,则不能真实地反映测得值的分散性,所以必须正确地判别和剔除异常值。
三、计量检定中异常值的判别与剔除(一)物理判别法在测量过程中,记错、读错、仪器突然跳动、突然震动等异常情况引起的已知原因的异常值,应该随时发现,随时剔除,即必须是已知原因的明显错误或突发事件造成的数据异常可以随时剔除。
(二)统计判别法有时仅仅是怀疑某个值,对于不能确定哪个是异常值时,必须采用统计判别法进行判别,判定为异常值的才能剔除。
判别异常值常用的统计方法有拉依达准则(或称3σ准则)、格拉布斯准则、狄克逊准则。
1.拉依达准则拉依达准则又称为3σ准则。
当重复观测次数充分大的前提下(n>>10),设按贝塞尔公式计算出的实验标准差为s,若某个可疑值与n个测得值的平均值之差的绝对值大于或等于3s时,判定为异常值,即应满足下式:2.格拉布斯准则设在一组重复观测值中,其残差的绝对值最大者为可疑值,在给定的包含概率为或,也就是显著水平为或时,判定为异常值时应满足下式:——与显著水平和重复观测次数有关的格拉布斯临界值,该临界值需要查格拉布斯准则的临界值表。

计量测试中异常数据剔除的措施计量测量,其本身便是一项对数据精准性有着极高要求的工作。
而要确保数据获取的精准性,除了需科学处理计量测量所得出的数据外,尚需找出其中的异常数据并将之剔除,如此方能作为相关科学的参考依据。
当前,国内已然根据计量测量中异常数据的出现原因提出了4种有针对性的异常数据剔除方法,这些方法可独立使用,亦可综合利用,其目的均在于判定异常值并将之剔除,以确保计量测量数据的准确性。
1 计量仪器出现误差的原因由于计量仪器对外部环境有着极高的要求,加之其本身也是一种高精密的仪器,因而任何外部环境的变化都可能导致仪器测试结果产生偏差,并最终影响到检测结果的准确性。
就当前的外部环境而言,可能導致计量仪器产生误差的原因主要包括以下几个方面:(1)仪器受到了外界诸如震动、机械动荡一类的自然或人为因素影响;(2)受电磁干扰或因供电电压不稳而导致的检测仪器出现故障;(3)操作人员本身经验不足,加之操作事物所因其的检测不准确;(4)仪器本身存在如元件损坏、零件松动一类的质量问题,这类问题一旦发生,将直接导致检测结果不准确,从而影响到工作人员的正常测量。
对于以上影响因素,操作人员在实际的操作过程中,务必全面排除,如此方能确保测量结果的准确性。
当然,在此过程中,针对异常值的剔除尚需注意采取合适的剔除方法,若剔除方法选择不当则可能收获适得其反的效果。
简言之,即针对异常值不同的产生原因需采取有针对性的剔除方法,方能确保仪器测量结果达到规定的使用标准。
在实际的判断异常值过程中,以下几种是当前人们最常用的异常值判断准则,即3∑准则、肖维勒准则、t检验法以及格拉布斯准则。
2 计量测试中异常数据剔除的措施以上所提准则,虽其实际内容各不相同,但却均是置信概率的运用基础,而所谓的置信概率,即随机变量于置信区间内的落入概率。
若实际的运用过程中,将置信区间内的测量数据实际范围用X来表示,那么以上所提之准则则能用以下方式来表达:2.1 3∑准则该式子所表达的含义为可疑数据与整租数据的算术平均差,其目的是要找出该差与3倍哒的绝对值之间的差异,若偏差较大则将此数值舍弃。

目录摘要...................................................... 错误!未定义书签。
关键词................................................... 错误!未定义书签。
1 引言...................................................... 错误!未定义书签。
2 异常值的判别方法..................................... 错误!未定义书签。
检验(3S)准则........................................ 错误!未定义书签。
狄克松(Dixon)准则.................................. 错误!未定义书签。
格拉布斯(Grubbs)准则.............................. 错误!未定义书签。
指数分布时异常值检验................................. 错误!未定义书签。
莱茵达准则(PanTa).................................. 错误!未定义书签。
肖维勒准则(Chauvenet)............................. 错误!未定义书签。
3 实验异常数据的处理 .................................. 错误!未定义书签。
4 结束语................................................... 错误!未定义书签。
参考文献.................................................... 错误!未定义书签。
试验数据异常值的检验及剔除方法摘要:在实验中不可避免会存在一些异常数据,而异常数据的存在会掩盖研究对象的变化规律和对分析结果产生重要的影响,异常值的检验与正确处理是保证原始数据可靠性、平均值与标准差计算准确性的前提.本文简述判别测量值异常的几种统计学方法,并利用DPS软件检验及剔除实验数据中异常值,此方法简单、直观、快捷,适合实验者用于实验的数据处理和分析.关键词:异常值检验;异常值剔除;DPS;测量数据1 引言在实验中,由于测量产生误差,从而导致个别数据出现异常,往往导致结果产生较大的误差,即出现数据的异常.而异常数据的出现会掩盖实验数据的变化规律,以致使研究对象变化规律异常,得出错误结论.因此,正确分析并剔除异常值有助于提高实验精度.判别实验数据中异常值的步骤是先要检验和分析原始数据的记录、操作方法、实验条件等过程,找出异常值出现的原因并予以剔除.利用计算机剔除异常值的方法许多专家做了详细的文献[1]报告.如王鑫,吴先球,用Origin 剔除线形拟合中实验数据的异常值;严昌顺.用计算机快速剔除含粗大误差的“环值”;运用了统计学中各种判别异常值的准则,各种准则的优劣程度将体现在下文.2 异常值的判别方法判别异常值的准则很多,常用的有t 检验(3S )准则、狄克松(Dixon )准则、格拉布斯(Grubbs )准则等准则.下面将一一简要介绍. 2.1 检验(3S )准则t 检验准则又称罗曼诺夫斯基准则,它是按t 分布的实际误差分布范围来判别异常值,对重复测量次数较少的情况比较合理.基本思想:首先剔除一个可疑值,然后安t 分布来检验被剔除的值是否为异常值.设样本数据为123,,n x x x x ,若认j x 为可疑值.计算余下1n -个数据平均值1n x -及标准差1n s -,即2111,1,1n n i n i i j x x s n --=≠=-∑.然后,按t 分布来判别被剔除的值j x 是否为异常值.若1(,)n j x x kn a -->,则j x 为异常值,应予剔除,否则为正常值,应予以保留.其中:a 为显著水平;n 数据个数;(,)k n a 为检验系数,可通过查表得到.2.2 狄克松(Dixon )准则设有一组测量数据123nx x x x ≤≤≤,且为正态分布,则可能为异常值的测量数据必然出现在两端,即1x 或n x .狄克松给出了不同样本数量n 时检验统计量的计算公式(见表1).当显著水平a 为1%或5%时,狄克松给出了其临界值1()a n D -.如果测量数据的检验统计量1()a n D D ->,则1x 为异常值,如果测量数据的检验统计量'1()a n D D ->,则n x 为异常值.2.3 格拉布斯(Grubbs )准则设有一组测量数据为正态分布,为了检验数据中是否存在异常值,将其按大小顺序排列,即123n x x x x ≤≤≤,可能为异常值的测量数据一定出现在最大或最小的数据中.若最小值1x 是可疑的,则检验统计量1()/G x x s =-.式中x 是均值、s 是标准差,即211,n i i x xs n ==∑. 对于检验统计量G ,格拉布斯导出了其统计分布,并给出了当显著水平a 为1%或5%时的临界值(1)()n G n -.(1)()n G n -称格拉布斯系数,可通过抽查表得到.当最小值1x 或最大值n x 对应的检验统计量G 大于临界值时,则认为与之对应的1x 或n x 为可疑异常值,应予以剔除.2.4 指数分布时异常值检验设一组测量数据为指数分布,为了检验数据中是否存在异常值,将其按大小顺序排列,即123n x x x x ≤≤≤.检验最小值或最大值是否为异常值的检验方法如下:当样本量100n ≤时,计算统计量()1/nn n n i i T x x ==∑及(1)11/nn i i T x x ==∑对于给定的显著水平a (通常取)和样本数量n ,通过查表得到()n n T 及(1)n T 分别对应的临界值()(1)n n T a -和(1)()n T a .若()()(1)n n n n T T a >-时,认为n x 为异常值;若(1)(1)()n n T T a <时,认为1x 为异常值. 当样本容量100n >时,计算统计量()111(1)()/()nn n n n i n i E n x x x x --==--+∑及(1)111(1)/()nn i i E n n x x n x ==-+∑. 对于给定显著水平a 和样本数量n ,若11()2,2~2,1(1)(1)n n n n aE F n a --->=--,则判断n x 为异常值;若11(1)2,22,(1)[(1)1]n n n a E F n a --->=---,则判断1x 为异常值. 2.5 莱茵达准则(PanTa )对于实验数据测出值123,,,,nx x x x ,求取其算术平均值11/ni i x n x ==∑及剩余误差值i i v x x =-,然后求出其均方根偏差21/2(/1)i v n σ=-∑. 判别依据(假设v 服从正态分布):3i x x σ->,则i x 相对而言误差较大,应舍去; 3i x x σ-≤,i x 为正常数据,应该保留.有概率论统计可知,如果误差服从正要分布,误差大于3σ的观测数据出现的概率小于,相当大于300次观测中有一次出现的可能.莱茵达准则只是进行粗略的剔除,取舍的概率较小,可能将不合理的异常值保留.2.6 肖维勒准则(Chauvenet )次准则也是建立在实验数据服从正态分布.假设多次测量的n 个测量值中,数据的参与误差i c v Z σ>,则剔除该数据.其中21/2(/1)i v n σ=-∑,样品容量为n 时的判别系数3c Z <,弥补了莱茵达准则的不足,故此准则优胜于莱茵达准则,但条件更为苛刻.3 实验异常数据的处理对于测定中异常数据的处理,必须慎重考虑,不能凭预感任意删除或添加.应该从所学知识上考虑,异常值有时能反映试验中的某些新现象.这类“异常值”正深化人们对客观事物的认识,如果随意删除它,可能深入了解和发现新事物的一次机会,那么对学者深入研究非常可惜.所以对任何异常数据都因首先在技术上寻找原因,如果在技术上发现原因,理应舍去.如在技术上无法作出判断,却可在上述准则中发现其高度异常,也因舍弃.其中,运用DPS 软件进行异常数据的检验与剔除特别方便,而且不许编写程序,它融合了SPSS 表格和EXCELL 表格,操作简单,实用性强.如图一下为DPS 数据处理系统对话框.图一 数据处理系统对话框只要执行菜单命令下的“数据分析——异常值检验”弹出如图二下图的窗口,然后进行选择检验分析方法及显著水平,点击确定即可.图二用户对话框在测定中,有时发现个别数据离群严重,上述检验原则为异常值,但它与其他测定值的差异在仪器的精度范围内,这种数据不应舍去,应予保留.而对于一些分析而言,需要估计总体参数,异常数据一般都要舍去.对于不同的之心度应作相应的处理,则要据实际情况而定.4结束语由上述可知,用DPS软件进行异常值检验和剔除的过程简单、直观、快捷,适用于大众学生进行各实验数据的处理和分析.将此软件运用于实验教学,可以使学生快速准确判断实验结果,也可以提高教学质量.参考文献[1] 王鑫,吴先球.用Origin剔除线形拟合中实验数据的异常值[J].山西师范大学学报,2003,17(1),56—57.[2] 严昌顺.用计算机快速剔除含粗大误差的“环值”[J].计量技术,1994(5),45—47.[3] 苏金明,傅荣华,周建斌.统计软件SPSS系列应用实战篇[M].电子工业出版社,2002[4] 唐起义.DPS数据处理系统——实验设计、统计分析及数据挖掘[M].科学出版社,2006[5] 何国伟等编著.误差分析方法.北京:国防工业出版社,1978。

经济统计数据的异常检验与处理方法在经济领域,统计数据的准确性和可靠性对于决策和预测具有重要意义。
然而,由于各种原因,经济统计数据中常常会出现异常值,即与其他观测值相比明显偏离的数据点。
这些异常值可能是由于测量误差、数据录入错误、样本选择偏差或者其他未知因素引起的。
为了确保统计数据的准确性,我们需要对这些异常值进行检验和处理。
一、异常值检验方法1. 离群值检验离群值检验是最常用的异常值检验方法之一。
它通过计算观测值与均值之间的偏差来确定异常值。
常用的离群值检验方法包括标准差法、箱线图法和Grubbs检验法等。
- 标准差法:根据正态分布的性质,我们可以将均值加减两倍标准差的范围定义为正常值的范围,超出这个范围的观测值可以被认为是异常值。
- 箱线图法:箱线图通过绘制数据的四分位数和中位数来展示数据的分布情况。
根据箱线图,我们可以将超出1.5倍四分位距的观测值定义为异常值。
- Grubbs检验法:Grubbs检验法基于统计学原理,通过计算观测值与均值之间的差异来确定异常值。
该方法可以检测出单个异常值或者多个异常值。
2. 趋势异常检验除了离群值检验,我们还可以通过趋势异常检验来发现数据中的异常情况。
趋势异常检验主要关注数据的变化趋势是否与历史数据相符。
常用的趋势异常检验方法包括移动平均法、指数平滑法和回归分析法等。
- 移动平均法:移动平均法通过计算一段时间内的平均值来观察数据的趋势。
如果某个观测值与移动平均值之间的偏差超过一定阈值,就可以认为该观测值存在异常。
- 指数平滑法:指数平滑法通过对数据进行加权平均来计算预测值。
如果某个观测值与预测值之间的偏差超过一定阈值,就可以认为该观测值存在异常。
- 回归分析法:回归分析法通过建立统计模型来预测数据的变化趋势。
如果某个观测值与回归模型的预测值之间的偏差超过一定阈值,就可以认为该观测值存在异常。
二、异常值处理方法1. 删除异常值一种常见的异常值处理方法是直接删除异常值。

处理异常值的方法引言:在数据分析和统计学中,异常值是指明显不符合预期模式或分布的数据点。
这些异常值可能是由于数据采集错误、测量误差、数据录入错误或真实世界中的异常情况引起的。
处理异常值对于保证数据的准确性和分析结果的可靠性非常重要。
本文将介绍一些常见的方法来处理异常值。
一、识别异常值在处理异常值之前,我们首先需要识别出数据中的异常值。
常见的识别方法包括:1. 基于统计学方法:使用统计学模型和方法,如标准差、箱线图、Z分数等,来识别数据中的异常值。
2. 基于可视化方法:通过绘制直方图、散点图、箱线图等可视化图表,来发现数据中的异常值。
3. 基于专家判断:依靠领域专家的经验和知识,对数据进行评估和筛选,识别出异常值。
二、处理异常值的方法一旦识别出异常值,我们可以采取以下几种方法进行处理:1. 删除异常值:最简单的方法是直接删除异常值。
但需要注意,在删除异常值之前,需要确保这些数据点确实是异常值,并非数据采集或录入错误。
删除异常值可能会导致数据量减少、样本偏差等问题,因此需要谨慎使用。
2. 替换异常值:替换异常值是常见的处理方法之一。
替换可以采用以下几种策略:- 均值或中位数替换:将异常值替换为数据的均值或中位数。
均值替换适用于数据近似正态分布的情况,中位数替换适用于数据存在较多离群值的情况。
- 分组均值或中位数替换:将异常值替换为相同分组数据的均值或中位数。
这种方法可以更准确地估计异常值所在分组的真实情况。
- 回归模型预测:使用回归模型对异常值进行预测,并将预测值作为替换值。
这种方法可以利用其他变量之间的关系来更准确地估计异常值。
3. 转换异常值:转换异常值是通过数学变换来调整异常值,使其符合数据分布的方法。
常见的转换方法包括:- 对数转换:对数据取对数,可以将右偏分布转换为接近正态分布。
- 偏度和峰度调整:通过调整数据的偏度和峰度,使其更接近正态分布。
- 区间缩放:通过将数据映射到特定区间,如[0, 1]或[-1, 1],来调整异常值。

异常值处理的四种方法异常值,也称为离群值,是指在一组数据中与其他数据显著不同的数值。
异常值的出现可能是由于测量误差、数据输入错误、系统故障或者真实存在的特殊情况等原因造成的。
在数据分析中,异常值会对结果产生影响,因此需要进行异常值处理。
本文将介绍四种常见的异常值处理方法。
一、删除异常值删除异常值是最简单的处理方法之一,直接将异常值从数据中删除。
这种方法适用于异常值数量很少的情况,删除后对数据分析结果的影响很小。
但是,如果异常值数量较多,删除后可能会导致数据量减少,从而影响分析结果的准确性。
二、替换异常值替换异常值是指用其他数值替换异常值。
替换的方法有多种,如用该变量的平均值、中位数或者众数替换异常值。
这种方法适用于异常值数量较多的情况,可以保持数据量不变,但如果替换的数值过于接近其他数据,可能会对结果产生误差。
三、分组处理异常值分组处理异常值是将数据按照一定的规则分组,然后对每个组的异常值进行处理。
这种方法可以避免异常值对整体数据的影响,同时可以更好地反映数据的真实情况。
例如,在统计某个城市的房价时,可以将房价按照不同区域分组,然后对每个区域的异常值进行处理。
四、使用统计方法处理异常值使用统计方法处理异常值是一种更为科学的方法,包括基于分布的方法和基于模型的方法。
基于分布的方法是指根据数据分布的特征来判断异常值,常用的方法有箱线图、Z分数法和3σ原则等。
基于模型的方法是指使用模型来判断异常值,例如线性回归模型、聚类模型等。
这种方法可以更好地反映数据的真实情况,但需要一定的统计知识和技能。
综上所述,异常值处理是数据分析中不可避免的一部分。
不同的处理方法适用于不同的情况,需要根据实际情况选择合适的方法。
同时,需要注意处理异常值的原则,不能简单地删除或替换异常值,应该根据数据的特点和分析目的来进行处理,保证数据分析结果的准确性和可靠性。
异常数据的判别和剔除在一个测呈列屮,误差超出极限值的测最数据称为异常数据。
它的出现,往往是由于某种错误或预测不到的环境突变引起的。
这些异常数据会歪曲实验或测量结果。
为了使测量数据能真实地反映实际情况,需要-个鉴别异常数据的科学标准,用一定的方法去鉴别并把异常数据剔除。
鉴别异常数据的基本思想是以一定置信水平确定一个置信限,凡是超过该限度的误差就认为它不属丁•随机误差的范出而予以剔除。
剔除一次异常数据Z后,对余卜•的数据重新检查, 航到测量列的其他数据都在规定的置信限内,才使用这些数据计算测量结果。
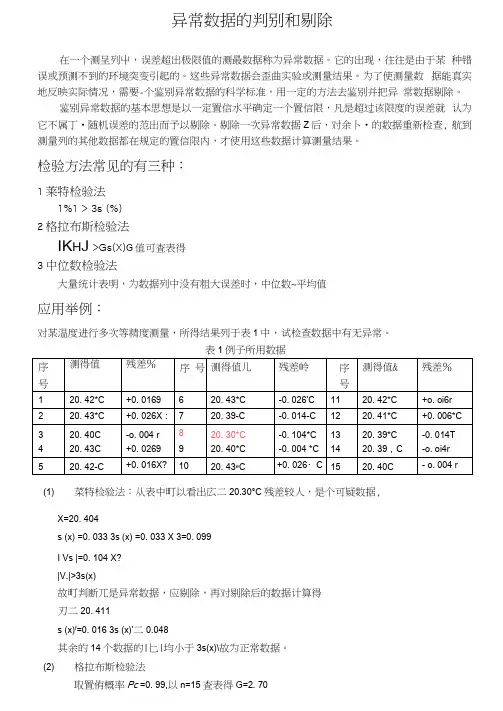
检验方法常见的有三种:1莱特检验法1%1 > 3s (%)2格拉布斯检验法IK H J >Gs(X)G值可査表得3中位数检验法大量统计表明,为数据列中没有粗大误差时,中位数~平均值应用举例:对某温度进行多次等精度测量,所得结果列于表1中,试检查数据中有无异常。
表1例子所用数据(1)菜特检验法:从表中町以看出広二20.30°C残差较人,是个可疑数据,X=20. 404s (x) =0. 033 3s (x) =0. 033 X 3=0. 099I Vs |=0. 104 X?|V.|>3s(x)故町判断兀是异常数据,应剔除,再对剔除后的数据计算得刃二20. 411s (x)f=0. 016 3s (x)'二0.048其余的14个数据的|匕|均小于3s(x)\故为正常数据。
(2)格拉布斯检验法取置侑概率Pc =0. 99,以n=15査表得G=2. 70Gs (x) =2. 70X0. 033=0. 09<|V«|,剔除上后重新计算判别得n=14, Pc =0. 99 下的G 值为 2. 66Gs (x)'=2. 66X0.016=0. 04 余卜墩据中无异常值。
(3)中位数检验法20. 30, 20. 39, 20. 39, 20. 39, 20. 40, 20. 40. 20. 40, 20.41, 20. 42, 20. 42, 20. 42,20.43, 20.43, 20.43, 20.43通过此例及以往经验我们应该注意几个问题:(1)所仃的检验法都是人为主观拟定的,至今尚未令统一的规定。
异常值处理方法异常值,也被称为离群点,是指在数据集中与其他数据点差别较大的数据点。
在数据分析中,异常值的存在会对结果产生干扰,因此需要对其进行处理。
本文将介绍常见的异常值处理方法。
一、删除异常值删除异常值是最常见的处理方法之一。
其基本思想是将异常值从数据集中删除。
但是,这种方法的缺点是会造成信息的损失,因为异常值可能携带有价值的信息。
此外,如果异常值数量较多,那么删除操作可能会导致数据集的样本量急剧减少,从而影响分析结果的可靠性。
二、替换异常值替换异常值是另一种处理方法。
其基本思想是将异常值替换成数据集中的其他值。
替换的方法有很多种,下面列举几种常见的方法:1.平均值替换法:用变量的平均值代替异常值。
2.中位数替换法:用变量的中位数代替异常值。
3.众数替换法:用变量的众数代替异常值。
4.分位数替换法:将变量按照大小排序,将异常值替换成处于某个分位数的值,如25%分位数、50%分位数、75%分位数等。
5.回归替换法:利用回归分析方法,将异常值用其他变量的值进行预测,然后将预测值代替异常值。
三、离群点检测离群点检测是一种更加精细的处理方法。
其基本思想是利用统计学方法,检测出哪些数据点是异常值,然后将其进行处理。
下面列举几种常见的离群点检测方法:1.均值-标准差检测法:假设数据集服从正态分布,用均值和标准差来检测异常值。
2.箱线图检测法:利用箱线图来检测异常值。
箱线图中,箱子表示数据集的四分位数,箱子上下的线表示上四分位数和下四分位数,箱子外的点表示异常值。
3.基于距离的检测法:利用距离来检测异常值。
常见的方法有k 近邻算法、DBSCAN算法等。
4.基于密度的检测法:利用密度来检测异常值。
常见的方法有LOF算法、HBOS算法等。
总之,异常值处理是数据分析中非常重要的一环。
不同的处理方法适用于不同的数据类型和分析目的,需要根据具体情况进行选择。
在处理异常值时,需要注意保持数据的完整性和可靠性。
剔除异常值的方法剔除异常值是指在数据分析中,对于偏离正常范围的极端数据进行处理或排除的方法。
异常值可能是由于测量或记录错误、无效数据、异常事件等原因导致的,如果将异常值包括在分析中,可能会对结果产生显著的偏差。
因此,剔除异常值是很重要的数据预处理步骤,下面是常用的剔除异常值的方法:1.标准差法:标准差是描述数据集合离散程度的统计量,如果一些数据点与平均值的偏离程度超过了一定的标准差范围,可以判定为异常值。
根据经验,在正态分布的情况下,采用平均值加减3倍标准差的范围内的数据是比较典型的数据集合。
2.箱线图法:箱线图是一种常用的异常值检测方法,它能够直观地显示数据的分组情况及异常值。
箱线图通过绘制数据集的上四分位数(Q3), 下四分位数(Q1)和中位数(Median)以及上下边界,可以看出数据中是否存在异常值。
根据箱线图,异常值被定义为小于Q1-1.5IQR或大于Q3+1.5IQR的数据点,其中IQR指的是四分位距。
3.3σ原则:3σ原则是指在正态分布的情况下,大约99.73%的数据位于平均值加减3倍标准差的范围之内。
因此,可以根据3σ原则剔除超出平均值加减3倍标准差范围之外的数据点。
4.多元异常值检测:多元异常值检测是指通过多个变量之间的关系检测异常值。
常用的方法有杠杆性和学生化残差。
杠杆性指的是一个数据点对回归结果的影响程度,可以使用杠杆值来判定异常值。
学生化残差是指将残差标准化后的值,可以通过学生化残差的阈值来检测异常值。
5.离群点分数法:离群点分数法是一种基于分位数的异常值检测方法,通过计算数据点相对于其他数据点的离散程度来评估异常值。
常用的离群点分数包括Z-Score、箱线图的方法以及帕累托法则。
6.局部离群点因子法:局部离群点因子(Local Outlier Factor, LOF)是一种基于密度的异常值检测方法。
LOF通过计算每个数据点相对于其邻居数据点的离散程度来评估异常值。
LOF值越大,表示越可能是异常值。
异常试验数据的剔除方法1.观察剔除法:观察剔除法是最简单直接的异常数据剔除方法,它基于对实验数据进行观察和分析的方法。
通过观察数据的分布情况和实验是否出现了明显的异常情况,可以剔除异常的试验数据。
2.3σ原则:3σ原则是一种常用的统计学剔除异常数据的方法。
这种方法假设试验数据服从正态分布,基于标准差进行判断。
根据3σ原则,平均值加减3倍标准差之外的数据可以被判定为异常数据,并进行剔除。
3.箱线图剔除法:箱线图剔除法是一种基于统计学的方法。
通过绘制箱线图,可以直观地观察数据的分布情况和是否存在异常值。
箱线图将数据的中位数、上下四分位数和离群值可视化,根据经验判断是否有离群值,从而进行剔除。
4. Grubbs检验:Grubbs检验是一种常用的单变量异常值检验方法。
它基于假设检验的思想,通过计算试验数据的离群程度,判断是否应该剔除该数据。
Grubbs检验根据试验数据的最大/最小值与均值的差异,计算统计量,并与临界值进行比较,从而判断数据是否异常。
5. Hampel校正:Hampel校正是一种鲁棒性更强的异常值处理方法。
它通过对数据的多次迭代,识别具有较大偏差的异常值,并对其进行剔除或修正。
这种方法不仅可以剔除异常值,还可以对异常值进行修正,提高数据的稳定性和可靠性。
需要注意的是,异常数据的剔除应该谨慎进行。
在进行剔除操作之前,需要对试验数据进行充分的分析和检验,确保剔除的准确性和合理性。
此外,剔除异常数据可能会导致原始数据的丢失,因此需要根据实际情况进行权衡和决策。
总结起来,异常试验数据的剔除是科学研究和数据分析中不可或缺的一项工作。
合理有效地剔除异常数据可以提高数据的准确性和可靠性,从而得出更加科学和可靠的结论。
以上介绍的方法只是其中的一部分,根据实际情况可以选择合适的方法进行异常数据的剔除。
异常数据4种剔除方法异常数据是指与其他数据不一致或不符合预期的数据。
在数据分析和建模过程中,异常数据可能会影响统计结果和模型的准确性。
因此,为了保证分析结果的可靠性,通常需要对异常数据进行剔除或修正。
以下是常见的四种剔除异常数据的方法。
1.箱线图检测异常值箱线图是一种常用的异常值检测方法,它以数据的分位数为基础,通过上下四分位距来判断数据是否异常。
根据箱线图,我们可以判断出数据中的异常值,并将其剔除。
首先,绘制箱线图以可视化数据的分布情况。
箱线图由一个箱体和两条触须组成。
箱体表示数据的四分位数范围,上触须和下触须分别表示上四分位数和下四分位数与最大非异常值和最小非异常值之间的距离。
根据箱线图,我们可以识别出在上下触须之外的数据点,这些点通常是异常值。
然后,我们可以将这些异常值从数据集中剔除,以保证后续分析的准确性。
2.3σ原则剔除异常值3σ原则是一种基于数据的均值和标准差的统计方法,用于判断数据是否异常。
在正态分布下,大约68%的数据位于均值的±1σ范围内,95%的数据位于均值的±2σ范围内,99.7%的数据位于均值的±3σ范围内。
因此,我们可以基于3σ原则来识别并剔除数据中的异常值。
首先,计算数据的均值和标准差。
然后,根据3σ原则,识别出超出3倍标准差范围之外的数据点,并将其从数据集中剔除。
3.离群点检测算法剔除异常值离群点检测算法是一种自动化的异常值识别方法。
常用的离群点检测算法包括聚类算法(如K-means算法)、孤立森林算法、LOF(局部异常因子)算法等。
这些算法可以根据数据的特征属性来识别出异常值,并将其从数据集中剔除。
4.领域知识和业务规则剔除异常值除了基于统计和算法的方法,领域知识和业务规则同样可以用于剔除异常值。
领域专家通常对数据的特点和业务规则有深入的了解,可以根据经验判断数据是否异常。
比如,在一些业务场景下,根据实际情况设定阈值,超出阈值的数据可以被视为异常并剔除。
异常样本剔除方法
异常样本是指与其他样本有明显差别的样本,通常是由数据采集错误、噪声或极端值等原因引起的。
在进行数据分析和建模时,如果不剔除异常样本,会导致模型的精确度降低,甚至使模型无法使用。
以下是常见的异常样本剔除方法:
1. 3σ原则:根据正态分布的特点,数据分布在平均值的±3σ范围内的概率为99.7%。
因此,可以将超出这个范围的数据视为异常值,并将其剔除。
2. 箱型图法:箱型图可以直观地显示数据的分布情况,通过观察箱型图中的异常值,可以将其剔除。
3. 离群点分析法:通过计算样本之间的距离或相似性,将距离或相似性较小的样本划分为一组,观察每组的数据分布情况,将分布与其他组显著不同的组视为异常组,并将其剔除。
4. 人工剔除法:经验丰富的分析师可以根据数据的特点和领域知识,通过人工观察数据,将异常样本进行剔除。
在进行异常样本剔除时,需要注意以下几点:
1. 剔除异常样本要基于充分的数据分析和判断,不能仅凭主观意见。
2. 剔除异常样本可能会影响样本的分布和数量,需要对后续分析和建模的影响进行评估。
3. 异常样本剔除不是万能的解决方案,有些异常值可能具有重要的信息和意义,需要根据实际情况进行判断。
异常值的处理方法异常值指的是与大部分样本明显不符的特殊观测值,可能是由于测量或记录错误、样本的异常属性或极端情况等原因引起的。
处理异常值的方法有很多种,下面我将详细介绍几种常见的异常值处理方法。
1. 舍弃法:舍弃法是指直接将异常值所在的数据记录删除或者不予考虑。
这种方法简单直接,适用于异常值对整体分布没有明显影响的情况。
但是需要注意的是,如果异常值占整体数据的比例较大,使用舍弃法可能会导致样本量过小,从而影响分析结果的可靠性。
2. 替代法:替代法是指用其他数值替代异常值。
常见的替代方法有以下几种:- 用中位数或均值替代异常值:计算整体样本的中位数或均值,将异常值替换成这些值。
优点是简便易行,但较大的异常值将会对均值产生较大影响。
- 用众数替代异常值:当样本变量是离散型数据或者呈现明显的分布情况时,可以用众数替代异常值。
众数是离散型数据中出现频率最高的值,替代异常值可以维持整体分布的连续性。
- 用线性插值或多项式替代法:将异常值视为缺失值,在异常值前后的点之间进行插值,可以使用线性插值或者更复杂的多项式插值方法进行替代。
3. 截断法:截断法又称为缩尾法,指通过设定阈值将超过阈值的异常值截断或缩尾。
具体方法有以下几种:- 上下截断法:设定上下阈值,大于上阈值的异常值设定为上阈值,小于下阈值的异常值设定为下阈值。
这种方法可以避免极端异常值对整体数据的影响,但可能会丢失一部分有用信息。
- 百分位数截断法:按照百分位数对数据进行分段,将超过一定百分位数的异常值设定为该百分位数的值。
比如将超过95%分位数的异常值设定为95%分位数的值。
这种方法可以保留数据的相对位置信息。
4. 基于模型的方法:基于模型的方法是通过建立数据的模型来识别和处理异常值。
常见的方法有:- 基于统计模型的方法:通过建立统计模型,比如正态分布模型或混合模型,对异常值进行识别和剔除。
这种方法适用于数据服从特定分布的情况。
- 基于机器学习的方法:使用机器学习算法对数据进行建模,然后根据模型预测的结果来判断哪些数据属于异常值。