§3扭转
- 格式:pps
- 大小:3.99 MB
- 文档页数:78



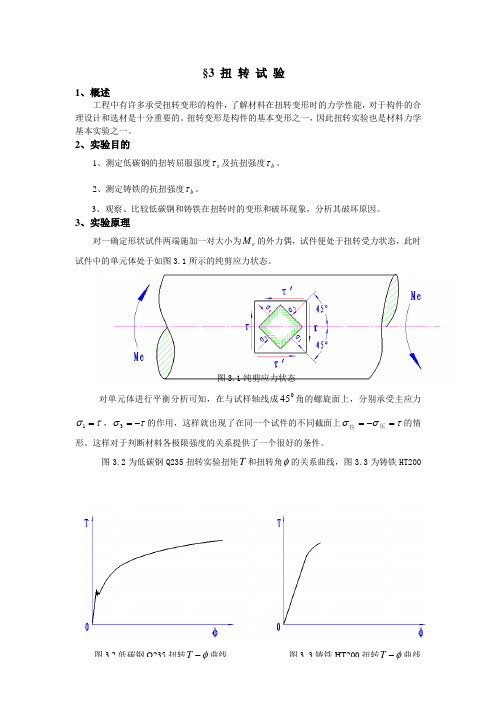
§3 扭 转 试 验1、概述工程中有许多承受扭转变形的构件,了解材料在扭转变形时的力学性能,对于构件的合理设计和选材是十分重要的。
扭转变形是构件的基本变形之一,因此扭转实验也是材料力学基本实验之一。
2、实验目的1、测定低碳钢的扭转屈服强度s τ及抗扭强度b τ。
2、测定铸铁的抗扭强度b τ。
3、观察、比较低碳钢和铸铁在扭转时的变形和破坏现象,分析其破坏原因。
3、实验原理对一确定形状试件两端施加一对大小为e M 的外力偶,试件便处于扭转受力状态,此时试件中的单元体处于如图3.1所示的纯剪应力状态。
图3.1纯剪应力状态对单元体进行平衡分析可知,在与试样轴线成045角的螺旋面上,分别承受主应力τσ=1,τσ-=3的作用,这样就出现了在同一个试件的不同截面上τσσ=-=压拉的情形。
这样对于判断材料各极限强度的关系提供了一个很好的条件。
图3.2为低碳钢Q235扭转实验扭矩T 和扭转角φ的关系曲线,图3.3为铸铁HT200图3.2低碳钢Q235扭转φ-T 曲线 图3. 3铸铁HT200扭转φ-T 曲线试件的扭转实验扭矩T 和扭转角φ的关系曲线。
图3.4为低碳钢和铸铁扭转破坏断口形式由图3.2低碳钢扭转φ-T 曲线可以看出,低碳钢Q235的扭转φ-T 曲线类似于拉伸的L F ∆-曲线,有明显的弹性阶段、流动屈服阶段及强化阶段。
在弹性阶段,根据扭矩平衡原理,由剪应力产生的合力矩需与外加扭矩相等,可得剪应力沿半径方向的分布ρτ为:PI T ρτρ*= 在弹性阶段剪应力的变化如图3.5所示在弹性阶段剪应力沿圆半径方向呈线性分布,据此可得PP W T I r T ==*max τ 当外缘剪应力增加到一定程度后,试件的边缘产生流动现象,试件承受的扭矩瞬间下降,应力重新分布至整个截面上的应力均匀一致,称之为屈服阶段,在屈服阶段剪应力的变化如图3.5 低碳钢扭转试件弹性阶段应力分布变化图3.4低碳钢和铸铁扭转破坏断口形式图3.6所示称达到均匀一致时的剪应力为剪切屈服强度(s τ),其对应的扭矩为屈服扭矩,习惯上将屈服段的最低点定义为屈服扭矩,同样根据扭矩平衡原理可得:Ps P s s W T I T 434*3==ρτ 应力均匀分布后,试件可承受更大的扭矩,试件整个截面上的应力均匀增加,直至试件剪切断裂,如图3.4所示,最大剪应力对应的扭矩为最大扭矩,定义最大剪应力为剪切强度。


第三章 扭 转 1 扭转的力学模型①构件特征——构件为圆截面直杆。
②受力特征——外力偶矩的作用面与杆件轴线相垂直。
③变形特征——杆件各横截面绕杆轴作相对转动。
2圆轴扭转时,横截面上的内力偶矩——扭矩 ①传动轴的速度、传递的功率与外力偶矩之间的关系为{}{}{}minr n KW P M mN e 9950=∙ ②扭矩——构件受扭时,横截面上的内力偶矩,以T 表示。
③扭矩的正负号规定——用右手螺旋法则,扭矩矢量的方向指向截面的为负,背离截面的为正。
④扭矩图——表示圆杆各截面上的扭矩沿杆轴线方向变化规律的图线。
3圆轴扭转时,横截面上的应力、强度条件 (1)横截面上的切应力①分布规律——一点的切应力的大小与该点到圆心的距离成正比,其方向与该点的半径相垂直。
②计算公式 ρτP I T =PP max W TR I T ==τ (2)极惯性矩与扭转截面系数, ①实心圆截面 432D I P π= , 316D W P π=②空心圆截面 ()()444413232αππ-=-=D dDI P ,()44116απ-=D WP式中, Dd =α (3)圆轴扭转的强度条件 []ττ≤=Pmax W T(4)强度计算的三类问题①强度校核 []ττ≤=Pmax W T②截面设计 []τTW P ≥,由P W 计算D⑧许可荷载计算 []P e W M τ≤,由T 计算e M 4.圆轴扭转时的变形,刚度条件 (1)圆轴扭转时的变形小变形时,圆轴的二任意横截面之间仅产生相对的角位移,称为相对扭转角。
① 相对扭转角 ()rad GI TLP=ϕ ②单位长度扭转角 ()m rad GI Tdx d P'==ϕϕ 计算相对扭转角ϕ的公式,应在长度L 范围内,T ,G 和P I 均为常数,若其中任意参数T 或G 或P I 不为常数,则应分段计算ϕ,然后叠加。
2)圆轴扭转时的刚度条件 []()()m GI max T max 'P '0180ϕπϕ≤⨯=5.矩形截面杆扭转的主要结果 (1)横截面上的最大切应力横截面上的最大切应力发生在矩形截面的长边中点处;即 3b Tmax βτ=式中,β为与比值h 有关的系数,可查文献1中表3—1获得。
第三章扭转§3.1 扭转的概念及实例§3.2 外力偶矩的计算扭矩及扭矩图§3.3 纯剪切§3.4 圆轴扭转时的应力及强度条件§3.5 圆轴扭转时的变形及刚度条件*§3.6 圆柱形密圈螺旋弹簧的应力和变形§3.7 非圆截面杆扭转的概念§3.8 薄壁杆件的自由扭转本章习题§3.1 扭转的概念及实例卡车的传动轴主传动轴卡车的方向盘扭转构件的受力特点:在垂直于杆件轴线的两个平面内,作用一对大小相等、转向相反的力偶。
…………变形特点:各横截面绕轴线发生相对转动。
A B O M e M e γOBA ϕ“轴”:以扭转为主要变形的直杆称为轴。
如:机器中的传动轴、石油钻机中的钻杆等。
外力偶矩M e 的计算)( 9549m N n P M e ⋅=其中:P —功率,(kW )n —转速,(rpm )所以已知传递功率P 、转速n 求外力偶矩M e :ω⨯=e M P 功率为力偶在单位时间内作的功:602n ⋅=πω其中:§3.2外力偶矩的计算单位:?(3.1)e e x M T M T M =∴=-=∑ 0:0 2、扭矩的求法——截面法:1、扭矩:轴的内力——内力偶矩,记作“T ”§3.2…… 扭矩及扭矩图M e M ex a a M e T x a a M eT x aa3、扭矩T的正负符号规定:“右手螺旋法则”右手拇指指向外法线方向为:正(+),反之为:负(-)。
4、扭矩图:形象表示沿杆件轴线各横截面上扭矩(T )变化规律的图形。
⑵|T |max 值及所在截面位置——(危险截面)⇒强度计算xT ⊕⑴内力的变化规律:作扭矩图的步骤:⑴求所有外力:支座反力;⑵分段求其内力:扭矩值;⑶分段作扭矩图。
100 Nm[]。
求:各段扭矩及画扭图,,,,如图已知例题 m kN 10 15 20 30: 4321⋅=⋅=⋅=⋅=m m kN m m kN m m kN m mkN m m T ⋅-=+-=+-= 102003 212mkN m T ⋅-=-= 30 11 E D C B A m 4m 3m 2m 1122段解:求AB 段求BC 11m1A T 122m 2 m 1T 2mkN m m m T ⋅=++-=++-= 5152030 3213mkN m m m m T ⋅=++++-=+++-= 1510152030 43214段求CD mkN m m T ⋅-=+-= 10212m kN m T ⋅-=-= 3011 E D C B Am 4m 3m 2 m 133T 3段求DE 44T 410kNm15kNm30kNm5kNm⊕⊕xTm kNm mmmT⋅=+ ++ -=154321 4E D C B Am4m3m2 m1 T4x T15 kNm+ 5 kNm+10 kNm-30 kNm-从左向右画:作该轴的扭矩图。
D C B Am 3m 2 m 1⊕xT3 kNm5 kNm⊕2 kNmT 作该轴的扭矩图。
A B C Dm 1m 2 m 3⊕xT3 kNm5 kNm2 kNm= ?薄壁圆筒:Rt 101一、薄壁圆筒扭转的时切应力:1)实验前:(1)纵向线:ab 、cd(2)圆周线:ac 、bd§3.3 纯剪切d xR2)实验后:2)实验后:(1)圆筒表面的各圆周线的形状、大小和间距均未改变,只是绕轴线作了相对转动,两端截面有相对扭转角φ。
(2)各纵向线均倾斜了同一微小角度γ。
(3)所有矩形网格均歪斜成同样的平行四边形。
ϕac ddx dy b·τττ’·τ’γ(1)无正应力;从上取一微小矩形单元体如图所示:(2)横截面上各点处,只产生垂直于半径的均匀分布的切应力τ,沿周向大小不变,方向与该截面的扭矩方向一致。
ϕacddx dy b·τττ’·τ’γ从上取一微小矩形单元体如图所示:3) ϕ与γ的关系:Rl ⋅=⋅ϕγ(3)称直角的改变量γ叫“切应变”。
4) 薄壁圆筒切应力τ与T 的关系:ττT R dA A=⋅⋅⎰τR4) 薄壁圆筒切应力τ与T 的关系:Tt R R dA R A =⋅⋅⋅=⋅⋅⎰ )2(πττtR T⋅=∴22 πτ注意该公式的应用条件:t ≤ R /10二、切应力互等定理:dy t dx τdx t dy τm z⋅⋅⋅'=⋅⋅⋅=∑)()( :0上式说明:在单元体相互垂直的两个截面上,剪应力必然成对出现,且数值相等,两者都垂直于两个面的交线,其方向则共同指向或共同背离该交线。
纯剪切应力状态——在单元体的四个侧面上只有剪应力而无正应力。
acddx dy b·τττ’·τ’zττ'=∴当剪应力不超过材料的剪切比例极限时(τ≤τp ),切应力τ与切应变γ成正比。
γτ⋅=G 三、剪切胡克定律:各向同性材料的各弹性量的关系:)1(2μ+=E G τγτpG —材料的剪切弹性模量通过材料的扭转实验可得下应力应变图:(3.3)四、剪切应变能:G/ τγγτ=⋅=G τγτp同理,我们也可得到剪切应变能:前面一章曾介绍了拉压应变能的概念:(2.19)2212Ev σεσε=⋅=(3.6)2212Gv τγτε=⋅=等直圆杆扭转实验观察:满足“平面假设”:§3.4圆轴扭转时的应力1) 变形几何关系:dxd ϕργρ=∴ 距圆心为ρ任一点处的γρ与到圆心的距离ρ成正比dxd ϕ——扭转角沿轴线方向变化率d m nρd ρRoxϕa a’G G’ϕργρd dx ⋅=⋅ dx2) 由物理关系——剪切胡克定律:γτ⋅=GdxdGdxdGGϕρϕργτρρ⋅=⋅=⋅=1) 由变形几何关系得:dxdϕργρ=代入可得:即距圆心为ρ任一点处的τρ与距圆心的ρ成正比:3) 静力学平衡关系可得:⎰⋅⋅=AdA T )(ρτρdxd GI pϕ=pGI Tdxd =ϕ得:dxd Gϕρτρ =OdAρ= I p为横截面的极惯性矩2) 由物理关系得:⎰⎰=⋅⋅=A A dA dx d G dA dx d G 2)(ρϕϕρρρτp I T ρτρ⋅=代入上式可得:(3.9)扭转剪应力分布:(实心截面)(空心截面)ρτρpIT=大小?方向?[例] 判断下列截面上的剪应力分布是否正确。
T()a T()b T()c T()d √×××一、圆轴扭转时的破坏现象低碳钢试件:沿横截面断开。
铸铁试件:沿与轴线约成45的螺旋线断开。
(a)(b)´´(c)(d)´ααx AAα’αxnt转角α符号规定:轴正向转至截面外法线逆时针为正;反之为负。
cos )sin (sin )cos (: 0=⋅⋅⋅'+⋅⋅⋅+⋅=∑ααταατσαdA dA dA Fnsin )sin (cos )cos (: 0=⋅⋅⋅'+⋅⋅⋅-⋅=∑ααταατταdA dA dA Ftττ'= 0sin2 =⋅⋅+⋅∴ατσαdA dA 0cos2=⋅⋅-⋅ατταdA dA: 0=∑nF: 0=∑tFsin2=⋅⋅+⋅ατσαdA dA 0cos2=⋅⋅-⋅ατταdA dA αττατσαα2cos 2sin =-=α’αxnt转角α符号规定:轴正向转至截面外法线逆时针为正;反之为负。
αττατσαα2cos 2sin =-=’450ασατα00τmax = τ450σmin = -τ0-450σmax = τ09000-τ(3.9)pI T ρτρ⋅=由pI R T D R ⋅=→===max max, 2ττρρρ有时当)2 ( 22 maxDI W W T D I T I D T p t t pp===⋅=∴其中令τt W T =maxτ二、圆轴扭转时的强度条件:(3.11)——抗扭截面模量;(mm 3 或m 3 ))2(maxDIRIWWTpptt===其中:得:τ实心圆截面:33162DRRIWptππ===空心圆截面:)1(16)1(24343απαπ-=-==DRRIWpt(3.9):pITρτρ⋅=由——抗扭截面模量(mm3 或m3 )对于等截面圆轴:][max ττ≤][maxmax ττ≤=tW T ( [τ] 称为许用切应力)(1) 强度校核:(2) 强度设计:(3) 强度计算许可载荷:][max maxττ≤=tW T ][maxτT W t ≥][max τ⋅≤t W T 强度条件:其强度计算的三方面工作:(3.15)pGI T dx d = ϕ⎰⎰==lpdxGI Td 0 ϕϕ§3.4 圆轴扭转时的变形p GI lT ⋅=ϕ1)相对扭转角φ:φl若上式中扭矩T 在整个l 段中为常数,即T 不变,而同时该段轴等截面积且同材料,则有:——等直圆杆的截面抗扭刚度(3.16)pGI l T ⋅=ϕ1)相对扭转角φ的计算:φl2)扭转变形的程度φ’ ( ——单位扭转角θ):(3.17)(rad/m) ' lGI T dx d p ϕϕϕ===(3.19) ]'[' maxmax ϕϕ≤⋅=pGI T 圆轴扭转时的刚度条件:pGI l T ⋅=ϕ1)相对扭转角φ的计算:φl2)扭转变形的程度φ’ ( ——单位扭转角θ):(3.17)(rad/m) ' p GI T dx d ==ϕϕ(3.20) /m)( ]'[ 180' max max ︒≤⨯=ϕπϕp GI T三、刚度条件:[φ’ ]称为许用单位扭转角[](rad/m) ' ' maxmax ϕϕ≤=pGI T []/m)( '180' max max ︒≤⋅=ϕπϕp GI T (1) 刚度校核:(2) 刚度设计:(3)刚度计算许可载荷:[]' ' max ϕϕ≤ ]'[ maxϕ⋅≥G T I p ]'[ max ϕ⋅≤p GI T 其刚度计算的三方面工作:[例1] 功率为150 kW ,转速为1200 rpm 的电动机转子轴,许用剪应力[τ]= 30 MPa , 试校核其强度n P M ⨯=9549m)(N 12001509549⋅⨯=解:(1)求外力扭矩:(3)强度计算:BD 3=135D 2=75D 1=70ACM M ][ 7170701661193)(3min max max τπτ≤=⨯==MPa ...W T t TxM⊕m)(N 61193⋅=.得:T max = M =1193.6 Nm(2)画扭矩图:满足强度要求。