统计学-统计指数【实用参考】

第八章统计指数通过本章学习掌握统计指数的概念和分类，各种指数的编制基础、编制原则、编制方法和应用条件【教学重点、难点】重点：统计指数的概念和分类，总指数的综合形式，总指数的平均形式，指数体系与因素分析等。

难点：各种指数（指数体系）编制的基础、编制的原则、编制的方法和应用的条件。

【教学用具】多媒体【教学过程】学习重点：主要讲授第一节统计指数的概念与分类一、统计指数的概念广义上说，指数是指用来反映研究所研究社会经济现象总体数量变动状况的相对数。

狭义上说，指数是指用来综合反映所研究社会经济现象复杂总体数量变动状况的相对数。

二、统计指数的分类按所反映的对象范围不同，统计指数分为个体指数和总指数。

按所表明现象的数量特征不同，统计指数分为数量指标指数和质量指标指数。

总指数按其所采用的指标形式不同，可以分为综合指数与平均指数。

按比较对象不同，统计指数可分时间性指数、地区性指数和计划完成指数。

在指数数列中按所采用的基期不同，统计指数可分为定基指数和环比指数。

三、统计指数的性质1.综合性。

2.代表性。

3.相对性。

4.平均性。

四、指数在经济分析中的作用1.综合地反映复杂经济现象总体的变动方向和程度。

2.分析在现象总体的变动中，各构成因素影响的大小。

第二节综合指数一、综合指数的概念及计算的一般原理指数方法论主要是研究总指数的计算问题，总指数的编制方法，其基本形式有两种：一是综合指数，二是平均指数。

两种方法有一定的联系，但各有其特点。

综合指数是对两个时期范围相同的复杂现象总体总量指标对比形成的指数，在总量指标中包含两个或两个以上的因素，将其中被研究因素以外的一个或一个以上的因素固定下来，仅观察被研究因素的变动，这样编制的指数，称为综合指数。

综合指数的重要意义，是它能够比较全面、准确地反映所研究的现象总体总的变动程度和随之产生的绝对数效果。

它的特点是先综合后对比。

其编制方法是：首先引入同度量因素，解决复杂总体在研究指标上不能直接综合的困难，使其可以计算出总体的综合总量；其次，将同度量因素固定，以消除同度量因素变动的影响；最后将两个时期的总量对比，其结果即为综合指数，也就综合地反映了复杂总体研究指标的变动。

统计学统计指数统计学是一门研究如何收集、整理、分析和解释数据的学科。

它是一门广泛应用于社交学科、自然科学、商务经济学及工程学等学科的学科。

通过合理地运用统计技术，我们能够更加客观、科学地分析和解读复杂的现象和实际问题。

在统计学中，有许多指数和统计量，它们可以有效地反映、衡量和比较实际问题的各种性质和特征，使得问题的定量分析成为可能。

今天，我们将主要简单介绍几种常见的统计指数。

一、基本指数基本指数是我们最常用、最基础的几个指标。

包括平均值、中位数、众数、最大值与最小值。

平均值：属于高频使用指数之一，是指所有数据之和除以数据的总数。

它是用于反映数据集合中心特征的一个重要指标。

平均值对于研究数据的趋势或规律，特别是用于对比两个或多个数据集时很有用。

中位数：中位数与平均数不同，是把一组数据从小到大排序后，位于中间位置上的数。

它的好处在于不会被极端值影响以及能够不失客观地反映数据的中间水平。

众数：众数与平均值和中位数不一样，是数据里出现最多的数字。

通常用于从大量数据中检测出明显的模式，帮助研究者了解整体数据的分布特征。

最大值与最小值：最大值与最小值是这组数据集合所包含的最大值和最小值。

在数据研究分析中，它们可用于参考不同数据之间的分布情况。

二、分散指数分散指数是用于衡量数据分布的不均匀程度。

其中包括方差和标准差。

方差：方差是数据集与其平均值的差的平方和除以数据总数的操作得到的指数。

方差越大，表示这组数据离散程度较大。

反之，越小则表明数据离散程度较小。

标准差：标准差是方差算术平方根的结果。

反映了数据集各数据与平均数的平均偏差值，是常用的反映数据集的离散程度的客观指标。

三、相关指数相关指数是用于度量数据的相似程度或关联程度。

其中包括相关系数和回归系数。

相关系数：相关系数是用来衡量两个数据集合之间的相关性或线性关系。

相关系数的取值范围为-1到+1之间，值越接近+1表示越正相关，值越接近-1表示越负相关。

当相关系数为0时，两个数据集之间无关联性。

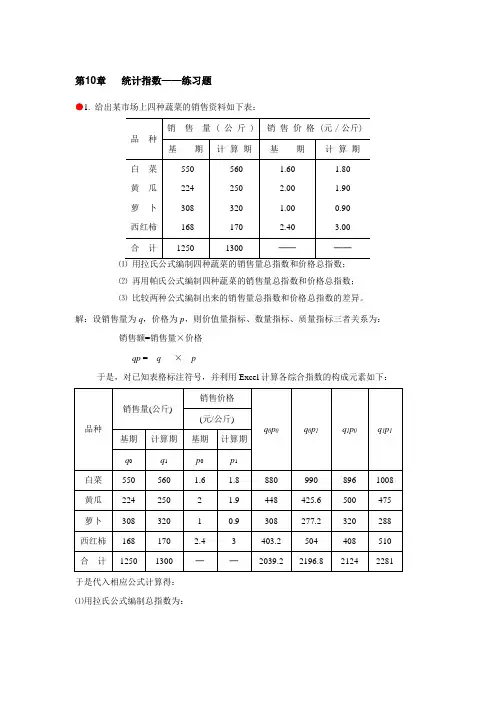
第 10章统计指数——练习题● 1. 给出某市场上四种蔬菜的销售资料以下表：销售量 ( 公斤 ) 销售价格 ( 元 / 公斤 )品种基期计算期基期计算期白菜550 560黄瓜224 250萝卜308 320西红柿168 170合计1250 1300 ────⑴ 用拉氏公式编制四种蔬菜的销售量总指数和价格总指数；⑵ 再用帕氏公式编制四种蔬菜的销售量总指数和价格总指数；⑶ 比较两种公式编制出来的销售量总指数和价格总指数的差异。

解：设销售量为q，价格为p，则价值量指标、数量指标、质量指标三者关系为：销售额 =销售量×价格qp = q×p于是，对已知表格注明符号，并利用Excel 计算各综合指数的构成元素以下：销售价格销售量 (公斤 )品种(元 /公斤 )q0p0 q0p1 q1p0 q1p1 基期计算期基期计算期q0 q1 p0 p1白菜550 560 880 990 896 1008 黄瓜224 250 2 448 500 475 萝卜308 320 1 308 320 288 西红柿168 170 3 504 408 510 合计1250 1300 ──2124 2281 于是代入相应公式计算得：⑴用拉氏公式编制总指数为：四种蔬菜的销售量总指数L qq1 p0 2124 104.16% ,q0 p0四种蔬菜的价格总指数L pq0 p1q0 p0107.73%⑵ 用帕氏公式编制总指数：四种蔬菜的销售量总指数为P qq1 p1 2281q0 p1103.83%四种蔬菜的价格总指数为P pq1 p1 2281q1 p0 107.39%2124⑶ 比较两种公式编制出来的销售量总指数和价格总指数，可见：拉氏指数＞帕氏指数在经济意义上，拉氏指数将同胸襟因素固定在基期。

销售量总指数说明花销者为保持与基期相同的花销价格，因调整增减的本质购买量而以致本质开支增减的百分比；价格总指数说明花销者为购买与基期相同数量的四种蔬菜，因价格的变化而以致本质开支增减的百分比。

统计学原理——统计指数统计指数是一项重要的统计学原理，它用于评估和比较不同群体或变量之间的相对差异。

通过统计指数，我们可以对数据进行更深入的分析，了解不同群体的差异以及其对总体的贡献。

在统计学中，常用的统计指数有多种，其中包括平均数、标准差、相关系数、协方差等。

这些指数可以帮助我们从不同角度对数据进行分析和解释。

首先，平均数是最常见的统计指数之一、它用于衡量一组数据的集中趋势和中心位置。

平均数可以通过将所有数据值相加并除以数据的个数来计算得到。

通过计算平均数，我们可以了解数据的总体特征和整体水平。

其次，标准差是用于衡量数据的离散程度和波动性的指数。

它衡量数据的每个数据点与平均数之间的距离，并计算这些距离的平均值。

标准差越大，表示数据的分布越分散；标准差越小，表示数据的分布越集中。

另外，相关系数是用于衡量两个变量之间相关性的指数。

它可以告诉我们两个变量之间的线性相关程度，取值范围从-1到1、当相关系数为正时，表示两个变量之间存在正相关关系；当相关系数为负时，表示两个变量之间存在负相关关系；当相关系数接近于0时，表示两个变量之间几乎没有相关性。

此外，协方差是用于衡量两个变量之间总体变化趋势的指数。

它可以告诉我们两个变量之间的总体变化方向和程度。

当协方差为正时，表示两个变量之间存在正相关关系；当协方差为负时，表示两个变量之间存在负相关关系；当协方差接近于0时，表示两个变量之间几乎没有线性关系。

这些统计指数对于统计学原理的应用非常重要。

通过计算和分析这些指数，我们可以从不同的角度深入了解数据的特征和关系，从而更好地进行数据的解释和应用。

在实际应用中，统计指数可以帮助我们研究不同群体之间的差异，并为决策提供依据。

例如，我们可以使用平均数和标准差来比较两个地区的人均收入水平和收入分布情况；我们可以使用相关系数和协方差来研究两个变量之间的相关性，如广告投资和销售额之间的关系。

总之，统计指数是统计学原理中重要的一部分，它可以帮助我们对数据进行更深入的分析和解释。

第10章统计指数——练习题●1. 给出某市场上四种蔬菜的销售资料如下表：⑵再用帕氏公式编制四种蔬菜的销售量总指数和价格总指数；⑶比较两种公式编制出来的销售量总指数和价格总指数的差异。

解：设销售量为q，价格为p，则价值量指标、数量指标、质量指标三者关系为：销售额=销售量×价格qp = q×p于是，对已知表格标注符号，并利用Excel计算各综合指数的构成元素如下：于是代入相应公式计算得：⑴用拉氏公式编制总指数为：四种蔬菜的销售量总指数 10002124104.16% , 2039.2q q p L q p===∑∑四种蔬菜的价格总指数 0102196.8107.73%2039.2p q p L q p===∑∑⑵ 用帕氏公式编制总指数：四种蔬菜的销售量总指数为 11012281103.83% 2196.8q q p P q p===∑∑四种蔬菜的价格总指数为 1112281107.39%2124pq p P q p===∑∑ ⑶ 比较两种公式编制出来的销售量总指数和价格总指数，可见：拉氏指数＞帕氏指数 在经济意义上，拉氏指数将同度量因素固定在基期。

销售量总指数说明消费者为保持与基期相同的消费价格，因调整增减的实际购买量而导致实际开支增减的百分比；价格总指数说明消费者为购买与基期相同数量的四种蔬菜，因价格的变化而导致实际开支增减的百分比。

帕氏指数将同度量因素固定在计算期。

销售量总指数说明消费者在计算期购买的四种蔬菜，因销售量的变化而导致实际开支增减的百分比；价格总指数说明消费者在计算期实际购买的四种蔬菜，因价格的变化而导致实际开支增减的百分比。

●2.依据上题的资料，试分别采用埃奇沃斯公式、理想公式和鲍莱公式编制销售量指数；然后，与拉氏指数和帕氏指数的结果进行比较，看看它们之间有什么关系。

解：采用埃奇沃斯公式编制销售量指数为：1011011101()()212422814405103.9896%2039.22196.84236q q pp q p q p E q pp q p q p++==+++===+∑∑∑∑∑∑采用理想公式编制销售量指数为：103.994869%q F ===采用鲍莱公式编制销售量指数为：1011000111()()22104.16%103.83%104.00%2q q q q p q p B L P q p q p =+=++==∑∑∑∑与拉氏销售量指数和帕氏销售量指数的结果进行比较，它们之间的关系是： q q q q q L B F E P >>>>即拉氏销售量指数最大，鲍莱销售量指数次大，理想销售量指数居中，埃奇沃斯销售量指数较小，帕氏销售量指数最小。

第十章统计指数一、填空题1．狭义指数是反映复杂现象总体变动的2.指数按其所反映的对象范围的不同，分为指数和指数。

3.指数按其所标明的指标性质的不同，分为指数和指数。

4.指数按其采用基期的不同，分为指数和指数。

5. 指数是在简单现象总体条件下存在的，指数是在复杂现象总体的条件下进行编制的。

6.总指数的计算形式有两种，一种是指数，一种是指数。

7.按照一般原则，编制数量指标指数时，同度量因素固定在，编制质量指标指数时，同度量因素固定在。

8.在编制质量指标指数时，指数化指标是指标，同度量因素是与之相联系的指标。

9.综合指数编制的特点，一是选择与指标相联系的同度量因素，二是把同度量因素的时期。

10.拉氏指数对于任何指数化指标的同度量因素都固定在，派氏指数对于任何指数化指标的同度量因素都固定在。

11.编制指数的一般方法是：指数是按拉氏指数公式编制的；指数是按派氏指数公式编制的。

12．综合指数的编制方法是先后。

13．编制综合指数时，与指数化指标相联系的因素称，还可以称为。

14.平均指数的计算形式为指数和指数。

15.平均指数是先计算出数量指标或质量指标的指数，然后再进行计算，来测定现象的总变动程度。

16.在编制平均指数时，算术平均数指数多用为权数，调和平均数指数多用为权数。

17.数量指标的算术平均数指数，在采用为权数的特定条件下，和一般综合指数的计算结论相同；而质量指标的调和平均数指数，在采用为权数的特定条件下，计算结果和综合指数一致。

18.编制数量指标平均指数，一是掌握，二是掌握。

19.编制质量指标平均指数，一是掌握，二是掌握。

20.在零售物价指数中，K表示，W表示。

21.平均指数既可依据资料编制，也可依据资料编制，同时还可用估算的权数比重进行编制计算。

22.因素分析包括数和数分析。

23.总量指标二因素分析是借助于来进行，即当总量指标是两个原因指标的时，才可据此进行因素分析。

24指数体系中，指数之间的数量对等关系表现在两个方面：一是结果指数等于因素指数的，二是结果指数的分子分母之差等于各因素指数的。