九年级数学上册 22.1.4 二次函数y=ax2bxc的图象和性质同步测试 (新版)新人教版

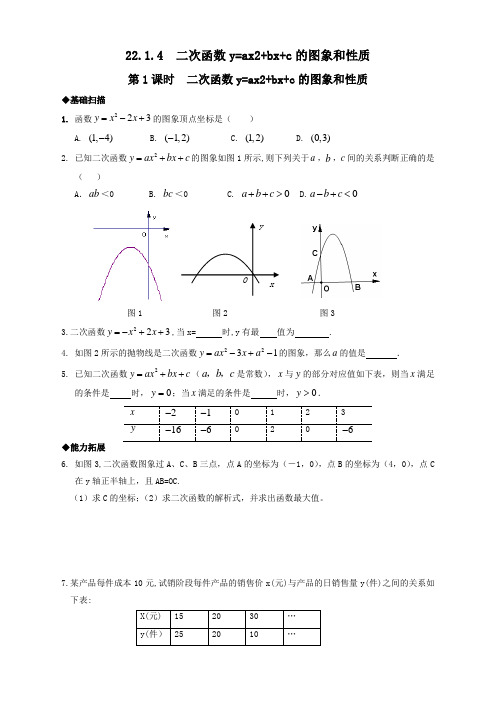
22.1.4 二次函数y=ax2+bx+c 的图象和性质第1课时 二次函数y=ax2+bx+c 的图象和性质◆基础扫描1. 函数223y x x =-+的图象顶点坐标是（ ）A. (1,4)-B. (1,2)-C. (1,2)D. (0,3)2. 已知二次函数2y ax bx c =++的图象如图1所示,则下列关于a ，b ，c 间的关系判断正确的是（ ）A ．ab ＜0 B. bc ＜0 C. 0a b c ++> D.0a b c -+<图1 图2 图3 3.二次函数223y x x =-++,当x= 时,y 有最 值为 .4. 如图2所示的抛物线是二次函数2231y ax x a =-+-的图象，那么a 的值是 ． 5. 已知二次函数2y ax bx c =++（a b c ，，是常数），x 与y 的部分对应值如下表，则当x 满足的条件是 时，0y =；当x 满足的条件是 时，0y >．x2- 1- 0 1 2 3y16-6-26-◆能力拓展6. 如图3,二次函数图象过A 、C 、B 三点，点A 的坐标为（－1，0），点B 的坐标为（4，0），点C 在y 轴正半轴上，且AB=OC.（1）求C 的坐标；（2）求二次函数的解析式，并求出函数最大值。

7.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:X(元) 15 20 30 … y(件） 252010…Oyx若日销售量y 是销售价x 的一次函数.(1)求出日销售量y(件)是销售价x(元)的函数关系式;(2)要使每日的销售利润最大,每件产品的销售价应定为多少元? 此时每日的销售利润是多少元?◆创新学习8．如图，对称轴为直线x ＝27的抛物线经过点A （6，0）和B （0，4）． （1）求抛物线解析式及顶点坐标；（2）设点E （x ，y ）是抛物线上一动点，且位于第四象限，四边形OEAF 是以OA 为对角线的平行四边形，求四边形OEAF 的面积S 与x 之间的函数关系式，并写出自变量x 的取值范围；（3）①当四边形OEAF 的面积为24时，请判断OEAF 是否为菱形？②是否存在点E ，使四边形OEAF 为正方形？若存在，求出点E 的坐标；若不存在，请说明理由．参考答案1．C 2．D 3．1x 大 4 4．－1 5．0或2 0＜x ＜2 6．(1)C(0,5)(2) 5(1)(4)4y x x =-+- 253125()4216x =--+7．(1)设此一次函数关系式为y kx b =+,则{15252020k b k b +=⎧⎨+=⎩,解得1,40k b =-=故一次函数的关系式为40y x =-+. (2)设所获利润为W 元,则22(10)(40)50400(25)225W x x x x x =--=-+-=--+ 所以产品的销售价应定为25元,此时每日的销售利润为225元． 8．（1）由抛物线的对称轴是72x =，可设解析式为27()2y a x k =-+． 把A 、B 两点坐标代入上式，得227(6)0,27(0) 4.2a k a k ⎧-+=⎪⎪⎨⎪-+=⎪⎩ 解之，得225,.36a k ==- 故抛物线解析式为22725()326y x =--，顶点为725(,).26- （2）∵点(,)E x y 在抛物线上，位于第四象限，且坐标适合.22725()326y x =--，∴y<0，即 －y>0,－y 表示点E 到OA 的距离． ∵OA 是OEAF Y 的对角线，∴2172264()2522OAE S S OA y y ==⨯⨯⋅=-=--+V ． 因为抛物线与x 轴的两个交点是（1，0）的（6，0）， 所以，自变量x 的取值范围是1＜x ＜6．①根据题意，当S = 24时，即274()25242x --+=． 化简，得271().24x -=解之，得123, 4.x x == 故所求的点E 有两个，分别为E 1（3，－4），E 2（4，－4）． 点E 1（3，－4）满足OE = AE ，所以OEAF Y 是菱形； 点E 2（4，－4）不满足OE = AE ，所以OEAF Y 不是菱形．Y是正方形，②当OA⊥EF，且OA = EF时，OEAF此时点E的坐标只能是（3，－3）．而坐标为（3，－3）的点不在抛物线上，Y为正方形．故不存在这样的点E，使OEAF。

人教版九年级数学上册第22章二次函数 22.1.4.1 二次函数y ＝ax ２＋bx ＋c 的图象和性质同步测试第Ⅰ卷（选择题）一、选择题（共10小题，3*10=30） 1.抛物线y ＝x 2－2x ＋2的顶点坐标为( )A ．(1，1)B ．(－1，1)C ．(1，3)D ．(－1，3)2．下列对二次函数y ＝x 2－x 的图象的描述，正确的是( ) A ．开口向下 B ．对称轴是y 轴C ．经过原点D ．在对称轴右侧部分是下降的3．已知二次函数y ＝－12x 2－7x ＋152.若自变量x 分别取x 1，x 2，x 3，且0＜x 1＜x 2＜x 3，则对应的函数值y 1，y 2，y 3的大小关系正确的是( ) A ．y 1＞y 2＞y 3 B ．y 1＜y 2＜y 3 C ．y 2＞y 3＞y 1 D ．y 2＜y 3＜y 14．用配方法将二次函数y ＝x 2－8x －9化为y ＝a(x －h)2＋k 的形式为 ( ) A ．y ＝(x －4)2＋7 B ．y ＝(x －4)2－25 C ．y ＝(x ＋4)2＋7 D ．y ＝(x ＋4)2－255. 二次函数y ＝ax 2＋bx ＋c(a ≠0)图象上部分点的坐标(x ，y)对应值列表如下：则该函数图象的对称轴是 ( ) A ．直线x ＝－3 B ．直线x ＝－2 C ．直线x ＝－1 D ．直线x ＝06．关于二次函数y＝2x2＋4x－1，下列说法正确的是( )A．图象与y轴的交点坐标为(0，1)B．图象的对称轴在y轴的右侧C．当x＜0时，y的值随x值的增大而减小D．y的最小值为－37. 点P1(－1，y1)，P2(3，y2)，P3(5，y3)均在二次函数y＝－x2＋2x＋c的图象上，则y1，y2，y3的大小关系是( )A．y3>y2>y1B．y3>y1＝y2C．y1>y2>y3D．y1＝y2>y38．如图，函数y＝ax2－2x＋1和y＝ax－a(a是常数，且a≠0)在同一平面直角坐标系的图象可能是( )9. 对于抛物线y＝ax2＋(2a－1)x＋a－3，当x＝1时，y＞0，则这条抛物线的顶点一定在( ) A．第一象限B．第二象限C．第三象限D．第四象限10. 已知二次函数y＝ax2＋bx＋c(a≠0)图象如图所示，下列结论：①abc＜0；②2a－b＜0；③b2＞(a ＋c)2；④点(－3，y1)，(1，y2)都在抛物线上，则有y1＞y2.其中正确的结论有( )A．4个B．3个C．2个D．1个第Ⅱ卷（非选择题）二．填空题（共8小题，3*8=24）11. 下列函数：①y＝x2；②y＝－x2；③y＝(x－1)2＋2，其中图象通过平移可以得到函数y＝x2＋2x－3的图象的有____.(填序号)12．已知二次函数y＝－2x2－8x－6，当x＝____时，y有最____值是___．13. 将抛物线y＝12x2－6x＋21向左平移2个单位长度后，得到抛物线的解析式为__________________.14．已知二次函数y＝x2＋2mx＋2，当x＞2时，y随x的增大而增大，则实数m的取值范围是__________.15. 在二次函数y＝－x2＋2x＋1的图象中．若y随x的增大而增大，则x的取值范围是__________.16. 二次函数y＝－x2＋bx＋c的图象如图所示．若点A(x1，y1)，B(x2，y2)在此函数的图象上，且x1<x2<1，则y1与y2的大小关系是__________.17．已知二次函数y＝ax2＋2ax＋3a2＋3(其中x是自变量)，当x≥2时，y随x的增大而增大，且－2≤x≤1时，y的最大值为9，则a的值为________.18. 如图，在平面直角坐标系中，抛物线y＝12x2经过平移得到抛物线y＝12x2－2x，其对称轴与两段抛物线所围成的阴影部分的面积为____.三．解答题（共7小题，46分）19．(6分) 把二次函数y＝3x2－6x－1化成y＝a(x－h)2＋k的形式，并指出其最值．20. (6分) 已知二次函数y＝x2－2kx＋k2＋k－2.(1)当实数k为何值时，图象经过原点？(2)当实数k在何范围取值时，函数图象的顶点在第四象限内？21. (6分) 已知抛物线y＝x2－4x＋4.(1)写出该抛物线的开口方向、对称轴和顶点；(2)画出此函数的图象；(3)说明该函数图象与二次函数y＝x2的图象之间的关系．22. (6分) 如图，抛物线y＝－x2＋bx＋c经过A(－1，0)，B(3，0)两点，交y轴于点C，点D为抛物线的顶点，连接BD，点H为BD的中点．请解答下列问题：(1)求抛物线的解析式及顶点D的坐标；(2)在y轴上找一点P，使PD＋PH的值最小，则PD＋PH的最小值为13.23．(6分)如图，抛物线y＝ax2－5ax＋4a与x轴相交于点A，B，且过点C(5，4)．(1)求a的值和该抛物线顶点P的坐标；(2)请你设计一种平移的方法，使平移后抛物线的顶点落在第二象限，并写出平移后抛物线的解析式．24．(8分) 抛物线y＝－13x2＋bx＋c经过点A(33，0)和点B(0，3)，且这个抛物线的对称轴为直线l，顶点为C.(1)求抛物线的解析式；(2)连接AB，AC，BC，求△ABC的面积．25．(8分) 如图，以D为顶点的抛物线y＝－x2＋bx＋c交x轴于A，B两点，交y轴于点C，直线BC的表达式为y＝－x＋3.(1)求抛物线的表达式并直接判断△DBC的形状(直接写出答案)；(2)在直线BC上有一点P，使PO＋PA的值最小，求点P的坐标．参考答案 1-5 ACABB 6-10 DDBCB 11. ①③ 12. －2 大 2 13. y ＝12(x －4)2＋3 14. m ≥－2 15. x ＜116. y 1<y 2 17. 1 18. 419. 解：y ＝3x 2－6x －1＝3(x 2－2x)－1＝3(x －1)2－4， ∴顶点坐标为(1，－4)， ∵开口向上， ∴有最小值为－420. 解：(1)∵图象过原点，∴k 2＋k －2＝0， ∴k 1＝－2，k 2＝1(2)y ＝x 2－2kx ＋k 2＋k －2＝(x －k)2＋k －2， 其顶点坐标为(k ，k －2)． ∵顶点在第四象限内，∴⎩⎪⎨⎪⎧k ＞0，k －2＜0， ∴0＜k ＜221. 解：(1)由已知得y ＝(x －2)2， ∵a ＝1＞0，∴开口向上，对称轴是直线x ＝2，顶点为(2，0) (2)画图象略(3)该函数图象与y ＝x 2的图象的形状、开口方向均相同， 将抛物线y ＝x 2向右平移2个单位得到抛物线y ＝x 2－4x ＋4 22. 解：(1)∵抛物线y ＝－x 2＋bx ＋c 过点A(－1，0)，B(3，0)，∴⎩⎪⎨⎪⎧－1－b ＋c ＝0，－9＋3b ＋c ＝0，解得⎩⎪⎨⎪⎧b ＝2，c ＝3， ∴所求函数的解析式为：y ＝－x 2＋2x ＋3， ∵y ＝－x 2＋2x ＋3＝－(x －1)2＋4， ∴顶点D(1，4)23. 解：(1)由抛物线过C(5，4)得25a －25a ＋4a ＝4，解得a ＝1， ∴该二次函数的解析式为y ＝x 2－5x ＋4.∵y ＝x 2－5x ＋4＝(x －52)2－94，∴顶点坐标为P(52，－94)(2)(答案不唯一，合理即正确)如：先向左平移3个单位长度，再向上平移4个单位长度，得到的二次函数解析式为y ＝(x －52＋3)2－94＋4，即y ＝(x ＋12)2＋74，也即y ＝x 2＋x ＋224. 解：(1)∵抛物线y ＝－13x 2＋bx ＋c 经过A(33，0)，B(0，3)，∴⎩⎨⎧－9＋33b ＋c ＝0，c ＝3，解得b ＝233，c ＝3.∴抛物线的解析式为y ＝－13x 2＋233x ＋3(2)由(1)知抛物线对称轴为直线x ＝3， 把x ＝3代入，y ＝－13x 2＋233x ＋3得y ＝4，则点C 坐标为(3，4)，设线段AB 所在直线为：y ＝kx ＋b ， 解得y ＝－33x ＋3， ∵线段AB 所在直线经过点A(3，3，0)，B(0，3)， 抛物线的对称轴l 与直线AB 交于点D. ∴设点D 的坐标为(3，m)， 将点D(3，m)代入y ＝－33x ＋3， 解得m ＝2，∴点D 坐标为(3，2)， ∴CD ＝CE －DE ＝2，过点B 作BF ⊥l 于点F ，BF ＝OE ＝3，∵BF ＋AE ＝OE ＋AE ＝OA ＝33，∵S △ABC ＝S △BCD ＋S △ACD ＝12CD ·BF ＋12CD ·AE ，∴S △ABC ＝12CD(BF ＋AE)＝12×2×33＝3 325. 解：(1)把x ＝0代入y ＝－x ＋3，得y ＝3. ∴C(0，3)．把y ＝0代入y ＝－x ＋3得：x ＝3. ∴B(3，0)．将C(0，3)，B(3，0)代入y ＝－x 2＋bx ＋c得：⎩⎪⎨⎪⎧－9＋3b ＋c ＝0，c ＝3，解得b ＝2，c ＝3.∴抛物线的解析式为y ＝－x 2＋2x ＋3，△DBC 为直角三角形 (2)如图所示：作点O 关于BC 的对称点O ′，则O ′(3，3)． ∵O ′与O 关于BC 对称，∴PO ＝PO ′.∴OP ＋AP ＝O ′P ＋AP ≤AO ′.∴当A ，P ，O ′在一条直线上时，OP ＋AP 有最小值． 设AP 的解析式为y ＝kx ＋b ，由(1)得A(－1，0)，则⎩⎪⎨⎪⎧－k ＋b ＝0，3k ＋b ＝3， 解得⎩⎨⎧k ＝34，b ＝34.∴AP 的解析式为y ＝34x ＋34.将y ＝34x ＋34与y ＝－x ＋3联立，解得⎩⎨⎧x ＝97.y ＝127，∴点P 的坐标为(97，127)。

22.1.4 二次函数y=ax²+bx+c的图象和性质一．选择题1．二次函数y＝x2﹣x﹣12与y轴的交点坐标为（）A．（﹣3，0）B．（6，0）C．（0，﹣12）D．（2，16）2．在同一平面直角坐标系内，二次函数y＝ax2+bx+b（a≠0）与一次函数y＝ax+b的图象可能是（）A．B．C．D．3．一次函数y＝acx+b与二次函数y＝ax2+bx+c在同一平面直角坐标系中的图象可能是（）A．B．C．D．4．已知点A（﹣2，y1），B（1，y2）在二次函数y＝x2+2x﹣m的图象上，则下列有关y1和y2的大小关系的结论中正确的是（）A．y1＝y2B．y1＜y2C．y1＞y2D．与m的值有关5．二次函数y＝ax2+bx+c的自变量x与函数值y的对应值如图，下列说法错误的是：（）x…﹣6﹣5﹣4﹣3﹣2﹣1…y…1040﹣2﹣20…A．抛物线开口向上B．抛物线与y轴的交点是（0，4）C．当x＜﹣2时，y随x的增大而减小D．当x＞﹣2时，y随x的增大而增大6．已知二次函数y＝x2﹣6x+1，关于该函数在﹣1≤x≤4的取值范围内，下列说法正确的是（）A．有最大值8，最小值﹣8B．有最大值8，最小值﹣7C．有最大值﹣7，最小值﹣8D．有最大值1，最小值﹣77．已知（﹣3，y1），（﹣2，y2），（1，y3）是抛物线y＝﹣3x2﹣12x+m上的点，则（）A．y3＜y2＜y1B．y3＜y1＜y2C．y2＜y3＜y1D．y1＜y3＜y28．已知二次函数y＝ax2+bx+c的图象如图所示，则下列6个代数式：ab，ac，a+b+c，a﹣b+c，2a+b，2a﹣b中，其值为正的式子的个数是（）A．2个B．3个C．4个D．5个9．二次函数y＝ax2+bx+c的图象如图所示，有如下结论：①abc＞0；②2a+b＝0；③3b﹣2c＜0；④am2+bm≥a+b（m为实数）．其中正确结论的个数是（）A．1个B．2个C．3个D．4个10．如图，二次函数y＝ax2+bx+c的图象经过点A（﹣3，0），其对称轴为直线x＝﹣1，有下列结论：①abc＜0；②a+b+c＜0；③5a+4c＜0；④4ac﹣b2＞0；⑤若P（﹣5，y1），Q（m，y2）是抛物线上两点，且y1＞y2，则实数m的取值范围是﹣5＜m＜3．其中正确结论的个数是（）A．1B．2C．3D．4二．填空题11．二次函数y＝x2+2x﹣4的图象的对称轴是，顶点坐标是．12．二次函数y＝x2﹣16x﹣8的最小值是．13．二次函数图象过A（﹣1，0），B（2，0），C（0，﹣2），则此二次函数的解析式是．14．某同学利用描点法画二次函数y＝ax2+bx+c（a≠0）的图象时，列出的部分数据如下表：序号①②③④⑤x01234y30﹣203经检查，发现表格中恰好有一组数据计算错误，请你找出错误的那组数据．（只填序号）15．若二次函数y＝ax2+bx+c（a≠0）的图象的顶点在第一象限，且过点（0，1）和（﹣1，0）．则S＝a+b+c的值的变化范围是．16．抛物线y＝ax2+bx+c（a＞0）过点（﹣1，0）和点（0，﹣4），且顶点在第四象限，则a 的取值范围是．17．当﹣1≤x≤3时，二次函数y＝x2﹣4x+5有最大值m，则m＝．18．如图，是二次函数y＝ax2+bx+c图象的一部分，其对称轴是x＝﹣1，且过点（﹣3，0），下列说法：①abc＜0；②2a﹣b＝0；③若（﹣5，y1），（3，y2）是抛物线上两点，则y1＝y2；④4a+2b+c＜0，其中说法正确的（填写序号）．三．解答题19．已知抛物线y＝ax2+bx+1经过点（1，﹣2），（﹣2，13）．（1）求a，b的值．（2）若（5，y1），（m，y2）是抛物线上不同的两点，且y2＝12﹣y1，求m的值．20．在平面直角坐标系xOy中，M（x1，y1），N（x2，y2）为抛物线y＝ax2+bx+c（a＞0）上任意两点，其中x1＜x2．（1）若抛物线的对称轴为x＝1，当x1，x2为何值时，y1＝y2＝c；（2）设抛物线的对称轴为x＝t，若对于x1+x2＞3，都有y1＜y2，求t的取值范围．21．已知抛物线y＝ax2﹣2ax﹣3+2a2（a≠0）．（1）求这条抛物线的对称轴；（2）若该抛物线的顶点在x轴上，求其解析式；（3）设点P（m，y1），Q（3，y2）在抛物线上，若y1＜y2，求m的取值范围．22．已知函数y＝ax2+bx+c（a≠0，a、b、c为常数）的图象经过点A（﹣1，0）、B（0，2）．（1）b＝（用含有a的代数式表示），c＝；（2）点O是坐标原点，点C是该函数图象的顶点，若△AOC的面积为1，则a＝；（3）若x＞1时，y＜5．结合图象，直接写出a的取值范围．23．如图，已知抛物线y＝﹣x2+bx+c经过点A（3，1）与点B（0，4）．（1）求该抛物线的解析式及顶点坐标；（2）在第三象限内的抛物线上有一点P，使得P A⊥AB，求点P的坐标；（3）若点C（m，n）在该抛物线上，当q≤m≤3时，1≤n≤5，请确定q的取值范围．参考答案一．选择题1．解：由图象与y轴相交则x＝0，代入得：y＝﹣12，∴与y轴交点坐标是（0，﹣12）；故选：C．2．解：A、二次函数图象开口向上，对称轴在y轴右侧，∴a＞0，b＜0，∴一次函数图象应该过第一、三、四象限，且与二次函数交于y轴负半轴的同一点，故A错误；B、∵二次函数图象开口向下，对称轴在y轴左侧，∴a＜0，b＜0，∴一次函数图象应该过第二、三、四象限，且与二次函数交于y轴负半轴的同一点，故B错误；C、二次函数图象开口向上，对称轴在y轴右侧，∴a＞0，b＜0，∴一次函数图象应该过第一、三、四象限，且与二次函数交于y轴负半轴的同一点，故C正确；∵D、二次函数图象开口向上，对称轴在y轴右侧，∴a＞0，b＜0，∴一次函数图象应该过第一、三、四象限，且与二次函数交于y轴负半轴的同一点，故D错误；故选：C．3．解：A、由抛物线可知，a＞0，b＜0，c＞0，则ac＞0，由直线可知，ac＞0，b＞0，故本选项不合题意；B、由抛物线可知，a＞0，b＞0，c＞0，则ac＞0，由直线可知，ac＞0，b＞0，故本选项符合题意；C、由抛物线可知，a＜0，b＞0，c＞0，则ac＜0，由直线可知，ac＜0，b＜0，故本选项不合题意；D、由抛物线可知，a＜0，b＜0，c＞0，则ac＜0，由直线可知，ac＞0，b＞0，故本选项不合题意．4．解：y＝x2+2x﹣m＝（x+1）2﹣1﹣m，∵点A（﹣2，y1）是二次函数y＝（x+1）2﹣1﹣m图象上的点，∴y1＝（﹣2+1）2﹣1﹣m＝1﹣1﹣m＝﹣m；∵点B（1，y2）是二次函数y＝（x+1）2﹣1﹣m图象上的点，∴y2＝（1+1）2﹣1﹣m＝4﹣1﹣m＝3﹣m．∴y1＜y2．故选：B．5．解：由表格可知，该抛物线的对称轴是直线x＝＝﹣，抛物线开口向上，故选项A正确；x＝0和x＝﹣5对应的函数值相等，故抛物线与y轴的交点是（0，4），故选项B正确；当x＜﹣时，y随x的增大而减小，故选项C错误；当x＞﹣时，y随x的增大而增大，故选项D正确；故选：C．6．解：∵y＝x2﹣6x+1＝（x﹣3）2﹣8，∴在﹣1≤x≤4的取值范围内，当x＝3时，有最小值﹣8，当x＝﹣1时，有最大值为y＝16﹣8＝8．故选：A．7．解：抛物线的对称轴为直线x＝﹣＝﹣2，∵a＝﹣3＜0，∴x＝﹣2时，函数值最大，又∵﹣3到﹣2的距离比1到﹣2的距离小，∴y3＜y1＜y2．故选：B．8．解：∵抛物线的开口向下，∴a＜0，∵与y轴的交点为在y轴的负半轴上，∴c＜0，∵对称轴为x＝＞0，∴a、b异号，即b＞0，∴ab＜0，当x＝1时，y＝a+b+c＞0，当x＝﹣1时，y＝a﹣b+c＜0，∵对称轴为x＝＜1，a＜0，∴2a+b＜0，∴a＜0，b＞0，∴2a﹣b＜0∴有2个正确．故选：A．9．解：①∵对称轴在y轴右侧，∴a、b异号，∴ab＜0，∵c＜0，∴abc＞0，故①正确；②∵对称轴x＝﹣＝1，∴2a+b＝0；故②正确；③∵2a+b＝0，∴a＝﹣b，∵当x＝﹣1时，y＝a﹣b+c＞0，∴﹣b﹣b+c＞0，∴3b﹣2c＜0，故③正确；④根据图象知，当x＝1时，y有最小值；当m为实数时，有am2+bm+c≥a+b+c，所以am2+bm≥a+b（m为实数）．故④正确．本题正确的结论有：①②③④，4个；故选：D．10．解：①观察图象可知：a＞0，b＞0，c＜0，∴abc＜0，∴①正确；②当x＝1时，y＝0，即a+b+c＝0，∴②错误；③对称轴x＝﹣1，即﹣＝﹣1得b＝2a，当x＝时，y＜0，即a+b+c＜0，即a+2b+4c＜0，∴5a+4c＜0．∴③正确；④因为抛物线与x轴有两个交点，所以△＞0，即b2﹣4ac＞0，∴4ac﹣b2＜0．∴④错误；⑤∵（﹣5，y1）关于直线x＝﹣1的对称点的坐标是（3，y1），∴当y1＞y2时，﹣5＜m＜3．∴⑤正确．故选：C．二．填空题11．解：∵y＝x2+2x﹣4＝（x+1）2﹣5，∴该函数图象的对称轴是直线x＝﹣1，顶点坐标为（﹣1，﹣5），故答案为：直线x＝﹣1，（﹣1，﹣5）．12．解：y＝x2﹣16x﹣8＝（x﹣8）2﹣72，由于函数开口向上，因此函数有最小值，且最小值为﹣72，故答案为：﹣72．13．解：∵二次函数图象经过A（﹣1，0），B（2，0），∴设二次函数解析式为y＝a（x+1）（x﹣2），将C（0，﹣2）代入，得：﹣2a＝﹣2，解得a＝1，则抛物线解析式为y＝（x+1）（x﹣2）＝x2﹣x﹣2，故答案为：y＝x2﹣x﹣2．14．解：由图表数据可知，①、⑤两点关于直线x＝2对称，②、④两点关于直线x＝2对称，所以，计算错误的一组数据应该是③，验证：由①②④数据可得，解得，∴该二次函数解析式为y＝x2﹣4x+3，当x＝2时，y＝22﹣4×2+3＝﹣1≠﹣2，所以③数据计算错误．故答案为：③．15．解：将点（0，1）和（﹣1，0）分别代入抛物线解析式，得c＝1，a＝b﹣1，∴S＝a+b+c＝2b，由题设知，对称轴x＝，∴2b＞0．又由b＝a+1及a＜0可知2b＝2a+2＜2．∴0＜S＜2．故本题答案为：0＜S＜2．16．解：∵抛物线y＝ax2+bx+c（a＞0）过点（﹣1，0）和点（0，﹣4），∴，所以，a﹣b＝4，b＝a﹣4，∵顶点在第四象限，∴，即﹣＞0①，＜0②，解不等式①得，a＜4，不等式②整理得，（a+4）2＞0，所以，a≠﹣4，所以，a的取值范围是0＜a＜4．故答案为：0＜a＜4．17．解：∵二次函数y＝x2﹣4x+5＝（x﹣2）2+1，∴该函数开口向上，对称轴为x＝2，∵当﹣1≤x≤3时，二次函数y＝x2﹣4x+5有最大值m，∴当x＝﹣1时，该函数取得最大值，此时m＝（﹣1﹣2）2+1＝10，故答案为：10．18．解：∵抛物线开口向上，∴a＞0，∵抛物线对称轴为直线x＝﹣＝﹣1，∴b＝2a＞0，则2a﹣b＝0，所以②正确；∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＜0，所以①正确；∵点（﹣5，y1）离对称轴的距离与点（3，y2）离对称轴的距离相等，∴y1＝y2，所以③正确．∵x＝2时，y＞0，∴4a+2b+c＞0，所以④错误；故答案为：①②③．三．解答题19．解：（1）把点（1，﹣2），（﹣2，13）代入y＝ax2+bx+1得，，解得：；（2）由（1）得函数解析式为y＝x2﹣4x+1，把x＝5代入y＝x2﹣4x+1得，y1＝6，∴y2＝12﹣y1＝6，∵y1＝y2，且对称轴为x＝2，∴m＝4﹣5＝﹣1．20．解：（1）由题意y1＝y2＝c，∴x1＝0，∵对称轴x＝1，∴M，N关于x＝1对称，∴x2＝2，∴x1＝0，x2＝2时，y1＝y2＝c．（2）①当x1≥t时，恒成立．②当x1≤t时，恒不成立．③当x1＜t．x2＞t时，∵抛物线的对称轴为x＝t，若对于x1+x2＞3，都有y1＜y2，当x1+x2＝3，且y1＝y2时，对称轴x＝，∴满足条件的值为：t≤．21．解：（1）∵抛物线y＝ax2﹣2ax﹣3+2a2＝a（x﹣1）2+2a2﹣a﹣3．∴抛物线的对称轴为直线x＝1；（2）∵抛物线的顶点在x轴上，∴2a2﹣a﹣3＝0，解得a＝或a＝﹣1，∴抛物线为y＝x2﹣3x+或y＝﹣x2+2x﹣1；（3）∵抛物线的对称轴为x＝1，则Q（3，y2）关于x＝1对称点的坐标为（﹣1，y2），∴当a＞0，﹣1＜m＜3时，y1＜y2；当a＜0，m＜﹣1或m＞3时，y1＜y2．22．解：（1）把点A（﹣1，0）、B（0，2）代入函数y＝ax2+bx+c，a﹣b+c＝0，c＝2，∴b＝a+2；c＝2．故答案为a+2，2；（2）∵点O是坐标原点，点C是该函数图象的顶点，∴y＝ax2+（a+2）x+2的顶点C的坐标为：（﹣，），∵△AOC的面积为1，即×1×||＝1解得：a＝﹣2或6﹣4或6+4．故答案为：a＝﹣2或6﹣4或6+4．（3）∵函数解析式为：y＝ax2+（a+2）x+2∴对称轴x＝﹣＝﹣，∵经过点A（﹣1，0）、B（0，2）且x＞1时，y＜5，∴a＜0．当对称轴在x＝1左侧时，如图1，解得a≤当对称轴在x＝1右侧时，如图2，解得﹣＜a＜﹣8+2，综上所述，a的取值范围是：a＜﹣8+2．23．解：（1）将A（3，1），B（0，4）代入y＝﹣x2+bx+c得，解得，∴所求的抛物线的解析式为：y＝﹣x2+2x+4，∵y＝﹣x2+2x+4＝﹣（x﹣1）2+5∴顶点坐标为（1，5）；（2）如图，分别过点B与点P作x轴的平行线BD、PE，过点A作x轴的垂线交BD于D、交PE于点E，∵P A⊥AB，∴∠P AB＝90°，∴∠DAB+∠P AE＝90°，由A（3，1）、B（0，4）知BD＝AD＝3，∴∠DAB＝45°，∴∠P AE＝90°﹣∠DAB＝90°﹣45°＝45°，∴∠P AE＝∠APE＝45°，∴AE＝PE，设点P的坐标为（m，﹣m2+2m+4），则AE＝，DE ＝x A﹣x E＝3﹣m∴m2﹣2m﹣3＝3﹣m解得：m＝﹣2或m＝3（点P在第三象限，不合题意，舍去），∴m＝﹣2时，﹣m2+2m+4＝﹣（﹣2）2+2×（﹣2）+4＝﹣4∴点P的坐标为（﹣2，﹣4）；（3）∵1≤n≤5且抛物线的顶点为（1，5），∴区间包含顶点，∴q的最大值为1，在y＝﹣x2+2x+4中，当y＝1时，x＝﹣1或者x＝3，∴q的最小值为﹣1，∴q的取值范围是：﹣1≤q≤1．。

人教版九年级数学上册《22.1.4二次函数y=ax²＋bx＋c的图象和性质》同步测试题带答案学校:___________班级：___________姓名：___________考号：___________一、选择题1．抛物线y=−2x2+4x+1的对称轴是（）A．直线x=2B．直线x=−2C．直线x=1D．直线x=−12．将二次函数y＝x2-4x+8转化为y＝a（x-m）2+k的形式，其结果为（）A．y＝（x-2）2+4 B．y＝（x+4）2+4C．y＝（x-4）2+8 D．y＝（x-2）2-43．如果抛物线的对称轴是直线x=2，与x轴的一个交点的坐标是(6，0)，那么它与x轴的一个交点的坐标是（）A．（-6，0）B．（-4，0）C．（-2，0）D．（4，0）4．已知二次函数y=−x2−2(b−2)x−b2+1的图象不经过第二象限，则实数b的取值范围是（）B．b≥1或b≤−1A．b≥54C．b≥2D．1≤b≤25．已知抛物线y=−x2−mx+n经过(−2，a)和(6，a)两点，则m的值为（）A．2 B．−4C．3 D．−66．若A(4,y1),B(1,y2),C(−1,y3)为二次函数y=x2−4x+3的图象上的三点，则y1,y2,y3的大小关系是（）A．y1<y2<y3B．y2<y1<y3C．y3<y1<y2D．y1<y3<y27．已知二次函数y=x2+(m−1)x+1，当x＞1时，y随x的增大而增大，而m的取值范围是（）A．m=−1B．m=3C．m≤−1D．m≥−1，与x轴交于点8．二次函数y=ax2+bx+c(a≠0)的部分图像如图所示，其对称轴为直线x=−12A，点A的坐标为(−2，0)，则2a+c的值为（）A．−2B．0 C．1 D．2二、填空题9．请写出一个开口向上，并且与y轴交于点(0，−2)的抛物线解析式．10．如图所示，抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1，且抛物线经过点P(3，0)，则抛物线与x轴的另一个交点为.11．已知二次函数y=x2−4x+k的图象的顶点在x轴下方，则实数k的取值范围是．12．已知抛物线y＝﹣x2﹣3x+3，点P（m，n）在抛物线上，则m+n的最大值是．13．已知二次函数y=x2+2x−3，当−4≤x≤1时，y的取值范围为.三、解答题14．已知抛物线y=x2−2x−2的顶点为A，与y轴的交点为B，求过A、B两点的直线的解析式. 15．已知二次函数y=12x2+x+4．（1）确定抛物线的开口方向、顶点坐标和对称轴方程；（2）当x取何值时，y随x的增大而增大？当x取何值时，y随x的增大而减小？16．已知抛物线y=ax2-2ax-3+2a2(a≠0)．（1）求这条抛物线的对称轴．（2）若该抛物线的顶点在x轴上，求其函数表达式．（3）设点P(m，y1)，Q(3，y2)在抛物线上，若y1<y2，求m的取值范围．17．已知抛物线y=x2+ax+a+1经过点A(−2，3)．（1）求a的值；（2）已知点P(m，y P)，Q(m−4，y Q)均在该抛物线上．①若m=0，请直接比较y P与y Q的大小关系；②当−3≤x≤m时，函数y的最大值是6，最小值是2，求m的取值范围．参考答案1．C2．A3．C4．B5．B6．B7．D8．B9．y =x 2−2（答案不唯一）．10．(−1，0)11．k <412．413．−4≤y ≤514．解：∵抛物线y=x 2-2x-2=（x-1）2-3∴抛物线顶点坐标为（1，-3），与y 轴的交点坐标为（0，-2） 即A （1，-3），B （0，-2）设所求直线的解析式为y=kx+b则 {−3=k ⋅1+b −2=k ⋅0+b解得 {k =−1b =−2∴所求直线的解析式为y=-x-2.15．（1）解：∵a =12>0∴抛物线开口向上∵−b 2a =−12x(−12)=−1 ∴抛物线的对称轴为直线x =−1∵当x =−1时∴顶点坐标为(−1，72)；（2）解：∵抛物线开口向上且对称轴为x =−1∴当x <−1时，y 随x 的增大而减小当x ≥−1时，y 随x 的增大而增大．16．（1）解：∵抛物线y=ax 2- 2ax- 3+2a 2=a(x- 1)2+2a 2-a-3∴抛物线的对称轴为直线x=1．（2）解：∵抛物线的顶点在x 轴上，∴2a 2-a-3=0 解得a= 32或a=-1，∴抛物线的函数表达式为y= 32x 2-3x+32或y=-x 2+2x-1；（3）解：∵抛物线的对称轴为直线x=1∴Q(3，y 2)关于直线x=1的对称点的坐标为(-1，y 2)． 当a>0时，∵y 1<y 2，∴-1<m<3；当a<0时，∵y 1<y 2，∴m<-1或m> 3．17．（1）解：将点(−2，3)代入y =x 2+ax +a +1中 得3=4−2a +a +1解得a =2；（2）解：①∵a =2∴抛物线为y =x 2+2x +3当m =0时，点P(m ，y P )，Q(m −4，y Q )为P(0，y P )，Q(−4，y Q ) ∴y P =0+0+3=3，y Q =16−8+3=11 ∴y P 与y Q 的大小关系为y P <y Q ；②y =x 2+2x +3=(x +1)2+2．当x 2+2x +3=6时x 1=−3，x 2=1． 根据图象和题意可得m 的取值范围是−1≤m ≤1．。

22.1.4二次函数y=ax^2+bx+c的图像和性质（培优）姓名：得分：日期：一、选择题（本大题共 7 小题）1、已知二次函数y=x2+（m-1）x+1，当x＞1时，y随x的增大而增大，而m的取值范围是（）A.m=-1B.m=3C.m≤-1D.m≥-12、已知二次函数y=x2−x+a(a>0)，当自变量x取m时，其相应的函数值小于0，那么当自变量x取m-1时，下列结论中正确的是( )A. m-1的函数值小于0B. m-1的函数值大于0C. m-1的函数值等于0D. m-1的函数值与0的大小关系不确定3、已知抛物线C1：y=2x2−4x+1，抛物线C2是由抛物线C1向右平移3个单位得到的，那我们我们可以得到抛物线C1和抛物线C2一定关于某条直线对称，则这条直线为( )A. x=3B. x=2C. x=52D. x=324、若二次函数y=x2−6x+9的图象经过A(−1，y1)，B(1，y2)，C(3+√3，y3)三点.则关于y1，y2，y3大小关系正确的是( )A. y1>y2>y3B. y1>y3>y2C. y2>y1>y3D. y3>y1>y25、二次函数y=x2+mx+n，若m-n=0，则它的图象必经过点( )A. (-1，1)B. (1，-1)C. (-1，-1)D. (1，1)6、如图，图中是抛物线形拱桥，当拱顶离水面2m时水面宽4m.水面下降1m，水面宽度为A.2√6mB.2√3mC.√6mD.√3m7、要将抛物线y=x2+2x+3平移后得到抛物线y=x2，下列平移方法正确的是( )A. 向左平移1个单位，再向上平移2个单位B.向左平移1个单位，再向下平移2个单位C. 向右平移1个单位，再向上平移2个单位D. 向右平移1个单位，再向下平移2个单位二、填空题（本大题共 8 小题）8、请写出一个开口向下，并且与y轴交于点（0，2）的抛物线的解析式，y=______．9、将二次函数y=ax2+(b+2)x+c的图象向左平移1个单位，再向上平移2个单位，得到y=x2+x−1的图象，则原二次函数解析式为________。

九年级数学上册22.1.4二次函数y=ax2+bx+c的图象和性质
同步检测含解析
2214 二次函数=ax2+bx+c的图象和性质
测试时间2经过平移得到抛物线=-x2,平移方法是( )
A向右平移1个单位,再向下平移1个单位 B向右平移1个单位,再向上平移1个单位
c向左平移1个单位,再向下平移1个单位 D向左平移1个单位,再向上平移1个单位
2(1的图象顶点坐标是( )
A(0,-1) B(2,-1) c D
3若点(-2,1),N(-1,2),P(8,3)在抛物线=-x2+2x上,则下列结论正确的是( )
A1 2 3 B2 1 3 c3 1 2 D1 3 2
4(x2+2x+7的最大值为
6(2ax-1的图象上,如果 n,那么a 0(用“ ”或“ ”连接)
三、解答题
7(4-228…
(1)求这个二次函数的解析式;
(2)用配方法求出这个二次函数图象的顶点坐标和对称轴
8已知抛物线=x2+bx+3经过点A(-1,8),顶点为
(1)求抛物线的表达式;
(2)设抛物线对称轴与x轴交于点B,连接AB、A,求△AB的面积
2214 二次函数=ax2+bx+c的图象和性质
一、选择题
1答案D ∵抛物线=-x2+2x-2=-(x-1)2-1的顶点坐标为(1,-1),又∵平移后抛物线=-x2的顶点坐标为(0,0),∴平移方法为向左平移1个单位,再向上平移1个单位故选D
2答案c ∵=2x2-x-1=2-,∴二次函数图象的顶点坐标为,故选c。

2019-2019学年数学人教版九年级上册22.1.4 y=ax2+bx+c的图象和性质同步训练一、选择题1. ( 2分) 抛物线y=x2﹣2x+1的顶点坐标是（）A.（1，0）B.（﹣1，0）C.（﹣2，1）D.（2，﹣1）【答案】A【考点】二次函数y=ax^2+bx+c的性质【解析】【解答】由原方程，得y=（x﹣1）2，∴该抛物线的顶点坐标是：（1，0）．故答案为：A．【分析】将二次函数的解析式转化为顶点式，就可求出顶点坐标。

或将a、b、c的值代入顶点式计算即可。

2. ( 2分) 用配方法将化成的形式为（）A. B. C. D.【答案】B【考点】二次函数y=ax^2+bx+c与二次函数y=a（x-h）^2+k的转化【解析】【解答】故答案为：：B【分析】在抛物线的解析式的右边加上一次项系数一半的平方，再减去一次项系数一半的平方，然后前三项利用完全平方公式分解因式，常数项合并在一起，即y = x2−8x+12=x2−8x+16−16+12= (x−4)2−4.3. ( 2分) 对二次函数y＝3x2－6x的性质及其图象，下列说法不正确的是（）A. 开口向上B. 对称轴为直线x＝1C. 顶点坐标为（1，－3）D. 最小值为3【答案】D【考点】二次函数的最值，二次函数y=ax^2+bx+c与二次函数y=a（x-h）^2+k的转化【解析】【解答】A. 二次函数开口向上，不符合题意.B.对称轴不符合题意.C.当时，顶点坐标为：不符合题意.D.二次函数的最小值为：符合题意.故答案为：：D【分析】首先将二次函数配成顶点式，根据顶点坐标式即可判断出其对称轴直线，顶点坐标，最值等问题，再根据二次项系数大于0，即可判断出抛物线的开口方向。

4. ( 2分) 二次函数y＝ax2＋bx－1(a≠0)的图象经过点(1，－3)，则代数式1＋a＋b的值为( )A. －3B. －1C. 2D. 5 【答案】B【考点】代数式求值，二次函数图象上点的坐标特征【解析】【解答】二次函数的图象经过点把点代入二次函数的解析式，得：故答案为：：B【分析】将点( 1 ，− 3 ) 得出代入二次函数的解析式+b=−2.，再整体代入代数式即可算出答案。

22 22.1.4 二次函数y=ax 2+bx+c 的图象和性质1.若抛物线 y=-x 2+bx+c 经过点(-2,3),则 2c-4b-9 的值是( )A.5B.-1C.4D.182.(2018·山东德州中考)如图,函数 y=ax 2-2x+1 和 y=ax-a (a 是常数,且 a ≠0)在同一平面直角坐标系中的图象可能是()3. 若抛物线 y=x 2-2x+3 不动,将平面直角坐标系 xOy 先沿水平方向向右平移 1 个单位长度,再沿竖直方向向上平移 3 个单位长度,则原抛物线对应的函数解析式应变为( )A.y=(x-2)2+3B.y=(x-2)2+5C.y=x 2-1D.y=x 2+44. 二次函数 y=1x 2+3x+5y=1x 2 的图象先向(左、右)平移个单位长度,再2的图象是由函数向 (上、下)平移个单位长度得到的.5.经过 A (4,0),B (-2,0),C (0,3)三点的抛物线解析式是.6. 如图,若抛物线 y=ax 2+bx+c 上的 P (4,0),Q 两点关于它的对称轴 x=1 对称,则点 Q 的坐标为 .7. 已知二次函数 y=ax 2+bx+c 的图象如图所示,则点 P (a ,bc )在第象限.8.已知二次函数y=ax2-5x+c 的图象如图所示.(1)试求该二次函数的解析式和它的图象的顶点坐标.(2)观察图象回答,何时y 随x 的增大而增大,何时y 随x 的增大而减小?(3)将图中抛物线先向左平移3 个单位长度,再向下平移4 个单位长度,试确定所得到的抛物线的解析式.9.已知抛物线y=x2-2mx-4(m>0)的顶点M 关于坐标原点O 的对称点为M',若点M'在这条抛物线上,则点M 的坐标为( )A.(1,-5)B.(3,-13)C.(2,-8)D.(4,-20)10.由于被墨水污染,一道数学题仅能见到如下文字:“已知二次函数y=x2+bx+c 的图象过点(1,0)……求证:这个二次函数的图象关于直线x=2 对称.”根据现有信息,题中的二次函数图象不具有的性质是( )A.过点(3,0)B.顶点是(2,-2)C.b<0D.c=311.若抛物线y=ax2+bx+c 的顶点是A(2,1),且经过点B(1,0),则抛物线的函数解析式为.12.二次函数y=ax2+bx+c 的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,则P,Q 的大小关系是.★13. 如图,四边形ABCD 是菱形,点D 的坐标是(0, 3),以点C 为顶点的抛物线y=ax2+bx+c 恰好经过x 轴上A,B 两点.(1)求A,B,C 三点的坐标.(2)求经过A,B,C 三点的抛物线的解析式.(3)若将上述抛物线沿其对称轴向上平移后恰好过点D,求平移后抛物线的解析式,并指出平移了多少个单位长度?★14.我们知道,经过原点的抛物线的解析式可以是y=ax2+bx(a≠0).(1)对于这样的抛物线:当顶点坐标为(1,1)时,a= ;当顶点坐标为(m,m)(m≠0)时,a 与m 之间的关系式是;(2)继续探究,若b≠0,且过原点的抛物线顶点在直线y=kx(k≠0)上,请用含k 的式子表示b;(3)现有一组过原点的抛物线,顶点A1,A2,…,A n在直线y=x 上,横坐标依次为1,2,…,n(n 为正整数,且n≤12),分别过每个顶点作x 轴的垂线,垂足记为B1,B2,…,B n,以线段A n B n为边向右作正方形A n B n C n D n, 若这组抛物线中有一条经过D n,求所有满足条件的正方形边长.参考答案夯基达标1.A ∵抛物线y=-x2+bx+c 经过点(-2,3),∴-(-2)2-2b+c=3,整理得,-2b+c=7,∴2c-4b-9=2(c-2b)-9=2×7-9=5,故选A.2.B A.由一次函数y=ax-a 的图象可得a<0,此时二次函数y=ax2-2x+1 的图象应该开口向下,故本选项错误;B.由一次函数y=ax-a 的图象可得a>0,此时二次函数y=ax2-2x+1 的图象应该开口向上,对称轴x=- -2 >0,故本选项正确;2�C.由一次函数y=ax-a 的图象可得a>0,此时二次函数y=ax2-2x+1 的图象应该开口向上,对称轴x=- -2 >0,和x 轴的正半轴相交,故本选项错误;2�D.由一次函数y=ax-a 的图象可得a>0,此时二次函数y=ax2-2x+1 的图象应该开口向上,故本选项错误.故选B.3.C 将平面直角坐标系xOy 先沿水平方向向右平移1 个单位长度,再沿竖直方向向上平移3 个单位长度,相当于把抛物线向左平移1 个单位长度,再向下平移3 个单位长度,因为y=x2-2x+3=(x-1)2+2,所以抛物线的顶点坐标为(1,2),向左平移1 个单位长度,再向下平移3 个单位长度,得到顶点(0,-1),所以原抛物线对应函数的解析式应变为y=x2-1.故选C.2�16�-20 + � =02 4. 左3 下 2 先将二次函数由一般式化成顶点式,再确定平移的单位长度.由于y=1x 2+3x+5 = 1(x 2+6x+5)=1(x 2+6x+9-9+5)=1(x+3)2-2,22222故抛物线 y=1x 2+3x+5 y=1x 2 先向左平移 3 个单位长度,再向下平移 2 个单位长度得到的.是由抛物线 2225. y=-3x 2+3x+3 根据题意设抛物线的解析式为 y=a (x+2)(x-4),84把 C (0,3)代入得-8a=3,即 a=-3,则抛物线的解析式为 y=-3(x+2)(x-4)=-3x 2+3x+3.88846.(-2,0) 由抛物线 y=ax 2+bx+c 上的 P (4,0),Q 两点关于它的对称轴 x=1 对称,可知 P ,Q 两点到对称轴x=1 的距离相等,所以点 Q 的坐标为(-2,0).7.三 ∵抛物线开口向下,∴a<0.∵- �<0,a<0,∴b<0.∵抛物线与 y 轴交于正半轴,∴c>0,∴P (a ,bc )在第三象限.8.解 (1)由题图知,抛物线过点(1,0),(4,0),代入函数解析式,得 �-5 + � = 0, ,解得 � = 1,= 4.故所求二次函数的解析式为 y=x 2-5x+4.又因为 y=x 2-5x+4= �− 9,所以函数图象的顶点坐标为4(2)由(1)知,a=1>0,抛物线的对称轴为直线 x=5,从图象知,当 x>5,y 随 x 的增大而增大;当 x<5,y 随 时 时 222x 的增大而减小.(3)由(1)知,y=x 2-5x+4= �- 52− 9,将抛物线先向左平移 3 个单位长度,再向下平移 4 个单位长度,则所4得抛物线的解析式为 y= �- 5 + 3 2− 9-4,即 y=x 2+x-6.24培优促能9.C ∵y=x 2-2mx-4=x 2-2mx+m 2-m 2-4=(x-m )2-m 2-4,2�2 2� ∴点 M (m ,-m 2-4).∴点 M'(-m ,m 2+4).∴m 2+2m 2-4=m 2+4.解得 m=±2.∵m>0,∴m=2.∴M (2,-8).故选 C .10.B 因为二次函数 y=x 2+bx+c 的图象过点(1,0),且关于直线 x=2 对称,所以 1+b+c=0,且图象过点(3,0),-�=2,则 b=-4<0;将 b=-4 代入 1+b+c=0,得 c=3.故 y=x 2-4x+3,顶点是(2,-1).211.y=-x 2+4x-3 设抛物线的解析式为 y=a (x-2)2+1,将 B (1,0)代入 y=a (x-2)2+1,得 a=-1.因此抛物线的函数解析式为 y=-(x-2)2+1,展开得 y=-x 2+4x-3.12. P>Q ∵抛物线的开口向下,∴a<0.∵- �>0,∴b>0.∴2a-b<0.∵- �=1,∴b+2a=0.x=1 时,a+b+c>0,x=-1 时,y=a-b+c<0.∴-1b-b+c<0.∴3b-2c>0.∵抛物线与 y 轴的正半轴相交,∴c>0.∴3b+2c>0,∴P=0+3b-2c=3b-2c>0,Q=b-2a-3b-2c=-2a-2b-2c=-2(a+b+c )<0.∴P>Q.13. 解 (1)由抛物线的对称性可知 AE=BE.在 Rt △AOD 和 Rt △BEC 中, 因为 OD=EC ,AD=BC , 所以 Rt △AOD ≌Rt △BEC (HL).2� 故 OA=EB=EA.设菱形的边长为 2m ,在 Rt △AOD 中,m 2+( 3)2=(2m )2,解得 m=1.所以 DC=2,OA=1,OB=3.故 A ,B ,C 三点的坐标分别为(1,0),(3,0),(2, 3).(2) 设抛物线的解析式为 y=a (x-2)2+ 3,代入点 A 的坐标(1,0),得 a=- 3,所以抛物线的解析式为 y=- 3(x-2)2+ 3.(3) 设平移后抛物线的解析式为 y=- 3(x-2)2+k ,代入点 D 的坐标(0, 3),得 k=5 3,所以平移后的抛物线的解析式为 y=- 3(x-2)2+5 3.所以平移了 5 3 − 3=4 3个单位长度.创新应用14.解 (1)-1 a=- 1(或 am+1=0)�(2) 因为 a ≠0,所以 y=ax2+bx=a � + �所以顶点坐标为 - � �22 − �2 . 4�2��因为顶点在直线 y=kx 上,所以 k · - =-�2.4�又因为 b ≠0,所以 b=2k.(3) 因为顶点 A n 在直线 y=x 上,所以可设 A n 的坐标为(n ,n ),点 D n 所在的抛物线顶点坐标为(t ,t ),由(1)(2)可得,点 D n 所在的抛物线解析式为 y=-1x 2+2x.�因为四边形 A n B n C n D n 是正方形,所以点 D n 的坐标为(2n ,n ).所以-1·(2n )2+2×2n=n.�所以 4n=3t.� 2�因为t,n 是正整数,且t≤12,n≤12,所以n 的值为3,6 或9. 所以满足条件的正方形边长为3,6 或9.。

二次函数y ＝ax2+bx+c 的图象和性质（时间：60分钟，满分90分）班级：___________姓名：___________得分：___________ 一、选择题（每题3分）1．对于二次函数y=x 2-4x+7的图象，下列说法正确的是（ ） A ．开口向下B ．对称轴是x=-2C ．顶点坐标是（2，3）D ．与x 轴有两个交点 【答案】C ． 【解析】试题解析：∵y=x 2-4x+7=（x-2）2+3， ∴对称轴为x=2，顶点坐标为（2，3）， 故B 错误，C 正确， 故选C ．考点：二次函数的性质．2．抛物线223y x x =-++的顶点坐标是 ( ) A ．(-1，4) B ．(1，3) C ．(-1，3) D ．(1，4) 【答案】D 【解析】试题分析：将二次函数配成顶点式为：y=－(2x －2x)+3=－(2x －2x+1－1)+3=－2(1)x -+4，则顶点坐标为(1,4)；本题也可以直接利用二次函数的顶点坐标(－2ba ，244acb a-)进行求解.考点：二次函数的顶点坐标3．已知抛物线y ＝ax 2＋bx ＋c 的开口向上，顶点坐标为(3，-2)，那么该抛物线有( ) A ．最小值-2 B ．最大值-2 C ．最小值3 D ．最大值3 【答案】A ． 【解析】试题解析：由抛物线y=ax2+bx+c 的开口向上，顶点坐标为（3，-2）， 可知该抛物线有最小值-2， 故选A ．考点：二次函数的最值．4．已知二次函数y=ax 2+bx+c （a ＜0）的图象如图所示，当-5≤x≤0时，下列说法正确的是（ ）A ．有最小值-5、最大值0B ．有最小值-3、最大值6C ．有最小值0、最大值6D ．有最小值2、最大值6 【答案】B ． 【解析】试题解析：由二次函数的图象可知， ∵-5≤x≤0，∴当x=-2时函数有最大值，y 最大=6； 当x=-5时函数值最小，y 最小=-3． 故选B ．考点：二次函数的最值．5．已知开口向下的抛物线的顶点坐标为（2，0），则函数y 随x 的增大而增大的取值范围为（ ）． A ．x ＞0 B ．x ＜0 C ．x ＞2 D ．x ＜2 【答案】D ． 【解析】试题分析：因为顶点坐标是（2，0），所以对称轴是直线x=2，又因为抛物线开口向下，所以在对称轴左侧，函数y 随x 的增大而增大，故自变量的取值范围是x ＜2，故选D ． 考点：函数的增减性．6．函数y=-2x 2-8x+m 的图象上有两点A （x 1，y 1），B （x 2，y 2），若-2＜x 1＜x 2，则 A ．21y y < B ．21y y >C ．21y y =D ．1y 、2y 的大小不确定【答案】B ． 【解析】试题解析：∵y=-2x 2-8x+m=-2（x+2）2+m+8，∴对称轴是x=-2，开口向下，距离对称轴越近，函数值越大， ∵-2＜x 1＜x 2， ∴y 1＞y 2． 故选B ．考点：1．二次函数图象上点的坐标特征；2．二次函数的性质．7．把二次函数y ＝－x 2－x ＋3用配方法化成y ＝a （x －h ）2＋k 的形式（ ） A ．y ＝－（x －2）2＋2 B ．y ＝（x －2）2＋4 C ．y ＝－（x ＋2）2＋4 D ．y ＝2＋3 【答案】C ． 【解析】试题分析：y=-x 2-x+3=-（x 2+4x+4）+1+3=- （x+2）2+4,故答案选C ． 考点：二次函数的解析式的三种形式．8．若b ＜0，则二次函数y=x 2-bx-1的图象的顶点在：A ．第一象限B ．第二象限C ．第三象限D ．第四象限 【答案】C ． 【解析】试题解析：二次函数y=x 2-bx-1的图象的顶点为（-21b -⨯，()()241141b ⨯⨯---⨯），即（2b ，244b --），∵b ＜0，∴2b＜0，244b --＜0，∴（2b ，244b --）在第三象限．故选C ．考点：二次函数图象与系数的关系．9．抛物线222y x x =-＋-经过平移得到2y x =-，平移方法是（ ） A ．向右平移1个单位，再向下平移1个单位 B ．向右平移1个单位，再向上平移1个单位 C ．向左平移1个单位，再向下平移1个单位 D ．向左平移1个单位，再向上平移1个单位 【答案】D 【解析】试题分析：因为2222(1)3y x x x ==----＋-，所以抛物线222y x x =-＋-向左平移1个单位，再向上平移1个单位可以得到2y x =-，故选：D ．考点：抛物线的平移．10．函数y=x 2+3x －4的图象与y 轴的交点坐标是 A ．（2，0） B ．（－2，0） C ．（0，4） D ．（0，－4） 【答案】D ． 【解析】试题解析：把x=0代入y=x 2+3x-4得y=-4，所以函数y= x 2+3x-4的图象与y 轴的交点坐标为（0，-4）． 考点：二次函数图象上点的坐标特征． 二、填空题（每题3分）11．抛物线y ＝2x 2-bx ＋3的对称轴是直线x ＝1，则b 的值为___ 【答案】-4. 【解析】 试题解析：∵-22b-⨯=-1， ∴b=-4考点：二次函数的性质．12．已知二次函数222y x mx =++，当x ＞2时，y 的值随x 值的增大而增大，则实数m 的取值范围 是_ _．【答案】2m ≥-． 【解析】试题分析：抛物线的对称轴为直线x=221m-⨯=﹣m ，∵当x ＞2时，y 的值随x 值的增大而增大，∴﹣m≤2，解得m≥﹣2．故答案为：m≥﹣2． 考点：二次函数的性质．13．二次函数226y x x =-+的最小值是__ __． 【答案】5． 【解析】试题分析：226y x x =-+=2(1)5x -+，可见，二次函数的最小值为5．故答案为：5． 考点：二次函数的最值．14．抛物线y=x 2﹣4x+3的顶点坐标是 ． 【答案】（2，-1） 【解析】试题分析：因为二次函数2()y a x h k =-+的顶点坐标是（h ，k ），所以函数y=x 2﹣4x+3=（ x-2）2-1的图象的顶点坐标是（2，－1）． 考点：二次函数的顶点坐标15．抛物线332-+-=x x y 与y 轴的交点坐标为___________．【答案】（0，-3）． 【解析】试题分析：因为抛物线与y 轴交点的横坐标是0，所以将x=0代入解析式，得y=-3，所以抛物线332-+-=x x y 与y 轴的交点坐标为（0，-3）． 考点：抛物线与坐标轴交点坐标的规律．16．二次函数y=x 2+2x 的顶点坐标为 ，对称轴是直线 ． 【答案】（-1，-1），x=-1． 【解析】试题分析：二次函数y=ax 2+bx+c 中，顶点坐标是（-a b 2，aac 4-4b 2），对称轴是直线x=-a b 2，所给二次函 数中，a=1，b=2，c=0，代入公式中，对称轴是直线x=-a b 2=-22=-1；顶点横坐标是-1，顶点纵坐标是 aac 4-4b 2=4-22=-1．所以顶点坐标为（-1，-1），对称轴是直线x=-1．考点：二次函数的对称轴与顶点坐标公式．17．将抛物线22y x x =-向上平移3个单位，再向右平移4个单位得到的抛物线是_______．【答案】2(5)2y x =-+或21027y x x =-+． 【解析】试题分析：22y x x =-=2(1)1x --，根据平移规律，向上平移3个单位，再向右平移4个单位得到的抛物线是：2(5)2y x =-+，将顶点式展开得，21027y x x =-+．故答案为：2(5)2y x =-+或21027y x x =-+．考点：1．二次函数图象与几何变换；2．压轴题；3．几何变换． 18．若二次函数24y ax x a -+＝的最小值是－3，则a ＝_________． 【答案】1 【解析】试题分析：因为二次函数24y ax x a -+＝的最小值是－3，所以241634a y a-==-，解得a=1或-4，又二次函数有最小值，所以a ＞0，所以a=1． 考点：二次函数的最值19．将二次函数y ＝2x －2x －3化为y ＝（x －h ）2＋k 的形式，则__________________．【答案】y ＝（x －1）2－4 【解析】试题分析：y ＝2x －2x －3=2x －2x+1-4=（x －1）2－4． 考点：配方法．20．已知A （﹣2，y 1）、B （0，y 2）、C （1，y 3）三点都在抛物线y=kx 2+2kx+k 2+k （k ＜0）的图象上，则y 1、y 2、y 3的大小关系是 ． 【答案】y 1=y 2＞y 3 【解析】试题分析：对称轴为直线x=﹣22kk⋅=﹣1， ∵A （﹣2，y 1）、B （0，y 2）， ∴A 、B 是对称点， ∴y 1=y 2， ∵k ＜0，∴x ＞﹣1时，y 的值随x 的增大而减小， ∴y 2＞y 3， ∴y 1=y 2＞y 3．故答案为：y 1=y 2＞y 3．考点：二次函数图象上点的坐标特征. 三、计算题（每题10分）21. 画出二次函数y=﹣x 2+2x+3的图像，并根据图像解答下列问题：（1）x 取何值时，函数值y 随x 的增大而减小； （2）x 取何值时，y ≤3． 【答案】正确画出图像；（1）x ≥1；（2）x ≤0或x ≥2 【解析】 试题分析：（1）确定出二次函数的对称轴即可解答；（2）利用图象直接解答即可．试题解析：（1）原式可化为：y=﹣x 2+2x+3=-（x-1）2+4，则函数图象的对称轴为x=1，∵函数图象开口向下，所以自变量x ≥1时，y 随x 的增大而减小；（2）由图可知当0＜x ＜2时，y ＞3，所以当x ≤0或x ≥2时，y ≤3．考点：二次函数的图像及性质． 22. 已知二次函数y=﹣x 2+x+4．（1）求抛物线的顶点坐标和对称轴；（2）当x 取何值时，y 随x 的增大而增大？当x 取何值时，y 随x 的增大而减小？当x 取何值时，y 有最大值还是最小值？是多少？ 【答案】（1）顶点坐标为（1，29），对称轴为x=1； （2）当x ＜1时，y 随x 的增大而增大；当x ＞1时y 随x 的增大而减小；函数有最大值为29． 【解析】 试题分析：（1）根据函数解析式可求出顶点坐标，对称轴及与坐标轴的交点； （2）根据确定的对称轴及顶点坐标确定其增减性即可． 试题解析：（1）∵y=﹣21x 2+x+4=﹣21（x 2﹣2x+1﹣1）+4=﹣21（x ﹣1）2+29，∴顶点坐标为（1，29），对称轴为x=1；（2）∵开口向下且对称轴为x=1，∴当x ＜1时，y 随x 的增大而增大；当x ＞1时y 随x 的增大而减小；函数有最大值为29． 考点：1.二次函数的性质；2.二次函数的最值． 23.如图，已知二次函数21232y x x =-+的图象的顶点为A ，且与y 轴交于点C ．（1）求点A 与点C 的坐标；（2）若将此函数的图象沿z 轴向右平移1个单位，再沿y 轴向下平移3个单位，请直接写出平移后图象所对应的函数关系式及点C 的对应点的坐标；（3）若A （m ，1y ），B （m ＋1，2y ）两点都在此函数的图象上，试比较1y 与2y 的大小． 【答案】（1）A(2，1)，C （0，3）；(2)21(3)22y x =-- ，C ′（1，0）；（3）当32m <时，12y y >，当32m =时，12y y =，当32m >时，12y y <． 【解析】 试题分析：（1）把抛物线的解析式配方即可得到顶点A 的坐标，令抛物线解析式的x=0，算出y ，即可得到抛物线y 轴交于点C 的坐标；（2）根据平移规律即可得到平移后的解析式和点C 对应点的坐标； （3）把m 和m+1代入抛物线解析式，算出2132y y m -=-，进行讨论即可． 试题解析：（1）21232y x x =-+=21(2)12x -+，∴顶点A 的坐标为(2，1)，在21232y x x =-+中，令x=0，得y=3，∴C （0，3）；（2）平移后的抛物线方程为：21(3)22y x =--，点C 的对应点的坐标为（1，0）； （3）211232y m m =-+，221(1)2(1)32y m m =+-++，2132y y m -=-，∴当32m <时，12y y >，当32m =时，12y y =，当32m >时，12y y <．考点：1．二次函数的图象；2．二次函数的性质；3．二次函数与几何变换．。

22.1.4二次函数y＝ax2＋bx＋c的图象和性质（2）一、夯实基础1.已知某二次函数的图象如图所示，则这个二次函数的解析式为( )A.y=2(x+1)2+8B.y=18(x+1)2-8C.y=(x-1)2+8D.y=2(x-1)2-82.如图所示，抛物线的函数表达式是( )A.y=x2-x+4B.y=-x2-x+4C.y=x2+x+4D.y=-x2+x+43.已知二次函数y=ax2+bx+c经过点(-1,0)，（0，-2），(1,-2).则这个二次函数的解析式为______.4.已知二次函数y=ax2+bx+c，当x=0时，y=1；当x=-1时，y=6；当x=1时，y=0.求这个二次函数的解析式.5.已知抛物线的顶点坐标为(4,-1)，与y轴交于点(0,3)，求这条抛物线的解析式.6.已知一个二次函数的图象与x轴的两个交点的坐标分别为(-1，0)和(2，0)，与y轴的交点坐标为(0，-2)，则该二次函数的解析式为______.7.抛物线的图象如图所示，根据图象可知，抛物线的解析式可能是( )A.y＝x2-x-2B.y＝-x2-x+2C.y＝-x2-x+1D.y＝-x2+x+2二、能力提升8.二次函数y=-x2+bx+c的图象的最高点是(-1，-3)，则b，c的值分别是( )A.b=2，c=4B.b=2，c=-4C.b=-2，c=4D.b=-2，c=-49.已知抛物线y＝ax2＋bx＋c(a≠0)的对称轴为x＝1，且抛物线经过A(-1，0)，B(0，-3)两点，则这条抛物线所对应的函数关系式为______.10.设抛物线y=ax2+bx+c(a≠0)过点A(0，2)，B(4，3)，C三点，其中点C在直线x=2上，且点C到抛物线的对称轴的距离等于1，则抛物线的函数解析式为______.11.如图，已知抛物线的顶点为A(1，4)，抛物线与y轴交于点B(0，3)，与x轴交于C、D两点.点P是x轴上的一个动点.(1)求此抛物线的解析式；(2)当PA+PB的值最小时，求点P的坐标.三、课外拓展12.已知抛物线y=ax2+bx+c与x轴交于点A(1，0)，B(3，0)，且过点C(0，-3).(1)求抛物线的解析式和顶点坐标；(2)请你写出一种平移的方法，使平移后抛物线的顶点落在直线y=-x上，并写出平移后抛物线的解析式.13.如图，2×2网格(每个小正方形的边长为1)中有A，B，C，D，E，F，G，H，O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).(1)n为奇数，且l经过点H(0，1)和C(2，1)，求b，c的值，并直接写出哪个格点是该抛物线上的顶点；(2)n为偶数，且l经过点A(1，0)和B(2，0)，通过计算说明点F(0，2)和H(0，1)是否在抛物线上；(3)若l经过这九个格点中的三个，直接写出满足这样条件的抛物线条数.四、中考链接1．（2016•沈阳）在平面直角坐标系中，二次函数y=x2+2x﹣3的图象如图所示，点A（x1，y1），B（x2，y2）是该二次函数图象上的两点，其中﹣3≤x1＜x2≤0，则下列结论正确的是（）A．y1＜y2B．y1＞y2C．y的最小值是﹣3 D．y的最小值是﹣42.（2016·四川眉山·3分）若抛物线y=x2﹣2x+3不动，将平面直角坐标系xOy先沿水平方向向右平移一个单位，再沿铅直方向向上平移三个单位，则原抛物线图象的解析式应变为（）A．y=（x﹣2）2+3 B．y=（x﹣2）2+5 C．y=x2﹣1 D．y=x2+43.（2016河南）已知A（0，3），B（2，3）是抛物线y=﹣x2+bx+c上两点，该抛物线的顶点坐标是．答案1.D2.D3.y=x2-x-2.4.由题意，得a+b+c=0,a-b+c=6,c=1.解得a=2,b=-3,c=1.∴二次函数的解析式为y=2x2-3x+1.5.依题意，设y=a(x-h)2+k.将顶点坐标(4,-1)和与y轴交点(0,3)代入，得3=a(0-4)2-1.解得a=.∴这条抛物线的解析式为y=(x-4)2-1.6.y=x2-x-2.7.D8.D9.y＝x2-2x-3.10.y=x2-x+2或y=-x2+x+2.11.(1)∵抛物线顶点坐标为(1,4)，∴设y=a(x-1)2+4.∵抛物线过点B(0，3)，∴3=a(0-1)2+4，解得a=-1.∴抛物线的解析式为y=-(x-1)2+4，即y=-x2+2x+3.(2)作点B关于x轴的对称点E(0，-3)，连接AE交x轴于点P.设AE解析式为y=kx+b，则k+b=4,b=-3,解得k=7,b=-3.∴y AE=7x-3.∵当y=0时，x=，∴点P的坐标为(，0).12.(1)∵A(1，0)，B(3，0)，∴设抛物线解析式为y=a(x-1)(x-3).∵抛物线过(0，-3)，∴-3=a(-1)×(-3).解得a=-1.∴y=-(x-1)(x-3)=-x2+4x-3.∵y=-x2+4x-3=-(x-2)2+1，∴顶点坐标为(2，1).(2)答案不唯一，如：先向左平移2个单位，再向下平移1个单位，得到的抛物线的解析式为y=-x2，平移后抛物线的顶点为(0，0)落在直线y=-x上.13.(1)因为n为奇数，则抛物线解析式为y=-x2+bx+c.将H(0，1)和C(2，1)代入上式，得b=2，c=1.所以抛物线解析式为y=-x2+2x+1.化为顶点式为y=-(x-1)2+2，其顶点坐标为(1，2)，所以顶点所在的格点为E.(2)因为n为偶数，则抛物线的解析式为y=x2+bx+c.将A(1，0)和B(2，0)代入上式，得b=-3，c=2.所以抛物线解析式为y=x2-3x+2.将x=0代入上式可得y=2，所以F点在该抛物线上，H点不在该抛物线上.(3) 8.中考链接：1解：y=x2+2x﹣3=（x+3）（x﹣1），则该抛物线与x轴的两交点横坐标分别是﹣3、1．又y=x2+2x﹣3=（x+1）2﹣4，∴该抛物线的顶点坐标是（﹣1，﹣4），对称轴为x=﹣1．A、无法确定点A、B离对称轴x=﹣1的远近，故无法判断y1与y2的大小，故本选项错误；B、无法确定点A、B离对称轴x=﹣1的远近，故无法判断y1与y2的大小，故本选项错误；C、y的最小值是﹣4，故本选项错误；D、y的最小值是﹣4，故本选项正确．故选：D．2.解：将平面直角坐标系xOy先沿水平方向向右平移一个单位，再沿铅直方向向上平移三个单位，这个相当于把抛物线向左平移有关单位，再向下平移3个单位，∵y=（x﹣1）2+2，∴原抛物线图象的解析式应变为y=（x﹣1+1）2+2﹣3=x2﹣1，故答案为C．3．解：∵A（0，3），B（2，3）是抛物线y=﹣x2+bx+c上两点，∴代入得：，解得：b=2，c=3，∴y=﹣x2+2x+3=﹣（x﹣1）2+4，顶点坐标为（1，4），故答案为：（1，4）．。