下载文档原格式
类比归纳专题：平面直角坐标系中图形面积的求法
——代几结合，突破面积及点的存在性问题
◆类型一有一边在坐标轴上或平行于坐
标轴的三角形直接求面积
1．如图，平面直角坐标系中△ABC的面积是()
A．2 B．4 C．8 D．6
2．如图，在平面直角坐标系xOy中，已知A(－1，5)，B(－1，0)，C(－4，3)，则△ABC的面积为________．
◆类型二利用补形法或分割法求图
形的面积【方法10】
3．如图，四边形ABCD的面积为()
A．16.5 B．21 C．17 D．18
4．(2016－2017·安陆市期中)如图所示，在平面直角坐标系中，点A(4，0)，B(3，4)，C(0，2)，则四边形ABCO的面积为________．
5．在如图所示的正方形网格中，每个小正方形的边长均为1，三角形ABC的三个顶点恰好是正方形网格的格点．
(1)写出三角形ABC各顶点的坐标；
(2)求出此三角形的面积．
◆类型三与图形面积相关的点的存
在性问题
6．如图，平面直角坐标系中，ABCD 为长方形，其中点A，C的坐标分别为(－4，2)，(1，－4)，且AD∥x轴交y轴于M点，AB∥y轴交x轴于N点．
(1)求B，D两点的坐标和长方形ABCD 的面积；
(2)一动点P从A点出发，以
1
2
个单位/秒的速度沿AB向B点运动，是否存在某一
时刻t，使△AMP的面积等于长方形ABCD。
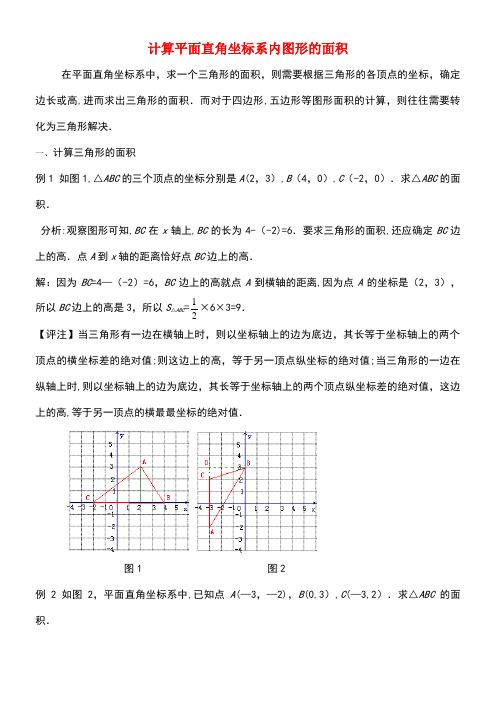
计算平面直角坐标系内图形的面积在平面直角坐标系中，求一个三角形的面积，则需要根据三角形的各顶点的坐标，确定边长或高,进而求出三角形的面积．而对于四边形,五边形等图形面积的计算，则往往需要转化为三角形解决．一、计算三角形的面积例1 如图1,△ABC 的三个顶点的坐标分别是A (2，3）,B （4，0）,C （-2，0）．求△ABC 的面积．分析:观察图形可知,BC 在x 轴上,BC 的长为4-（-2)=6．要求三角形的面积,还应确定BC 边上的高．点A 到x 轴的距离恰好点BC 边上的高．解：因为BC =4—（-2）=6，BC 边上的高就点A 到横轴的距离,因为点A 的坐标是（2，3），所以BC 边上的高是3，所以S △ABC =21×6×3=9． 【评注】当三角形有一边在横轴上时，则以坐标轴上的边为底边，其长等于坐标轴上的两个顶点的横坐标差的绝对值;则这边上的高，等于另一顶点纵坐标的绝对值;当三角形的一边在纵轴上时,则以坐标轴上的边为底边，其长等于坐标轴上的两个顶点纵坐标差的绝对值，这边上的高,等于另一顶点的横最最坐标的绝对值．图1 图2例 2 如图2，平面直角坐标系中,已知点A (—3，—2)，B (0,3）,C (—3,2）．求△ABC 的面积．分析：在△ABC 中只有边AC 的长度是比较求得的，所以找到AC 边上的高,而点A 到纵坐标的距离恰好是AC 边上的高．解:AC =|2-（—2）｜=4，作AC 边上的高BD ，而BD 就等于点A 到纵轴的距离，因为点A 的坐标是（-3，-2），所以BD =｜—3｜=3，所以S △ABC =21×4×3=6． 【评注】当三角形的一边和坐标轴平行时，这条边的长等于两个顶点横坐标（平行横轴）或纵坐标(平行纵轴）的差的绝对值;这边上的高等于平行坐标轴的边与坐标轴的距离．例3 如图3,平面直角坐标系中，已知△ABC 三个顶点的坐标分别是A (-3，-1)，B （1，3)，C （2，—3)．求△ABC 的面积．分析：三角形的三边都不和坐标轴平行,根据平面直角坐标系的特点，可以将三角形面积转化为梯形或长方形的面积减去多余的直角三角形的面积，即可求到此三角形的面积．解:过点A ，C 分别作平行于y 轴的直线，与过B 点作平行于x 轴的直线交于点D 、E ．则四边形ACED 为梯形．根据点A (-3,-1),B (1，3），C (2，-3)， 可求得AD =4,CE =6, DB =4,BE =1,DE =5,所以△ABC 的面积为：S △ABC =21（AD +CE ）·DE —21AD ·DB -21CE ·BE =21(4+6)×5—21×4×4—21×6×1=14．【评注】当三角形的三边都不和坐标轴平行时,可将通过过三角形的顶点作坐标轴的平行线,将三角形的面积转化为梯形或长方形的面积与直角三角形的面积差求解．图3 图4例4 如图4,四边形ABCD 的四个顶点的坐标分别是A （4，2)，B （4，-2）,C （0,-4），D(0，1）．求四边形ABCD 的面积．分析：因为点A 、B 的横坐标相同,点CD 在纵轴上，所以AB //CD ，则四边形ABCD 为梯形，可以过A 作CD 上的高AE ，则AE 的长就是点A 到y 轴的距离．解：因为CD =1-（-4)=5，AB =2-（-2)=4,AE =4，S ABCD =21（AB +CD ）·AE =21（5+4）×4=18．【评注】一般四边形的面积的计算,可将四边形的面积转化为特殊的四边形(如梯形）与特殊的三角形(如直角三角形）的面积和或差的形式计算． 尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。
