双曲线的焦半径PPT课件

在双曲线中，焦点是指距离双曲线中心最近的两个点。

双曲线焦点之间的距离称为焦距，而焦点到双曲线中心的距离称为焦半径。

焦半径在双曲线的方程中扮演着重要角色，它是定义双曲线形状和尺寸的关键参数之一。

焦半径的计算可以根据双曲线的参数方程进行求解。

对于标准的水平双曲线（具有中心在原点的双曲线），焦半径的计算公式如下：
1.水平双曲线焦半径：对于水平双曲线，焦半径等于双曲线焦点到原点的距
离，可以通过下面的公式来计算：
其中，c 表示焦半径，a 和 b 分别表示双曲线的两条分支在 x 轴和 y 轴上的
长度。

对于垂直双曲线（具有中心在原点的双曲线），焦半径的计算公式为：
1.垂直双曲线焦半径：对于垂直双曲线，焦半径可以通过下面的公式计算：
在这里，c 仍然表示焦半径，a 和 b 分别表示双曲线的两条分支在 x 轴和 y
轴上的长度。

要注意的是，焦半径的正负取决于双曲线的方程类型以及焦点的位置。

因此，在计算双曲线焦半径时，需要根据具体情况选择适当的公式并注意方程参数的正负性。

焦半径是描述双曲线形状和属性的重要指标，它有助于理解双曲线的几何特征和结构。

第8讲 椭圆、双曲线的角版焦半径、焦点弦公式知识与方法1．椭圆()222210x y a b a b +=>>的一个焦点为F ，P 为椭圆上任意一点，设PFO α∠=，则椭圆的焦半径2cos b PF a c α=−，若延长PF 交椭圆于另一点Q ，则椭圆的焦点弦22222cos ab PQ a c α=−. 2．双曲线()222210,0x y a b a b −=>>的一个焦点为F ，P 为双曲线上任意一点，设PFO α∠=，则双曲线的焦半径2cos b PF c aα=±，若直线PF 交双曲线于另一点Q ，则双曲线的焦点弦22222cos ab PQ a c α=−.（焦半径公式中取“+”还是取“－”由P 和F 是否位于y 轴同侧决定，同正异负）典型例题【例1】已知椭圆22:142x y C +=的左焦点为F ，过F 且倾斜角为45°的直线l 交椭圆C 于A 、B 两点，则AB =______；若AF BF >，则:AF BF =______. 【解析】如图，设AFO α∠=，则45α=︒由焦点弦公式，2222222228cos 42cos 453ab AB a c α︒⨯⨯===−−⨯，由焦半径公式，22cos b AF a c α===−，23BF ==，所以:3:1AF BF =.【答案】83，3:1变式1 已知椭圆22:142x y C +=的左焦点为F ，过F 且斜率为2的直线l 交椭圆C 于A 、B 两点，则AB =______【解析】设直线l 的倾斜角为α，则tan 2α=，所以cos α=，由焦点弦公式，22222222220cos 942ab AB a c α⨯⨯===−−⨯⎝⎭. 【答案】209变式2 已知椭圆22:142x y C +=的左焦点为F ，过F 的直线l 交椭圆C 于A 、B 两点，若3AF =，则AB =______.【解析】设AFO α∠=，则由焦半径公式，23cos b AF a c α===−，解得：cos 3α=，由焦点弦公式，2222218cos 5ab AB a c α==−. 【答案】185变式3 已知椭圆22:142x y C +=的左焦点为F ，过F 的直线l 交椭圆C 于A 、B 两点，若AF BF AF BF λ+=⋅，则λ=________.【解析】设AFO α∠=，则BFO πα∠=−，由焦半径公式，2cos b AF a c α==−，()2cos b BF a c πα==−−，所以112AF BF +==，从而2AF BF AF BF +=⋅，即2λ=.【反思】一般地，设椭圆()2222:10x y C a b a b+=>>的一个焦点为F ，过F 的直线l 交椭圆C于A 、B 两点，则2112aAF BF b +=.变式4 已知椭圆222:14x y C b+=()02b <<的右焦点为F ，过F 且倾斜角为60°的直线l 交椭圆C 于A 、B 两点，若167AB =，则椭圆C 的离心率为________. 【解析】由焦点弦公式，()222222222216cos 744cos 60ab b AB a c b α⨯⨯===−−−⨯︒，解得：22b =，所以e =.变式5 已知椭圆()222210x y a b a b+=>>的左、右焦点分别为1F 、2F ，过1F 且斜率为1的直线l 交椭圆C 于A 、B 两点，若2AF 、AB 、2BF 成等差数列，则椭圆C 的离心率为______. 【解析】直线l 的斜率为1l ⇒的倾斜角45α=︒，由焦点弦公式，22222cos 45ab AB a c =−︒，2AF 、AB 、2BF 成等差数列222223AB AF BF AB AF BF AB ⇒=+⇒=++， 如图，由椭圆定义可得224AF BF AB a ++=， 所以34AB a =，故222264cos 45ab a a c =−︒， 化简得：22232b a c =−，所以2222332a c a c −=−，从而224a c =，故椭圆C 的离心率12c e a ==.【答案】12【例2】过双曲线22:142x y C −=的右焦点且斜率为的直线截该双曲线所得的弦长为【解析】k =⇒直线的倾斜角60α=︒，由焦点弦公式，222222222165cos 46cos 60ab AB a c α⨯⨯===−−︒. 【答案】165变式1 过双曲线22:142x y C −=的右焦点F 的直线l 与双曲线C 交于A 、B 两点，若8AB =，则直线l 的方程为_______.【解析】由题意，2a =，b =，c =)F，设直线AFO α∠=，则由焦点弦公式，22222248cos 23cos ab AB a c αα===−−，解得：25cos 6α=或12，若25cos 6α=，则21sin 6α=，所以21tan 5α=，从而直线l 的斜率tan 5k α==，故直线l 的方程为y x =−； 若21cos 2α=，则21sin 2α=，所以2tan 1α=，从而直线l 的斜率tan 1k α==±，故直线l 的方程为(y x =±；综上所述，直线l 的方程为5y x =或(y x =±【答案】5y x =±−或(y x =± 变式2 过双曲线22:142x y C −=的右焦点F 的直线l 与双曲线C 交于A 、B 两点，若23AF =，则BF =______.【解析】设AFO α∠=，因为23AF =，所以点A 必在双曲线右支上，由焦半径公式，22cos 3b AF c a α===+，解得：cos α=，所以sin α=，从而tan αC 的渐近线的斜率为2±，2>，所以点B 也在双曲线的右支上，如图， 由图可知，BFO AFO ππα∠=−∠=− 所以()22cos b BF c a πα==−+.【答案】2强化训练1.（★★）已知椭圆22:143x y C +=的左焦点为F ，过F 且倾斜角为60°的直线l 交椭圆C 于A 、B 两点，则AB =_______.【解析】由焦点弦公式，22222222316cos 51412ab AB a c α⨯⨯===−⎛⎫−⨯ ⎪⎝⎭. 【答案】1652.（★★）已知椭圆22:193x y C +=的左焦点为F ，过F 的直线l 交椭圆C 于A 、B 两点，若3AB =，则直线l 的方程为________.【解析】设直线l 的倾斜角为α，由焦点弦公式，2222222333cos 96cos ab AB a c αα⨯⨯===−−⨯，从而cos 2α=，所以45α=︒或135°，从而直线l 的斜率为1±，显然()F ，故直线l的方程为y x =+或y x =−.【答案】y x =+或y x =−−3.（★★★）已知椭圆22:142x y C +=的左、右焦点分别为1F 、2F ，过1F 且倾斜角为45°的直线l 交椭圆C 于A 、B 两点，则2ABF 的面积为________. 【解析】如图，由焦点弦公式，222228cos 3ab AB a c α==−， 所以21218sin 4523ABF SF F AB =⋅⋅︒=.【答案】834.（★★★）已知椭圆()2222:10x y C a b a b+=>>一个焦点为F ，过F 且斜率为1的直线l 交椭圆C 于A 、B 两点，若34AB a =，则椭圆C 的离心率为________.【解析】由题意，直线l 的倾斜角为45°，由焦点弦公式，22222cos 45ab AB a c =−︒，因为34AB a =，所以222264cos 45ab a a c =−︒，结合222b a c =−化简得：222a c =，故离心率2c e a ==.【答案】25.（★★★）已知F 是椭圆22:142x y C +=的左焦点，过F 且不与x 轴垂直的直线交椭圆于A 、B 两点，弦AB 的中垂线交x 轴于点M ，则AB FM=________.【解析】解法1：如图，由对称性，不妨设直线的倾斜角为锐角，A 在x 轴下方， 则22222442cos 2cos AB αα⨯⨯==−−，AF ==，所以21222cos FN AN AF AB AF α=−=−==−，从而cos FN FM α==AB FM=解法2（特值法）：考虑AB y ⊥的情形，此时4AB =，M与原点重合，所以FM =AB FM=【答案】6.（★★★）如图，椭圆22:12x C y +=的左焦点为F ，过F 作两条互相垂直的直线分别与椭圆交于A 、B 和D 、E 四点，则四边形ADBE 的面积的取值范围是________.【解析】设AFO α=，不妨假设02πα≤≤，则2EFO πα∠=+，由焦点弦公式，AB =22cos 2DE α=−+ ⎪⎝⎭， 所以四边形ADBE 的面积()()2222114222cos 2sin 2cos 2sin S AB DE αααα=⋅=⨯⨯=−−−− 2222241642sin 2cos sin cos 8sin 2ααααα==−−++，显然20sin 21α≤≤，所以1629S ≤≤，即四边形ADBE 的面积的取值范围是16,29⎡⎤⎢⎥⎣⎦. 【答案】16,29⎡⎤⎢⎥⎣⎦7.（★★★）双曲线22:1C x y −=的右焦点为F ，过F 的直线l 与双曲线C 交于A 、B 两点，若4AB =，则直线l 的方程为________. 【解析】由题意，1a b ==，c =)F，设直线AFO α∠=，则由焦点弦公式，22222224cos 12cos ab AB a c αα===−−，解得：23cos 4α=或14， 若23cos 4α=，则21sin 4α=，所以21tan 3α=，从而直线l的斜率tan k α==， 故直线l的方程为y x =；若21cos 4α=，则23sin 4α=，所以2tan 3α=，从而直线l的斜率tan k α==故直线l的方程为y x =，综上所述，直线l的方程为y x =或3y x =±【答案】y x =−或3y x = 8.（★★★）双曲线22:163x y C −=的左、右焦点分别为1F 、2F ，过1F 的直线l 与双曲线C 交于A 、B 两点，若213AF AF =，则2BF =________.【解析】由题意，21213AF AF AF AF ⎧=⎪⎨−=⎪⎩，所以1AF =1AFO α∠=，则21cos b AF c a α==+，所以=，解得：cos α=，从而sin α==sin tan cos ααα==C的渐近线斜率为，因为<，所以点B 也在左支上，且1BFO πα∠=−， 故()22cos b BF c aπα===−+【答案】39.（★★★）双曲线22:13y C x −=的左焦点为F ，点P 在双曲线C 的右支上，且5PF =，则PFO 的面积为________.【解析】解法1：由题意，1a =，b =2c =，设PFO α∠=，由焦半径公式，23cos 2cos 1b PFc a αα==−−，又5PF =，所以352cos 1α=−，解得：4cos 5α=，所以3sin 5α=，如图，显然113sin 523225PFOSPF OF α=⋅⋅=⨯⨯⨯=. 解法2：由题意，1a =，2c =，离心率2e =，设()00,P x y ，由焦半径公式，0125PF x =+=，又5PF =，所以0125x +=，解得：02x =或3−，因为P 在右支上，所以02x =， 代入双曲线方程可求得03y =±，所以01123322PFOSOF y =⋅=⨯⨯±=. 解法3：如图，设双曲线C 的右焦点为1F ，由双曲线定义，12PF PF −=，又5PF =，所以13PF =， 易求得14FF =，所以22211PF FF PF +=，故11PF FF ⊥， 所以1111143622PFF SFF PF =⋅=⨯⨯=， 显然O 是1FF 的中点，所以1132PFOPFF SS ==.【答案】3。

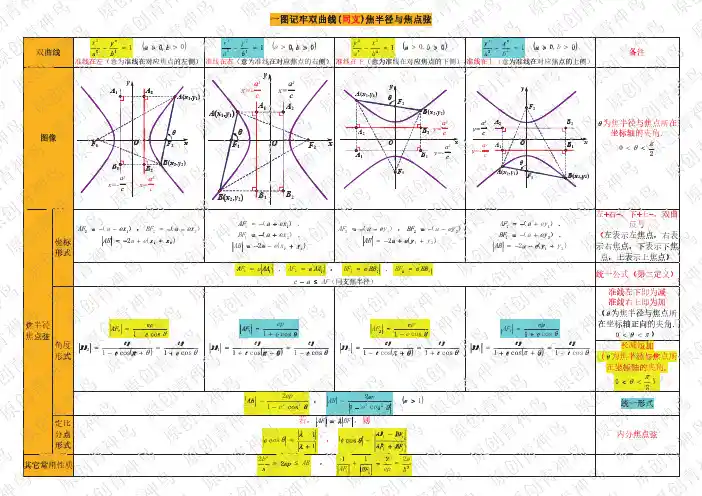
双曲线焦半径
双曲线的焦半径公式是r=|a－ex|。

连接圆锥曲线包括椭圆，双曲线，抛物线上一点与对应焦点的线段的长度，叫做圆锥曲线焦半径。

双曲线上任意一点P与双曲线焦点的连线段，叫做双曲线的焦半径。

圆锥曲线上一点到焦点的距离不是定值。

焦半径：曲线上任意一点与焦点的连线段焦点弦，过一个焦点的弦通径。

过焦点并垂直于轴的弦圆锥曲线中，过焦点并垂直于轴的弦。

扩展资料
双曲线的焦半径及其应用
1：定义：双曲线上任意一点P与双曲线焦点的连线段，叫做双曲线的焦半径。

2．已知双曲线标准方程，x²/a²-y²/b²=1，且F1为左焦点，F2为右焦点，e为双曲线的离心率。

总说：│PF1│=|(ex+a)| ；│PF2│=|(ex-a)|（对任意x而言）
具体点P(x,y)在右支上，│PF1│=ex+a ；│PF2│=ex-a；点P(x,y)在左支上，│PF1│=-(ex+a) ；│PF2│=-(ex-a)。

聚焦双曲线的“焦半径”设双曲线22221x y a b-=的左右焦点分别为1F ,2F ，00(,)P x y 是其上一点，我们称12||||PF PF 、为双曲线的焦半径，利用第二定义可得10||PF ex a =±+（），20||PF ex a =±-（），当点P 在左支上时取“-”，在右支上时取“+”，若双曲线焦点在y 轴只需将0x 换为0y 即可，凡涉及到动点与焦点距离的问题时都可利用到焦半径公式，能大大降低运算量. 例：设双曲线22122x y -=的两个焦点分别为1F ,2F ，P 为双曲线上任意一点，求证：12||,||,||PF PO PF 成等比数列证明：设00(,)P x y ，则||PO =，当P 在左支上时由焦半径公式得，10||PF ex a =-+（），20||PF ex a =--（），易得双曲线的离心率e =22a =，于是2222222120000||||22||PF PF e x a x x y PO =-=-=+=,对于P 在右支的情况同理可证，故12||,||,||PF PO PF 成等比数列跟踪训练题1、双曲线22221x y a b-=（a ＞0,b ＞0）的左右焦点分别为1F ,2F ，若P 为其上一点，且12||3||PF PF =,则双曲线离心率的取值范围为（ ）A. (1,2)B.(]1,2C. (2,)+∞D.[)2,+∞ 2、设双曲线221x y -=的右焦点为F ，作F 一直线l 与右支交于A,B 两点，若||FA ,||FB 均是整数，则这样的直线（ ）A. 不存在B. 有无数条C. 只有一条D. 有限条但多于一条3、设F 为双曲线2213x y -=的左焦点，A,B,C 为左支上不同的三个点，若ABC ∆的重心恰为F ，则||||||FA FB FC ++等于4、在双曲线22145x y -=的右支上有两个动点A 、B ，满足||||8FA FB +=，其中F 为右焦点，则线段AB 的中点的横坐标为5、设双曲线2213y x -=的左右焦点分别为1F ,2F ，P 为双曲线右支上一点，设P 到右准线的距离为d ，则12||,||,PF PF d 这三者能否以某种顺序构成等差数列？若存在这样的点P 请求出，若不存在请说明理由.答案：1、答案：B解析：设00(,)P x y ，易知P 在右支上，所以有0x a ≥，由焦半径公式得10||PF ex a =+，20||PF ex a =-，由12||3||PF PF =，得003()ex a ex a +=-，所以022a e x =≤，故e 的范围是(]1,2，选B2、答案：C 解析：易得右焦点F的坐标是，设11(,)A x y ,22(,)B x y ,则11||1FA ex a =-=-，同理2||1FB =-,当直线l 与x轴垂直时，12x x ==，此时||FA ,||FB 均是整数;若直线l 不与x 轴垂直时，从图形可以判断在12,x x，因此||FA ,||FB 不可能同时为整数，故符合要求的直线只有一条,选C3解：设11(,)A x y ,22(,)B x y ，33(,)C x y ，易得F 的坐标是(2,0)-，由重心坐标公式得1236x x x ++=-，而123||||||()()()FA FB FC ex a ex a ex a ++=--+--+--，233e =a=||||||FA FB FC ++=4、答案：4解：设11(,)A x y ,22(,)B x y ，由焦半径公式得，1||FA ex a =-，2||FB ex a =-，而32e =，2a =，由||||8FA FB +=，得12x x +=8，故线段AB 的中点的横坐标为45、解：设00(,)P x y ,由双曲线的性质易知，12||||PF PF d >>，假设存在这样的点P 使三者能构成等差数列，则顺序只能是12||,||,PF PF d 或21,||,||d PF PF ,总之有212||||PF d PF =+，由焦半径公式得10||PF ex a =+，20||PF ex a =-，2a d x c=-，2e =，1a =，于是00012(21)212x x x -=++-，解得0512x =>，故在右支上存在这样的点P ，使12||,||,PF PF d 或21,||,||d PF PF 成等差数列备用题1、双曲线221169x y -=的左焦点为F ,P 为其右支上一点，若||14PF <,则点P 的横坐标的取值范围是（ ）A. (0,8)B.(4,)+∞C. [4,8)D.72[4,)5 答案：C解析：设00(,)P x y ，则005||4144PF ex a x =+=+<，解得08x <，因为P 在右支上，故048x ≤<，选C2、设221412x y -=的左焦点为F ，A 、B 、C 是左支上不同的三个点，若||,||,||FA FB FC 恰能构成直角三角形，请写出一组符合条件的三个点的横坐标 .(写出满足条件的一组值即可不必考虑所有情况)答案：4,5,6---解：由焦半径公式知左支上的点00(,)x y 到左焦点的距离00||22)PF ex a x =-+=-+（）（，设A 、B 、C 的横坐标分别为123,,x x x ，不妨令222||||||FA FB FC =+，可得222123(1)(1)(1)x x x +=+++，符合此条件的有无数组，如6,5,4---，11,9,7---等3、已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ，直线00(0)y y y =≠与双曲线的左右支分别交于A,B 两点，求证：||||||AF BF AB +是定值 证明：由双曲线对称性可知，A,B 两点关于y 轴对称，不妨设00(,)A x y ,则B 的坐标是00(,)x y -,由焦半径公式得0||AF ex a =--，0||BF ex a =-+,则0||||2AF BF ex +=，而0||2AB x =-，故002||||||2ex AF BF e AB x -+===-为定值。