当前位置：文档之家 › 留数定理计算积分

留数定理计算积分

  • 格式：ppt
  • 大小：1.80 MB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

留数定理公式总结

留数定理公式总结

留数定理公式总结留数定理是复变函数论中的一个重要定理，在数学分析和工程技术等领域都有着广泛的应用。

咱们先来瞅瞅留数定理的公式到底是啥样的。

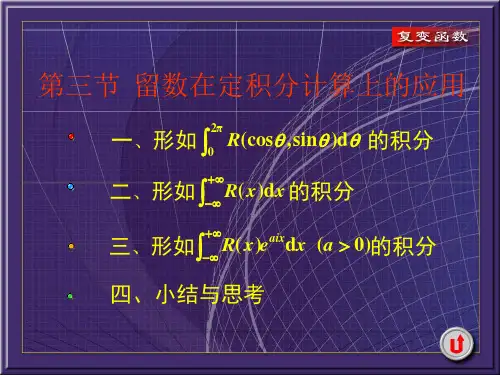
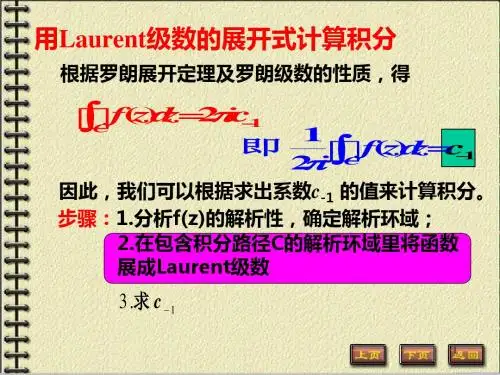
留数定理表述为：设函数$f(z)$在区域$D$内除有限个孤立奇点$z_1,z_2,\cdots,z_n$外处处解析，$C$是$D$内包围诸奇点的一条正向简单闭曲线，那$f(z)$沿$C$的积分就等于$2\pi i$乘以$f(z)$在$C$内各奇点的留数之和，即：$\oint_C f(z)dz = 2\pi i \sum_{k = 1}^{n}Res[f,z_k]$这里的$Res[f,z_k]$表示$f(z)$在奇点$z_k$处的留数。

那留数又咋算呢？对于孤立奇点$z_0$，如果它是可去奇点，那留数为$0$；如果是$m$阶极点，就有公式$Res[f,z_0] = \frac{1}{(m -1)!}\lim_{z \to z_0}\frac{d^{m - 1}}{dz^{m - 1}}[(z - z_0)^mf(z)]$。

咱们通过一个具体例子来感受一下留数定理的魅力。

比如说，计算积分$\int_{|z| = 2} \frac{e^z}{z(z - 1)}dz$。

首先得找出被积函数的奇点，很明显，$z = 0$和$z = 1$是奇点。

对于$z = 0$，它是一阶极点，$Res[f,0] = \lim_{z \to 0} z\frac{e^z}{z(z - 1)} = -1$；对于$z = 1$，也是一阶极点，$Res[f,1] = \lim_{z \to 1} (z - 1)\frac{e^z}{z(z - 1)} = e$。

然后根据留数定理，原积分就等于$2\pi i (-1 + e)$。

留数定理在解决一些复杂的积分问题时特别有用。

比如说，计算一些实函数在无穷区间上的积分，通过巧妙地构造复变函数和积分路径，然后利用留数定理就能轻松搞定。

我记得有一次给学生们讲留数定理的应用，有个学生就特别迷糊，怎么都搞不明白。

留数及留数定理

留数及留数定理
ez − 1 1 z 2 z 3 z4 z5 z6 = 5 1 + z + + + + + + L − 1 5 2! 3! 4! 5! 6! z z 1 1 1 1 1 z = 4+ + + + L, 3 + 2 + z 2! z 3! z 4! z 5! 6!
其中n=4的项的系数为 -1=1/4!, 从而也有 的项的系数为c 其中 的项的系数为 ,
d4 z 1 1 Res[ f1 ( z ),0] = lim 4 (e − 1) = 4! z → 0 dz 4!
14
例3．求下列函数在指定点处的留数 (1) f1 ( z ) = (e z − 1) z 5 , z0 = 0 ; 另解： 另解： f1 ( z ) 在点 z0 = 0 的去心邻域 0 < z < ∞内的 Laurent级数为 级数为
Res[ f1 ( z ),0] = c−1 = 1 4!
15
(2)f 4 ( z ) = sin(1 z ) , z0 = 0 ; 解 ： f 4 ( z ) 在点 z0 = 0 的去心邻域 0 < z < ∞ 内的 Laurent级数为 级数为
1 ∞ ( −1) n z −2 n −1 sin = ∑ z n= 0 ( 2n + 1)!
2πi 0 (高阶导数公式 高阶导数公式) 高阶导数公式 + ∫ c0dz + ∫ c1 ( z − z0 )dz + + ∫ cn ( z − z0 )n dz + L
C C C
= 2πic−1
0 (柯西积分定理) 柯西积分定理)

课件：用留数计算定积分

课件：用留数计算定积分

( z
1 ai )2 ( z 2
b2
)
1 2bi(a2
b2
)2
,
zai
16
Res[ R(z),bi]
(z2
1 a2 )2(z
bi)
zbi
b2 3a2 4a3i(b2 a2 )2
,
所以
dx
( x2 a2 )2( x2 b2 )
2π i{Res[R(z),bi] Res[R(z),ai]}
2
分析
可先讨论
R
R( x)dx,
R
最后令 R 即可 .
11
R
R R( x)dx
f (z)dz
C
1. 被积函数的转化: 可取 f(z)=R(z) .
(当z在实轴上的区间内变动时 , R(z)=R(x))
2. 积分区域的转化:
取一条连接区间两端的按段光滑曲线, 使与区间
一起构成一条封闭曲线, 并使R(z)在其内部除有
sin
)d
z2 1 z2 1 dz
R z 1
2z
,
2iz
iz
n
f (z)dz 2π i Res f (z), zk .
z 1
k 1
z的有理函数 , 且在 单位圆周上分母不
为零 , 满足留数定 理的条件 .
包围在单位圆周 内的诸孤立奇点.
4
例1
计算积分
2π
0
a
s in2 bcos
1 2 pcos p2 (1 p)2 2 p(1 cos )
在0 2π内不为零， 故积分有意义.
由于 cos 2 1 (e2i e2i ) 1 (z2 z2 ),
2

5-第五章-留数定理

5-第五章-留数定理

因此
z ez
e e1
C
z2
dz 1
2 π i( 2
) 2 πi ch1 2
： 我们也可以用规则III来求留数
| Res[ f (z),1] z ez e ; 2z z1 2
| Res[ f (z),1] z ez e1 . 2z z1 2
这比用规则1要简单些，但要注意应用的条件。
z
例7
环域内绕原点的任何一条简单闭曲线，则积分
1
2π i f (z) d z C
称其为f (z)在点的留数，记作
1
Res[ f (z), ]
f (z)d z
2i C
这里积分路径的方向是顺时针方向，这个方向很自然
地可以看作是围绕无穷远点的正向。
将 f (z)在 R<|z|<+∞内的罗朗展式为
f
(z)
z 4z3
1 4z2
,故z1111C源自z4d 1z
2π
i( 4
4
4
4)
0
Ñ 例 8
计算积分
C
ez z(z 1)2
dz,
C
为正向圆周|z|=2.
[解] z=0为被积函数的一级极点, z=1为二级极点, 而
Res[ f (z),0] lim z0
z
ez z(z 1)2
lim z0
ez (z 1)2
1.
一、 留数的定义
定义 若f (z)在去心邻域 0 z z0 R内解析，
z0是f (z)的孤立奇点，C是 0 z z0内 包R 围z0的
任意一条正向简单闭曲线，定义积分
1
2i
C
f
(z)d
z

留数的定义,性质以及应用

留数的定义,性质以及应用

P( z ) ( z − z0 ) f ( z ) = Q ( z ) − Q ( z0 ) 因为 z − z0
令 z→z0 即得(5.2.6)
9
ze dz 2 ∫ 例 1 计算积分 C z − 1 , C 为正向圆周|z|=2.
z ez f ( z) = 2 [解] 由于 z − 1 有两个一级极点+1,−1, 而
z
[解] z=0 为被积函数的一级极点, z=1 为二级 极点, 而 z z e e Res[ f ( z ),0] = lim z ⋅ = lim = 1. 2 2 z →0 z → 0 ( z − 1) z ( z − 1)
15
⎤ 1 d ⎡ e 2 Res[ f ( z ),1] = lim ( z − 1) ⎢ 2⎥ (2 − 1)! z →1 d z ⎣ z ( z − 1) ⎦
6
2. 留数的计算规则 规则1 如果z0为f(z)的一级极点, 则
Res[ f ( z ), z0 ] = lim ( z − z0 ) f ( z )
z → z0
m −1
(5.2.4)
规则2 如果z0为f(z)的m级极点, 则
d 1 m Res[ f ( z ), z0 ] = lim m −1 {( z − z0 ) f ( z )} (m − 1)! z → z0 d z (5.2.5)
例1 例2 例3 例4 计算积分 计算积分 计算积分
| z | =1
∫
dz (0 < ε < 1) 2 ε z + 2z + ε
ze z dz 2 z −1 z dz 4 z −1
| z|= 2
∫
| z| = 2
∫

留数定理

留数定理

求出函数在
这些极点的留数.
解
f (z) = z + 2i z5 + 4z3
=
z + 2i z3 (z2 + 4)
=
z3(z
z + 2i + 2i)(z
− 2i)
=
1 z3 (z − 2i)
(1)、当z→2i时，f(z) →∞，所以z=2i是f(z)的极点，
lim ( z
z→2i
− 2i)
f
(z)
=
lim
∫l f (z)dz = −2π ia−1
Re sf (∞) = −a−1
二、全平面的留数和为零
∞
∑ f (z) = ak z k k =−∞ (R < z < ∞)
函数f(z)在全平面上所有各点的留数之和为0。 这里的所有各点包括无限远点和有限远的奇点。
{ f (z)在所有有限远奇点上的留数和 + Re sf (∞)} = 0
n
∫ ∑ l
f
( z )dz
=
2π i
Re sf
j =1
(bj )
注意: 左边的积分是沿l 的正向进行的；
右边的奇点是指l 所围区域内的，并非是f(z)所有
的奇点。
7
留数定理对于无限远点也成立：
∞
∞
∫ ∫ ∑ ∑ ∫ f (z)dz = l
l k =−∞ ak z k dz = k =−∞ ak
l zk dz = 2π ia−1
∫ dz
z =1 ε z2 + 2z + ε
(0 < ε < 1)
∫ dz = πi
z =1 ε z2 + 2z + ε 1− ε 2

留数及留数定理

留数及留数定理
R esf(z),z0=(m 1 -1 )!z li m z0d d z m m -1 -1[(z-z0)m f(z)]
由于f(z)=(z(zz)0)n，由高阶导数定理可得
Res[f(z),z0]=21πiC(zφ -(zz0))n
dz=φ(n-1)(z0 ) (n-1)!
8
规则3
设 为 f (z) 的一个孤立奇点;
的某去心邻域 r z
内的任一条正向简单闭曲线C: | z |= ρ > r
定义
若 f ( z ) 在 的 去 心 邻 域 r < | z | < + 内 解 析
则 称 1
记
2 π i f ( z ) d z Res[f (z),].= -C -1
分析 P ( 0 ) P ( 0 ) P ( 0 ) 0 , P(0)0. z0是 zsizn的三级零点
所以 z0是f(z)的三级极 由规点则， 2得 Rfe (z)s 0 ] , [(3 1 1 )lz !i0d d m z 2 2 z3z z s 6iz n . 计算较麻烦.
其中n=4的项的系数为c-1=1/4!, 从而也有
R [f1 e (z)s 0 ] , c 1 14 !
16
(2) f4(z)s, i1 nz;() z0 0
解： f4(在z)点 数为
的z0 去 0心邻域
内0的 zLaurent级
1 (1)nz2n1
sin z n0 (2n1)!
即
1
2i
Cf(z)dzc1
因此，我们可以根据求出系数c-1 的值来计算积分。 步骤：1.分析f(z)的解析性，确定解析环域；
2.在包含积分路径C的解析环域里将函数 展成Laurent级数

留数和留数定理

留数和留数定理
C C
0 (高阶导数公式)
C C C
2i
c0dz c1 ( z z0 )dz cn ( z z0 )n dz
0 (柯西-古萨定理)
2ic1
Laurent级数中负幂项c1 ( z z0 ) 的系数
3
1
1 即 c 1 2i C
f ( z ) 在 z0 的留数 f ( z )dz Res[ f ( z ), z0 ]
f ( z ) c n ( z z0 ) n c1 ( z z0 )1 c0 c1 ( z z0 ) cn ( z z0 )n
2
积分 f ( z )dz
C
c n ( z z 0 ) n d z c 1 ( z z 0 ) 1 d z
1 . ( n 1)!
11
例2 计算积分 解 函数f ( z )
C

ze z dz, 2 z 1
C为正向圆周: z 2.
C

ze z dz有两个一级极点 1， 1， 2 z 1
而这两个极点都在圆周 z 2内，所以
域内的Laurent级数中负幂项c1 ( z z0 )1 的系数.)
4
留数定理
函数 f ( z ) 在区域 D内除有限个孤立
奇点 z1 , z2 ,, zn 外处处解析, C 是 D内包围诸奇 点的一条正向简单闭曲线, 那么
C
Res[ f ( z ), zk ]. f ( z )dz 2i k 1
用 (z-z0 ) 乘上式的两端得 ( z z0 )m f z cm cm1 ( z z0 )
(0 z z0 )

5.4利用留数计算实积分

5.4利用留数计算实积分
封闭路线的积分 . 两个重要工作: 1) 被积函数的转化
2) 积分路径的转化
2
2π
0 R(cos ,sin )d
令 z ei
dz iei d
sin 1 (ei ei ) z2 1 ,
2i
2iz
d dz ,
iz
cos 1 (ei ei ) z2 1,
2
2z
当 历经变程 [0,2π ] 时,
e ix
( x2 1)( x2 9) dx
2 i{Res[ f (z)eiz ,i] Res[ f (z)eiz ,3i]}
14
2
)( z 2
9)
lim
z3i
(z2
e iz 1)( z
3i)
2 i
e 1 16i
e 3 48i
24e 3
3e2 1 .
z 1 3z2
2 10iz
dz 3
2 3
z 1 ( z
i
1 )( z
3i)
dz
3
5
I
2 3
z 1
(z
i
1 )( z
3i)
dz
3
记
f (z)
(z
1 i )(z 3i)
，则
3
I
2 3
2πiRes
f
( z ),
i 3
2 2i( 3i )
3
82
6
R(x)dx
其中R(x)是有理函数，其分母至少比分子高两次,
a2 b2
. ab
11
R( x) eaixdx (a 0)
积分存在要求: R(x) 是 x 的有理函数，且分母的

留数定理在积分计算和级数求和中的应用

留数定理在积分计算和级数求和中的应用

内解析，为ｚ ｃ ０ 邻域内任意一条简单闭曲线， 则积分 。｝ｆ ｄ的值， ＿ ｌ （ｚ ｚ ）
称为函数 ｚ 点 ｚｚ处的 留数 ， ） 在 －ｏ 记作 Ｒ ｓ （，Ｊ ｅ ）即 Ｒ ｓ（ ， ｅ【ｚｚ或Ｒ ｓ ， ｅ［ ） ｆ ）ｏ ｚ ｆ ｚ
＝
ｆｚ ） ｃ ｆ （
三
｛Ｒ ｆ ＋（ ＊
，
特别地 ， Ｒｘ 若 （ 为偶 函数 ， ） 则有
， ＋＊
ｆ （ｄ ￣ Ｒｓ（ｚ Ｒ ）＝ｉ ｅＲ）】 ｘｘｒ ［ｚｋ ，
（ ２ ）
｝ｆ ｄ ２ｉ２ ｅ （， （ ｚ ￣２ Ｒｓ ｚ ｚ ＝ ） ｆ 。 ｉ）
注 １除上述关于 留数 的定义外， 留数还 可定义为 Ｒ ｓ（， ： 其 ｅｆ ）ｏ ｃ ｆ ｚ ｚ ］ 中 ｃ 是 ｆ１ 一 （ 在以 Ｚ为中心的圆环域 内的洛 朗级数 中负幂项 ｃ （ ｚ ０ 的 系数。
ｘｄ＝ ￣ Ｒ ｓ （ ， ）ｘ ２ｒ ｉ ｅ［ ｚｚ Ｒ ）ｄ
三
（） １
定理 １留数 定理【 设 函数 ｆ ） （ ２ １ ） （ 在区域 Ｄ内除有 限个孤 立奇 点 ｚ ｚ － ， ｚ …＇ 外处处解析。 是 Ｄ内包 围诸奇点 的一条正 向简单闭 曲线 ， ｚ ， ｎ ｃ 那么
Ｒ＿ ｊ Ｃ Ｒ
半圆周。 现在我们来考察几种常见的实积分类 型，其结果均可 由引理 １定 、 理 １和定理 ３推得。
１计算 ｊ Ｒｘ ｘ型积分 ） （ｄ ）
当被积 函数 Ｒ ｘ ｘ的有 理 函数 ， ｆ是 ］ 其分母 的次数至 少 比分 子高二 次 ， Ｒｘ 且 （ 在实轴上 没有奇点 ， ） 积分存在时 。 若设 Ｒｚ （在上半平 面 ｌ ｚ ０ ） ｍ＞ 的极点为 Ｚ ・ 则 ｔ ，， ＊ ｚ Ｚ

复变函数第11讲用留数计算实积分

复变函数第11讲用留数计算实积分

z −1
+
p2
⋅
dz iz
2
1+ z4
∫ ∫ =
| z|=1
2iz2
(1 −
pz )( z
−
p)
d
z
=
f
| z|=1
(z)
d
z
4
在被积函数的三个极点z=0,p,1/p中只有前两 个在圆周|z|=1内, 其中z=0为二级极点, z=p为 一级极点.
Res[
f
(z),0] =
lim
z→0
d dz
⎡ ⎢
=
λ
,
r→∞
∫ 则 lim r →∞
Cr R( z)dz = i(θ 2 − θ1 )λ
14
+∞
∫ 3. 形如 R( x)eaixd x(a > 0) 的积分 −∞
当R(x)是x的有理函数而分母的次数至少比 分子的次数高一次, 且R(x)在实数轴上没有 奇点时, 积分是存在的象2中处理的一样, 由 于m−n≥1, 故对充分大的|z|有
Cr
Cr
r2
2π = r ⎯r⎯⎯→∞→ 0
+∞
因此 ∫−∞ R( x)d x = 2 π i∑ Res[R(z), zk ].
如果R( x)为偶函数,
+∞
∫0R( x)d x = π i∑ Res[R(z), zk ]
10
例 计算
的值.
解 这里 m=4,n=2,m−n=2,并且实轴上 R(z)没有 孤立奇点, 因此积分是存在的. 函数
有理函数, 而分母的次数至少比分子的次数高
+ 二次, 并且 R(x)在实轴上没有孤立奇点时, 积

第四章留数定理

第四章留数定理
第四章 留数定理
重点
1、留数的概念与留数定理； 2、应用留数定理计算复变函数的积分； 3、应用留数定理计算实变函数的积分
§4.1 留数定理
一 、留数及留数定理
1.留数
如果函数f(z)在z0的邻域内解析, 那么根据Cauchy定理
f (z) d z 0.
l
但是, 如果z0为f(z)的一个孤立奇点, 则沿在z0的某个去 心邻域0<|z-z0|<R内包含z0的任意一条正向闭曲线的积分
l
l1
l2
ln
f (z) d z 2πi[Res f (z1) Res f (z2 ) Res f (zn )]
l
n
即 f (z) d z 2 π i Res f (z j ).
l
j 1
zn l3 z3
ln z1 l2 z2
l1
D
l
求函数在奇点z0处的留数即求它在以z0为中心的圆环域内
令 z ei
dz iei d d dz ,
iz
sin 1 (ei ei ) z - z-1 ,
2i
2i
cos 1 (ei ei )
z z1
,
2
2
当 历经变程 [0,2π ] 时,
z 沿单位圆周 z 1的 正方向绕行一周.
2π
0
R(cos
,
sin
)d
z
1
R
z
2 2z
1
,
z
2 2iz
(1)n
例4 计算积分
z
zez 2
1
d
z
，C为正向圆周|z|=2.
C
解
由于
f (z)

留数定理

留数定理

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

5-2留数和留数定理

5-2留数和留数定理

函数 f (z) 在区域 D内除有限个孤立 内除有限个孤立
奇点 z1 , z2 ,L, zn 外处处解析 C 是 D内包围诸奇 外处处解析, 内包围诸奇 点的一条正向简单闭曲线, 点的一条正向简单闭曲线 那么
C
∫ f (z)dz = 2πi∑Res[ f (z), zk ]. k=1
n
注:
留数定理将沿封闭曲线C积分转化为求 留数定理将沿封闭曲线 积分转化为求 被积函数在C内各孤立奇点处的留数 被积函数在 内各孤立奇点处的留数. 内各孤立奇点处的留数
3
1 即 c −1 = ∫ 2πi C
f (z)在z0的 数 留 f ( z )dz = Res[ f (z), z0]
定义 如果 z0 为函数 f ( z ) 的一个孤立奇点 则沿 的一个孤立奇点,
z0 的某个去心邻域 0 < z − z0 < R 内，包含 z0 的
任意一条简单闭曲线 C 的积分
z 1 1 1 1 ∫ z 4 − 1 dz = 2πi 4 + 4 − 4 − 4 = 0 . C
14
ez 例4 计算积分 ∫ 为正向圆周: 为正向圆周 2 dz , C为正向圆周 z = 2. z ( z − 1) C
为一级极点, 解 z = 0 为一级极点
z = 1 为二级极点 为二级极点,
10
3 典型例题
ez 的留数. 例1 求 f ( z ) = n 在 z = 0 的留数 z
解
阶极点， 因为 z = 0 是 f ( z )的 n 阶极点，
1 d n −1 n e z ez lim n−1 z ⋅ n 所以 Res n ,0 = z z ( n − 1)! z →0 dz

4-1留数定理

4-1留数定理

4 z / 4 cos2z
z / 4 2 sin 2z
/ 4

zdz |z|2 1/ 2 sin 2
z

2i[Re sf
(
/ 4) Re sf
(
/ 4)]
2i
例5：计算
I
z15dz |z|4 ( z 2 1)2 ( z 4 2)3
z1
z n1

1 zn2 ...
z
1

1 n
另解：
Re
sf
(1)

lim
z 1
1 (zn 1)

lim
z 1
1 nz n 1

1 n
例2：确定函数 f (z) ez 的奇点，求在奇点的留数。
1 z
解：∵ lim ez ∴ z=-1是f(z)的极点
z11 z

1 z
1 2
1 z2
...1 3
2 z4
...
则： a-1=1
Re sf () 1 I 2i[ Re sf ()] 2i
作业：P55-56：1－－（2）、（4）、（5） 2－－（2）、（3）
，l的方程是x2+y2-2x-2y=0
1)2
解：方程化为(x-1)2+(y-1)2=2
f (z)
(z2
1 1)( z 1)2
有两个单极点z0=±i和一
个二阶极点z0=1，其中z0=-i不在l内。
Re
sf
(i)

lim[(z
zi

i)
(z2
1 1)(z
1) 2
]
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

sinxd x, sinx2 d x, e a xc o sb x d x,
0x 0
0
数学分析计算这些积分麻烦,无统一方法;用
留数计算,较简捷.
这 种 方 法 的 基 本 思 路 是 ,先 取 辅 助 函 数 g(z)(在 [a,b]上 g(z)的 实
部 或 虚 部 为 f(x))在 有 限 区 间 [a,b]上 的 定 积 分 ,再 引 入 辅 助 曲 线 ,
4(a 2 1) 2
2020/12/1
9
由留数定理
2π 0
(a
1
cos)2
d
4 i z1(z2
z
dz
2az1)2
4 i
2iRes f (z) 8 z 2π dx
a
3
4(a 2 1)2
2 a 3.
(a 2 1) 2
例3
计算 I
0
. 1cos2 x
解 令 z eix ,
I
2 1
0
z2 2 a z 1 0 的 二 相 异 实 根 ,
由 1 ,且 显 然 ,故 必 有 1 , 1 ;
于 是 f(z)(z)2z(z)2在 z1上 无 奇 点 ,
在z1内 只 有 一 个 二 阶 极 点 z,由 推 论 6.4得
Rzesf(z)[(zz)2]' |z
(
)3
a
3
0 R (sin ,c o s)d 1 2 R (sin ,c o s)d .
例4 计算积分Iπ cosm xdx (m 为 正 整 数 ) .
054cosx
解I 1 π cosmx dx1Re π eimx dx
2 54cosx 2 54cosx
令z eix,则
J
π
eimx
dx
54cosx
2i
2 iz
d dz ,
iz
2020/12/1
3
cos1(eiei) z 2 1 ,
2

2z
当 历经变程 [0,2π]时,
z 沿单位圆周 z 1的正方向绕行一周.
n
02πR(co,ssin)d f (z)dz z 1
2i Res f (z). k1 zak
z的有理函数 , 且在单位圆周上分 包围在单位圆周 母不为零 , 满足留数定理的条 内的诸孤立奇点.
留数定理计算积分
留数定理的应用--积分的计算:
利用留数计算积分的特点： （1）、利用留数定理，我们把计算一些积分的问题， 转化为计算某些解析函数在孤立奇点的留数，从而大大 化简了计算；
（2）、利用留数计算积分，没有一些通用的方法，
我们主要通过例子进行讨论；
（3）我们只讨论应用单值解析函数来计算积分，应 用多值解析函数来计算积分在课本中有讨论。由于时 间的关系，我们不讨论应用多值解析函数来计算积分
2pi
z0
z1
p
例2
计算积分
I
2π
1 d
0 (acos)2
(a1).
解
令zei,
则
cos
z2 1 ,
2z
d
dz , iz
I
2π 0
(ac1os)2d
z 1 (a
1 z2
1)2
dz iz
4 i
z
1
(z2
z 2az
1)2dz
2z
2020/12/1
8
4i z1(z)2z(z)2 dz
其 中 aa 2 1 ), aa 2 1 )为 实 二 次 方 程
u R3es8u f2 ( u6 ) u (1 u2 61u1)'
|
u3
8
1 28
1, 42
由留数定理
4
du
I
i
u2
u 1
6u 1
4 2i Res f(u)
i
u3 8
2 .
2020/12/1
11
注 :若 R (sin,cos)为 的 偶 函 数 ,则 0 R (sin,cos)d
亦 可 用 上 述 方 法 求
'
1 z4
Res z0
f
(z)
(z
1)(z
p)
|z0
1
p p
2
,
p
Res
zp
f (z)
1 z4 z2(z 1
)
|zp
1 p4 p (1 p 2 )
,
p
因此I21pi2πi1pp2p1(1pp22)
2π 1
p2 p2
.
2020/12/1
7
注此时: 若 I p1 1,则 2fπ(iz [)R 在 eszf (z1 )内 奇 Re点 sf为 (zz)]0 ,1 p
1cos2
dx x
1 z 11 ( z2 1)2
dz iz
2z
2020/12/1
10
2 i
z4
z 1
2zdz 6z2 1
2 i
z4
z 1
dz 2 6z2
1
令 z2 u, 则 当 z 绕 z 1 正 向 一 周 时 ,u 绕 u 1 正 向 二 周 ;
f( u ) 2i1 2 u 1 u在 2 u d6u u1 内 1有 , 一 个 一 阶 极 点 u 3 8 ,且
解 由于0 p 1,
1 2 p co p 2 s ( 1 p ) 2 2 p ( 1 c) os
在02π内不为零故， 积分有意义.
由c于 o 2s 1 2(e2ie2i)12(z2 z2),
Iz1z2 2z212pz1 z1p2d izz
2
2020/12/1
5
z2z2
1
dz
I
z1
2 12pzz1p2iz
2
1
1z4
dz 1
f (z)dz.
2pi z1 z2(z 1)(zp)
2 pi z 1
p
被积函数的三个 z极 0, p点 ,1, p
z0,p,在圆 z1内 周，
且 z0为二级 z极 p为点 一， 级极点，
2020/12/1
6
所以在圆 z 周 1上被积函数无奇点，
注件:关 .键 是 引 进 代 换 z e i,R (sin ,c o s)在 [0 ,2 ]上 连 续 可
不 必 检 验 ,只 要 看 变 换 后 被 积 函 数 在 z 1 是 否 有 奇 点 .
2020/12/1
4
例1 计 算 积 分 I 0 2 π 1 2 p c o c o s 2 s p 2d(0 p 1 ) 的 值 .
1 i
z
1
5z
zm 2z2
dz 2
2020/12/1
12
i
zm
dz i 2iRes
zm
2 z 1 (z 1)(z 2)
2
z1 2
(z 1)(z 2)
2
2
zm
z
2
|
z
1
2
3
2 m 1
,
所以I 1 ReJ 2
3 2m .
2020/12/1
13
在许多实际问题中，往往要求计算反常积分的值，如
的问题，同学们可以自学。
2020/12/1
2
一 计 算 0 2 πR (c o s,sin )d 型 积 分
思想方法 : 把定积分化为一个复变函数沿某条
封闭路线的积分 .
两个重要工作: 1) 积分区域的转化
2) 被积函数的转化
形如02πR(co,ssin)d
令zei dzieid
sin1(eiei) z 2 1 ,