1---50平方、立方、平方根、立方根表
- 格式：doc
- 大小：35.50 KB
- 文档页数：3
下载文档原格式
合集下载
常用的平方根表立方根表
常用的平方根表立方根表在数学的世界里，平方根和立方根是非常重要的概念。
它们在各种数学计算、科学研究以及实际生活中都有着广泛的应用。
为了方便计算和查询，人们常常会编制平方根表和立方根表。
平方根，简单来说，就是一个数的平方等于另一个数，那么这个数就是另一个数的平方根。
例如，2 的平方是 4，所以 2 是 4 的平方根。
同时，因为（－2) 的平方也是 4，所以－2 也是 4 的平方根。
一个正数有两个平方根，它们互为相反数；0 的平方根是 0；负数在实数范围内没有平方根。
立方根则是指一个数的立方等于另一个数，那么这个数就是另一个数的立方根。
比如，2 的立方是 8，所以 2 是 8 的立方根。
与平方根不同的是，任何实数都有唯一的一个立方根。
平方根表通常列出了从 1 到某个较大整数的平方根的值。
以常见的平方根表为例，它会依次给出 1 到 100 这些整数的平方根。
比如，1 的平方根是 1，4 的平方根是 2，9 的平方根是 3 等等。
在实际使用中，如果我们要计算一个不是整数的数的平方根，比如 25 的平方根，我们可以先找到最接近 25 的两个整数的平方根，然后通过插值的方法来估算。
立方根表的编制方式与平方根表类似，也是列出从 1 到一定整数的立方根的值。
比如，1 的立方根是 1，8 的立方根是 2，27 的立方根是3 等等。
那么，这些平方根表和立方根表在哪些方面有用呢？在数学计算中，它们可以大大提高计算速度和准确性。
特别是在一些复杂的计算中，如果需要多次用到某个数的平方根或立方根，直接从表中查找可以节省时间，避免繁琐的计算过程。
在科学研究中，平方根和立方根的概念经常出现。
比如在物理学中，计算物体的速度、加速度等常常会涉及到平方根；在化学中，计算物质的密度、体积等可能会用到立方根。
有了平方根表和立方根表，科学家们可以更高效地进行数据处理和分析。
在工程领域，如建筑、机械制造等，也经常需要用到平方根和立方根的计算。
实用的平方根表立方根表.pdf
，检查合同的履行情况；
4.5.4 保管法人代表授权委托书、合同专用章，并按编号归口使用；
4.5.5 建立合同管理台帐，对合同文本资料进行编号统计管理；
4.5.6 组织对法规、制度的学习和贯彻执行，定期向有关领导和部门报告工作；
4.5.7 在总经理领导下，做好合同管理的其他工作，
4.6 工程技术部：专职合同管理员及材料、燃料供应部兼职合同管理员履行以下职责：
4.2 工程部：是发电厂建设施工安装等工程合同签订管理部门；负责签订管理基建、安装、人工技术的工程合同。
4.3 经营部：是合同签订管理部门，负责管理设备、材料、物资的订购合同。
4.5 合同管理部门履行以下职责：
4.5.1 建立健全合同管理办法并逐步完善规范；
4.5.2 参与合同的洽谈、起草、审查、签约、变更、解除以及合同的签证、公证、调解、诉讼等活动，全程跟踪和检查合同的履行质量； 4.5.3 审查、登记合同对方单位代表资格及单位资质，包括营业执照、经营范围、技术装备、信誉、越区域经营许可等证件及履约能力（必要时要求对方提供担保）
立方根 √3 1 = 1 √ 2 = 1.260 √ 3 = 1.442 √ 4 = 1.587 √ 5 = 1.710 √ 6 = 1.817 √ 7 = 1.913 √8 = 2 √ 9 = 2.080 √ 10 = 2.154 √ 11 = 2.224 √ 12 = 2.289 √ 13 = 2.351 √ 14 = 2.410 √ 15 = 2.466 √ 16 = 2.520 √ 17 = 2.571 √ 18 = 2.621 √ 19 = 2.668 √ 20 = 2.714
平方根 √1＝1 √2＝ 1.414 √3＝ 1.732 √4＝2 √5＝ 2.236 √6＝ 2.449 √7＝ 2.646 √8＝ 2.828 √9＝3 √10＝3.162 √11 = 3.317 √12 = 3.464 √13 = 3.606 √14 = 3.742 √15 = 3.873 √16 = 4 √17 = 4.123 √18 = 4.243 √19 = 4.359 √20 = 4.472
平方根立方根背诵表
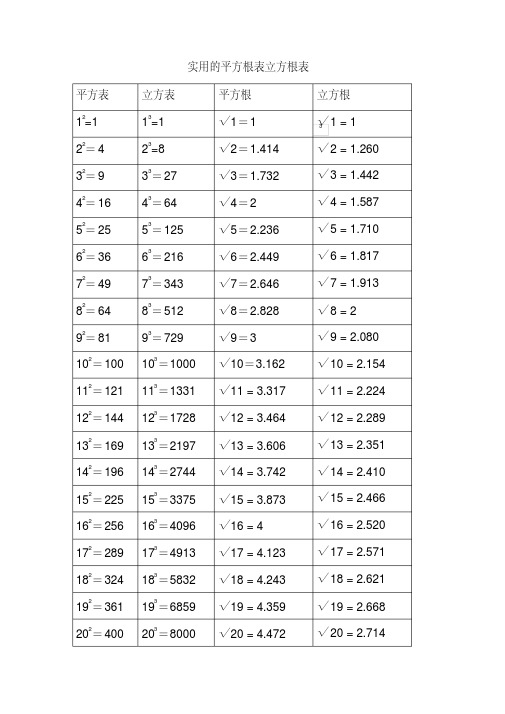
平方根立方根背诵表
嘿，朋友们！今天咱们来聊聊平方根立方根背诵表。
说起这个平方根立方根啊，是不是有时候觉得脑袋都大啦？其实呀，只要咱们掌握了规律，也没那么可怕！
先看看平方根，像 1 的平方根就是 1 和 1 ，这很简单对吧？2 的平方根呢，就是约等于 1.414 和 1.414 。
3 的平方根约是 1.732 和 1.732 。
4 的平方根就很清楚啦，是 2 和 2 。
再来说说立方根，1 的立方根还是 1 ，这个好记。
2 的立方根约是 1.260 。
3 的立方根约是 1.442 。
可别觉得记这些数字很枯燥哦，咱们要是能熟练掌握，做题的时候那可就像开了挂一样顺溜！
你想想，考试的时候，别人还在那里苦思冥想，咱们一下子就能算出答案，多牛呀！
而且哦，平时生活中说不定也能用上呢。
比如说算个什么体积、面积啥的。
其实呀，多背几遍，多做几道题，这些数字就会乖乖地待在咱们的脑袋里啦。
每次背的时候，可以把它们想象成一个个可爱的小精灵，和它们交上朋友，这样就更容易记住啦。
怎么样，是不是觉得平方根立方根也没那么可怕啦？咱们一起加油，把这个背诵表拿下！。
实用的平方根表立方根表
实用的平方根表立方根表
（表示根号0等于0，下平方根表立方根表
√1 = 1
√2 = 1.414
√3 = 1.732
√4 = 2
√5 = 2.236
√6 = 2.449
√7 = 2.646
√8 = 2.828
√9 = 3
√10 = 3.162
√11 = 3.317
√12 = 3.464
√13 = 3.606
√14 = 3.742
√15 = 3.873
√16 = 4
√17 = 4.123
√18 = 4.243
√19 = 4.359
√20 = 4.472
大家都来到荷塘，挖莲藕抓鱼虾，捉泥鳅捡螃蟹，人声鼎沸，笑语欢声，相互谈说着要如何弄出一顿顿可口的美味。
光是莲藕的吃法就有很多：熬汤炖肉八宝酿、清炒生吃蜜饯糖，还可以磨成藕粉，加入砂糖或蜂蜜，在温水里一泡，就是一杯清凉清甜的解暑饮料。
用鲜莲叶来熬粥，蒸饭蒸鸡，或蒸其它肉类味道都是极鲜美的，做出来的食物均带着一股淡淡的莲叶清香。
人们那么喜欢荷花，不单单是因为它的芳香美丽洁净高雅，更因为它全身是宝，每一处都可食可药可用。
我最喜欢的是生鲜莲子羹。
把剥好的莲子对半打开去芯，莲子芯很苦，可以药用，没有芯的莲子是甜的，正好用它熬糖水。
把足量的生莲子洗净，和着一小片生姜一片鲜莲叶，放进清水锅里，盖着盖子大火烧滚，转小火熬二十分钟，捞起莲叶，加入冰糖，小火慢熬，边熬边搅拌，十五分钟后，一款既清香甘美又消暑解渴的莲子羹就做成了。
这样的汤水，在炎热的夏季里，只要喝过一次都不会忘记。
常用的平方根表立方根表
常用的平方根表立方根表在数学的世界里，平方根和立方根是非常重要的概念。
为了更方便地进行计算和解决问题，人们常常会用到平方根表和立方根表。
平方根，简单来说，就是一个数的平方的逆运算。
比如，如果一个数的平方是 9，那么这个数就是 9 的平方根，即 3 或者－3。
平方根表就是把一些常见数字的平方根整理在一起，方便我们查阅和使用。
立方根呢，则是一个数的立方的逆运算。
例如，若一个数的立方是8，那么这个数就是 8 的立方根，即 2。
立方根表就是将常见数字的立方根罗列出来的表格。
平方根表通常包含从 1 到一定数值范围内数字的平方根。
比如说，对于数字 1，它的平方根就是 1；数字 4 的平方根是 2；数字 9 的平方根是 3。
当数字不是完全平方数时，平方根就会是一个无理数，这时候平方根表中会给出其近似值。
比如，2 的平方根约为 1414，3 的平方根约为 1732 等等。
立方根表的构成和平方根表类似，只不过是关于数字的立方根。
像1 的立方根还是 1，8 的立方根是 2，27 的立方根是 3。
对于不是完全立方数的数字，立方根表也会给出相应的近似值。
这些平方根表和立方根表在很多领域都有着广泛的应用。
在数学计算中，当我们需要快速得到一个数的平方根或立方根的值时，它们可以节省我们大量的计算时间。
特别是在一些复杂的数学问题中，或者在需要精确计算的科学研究中，这些表格能发挥重要作用。
在工程领域，平方根和立方根的计算也经常出现。
比如在建筑设计中，计算结构的受力、材料的用量等，都可能会用到平方根和立方根。
有了平方根表和立方根表，工程师们能够更高效地完成设计和计算工作，确保工程的准确性和安全性。
在物理学中，平方根和立方根的概念同样不可或缺。
例如在研究物体的运动、能量的转换等方面，常常需要进行相关的计算。
此时，平方根表和立方根表可以为物理学家们提供便利，帮助他们更专注于理论的研究和实验的分析。
在日常生活中，平方根和立方根的应用也并不少见。
实用的平方根表立方根表
3 实用的平方根表立方根表平方表立方表平方根立方根12=1 13=1 √1＝1 √1 = 1 22＝4 23=8 √2＝1.414 √2 = 1.260 32＝9 33＝27 √3＝1.732 √3 = 1.442 42＝16 43＝64 √4＝2 √4 = 1.587 52＝25 53＝125 √5＝2.236 √5 = 1.710 62＝36 63＝216 √6＝2.449 √6 = 1.817 72＝49 73＝343 √7＝2.646 √7 = 1.913 82＝64 83＝512 √8＝2.828 √8 = 2 92＝81 93＝729 √9＝3 √9 = 2.080 102＝100 103＝1000 √10＝3.162 √10 = 2.154 112＝121 113＝1331 √11 = 3.317 √11 = 2.224 122＝144 123＝1728 √12 = 3.464 √12 = 2.289 132＝169 133＝2197 √13 = 3.606 √13 = 2.351 142＝196 143＝2744 √14 = 3.742 √14 = 2.410 152＝225 153＝3375 √15 = 3.873 √15 = 2.466 162＝256 163＝4096 √16 = 4 √16 = 2.520 172＝289 173＝4913 √17 = 4.123 √17 = 2.571 182＝324 183＝5832 √18 = 4.243 √18 = 2.621 192＝361 193＝6859 √19 = 4.359 √19 = 2.668 202＝400203＝8000√20 = 4.472√20 = 2.7143√0 = 0（表示根号0等于0，下平方根表立方根表√1 = 1√2 = 1.414√3 = 1.732√4 = 2√5 = 2.236√6 = 2.449√7 = 2.646√8 = 2.828√9 = 3√10 = 3.162√11 = 3.317√12 = 3.464√13 = 3.606√14 = 3.742√15 = 3.873√16 = 4√17 = 4.123√18 = 4.243√19 = 4.359√20 = 4.472其中专业理论知识内容包括：保安理论知识、消防业务知识、职业道德、法律常识、保安礼仪、救护知识。
常用的平方根表立方根表
常用的平方根表立方根表在数学的世界里，平方根和立方根是非常重要的概念。
它们在各种数学计算、科学研究以及实际生活中都有着广泛的应用。
为了方便计算和查询，人们常常会编制平方根表和立方根表。
平方根，简单来说，就是一个数的平方等于另一个数，那么这个数就是另一个数的平方根。
例如，因为 2 的平方等于 4，所以 2 是 4 的平方根。
同时，－2 也是 4 的平方根，因为（－2) 的平方也等于 4。
正数有两个平方根，它们互为相反数；0 的平方根是 0；负数在实数范围内没有平方根。
立方根则是一个数的立方等于另一个数，那么这个数就是另一个数的立方根。
比如，因为 2 的立方等于 8，所以 2 是 8 的立方根。
与平方根不同的是，任何实数都有唯一的立方根。
平方根表通常列出了从 1 到一定数值（比如 1000）的整数的平方根。
以常见的平方根表为例，它会按照数字的顺序依次列出每个数的平方根。
例如，1 的平方根是 1，2 的平方根约为 1414，3 的平方根约为1732 等等。
这些数值都是经过精确计算得出的，为我们在计算中提供了极大的便利。
立方根表的形式与平方根表类似，也是按照数字顺序列出一定范围内整数的立方根。
比如 1 的立方根是 1，2 的立方根约为 1260，3 的立方根约为 1442 等等。
那么，这些平方根表和立方根表在哪些方面能帮助我们呢？首先，在数学计算中，如果我们需要频繁计算某个数的平方根或立方根，直接查询表格可以节省大量的计算时间。
特别是在一些复杂的数学问题中，快速准确地获取平方根和立方根的值能够提高解题的效率。
其次，在科学研究和工程领域，很多数据的处理和分析都涉及到平方根和立方根的计算。
例如，物理学中的力学、电学计算，化学中的浓度计算，以及工程学中的结构设计等。
有了平方根表和立方根表，科研人员和工程师们可以更快速地得到准确的结果，从而推进研究和项目的进展。
在日常生活中，平方根和立方根的应用也不少。
比如在建筑施工中，计算房间的面积、体积时就可能用到；在制定预算时，计算成本的平方根或立方根来评估价格的合理性等等。