当前位置：文档之家 › 光波在介质中界面上的反射及透射特性的仿真

光波在介质中界面上的反射及透射特性的仿真

  • 格式：doc
  • 大小：664.78 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

光课程设计——光波在介质中界面上的反射及透射特性的仿真教学提纲

光课程设计——光波在介质中界面上的反射及透射特性的仿真教学提纲

光课程设计——光波在介质中界面上的反射及透射特性的仿真西安邮电大学光学报告学院：电子工程学生姓名：专业名称：光信息科学与技术班级：光信1103班设计名称：光波在介质中界面上的反射及透射特性的仿真一、课程设计目的1．掌握反射系数及透射系数的概念；2．掌握反射光与透射光振幅和相位的变化规律；3．掌握布儒斯特角和全反射临界角的概念。

二、任务与要求对n1=1、n2=1.52及n1=1.52、n2=1的两种情况下，分别计算反射光与透射光振幅和相位的变化，绘出变化曲线并总结规律。

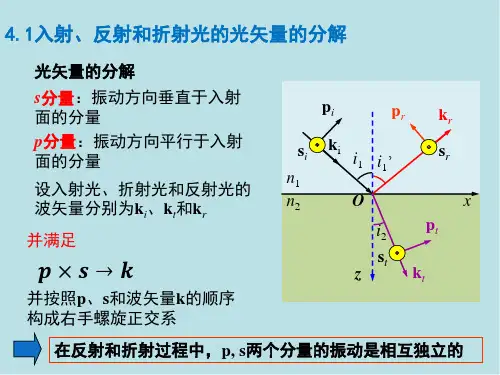
三、课程设计原理光在介质界面上的反射和折射特性与电矢量的振动方向密切相关。

由于平面光波的横波特性，电矢量可在垂直传播方向的平面内的任意方向上振动，而它总可以p s m E Et E E r imtm m im rm m ,,,0000===分解成垂直于入射面振动的分量和平行于入射面振动的分量，一旦这两个分量的反射、折射特性确定，则任意方向上的振动的光的反射、折射特性也即确定。

菲涅耳公式就是确定这两个振动分量反射、折射特性的定量关系式。

（1）s 分量和p 分量垂直入射面的振动分量- -s 分量平行入射面的振动分量- -p 分量定义：s 分量、p 分量的反射系数、透射系数分别为（2）反射系数和透射系数定义：s 分量、p 分量的反射系数、透射系数分别为p s m E Et E E r imtm m im rm m ,,,0000===（3）菲涅耳公式已知界面两侧的折射率21n n 、和入射角1θ，就可由折射定律确定折射角2θ；进而可由菲涅耳公式求出反射系数和透射系数。

绘出如下按光学玻璃（n=1.5）和空气界面计算，在21n n <（光由光疏介质射向光密介质）和21n n >（光由光密介质射向光疏介质）两种情况下，反射系数、透射系数随入射角1θ的变化曲线。

(a)光由光疏介质射向光密介质 (b)光由光密介质射向光疏介反射光与入射光中s,p 分量的相位关系： （1）n1＜n2时，光疏入射光密 s 分量的反射系数s r ：反射光中的s 分量与入射光中的s 分量相位相反；反射光中的s 分量相对入射光中的s 分量存在一个π相位突变(rs ϕ=π)； p 分量的反射系数p r ：在1θ<B θ范围内,p r ＞0，反射光中的p 分p 量与入射光中的分量相位相同(rp ϕ=0)；在1θ>B θ范围内,p r <0，反射光中的p 分量相对入射光中的p 分量有π相位突变(rp ϕ=π)；（2）n1>n2时，光密入射光疏 s 分量的反射系数s r ：入射角1θ在0到C θ(临界角，12/sin n n C =θ）的范围内，s 分量的反射系数s r ＞0。

基础光学第4章光波在界面的反射和折射规律课件

基础光学第4章光波在界面的反射和折射规律课件

无论 n1 n2 或 n1 n2
透射光1’和2’振动方
向相同。即无半波损失。
只要光线2存在，光线1
和2的振动方向总是相
反的，即1和2的光程之
间存在半波损失。
光在多层透明介质界面的反射和折射
n1 < n2< n3 或n3 < n2< n1
时，光线1和2之间的光程
没有半波损失。
当折射率不按顺序排列时，
p
s
n2 n1
t p ts
2n1
n2 n1
入射
反射
约定
n1 < n2 n1 > n2
rp
rs
tp
ts
+
+
+
+
+
约定
实际
实际
+
反射
入射
n1
n2
约定
实际
透射
(a) n1 < n2
n1 < n2 时反射光与入射光振动方向相反
n1 > n2 时反射光与入射光振动方向相同
在任何情况下，透射光的方向和入射光相同
中的多次反射，分别求光从空气（折射率为1.0）正入射到玻
璃上表面，以及光从玻璃下表面射出时的振幅反射率、光强
反射率、振幅透射率和光强透射率。
【解】 正入射： i1 i2 0
n n
2n1
rp 2 1 rs ， t p ts
n2 n1
n2 n1
2
n2 n1
在反射和折射过程中，p, s两个分量的振动是相互独立的
4.2 菲涅尔反射和折射公式
n cos i1 n1 cos i2

光波场在2种介质界面反射时的半波损失

光波场在2种介质界面反射时的半波损失

光波场在2种介质界面反射时的半波损失
庹有康;陈希明
【期刊名称】《重庆邮电大学学报（自然科学版）》
【年(卷),期】2004(016)006
【摘要】在波动光学中常常会遇到光波场在2种介质分界面上反射时的半波损失问题,而大多数教科书并未能从理论上阐明半波损失产生的条件和原因.从电磁场的基本理论出发,分析和讨论了光波场在两种界面上反射时的半波损失问题,从本质上全面、合理地解释了在实验中产生半波损失的实验结果.
【总页数】3页(P36-38)
【作者】庹有康;陈希明
【作者单位】重庆邮电学院,重庆,400065;重庆邮电学院,重庆,400065
【正文语种】中文
【中图分类】O431.1
【相关文献】
1.光从晶体到各向同性介质界面的反射和透射 [J], 裴芳芳;陈西园
2.论光在介质表面反射时的半波损失问题--兼与张静江先生商榷 [J], 陶志伟;刘涵哲
3.半波损失——平面偏振光在界面反射时的相位变化 [J], 龙海燕
4.半波损失——平面偏振光在界面反射时的相位变化 [J], 龙海燕;
5.光波入射到光疏—光密界面时反射光与折射光电矢量分析 [J], 陶志伟;高飞
因版权原因，仅展示原文概要，查看原文内容请购买。

光波在介质中界面的反射及透射的特性仿真实验题

光波在介质中界面的反射及透射的特性仿真实验题

1. 如何确定入射面?答：入射光与反射光以及法线共同构成的平面即入射面2.什么是临界角?临界角是光疏到光密，还是光密到光疏时发生?答：临界角就是全反射角，他指的是光线由光密介质入射到光疏介质时正好发生全反射时的入射角。

3.利用全反射现象能否产生圆偏振光?答；利用全反射现象可以产生圆偏振光，一个偏振光在一定角度上经过两次全反射可以产生圆偏振光，菲涅耳棱镜就是利用这个原理所制成的。

4.解释反射系数及透射系数的概念。

答：当电磁波由一个磁导率为μ1、介电常数为ε1的均匀介质，进入另一个具有磁导率为μ2、介电常数为ε2的均匀介质时，一部分电磁波在界面上被反射回来，另一分电磁波则透射过去。

反射波与透射波的振幅同入射波振幅之比，分别称之为反射系数与透射系数。

5.根据仿真曲线解释反射及透射光的相位变化规律。

答：图中反应了他们的相位的变化规律，例如图三所示在布儒斯特角处它的相位发生了π的跃变，而根据一个确定的波的表达式来看它是由余弦函数的的变化来确定的，而rp在菲涅耳表达式中是两个确定的余弦函数之比，所以rp由正变为负的时候，其中有一个余弦函数肯定相位发生了变化（奇变偶不变，符号看象限），且在布儒斯特角处，而在全反射角处也会发生变化，而且是逐渐变化的，这是因为当入射角逐渐增大的时候，它满足一个公式tan(fai/2)=-√((sin θ)^2-n^2)/cosθ),从公式可以看出相位会随着入射角的变化而渐变，当θ=π/2时，tan(fai/2)为无穷，所以fai=π。

6.试说明布儒斯特角的概念。

答：布儒斯特角，又称偏振角，是自然光经电介质界面反射后，反射光为线偏振光所应满足的条件。

7.试分析布儒斯特角与临界角哪个大。

答：临界角大于布儒斯特角，我们从它们的公式可以简单的推导出来，布儒斯特角为arctan(n2/n1),全反射角为arcsin(n2/n2), 假设n2/n1=x,因为有光密入射到光疏，所以n2>n1，因此x>1，此时布儒斯特角为arctan(x),全反射角为arcsin(x),我们对它两个同时求导得到：（arctan(x)）’=1/(1+x^2),而（arcsin(x)）’=1/√(1+x^2),由此我们可以得出全反射角公式的倒数大，也就是说，在相同变量的情况下它的数值大，从而我们也就说明了临界角大于布儒斯特角。

第二章-理想平板介质光波导中的光传播特性及仿真

第二章-理想平板介质光波导中的光传播特性及仿真

第2章介质光波导分析方法2.1 平板介质光波导一般概念2.1 平板介质光波导一般概念波动理论法则是把平板介质光波导中的光波看作是满足波导边界条件的麦克斯韦方程组的解。

2.2 平板光波导分析的射线法振幅反射率和附加相移振幅反射率和附加相移S 波（TE 波——电矢量平行于界面）振幅反射率：光传播过程相位变化：光波不仅在介质中传播过程中相位会发生改变，在界面上反射时相位也会变化。

对于θ1 ＜ θ1c ，界面上发生全反射，此时上式的分子和分母中第二个平方根内为负数，因此得到的振幅反射率r 为复数。

1.106分子分母同乘k ）振幅反射率和附加相移振幅反射率和附加相移s 波（ TE波——电矢量平行于界面） 附加相移为：p 波（ TM波——磁矢量平行于界面）在界面发生全反射时引起的附加相移为：（1.145）（1.144）界面：n1、n2、n3的界面，不是入射面平板波导中的其他光场均可视为TEM 模：模式只有横向分量，而无纵导模特征方程导模特征方程入射光线两次反射后与入射光线同方向传输特征方程特征方程A、B 两点的距离为:C、D两点的距离为:光线CD 还经历了两个附加相移:分别是介质1、3 界面处全反射的附加相移ϕ3 和介质1、2 界面处全反射的附加相移ϕ2.平板光波导的特征方程：特征方程特征方程 界面处的附加相移会因入射光偏振方向的不同而有所差异，因此就能够得到两个不同模式下的特征方程电矢量平行于界面的导波式中：特征方程特征方程同样地，磁矢量平行于界面的导波TM 模的特征方程（代入ΦM2和ΦM3） ：这里采用的是简单光线传播的射线理论。

实际上，从麦克斯韦方程出发，结合介质界面处的边界条件也可以推导出以上特征方程。

引入的几个重要参数——都是θ的函数,得到一个光波模式的波矢就可以求解其他引入的几个重要参数——都是θ的函数,得到一个光波模式的波矢就可以求解其他纵向波矢横向波矢衰减系数< n 1kn 2k << n 1k2.3 平板光波导中的TE模TE模的电磁理论求解TE模的电磁理论求解平板光波导中的TE模仅有E y由麦克斯韦方程：(2.30)TE模的电磁理论求解TE模的电磁理论求解的式子因此可以将H的分量表示为Ey代入式(2.30)，可以得到关于Ey的波动方程，j = 1;2;3 表示分别是在芯层、衬底和覆盖层。

光波在介质界面上的反射和折射 PPT课件

光波在介质界面上的反射和折射 PPT课件

(2) 大小
i t / 2 n1 sini n2 sint
tan B
n2 n1
n21
(3) 应用
3、全反射
•
设光波从光密介质射向光疏介质(n1>n2)，
折射角θ2大于入射角θ1。当sinθ1＝n2/n1时，θ2
为90o，这时折射角沿界面掠过。若入射角再增
大，使sinθ1>n2/n1 ，这时不能定义实数的折射 角。使θ2=90o的入射角θ1称为临界角，记作θc 即
E0ip cosi E0rp cosr＝Et0 p cost
2、反射系数和透射系数
rp
E0rp E0ip
n2 cos1 n1 cos2 n2 cos1 n1 cos2
tan(1 2 ) tan(1 2 )
tp
E0tp E0ip
2n1 cos1 n2 cos1 n1 cos2
2 cos1 sin 2 sin(1 2) cos(1 2)
RT 1
四、反射率和透射率
3、反射率随入射角变化关系
R随入射角θ1的变化关系
11日出生于苏格兰杰德伯勒，1800年毕业于爱
丁堡大学，曾任“爱丁堡杂志”、“苏格兰杂 志”、“爱丁堡百科全书”编辑，爱丁堡大学
教授、校长等。1815年被选为皇家学会会员， 1819年获冉福德奖章。
•
布儒斯特主要从事光学方面的研究。1812
年发现当入射角的正切等于媒质的相对折射率 时，反射光线将为线偏振光（现称为布儒斯特
Ets Eis Ers
n H2 H1 0
n Htp cost Hip cosi Hrp cosr 0
Hip cosi H rp cosr Htp cost
7

光波在各向同性介质界面的反射和折射 ppt课件

光波在各向同性介质界面的反射和折射 ppt课件

ppt课件
17
(2)大角度入射(掠射)的反射特性

由图1-24(a)，有
n1＜n2，光疏到光密。θ 1≈900的掠射情况。
rs 0, rp 0

在入射点处，反射光矢量Er与入射光矢量Ei方向近似相 反，将产生半波损失。 n1>n2，光密到光疏。掠射θ 1≈900>θ c。全反射。 在入射点处，反射光产生半波损失的条件：
ki sin i kr sin r , ki sin i kt sin t n1 sin i n1 sin r , n1 sin i n2 sin t
反射定律
T 1-21
折射定律

描述光在介质面上的传播方向
ppt课件 3
1.2.2 菲涅耳公式
描述入射光、反射光和折射光 之间的振幅、相位关系。 1.s分量和p分量 垂直入射面的振动分量- -s分量 T 1-23 平行入射面的振动分量- -p分量 规定分量和分量的正方向如图所示 2.反射系数和透射系数 定义：s分量、p分量的反射系数、透射系数分别为
① n1＜n2，光疏到光密。先考察θ 1=00的正入射情况。 由图1-24(a)，有
rs 0, rp 0
考虑P30 T1-23，有关光场振动正方向的规定，则有
可见：在入射点处，合成的反射光矢量Er相对入射光场Ei反 向，相位发生π突变，或半波损失。 对于θ 1非零、小角度入射时，都将近似产生π相位突变，或 半波损失。

入射光中s分量和p分量的透射率(不相同)为
n2 cos 2 2 sin 21 sin 2 2 Ts ts n1 cos1 sin 2 (1 2 )
n2 cos 2 2 sin 21 sin 2 2 Tp tp 2 n1 cos1 sin (1 2 ) cos2 (1 2 )

平面光波在电介质表面的反射特性仿真研究

平面光波在电介质表面的反射特性仿真研究
一
１ Байду номын сангаас— １
《 电子设 计 工程 ） ０ ２年 第 １ ２１ １期
透射波 ： Ｅ＝ ，ｘ ｋ（ｉ —ｏ ）【 ， ｏ ｐｉ ２ｓ ｃｓ Ｅｅ ［ ｎ 一ｏ 胡 （） ４
１２ ８ ３年 ） 。其 中 ， （ １ 和 式 （ ３ 是 反 射 公 式 ， （ ２ 和 式 式 １） １） 式 １）
Ｅ ｅｐｉ １ｓ ０ — Ｏ０ｙ一 ｔ ； ｘ ｋ（ｉ ｒ ＣＳｒ）ｔ】 ［ ｎｘ Ｏ
（） ３
基 金 项 目： 军队 重 点科 研 项 目（ Ｊ ５ ３ ） Ｋ ０ １８ 作 者 简 介 ： 昊 鹏 （９ ７ ） 男 ， 宁 沈 阳人 ， 士 研 究 生 。研 究 方 向 ： 确 制 导 武 器 的作 战 使 用与 仿 真 。 王 １８ 一 ， 辽 硕 精
ｃ ｓ 矿ｃ ｓ ｏ ０悱 ｃｓ ０ ｏ （ ６）
失问题 。
２ 平面 光 波在 电 介质 表 面 的 反射 和 折 射
２１ 电矢 量 平行 入 射 面 ．
平 面 光 波 的 电 矢 量 平 行 于入 射 面 ， 此 其 电场 只有 Ｐ分 因 量 ， 磁 场 垂 直 于 入 射 面 ， 此 只 有 Ｓ分 量 ， 面 光 波 传 输 其 因 平 方 向矢 量 ｜ 在 入 射 面 内 ， 与 ： 平 行 。 以 、 和 曰所 确定 ｊ ｝ 轴 Ｅ
ｃｓｉ ｅｐｉ ｉｉ０－ ｃｓ Ｅ０ ｐｉ ｉｉ０－ｔ ｏＯ ￣ｘ ｋｓ ｎｒ Ｉ一 ｏ ，ｘ ｋ ｓ ｃ 】 Ｅ ［ ｓ （ ） ｅ ［ｓ ｎ ｏ ＝ ｏ０ ￣ｘ ｋｓｉＯ－ ｔ ｃｓ， ｅｐｉ ２ ｎｒｏ］ Ｅ ［ ｓ ｔ 再 结 合 ｊ＝ ￣ ｌ 和 ｋ＝ ￣ Ｊ 代 人 （ ） 简 可 得 ： ｝ ２ｒ １ ｎ ２２ ｎ Ａ， ５化

正负折射率介质分界面反射和折射的仿真

正负折射率介质分界面反射和折射的仿真

正负折射率介质分界面反射和折射的仿真马慧许雪艳【摘要】电磁波在负折射率介质中传播时，材料的介电常数和磁导率均为负数，从而表现出一些奇特的特性。

为详细了解电磁波在正负折射率介质分界面的反常折射现象，文章讨论了正负折射率介质分界面的反射和折射规律，并用有限元软件Comsol Multiphysics对反射和折射现象进行仿真，同时对与理论分析一致的仿真结果以图像形式进行了显示。

【期刊名称】巢湖学院学报【年(卷),期】2014(000)006【总页数】4【关键词】负折射率介质；反射和折射；有限元软件1 引言早在1968年，前苏联物理学家Veselago就预言：对于无能量损耗的介质，当介电常数和磁导率同时为负值时，将具有负群速度、负折射率、负光压、逆多普勒效应、逆切伦科夫辐射、倏逝波放大、理想成像等一些反常的物理现象，这种材料被称之为负折射率材料(NIM）。

在此材料中，电场、磁场和波矢之间构成左手关系，又称之为左手材料(LHM）[1]。

由于自然界中难以找到介电常数和磁导率同时为负的物质，因此Veselago的研究没有引起学术界太多的注意；直到1996年，英国皇家学院的John Pendry等人从理论上证明了周期性排列的金属条和金属开口谐振环组成的结构能够在一定频率范围内产生负等效介电常数和负等效磁导率[2]，这一现象才引起人们的重视。

2000年，美国加州大学的David Smith研究小组首次利用以铜为主的复合材料人工合成了世界上第一块在微波波段具有负折射率的物质，从而证明了负折射率材料的存在[3]。

到目前为止，负折射率材料已经在微波、太赫兹波、红外线及可见光波段被证实，并开始进行应用领域的研究和探索，如用来制造高指向性的天线，实现完美透镜，制成吸波材料实现电磁波的隐身，制造各种新颖的微波或光波器件等[4-7]。

因此，深入研究负折射率材料的电磁特性，为研究、制作新型的电磁器件和光子器件提供理论依据。

由于很难获得理想的负折射率材料，通过数值仿真验证负折射率材料的奇特性质，对人们认识负折射率材料正发挥着越来越重要的作用[8-9]。

第一篇-第二章平面光波在两介质分界平面上的反射与透射.

第一篇-第二章平面光波在两介质分界平面上的反射与透射.

对于S-波偏振，引入介质界面两侧光学 有效导纳
n1 n2 s r n1 n2 2n1 ts n1 n2
（2-19）
（2-20）
1 n1 cos1 , 2 n2 cos2
（2-21）
则式（2-17）和式（2-18）改写为
薄膜光学与薄膜技术基础
1 2 s r 1 2
薄膜光学与薄膜技术基础
则式（2-36）和式（2-37）改写为
2 1 cos 1 tp 1 2 cos 2
1 2 p r 1 2
（2-39） （2-40）
需要注意的是P-波偏振情况下，用光学有效 导纳表示的透射系数与垂直入射情况下的透 射系数公式相差因子 cos1 cos2。 2.2 各向同性吸收介质界面的反射与透射 2.2.1 S-波反射与透射 s 2 ? 0 ，在平面 假设介质电导率 s 1 ? 0，
i
（2-1）
是电场在r=0处的幅值，k 为介质 式中 E 1 1 1 0i 1中的波数，1为介质1的本征阻抗。由图2-1， 在直角坐标下，入射波传播方向的单位矢量。 由图2-1，在直角坐标下，入射波传播方向的 i k 单位矢量 0 写成分量形式，有 ki0 sin 1ex cos1ez （2-2）
（2-25）
同理，可得反射波与透射波电场和磁场 复振幅矢量表达式为
jk1 x sin1 z cos1 Er (r ) e x cos1 e z sin 1 E0r e jk1 x sin1 z cos1 E H r (r ) e y 0 r e 1 (r ) e cos e sin E e jk2 x sin2 z cos2 E t x 2 z 2 0t jk x sin z cos E 0t 2 2 e 2 Ht (r ) e y 2

平面光波在平界面层状介质薄膜中反射和透射

平面光波在平界面层状介质薄膜中反射和透射

2
n0 n0
n12 n1取偶数，式（3-34）化为
B 1 0 1
C
0
1
nG
得
(3-47)
B 1, C nG
（3-48）
代入式（3-39），有
R
Rs
Rp
n0 n0
nG nG
2
（3-49）
（1）当m取奇数时，由式（3-42）可知，
1
2
n1d1
cos1
2
n1d1
m
2
(3-41)
或
n1d1 m 4
(3-42)
即薄膜的光学厚度 n1d1取四分之一波长的整数
倍，此时
cos 1
0, 1,
m 1,3,5, m 2, 4,6,
,
sin
1
1, 0,
m 1,3,5, m 2, 4,6,
(3-43)
因此，当 m 取奇数，式（3-34）化为
为了引入光学有效导纳的概念，首先定义 切向阻抗）。定义为平面电磁波在分界平面上 电场切向分量与磁场切向分量之比，即
t
Et Ht
(3-1)
注意此处的下标 t 指切向分量，而不是透射分
量。显然，法向阻抗与本征阻抗 具有相同
的量纲。那么，在斜入射S-波偏振的情况下，
对入射波，由图2-1可知
E1t Ei , H1t Hi cos1
Er cos1
Hr
1 cos1 ip
（3-9）
如果不考虑场矢量的方向性（反射系数和透射
系数已考虑场矢量的方向性），可定义S-波偏
振界面上侧介质1中的法向阻抗为
1s
1 cos1
（3-10）
而P-波偏振界面上侧介质1中的法向阻抗为

光在两介质分界面上的反射与折射.ppt

光在两介质分界面上的反射与折射.ppt

A1 exp A1 ' exp A2 exp
iii(((kkk12'1rrr1t2')t1)t
)
§1-7 光在两个介质面上的
反射和折射
注：
1.位置矢量的原点可选取为分界面上的某 点O；
2.由于三个波的初位相可以不同，故振幅 一般为复数；
3.介质1中的电场强度是入射波和反射波
则电：场应强用度边之值和关。系：n
为
，
在介质1、2中光波的位相速度分别为
则： 由
n
k1
θ1 θ΄1
k΄1
1
o 2
界面
θ2 k2
n
k1
θ1 θ΄1
k΄1
1
o
界面
2
在界面上的投影相等。 θ2 k2 由三角函数和矢量关系可知：
则有： 即为入射角等于反射角――反射定律；
即为折射定律
§1-7 光在两个介质面上的 反射和折射
这样，我们就解决了平面光波在两个介质 分界面上的传播方向问题。
0
0
把上式代入磁场边界条件表达式，可以得 到关于三个电场振幅的另一个关系式：
n E n E n E cos
cos
cos
1 1s
1 1 1s
1
2 2s
2
联立两个关于E分量的方程，
§1-7光在两个介质分界面上的
反射和折射
则
E E E 1s
1s
2s
n E n E n E cos
cos
E1s E1s E2s
为了解出两个未知量，还需利用磁场的边
界条件：
H H H cos cos cos
1p
1
1p

第1章 波动光学基础 1-5 光在介质界面的反射与折射 物理光学课件

第1章 波动光学基础 1-5 光在介质界面的反射与折射 物理光学课件

1.5.7 反射光与透射光的能量分配
1 波动光学基础
1.5 光在介质界面的反射与折射
• 1.5.８ 光在吸收介质界面上的反射和折射
R r 2 1n 1 n
n n 1 i
• 1.5.９光的吸收、色散和散射
• １、吸收介质内
E
A exp
i
n
z c
t
A exp
i
n 1
i
z c
t
A
exp
1 波动光学基础
1.5.1 光在介质界面的反射与折射
二、反射和折射定律 •设（如图）：入射、反射、折射光波的电场矢量的S-分量分别为：
E1s E1y A1s exp[i(k1 r t)] A1s exp{i[k1(x sin i1 z cos i1) 1t]} E1's E1'y A1's exp[i(k1' r 1' t)] A1' s exp{i[k1' (x sin i1' z cos i1' ) 1' t]} E2s E2y A2s exp[i(k2 r 2t)] A2s exp{i[k2 (x sin i2 z cos i2 ) 2t]}
2、入射波透入介质2约一个波长的深度， 透射波沿界面传播约半个波长， 然后返回介质1。
1 波动光学基础
• 三、近场扫描光学显微镜（NSOM）
• NSOM原理：
1.5.6 全反射现象与应用
1 波动光学基础
1.5.6 全反射现象与应用
• NSOM独特功能：
• 1、高分辨 • 突破衍射极限（200nm）, 实现12nm分辨。 • ２、样品宽容 • 固、液、绝缘体、金属、半导体，无需特殊加工。 • ３、环境宽松 • 无需真空环境。 • ４、照明方式多样，倏逝波广泛存在。

光学课程设计 光波在介质中界面上的反射及透射特性的仿真

光学课程设计 光波在介质中界面上的反射及透射特性的仿真

西安邮电大学光学报告学院：电子工程学生姓名：专业名称：光信息科学与技术班级：光信1103班光波在介质中界面上的反射及透射特性的仿真一、课程设计目的1．掌握反射系数及透射系数的概念；2．掌握反射光与透射光振幅和相位的变化规律；3．掌握布儒斯特角和全反射临界角的概念。

二、任务与要求对n1=1、n2=1.52及n1=1.52、n2=1的两种情况下，分别计算反射光与透射光振幅和相位的变化，绘出变化曲线并总结规律三、课程设计原理根据麦克斯韦电磁理论，利用电矢量和磁矢量来分析光波在两介质表面的反射特性，把平面光波的入射波、反射波和折射波的电矢量分成两个分量：一个平行于入射角，另一个垂直于入射角，对平面光波在电介质表面的反射和折射进行分析，推导了菲涅尔公式，并结合MATLAB研究光波从光疏介质进入光密介质，以及光波从光密介质进入光疏介质时的反射率、透射率、相位等随入射角度的变换关系。

同时对光波在不同介质中传播时的特性变化进行仿真研究，根据仿真结果分析了布鲁斯特角、全反射现象及相位变化的特点。

有关各量的平行分量与垂直分量依次用指标p和s来表示，s分量、p分量和传播方向三者构成右螺旋关系。

假设界面上的入射光，反射光和折射光同相位，根据电磁场的边界条件及S分量，P分量的正方向规定，可得Eis+Ers=Ets. 由著名的菲涅耳公式：rs=E0rs/E0is=-(tanθ1-tanθ2)/(tanθ1+tanθ2);rp=E0rp/E0ip=(sin2θ1-sin2θ2)/ (sin2θ1+sin2θ2);ts=E0ts/E0is=2n1cosθ1/n1cosθ1+n2cosθ2;tp=E0tp/E0ip=2n1cosθ1/n2cosθ1+n1cosθ2;反射与折射的相位特性1.折射光与入射光的相位关系S分量与P分量的透射系数t总是取正值，因此，折射光总是与入射光同相位。

2.反射光与入射光的相位关系1）光波由光疏介质射向光密介质n1<n2时，反射系数rs<0,说明反射光中的s分量与入射光中的s分量相位相反，即存在一个π的相位突变。

(整理)光电课程设计_光学仿真.

(整理)光电课程设计_光学仿真.

概述：一、光源在光纤通信系统中，光源器件可实现从电信号到光信号的转换，是光发射机以及光纤通信系统的核心器件，它的性能直接关系到光纤通信系统的性能和质量指标。

光纤通信系统要求光源具有合适的发射波长，处在光纤的低损耗窗口之中；有足够大的输出功率，从而有较长的传输距离；有较窄的发光谱线，可以减少光纤的色散对信号传输质量的影响；易于与光纤耦合，确保更多的光功率进入光纤；易于调制，响应速度要快，调制失真小，带宽大；在室温下能连续工作，可靠性高，寿命至少在10万小时以上。

下面简单介绍已广泛应用的两类半导体光源：半导体发光二极管（LED ）和半导体激光二极管（LD ）。

1 发光二极管（LED ）发光二极管（LED ）是低速、短距离光波通信系统中常用的光源。

其寿命很长，受温度影响较小，输出光功率与注入电流的线性关系较好，价格也比较便宜。

驱动电路简单，不存在模式噪声等问 题。

发光二极管结构简单，是一个正向偏置的PN 同质结，电子-空穴对在耗尽区辐射复合发光，称为电致发光。

发出的部分光耦合进入光纤供传输使用。

LED 所发出的光是非相干光，具有较宽的谱宽（30～60nm ）和较大的发射角（≈100°）。

自发辐射产生的功率是由正向偏置电压产生的注入电流提供的，当注入电流为I ，在稳态时，电子-空穴对通过辐射和非辐射复合，其复合率等于载流子注入率I/q ，其中发射电子的复合率决定于内量子效率ηint ，光子产生率为(I ηint/q)，因此LED 内产生的光功率为()int int /P w q η= (2.1)式中，ω 为光量子能量。

假定所有发射的光子能量近似相等，并设从LED 逸出的功率占内部产生功率的份额为ηext ，则LED 的发射功率为()int int /e ext ext P P w q I ηηη== (2.2) ηext 亦称为外量子效率。

由上式可知，LED 发射功率P 和注入电流I 成正比。

光波及其在各向同性介质界面的反射和折射

光波及其在各向同性介质界面的反射和折射

2020年2月8日
7
光学教程专题 光波及其在各向同性介质界面的反射和折射
菲涅耳公式： 反射比与透射比关系：
rp t p 1; rs ts 1
正入射时：
rp

rs

n2 n2
n1 n1
tp

ts

2n1 n2 n1
2020年2月8日
8
光学教程专题 光波及其在各向同性介质界面的反射和折射
沿z轴方向传播的一维平面简谐波的波函数：
E(
p, t )

A c os [ (t

z) v
0
]
E hv,T 2 , h / 2 , P h /
k 2 , v
E(
p, t )

A exp
i [Et

P
r0 ]
2020年2月8日
2
E
2020年2月8日
A
exp
i[
(t

z v
)

0
E* Aexp{i[(t
] z
v
)

0
]}
4
光学教程专题 光波及其在各向同性介质界面的反射和折射
波函数的复数表达 复振幅：
当略去含有时间的指数因子时：
E~

Aexpi[k
r 0
]
称为复振幅。而根据复函数的运算法则：
相位突变 对入射波和反射波而言，则因：
rp

E1p ' E1 p

n2 n2
cosi1 cosi1
n1 cosi2 n1 cosi2
rs

光波在介质界面上的反射和折射 菲涅耳公式

光波在介质界面上的反射和折射 菲涅耳公式

在讨论过程中，不计吸收、散射等能量损耗，因此， 入射光能量在反射光和折射光中重新分配，而总能 量保持不变。
2. 3 反射率和透射率 (Reflectivity and transmissivity) 若有一个平面光波以入射角1 斜入射介质分界面， 平面光波的强度为 Ii，则每秒入射到界面上单位面积 的能量为
代入边值关系 n Ei Er n Et ，该式总是成立，故
i r t
( ki k r ) r 0 ( ki k t ) r 0 (120) (121) (122)
2.1 反射定律和折射定律 进一步，根据图所示的几何关系，可得可由（121） 式和（122）式得到
Eis Ers Ets
(131)
(Eis Ers )n1cos1 Ets n2 cos 2 (133)
3. 菲涅耳公式 将 （128）式代入上式，利用（121）式关系，并根据 反射系数定义，得到
sin (1 2 ) rs =sin (1 2 )
Elm E0lm e－i(l t－kl r )
ki sini kr sin r ki sini kt sin t
( ki k r ) r 0 ( ki k t ) r 0
(123) (124)
n1 n2 O
kr ki kt
r
B
分界面
(121) (122)
i
t
A C
2.1 反射定律和折射定律 又因为 k n / c ，可将上二式改写为
Ers sin ( 2 1 ) Eis sin ( 2 1 )
(ki kr ) r 0 (121)
(134)
m s, p
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

西安邮电大学光学报告学院：电子工程学生姓名：专业名称：光信息科学与技术班级：光信1103班设计名称：光波在介质中界面上的反射及透射特性的仿真一、课程设计目的1．掌握反射系数及透射系数的概念；2．掌握反射光与透射光振幅和相位的变化规律；3．掌握布儒斯特角和全反射临界角的概念。

二、任务与要求对n1=1、n2=1.52及n1=1.52、n2=1的两种情况下，分别计算反射光与透射光振幅和相位的变化，绘出变化曲线并总结规律。

三、课程设计原理光在介质界面上的反射和折射特性与电矢量的振动方向密切相关。

由于平面光波的横波特性，电矢量可在垂直传播方向的平面内的任意方向上振动，而它总可以分解成垂直于入射面振动的分量和平行于入射面振动的分量，一旦这两个分量的反射、折射特性确定，则任意方向上的振动的光的反射、折射特性也即确定。

菲涅耳公式就是确定这两个振动分量反射、折射特性的定量关系式。

（1）s分量和p分量p s m E Et E E r imtm m im rm m ,,,0000===垂直入射面的振动分量- -s 分量平行入射面的振动分量- -p 分量定义：s 分量、p 分量的反射系数、透射系数分别为（2）反射系数和透射系数定义：s 分量、p 分量的反射系数、透射系数分别为p s m E E t E E r imtm m im rm m ,,,0000===（3）菲涅耳公式已知界面两侧的折射率21n n 、和入射角1θ，就可由折射定律确定折射角2θ；进而可由菲涅耳公式求出反射系数和透射系数。

绘出如下按光学玻璃（n=1.5）和空气界面计算，在21n n <（光由光疏介质射向光密介质）和21n n >（光由光密介质射向光疏介质）两种情况下，反射系数、透射系数随入射角1θ的变化曲线。

(a)光由光疏介质射向光密介质 (b)光由光密介质射向光疏介反射光与入射光中s,p 分量的相位关系： （1）n1＜n2时，光疏入射光密 s 分量的反射系数s r ：反射光中的s 分量与入射光中的s 分量相位相反；反射光中的s 分量相对入射光中的s 分量存在一个π相位突变(rs ϕ=π)； p 分量的反射系数p r ：在1θ<B θ范围内,p r ＞0，反射光中的p 分p 量与入射光中的分量相位相同(rp ϕ=0)；在1θ>B θ范围内,p r <0，反射光中的p 分量相对入射光中的p 分量有π相位突变(rp ϕ=π)；（2）n1>n2时，光密入射光疏 s 分量的反射系数s r ：入射角1θ在0到C θ(临界角，12/sin n n C =θ）的范围内，s 分量的反射系数s r ＞0。

反射光中的s 分量与入射光中的s 分量同相位，rs ϕ=0；入射角1θ>C θ时，发生全反射，1212cos sin 2tan θθϕn rs--=（21/n n n =）； p 分量的反射系数p r ：在1θ＜B θ范围内，p r <0，反射光中的p 分量相对入射光中的p 分量有π相位突变（rp ϕ=π)；在B θ<1θ<C θ范围内，p r >0，反射光中的p 分量与入射光中的p 分量相位相同(rp ϕ=0)；入射角1θ>C θ时，发生全反射，12122cos sin 2tan θθϕn n rp--=； 四、课程设计步骤（流程图）（1）定义变量n1,n2,f1.（2）给变量赋值,其中n1=1,n2=1.52,还有一种情况其中n1=1.52,n2=1（3）设计for 循环，使f1每循环一次加 /1000，实现在f1每变化一次下，得出相应的反射系数，透射系数的值，从而得出程序的循环（4）根据程序仿真结果五、仿真结果分析102030405060708090-1-0.500.51Fn1<n2s/p 分量与相位的关系010203040506070809001234Ff r s010203040506070809001234Ff r p0102030405060708090-11234n1>n2s/p 分量与相位的关系F01020304050607080901234Ff r s01020304050607080901234Ff r p结论：光在介质面上的反射、透射特性有三个因素决定：入射光的偏振态，入射角，界面两侧介质的折射率。

(1)光波由光疏介质射向光密介质（n1<n2）a.n1<n2时，反射系数rs<0,说明反射光中的s 分量与入射光中的s 分量相位相反。

(即frs=π)b.而p分量的反射系数rp在f1<fb范围内，rp>0,说明反射光中的p 分量与入射光中的p分量相位相同。

（即frp=0）c.在f1>fb范围内，rp<0,说明反射光中的p分量与入射光中的p分量π相位突变。

（即frp=π）(2)光波由光密介质射向光疏介质（n1>n2）a.入射角f1在0到fc的范围内，s分量的反射系数rs>0,说明反射光中s分量与入射光中的s分量同相位。

（即frs=0）b.P分量的反射系数rp在f1<fb范围内，rp<0,说明反射光中的p分量相对入射光中的p分量有π相位突变。

（即frp=π）c.在fb<f1<fc范围内，rp>0,说明反射光中的p分量与入射光中的p分量相位相同。

六、仿真小结光在介质界面上的反射、透射特性由三个因素决定：（1）入射光的偏振态；（2）入射角;（3）界面两侧介质的折射率。

由rs、rp、ts、tp随入射角的变化曲线可知，在入射角从0度到90度的变化范围内，不论光波以什么角度入射至界面，也不论界面两侧折射率大小如何，s分量和p分量的透射系数t总是取正值，因此，折射光总是与入射光同相位。

通过本次实验，掌握了反射系数及透射系数的概念，反射光与透射光振幅和相位的变化规律，布儒斯特角和全反射临界角的概念。

七、程序clear all;%n1=1;%n2=1.52;n1=1.52;n2=1;n=n2./n1;if n1<n2subplot(1,3,1)qa=0:pi/100:pi/2;qb=asin(n1.*sin(qa)./n2);rs=-sin(qa-qb)./sin(qa+qb);rp=tan(qa-qb)./tan(qa+qb);ts=2.*cos(qa).*sin(qb)./sin(qa+qb);tp=2.*cos(qa).*sin(qb)./sin(qa+qb)./cos(qa-qb);plot(qa*180./pi,rs,'r',qa*180./pi,rp,'c',qa*180./pi,ts,'b',qa*180./pi ,tp,'g')legend('rs','rp','ts','tp')%rssubplot(1,3,2)for qa=0:pi/1000:pi/2qb=asin(n1.*sin(qa)./n2);rs=-sin(qa-qb)./sin(qa+qb);if rs<=0Frs=pi;elseFrs=0;endplot(qa*180./pi,Frs,'r')hold onendlegend('Frs')%rpsubplot(1,3,3)for qa=0:pi/1000:pi/2qb=asin(n1.*sin(qa)./n2);rp=tan(qa-qb)./tan(qa+qb);if rp<=0Frp=pi;elseFrp=0;endplot(qa*180./pi,Frp,'b')hold onendlegend('Frp')elsesubplot(1,3,1)qc=asin(n2./n1);qa=0:0.0001:qc;qb=asin(n1.*sin(qa)./n2);rs=-sin(qa-qb)./sin(qa+qb);rp=tan(qa-qb)./tan(qa+qb);ts=2.*cos(qa).*sin(qb)./sin(qa+qb);tp=2.*cos(qa).*sin(qb)./sin(qa+qb)./cos(qa-qb);plot(qa*180./pi,rs,'r',qa*180./pi,rp,'c',qa*180./pi,ts,'b',qa*180./pi ,tp,'g')hold onqa=qc:0.0001:pi/2;tp=0;ts=0;rs=1;rp=1;plot(qa*180./pi,rs,'r',qa*180./pi,rp,'c',qa*180./pi,ts,'b',qa*180./pi ,tp,'g')hold onlegend('rs','rp','ts','tp')%rsqc=asin(n2./n1);subplot(1,3,2)for qa=0:pi/1000:qcqb=asin(n1.*sin(qa)./n2);rs=-sin(qa-qb)./sin(qa+qb);if rs<=0Frs=pi;elseFrs=0;endplot(qa*180./pi,Frs,'r')hold onendqa=qc:pi/1000:pi/2;Frs= 2.*atan(sqrt(sin(qa).^2-(n.^2))./cos(qa));plot(qa*180./pi,Frs,'r')hold onlegend('Frs')%rpsubplot(1,3,3)for qa=0:pi/1000:qc;qb=asin(n1.*sin(qa)./n2);rp=tan(qa-qb)./tan(qa+qb);if rp<=0Frp=pi;elseFrp=0;endplot(qa*180./pi,Frp,'b')hold onendqa=qc:pi/1000:pi/2;Frp= 2.*atan(sqrt(sin(qa).^2-(n.^2))./cos(qa)./n.^2); plot(qa*180./pi,Frp,'b')hold onlegend('Frp')end。