量子力学中的量子态与量子数
- 格式:docx
- 大小:37.64 KB
- 文档页数:3

主量子数,角量子数,磁量子数,自旋量子数主量子数、角量子数、磁量子数、自旋量子数是量子力学中非常重要的四个概念。
这四个量子数决定了原子的能级和电子的行为,是解释化学现象的基础,下面我们从四个方面分别来介绍一下这四个量子数的意义和特点。
一、主量子数(n)主量子数n是第一个确定一个原子的能级的量子数,它决定原子的大小和能量。
主量子数n可取值为1,2,3,4,......,其中1为基态,从2开始的状态称为激发态。
主量子数越大,能量越高,原子越大,电子距离原子核越远,所占的体积越大。
电子激发到高能级时需要吸收能量,回到基态时需要释放能量。
例如,氢原子的第一个能级是基态,n=1,能量最低;第二个能级为一级激发态,n=2,能量稍高;第三个能级为二级激发态,n=3,能量更高。
二、角量子数(l)角量子数l是第二个确定一个原子能级的量子数,它决定了电子在原子空间中的运动轨迹和形状。
角量子数l的取值一般从0开始,直到n-1。
l=0时,电子的轨迹是一个球形壳,称为S轨道;l=1时,电子在原子空间中运动的轨迹形状类似于一颗手环,称为P轨道;l=2时,电子的轨迹形状类似于一个双叶草,称为D轨道;l=3时,电子的轨迹形状类似于一个直角棱柱,称为F轨道。
以此类推。
不同的轨道形状决定了电子在原子空间中的分布情况,从而影响了电子与其他原子的反应。
三、磁量子数(ml)磁量子数ml是第三个确定能级的量子数,它决定了电子在空间中的定向。
ml的取值范围为- l, - l+1,…,0,…,l-1, l。
角量子数l的取值为2时,电子轨道形状是D轨道。
D轨道有五个方向,所以对应的磁量子数ml的取值有5个,分别为-2,-1,0,1,2。
磁量子数的变化影响了电子在原子中的分布情况,从而影响了原子的化学性质和反应。
四、自旋量子数(ms)自旋量子数ms用来描述电子自转的方向,它有两个可能取值:+1/2和-1/2。
一个原子最多容纳两个电子占据同一个轨道,而它们的自旋量子数必须相反,这被称为洪特规则。

量子力学复习提纲一、简答题1、什么是黑体?答:在任何温度下,对入射的任何波长的辐射全部吸收的物体。
2、简述光的波粒二象性。
答:吸收、发射以微粒形式,传播 c 。
描述波动性的力学量λν,与描述粒子的力学量p E ,之间的联系为νh E =,λhp =。
3、试简述Bohr 的量子理论。
答:(1)定态假设:电子只能在一组特殊的轨道上运动,在这组轨道上电子处于稳定状态,简称定态。
(2)频率条件:当电子从一个定态跃迁到另一个定态时,吸收或发射的辐射频率满足:νh E E n m =- 。
(3)量子化条件:电子在轨道上运动时,其角动量必须是h 的整数倍。
4、简述德布罗意假设。
答:具有能量E 和动量P的自由粒子与一个频率为ν、波长为λ的平面波相联系。
νh E =,λhp =。
5、粒子的德布罗意波长是否可以比其本身线度长或短?答:由基本假设ph =λ,波长仅取决于粒子的动量而与粒子本身线度无必然联系。
6、波函数模的平方()2,t rψ的物理意义是什么?答:()2,t r ψ表示在t 时刻r点附近单位体积中粒子出现的概率,即概率密度。
7、按照波函数的统计解释,试给出波函数应满足的条件。
答:波函数应满足的条件是:连续,有限,单值。
8、简述态叠加原理。
答:若n ψψψ,,,21 是体系的可能状态,则n n C C C ψψψψ+++= 2211也是体系的可能状态。
这一结论称为态叠加原理。
9.何谓定态?答:能量具有确定值的状态称为定态。
它用定态波函数()()iEt er t r -=ψψ,描写。
10、简述定态的特性。
答:定态的特性有:①能量具有确定值。
②几率密度及几率流密度不随t 变化。
③任何力学量(不含t )的平均值不随t 变化。
④任何力学量(不含t )取各种可能测量值的几率分布不随t 变化。
11、简要解释一维线性谐振子的零点能。
答:一维线性谐振子的零点能为ω210=E ,它是谐振子基态的能量,是一种量子效应,是测不准关系所要求的最小能量,是粒子具有波粒二象性的具体体现,谐振子永远不会静止。

四个量子数的物理意义和量子化条件量子力学,这个听起来高深莫测的词,其实就像一把钥匙,打开了微观世界的奇妙大门。
四个量子数就像是这个世界的小精灵,它们各自有各自的故事和角色。
你知道吗?在原子的舞台上,每个电子都在按照它们的规则跳舞,简直像是在进行一场宇宙的芭蕾舞演出。
我们来说说第一个量子数,主量子数。
它就像是一张身份证,告诉我们电子离原子核有多远。
数值越大,电子就越“潇洒”,离核越远,活得越自在。
想象一下,一个孩子在游乐场玩耍,离家越远越开心,主量子数就是那份自由的象征。
主量子数可不仅仅是个数字哦,它是决定能量级的关键。
能量高了,电子就像开了挂一样,飞得更远,能量低了,它们就得乖乖待在家里,跟原子核亲密接触。
接下来就是角量子数了。
它就像电子在“舞池”里跳舞时的舞步样式。
这个数决定了电子的轨道形状,像是个舞者的风格,有的优雅,有的张扬。
它的数值越高,舞姿越复杂,像极了现代舞中的那些神奇动作。
想象一下,如果电子是舞者,那角量子数就是他们的舞伴,伴随他们在空间中旋转、跳跃。
每个舞者都有自己的特色,电子也是如此。
无论是s轨道的圆润,还是p轨道的优雅,每一种形状都能带来不同的能量感受。
然后是磁量子数,这个有点像是电子的朝向。
在这个舞池中,舞者不仅要有风格,还要知道朝哪儿转。
这个量子数告诉我们电子在空间中的取向,就像是一名舞者在舞台上的位置。
如果你想象一下,舞者在不同的方向旋转,那种感觉是不是特别棒?每个方向都有独特的魅力。
磁量子数可以有很多种选择,每个选择都像是给舞者添加了不同的舞台效果,让整体的演出更加丰富多彩。
就是自旋量子数,听起来有点神秘对吧?它就是电子自身的旋转状态。
想象一下,电子就像个小陀螺,不停地旋转。
这个旋转的方向可以是顺时针或者逆时针,仿佛给了电子一种独特的个性。
自旋量子数的存在让电子在微观世界中显得更加活泼。
正因为这个小家伙的存在,电子才能在整个原子中找到自己的位置,和其他电子一起和谐共存。


量子力学一、量子力学的实验基础1.卢瑟福实验:a 粒子的质量远大于电子,两者的质心几乎就在a 粒子上。
虽然二体系统有内部的相互作用,但它们的质心是自由运动的,故电子对a 粒子的作用不影响a 粒子的运动。
a 粒子散射时,原子的正电荷部分受到反冲力,导致薄片晶格的振动。
2.原子光谱是原子内部电子运动情态的反映。
光谱项T。
氢原子光谱的频谱是离散的,且不是连续谱亦非由基频和倍频构成的频谱,这个性质直接来源于原子中电子运动具有能级的特性以及光具有粒子性。
3.光电效应实验中无法用经典物理学解释的现象:(1)反向遏止电压和入射光强无关;(2)反向遏止电压和入射光的频率呈线性关系;(3)电子逸出相对于光的照射而言几乎无时间延迟。
4.爱因斯坦方程:φω−=ℏT ,表示金属电子吸收一份光能量而获得T 的动能逸出金属,φ为脱出功,与材料有关。
5.光子:(1)博特实验(W.Bothe experiment)表明每份光能量是集中的;(2)贾诺希实验(L.Janossy experiment)表明每份光子落在何处是偶然事件,也就是说电磁波是光子的概率幅波。
(量子力学有整体性,光子的运动受到整个环境的影响。
)6.爱因斯坦关系:ωℏℏ==E k p ,。
P 和E 描写光子,k 和ω描写单色波。
【注意:说光有波粒二象性是沿用经典物理的语言。
光有波动性,是指光的运动没有轨道;光具有粒子性,是指光与电子相互作用时像粒子那样,而不像经典的波场那般。
】7.康普顿(pton)效应应用了“静电子模型”(靶原子的外层电子)。
康普顿波长:�ℏA mc0242621.02==Λπ。
计算过程中考虑了能量守恒(相对论力学)和动量守恒(矢量力学),2sin 22θλΛ=∆。
(1)对于原子内层的“束缚电子”,由于它们与原子核束缚的紧,应作为一个整体看待,“静电子模型”不成立。
光子撞不动整个原子,只是自己改变方向。
因此实验中出现了0=∆λ的成分。
(2)对于可见光,能量和动量小,靶原子的外层电子应作束缚电子看待,“静电子模型”不成立。
量子力学知识点量子力学是20世纪初发展起来的一种物理学理论,它主要描述微观粒子如原子、电子等的行为。
量子力学的核心概念包括波函数、量子态、不确定性原理、量子纠缠等。
以下是量子力学的一些主要知识点总结:1. 波函数:量子力学中,一个粒子的状态由波函数描述,波函数是一个复数函数,其模的平方给出了粒子在某个位置被发现的概率密度。
2. 薛定谔方程:这是量子力学中描述粒子波函数随时间演化的基本方程。
薛定谔方程是量子力学的核心,它是一个偏微分方程,能够预测粒子的行为。
3. 量子态:量子系统的状态可以由波函数表示,这些状态是离散的,并且遵循一定的量子数规则。
4. 量子叠加原理:量子系统可以同时处于多个可能的状态,这些状态的叠加构成了系统的总状态。
5. 不确定性原理:由海森堡提出,指出无法同时精确测量粒子的位置和动量。
这是量子力学与经典力学的一个根本区别。
6. 量子纠缠:两个或多个粒子可以处于一种特殊的相关状态,即使它们相隔很远,一个粒子的状态改变也会立即影响到另一个粒子的状态。
7. 量子隧道效应:粒子有可能穿过一个经典力学中不可能穿越的势垒,这是量子力学中的一个非直观现象。
8. 波粒二象性:量子力学中的粒子既表现出波动性也表现出粒子性,这种性质由德布罗意提出。
9. 量子力学的诠释:包括哥本哈根诠释、多世界诠释等,不同的诠释试图解释量子力学中观察到的现象。
10. 量子计算:利用量子力学原理进行信息处理的技术,量子计算机能够执行某些特定类型的计算任务,速度远超传统计算机。
11. 量子纠缠与量子通信:量子纠缠是量子通信的基础,可以实现安全的信息传输。
12. 量子退相干:量子系统与环境相互作用,导致量子态的相干性丧失,是量子系统向经典系统过渡的过程。
13. 量子场论:将量子力学与相对论结合起来,描述粒子的产生和湮灭过程。
14. 量子信息:研究量子系统在信息处理中的应用,包括量子密码学、量子通信等。
15. 量子测量:量子力学中的测量问题涉及到波函数的坍缩,即测量过程会导致量子态的不确定性减少。
nlm三个量子数的取值范围相互关系和物理意义量子力学中,电子的状态可以用三个量子数来描述,分别是主量子数(n)、角量子数(l)和磁量子数(m)。
这些量子数的取值范围相互关系复杂且存在物理意义。
在本文中,我将简要介绍这些量子数的取值范围和它们之间的关系及其物理意义。
主量子数(n)主量子数(n)是一个正整数,用来描述电子的能量状态。
n的取值范围是1、2、3、4...,没有上限。
n越大,对应能量越高,并且电子离原子核越远。
每一电子壳层有不同的n值,例如第一壳层的n值为1,第二壳层的n值为2,以此类推。
角量子数(l)是与角动量有关的量子数。
l的取值范围是0、1、2、3...、(n-1),其中n为主量子数。
角量子数l规定了电子绕原子核运动时的动量角动量和其运动轨道形态。
当l=0时,电子处于与原子核距离最近的s轨道,这种轨道形状呈球形,称为原子的s壳层;当l=1时,电子位于p轨道,它在三维空间中形成一个双叶片状的结构;当l=2时,电子位于d轨道,它在三维空间中形成更为复杂的四叶花瓣状结构,以此类推。
磁量子数(m)描述了运动电子在轨道上的空间定向,可以理解为轨道上的电子所在位置相对于磁场的方向。
它的取值范围是-l,-l+1,...0,...l-1,l。
例如,当l=1时,m的取值可以是-1、0或+1,分别代表电子在p轨道上相对于一个磁场可以处于x、y或z方向。
如果l=2,则m可取-2、-1、0、1或+2。
相互关系和物理意义每个电子的状态都可以用这三个量子数来描述。
它们的取值范围和关系有以下规律:1. 主量子数和角量子数的关系:根据定义,角量子数的取值范围是从0到n-1,因此每个主量子数对应一定数量的角量子数。
例如,当n=1时,只有l=0,因此只有一种可能的电子构型(1s)。
当n=2时,l的取值可以是0或1,因此有两个可能的电子构型(2s和2p)。
2. 角量子数和磁量子数的关系:有多少个l值,就有多少个可能的m值。
量子力学中的量子态与量子数量子力学是研究微观粒子行为的物理学分支,它提出了独特的数学
框架,用于描述微观世界中的粒子行为。
在量子力学中,一个粒子的
状态可以由其量子态和量子数来完整描述。
本文将介绍量子态与量子
数的概念,并探讨它们在量子力学中的重要性。
一、量子态与量子数的概念
量子态是描述微观粒子状态的数学概念。
在量子力学中,一个粒子
的量子态可以用波函数来表示。
波函数是一个数学函数,可以描述粒
子的位置、动量和其他物理性质。
根据波函数的性质,一个粒子的量
子态可以是定态或叠加态。
定态是指一个粒子的波函数处于一个确定的状态,具有确定的能量、动量和其他物理量。
定态可以通过量子数来描述,量子数代表了一个
物理量的取值。
例如,对于一个具有自旋的粒子,其自旋量子数可以
是+1/2或-1/2。
叠加态是指一个粒子的波函数可以处于多个态之间的叠加状态。
在
叠加态中,粒子处于多个状态的叠加,它们的概率振幅可以正相加或
负相加,产生干涉效应。
叠加态的概念在双缝实验等实验中得到了验证。
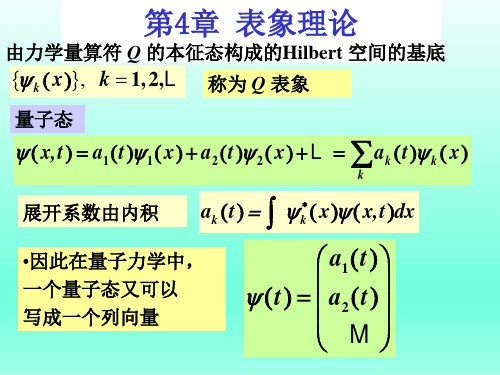
二、量子态的表示
量子态可以用矢量表示,这是量子力学中常用的表示方法。
一个粒
子的量子态可以用一个希尔伯特空间中的矢量表示,这个空间称为态
空间。
态空间是一个复数线性空间,其维度与粒子的状态数有关。
对于一个粒子的定态,可以用一个独立的态矢量表示。
例如,对于
一个自旋为1/2的粒子,其量子态可以用两个正交的矢量表示,分别代表自旋向上和自旋向下的态。
叠加态可以用态矢量的叠加表示。
例如,对于一个粒子的自旋,如
果它处于自旋向上和自旋向下的叠加态,可以用两个矢量的线性组合
来表示。
这个线性组合需要满足归一化条件,使得概率振幅的平方之
和为1。
三、量子数与测量
量子数是描述量子物理系统某个物理量取值的标记。
在量子力学中,物理量的取值是离散的,而不是连续的。
每个物理量都对应着一个或
多个可观测值,并且每个可观测值都对应着一个量子数。
量子数可以用来描述系统的宇称、自旋、角动量等性质。
例如,对
于电子,它的自旋量子数可以是+1/2或-1/2。
量子数的取值通过测量得到,测量会导致量子态的坍缩,即从叠加态坍缩到定态。
四、量子态的演化与相互作用
在量子力学中,量子态随着时间的演化而变化。
量子态的演化由薛
定谔方程描述,它可以用来计算波函数的时间演化。
薛定谔方程是一
个偏微分方程,它描述了波函数随时间的变化规律。
量子态的演化还可以由相互作用描述。
在量子力学中,粒子之间的
相互作用可以用哈密顿量来表示。
哈密顿量包含了粒子之间的相互作
用势能,它会影响粒子的量子态演化过程。
五、量子态的纠缠与量子计算
量子态的纠缠是量子力学的一种独特现象。
当两个或多个粒子处于
纠缠态时,它们之间的量子态是相互关联的,无论它们之间的距离有
多远。
纠缠态的应用包括量子通信、量子计算和量子隐形传态等领域。
量子计算是利用量子力学的特性进行计算的一种新型计算模式。
在
传统的计算机中,信息以比特的形式存储和处理,而在量子计算中,
信息以量子比特或量子态的形式存储和处理。
量子计算的优势在于可
以进行并行计算和量子纠错,对于某些特定问题有着巨大的计算优势。
六、结论
量子态与量子数是量子力学中重要的概念,它们用于描述微观粒子
的状态和性质。
量子态可以用矢量表示,其中定态和叠加态可以描述
粒子的确定状态和多态叠加状态。
量子数用于标记物理量的取值,并
通过测量来确定。
量子态的演化和相互作用描述了粒子随时间变化和相互影响的规律。
量子态的纠缠和量子计算则展示了量子力学的独特性质和潜在应用。
通过深入理解量子态与量子数,我们能更好地掌握和应用量子力学的
原理和方法。