正方体的展开与折叠规律方法
- 格式:docx
- 大小:280.23 KB
- 文档页数:4

巧记口诀确定正方体表面展开图正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明:四方成线两相卫,六种图形巧组合;跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图:一、四方成线两相卫,六种图形巧组合(1) (2) (3) (4)(5) (6)以上六种展开图可归结为四方连线,即块在四个方块的上下两侧,共六种情况。
二、跃马失蹄四分开(1) (2) (3) (4)以上四种情况可归结为五个小方块组成“三二相连”的基本图形(如图),另外一个小方块的位置有四种情况,即图中四个小方块中的任意一个,这一图形有点像失蹄的马,故称为“跃马失蹄”。
三、两两错开一阶梯这一种图形是两个小方块一组,两两错开,像阶梯一样,故称“两两错开一阶梯”。
四、对面相隔不相连这是确定展开图的又一种方法,也是确定展开图中的对面的一种方法。
如果出现三个相连,则1号面与3号面是对面,中间隔了一个2号面,并且是对面的一定不相连。
五、识图巧排“7”、“凹”、“田”(1) (2) (3)这里介绍的是一种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正方体展开图的,因为图中1号面与3号面是对面,3号面又与5号面是对面,出现矛盾。
如果图中出现象图(2)中的“田”形结构的图形不可能是正方体展开图的,因为同一顶点处不可能出现四个面的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正方体展开图的,因为如果把该图形折叠起来将有两个面重合。
例1.下面的平面图形中,是正方体的平面展开图的是( )解析:本题可用“识图巧排 ‘7’、‘田’、‘凹’”来解决。
A 、D 都有“凹”形结构,B 有“田”形结构,故应选C例2.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如右图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示.) 解析:本题可用“跃马失蹄四分开”来解决。

图形的展开一、正方形展开第一类,中间四连方,两侧各一个,共六种。
第二类,中间三连方,两侧各有一、二个,共三种。
第三类,中间二连方,两侧各有二个,只有一种。
第四类,两排各三个,只有一种。
以上是一个立方体的11种平面展开图。
虽然一个立方体可能还会有更多的展开图,但从上面这些图中,我们基本可以看出它的规律。
1、一个立方体的表面展开图必定6个正方形连接组成,缺一不可,多一个也不对,展开图折叠后,必须覆盖立方体的6个表面。
2、展开图沿横、竖方向展开时,一个方向必定由4个正方形组成,而另一个方向必须是3个正方形(一种例外)。
3、相对的面不相连。
正方体展开头记忆口诀:正方体盒巧展开,六个面儿七刀裁;十四条边布周围,十一类图记分明;四方成线两相卫,六种图形巧组合;跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
二、长方体展开典型例题1、看左图回答问题.(1)A面与_____面相对; (2)B面与_____面相对; (3)C面与_____面相对.答案:D E F解析:这是一个长方体的展开图,把它折叠成长方体时,(1)A面与D面相对;(2)B面与E面相对;(3)C面与F面相对.解:(1)A面与D面相对;(2)B面与E面相对;(3)C面与F面相对;故答案为:D,E,F.2、下面各图中,是正方体的平面展开图的是_A_C___;是长方体的平面展开图的是__B__D_.长方体和长方体的关系如图所示:三、圆柱体展开图(侧面+两个同样大小的圆)(可以看作是一个矩形(长方形,正方形)旋转得到的。
侧面展开有三种图形:(正方形,长方形,平行四边形)一般展开图四、圆锥展开(一个扇形+一个圆)1、从侧面看是一个等腰三角形。
2、直角三角形以直角边旋转一周得到一个圆锥体。
3、从上面看一个圆锥体,看到的是一个圆。
数与图探索规律探索规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。

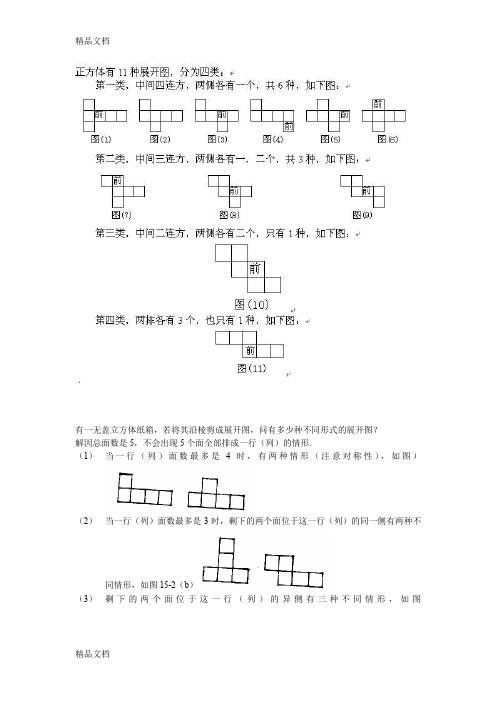
有一无盖立方体纸箱,若将其沿棱剪成展开图,问有多少种不同形式的展开图?解因总面数是5,不会出现5个面全部排成一行(列)的情形.(1)当一行(列)面数最多是4时,有两种情形(注意对称性),如图)(2)当一行(列)面数最多是3时,剩下的两个面位于这一行(列)的同一侧有两种不(3)剩下的两个面位于这一行(列)的异侧有三种不同情形,如图(4)当一行(列)的面数最多是2时,仅一种情形,如图所示.总数为2+2+3+1=8种,即有8种不同的展开形式.探究正方体的展开图将一个正方体的表面沿某些棱剪开,展成一个平面,共有哪些不同的图形呢?要搞清这个问题,最好是动手实践,比如找一些正方体纸盒,沿着棱按不同方式将其剪开(但不要剪断,六个面要通过边连在一起),展成平面,再观察、对比一下不同形状的图形有哪些。
如果不容易找到足够的正方体纸盒,还可以找一些不太厚、易折叠的正方体纸板,利用逆向思维,先猜测正方体展开图会有哪些不同形状,并将它们画在纸板上,再将周围多余部分剪去,然后沿所画直线直行折叠,看看哪些图形纸板可以折叠成正方体。
这种探究方法虽然有点麻烦,但操作简便易行,快速有效。
事先可多画一些纸板(六个正方形边与边对齐,任意连接成不同的平面图形),经过逐个验证,记录下所有可以折叠成正方体的图形,再将这些图形分类,总结并寻找出其中的规律。
那么,沿棱剪开展开一个正方体,究竟有哪些不同的形状呢?如果不考虑由于旋转或翻折等造成相对位置的不同,只从本质上讲,有以下三类共11种。
一、“141型”(共6种)特点:这类展开图中,最长的一行(或一列)有4个正方形(图1~图6)。
理解:有4个面直线相连,其余2个面分别在“直线”两旁,位置任意。
二、“231型”与“33型”(共4种)特点:这类展开图中,最长的一行(或一列)有3个正方形(如图7~图10)。
理解:在“231型”中,“3”所在的行(列)必须在中间,“2”、“1”所在行(列)分属两边(前后不分),且“2”与“3”同向,“1”可以放在“3”的任意一个正方形格旁边,这种情况共有3种,而“33型”只有1种。

巧记口诀确定正方体表面展开图6个相连的正方形组成的平面图形,经折叠能否围城正方体问题,是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手,现将确定正方体展开图的方法以口诀的方式总结出来,供大家参考:正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明:四方成线两相卫,六种图形巧组合;跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图:一、四方成线两相卫,六种图形巧组合(1)(2)(3)(4)(5)(6)以上六种展开图可归结为四方连线,即另外两个小方块在四个方块的上下两侧,共六种情况。
二、跃马失蹄四分开(1)(2)(3)(4)以上四种情况可归结为五个小方块组成“三二相连”的基本图形(如图),另外一个小方块的位置有四种情况,即图中四个小方块中的任意一个,这一图形有点像失蹄的马,故称为“跃马失蹄”。
三、两两错开一阶梯这一种图形是两个小方块一组,两两错开,像阶梯一样,故称“两两错开一阶梯”。
四、对面相隔不相连这是确定展开图的又一种方法,也是确定展开图中的对面的一种方法。
如果出现三个相连,则1号面与3号面是对面,中间隔了一个2号面,并且是对面的一定不相连。
五、识图巧排“7”、“凹”、“田”(1) (2) (3)这里介绍的是一种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正方体展开图的,因为图中1号面与3号面是对面,3号面又与5号面是对面,出现矛盾。
如果图中出现象图(2)中的“田”形结构的图形不可能是正方体展开图的,因为同一顶点处不可能出现四个面的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正方体展开图的,因为如果把该图形折叠起来将有两个面重合。
现举例说明:例1.(2004海口市实验区)下面的平面图形中,是正方体的平面展开图的是( )解析:本题可用“识图巧排 ‘7’、‘田’、‘凹’”来解决。

将一个正方体地表面沿某些棱剪开,展成一个平面,共有哪些不同地图形呢?要搞清这个问题,最好是动手实践,比如找一些正方体纸盒,沿着棱按不同方式将其剪开(但不要剪断,六个面要通过边连在一起),展成平面,再观察、对比一下不同形状地图形有哪些.个人收集整理勿做商业用途如果不容易找到足够地正方体纸盒,还可以找一些不太厚、易折叠地正方体纸板,利用逆向思维,先猜测正方体展开图会有哪些不同形状,并将它们画在纸板上,再将周围多余部分剪去,然后沿所画直线直行折叠,看看哪些图形纸板可以折叠成正方体.这种探究方法虽然有点麻烦,但操作简便易行,快速有效.事先可多画一些纸板(六个正方形边与边对齐,任意连接成不同地平面图形),经过逐个验证,记录下所有可以折叠成正方体地图形,再将这些图形分类,总结并寻找出其中地规律.个人收集整理勿做商业用途那么,沿棱剪开展开一个正方体,究竟有哪些不同地形状呢?如果不考虑由于旋转或翻折等造成相对位置地不同,只从本质上讲,有以下三类共种.个人收集整理勿做商业用途一、“型”(共种)特点:这类展开图中,最长地一行(或一列)有个正方形(图~图).理解:有个面直线相连,其余个面分别在“直线”两旁,位置任意.二、“型”与“型”(共种)特点:这类展开图中,最长地一行(或一列)有个正方形(如图~图).理解:在“型”中,“”所在地行(列)必须在中间,“”、“”所在行(列)分属两边(前后不分),且“”与“”同向,“”可以放在“”地任意一个正方形格旁边,这种情况共有种,而“型”只有种.个人收集整理勿做商业用途三、“型”(只有种)特点:展开图中,最多只有个面直线相连(图).评注:⑴将上面个图中地任意一个,旋转一定角度或翻过来,看上去都与原图似有不同,但这只是图形放置地位置或方式不同.实际上,它与原图能够完全重合,不能算作一个独立地新图,而从上面个图中任取两个,不论怎样操作(旋转、翻折、平移等),它们都不可能完全重合,即彼此是独立地、不同地图形.个人收集整理勿做商业用途⑵对于由大小一样地六个正方形通过边对齐相连组成地平面图,如果图中含有“一”字型、“”字型、“田”字型、“凹”字型,就一定不能折成正方体.概括地说,只要不符合上述“”、“”和“”、“”地特点,就不能折成正方体.如图,如果将其看作“”型,那么,无论怎么看,“”和“”都不是同向,故不能折成正方体.其实,它属于“”(或“”)型.个人收集整理勿做商业用途。
折成正方体的规律
将一个正方形纸张折成正方体的规律如下:
1. 将正方形纸张折叠成两半,使两个对角线对齐。
2. 沿着折痕将下方的一角折向上方,使顶点与纸边对齐。
3. 将纸张快速展开,变成一个直角三角形。
4. 将直角边再次对折,使纸张变成一个等腰直角三角形。
5. 将纸张最长边沿着对角线线对齐,使纸张变为长方形。
6. 将长方形的下方翻折至上方,使两条短边对齐。
7. 最后,将纸张的两侧向内折叠,使纸张形成一个正方体。
通过以上步骤,可以将一个正方形纸张折成一个正方体。
正方体的展开与折叠总共有四类情况,分别是1,4,1型;1,3,2型;2,2,2型和3、3型。
第一类:(1,4,1型),共6种。
记忆口诀:中间四个面,上下各一面。
第二类:(1,3,2型),共3种。
记忆口诀:中间三个面,一二隔河见。
第三类:(2,2,2型),共1种。
记忆口诀:中间两个面,楼梯天天见。
第四类:(3,3型),共1种。
记忆口诀:中间没有面,三三连一线。
解题技巧背一背
1、寻找正方体相对面
解题技巧:“I”型图不相连;“Z”型图在两端。
2、判断是否可以围成正方体
一线不过四(一条直线上的小正方形的个数不会超过四个);“7”、“田”、“凹”应弃之(在正方体展开图中,不会有“7”字型、“田”字型、“凹”字型)。
正方体的性质
1、正方体有有6个面,12条棱,8个顶点。
2、正方体一般指正六面体,用六个完全相同的正方形围成的立体图形叫正六面体,也称立方体、正方体。
3、且正方体的每个面都相等,展开之后的表面积也相等。