当前位置：文档之家 › 不等式的证明3(切线放缩) 高中数学课堂教学ppT课件

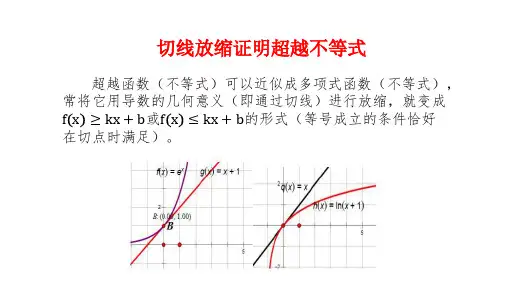
不等式的证明3(切线放缩) 高中数学课堂教学ppT课件

  • 格式：ppt
  • 大小：559.50 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

第12讲 切线放缩

第12讲 切线放缩

第12讲切线放缩本讲义由作业帮周永亮老师（白哥）独家编撰，侵权必究知识导航1．两个常见的切线放缩公式（1） ;（2）2．切线放缩在求导过程中的应用在求导的过程中，我们很多时候需要求二次导，乃至三次或多次，其实，对于几乎所有的问题，如果我们能够很好的利用放缩的技巧的话，我们最多只需要求二次导就可以了.3．切线放缩在数列不等式中的应用数列不等式有很多种，其中有一种最常见的叫做“拆和之函数放缩”，而这个函数，一般都是由我们这两个最常见的切线放缩公式演变而来的．知识札记例2（★★★☆☆）（2018·河北石家庄市一模）已知函数（）在处的切线方程为．（1）求，．（2）若，证明：．例1（★★★☆☆）（2018·河北保定市模拟【文】）已知函数，函数，证明：当且时，．考点1 切线放缩的基础应用注：本讲对于切线放缩公式的应用，都写了易证，但在正常考试中，需要同学们证明.经典例题例5（★★★★☆）（2017·黑龙江大庆市期中【文】）已知，求证：当时，恒成立．例4（★★★★☆）已知函数，在点处的切线方程为．（1）求，；（2）证明：．例3（★★★★☆）证明：．考点2 切线放缩拓展应用例8（★★★★☆）证明：当，时，．考点3 切线放缩在数列不等式中的应用例7（★★★★★）证明：．例6（★★★★★）（2018·江苏泰州市期末【文】）已知函数，（，），当，时，求证：．例11（★★★★☆）（2013·安徽合肥市月考【理】）设函数（），数列满足：，（）．（1）求数列的通项公式；（2）求证：．例10（★★★★☆）（2018·辽宁月考【文】）求证：（）．例9（★★★★☆）（2016·湖南模拟【理】）证明不等式：（）．课后练习练1（★★★☆☆）（2017·贵州一模【文】）已知函数，证明：对任意，成立．练2（★★★★★）（2017·重庆渝中区模拟【理】）已知函数（为实数，为自然对数的底数），曲线在处的切线与直线平行．（1）求实数的值；（2）证明：当时，．练3（★★★★☆）（2016·全国卷）求证：当且时，．。

《不等式的证明》PPT课件

《不等式的证明》PPT课件
2
∵-1<a<1,-1<b<1, ∴(a-b)2≥0, 1+ab>0， 1-a2>0,1-b2>0, 1-ab>0. 所以，(1-a2)(1-b2)(1-ab)>0,
(a-b)2(1+ab)≥0.
1 1 2 故 2 2 1 a 1 b 1 ab
证明二:分析法 证明三:综合法 ∵a2+b2≥2ab, ∴-a2-b2≤-2ab. 从而0<1+a2b2-a2-b2≤1+a2b2-2ab=(1-ab)2,1-ab>0. 1 1 1 1 2 2 2 2 1 a 1 b 1 a 1 b2
证明二：(分析法)
证明三：(综合法)
一般地,对任意实数ai,bi(i=1,2,3, …,n),都有:
(a12+a22+…+an2)(b12+b22+…+bn2)
≥(a1b1+a2b2+…+anbn) 2.(柯西不等式)
【例4】设-1<a<1,-1<b<1,求证: 1 1 2 . 2 2 1 a 1 b 1 ab
证明二：比较法（作商） ∵a2+b2≥2ab，
2 2 3 3 ( a b )( a b ab) a b ∴ 2 2 ab(a b) a b ab 2 2 a b ab 2ab ab 1 ab ab
又a>0，b>0，所以ab>0，
故a3+b3≥a2b+ab2.
证明一:比较法(作差)
1 1 2 2 2 1 a 1 b 1 ab
(1 b 2 )(1 ab) (1 a 2 )(1 ab) 2(1 a 2 )(1 b 2 ) (1 a 2 )(1 b 2 )(1 ab)

高中数学 放缩法与反证法证明不等式课件 新人教A选修45

高中数学 放缩法与反证法证明不等式课件 新人教A选修45
abc
(c a )2 2
小结
• 在证明不等式过程中，有时为了证明 的需要，可对有关式子适当进行放大或缩 小，实现证明。例如：
• 要证b<c,只须寻找b1使b<b1且b1≤c(放大) • 要证b>a,只须寻找b2使b>b2且b2≥a(缩小)
• 这种证明方法,我们称之为放缩法。 • 放缩法的依据就是定理2（传递性性质）
•
再寻求矛盾，推翻假设，从而证明结
•
论成立的方法。
又∵0 < a, b, c < 1 ∴0(1a)a(1a 2)a21 4
同理： (1 b)b 1 (1 c)c 1
4
4
1
以上三式相乘： (1 a)a•(1 b)b•(1 c)c≤ 64
与①矛盾∴结论成立
放缩法
• 在证明不等式过程中，有时为了证明 的需要，可对有关式子适当进行放大或缩 小，实现证明。例如：
ab .
1a b 1a b 1 a 1 b
法３：函数的方法
例4、巳知：a、b、c∈ R ，求证：
a 2 a b b 2a 2 a c c 2 a b c
略
解 a2 ab b2 a2 ac c2
ห้องสมุดไป่ตู้
(b a )2 3 a 2 (c a )2 3 a 2
24
24
(b a )2 2
•11、凡为教者必期于达到不须教。对人以诚信，人不欺我;对事以诚信，事无不成。 •12、首先是教师品格的陶冶，行为的教育，然后才是专门知识和技能的训练。 •13、在教师手里操着幼年人的命运，便操着民族和人类的命运。2022/1/182022/1/18January 18, 2022 •14、孩子在快乐的时候，他学习任何东西都比较容易。 •15、纪律是集体的面貌，集体的声音，集体的动作，集体的表情，集体的信念。 •16、一个人所受的教育超过了自己的智力，这样的人才有学问。 •17、好奇是儿童的原始本性，感知会使儿童心灵升华，为其为了探究事物藏下本源。2022年1月2022/1/182022/1/182022/1/181/18/2022 •18、人自身有一种力量，用许多方式按照本人意愿控制和影响这种力量，一旦他这样做，就会影响到对他的教育和对他发生作用的环境。 2022/1/182022/1/18

切线放缩证明超越不等式

切线放缩证明超越不等式
f ( x) 0成立
（3）难点在于合理拆分函数，寻找它们的斜率相等的公
切线隔板----以直代曲，
注：切线放缩的一般原则：（1）先对数后指数；（2）合理选用放缩
（一般用得最多指数对数加减）
技能拓展：常见超越不等式谱系图

≥1++
2

≤


以
2
换

以

换

以 −≥
1 换
1
2 证明：当 ≥ 时， ≥ 0.

注：含参函数有时需要根据函数特征将原函数进行适当放缩.
【题2】 2018 ∙ 新课标Ⅲ ∙ 文 已知函数 =
2 证明：当 ≥ 1时， + ≥ 0.
2 +−1

注：复杂形式的函数需要将函数适当转化后再进行放缩.
课堂小结
1.切线放缩法实质是以直（切线）代曲ቤተ መጻሕፍቲ ባይዱ原函数）；
2.切线放缩法中常用的两个定理必须先证明后使用；
3.证明流程为：求切线—构造差函数—证明差函数恒正（负）
--原不等式成立．
4.对于较为简单的导数试题，往往只涉及到一次切线放缩，但是
有些压轴试题涉及到两次不同的切线放缩．
+）
注意事项：
g ( x) min g (0) 0,
（1）适用于凹函数与凸函数且它们的凹凸性相反的
问题（需合理拆成两个函数）----数形结合；
g ( x) 0,
（2）两函数有斜率相同的切线，通过引入一个中间量
又 等号不能同时取到
分别证明两个不等式成立，然后利用传递性就可以了；
切线放缩证明超越不等式
超越函数（不等式）可以近似成多项式函数（不等式），

不等式ppt课件

不等式ppt课件

不等式的应用场景
01
02
03
04
数学领域
解决各种不等关系的问题，如 最值、范围等。
物理领域
描述物理现象和规律，如力学 、电磁学等。
经济领域
描述经济变量之间的关系，如 价格、成本等。
实际生活
描述日常生活中的不等关系， 如时间、距离等。
02
不等式的类型
算术平均数与几何平均数的不等式
总结词
算术平均数与几何平均数的不等式是一种基本的不等式，它反映了平均值与方 差之间的关系。
实际应用定义
描述实际生活中两个量之 间的不等关系，如价格、 距离等。
不等式的性质
加法单调性
即同向不等式相加，不等号不 改变方向。
反身性
任何实数都大于它本身。
传递性
如果a>b，b>c，则a>c。
乘法单调性
即不等式乘以一个正数，不等 号不改变方向；乘以一个负数 ，不等号改变方向。
非空性
不等式的两边都可以取无穷大 或无穷小。
03
不等式的证明方法
利用导数证明不等式
总结词
导数是一阶导数的简称，它描述了函数在某一点的变化率， 可以用来判断函数的单调性和凹凸性，从而帮助我们证明不 等式。
详细描述
首先，我们需要找到不等式两边的函数，然后求导，通过比 较导数值的大小来判断函数的单调性，从而得出不等式的证 明结论。
利用拉格朗日中值定理证明不等式
详细描述
柯西不等式表明，对于任何实数x 和y，都有$x^2+y^2 \geq 2xy$ ，当且仅当x=y时等号成立。这 个不等式在解决一些最优化问题 时非常有用。
排序不等式
总结词
排序不等式是一种基于排序原理的不 等式，它反映了有序实数之间的差值 与乘积之间的关系。

导数证明单变量不等式ppt课件

导数证明单变量不等式ppt课件

证明： 易知，不等式中x (0,1) (1, )
当0 x 1时，易证ex x 1 0，ln x x 1 0
所以 e x
x1 1
x1
ln x
当x 1时，只需证ex ln x x2 1
令f ( x) e x ln x x2 1, x 1
求导得f ( x) (ln x 1 )e x 2x, x 1 x
2e x )
2e x
令t 1+2e x ,只证ln t t 1
换元后再构造
1
方法梳理
FANGFASHULI
三、切线放缩法证明
步骤 对不等式切线放缩
构造函数
导数研究函数最值、单调性 获得不等式结论
例3. 求证：xex x ln x 1 0
证明：因为xe x x ln x 1 0 e xln x x ln x 1 0 令t x+ ln x,只需证et t 1 0， 构造f (t ) et t 1，
易证，当x 1时，ln x 1 1 x
所以f ( x) (ln x 1 )e x 2x e x 2x x
令g( x) e x 2x, x 1， 求导得g( x) e x 2 e 2 0, x 1
所以g( x)在区间(1, )上为增函数，因此g( x) g(1) e 2 0
y ex x,
常见有界函数
y ln x x,
y xe x , y x ln x,
ex y ,
x y ln x ,
x
x y ex y x
ln x
1
方法梳理
FANGFASHULI
六、隐零点法证明
步骤 构造函数
二 阶求导
导函数隐零点的存在性 整体代换

不等式的证明ppt课件


不等式证明——解答题13
1 1 证明 : f ( x1 ) f ( x2 ) (loga x1 loga x2 ) 2 2 x1 x2 x1 x2 loga x1 x2 , f ( ) loga 2 2 1 x1 x2 当a 1时， f ( x1 ) f ( x2 ) f 2 2 1 x1 x2 当0 a 1时， f ( x1 ) f ( x2 ) f ( ) 2 2
2 2 (b c) (c a ) 2 ( a b c ) 2 2 2
13.已知f ( x) loga x(a 0且a 1), 若x1 , x2 R* , 1 x1 x2 比较 f ( x1 ) f ( x2 )与f ( )的大小，并证明 . 2 2
2
a b 15.已知a b 0, 求证：
不等式证明——解答题15
2
8a
ab ab 2
证明：要证明原不等式成立
a b 8a 2 a b a b 只需证明： 2 2 a 2
a b 只要证明：
2


2
只需证明： 2 ab ຫໍສະໝຸດ a b a b 0 2 ab a b成立
m 0 此不等式无解 4 4m(m 1) 0
不存在实数m，能使不等式恒成立
恒成立问题——解答题11（1）
(2)若对于m 2,2不等式恒成立，求实数 x的范围
(2)原不等式变为： m( x2 1) 2x 1 0
令f (m) m( x 1) 2 x 1
16 14.已知a b 0, 求证：a 16 b( a b)
2
不等式证明——解答题14

20181207放缩法证明不等式

2
（2）若 f (x) 在定义域内为增函数，求a 的取值范围；
（3）设 g(x) f (x) x2 1 ，当a 1 时，
求证：① g(x) 0在其定义域内恒成立；
求证：②
ln 22 ln 32 22 32

ln n2 n2

2n2 n 1
2n 1
。
例4. 证明： x2ex－lnx＞1 .
O
1
x
x 1
x 1
x
≤lnx≤ x ≤ 1
y x
y
2
y＝x－1
y＝lnx
y x1 x
O
1
x
x1 ≤
x 1 x≤lnx≤ x－1
x
2
(0＜x≤1)
6．（本小题满分 14 分）设函数 f (x) ln x x2 ax 。 （1）若 f (x) 在x 1 处取得极值，求a 的值；
O
1
x
方法三：
方法四：
又由
f '(x0)＝0
得：( x02
2 x0 ) ex0

1 x0

0
e x0

1 x02 ( x0
2)
x02 e x0

1 x0 2
f (x)≥ f (x0)＝
x02ex0 ln x0 ＝
1 x0 2 ln x0
构造函数 h(x)＝
1 ln x x2
,
x


放缩法证明不等式
放缩的方法
1。运用基本不等式和常见结论进行放缩 2。运用切线方程进行放缩 3。运用题目给出的不等式进行放缩。 4。运用参数范围进行放缩
切线放缩原理及常见的切线放缩
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

法二：分离参数后考察没有零点
另例：已知函数f (x) x ln x a(x 1)(a 0)在区间(0, 2)有一个零点， 求a的取值范围. 解：令f (x) 0, f (1) 0, x 1是函数在区间(0, 2)的一个零点, 满足题意a 0
当x
1时,由a
x ln x x 1
, 令 y1
x 0 , y2 0; x 1 , y2 1(如下); x 2 , y2 2 ln 2
(洛必达法则lim f (x) 0 lim f (x) 即x 1 , lim x ln x = lim ln x 1 1);
g(x) 0
g ( x)
x 1
1
第二种处理：
切线不等式x
1
ln
x，从而直接判断
a,
y2
x ln x x 1
y2
(1
ln
x)(x 1) (x 1)2
x ln
x
ln x x 1 (x 1)2
第一种处理：二次求导g(x) ln x x 1, g(x) 1 1 x 1
x
x
g(x)在区间(0,1) (1, ) , g(x)min g(1) 0
g(x) 0,即有y2 0, y2在区间(0,1), (1, ) 现在画图了，
x f (x)在区间(0, 2)上单调递增 当x 0+，f (x) ，故只需讨论f (2) 1+ ln 2 a的正负即可 当f (2) 1+ ln 2 a 0,即a 1+ ln 2故f (x)在(0, 2)上单调递减，又 f (1)=0 f (x)有唯一零点1，且f (2)=2 ln 2 a பைடு நூலகம்0即a 2 ln 2 综上：a 2 ln 2 当f (2) 1+ ln 2 a 0,即a 1+ ln 2,故f (x)在(0, 2)上有唯一零点x0， 故f (x0 )=0，1+ ln x0 a=0，又 f (1)=0a=1 综上可得：a=1，a 2 ln 2
注：切线放缩的一般原则：（1）先对数后指数；（2）合理选用 放缩（一般用得最多指数对数加减）
例：已知函数f (x) ex ln(x 2), 证明f (x) 0.
证明： ln(x 2) x （1 x -1时取等号）
f (x) ex ln(x 2) ex (x 1)
令g(x) ex (x 1)
g(x) ex 1 0 x 0
g(x)在（-，0） ，（0，+）
g(x)min g(0) 0, g(x) 0, 又 等号不能同时取到
注：采用切线不等式， 还是需要用构造差函数 进行最值证明。
f (x) 0成立
法一：单调性讨论法
解： f (x) x ln x a(x 1) f (x) 1+ ln x a，f (x) 1 0
数学课安排
1. 不等式的证明3 2. 切线放缩法（网课期间不讲）
学习目标
1.会对函数进行重新构建与切线不等式的应用 2. 求函数的最值要精准熟练
法一，隐零点问题，即零点求不出来，但存在零点（代数法证明）
一、切线不等式的介绍
法二，公切线隔离法（几何证明法） 也称为：“切线放缩”
注：（1）适用于凹函数与凸函数且它们的凹凸性相反的 问题（拆成两个函数）； （2）两函数有斜率相同的切线，这是切线放缩的本质。 引入一个中间量，分别证明两个不等式成立，然后利用不 等式的传递性就可以了； （3）难点在合理拆分函数，寻找它们斜率相等的切线隔板
ln x x 1 (x 1)2
0
y2 0, (0,1), (1, )
若改为（1,2）内有一个零点
另例：已知函数f (x) x ln x a(x 1)(a 0)在区间(0, 2)有一个零点， 求a的取值范围.
法三：不分离切线法
解：如图当a 1时，u(x) x ln x与v(x) x 1相切满足题意； 由x （0,2），当v(x)=a(x 1)过点（2,2ln 2）时，u(x)与v(x)有 两个交点； 要使u(x)与v(x)有一个交点，则a 2ln 2； 综上所述：a 1或a 2ln 2