2017年黑龙江省绥化市中考数学真题试题

绥化中考数学试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 2B. √2C. 0.33333D. 3.14答案：B2. 如果一个三角形的两边长分别为3和4，且第三边长是整数，那么第三边长可能是多少？A. 1B. 2C. 5D. 7答案：C3. 一个数的平方是16，那么这个数是？A. 4B. -4C. 4或-4D. 以上都不对答案：C4. 函数y=2x+3的图象经过点（0,3），那么这个函数的斜率是多少？A. 2B. 3C. 0.5D. 1答案：A5. 一个圆的直径是10cm，那么它的半径是多少？A. 5cmB. 10cmC. 15cmD. 20cm答案：A6. 下列哪个选项是方程2x-3=7的解？A. x=5B. x=3C. x=-1D. x=7答案：A7. 一个等腰三角形的底边长为6cm，腰长为5cm，那么它的高是多少？A. 4cmB. 3cmC. 2cmD. 1cm答案：B8. 一个数的立方是-27，那么这个数是？A. 3B. -3C. 3或-3D. 以上都不对答案：B9. 函数y=x^2-4x+3的顶点坐标是多少？A. (2, -1)B. (-2, -1)C. (2, 1)D. (-2, 1)答案：A10. 一个矩形的长是10cm，宽是5cm，那么它的面积是多少？A. 25cm²B. 50cm²C. 100cm²D. 200cm²答案：B二、填空题（每题4分，共20分）11. 一个数的相反数是-5，那么这个数是________。

答案：512. 一个数的绝对值是8，那么这个数可能是________或________。

答案：8 或 -813. 一个数的平方根是4，那么这个数是________。

答案：1614. 如果一个角的补角是120°，那么这个角的大小是________。

答案：60°15. 一个数的立方根是2，那么这个数是________。

文件清单：2017年黑龙江省佳木斯市中考数学试卷（含答案）2017年黑龙江省哈尔滨市中考数学试题（含答案）2017年黑龙江省鹤岗市中考数学试卷（农垦、森工用）（含答案）2017年黑龙江省齐齐哈尔市中考数学试题（含答案）黑龙江省绥化市2017年中考数学试题（含答案）黑龙江省龙东地区2017年中考数学试卷及答案（含答案）2017年黑龙江省佳木斯市中考数学试卷一、填空题（每题3分，满分30分）1．“可燃冰”的开发成功，拉开了我国开发新能源的大门，目前发现我国南海“可燃冰”储存量达到800亿吨，将800亿吨用科学记数法可表示为吨．2．在函数y=中，自变量x的取值范围是．3．如图，BC∥EF，AC∥DF，添加一个条件，使得△ABC≌△DEF．4．在一个不透明的袋子中装有除颜色外完全相同的3个白球、若干红球，从中随机摸取1个球，摸到红球的概率是，则这个袋子中有红球个．5．若关于x的一元一次不等式组无解，则a的取值范围是．6．为了鼓励居民节约用水，某自来水公司采取分段计费，每月每户用水不超过10吨，每吨2.2元；超过10吨的部分，每吨加收1.3元．小明家4月份用水15吨，应交水费元．7．如图，BD是⊙O的切线，B为切点，连接DO与⊙O交于点C，AB为⊙O的直径，连接CA，若∠D=30°，⊙O的半径为4，则图中阴影部分的面积为．8．圆锥的底面半径为2cm，圆锥高为3cm，则此圆锥侧面展开图的周长为cm．9．如图，在△ABC中，AB=BC=8，AO=BO，点M是射线CO上的一个动点，∠AOC=60°，则当△ABM为直角三角形时，AM的长为．10．如图，四条直线l 1：y1=x，l2：y2=x，l3：y3=﹣x，l4：y4=﹣x，OA1=1，过点A1作A1A2⊥x轴，交l1于点A2，再过点A1作A1A2⊥l1交l2于点A2，再过点A2作A2A3⊥l3交y轴于点A3…，则点A2017坐标为．二、选择题（每题3分，满分30分）11．下列运算中，计算正确的是（）A．（a2b）3=a5b3B．（3a2）3=27a6C．x6÷x2=x3D．（a+b）2=a2+b2 12．下列图形中，既是轴对称图形又是中心对称图形的是（）A． B． C．D．13．如图，是由若干个相同的小立方体搭成的几何体体俯视图和左视图．则小立方体的个数可能是（）A．5或6 B．5或7 C．4或5或6 D．5或6或714．某市4月份日平均气温统计图情况如图所示，则在日平均气温这组数据中，众数和中位数分别是（）A．13，13 B．13，13.5 C．13，14 D．16，1315．如图，某工厂有甲、乙两个大小相同的蓄水池，且中间有管道连通，现要向甲池中注水，若单位时间内的注水量不变，那么从注水开始，乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是（）A．B．C．D．16．反比例函数y=图象上三个点的坐标为（x1，y1）、（x2，y2）、（x3，y3），若x1＜x2＜0＜x3，则y1，y2，y3的大小关系是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y2＜y3＜y1D．y1＜y3＜y217．已知关于x的分式方程=的解是非负数，那么a的取值范围是（）A．a＞1 B．a≥1 C．a≥1且a≠9 D．a≤118．如图，在矩形ABCD中，AD=4，∠DAC=30°，点P、E分别在AC、AD 上，则PE+PD的最小值是（）A．2 B．2C．4 D．19．“双11”促销活动中，小芳的妈妈计划用1000元在唯品会购买价格分别为80元和120元的两种商品，则可供小芳妈妈选择的购买方案有（）A．4种 B．5种 C．6种 D．7种20．如图，在边长为4的正方形ABCD中，E、F是AD边上的两个动点，且AE=FD，连接BE、CF、BD，CF与BD交于点G，连接AG交BE于点H，连接DH，下列结论正确的个数是（）①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG ：S△HBG=tan∠DAG ⑤线段DH的最小值是2﹣2．A．2 B．3 C．4 D．5三、解答题（满分60分）21．先化简，再求值：÷﹣，其中a=1+2cos60°．22．如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，2）请解答下列问题：（1）画出△ABC关于y轴对称的△A1B1C1，并写出A1的坐标．（2）画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2，并写出A2的坐标．（3）画出△A2B2C2关于原点O成中心对称的△A3B3C3，并写出A3的坐标．23．如图，Rt△AOB的直角边OA在x轴上，OA=2，AB=1，将Rt△AOB绕点O逆时针旋转90°得到Rt△COD，抛物线y=﹣x2+bx+c经过B、D两点．（1）求二次函数的解析式；（2）连接BD，点P是抛物线上一点，直线OP把△BOD的周长分成相等的两部分，求点P的坐标．24．我市某中学为了了解孩子们对《中国诗词大会》，《挑战不可能》，《最强大脑》，《超级演说家》，《地理中国》五种电视节目的喜爱程度，随机在七、八、九年级抽取了部分学生进行调查（每人只能选择一种喜爱的电视节目），并将获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据两幅统计图中的信息回答下列问题：（1）本次调查中共抽取了名学生．（2）补全条形统计图．（3）在扇形统计图中，喜爱《地理中国》节目的人数所在的扇形的圆心角是度．（4）若该学校有2000人，请你估计该学校喜欢《最强大脑》节目的学生人数是多少人？．25．在甲、乙两城市之间有一服务区，一辆客车从甲地驶往乙地，一辆货车从乙地驶往甲地．两车同时出发，匀速行驶，客车、货车离服务区的距离y1（千米），y2（千米）与行驶的时间x（小时）的函数关系图象如图1所示．（1）甲、乙两地相距千米．（2）求出发3小时后，货车离服务区的路程y2（千米）与行驶时间x（小时）之间的函数关系式．（3）在客车和货车出发的同时，有一辆邮政车从服务区匀速去甲地取货后返回乙地（取货的时间忽略不计），邮政车离服务区的距离y3（千米）与行驶时间x（小时）之间的函数关系图线如图2中的虚线所示，直接写出在行驶的过程中，经过多长时间邮政车与客车和货车的距离相等？26．已知：△AOB和△COD均为等腰直角三角形，∠AOB=∠COD=90°．连接AD，BC，点H为BC中点，连接OH．（1）如图1所示，易证：OH=AD且OH⊥AD（不需证明）（2）将△COD绕点O旋转到图2，图3所示位置时，线段OH与AD又有怎样的关系，并选择一个图形证明你的结论．27．为了推动“龙江经济带”建设，我省某蔬菜企业决定通过加大种植面积、增加种植种类，促进经济发展．2017年春，预计种植西红柿、马铃薯、青椒共100公顷（三种蔬菜的种植面积均为整数），青椒的种植面积是西红柿种植面积的2倍，经预算，种植西红柿的利润可达1万元/公顷，青椒1.5万元/公顷，马铃薯2万元/公顷，设种植西红柿x公顷，总利润为y万元．（1）求总利润y（万元）与种植西红柿的面积x（公顷）之间的关系式．（2）若预计总利润不低于180万元，西红柿的种植面积不低于8公顷，有多少种种植方案？（3）在（2）的前提下，该企业决定投资不超过获得最大利润的在冬季同时建造A、B两种类型的温室大棚，开辟新的经济增长点，经测算，投资A种类型的大棚5万元/个，B种类型的大棚8万元/个，请直接写出有哪几种建造方案？28．如图，矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上，线段OA、OC的长度满足方程|x﹣15|+=0（OA＞OC），直线y=kx+b分别与x轴、y 轴交于M、N两点，将△BCN沿直线BN折叠，点C恰好落在直线MN上的点D 处，且tan∠CBD=（1）求点B的坐标；（2）求直线BN的解析式；（3）将直线BN以每秒1个单位长度的速度沿y轴向下平移，求直线BN扫过矩形AOCB的面积S关于运动的时间t（0＜t≤13）的函数关系式．2017年黑龙江省佳木斯市中考数学试卷参考答案与试题解析一、填空题（每题3分，满分30分）1．“可燃冰”的开发成功，拉开了我国开发新能源的大门，目前发现我国南海“可燃冰”储存量达到800亿吨，将800亿吨用科学记数法可表示为8×1010吨．【考点】1I：科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：800亿=8×1010．故答案为：8×1010．2．在函数y=中，自变量x的取值范围是x≠1．【考点】E4：函数自变量的取值范围．【分析】根据分母不等于0列式计算即可得解．【解答】解：由题意得，x﹣1≠0，解得x≠1．故答案为：x≠1．3．如图，BC∥EF，AC∥DF，添加一个条件AB=DE或BC=EF或AC=DF 或AD=BE（只需添加一个即可），使得△ABC≌△DEF．【考点】KB：全等三角形的判定．【分析】本题要判定△ABC≌△DEF，易证∠A=∠EDF，∠ABC=∠E，故添加AB=DE、BC=EF或AC=DF根据ASA、AAS即可解题．【解答】解：∵BC∥EF，∴∠ABC=∠E，∵AC∥DF，∴∠A=∠EDF，∵在△ABC和△DEF中，，∴△ABC≌△DEF，同理，BC=EF或AC=DF也可证△ABC≌△DEF．故答案为AB=DE或BC=EF或AC=DF或AD=BE（只需添加一个即可）．4．在一个不透明的袋子中装有除颜色外完全相同的3个白球、若干红球，从中随机摸取1个球，摸到红球的概率是，则这个袋子中有红球5个．【考点】X4：概率公式．【分析】设这个袋子中有红球x个，根据已知条件列方程即可得到结论．【解答】解：设这个袋子中有红球x个，∵摸到红球的概率是，∴=，∴x=5，故答案为：5．5．若关于x的一元一次不等式组无解，则a的取值范围是a≥2．【考点】CB：解一元一次不等式组．【分析】先求出各不等式的解集，再与已知解集相比较求出a的取值范围．【解答】解：由x﹣a＞0得，x＞a；由1﹣x＞x﹣1得，x＜2，∵此不等式组的解集是空集，∴a≥2．故答案为：a≥2．6．为了鼓励居民节约用水，某自来水公司采取分段计费，每月每户用水不超过10吨，每吨2.2元；超过10吨的部分，每吨加收1.3元．小明家4月份用水15吨，应交水费39.5元．【考点】1G：有理数的混合运算．【分析】先根据单价×数量=总价求出10吨的水费，再根据单价×数量=总价加上超过10吨的部分的水费，再把它们相加即可解答．【解答】解：2.2×10+（2.2+1.3）×（15﹣10）=22+3.5×5=22+17.5=39.5（元）．答：应交水费39.5元．故答案为：39.5．7．如图，BD是⊙O的切线，B为切点，连接DO与⊙O交于点C，AB为⊙O的直径，连接CA，若∠D=30°，⊙O的半径为4，则图中阴影部分的面积为．【考点】MC：切线的性质；MO：扇形面积的计算．【分析】由条件可求得∠COA的度数，过O作OE⊥CA于点E，则可求得OE的长和CA的长，再利用S阴影=S扇形COA﹣S△COA可求得答案．【解答】解：如图，过O作OE⊥CA于点E，∵DB为⊙O的切线，∴∠DBA=90°，∵∠D=30°，∴∠BOC=60°，∴∠COA=120°，∵OC=OA=4，∴∠OAE=30°，∴OE=2，CA=2AE=4∴S阴影=S扇形COA﹣S△COA=﹣×2×4=π﹣4，故答案为：π﹣4．8．圆锥的底面半径为2cm，圆锥高为3cm，则此圆锥侧面展开图的周长为（2+4π）cm．【考点】MP：圆锥的计算．【分析】利用勾股定理易得圆锥的母线长，圆锥周长=弧长+2母线长．【解答】解：∵圆锥的底面半径是2，高是3，∴圆锥的母线长为： =，∴这个圆锥的侧面展开图的周长=2×+2π×2=2+4π．故答案为2+4π．9．如图，在△ABC中，AB=BC=8，AO=BO，点M是射线CO上的一个动点，∠AOC=60°，则当△ABM为直角三角形时，AM的长为4或4或4．【考点】KQ：勾股定理；KH：等腰三角形的性质．【分析】分三种情况讨论：①当M在AB下方且∠AMB=90°时，②当M在AB上方且∠AMB=90°时，③当∠ABM=90°时，分别根据含30°直角三角形的性质、直角三角形斜边的中线的性质或勾股定理，进行计算求解即可．【解答】解：如图1，当∠AMB=90°时，∵O是AB的中点，AB=8，∴OM=OB=4，又∵∠AOC=∠BOM=60°，∴△BOM是等边三角形，∴BM=BO=4，∴Rt△ABM中，AM==4；如图2，当∠AMB=90°时，∵O是AB的中点，AB=8，∴OM=OA=4，又∵∠AOC=60°，∴△AOM是等边三角形，∴AM=AO=4；如图3，当∠ABM=90°时，∵∠BOM=∠AOC=60°，∴∠BMO=30°，∴MO=2BO=2×4=8，∴Rt△BOM中，BM==4，∴Rt△ABM中，AM==4，综上所述，当△ABM为直角三角形时，AM的长为4或4或4．故答案为：4或4或4．10．如图，四条直线l 1：y1=x，l2：y2=x，l3：y3=﹣x，l4：y4=﹣x，OA1=1，过点A1作A1A2⊥x轴，交l1于点A2，再过点A1作A1A2⊥l1交l2于点A2，再过点A2作A2A3⊥l3交y轴于点A3…，则点A2017坐标为[（）2015，（）2016]．【考点】D2：规律型：点的坐标．【分析】先利用各直线的解析式得到x轴、l1、l2、y轴、l3、l4依次相交为30的角，各点的位置是每12个一循环，由于2017=168×12+1，则可判定点A2016在x轴的正半轴上，再规律得到OA2016=（）2015，然后表示出点A2017坐标．【解答】解：∵y 1=x，l2：y2=x，l3：y3=﹣x，l4：y4=﹣x，∴x轴、l1、l2、y轴、l3、l4依次相交为30的角，∵2017=168×12+1，∴点A2016在x轴的正半轴上，∵OA2==，OA3=（）2，OA4=（）3，…OA2016=（）2015，∴点A2017坐标为[（）2015，（）2016]．故答案为[（）2015，（）2016]．二、选择题（每题3分，满分30分）11．下列运算中，计算正确的是（）A．（a2b）3=a5b3B．（3a2）3=27a6C．x6÷x2=x3D．（a+b）2=a2+b2【考点】4I：整式的混合运算．【分析】各项计算得到结果，即可作出判断．【解答】解：A、原式=a6b3，不符合题意；B、原式=27a6，符合题意；C、原式=x4，不符合题意；D、原式=a2+2ab+b2，不符合题意，故选B12．下列图形中，既是轴对称图形又是中心对称图形的是（）A． B． C．D．【考点】R5：中心对称图形；P3：轴对称图形．【分析】利用中心对称图形与轴对称图形性质判断即可．【解答】解：既是轴对称图形又是中心对称图形的是，故选A13．如图，是由若干个相同的小立方体搭成的几何体体俯视图和左视图．则小立方体的个数可能是（）A．5或6 B．5或7 C．4或5或6 D．5或6或7【考点】U3：由三视图判断几何体．【分析】易得这个几何体共有2层，由俯视图可得第一层立方体的个数，由左视图可得第二层最多和最少小立方体的个数，相加即可．【解答】解：由俯视图易得最底层有4个小立方体，由左视图易得第二层最多有3个小立方体和最少有1个小立方体，那么小立方体的个数可能是5个或6个或7个．故选D．14．某市4月份日平均气温统计图情况如图所示，则在日平均气温这组数据中，众数和中位数分别是（）A．13，13 B．13，13.5 C．13，14 D．16，13【考点】W5：众数；W4：中位数．【分析】根据条形统计图得到各数据的权，然后根据众数和中位数的定义求解．【解答】解：这组数据中，13出现了10次，出现次数最多，所以众数为13，第15个数和第16个数都是14，所以中位数是14．故选C．15．如图，某工厂有甲、乙两个大小相同的蓄水池，且中间有管道连通，现要向甲池中注水，若单位时间内的注水量不变，那么从注水开始，乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是（）A．B．C．D．【考点】E6：函数的图象．【分析】根据特殊点的实际意义即可求出答案．【解答】解：先注甲时水未达连接地方是，乙水池中的水面高度没变化；当甲池中水到达连接的地方，乙水池中水面上升比较快；当两水池水面不持平时，乙水池的水面持续增长较慢，最后两池水面持平后继续快速上升，故选：D．16．反比例函数y=图象上三个点的坐标为（x1，y1）、（x2，y2）、（x3，y3），若x1＜x2＜0＜x3，则y1，y2，y3的大小关系是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y2＜y3＜y1D．y1＜y3＜y2【考点】G6：反比例函数图象上点的坐标特征．【分析】先根据反比例函数的解析式判断出函数图象所在的象限及其增减性，再根据x1＜x2＜0＜x3即可得出结论．【解答】解：∵反比例函数y=中，k=3＞0，∴此函数图象的两个分支分别位于第一三象限，且在每一象限内y随x的增大而减小．∵x1＜x2＜0＜x3，∴（x1，y1）、（x2，y2）在第三象限，（x3，y3）在第一象限，∴y2＜y1＜0＜y3．故选B．17．已知关于x的分式方程=的解是非负数，那么a的取值范围是（）A．a＞1 B．a≥1 C．a≥1且a≠9 D．a≤1【考点】B2：分式方程的解；C6：解一元一次不等式．【分析】根据分式方程的解法即可求出a的取值范围；【解答】解：3（3x﹣a）=x﹣3，9x﹣3a=x﹣3，8x=3a﹣3∴x=，由于该分式方程有解，令x=代入x﹣3≠0，∴a≠9，∵该方程的解是非负数解，∴≥0，∴a≥1，∴a的范围为：a≥1且a≠9，故选（C）18．如图，在矩形ABCD中，AD=4，∠DAC=30°，点P、E分别在AC、AD 上，则PE+PD的最小值是（）A．2 B．2C．4 D．【考点】PA：轴对称﹣最短路线问题；LB：矩形的性质．【分析】作D关于直线AC的对称点D′，过D′作D′E⊥AD于E，则D′E=PE+PD的最小值，解直角三角形得到即可得到结论．【解答】解：作D关于直线AC的对称点D′，过D′作D′E⊥AD于E，则D′E=PE+PD的最小值，∵四边形ABCD是矩形，∴∠ADC=90°，∵AD=4，∠DAC=30°，∴CD=，∵DD′⊥AC，∴∠CDD′=30°，∴∠ADD′=60°，∴DD′=4，∴D′E=2，故选B．19．“双11”促销活动中，小芳的妈妈计划用1000元在唯品会购买价格分别为80元和120元的两种商品，则可供小芳妈妈选择的购买方案有（）A．4种 B．5种 C．6种 D．7种【考点】95：二元一次方程的应用．【分析】设购买80元的商品数量为x，购买120元的商品数量为y，根据总费用是1000元列出方程，求得正整数x、y的值即可．【解答】解：设购买80元的商品数量为x，购买120元的商品数量为y，依题意得：80x+120y=1000，整理，得y=．因为x是正整数，所以当x=2时，y=7．当x=5时，y=5．当x=8时，y=3．当x=11时，y=1．即有4种购买方案．故选：A．20．如图，在边长为4的正方形ABCD中，E、F是AD边上的两个动点，且AE=FD，连接BE、CF、BD，CF与BD交于点G，连接AG交BE于点H，连接DH，下列结论正确的个数是（）①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG ：S△HBG=tan∠DAG ⑤线段DH的最小值是2﹣2．A．2 B．3 C．4 D．5【考点】S9：相似三角形的判定与性质；KD：全等三角形的判定与性质；LE：正方形的性质；T7：解直角三角形．【分析】首先证明△ABE≌△DCF，△ADG≌△CDG（SAS），△AGB≌△CGB，利用全等三角形的性质，等高模型、三边关系一一判断即可．【解答】解：∵四边形ABCD是正方形，∴AB=CD，∠BAD=∠ADC=90°，∠ADB=∠CDB=45°，在△ABE和△DCF中，，∴△ABE≌△DCF（SAS），∴∠ABE=∠DCF，在△ADG和△CDG中，，∴△ADG≌△CDG（SAS），∴∠DAG=∠DCF，∴∠ABE=∠DAG，∵∠DAG+∠BAH=90°，∴∠BAE+∠BAH=90°，∴∠AHB=90°，∴AG⊥BE，故③正确，同法可证：△AGB≌△CGB，∵DF∥CB，∴△CBG∽△FDG，∴△ABG∽△FDG，故①正确，∵S△HDG ：S△HBG=DG：BG=DF：BC=DF：CD=tan∠FCD，又∵∠DAG=∠FCD，∴S△HDG ：S△HBG=tan∠FCD，tan∠DAG，故④正确取AB的中点O，连接OD、OH，∵正方形的边长为4，∴AO=OH=×4=2，由勾股定理得，OD==2，由三角形的三边关系得，O、D、H三点共线时，DH最小，DH 最小=2﹣2．无法证明DH平分∠EHG，故②错误，故①③④⑤正确，故选C．三、解答题（满分60分）21．先化简，再求值：÷﹣，其中a=1+2cos60°．【考点】6D：分式的化简求值；T5：特殊角的三角函数值．【分析】根据分式的除法和减法可以化简题目中的式子，然后将a的值代入即可解答本题．【解答】解：÷﹣===，当a=1+2cos60°=1+2×=1+1=2时，原式=．22．如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，2）请解答下列问题：（1）画出△ABC关于y轴对称的△A1B1C1，并写出A1的坐标．（2）画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2，并写出A2的坐标．（3）画出△A2B2C2关于原点O成中心对称的△A3B3C3，并写出A3的坐标．【考点】R8：作图﹣旋转变换；P7：作图﹣轴对称变换．【分析】根据题意画出相应的三角形，确定出所求点坐标即可．【解答】解：（1）画出△ABC关于y轴对称的△A1B1C1，如图所示，此时A1的坐标为（﹣2，2）；（2）画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2，如图所示，此时A2的坐标为（4，0）；（3）画出△A2B2C2关于原点O成中心对称的△A3B3C3，如图所示，此时A3的坐标为（﹣4，0）．23．如图，Rt△AOB的直角边OA在x轴上，OA=2，AB=1，将Rt△AOB绕点O逆时针旋转90°得到Rt△COD，抛物线y=﹣x2+bx+c经过B、D两点．（1）求二次函数的解析式；（2）连接BD，点P是抛物线上一点，直线OP把△BOD的周长分成相等的两部分，求点P的坐标．【考点】H8：待定系数法求二次函数解析式；H5：二次函数图象上点的坐标特征；R7：坐标与图形变化﹣旋转．【分析】（1）由旋转性质可得CD=AB=1、OA=OC=2，从而得出点B、D坐标，代入解析式即可得出答案；（2）由直线OP把△BOD的周长分成相等的两部分且OB=OD，知DQ=BQ，即点Q为BD的中点，从而得出点Q坐标，求得直线OP解析式，代入抛物线解析式可得点P坐标．【解答】解：（1）∵Rt△AOB绕点O逆时针旋转90°得到Rt△COD，∴CD=AB=1、OA=OC=2，则点B（2，1）、D（﹣1，2），代入解析式，得：，解得：，∴二次函数的解析式为y=﹣x2+x+；（2）如图，∵直线OP把△BOD的周长分成相等的两部分，且OB=OD，∴DQ=BQ，即点Q为BD的中点，∴点Q坐标为（，），设直线OP解析式为y=kx，将点Q坐标代入，得： k=，解得：k=3，∴直线OP的解析式为y=3x，代入y=﹣x2+x+，得：﹣ x2+x+=3x，解得：x=1或x=﹣4（舍），当x=1时，y=3，∴点P坐标为（1，3）．24．我市某中学为了了解孩子们对《中国诗词大会》，《挑战不可能》，《最强大脑》，《超级演说家》，《地理中国》五种电视节目的喜爱程度，随机在七、八、九年级抽取了部分学生进行调查（每人只能选择一种喜爱的电视节目），并将获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据两幅统计图中的信息回答下列问题：（1）本次调查中共抽取了200名学生．（2）补全条形统计图．（3）在扇形统计图中，喜爱《地理中国》节目的人数所在的扇形的圆心角是36度．（4）若该学校有2000人，请你估计该学校喜欢《最强大脑》节目的学生人数是多少人？．【考点】VC：条形统计图；V5：用样本估计总体；VB：扇形统计图．【分析】（1）根据题意列式计算即可；（2）求得喜爱《挑战不可能》节目的人数，将条形统计图补充完整即可；（3）用360°×喜爱《地理中国》节目的人数占总人数的百分数即可得到结论；（4）直接利用样本估计总体的方法求解即可求得答案．【解答】解：（1）30÷15%=200名，答：本次调查中共抽取了200名学生；故答案为：200；（2）喜爱《挑战不可能》节目的人数=200﹣20﹣60﹣40﹣30=50名，补全条形统计图如图所示；（3）喜爱《地理中国》节目的人数所在的扇形的圆心角是360°×=36度；故答案为：36；（4）2000×=600名，答：该学校喜欢《最强大脑》节目的学生人数是600人．25．在甲、乙两城市之间有一服务区，一辆客车从甲地驶往乙地，一辆货车从乙地驶往甲地．两车同时出发，匀速行驶，客车、货车离服务区的距离y1（千米），y2（千米）与行驶的时间x（小时）的函数关系图象如图1所示．（1）甲、乙两地相距480千米．（2）求出发3小时后，货车离服务区的路程y2（千米）与行驶时间x（小时）之间的函数关系式．（3）在客车和货车出发的同时，有一辆邮政车从服务区匀速去甲地取货后返回乙地（取货的时间忽略不计），邮政车离服务区的距离y3（千米）与行驶时间x（小时）之间的函数关系图线如图2中的虚线所示，直接写出在行驶的过程中，经过多长时间邮政车与客车和货车的距离相等？【考点】FH：一次函数的应用．。

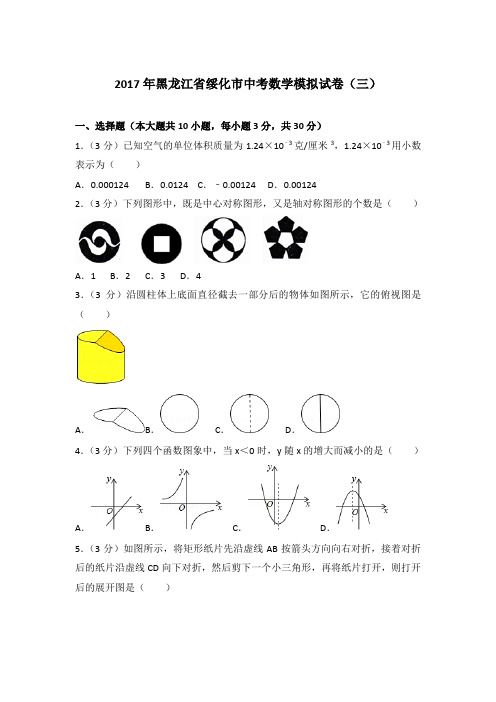
2017年黑龙江省绥化市中考数学模拟试卷（三）一、选择题（本大题共10小题，每小题3分，共30分）1．（3分）已知空气的单位体积质量为1.24×10﹣3克/厘米3，1.24×10﹣3用小数表示为（）A．0.000124 B．0.0124 C．﹣0.00124 D．0.001242．（3分）下列图形中，既是中心对称图形，又是轴对称图形的个数是（）A．1 B．2 C．3 D．43．（3分）沿圆柱体上底面直径截去一部分后的物体如图所示，它的俯视图是（）A．B．C．D．4．（3分）下列四个函数图象中，当x＜0时，y随x的增大而减小的是（）A．B．C．D．5．（3分）如图所示，将矩形纸片先沿虚线AB按箭头方向向右对折，接着对折后的纸片沿虚线CD向下对折，然后剪下一个小三角形，再将纸片打开，则打开后的展开图是（）A．B． C． D．6．（3分）如图，海关缉私艇在A处接到情报，在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行，于是该艇立即沿北偏西45°的方向前进，经过1小时航行，恰好在C处截住可疑船只，则缉私艇的速度为（）A．（12+12）海里/时B．（12+12）海里/时C．（12+12）海里/时D．（8+8）海里/时7．（3分）在函数y=中，自变量x的取值范围是（）A．x＜5且x≠2 B．x≥5 C．x≤5且x≠﹣2 D．x≠﹣28．（3分）某种高端品牌的家用电器，若按标价打八折销售该电器一件，则可获利润500元，其利润率为20%．现如果按同一标价打九折销售该电器一件，那么获得的纯利润为（）A．562.5元 B．875元C．550元D．750元9．（3分）化简+的结果是（）A．m﹣3 B．m+3 C． D．10．（3分）如图，菱形ABCD的周长为16，∠ABC=120°，则AC的长为（）A．4 B．4 C．2 D．2二、填空题（每小题3分，共33分）11．（3分）﹣的绝对值的相反数是．12．（3分）今年某校约有2000名学生参加中考，为了解这2000名学生的数学成绩，准备从中随机抽取200名学生的数学成绩进行统计分析，那么你的数学成绩被抽中的概率为．13．（3分）如图，直线a∥b，∠1=70°，∠2=35°，则∠3的度数是．14．（3分）在一次数学测验中，随机抽取了8份试卷，其得分如下表：则这8名考生得分的中位数是分．15．（3分）计算：|﹣2|+（﹣2）0+2sin30°﹣（）﹣2=．16．（3分）把抛物线C先向左平移1个单位长度，再向上平移3个单位长度，所得新抛物线的解析式为y=﹣x2，则抛物线C的解析式为．17．（3分）在直径为150cm的圆柱形油槽内装入一些油后，截面如图所示，如果油的最大深度DC为30cm，那么油面宽度AB是cm．18．（3分）圆锥的轴截面是一个边长为6cm的等边三角形，则这个圆锥的侧面积是．19．（3分）如图，△AOB中，∠AOB=90°，AO=3，BO=6，△AOB绕顶点O逆时针旋转到△A′OB′处，此时线段A′B′与BO的交点E为BO的中点，则线段B′E的长度为．20．（3分）如图所示是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，…，第n（n是正整数）个图案中的基础图形个数为（用含n的式子表示）．21．（3分）如图，正方形ABCD的边长为3cm，E为CD边上一点，∠DAE=30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q．若PQ=AE，则AP等于cm．三、解答题（满分57分）22．（5分）两个城镇A、B与两条公路l1、l2位置如图所示，电信部门需在C处修建一座信号发射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路l1，l2的距离也必须相等，那么点C应选在何处？请在图中，用尺规作图找出所有符合条件的点C．（不写已知、求作、作法，只保留作图痕迹）23．（7分）已知关于x的一元二次方程x2+（2m﹣1）x+m2+3=0（1）若方程有两个实数根，求m的取值范围；（2）若方程有两个实数根x1，x2，且x12+x22=25，求m的值．24．（7分）在农村的“村村通”的道路改键工程中，某路段长4000米，由甲、乙两个工程队拟在30天内（含30天）合作完成，已知两个工程队各有10名工人，设甲、乙两个工程队的工人全部参与生产，且甲、乙两个工程队每天各自的工作量相同，甲工程队1天，乙工程队2天共修路200米，甲工程队2天，乙工程队3天共修路350米．（1）求甲、乙两个工程队每天分别修路多少米？（2）甲、乙两个工程队施工10天后，由于工作需要，需从甲队抽调m人去学校新技术，总部要求在规定时间内完成，求甲队可以抽调多少人？（3）已知甲工程队每天的施工费用为0.6万元，乙工程队每天的施工费用为0.35万元，要使该工程的施工费用最低，则甲、乙两个工程队各做多少天？最低费用为多少？25．（8分）如图，△ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD 延长线上的一点，且AP=AC．（1）求证：PA是⊙O的切线；（2）若PD=，求⊙O的直径．26．（9分）一列快车从甲地驶往乙地，一列慢车沿同一条公路从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（单位：h），两车之间的距离为y（单位：km），图中的折线表示y与x之间的函数关系．根据图象解答下列问题：（1）甲、乙两地之间的距离为km；（2）请解释图中点B的实际意义；（3）求慢车和快车的速度（4）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同，在第一列快车与慢车相遇30min后，第二列快车与慢车相遇，求第二列快车比第一列快车晚出发多少小时？27．（10分）如图，已知矩形，在BC上取两点E，F（E在F 左边），以EF为边作等边三角形PEF，使顶点P在AD上，PE，PF分别交AC于点G，H．（1）求△PEF的边长；（2）求证：；（3）若△PEF的边EF在线段BC上移动．试猜想：PH与BE有何数量关系？并证明你猜想的结论．28．（11分）抛物线y=ax2+bx+c交x轴于A，B两点，交y轴于点C，已知抛物线的对称轴为x=1，点B的坐标为（3，0），点C的坐标为（0，﹣3）（1）求抛物线的解析式；（2）在抛物线对称轴上是否存在一点P，使点P到B、C两点距离之差最大？若存在，求出P点坐标；若不存在，请说明理由；（3）平行于x轴的一条直线交抛物线于M、N两点，（点M在点N左侧），若以MN为直径的圆恰好与x轴相切，求此圆的半径．2017年黑龙江省绥化市中考数学模拟试卷（三）参考答案与试题解析一、选择题（本大题共10小题，每小题3分，共30分）1．（3分）已知空气的单位体积质量为1.24×10﹣3克/厘米3，1.24×10﹣3用小数表示为（）A．0.000124 B．0.0124 C．﹣0.00124 D．0.00124【解答】解：把数据“1.24×10﹣3中1.24的小数点向左移动3位就可以得到为0.001 24．故选D．2．（3分）下列图形中，既是中心对称图形，又是轴对称图形的个数是（）A．1 B．2 C．3 D．4【解答】解：第一个图形是中心对称图形，第二个图形、第三个图形既是中心对称图形，又是轴对称图形，第四个图形是轴对称图形，共2个，故选：B．3．（3分）沿圆柱体上底面直径截去一部分后的物体如图所示，它的俯视图是（）A．B．C．D．【解答】解：从上面看依然可得到两个半圆的组合图形，故选：D．4．（3分）下列四个函数图象中，当x＜0时，y随x的增大而减小的是（）A．B．C．D．【解答】解：当x＜0时，y随x的增大而减小的是，故选C．5．（3分）如图所示，将矩形纸片先沿虚线AB按箭头方向向右对折，接着对折后的纸片沿虚线CD向下对折，然后剪下一个小三角形，再将纸片打开，则打开后的展开图是（）A．B． C． D．【解答】解：∵第三个图形是三角形，∴将第三个图形展开，可得，即可排除答案A，∵再展开可知两个短边正对着，∴选择答案D，排除B与C．故选：D．6．（3分）如图，海关缉私艇在A处接到情报，在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行，于是该艇立即沿北偏西45°的方向前进，经过1小时航行，恰好在C处截住可疑船只，则缉私艇的速度为（）A．（12+12）海里/时B．（12+12）海里/时C．（12+12）海里/时D．（8+8）海里/时【解答】解：由题意得，BC=24海里，设AD=x海里，在Rt△ABD中，BD==x，在Rt△ACD中，∠ACD=45°，∴CD=AD=x，则x﹣x=24，解得，x=12+12，∴AC=x=12+12，∴缉私艇的速度为（12+12）海里/时，故选：A．7．（3分）在函数y=中，自变量x的取值范围是（）A．x＜5且x≠2 B．x≥5 C．x≤5且x≠﹣2 D．x≠﹣2【解答】解：由题意得，5﹣x≥0且x+2≠0，解得x≤5且x≠﹣2．故选C．8．（3分）某种高端品牌的家用电器，若按标价打八折销售该电器一件，则可获利润500元，其利润率为20%．现如果按同一标价打九折销售该电器一件，那么获得的纯利润为（）A．562.5元 B．875元C．550元D．750元【解答】解：设该商品的进价为x元，标价为y元，由题意得，解得：x=2500，y=3750．则3750×0.9﹣2500=875（元）．故选：B9．（3分）化简+的结果是（）A．m﹣3 B．m+3 C． D．【解答】解：+=﹣==m+3．故选：B．10．（3分）如图，菱形ABCD的周长为16，∠ABC=120°，则AC的长为（）A．4 B．4 C．2 D．2【解答】解：在菱形ABCD中，∵∠ABC=120°，∴∠ABE=60°，AC⊥BD，∵菱形ABCD的周长为16，∴AB=4，在RT△ABE中，AE=ABsin∠ABE=4×=2，故可得AC=2AE=4．故选A．二、填空题（每小题3分，共33分）11．（3分）﹣的绝对值的相反数是﹣．【解答】解：﹣的绝对值的相反数是﹣|﹣|=﹣，故答案为：﹣．12．（3分）今年某校约有2000名学生参加中考，为了解这2000名学生的数学成绩，准备从中随机抽取200名学生的数学成绩进行统计分析，那么你的数学成绩被抽中的概率为．【解答】解：∵为了了解这2000名学生的数学成绩，准备从中随机抽取200名学生的数学成绩进行统计分析，∴数学成绩被抽中的概率为：=．故答案为：．13．（3分）如图，直线a∥b，∠1=70°，∠2=35°，则∠3的度数是35°．【解答】解：∵直线a∥b，∠1=70°，∴∠4=∠1=70°，∵∠2+∠3=∠4，∴∠3=∠4﹣∠2=70°﹣35°=35°．故答案为：35°．14．（3分）在一次数学测验中，随机抽取了8份试卷，其得分如下表：则这8名考生得分的中位数是86分．【解答】解：这8名考生得分的中位数是=86（分），故答案为：86．15．（3分）计算：|﹣2|+（﹣2）0+2sin30°﹣（）﹣2=0．【解答】解：|﹣2|+（﹣2）0+2sin30°﹣（）﹣2=2+1+2×﹣4=3+1﹣4=0故答案为：0．16．（3分）把抛物线C先向左平移1个单位长度，再向上平移3个单位长度，所得新抛物线的解析式为y=﹣x2，则抛物线C的解析式为y=﹣（x﹣1）2﹣3．【解答】解：将抛物线y=﹣x2向下平移3个单位长度，再向右平移1个单位长度，所得抛物线的函数解析式为y=﹣（x﹣1）2﹣3，故答案是：y=﹣（x﹣1）2﹣3．17．（3分）在直径为150cm的圆柱形油槽内装入一些油后，截面如图所示，如果油的最大深度DC为30cm，那么油面宽度AB是120cm．【解答】解：则OC⊥AB于点D，OC=OB=×150=75cm，OD=OC﹣CD=75﹣30=45cm．在直角△OBD中，BD===60（cm），则AB=2BD=120cm．故答案是：120．18．（3分）圆锥的轴截面是一个边长为6cm的等边三角形，则这个圆锥的侧面积是18πcm2．【解答】解：∵圆锥的轴截面是一个边长为6的等边三角形，∴底面半径=3，底面周长=6π，∴圆锥的侧面积=×6π×6=18πcm2．故答案为：18πcm2．19．（3分）如图，△AOB中，∠AOB=90°，AO=3，BO=6，△AOB绕顶点O逆时针旋转到△A′OB′处，此时线段A′B′与BO的交点E为BO的中点，则线段B′E的长度为．【解答】解：∵∠AOB=90°，AO=3，BO=6，∴AB===3，∵△AOB绕顶点O逆时针旋转到△A′OB′处，∴AO=A′O=3，A′B′=AB=3，∵点E为BO的中点，∴OE=BO=×6=3，∴OE=A′O，过点O作OF⊥A′B′于F，S△A′OB′=×3•OF=×3×6，解得OF=，在Rt△EOF中，EF===，∵OE=A′O，OF⊥A′B′，∴A′E=2EF=2×=（等腰三角形三线合一），∴B′E=A′B′﹣A′E=3﹣=．故答案为：．20．（3分）如图所示是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，…，第n（n是正整数）个图案中的基础图形个数为3n+1（用含n的式子表示）．【解答】解：观察可知，第1个图案由4个基础图形组成，4=3+1第2个图案由7个基础图形组成，7=3×2+1，第3个图案由10个基础图形组成，10=3×3+1，…，第n个图案中基础图形有：3n+1，故答案为：3n+1．21．（3分）如图，正方形ABCD的边长为3cm，E为CD边上一点，∠DAE=30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q．若PQ=AE，则AP等于1或2cm．【解答】解：根据题意画出图形，过P作PN⊥BC，交BC于点N，∵四边形ABCD为正方形，∴AD=DC=PN，在Rt△ADE中，∠DAE=30°，AD=3cm，∴tan30°=，即DE=cm，根据勾股定理得：AE==2cm，∵M为AE的中点，∴AM=AE=cm，在Rt△ADE和Rt△PNQ中，，∴Rt△ADE≌Rt△PNQ（HL），∴DE=NQ，∠DAE=∠NPQ=30°，∵PN∥DC，∴∠PFA=∠DEA=60°，∴∠PMF=90°，即PM⊥AF，在Rt△AMP中，∠MAP=30°，cos30°=，∴AP===2cm；由对称性得到AP′=DP=AD﹣AP=3﹣2=1cm，综上，AP等于1cm或2cm．故答案为：1或2．三、解答题（满分57分）22．（5分）两个城镇A、B与两条公路l1、l2位置如图所示，电信部门需在C处修建一座信号发射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路l1，l2的距离也必须相等，那么点C应选在何处？请在图中，用尺规作图找出所有符合条件的点C．（不写已知、求作、作法，只保留作图痕迹）【解答】解：（1）作出线段AB的垂直平分线；（2）作出角的平分线；它们的交点即为所求作的点C（2个）．23．（7分）已知关于x的一元二次方程x2+（2m﹣1）x+m2+3=0（1）若方程有两个实数根，求m的取值范围；（2）若方程有两个实数根x1，x2，且x12+x22=25，求m的值．【解答】解：（1）∵关于x的一元二次方程x2+（2m﹣1）x+m2+3=0有两个实数根，∴△=（2m﹣1）2﹣4×1×（m2+3）=﹣4m﹣11≥0，解得：m≤﹣．∴m的取值范围为m≤﹣．（2）∵方程x2+（2m﹣1）x+m2+3=0的实数根为x1，x2，∴x1+x2=﹣（2m﹣1），x1•x2=m2+3．又∵x12+x22=（x1+x2）2﹣2x1•x2=25，∴[﹣（2m﹣1）]2﹣2（m2+3）=25，解得：m1=﹣3，m2=5．∴m的值为﹣3．24．（7分）在农村的“村村通”的道路改键工程中，某路段长4000米，由甲、乙两个工程队拟在30天内（含30天）合作完成，已知两个工程队各有10名工人，设甲、乙两个工程队的工人全部参与生产，且甲、乙两个工程队每天各自的工作量相同，甲工程队1天，乙工程队2天共修路200米，甲工程队2天，乙工程队3天共修路350米．（1）求甲、乙两个工程队每天分别修路多少米？（2）甲、乙两个工程队施工10天后，由于工作需要，需从甲队抽调m人去学校新技术，总部要求在规定时间内完成，求甲队可以抽调多少人？（3）已知甲工程队每天的施工费用为0.6万元，乙工程队每天的施工费用为0.35万元，要使该工程的施工费用最低，则甲、乙两个工程队各做多少天？最低费用为多少？【解答】解：（1）设甲队每天修路x米，乙队每天修路y米，依题意得，解得．答：甲工程队每天修路100米，乙工程队每天修路50米；（2）依题意得，10×100+20××100+30×50≥4000，解得m≤，∵0＜m＜10，∴0＜m≤，∵m为正整数，∴m=1或2，∴甲队可以抽调1人或2人；（3）设甲工程队修a天，乙工程队修b天，依题意得，100a+50b=4000，所以，b=80﹣2a，∴0≤80﹣2a≤30，解得25≤a≤40，又∵0≤a≤30，∴25≤a≤30，设总费用为W元，依题意得，W=0.6a+0.35b，=0.6a+0.35（80﹣2a），=﹣0.1a+28，∵﹣0.1＜0，=﹣0.1×30+28=25（万元），∴当a=30时，W最小此时b=80﹣2a=80﹣2×30=20（天）．答：甲工程队需做30天，乙工程队需做20天，最低费用为25万元．25．（8分）如图，△ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD 延长线上的一点，且AP=AC．（1）求证：PA是⊙O的切线；（2）若PD=，求⊙O的直径．【解答】（1）证明：连接OA，∵∠B=60°，∴∠AOC=2∠B=120°，又∵OA=OC，∴∠OAC=∠OCA=30°，又∵AP=AC，∴∠P=∠ACP=30°，∴∠OAP=∠AOC﹣∠P=90°，∴OA⊥PA，∴PA是⊙O的切线．（2）在Rt△OAP中，∵∠P=30°，∴PO=2OA=OD+PD，又∵OA=OD，∴PD=OA，∵，∴．∴⊙O的直径为．26．（9分）一列快车从甲地驶往乙地，一列慢车沿同一条公路从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（单位：h），两车之间的距离为y（单位：km），图中的折线表示y与x之间的函数关系．根据图象解答下列问题：（1）甲、乙两地之间的距离为900km；（2）请解释图中点B的实际意义；（3）求慢车和快车的速度（4）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同，在第一列快车与慢车相遇30min后，第二列快车与慢车相遇，求第二列快车比第一列快车晚出发多少小时？【解答】解：（1）∵当x=0时，y=900，∴甲、乙两地之间的距离为900千米．故答案为：900．（2）图中点B的实际意义是当两车出发4小时时，慢车和快车相遇．（3）慢车的速度为900÷12=75（千米/小时），快车的速度为900÷4﹣75=150（千米/小时）．（4）设第二列快车比第一列快车晚出发m小时，则第二列快车与慢车相遇时，慢车行驶了4.5小时、第二列快车行驶了（4.5﹣m）小时，根据题意得：75×4.5+150×（4.5﹣m）=900，解得：m=0.75．答：第二列快车比第一列快车晚出发0.75小时．27．（10分）如图，已知矩形，在BC上取两点E，F（E在F 左边），以EF为边作等边三角形PEF，使顶点P在AD上，PE，PF分别交AC于点G，H．（1）求△PEF的边长；（2）求证：；（3）若△PEF的边EF在线段BC上移动．试猜想：PH与BE有何数量关系？并证明你猜想的结论．【解答】解：（1）过P作PQ⊥BC于Q（1分）∵四边形ABCD为矩形，∴∠B=90°，即AB⊥BC，又AD∥BC，∴，∵△PEF是等边三角形，∴∠PEQ=60°，在Rt△PEQ中，，（2分）∴PE=2，∴△PEF的边长为2．（1分）（2）在Rt△ABC中，∵tan∠ACB=，∴∠ACB=30°（1分）∵∠PEQ=60°，∴∠EGC=90°，∠PGH=90°，（1分）又∵△PEF是等边三角形，∴∠GEC=∠GPH，∴cot∠GEC=cot∠GPH，（2分）∴，（1分）（3）猜想：PH与BE的数量关系是：PH﹣BE=1（1分）证法1：如图，由（2），知∠1=30°∵△PEF是等边三角形∴∠PFE=60°，PF=EF=2，∵∠PFE=∠FHC+∠FCH，在直角三角形ABC中，∠EGC=90°，∠EPF=60°，∴∠FHC=30°（1分）∴∠FHC=∠FCH，∴FC=FH（1分）∵PH+FH=2，BE+EF+FC=3（2分）∴PH﹣BE=1证法2：由（2），知∠FCH=30°，∠EGC=90°，∴在Rt△CEG中，，即（2分）∵在Rt△PGH中，∠7=30°∴∴（2分）∴PH﹣BE=1证法3：可证：∠PEF=∠EPF=60°∠EGC=∠PGC=90°，∴△EGC∽△PGH∴∴①（2分）∵∠ACB=∠ACB，∠B=∠EGC=90°，∴△CEG∽△CAB，∴，即，∴②（2分）把②代入①得，，∴PH﹣BE=1．28．（11分）抛物线y=ax2+bx+c交x轴于A，B两点，交y轴于点C，已知抛物线的对称轴为x=1，点B的坐标为（3，0），点C的坐标为（0，﹣3）（1）求抛物线的解析式；（2）在抛物线对称轴上是否存在一点P，使点P到B、C两点距离之差最大？若存在，求出P点坐标；若不存在，请说明理由；（3）平行于x轴的一条直线交抛物线于M、N两点，（点M在点N左侧），若以MN为直径的圆恰好与x轴相切，求此圆的半径．【解答】解：（1）∵y=ax2+bx+c交x轴于A，B两点，交y轴于点C，抛物线的对称轴为x=1，点B的坐标为（3，0），点C的坐标为（0，﹣3），∴，∴，∴抛物线的解析式为：y=x2﹣2x﹣3；（2）存在，如图，连接AC并延长交对称轴于P，则点P即为P到B、C两点距离之差最大的点，∵抛物线的对称轴为x=1，点B的坐标为（3，0），∴A（﹣1，0），∵点C的坐标为（0，﹣3），∴直线AC的解析式为：y=﹣3x﹣3，∵P在对称轴上，∴P（1．﹣6）；（3）设M（x1，y），N（x2，y），圆的半径为：r，则x2﹣x1=2r，①∵对称轴为x=1，∴x1+x2=2，②由①，②得，x2=r+1，将N（r+1，y）代入y=x2﹣2x﹣3得，y=r2﹣4，∵r=|y|，∴当y＞0时，r2﹣r﹣4=0，∴r1=，r2=（舍去），当y＜0时，r2+r﹣4﹣0，∴r3=，r4=（舍去），∴圆的半径为：或．赠送：初中数学几何模型举例【模型四】几何最值模型：图形特征：l运用举例：1. △ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为AP的中点，则MF的最小值为EM FB2.如图，在边长为6的菱形ABCD中，∠BAD＝60°，E为AB的中点，F为AC上一动点，则EF+BF的最小值为_________。

[2017中考真题数学]2017中考真题以及答案-一、选择题1. (2017湖北宜昌,第2题3分)在﹣2，0，3，A.﹣2 0B. 3C. 这四个数中，最大的数是( )D.2. (__?湖北宜昌,第14题3分)如图，M，N两点在数轴上表示的数分别是m，n，则下列式子中成立的是( )A.m+n0B. ﹣m﹣nC. |m|﹣|n|0D. 2+m2+n3. (2017?湖南永州,第5题3分)若用湘教版初中数学教材上使用的某种计算器进行计算，则按键的结果为( )4. (2017河北，第5题2分)a，b是两个连续整数，若a5.(2014?陕西,第1题3分)4的算术平方根是( )A.﹣2B. 2C. ±2D. 166.(2017重庆A,第1题4分)实数﹣17的相反数是( )A.17B.C. ﹣17D. ﹣7.(2017湖北黄冈,第1题3分)﹣8的立方根是( )8. (2014?湖北荆门,第2题3分)下列运算正确的是( )A.31=﹣3 ﹣B. =±3C. (ab2)3=a3b6D. a6÷a2=a39.(2017莱芜，第1题3分)下列四个实数中，是无理数的为()10. (2017青岛，第1题3分)﹣7的绝对值是()11. (2017乐山，第1题3分)﹣2的绝对值是()12. (2017攀枝花，第1题3分)2的绝对值是( )内容需要下载文档才能查看13.(2017广西来宾，第2题3分)去年我市参加中考人数约__人，这个数用科学记数法表示是( )14.(2017黔南州，第1题4分)在﹣2，﹣3，0.1四个数中，最小的实数是( )A.﹣3B. ﹣2 0C. 1D.15.(2014年广西钦州，第3题3分)我市2014年参加中考的考生人数约为__人，将__用科学记数法表示为( )A.434×102B. 43.4×103C. 4.34×104D. 0.434×10516.(2017年广西南宁，第3题3分)南宁东高铁火车站位于南宁青秀区凤岭北路，火车站总建筑面积约为__平方米，其中数据__用科学记数法表示为( )A.26.7×104B.2.67×104 C. 2.67×105 D. 0.267×10617.(2017年贵州安顺，第2题3分)地球上的陆地而积约为__0km2.将__0用科学记数法表示为( )A.1.49×106二、填空题1. (2014?随州，第11题3分)计算：|﹣3|++(﹣1)0= B.1.49×107 C. 1.49×108 D. 1.49×1092.(2017江西，第7题3_______3.(2017陕西,第14题3分)用科学计算器计算：4.(2014?四川成都,第11题4分)计算：|﹣5.(2017黑龙江牡丹江, 第11题3分)计算|1﹣6. (2017湖北黄石,第17题7分)计算：|+3tan56°≈(结果精确到0.01) |=. |+(﹣1)0﹣()1= ﹣﹣﹣5|+2cos30°()1+(9﹣﹣)0+. 7. (2017年湖北荆门) (2014?湖北荆门,第13题3分)若﹣2xmny2与3x4y2m+n是同类项，则m﹣3n的立方根是 .8.(2017莱芜，第14题4分)计算：三、解答题1. (2017黑龙江绥化,第19题5分)计算：2. (2017湖北宜昌,第16题6分)计算：+|﹣2|+(﹣6)×(﹣). . =.3. (2017湖南永州,第17题6分)计算：﹣4cos30°+(π﹣3.14)0+4. (2017无锡，第19题8分)(1)(2)(x+1)(x﹣1)﹣(x﹣2)2.5.(2017宁夏，第17题6分)计算：(﹣)2+﹣. ﹣|﹣2|+(﹣2)0; ﹣2sin45°﹣|1﹣﹣5)0﹣﹣4sin45°﹣|. cos30°. +.﹣2|. . 6.(2017四川广安,第17题5分)+(﹣)1+(﹣7.(2014?浙江绍兴,第17题4分)(1)计算：8.(2017重庆A,第19题7分)计算：+(﹣3)2﹣__×|﹣4|+﹣9.(2017贵州黔西南州, 第21题6分)(1)计算：()2+(π﹣2014)0+sin60°+|10.(2017山西，第17题(1)5分)计算：(﹣2)2?sin60°﹣()1×﹣;11. (2017乐山，第17题9分)计算：+(﹣2014)0﹣2cos30°﹣()﹣1.)0+. 12. (2017攀枝花，第17题6分)计算：(﹣1)2014+()﹣1+(13. (2017丽水，第17题6分)计算：(﹣)2+|﹣4|×21﹣(﹣﹣1)0.|+﹣(﹣π)0; 14.(2017广西来宾，第19题12分)(1)计算：(﹣1)2014﹣|﹣(2)先化简，再求值：(2x﹣1)2﹣2(3﹣2x)，其中x=﹣2.15.(2017年广西南宁，第19题6分)计算：(﹣1)2﹣4sin45°+|﹣3|+16.(2017年广西钦州，第19题5分)计算：(﹣2)2+(﹣3)×2﹣17.(2017年贵州安顺，第19题8分)计算：(18.1. (2017海南,第19题10分)计算：(1)12×(﹣)+8×22﹣(﹣1)2 ﹣﹣. . ﹣| ﹣2)0+()1+4cos30°﹣|。