下载文档原格式
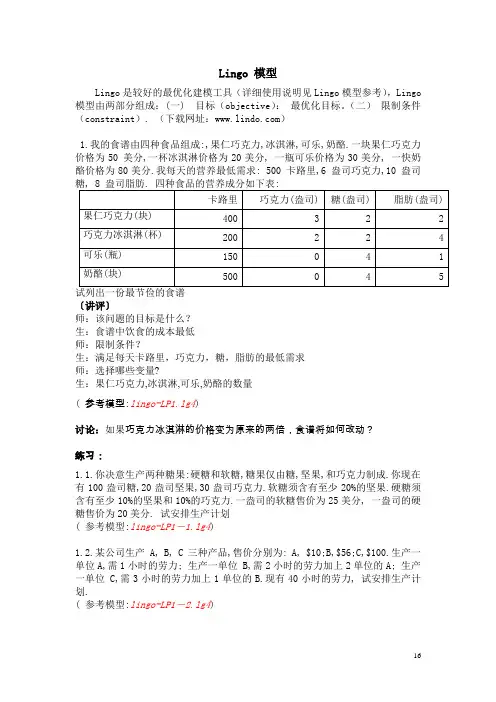
Lingo 模型Lingo 是较好的最优化建模工具（详细使用说明见Lingo模型参考），Lingo 模型由两部分组成：(一) 目标（objective）：最优化目标。
（二）限制条件（constraint）. （下载网址：）1.我的食谱由四种食品组成:,果仁巧克力,冰淇淋,可乐,奶酪.一块果仁巧克力价格为50 美分,一杯冰淇淋价格为20美分, 一瓶可乐价格为30美分, 一快奶酪价格为80美分.我每天的营养最低需求: 500 卡路里,6 盎司巧克力,10 盎司〔讲评〕师：该问题的目标是什么？生：食谱中饮食的成本最低师：限制条件？生：满足每天卡路里，巧克力，糖，脂肪的最低需求师：选择哪些变量?生：果仁巧克力,冰淇淋,可乐,奶酪的数量( 参考模型:lingo-LP1.lg4)讨论：如果巧克力冰淇淋的价格变为原来的两倍，食谱将如何改动？练习：1.1.你决意生产两种糖果:硬糖和软糖,糖果仅由糖,坚果,和巧克力制成.你现在有100盎司糖,20盎司坚果,30盎司巧克力.软糖须含有至少20%的坚果.硬糖须含有至少10%的坚果和10%的巧克力.一盎司的软糖售价为25美分, 一盎司的硬糖售价为20美分. 试安排生产计划( 参考模型:lingo-LP1－1.lg4)1.2.某公司生产 A, B, C 三种产品,售价分别为: A, $10;B,$56;C,$100.生产一单位A,需1小时的劳力; 生产一单位 B,需2小时的劳力加上2单位的A; 生产一单位 C,需3小时的劳力加上1单位的B.现有40小时的劳力, 试安排生产计划.( 参考模型:lingo-LP1－2.lg4)2.Donovan公司生产一种电子产品.已知明年四季度的需求(须按时交货):季度1,4000件; 季度2,2000件; 季度3,3000件; 季度4,10000件;公司员工每年有一个季度休假,每个员工年薪为$30,000,每季度最多可生产500件产品.每个季度末公司须为每件存货付存储费$30.公司现有600件产品,如何安排明年的生产?〔讲评〕师：该问题的目标是什么？生：员工年薪与存储费总和最低师：限制条件？生：每季度初的库存与该季度生产量的和须满足该季度的需求师：如何表示员工总数?生甲：各季度上班的员工x(1),x(2)，x(3),x(4)总和生乙：甲的总和是员工总数的3倍，因为每个员工工作3个季度。
第Ⅱ部分运筹学实验§1 LINGO快速入门一、LINDO/LINGO软件简介LINDO和LINGO是美国LINDO系统公司开发的一套专门用于求解最优化问题的软件，这源于芝加哥大学的Linus Schrage教授于1980年前后开发的一套专门用于求解最优化问题的软件包.LINDO用于求解线性规划和二次规划.目前LINGO除了具有LINDO的全部功能外，还可以用于求解非线性规划，也可以用于一些线性和非线性方程组的求解以及代数方程求根等.LINDO和LINGO软件的最大特色是可以求解决策变量为整数的优化问题，而且执行速度很快. LINGO实际上是一种最优化问题的建模语言，简单易学、包括许多常用的函数可调用，并提供与其它数据文件的接口，易于输入、求解和分析大规模最优化问题. 由于这些特点，LINDO和LINGO软件在教学、科研、工业、商业和服务等领域得到广泛应用.本章着重在Microsoft Windows系统下，介绍lingo9.0在运筹学中的使用和课本中相关问题求解的LINGO实现.二、LINGO软件的安装LINGO软件的安装非常简单，在Windows系统下双击运行安装光盘（或其它源）中的安装程序setup.exe，接受安装协议，选择安装目录,选择默认的LINGO 语法(recommended)，最后完成（finish）安装.安装完成后，第一次运行LINGO软件，这时提示要输入密码，输入正版的密码输入，即可以使用LINGO软件；当然可以选择测试/试用（demo）版本，这时求解变量不能超过300个.运行成功后得到如下窗口：图1.1图1.1中：File(文件)、Edit（编辑）、LINGO、Window（窗口）和Help为下拉菜单项，下面一行为菜单项中的一些快捷工具按钮.主窗口LINGO Model为输入模型的窗口，在没有命名保存(save)模型时，LINGO自动命名为LINGO1，LINGO2等.点击help菜单的About LINGO 可以获得版本的相关信息，如约束(constrain)、变量(variable)、整数变量(integer variable)、非线性变量(nonlinear variable)的限定个数，可用内存（generator memory）使用等.§2求解规划问题一、LINGO 求解LP 问题下面就用简单的例子来说明LINGO 中线性规划问题的求解. 例2.1求如下线性规划问题：2132min x x z +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥≥+0,600210035026..2121121x x x x x x x t s 在LINGO 模型窗口中图2.1输入：图2.1学习要点：（1） 输入max ，min 后LINGO 就会识别优化类型；数学运算符“乘号，除号，乘方”分别输入“*，/，^”； 关系运算符“≥，≤”分别输入“>=,<=” 来表示; 每行命令结束用“；”来表示.（2）算术运算符按优先级从高到低排序为：-（负号）；^；*，/；+，-（减号） （3）关系运算符按优先级从高到低排序为：<，=，>. 输入完毕后，点击求解按钮(或依次点击菜单LINGO/Solve ，或按Ctrl+S)，求解状态窗口（LINGO Solve Status ）被激活，如图2.2：图2.2此窗口显示：当前的求解状态，包括模型的类型（Model ），解的状态类型（State ），目标值（objective ）等，如果模型由于陷入循环等一时无法得到解，可以点击中断求解按钮（Interrupt Solver ）.学习要点：（1）LINGO 默认所有变量非负.（2）LINGO 关于求解的种类一般有如下几种（在asibility 处显示）：0 全局最优（Global Optimum ） 1 不可行（Infeasible ） 2 无界（Unbounded ）3 不确定（Undetermined ）4 可行（Feasible ）5 可行或者无界（Infeasible or Unbounded ）6 局部最优（Local Optimum ）7 局部不可行（Locally Infeasible ） 8 目标函数的截断值被达到（Cutoff ） 9 算术运算错误而停止（Numeric Error ）当关闭（Close ）求解状态窗口时，求解报告窗口（Solution Report ）被激活，如图2.3：图2.3求解报告显示：求解所需的迭代次数（iteration ）（线性规划默认单纯形法）；变量的值（value ）；及变量变化一个单位时，目标值发生的变化量（Reduced Cost ）；以及松弛或剩余变量（Slack or Surplus ，按模型输入行的顺序显示）的值和对偶价格（Dual Price ）.二、LINGO 求解ILP 问题例2.2 求如下整数规划问题：2123max x x z +=⎪⎩⎪⎨⎧≥≤+≤+且为整数0,14325.45.0..212121x x x x x x t s 在LINGO 模型窗口中按如图2.4输入：图2.4点击求解按钮，就会得到：求解状态窗口显示为纯整数规划（PILP ），全局最优解得到.求解报告窗口显示最优解为x1=4，x2=1，最优值为14. 学习要点：（1）“！”后面可添加为注释语句(注释以英文标识下“；” 结束)； “title ” 命令可以添加文档的标题和注释，在解的报告里会显示； LINGO 只有在“！”和“title ” 命令后才可以使用中文字符. （2）LINGO 不区分大小写；（3）LINGO 模型的目标、约束和约束之间的顺序可以颠倒； （4）变量界定函数：@gin(x) ：限制x 为整数. @bin(x) ： 限制x 为0或1； @bnd(L,x,U) ： 限制L ≤ x ≤ U ；@free(x) ： 取消对变量x 的默认下界为0的限制，即x 可以为任意 实数；其中符号“@”表示调用函数；三、LINGO 求解非线性规划(NLP)问题例2.3 求如下非线性规划问题：322312119210max x x x x x z -+-+= ⎩⎨⎧≥≤+0,5..2121x x x x t s在模型窗口中输入:max=10*x1+2*x1^2-*x1^3+9*x2-x2^3;x1+x2<=5;运行结果为：x1=2.61，x2=1.73，z=32.33.§3 灵敏度分析对模型的目标函数的系数，约束右端项进行灵敏度分析，首先要激活灵敏度分析.依次点击菜单LINGO|Option|General Solver Tab ，在Dual Computations 列表框中，选择Prices and Ranges 选项.当求解模型时，也作出了灵敏度分析，可以点击菜单LINGO 中的Range （Ctrl+R ）来查看.例2.4 对例1.1的线性规划模型，按照上述步骤作灵敏度分析，打开灵敏度分析报告（Range Report ）显示如图3.1：图3.1灵敏度分析报告中显示，当前模型中的目标系数(Current Coefficient),约束右端项( Current RHS), 对应参数在其它条件不变的情况下，可允许的增加量和减少量(Allowable Increase, Allowable Decrease),INFINITY 表示无穷.本例显示在其它参数不变的情况下，参数在下列变化范围内，最优基保持不变：目标函数中1x 的系数为2，其允许变化范围为)0,()22,(-∞=--∞，2x 的系数为3，其允许变化范围为)0,()33,(-∞=--∞；第一个约束右端项为350，其允许变化范围为)600,()250350,(-∞=+-∞，第二个右端项为100，其可变化范围为)300,3333.58()200100,6667.41100(=+-，第三个右端项600，其可变化范围为),200(),400600(+∞=+∞-.§4 LINGO中集合的定义与操作当模型的变量、数据较多时，按照前面按照模型逐个输入的办法，就显得力不从心了.LINGO是一种建模语言，使用LINGO语言可以通过输入简单的文字而代替大规模变量和约束，处理大型问题就得心应手.理解LINGO语言，最重要的是理解集合（sets）和属性（atrribute）的概念.下面我们从简单例子出发来说明这些问题.一、定义一个基本集（原始集）基本集的格式为：集合名/成员1，成员2，…/：属性1，属性2，…;例 4.1 产生表示价格的向量x=[35 26 45 78 69 66]：在模型窗口中输入如图4.1：图4.1运行得到：Variable ValueX(1) 35.00000X(2) 26.00000X(3) 45.00000X(4) 78.00000X(5) 69.00000X(6) 66.00000例 4.2 定义一个名为产品的的基本集（可记为products），包括三种产品A,B和C（即它具有成员A,B和C），现在想研究它们对应的单位价格120、100和80以及对应的质量等级1、2和3（即属性可以记为price, quality）在模型窗口中输入如图4.2：图4.2运行结果为：Variable ValuePRICE(A) 120.0000PRICE(B) 100.0000 PRICE(C) 80.00000 QUALITY(A) 1.000000 QUALITY(B) 2.000000 QUALITY(C) 3.000000学习要点：（1）定义一个基本集：集合名/集合的成员/：属性，属性，…，属性; （2）集合要夹在sets 和endsets 之间；（3）连续可编号的n 个成员可以使用1..n 或用带字母的编号表示如w1..wn 来输入，也可以直接以逗号间隔，将n 个成员输入为w1，…，wn ；（4）数据部分要夹在data 和enddata 之间； （5）成员可以当作数据输入.二、定义一个派生集派生集的基本格式：派生集名（基本集1，基本集2，…）：属性1，属性2，…;例4.3 导入矩阵⎥⎦⎤⎢⎣⎡=645241A . 在模型窗口中输入如图4.3：图4.3运行结果为：Variable Value A(1,1) 1.000000 A(1,2) 2.000000 A(1,3) 4.000000 A(2,1) 4.000000 A(2,2) 5.000000 A(2,3) 6.000000例4.4 产生矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=314022221221B ，其中“-”表示对应位置没有数据. 在模型窗口中输入如图4.4：图4.4运行结果为：Variable ValueB(1,1) 21.00000B(1,3) 40.00000B(2,1) 12.00000B(2,2) 22.00000B(3,2) 22.00000B(3,3) 31.00000例4.5 在模型窗口中输入：sets:product/1..2/;quality/1..2/;cost/1..2/;links(product,quality,cost):x;endsets运行后会发现：派生集合links产生八个成员：(1,1,1)， (1,1,2)，(1,2,1)，(1,2,2) ，(2,1,1)，(2,1,2)，(2,2,1)，(2,2,2).学习要点：（1）派生集的基本格式为：派生集名（基本集1，基本集2）：属性1，属性2，…，属性n;利用派生集可以产生多维数组，它是基本集合成员的所有可能组合；（2）对于派生集，可以定义其具体的成员，其格式与基本集的格式类似：派生集名（基本集1，基本集2）/成员/：属性1，属性2，…，属性n;（3）在例4.4中只取了派生集links中的一些元素，也称为稀疏集.三、集循环函数集循环函数是指对集合的元素进行循环操作的函数，其格式为：@函数名（集合（指标）|过滤条件：表达式）函数有for，max，min，prod，sum五种，分别表示对集合满足过滤条件的每一元素：独立生成表达式，求最大元素，求最小元素，计算乘积，求和.下面以简单例子来介绍@for和@sum函数的使用：1、@for例4.6 产生序列{4 9 16 25 36 49}.在模型窗口中输入：model:sets:number/1..7/:x;endsets@for(number(i)|i#ge#2:x(i)=i^2);end运行结果为：X(2) 4.000000X(3) 9.000000X(4) 16.00000X(5) 25.00000X(6) 36.00000X(7) 49.000002)@sum 求和例4.7 对数列1 2 5 4 6求和.在模型窗口中输入：model:sets:number/1..5/:x;endsetsS=@sum(number(I):x(I));data:x=1 2 5 4 6 ;enddataend运行结果为：Variable ValueS 18.00000X(1) 1.000000X(2) 2.000000X(3) 5.000000X(4) 4.000000X(5) 6.000000学习要点：（1）一个模型可写在model和end之间，这是为了表示一个完整的模型，不至于与模型窗口中的其它模型混淆；（2）集合中使用符号“|”表示其后为过滤条件，只有集合中满足条件的指标才执行其后的表达式；（3）如使用循环函数时，其中number(i) 表示集合number中的第i个元素，循环函数就会遍历number中满足条件的每个元素，执行其后所有表达式；（4）“ge”为逻辑符号，表示“大于等于”，逻辑运算符使用时要夹在“#”之间；所有逻辑运算符按优先级顺序由高到低排序为：not（非）；eq（等于），ne（不等于），gt（大于），lt（小于）；ge（大于等于），le（小于等于）；and（与），or（或）.§5 求解运输问题学习了LINGO的集合操作之后，运输问题就可以编写成简单的LINGO程序来求解.例5.1计算有5个产地A1—A5，8个销地B1-B8的运输问题的最优调运方案.分析：六个产地的总产量和为160，8个销售地的销量和为264，故产销不平衡，销大于产.定义集合workshop为有六个成员的产地，shop为有八个成员的销地，a为产量，b为销量，c为单位运价，x为待求调运量，编写程序如图5.1：图5.1运行部分结果为：Objective value: 272.0000X(W1,V1) 0.000000X(W1,V2) 0.000000X(W1,V3) 8.000000X(W1,V4) 0.000000X(W1,V5) 12.00000. . . . . . . .X(W5,V5) 0.000000X(W5,V6) 0.000000X(W5,V7) 0.000000X(W5,V8) 0.000000学习要点：（1）当销大于产时，对任意的销地j，从各个产地调往j的调运量之和不大于b（j），即有需求约束中为小于等于号；若产大于销，则产量约束中为小于等于号；（2）目标函数可以进一步简化为：min=@sum(links: c*x)不影响结果.§6求解网络问题一、最短路问题例6.1 用LINGO 求解图论中§6.3中例6.3.1所示的图6.3.1中从始点1到终点8的最短路问题的求解.分析：图中有8个顶点，需求出从结点1到结点8的最短路；设决策变量⎩⎨⎧=其它，的最短路上到于结点）（当081位,弧,1j i x ij 可把最短问题转化成一个规划问题，∑∈=Ej i ijijxw z ),(min⎪⎪⎩⎪⎪⎨⎧∈≥⎪⎩⎪⎨⎧-=-∑∑∈=∈=E j i x i ，i ，i ，x x ijEi j j ji Ej i j ij ),(,008111s.t.8),(18),(1为中间点为终点为始点 其中ij w 为弧),(j i 上的权（即结点i 与结点j 之间的距离） 在模型窗口中编写程序如图6.1：图6.1运行后部分结果为：Objective value: 12.00000Variable ValueX(1,6) 1.000000 X(5,8) 1.000000 X(6,7) 1.000000 X(7,5) 1.000000这表明路线85761→→→→为从始点1到终点8的最短路，长度为12.学习要点：（1）对无向图要把始点出发的弧和到达终点的弧当作单向弧，其余的等价为双向弧；（2）终点约束与其余约束线性相关可以省略；二、最大流问题例6.2下面介绍运用LINGO 求解§6.4中例6.4.1中图6.4.1所示的从始点s 到终点t 的最大流问题的求解.分析：根据最大流问题的要求和平衡条件，用flow 表示可行流量，可以把它转化成一个规划问题，flow max⎪⎪⎩⎪⎪⎨⎧∈≤≤⎪⎩⎪⎨⎧-=-∑∑∈∈∈∈Aj i c f i ，ti flow ，s i flow ，f f ij ij Ai j V i ji Aj i V j ij ),(,00s.t.),(),(为中间点为终点为始点 在模型窗口中编写程序如图6.2：图6.2运行得到一种最大流方案为：FLOW 22.00000F(S,4) 8.000000 F(2,3) 4.000000F(2,5) 10.00000 F(3,T) 4.000000 F(4,5) 8.000000 F(5,3) 0.000000 F(5,T) 18.00000三、最小费用最大流问题例6.3用LINGO 求解书中§6.5中图6.5.1所示的从始点s 到终点t 的最小费用最大流问题的求解.分析：根据最大流问题的要求和平衡条件，用F 表最大流量，可以把它转化成一个规划问题，∑∈Aj i ij ijf b),(min⎪⎪⎩⎪⎪⎨⎧∈≤≤⎪⎩⎪⎨⎧-=-∑∑∈∈∈∈Aj i c f i ，ti F ，s i F ，f f ij ij Ai j V i ji A j i V j ij ),(,00s.t.),(),(为中间点为终点为始点 根据最大流的求法可求得此网络的最大流量Q=15，编写程序如图6.3：图6.3运行得到一种最小费用最大流方案为：Objective value: 69.00000 F(S,2) 8.000000 F(S,3) 7.000000 F(2,3) 0.000000F(3,4) 7.000000F(4,2) 1.000000F(4,T) 6.000000这与增广链和最短路标号法求得的结果一致.§7 LINGO中外部数据文件的调用一、LINGO中调用文本文件数据调用文本数据函数@file(‘filename’)用于将文本文件中的数据调入LINGO 模型中，可以写相对和绝对路径，文件中的每组数据之间用符号“~”间隔，LINGO 将按照此函数在模型中出现的顺序依次读取每组数据.下面以简例说明之.例7.1 对x=[2 5 8]求和，对y=[3 6 1 4]取其最小元.按如图7.1在模型窗口中编写程序：图7.1其中data1.txt文件与此模型放在同一目录下，内容编写如图7.2：图7.2运行结果可得：S 15.00000，P 1.000000二、LINGO中调用excel数据电子表格数据调用函数@ole(‘filename’)用于将excel表中的数据导入LINGO，文件路径设置与@file函数一致，例7.2 对例7.1，可编程如图7.3：图7.3其中data2.xls文件与模型放在同一目录，编辑如图7.4：图7.4其中要定义单元格A3：A5为集合的名称price，B3：B5定义为x，C3：C6定义为y.定义单元格名称的方法是：选定要定义的单元格，依次打开菜单插入|名称|定义，输入想要定义的名称即可.学习要点：（1）@file和@ole函数可以在模型的集合段，数据段和开始段使用，其他段落不能使用.（2）@ole函数的完整格式为：@ole(‘filename.xls’，[rangelist])，其中rangelist为包含数据的单元范围（与excel表格中的记法一致）（3）这两个函数在集合段可以直接采用@file(‘filename’)和@ole(‘filename’)的形式，而在数据段要采用x=@file(‘filename’)或@ole(‘filename’)格式.。
lingo课程设计分析一、教学目标本课程的教学目标是使学生掌握Lingo语言的基本语法、词汇和句型，能够运用Lingo语言进行简单的交流和表达。
具体目标如下：1.掌握Lingo语言的基本语法结构。
2.学习并掌握100个以上Lingo语言的常用词汇。
3.了解Lingo语言的文化背景和用法。
4.能够用Lingo语言进行简单的自我介绍和日常交流。
5.能够阅读并理解简单的Lingo语言文本。
6.能够用Lingo语言撰写简单的句子和段落。
情感态度价值观目标：1.培养学生对Lingo语言的兴趣和学习的积极性。
2.培养学生跨文化交流的意识和能力。
3.培养学生合作学习和自主学习的能力。
二、教学内容根据课程目标，教学内容主要包括以下几个方面：1.Lingo语言的基本语法结构，包括词序、时态、语态等。
2.Lingo语言的常用词汇，包括日常生活、工作、学习等方面的词汇。
3.Lingo语言的文化背景和用法，包括礼仪、习惯、表达方式等。
教学大纲安排如下：第一周：Lingo语言的基本语法结构。
第二周：Lingo语言的词汇学习。
第三周：Lingo语言的文化背景和用法。
第四周：综合练习和复习。
三、教学方法本课程采用多种教学方法，以激发学生的学习兴趣和主动性：1.讲授法：教师讲解Lingo语言的基本语法和词汇，引导学生理解和掌握。
2.讨论法：学生分组讨论Lingo语言的用法和表达方式，促进交流和合作。
3.案例分析法：教师提供真实的Lingo语言使用场景，学生分析并运用所学知识解决问题。
4.实验法：学生通过模拟情景，进行Lingo语言的实际操作和练习。
四、教学资源本课程所需教学资源包括：1.教材：选用权威出版的Lingo语言学习教材。
2.参考书：提供Lingo语言的语法、词汇等方面的参考书籍。
3.多媒体资料：制作精美的PPT、视频、音频等多媒体教学资料。
4.实验设备：提供计算机、投影仪等实验设备，以便进行实验和实践操作。
五、教学评估本课程的评估方式包括以下几个方面，以保证评估的客观性和公正性：1.平时表现：通过观察学生在课堂上的参与度、发言情况等，评估学生的学习态度和积极性。
LINGO 使用教程LINGO 是用来求解线性和非线性优化问题的简易工具。
LINGO 内置了一种建立最优化模型的语言，可以简便地表达大规模问题，利用LINGO 高效的求解器可快速求解并分析结果。
§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时，会得到类似下面的一个窗口：外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口，建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例1.1 如何在LINGO 中求解如下的LP 问题：,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码： min =2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。
例1.2 使用LINGO 软件计算6个发点8个收点的最小费用运输问题。
产销单位运价如model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。
