第七章多目标函数的优化设计方法7.1多目标最优化数学模型-Read
- 格式:ppt
- 大小:2.00 MB
- 文档页数:24

第七章多目标函数的优化设计在实际问题的解决过程中,往往会面临多个目标的优化设计。
传统的优化方法常常只关注单一目标的优化,无法同时兼顾多个目标的需求。
因此,多目标函数的优化设计成为了一个重要的研究领域。
多目标函数的优化设计涉及到多个目标函数的最优化问题,称为多目标优化问题。
多目标优化问题的解决方法有两类:一类是将多目标优化问题转化为单目标优化问题,另一类是直接解决多目标优化问题。
第一种方法是将多目标优化问题转化为单目标优化问题。
这种方法通常会使用一些合成目标函数或加权目标函数的方式来将多个目标函数合并为一个单目标函数。
常用的方法有加权和法、Tchebycheff法、罚函数法等。
但是这种方法不仅涉及到目标函数之间的比重问题,而且通常只能得到近似解,并不能完全解决多目标优化问题。
第二种方法是直接解决多目标优化问题。
这种方法通常会利用一些优化算法来求解多目标优化问题,如遗传算法、粒子群算法、蚁群算法等。
这些算法通常是基于群体智能的思想,通过不断的迭代来寻找最优解的近似解。
这些算法通常会生成一组近似最优解,即所谓的帕累托解集。
帕累托解集是多目标优化问题的解集,其中的解称为帕累托解。
帕累托解的定义是指在解集中没有其他解能够改进一个解的一些目标函数值而不损害其他目标函数值的解。
帕累托解集的大小和分布会影响多目标优化问题的解决质量。
因此,如何有效地生成帕累托解集成为了多目标优化问题研究的一个重要方向。
除了解决多目标优化问题的方法外,还需要考虑如何对多目标优化问题的解进行评价。
常用的评价指标有全局评价指标和局部评价指标。
全局评价指标能够反映整个帕累托解集的性能,常用的指标有最小距离、全局适应度值、发散度等。
局部评价指标用于评价帕累托解集中的个体解的性能,常用的指标有支配关系、可行性等。
总结起来,多目标函数的优化设计是一个重要的研究领域,涉及到多个目标函数的最优化问题。
解决多目标函数的优化设计可以采用将多目标优化问题转化为单目标优化问题的方法或者直接解决多目标优化问题的方法。

7多目标优化方法多目标优化是指同时优化多个目标函数的问题,它在很多实际问题中具有重要的应用价值。
以下是七种常见的多目标优化方法:1.加权方法:加权方法是最简单的多目标优化方法之一、它将多个目标函数线性组合成一个单独的目标函数,并通过加权系数来控制各个目标函数的重要程度。
这种方法的优点是简单易实现,但需要根据问题的具体情况确定权重。
2.建模和求解方法:建模和求解方法将多目标优化问题转化为单目标优化问题,通过建立适当的模型和求解算法来解决。
其中一个常见的方法是基于遗传算法的多目标优化方法,通过遗传算法的进化过程来目标函数的近似最优解。
3. Pareto优化方法:Pareto优化方法是一种非支配排序方法,通过对解集进行排序和筛选,找到Pareto最优解集合。
Pareto最优解是指在没有劣化其他目标函数的情况下,无法通过优化任何一个目标函数而使得其他目标函数有所改善的解。
这种方法能够找到问题的一些最优解,但可能无法找到所有的最优解。
4.基于指标的方法:基于指标的方法通过定义一些评价指标来度量解的质量,并根据这些指标来选择最优解。
常用的指标包括距离指标、占优比例指标等。
这种方法能够在有限的时间内找到一些较优的解,但在有些情况下可能会丢失一些最优解。
5.多目标粒子群优化方法:多目标粒子群优化方法是一种基于粒子群算法的多目标优化方法。
它通过多种策略来维护多个最优解,并通过粒子调整和更新来逐步逼近Pareto最优解。
这种方法具有较好的全局能力和收敛性能。
6.模糊多目标优化方法:模糊多目标优化方法将隶属度函数引入多目标优化问题中,通过模糊规则和模糊推理来处理多目标优化问题。
它能够处理含有不精确信息或不确定参数的多目标优化问题。
7.多目标进化算法:多目标进化算法是一类通过模拟生物进化过程来解决多目标优化问题的方法,其中包括多目标遗传算法、多目标蚁群算法、多目标粒子群优化等。
这些方法通过维护一个种群来Pareto最优解,通过进化操作(如交叉、变异等)来逐步优化解的质量。

多目标优化数学模型是指在优化问题中存在多个目标函数的情况下,通过数学建模来求解最优解。
多目标优化问题可以形式化为如下形式:
$$
\begin{align*}
\text{minimize} \quad f_1(x) \\
\text{subject to} \quad f_2(x) \leq 0 \\
\quad f_3(x) \leq 0 \\
\quad \vdots \\
\quad f_m(x) \leq 0 \\
\end{align*}
$$
其中,$x$是决策变量,$f_1(x), f_2(x), \ldots, f_m(x)$是目标函数,$m$是目标函数的个数。
在多目标优化中,通常存在多个不同的最优解,这些最优解构成了一个被称为Pareto前沿(Pareto front)的集合。
Pareto前沿是指在所有满足约束条件的解中,无法通过改变一个目标函数的值而使其他目标函数的值变得更好的解。
求解多目标优化问题的常用方法包括遗传算法、粒子群算法、模拟退
火算法等。
这些算法通过在解空间中搜索,逐步逼近Pareto前沿,从而得到一组近似最优解。
多目标优化数学模型的应用非常广泛,例如在工程设计中,可以通过多目标优化来平衡不同的设计目标,如成本、性能、可靠性等;在金融投资中,可以通过多目标优化来平衡风险和收益等。






最优化_第7章多目标及离散变量优化方法在实际问题中,往往存在多个相互关联的优化目标,这就引出了多目标优化问题。
与单目标优化问题相比,多目标优化问题更加复杂,需要综合考虑多个目标之间的平衡和权衡。
多目标优化方法可以分为基于加权法的方法和基于多目标遗传算法的方法。
其中,基于加权法的方法将多个目标函数转化为单一的综合目标函数,通过对综合目标函数的优化来求解多目标优化问题。
而基于多目标遗传算法的方法则直接将多目标函数进行优化,通过一系列的遗传算子(如选择、交叉和变异)来逐步逼近多目标的最优解。
在多目标优化问题中,离散变量的存在进一步增加了问题的复杂性。
离散变量是指变量的取值只能是有限个数中的一个,与连续变量不同。
针对离散变量的多目标优化问题,可以采用遗传算法、粒子群算法等进化计算方法进行求解。
这些算法通常会使用染色体编码来表示离散变量,采用相应的遗传算子对染色体进行进化操作。
在实际应用中,多目标及离散变量优化方法可以应用于多个领域。
举个例子,对于资源分配问题,可以将资源的分配方案和目标函数(如成本、效益、风险等)作为多个目标进行优化,得到最优的资源分配方案。
又比如,在工程设计中,可以将设计方案的多个目标(如性能、重量、成本等)作为优化目标,找到最优的设计方案。
总之,多目标及离散变量优化方法是解决实际问题中复杂优化问题的有效手段。
通过综合考虑多个目标和处理离散变量,可以得到更加全面和合理的最优解,提高问题的解决效果。
在实际应用中,需要选择合适的优化方法和算法,并针对具体问题进行适当的调整和改进,以获得更好的优化结果。

第9章 多目标函数的优化设计方法Chapter 9 Multi-object Optimal Design在实际的机械设计中,往往期望在某些限制条件下,多项设计指标同时达到最优,这类问题称为多目标优化设计问题。
与前面单目标优化设计不同的是,多目标优化设计有着多种提法和模式,即数学模型。
因此,解决起来要比单目标问题复杂的多。
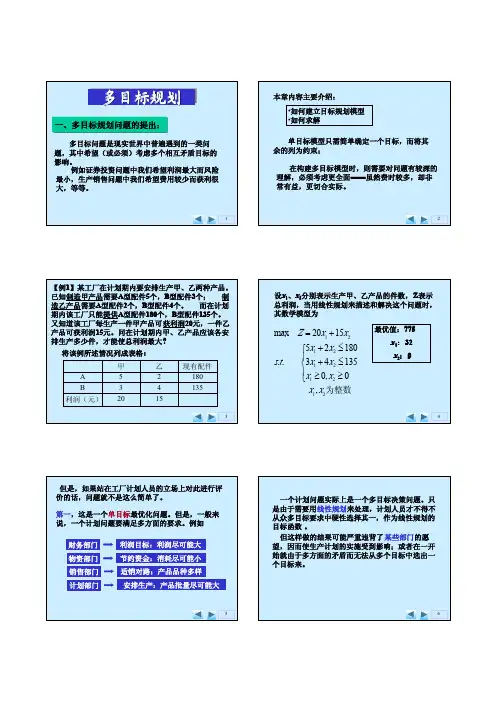
9.1 多目标最优化模型9.1.1 问题举例例9-1 生产计划问题 某工厂生产n (2≥n )种产品:1号品、2号品、...、n 号品。
已知:该厂生产)...,,2,1(n i i =号品的生产能力是i a 吨/小时; 生产一吨)...,,2,1(n i i =号品可获利润i α元;根据市场预测,下月i 号品的最大销售量为)...,,2(n i b i =吨; 工厂下月的开工能力为T 小时; 下月市场需要尽可能多的1号品。
问题:应如何安排下月的生产计划,在避免开工不足的条件下,使 工人加班时间尽可能的地少;工厂获得最大利润;满足市场对1号品尽可能多地要求。
为制定下月的生产计划,设该厂下月生产i 号品的时间为)...,,1(n i x i =小时。
9.1.2 基本概念如图9.1所示,两个目标函数f 1,f 2中的若干个设计中,3,4称为非劣解,若)(min{)(*x f x f j j ≤S.t .0)(≤x g u u=1,2,………….m成立,则称*x 为非劣解。
若不存在一个方向,同时满足:0)(*≤*∇s x f (目标函数值下降0)(*≤*∇s x g (不破坏约束)图9.1则称*x 为约束多目标优化设计问题的K-T 非劣解。
这样,多目标优化设计问题的求解过程为:先求出满足K-T 条件的非劣解,再从众多的非劣解确定一个选好解。
多目标优化的数学模型:T r x f x f x f X F V )](),........(),([)(min 21=--S.t .0)(≤x g u u=1,2,………….m0)(=x h v v=1,2,……….p式中:)(X F 是向量目标函数。
第六章最优化数学模型§ 1最优化问题1. 1最优化问题概念1. 2最优化问题分类1. 3最优化问题数学模型§ 2经典最优化方法2. 1无约束条件极值2. 2等式约束条件极值2. 3不等式约束条件极值§ 3线性规划3. 1线性规划3. 2整数规划§ 4最优化问题数值算法4. 1直接搜索法4. 2梯度法4. 3罚函数法§ 5多目标优化问题5. 1多目标优化问题5. 2单目标化解法5. 3多重优化解法5. 4目标关联函数解法5. 5投资收益风险问题第八早最优化冋题数学模§ 1最优化问题1. 1最优化问题概念(1)最优化问题在工业、农业、交通运输、商业、国防、建筑、通信、政府机关等各部门各领域的实际工作中,我们经常会遇到求函数的极值或最大值最小值问题,这一类问题我们称之为最优化问题。
而求解最优化问题的数学方法被称为最优化方法。
它主要解决最优生产计划、最优分配、最佳设计、最优决策、最优管理等求函数最大值最小值问题。
最优化问题的目的有两个:①求出满足一定条件下,函数的极值或最大值最小值;②求出取得极值时变量的取值。
最优化问题所涉及的内容种类繁多,有的十分复杂,但是它们都有共同的关键因素:变量,约束条件和目标函数。
(2)变量变量是指最优化问题中所涉及的与约束条件和目标函数有关的待确定的量。
一般来说,它们都有一些限制条件(约束条件),与目标函数紧密关联。
设问题中涉及的变量为X1,X2, ,X n ;我们常常也用X =(X1,X2,…,X n)表示。
(3)约束条件在最优化问题中,求目标函数的极值时,变量必须满足的限制称为约束条件例如,许多实际问题变量要求必须非负,这是一种限制;在研究电路优化设计问题时,变量必须服从电路基本定律,这也是一种限制等等。
在研究问题时, 这些限制我们必须用数学表达式准确地描述它们。
用数学语言描述约束条件一般来说有两种: 等式约束条件 g j (X)=o, i =1,2- ,m 不等式约束条件hj(X) _o,i =12…,r 或 h j (X)乞 0,i =1,2,…,r注:在最优化问题研究中,由于解的存在性十分复杂,一般来说,我们不考虑不 等式约束条件h(X) 0或h(X):::0。
第七章多目标及离散变量优化方法第七章主要介绍了多目标优化和离散变量优化的方法。
在传统的单目标优化问题中,目标函数是一个标量,优化的目标是找到使得目标函数取得最小或最大值的输入变量。
然而,在实际应用中,很多问题往往涉及到多个冲突的目标,而且这些目标往往是矛盾的,即优化一个目标会损害其他目标的性能。
为了解决这种多目标优化问题,有许多方法被提出。
其中一个常用的方法是将多目标优化问题转化为单目标优化问题,通过将多个目标函数组合成为一个综合目标函数来进行优化。
常用的组合方法有加权求和、加权乘积、最大最小法等。
这些方法的主要问题在于需要确定每个目标函数的权重或权值,这在实际应用中是非常困难的。
另一种方法是通过引入Pareto优化的概念来解决多目标优化问题。
Pareto优化是通过找到一组解集,使得没有其他解能同时改善所有的目标函数,从而得到一组最优解。
这些解被称为Pareto最优解,而Pareto 最优解集合则被称为Pareto前沿。
Pareto最优解集合是一个非支配解集合,其中的解没有一个目标函数比其他解更好,并且至少有一个目标函数比其他解更好。
离散变量优化是另一个经典的优化问题。
离散变量是指变量的取值是有限的、离散的。
这种问题在实际应用中非常普遍,比如组合优化、路径规划等问题。
离散变量优化的一个常用方法是使用遗传算法。
遗传算法是一种模拟生物进化过程的优化方法,通过模拟选择、交叉和变异的过程来最优解。
在离散变量优化中,变异操作通常被定义为在一些变量的取值范围中随机选择一个取值,然后替换原来的取值。
除了遗传算法,其他的优化方法如模拟退火算法、粒子群算法等也可以用于离散变量优化。
这些方法在解决离散变量优化问题时通常需要定义合适的邻域关系和评估函数,以在空间中进行。
综上所述,多目标和离散变量优化是优化问题中常见的两个特殊情况。
多目标优化需要考虑多个冲突的目标函数,而离散变量优化需要考虑变量取值的离散性。
针对这两个问题,有很多方法被提出,并且在实际应用中得到了广泛的应用。