系统辨识总结

系统辨识的读书报告经过对系统辨识半个学期的课上学习和课下的论文查阅，我已经对系统辨识有了一定的认识和了解。

它是伴随着现代控制理论的产生而发展起来的一门独立的学科，系统辨识(System Identification)就是假设系统输入U(t)和输出Y(t)已知，求系统的传递函数G(s)，即通过采集系统的输入输出数据来研究确定系统数学模型的理论和方法。

系统辨识有很多用途，在现代社会中也变得越来越重要。

凡是需要通过实验数据确定数学模型和估计参数的场合都要利用辨识技术，辨识技术现在已经推广到工程和非工程的许多领域，如化学化工过程、核反应堆、电力系统、航空航天飞行器、生物医学系统、社会经济系统、环境系统、生态系统等。

在预测方面，系统辨识的目的是用系统的可测量的输入和输出去预测系统输出的未来的演变。

例如最常见的气象预报，洪水预报，其他如太阳黑子预报，市场价格的预测，河流污染物含量的预测等。

而在控制领域，系统辨识是利用描述控制系统动态特性的数学模型设计控制器，来更好的对系统进行控制。

系统辨识的核心就是采集系统的输入输出数据来研究确定系统数学模型，由于建立数学描述的目的是要帮助分析和解决实际问题，认识客观世界，因此，所构建的模型最终要应用到现实世界中去，也就是说，作为被控对象进行控制，抽象出的模型必须能够代表原系统。

建立研究对象的数学模型主要有两条途径。

第一条途径是利用人们已有的关于对象的知识(如利用物理规律、能量和质量守恒方程及系统部件之间的关系等)，通过对对象自身运动机理的分析确定研究对象的数学结构和参数，从理论上推导出对象的数学模型，得到的模型称为理论模型。

由于客观世界运动关系的复杂和人类认识水平的局限，理论模型的建立特别是对复杂对象来说是非常困难的，一般都需要大量简化条件和假设，而且这类模型的数学求解过程异常复杂，难以理解，甚至不可获得，更难以指导实践和在实际工程中推广应用。

建立数学模型的第二条途径源于现代系统理论的发展与应用，它是根据对一个已经存在的对象或系统的观察、测量所得到的大量的输入、输出数据，推断出被研究对象的数学模型，这就是系统辨识过程，得到的数学模型称为经验模型。

系统辨识算法一、引言系统辨识是指通过对系统输入输出数据进行观测和分析，从而建立数学模型以描述和预测系统行为的过程。

系统辨识算法是在给定输入输出数据的基础上，利用数学方法和计算机模拟技术，对系统的结构和参数进行估计和辨识的算法。

系统辨识算法在控制工程、信号处理、机器学习等领域具有广泛的应用。

二、系统辨识方法系统辨识方法可以分为参数辨识和非参数辨识两类。

1. 参数辨识参数辨识是指通过对系统模型中的参数进行估计，来描述和预测系统的行为。

常用的参数辨识方法有最小二乘法、最大似然估计法、递推最小二乘法等。

最小二乘法是一种基于最小化误差平方和的优化方法，通过优化目标函数来估计参数值。

最大似然估计法是一种基于概率统计理论的方法，通过似然函数最大化来估计参数值。

递推最小二乘法是一种基于递推迭代的方法，通过更新参数估计值来逼近真实参数值。

2. 非参数辨识非参数辨识是指通过对系统的输入输出数据进行分析，来估计系统的结构和参数。

常用的非参数辨识方法有频域分析法、时域分析法、小波分析法等。

频域分析法是一种基于信号频谱特性的方法，通过对输入输出信号的频谱进行分析，来估计系统的频率响应。

时域分析法是一种基于信号时域特性的方法，通过对输入输出信号的时序关系进行分析，来估计系统的时域特性。

小波分析法是一种基于小波变换的方法，通过对输入输出信号的小波变换系数进行分析，来估计系统的时频特性。

三、系统辨识应用系统辨识算法在实际工程中有着广泛的应用。

1. 控制工程系统辨识算法在控制系统设计中起到关键作用。

通过对控制对象进行辨识，可以建立准确的数学模型，从而设计出性能优良的控制器。

例如，在自适应控制中，可以利用系统辨识算法来实时辨识系统模型，从而根据实际系统特性调整控制器参数。

2. 信号处理系统辨识算法在信号处理领域有重要应用。

通过对信号进行辨识，可以提取信号的特征和结构，从而实现信号去噪、信号分析、信号识别等目标。

例如，在语音信号处理中，可以利用系统辨识算法来建立语音模型，进而实现语音识别和语音合成。

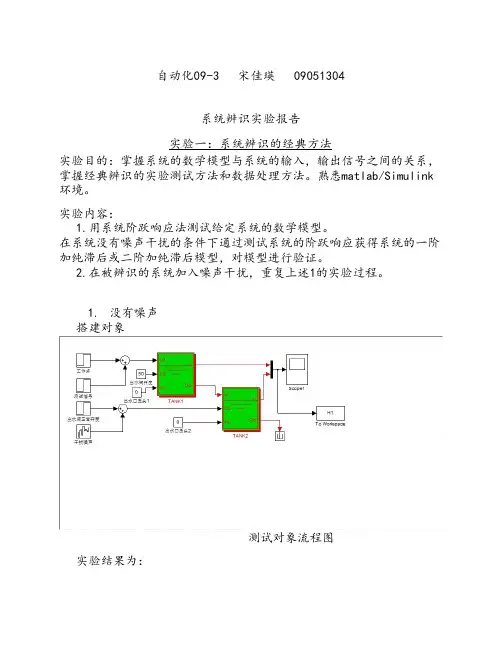
系统辨识根底复习资料知识点汇总：1.所谓系统，按通常的意义去理解，就是按某种相互依赖关系联系在一起的客体的集合。

2.所谓系统辨识，利用对未知系统的试验数据或在线运行数据〔输入/输出数据〕以及原理和原则建立系统的〔数学〕模型的科学。

3.系统辨识的步骤：〔1〕先验知识和建模目的的依据；〔2〕实验设计；〔3〕结构辨识；〔4〕参数估量；〔5〕模型适用性检验。

4.系统的数学模型，描述系统输入与输出之间数量关系的数学表达式称为系统的数学模型。

5. 目前最流行的操纵系统辅助工具是Matlab。

6.机理分析和系统辨识相结合建模方法也称为“灰箱问题〞。

7.机理建模这种建模方法也称为“白箱问题〞。

8.频谱覆盖宽、能量均匀分布是白噪声信号的特点。

9.最小二乘法辨识方法不属于系统辨识的经典方法。

10.关于多阶最小二乘法，描述错误的选项是计算简单，计算量小，只用五步根本的最小二乘法可获得较好的结果。

11.渐消记忆法是指对旧数据加上遗忘因子，按指数加权来使得旧数据的作用衰减。

12.脉冲响应数学模型属于非参数型。

13.检验模型的标准是模型的实际效果，检验应从不同的侧面检验其可靠性。

14.与周期测试信号相比，阶跃响应法不能够比拟精确地反映对象的动态特性。

15.闭环系统前向通道的阶次不是可辨识的。

16.使辨识系统可被辨识的X要求是辨识时间内系统的动态必须被输入信号延续鼓励。

17.观测数据内容不属于系统辨识的根本内容。

18.输入数据不属于系统辨识过程中的3大要素。

19.棕箱不属于按提供的实验信息分类的建模方法。

20.数学建模不属于现代操纵论的三大支柱。

21.不属于传递函数辨识的时域方法的是时间图索法。

22.关于递推算法收敛性的结论错误的选项是递推辅助变量法收敛于非真值。

23.设A为n×n矩阵，B为n×m矩阵，C为m×n矩阵，并且A，A+BC和I+CA-1B 都是非奇异矩阵，则以下等式横成立的是A+BC-1=A-1-A-1BI+CA-1B]-1CA-1。

第02讲系统辨识三要素系统辨识是指通过对系统输入和输出数据的观测和分析，求解出系统的数学模型的过程。

系统辨识主要有两种方法：非参数辨识和参数辨识。

在进行参数辨识时，需要确定三个基本要素，分别是模型结构、参数估计方法和误差分析方法。

本文将详细介绍这三个要素。

首先，模型结构是系统辨识的核心要素之一、模型结构决定了辨识出的数学模型与实际系统之间的对应关系。

模型结构的选择需要根据实际问题和已有的知识和经验来确定。

常用的模型结构包括线性模型、非线性模型、时变模型等。

例如，对于一个物理系统来说，可以尝试使用一阶惯性环节、二阶惯性环节等常见的线性模型结构进行辨识；对于一个生物系统来说，可以采用Lotka-Volterra模型等非线性模型结构进行辨识。

选择合适的模型结构可以提高系统辨识的精度和可靠性。

其次，参数估计方法是指在给定模型结构的情况下，通过对系统输入和输出数据进行处理和分析，求解出模型参数的过程。

参数估计方法分为两类：最小二乘法和最大似然法。

最小二乘法通过最小化观测数据与模型预测数据之间的残差平方和来估计模型参数；最大似然法通过最大化观测数据的似然函数来估计模型参数。

当观测数据服从高斯分布时，最小二乘法和最大似然法等效。

参数估计方法的选择需要根据数据性质和实际问题来确定。

对于小样本数据，最大似然法常常具有更好的效果；对于大样本数据，最小二乘法通常是更好的选择。

最后，误差分析方法是指用来评估辨识结果的准确性和可信度的方法。

误差分析方法主要包括残差分析、模型检验和辨识结果评价等。

残差分析是通过分析辨识结果与观测数据之间的差异来评估模型拟合程度的方法。

模型检验是通过将辨识结果应用到实际应用中，观察其预测能力和鲁棒性来评价模型的有效性。

辨识结果评价是通过计算模型的性能指标，如均方误差、决定系数等来评估辨识结果的准确性和可靠性。

误差分析方法的选择需要根据实际问题和辨识结果的要求来确定。

对于较为简单的问题，可以选择较为简单的误差分析方法；对于复杂的问题，需要选择更为精确和全面的误差分析方法。

机械系统动力学系统辨识方法综述在机械工程领域，对机械系统动力学特性的准确了解是优化设计、故障诊断、性能预测和控制策略制定的关键。

机械系统动力学系统辨识作为获取系统动态特性的重要手段，一直以来都是研究的热点。

本文将对常见的机械系统动力学系统辨识方法进行综述。

机械系统动力学系统辨识的基本任务是根据系统的输入和输出数据，建立能够准确描述系统动态特性的数学模型。

常见的辨识方法可以大致分为基于时域的方法和基于频域的方法。

时域辨识方法中，脉冲响应函数法是一种常用的技术。

它通过对系统施加一个短脉冲输入，并测量系统的输出响应，从而得到系统的脉冲响应函数。

脉冲响应函数直接反映了系统的动态特性，通过对其进行分析和处理，可以得到系统的数学模型参数。

最小二乘法在时域辨识中也应用广泛。

它基于输入输出数据，通过最小化误差的平方和来估计模型参数。

这种方法计算相对简单，并且在一定条件下具有较好的估计精度。

然而，它对噪声比较敏感，当测量数据中存在噪声时，可能会导致辨识结果的偏差。

卡尔曼滤波法是一种基于状态空间模型的时域辨识方法。

它能够在存在测量噪声和系统不确定性的情况下，对系统状态进行最优估计，并同时估计模型参数。

这种方法在处理多变量系统和时变系统时具有优势。

在频域辨识方法中，频率响应函数法是基础且重要的手段。

通过对系统施加不同频率的正弦输入，并测量系统的稳态输出响应，可以得到系统的频率响应函数。

频率响应函数包含了系统在不同频率下的幅频和相频特性，通过对其进行拟合和分析，可以获得系统的模型参数。

谐波平衡法常用于非线性系统的频域辨识。

它假设系统的响应可以表示为多个谐波的叠加，通过求解非线性方程来确定谐波的系数，从而得到系统的模型。

相干函数分析则用于评估输入和输出之间的线性相关性，帮助判断辨识结果的可靠性。

除了上述传统的辨识方法，近年来还发展出了一些新的技术和方法。

例如，基于神经网络的辨识方法利用神经网络强大的非线性拟合能力，能够处理复杂的非线性机械系统。

系统辨识的常用方法系统辨识是根据系统的输入输出时间函数来确定描述系统行为的数学模型，是现代控制理论中的一个分支。

对系统进行分析的主要问题是根据输入时间函数和系统的特性来确定输出信号。

传统的系统辨识方法（1）脉冲响应脉冲响应一般是指系统在输入为单位冲激函数时的输出（响应）。

对于连续时间系统来说，冲激响应一般用函数h(t)来表示。

对于无随机噪声的确定性线性系统，当输入信号为一脉冲函数δ（t）时，系统的输出响应 h（t）称为脉冲响应函数。

辨识脉冲响应函数的方法分为直接法、相关法和间接法。

①直接法：将波形较理想的脉冲信号输入系统，按时域的响应方式记录下系统的输出响应，可以是响应曲线或离散值。

②相关法：由著名的维纳-霍夫方程得知:如果输入信号u(t)的自相关函数R(t)是一个脉冲函数kδ(t), 则脉冲响应函数在忽略一个常数因子意义下等于输入输出的互相关函数,即h(t)=(1/k)Ruy(t)。

实际使用相关法辨识系统的脉冲响应时，常用伪随机信号作为输入信号，由相关仪或数字计算机可获得输入输出的互相关函数Ruy(t),因为伪随机信号的自相关函数 R(t)近似为一个脉冲函数，于是h(t)=(1/k)Ruy(t)。

这是比较通用的方法。

也可以输入一个带宽足够宽的近似白噪声信号，得到h(t)的近似表示。

③间接法：可以利用功率谱分析方法，先估计出频率响应函数H（ω）, 然后利用傅里叶逆变换将它变换到时域上，于是便得到脉冲响应h(t)。

（2）最小二乘法最小二乘法(LS)是一种经典的数据处理方法, 但由于最小二乘估计是非一致的、有偏差的, 因而为了克服它的不足, 形成了一些以最小二乘法为基础的辨识方法:广义最小二乘法(GLS)、辅助变量法(IVA)和增广矩阵法(EM), 以及将一般的最小二乘法与其它方法相结合的方法,有相关分析———最小二乘两步法(COR -LS)和随机逼近算法。

（3）极大似然法极大似然法(ML)对特殊的噪声模型有很好的性能, 具有很好的理论保证;但计算耗费大, 可能得到的是损失函数的局部极小值。

世京工商K段《系疣辨徂》信福调研赧告题目类别：系统建模的分类现代辨识方法报告题目：基于神经网络与模糊控制的辨识方法调研目录第一章系统辨识理论综述 (2)1.1系统辨识的基本原理 (2)1.2系统辨识的经典方法 (2)13神经网络系统辨识综述 (3)1.3.2神经网络在非线性系统辨识中的应用 (3)14模糊系统辨识综述 (3)14.1模糊系统的结构辨识 (3)1.3.3参数优化的方法 (4)1.3.4模糊规则库的化简 (4)1.5小结 (4)第二章模糊模型辨识方法的研究 (5)2.1模糊模型辨识流程 (5)2.2模糊模型结构辨识方法 (5)2.3模糊模型参数辨识方法 (6)2.4模糊系统辨识中的其它问题 (6)2.4.1衡量非线性建模方法好坏的几个方面 (6)2.4.2模糊辨识算法在实际系统应用中的几个问题 (6)2.4.3模糊模型的品质指标 (6)2.5小结 (7)第三章基于两种模型的自行车机器人系统辨识 (7)3.1基于ARX模型的自行车机器人系统辨识 (7)3.2基于ANFIs模糊神经网络的自行车机器人系统辨识 (7)3.3展望 (7)第一章系统辨识理论综述1.1系统辨识的基本原理根据1A.zade1的系统辨识的定义(1962):系统辨识就是在输入和输出数据的基础上，从一组给定的模型类中，确定一个与所测系统等价的模型”系统辨识有三大要素：(1)数据。

能观测到的被辨识系统的输入或输出数据,他们是辨识的基础。

(2)模型类。

寻找的模型范围,即所考虑的模型的结构。

(3)等价准则。

等价准则一辨识的优化目标用来衡量模型接近实际系统的标准。

1.2系统辨识的经典方法1、阶跃响应法系统辨识；2、频率响应法系统辨识；3、相关分析法系统辨识；4、系统辨识的其他常用方法;1.3神经网络系统辨识综述1.3.1神经网络在线性系统辨识中的应用自适应线性(Ada11ne—Mada1ine)神经网络作为神经网络的初期模型与感知机模型相对应，是以连续线性模拟量为输入模式，在拓扑结构上与感知机网络十分相似的一种连续时间型线性神经网络。

系统辨识综述一、系统辨识概述辨识、状态估计和控制理论是现代控制理论三个互相渗透的领域。

辨识和状态估计离不开控制理论的支持，控制理论的应用又几乎不能没有辨识和状态估计技术。

随着控制过程复杂性的提高，控制理论的应用日益广泛，但其实际应用不能脱离被控对象的数学模型。

然而在大多数情况下，被控对象的数学模型是不知道的，或者在正常运行期间模型的参数可能发生变化，因此利用控制理论去解决实际问题时，首先需要建立被控对象的数学模型。

系统辨识正是适应这一需要而形成的，他是现代控制理论中一个很活跃的分支。

社会科学和自然科学领域已经投入相当多的人力和物力去观察、研究有关的系统辨识问题。

系统辨识是建模的一种方法，不同的学科领域，对应着不同的数学模型。

从某种意义上来说，不同学科的发展过程就是建立他的数学模型的过程。

辨识问题可以归结为用一个模型来表示客观系统(或将要构造的系统)本质特征的一种演算，并用这个模型把对客观系统的理解表示成有用的形式。

当然也可以有另外的描述，辨识有三个要素：数据，模型类和准则。

辨识就是按照一个准则在一组模型类中选择一个与数据拟合得最好的模型。

总而言之，辨识的实质就是从一组模型类中选择一个模型，按照某种准则，使之能最好地拟合所关心的实际过程的静态或动态特性。

通过辨识建立数学模型的目的是估计表征系统行为的重要参数，建立一个能模仿真实系统行为的模型，用当前可测量的系统的输入和输出预测系统输出的未来演变，以及设计控制器。

对系统进行分析的主要问题是根据输入时间函数和系统的特性来确定输出信号。

对系统进行控制的主要问题是根据系统的特性设计控制输入，使输出满足预先规定的要求。

而系统辨识所研究的问题恰好是这些问题的逆问题。

通常，预先给定一个模型类μ=｛M｝（即给定一类已知结构的模型），一类输入信号u和等价准则J＝L(y，yM)(一般情况下，J是误差函数，是过程输出y和模型输出yM的一个泛函)；然后选择使误差函数J达到最小的模型，作为辨识所要求的结果。

系统辨识辨识方法性能分析引言系统辨识是指通过观测系统的输入和输出，利用数学模型对系统的动态行为进行建模和预测的过程。

辨识方法的性能分析是评估辨识方法的优劣和适用范围的过程，对于选择合适的辨识方法和优化辨识结果具有重要意义。

本文将对系统辨识中常用的几种方法进行性能分析，包括参数辨识方法、非参数辨识方法和半参数辨识方法。

参数辨识方法参数辨识方法是指通过估计系统的参数来建立系统模型。

常见的参数辨识方法包括最小二乘法、极大似然法和支持向量回归等。

这些方法通过寻找最优参数来拟合系统的输入和输出数据，从而得到系统的数学模型。

对于参数辨识方法的性能分析，可以从以下几个方面进行评估：1.拟合优度：拟合优度是指辨识方法得到的模型与实际系统之间的拟合程度。

可以通过计算模型的残差平方和或R方值来评估拟合优度，拟合优度越高，模型与实际系统的拟合程度越好。

2.参数估计误差：参数估计误差反映了辨识方法对系统参数的估计准确程度。

可以通过计算参数估计误差的均方根误差或标准偏差来评估辨识方法的参数估计精度，参数估计误差越小，辨识方法的性能越好。

3.参数可辨识性：参数可辨识性指的是辨识方法是否能够准确地估计系统的参数。

对于具有多个参数的系统，如果某些参数之间存在相关性或冗余性，辨识方法可能无法准确地估计这些参数。

因此，参数可辨识性是评估辨识方法是否适用于系统辨识的重要指标。

非参数辨识方法非参数辨识方法是指通过不对系统模型做任何假设，直接从输入和输出数据中提取系统的特征来进行辨识。

常见的非参数辨识方法包括频域方法、时域方法和小波分析等。

这些方法不需要对系统进行具体的数学建模，对系统的特征进行直接提取和分析。

对于非参数辨识方法的性能分析，可以从以下几个方面进行评估：1.频谱分辨能力：频谱分辨能力是指辨识方法对系统频域特征的提取能力。

通过计算频谱分辨能力指标，可以评估辨识方法在不同频率下对系统信息的提取精度，频谱分辨能力越高，辨识方法对系统频域特征的分析能力越强。

系统辨识三要素举例引言在系统辨识中，三要素是指系统的输入、输出和系统模型。

本文将依次介绍这三个要素，并通过实例进行详细探讨。

输入系统的输入是指对系统产生作用的影响或刺激。

输入可以是物质的，也可以是能量的，还可以是信息的。

下面通过几个例子来说明。

例子1：水龙头的流水当我们打开水龙头，水就会从水龙头中流出，这里的水流就是系统的输入。

水的流动对于水管系统来说，是一个重要的输入信号，系统会根据这个输入信号进行相应的处理和控制。

例子2：摄影机的光线对于一个摄影机来说，光线是其输入的重要因素之一。

当我们拍摄照片或录制视频时，摄影机会通过镜头接收到光线，将光线转化为电信号，并进行进一步的处理和记录。

例子3：人体感应灯的触发人体感应灯是一种智能照明设备，它可以根据人体的活动来自动感应开关。

当有人经过时，人体感应灯会检测到人体的热量和运动，从而触发开关动作。

这里的人体活动就是系统的输入。

输出系统的输出是指系统对输入作用的响应或处理结果。

输出可以是物质的，也可以是能量的，还可以是信息的。

下面通过几个例子来说明。

例子1：电饭煲的煮饭当我们把米和水放入电饭煲中，并设置好煮饭的时间和火力，电饭煲会通过控制加热和保温等操作，将米饭煮熟并保持在适宜的温度，这里的煮熟的米饭就是系统的输出。

例子2：汽车的速度当我们踩下汽车的油门，汽车会根据输入的油门信号，通过引擎和传动系统的协同工作，将化学能转化为机械能，将汽车推动前进。

这里汽车前进的速度就是系统的输出。

例子3：电视的图像和声音当我们打开电视，通过电视的天线、有线、光盘或网络等输入信号，电视会解码和处理这些信号，并将其转化为图像和声音，供我们观看和聆听。

这里的图像和声音就是电视的输出。

系统模型系统模型是对系统输入与输出关系的抽象描述和数学表达。

通过建立系统模型，可以更好地理解和分析系统的行为特性。

下面通过几个例子来说明。

例子1：弹簧振子弹簧振子是一个经典的力学系统，由质点和弹簧组成。

非线性控制系统的系统辨识方法综述摘要：系统辨识是一种从已知输入输出数据中估计出系统动力学模型的方法，用于非线性控制系统的设计和分析。

本文将综述非线性控制系统的系统辨识方法，包括参数辨识、状态辨识和混合辨识等。

首先介绍了参数辨识方法中的基本思想和常用算法，例如最小二乘法和极大似然法。

然后探讨了状态辨识方法中的系统辨识问题，包括基于最优控制理论的观测器设计和状态估计方法。

最后讨论了混合辨识方法在非线性控制系统中的应用以及其他相关研究领域的发展趋势。

1. 引言随着科技的不断发展，非线性控制系统的研究和应用越来越广泛。

而系统辨识作为非线性控制系统设计的关键环节之一，具有重要的理论和实际意义。

系统辨识可以通过从输入输出数据中估计出系统的数学模型，进而实现对系统的建模、分析和控制。

因此，非线性控制系统的系统辨识方法成为了一个研究热点。

2. 参数辨识方法参数辨识是一种从已知的输入输出数据中估计出系统参数的方法。

常用的参数辨识方法包括最小二乘法、极大似然法和频域分析法等。

其中，最小二乘法是一种常见的参数辨识方法，它通过最小化观测值与数学模型输出之间的差异来估计系统的参数。

极大似然法是另一种常见的参数辨识方法，它基于观测值的概率分布模型，通过最大化似然函数来估计系统的参数。

频域分析法则是通过对输入输出信号进行频谱分析，得到系统的频率特性，进而估计出系统的参数。

3. 状态辨识方法状态辨识是一种从已知的输入输出数据中估计出系统状态的方法，其基本思想是通过观测器设计和状态估计方法来实现。

观测器设计是一种通过补偿观测误差来估计系统状态的方法，其中常用的观测器设计方法包括最小二乘法、卡尔曼滤波器和无模型自适应控制等。

状态估计则是一种通过对系统动态方程进行求解，估计出系统状态的方法，常用的状态估计方法包括扩展卡尔曼滤波器和粒子滤波器等。

4. 混合辨识方法混合辨识方法是指将参数辨识和状态辨识方法相结合的方法。

通过将参数辨识和状态辨识方法相互补充，可以在一定程度上提高辨识结果的准确性。