LINGO软件的基本使用方法

16
LINGO 教 程
LINGO早期版本对LINDO的兼容问题
在LINGO 9.0以前的版本中不能直接用File|Open命令打开LINDO 模型，但由FILE | IMPORT LINDO FILE (F12)命令可以直接把 LINDO的模型文件转化成LINGO模型。运行后屏幕上会显示一 个标准的“打开文件”的对话框，打开EXAM0201.LTX，在 LINGO主窗口中又打开了命令窗口(Command Window)显示原始 文件，名为“exam0201”的模型窗口显示的是等价的LINGO模型。 当前光标位于命令窗口。
在LINGO中使用LINDO模型
④
运行程序的LINGO报告窗口（如下图）
12
注：LINGO不询问是否进行敏感性分析，敏感性分析 需要将来通过修改系统选项启动敏感性分析后，再调 用“REPORT|RANGE”菜单命令来实现。现在同样可 以把模型和结果报告保存在文件中。
LINGO 教 程
• 运行状态窗口
Variables（变量数量）： 变量总数（Total）、 非线性变量数（Nonlinear）、 整数变量数（Integer）。 Constraints（约束数量）： 约束总数（Total）、 非线性约束个数(Nonlinear)。 Nonzeros（非零系数数量）： 总数（Total）、 非线性项系数个数(Nonlinear)。 Generator Memory Used (K) (内存使用 量)
注：LINDO中没有数组，只能对每个季度分别定义变量， 如正常产量就要有RP1，RP2，RP3，RP4 4个变量等。 写起来就比较麻烦，尤其是更多(如1000个季度)的时候。 记四个季度组成的集合QUARTERS={1，2，3，4}， 它们就是上面数组的下标集合，而数组DEM,RP,OP, INV 对集合QUARTERS中的每个元素1，2，3，4分别对应于 一个值。LINGO正是充分利用了这种数组及其下标的关 系，引入了“集合”及其“属性”的概念，把 QUARTERS={1，2，3，4}称为集合，把DEM,RP,OP, INV称为该集合的属性(即定义在该集合上的属性)。

LINGO 是用来求解线性和非线性优化问题的简易工具。

LINGO 内置了一种建立最优化模型的语言，可以简便地表达大规模问题，利用LINGO 高效的求解器可快速求解并分析结果。

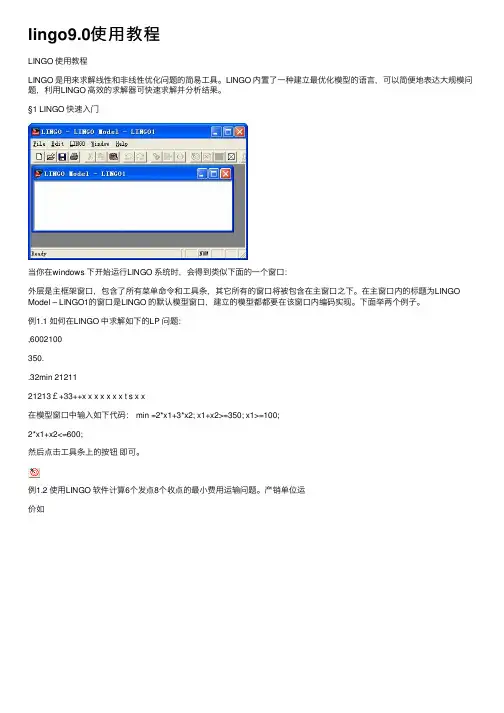
§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时，会得到类似下面的一个窗口：外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在主窗口之下。

在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口，建立的模型都都要在该窗口内编码实现。

下面举两个例子。

例 1.1 如何在LINGO 中求解如下的LP 问题：在模型窗口中输入如下代码：,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x xmin=2*x1+3*x2;x1+x2>=350;x1>=100;2*x1+x2<=600;然后点击工具条上的按钮即可。

例1.2使用LINGO软件计算6个发点8个收点的最小费用model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。

否则为flase #or# 仅当两个参数都为false时，结果为false； 否则为true
一、基本语法--- Lingo的内部函数
◆ 关系运算符 “=” 表示等于关系 “<=” 表示小于等于关系 “>=” 表示大于等于关系
◆ 数学函数 @abs(x) 返回x的绝对值
@sin(x) 返回x的正弦值，x采用弧度制
7 i 1
7
5
154 x ij s ij x ij q j j 1, 2 , , 5 i 1, 2 , , 7 i 1, 2 , , 7 j 1, 2 , , 5 j 1, 2 , , 5
i 1 j 1
Hale Waihona Puke x i 1 x i 2 x i 5 ks i x i 3 x i 4 ys i
一、基本语法---程序结构的三个部分
◆ 目标函数与约束条件部分 按模型中的目标函数及约束条件逐句写入 格式：max = …… 或 min =……
利用lingo中的内部函数组织目标函数及约束
条件的具体内容
例 sets: factory/1..60/:cost, volume; endsets min=@sum(factory(i): cost(i)*volume(i));
返回x1，x2，…，xn中的最大值
@smin(x1,x2,…,xn)
返回x1，x2，…，xn中的最小值
一、基本语法--- Lingo的内部函数
◆ 集循环函数 集循环函数遍历整个集进行操作。其语法为 @function(setname[(set_index_list)
集循环函数名 集合名 循环控制变量
◆ 输入和输出函数 输入和输出函数可以把程序和外部数据文件， 如文本文件、电子表格等连接起来。 @file 格式：@file(’文件名’) 功能：从指定的外部文本文件中输入数据 在数据文件中，以”~”作为一批数据结束的标 记，同一文件中，可以含多批数据，系统依次 打开数据文件时，依次读取各批数据

用“LINGO | Solve （Ctrl +S）”命令来 运行这个程序。 （如果想要了解运行状 态窗口中各项的含义， 可先点击工具栏上的图 标 ，再点击运行状 态窗口，屏幕上自动弹 出运行状态窗口的帮助 信息。）
求解结果报告窗口
3 敏感性分析


敏感性分析的作用是给出“Ranges in which the basis is unchanged”，即研究当目标函数的系数 和约束右端项在什么范围变化（此时假定其他系数 保持不变）时，最优基（矩阵）保持不变。 注意：这里LINGO不询问是否进行敏感性分析。如 果需要进行敏感性分析，必须用“LINGO |Options”命令打开系统选项对话框，在“General Solver”标签下的“Dual Computations”下拉列表 中选中“Prices & Range”，再按下“OK”按钮激 活敏感性分析功能。修改了系统选项后，以后只需 调用“LINGO |Range”命令即可进行敏感性分析了。
l5
Z=0
x1 D Z=2400
z=c (常数) ~等值线
在B(20,30)点得到最优解 最优解一定在凸多边 形的某个顶点取得。
目标函数和约束条件是线性函数 可行域为直线段围成的凸多边形 目标函数的等值线为直线
Lingo优化模型
这是一个（连 续）线性规划（LP）问题
（1）若用35元可以买到1桶牛奶，是否作这项投资？若投资，每天最多购买多 少桶牛奶？ （2）若可以聘用临时工人以增加劳动时间，付给临时工人的工资最多是每小时 几元？ （3）由于市场需求变化，每千克A1的获利增加到30元，是否应该改变生产计 划？
DEM——需求量，RP——正常生产的产量，OP——加班 生产的产量，INV——库存量 目标函数：

• 当前光标 的位置 •模型窗口（Model Window），用于输入 LINGO优化模型（即 LINGO程序）。
•状态行（最左边显示 “Ready”，表示 “准 备就绪”）
•.LG4：LINGO格式的模型文件，保存了模型窗口中所 能够看到的所有文本和其他对象及其格式信息； •.LNG：文本格式的模型文件，不保存模型中的格式信 息（如字体、颜色、嵌入对象等）； •.LDT：LINGO数据文件； •.LTF：LINGO命令脚本文件； •.LGR：LINGO报告文件； •.LTX： LINDO格式的模型文件；
问题的模型(可以看出是LP模型 )
目标函数是所有费用的和
MIN
I 1, 2,3, 4
{400RP(I ) 450OP(I ) 20INV (I )}
约束条件主要有两个： 1）能力限制： RP( I ) 40, I 1,2,3,4
2）产品数量的平衡方程：
INV ( I ) INV ( I 1) RP( I ) OP( I ) DEM ( I ), I 1,2,3,4
1、LINGO软件的安装
在安装LINGO时
首先要打上破解补
丁，如图所示：
LINGO软件的主要特色
两种命令模式 Windows模式： 通过下拉式菜单命令驱动LINGO运
行（多数菜单命令有快捷键，常用的菜单命令有快捷
按钮），图形界面，使用方便； (主要使用模式) 命令行 模式：仅在命令窗口(Command Window)下操 作，通过输入行命令驱动LINGO运行 。
对语句中冒号“：”后面的表达式，按照“：”前 面的集合指定的下标（元素）进行求和。 本例中目标函数也可以等价地写成
@SUM(QUARTERS(i): 400*RP(i) +450*OP(i) +20*INV(i) )；

@SMIN(list)：最小值函数，返回一列数(list)的最小值。 @FLOOR(X)：返回X的整数部分(向最靠近0的方向取整)。 @LGM(X) ：返回X的伽玛(gamma)函数的自然对数值(当X为 整数时LGM(X) = LOG(X-1)！；当X不为整数时 ，采用线性插值得到结果)。
华中农业大学建模基地
*.MPS：示MPS（数学规划系统）格式的模型文件。
华中农业大学建模基地
LINGO实验
－求解器状态窗口－
LP，QP，ILP，IQP，PILP， PIQP，NLP，INLP，PINLP 变量数量 模型类型 当前解状态 当前目标函数值 Ob Infe Ite T 约束不满足的总量 目前为止的迭代次数 T Type Obj N B-and-B Global Multistart N 非零系数数量 可直接求 解的变量 不作为决 策变量。 Class T N In 约束数量 "Global Optimum", "Local Optimum", "Feasible", "Infeasible“(不可行), "Unbounded“(无界), "Interrupted“(中断), "Undetermined“(未确定)
Model: Title:傻瓜输入法; !小程序可用，大程序不提倡; [st1]x1+x2<100; [opt]max=98*x1+277*x2-x1^2-0.3*x1*x2-2*x2^2; [st2]x1<=2*x2; @gin(x1);@gin(x2); end
华中农业大学建模基地
LINGO实验
华中农业大学建模基地
LINGO实验

lingo9.0使⽤教程LINGO 使⽤教程LINGO 是⽤来求解线性和⾮线性优化问题的简易⼯具。

LINGO 内置了⼀种建⽴最优化模型的语⾔，可以简便地表达⼤规模问题，利⽤LINGO ⾼效的求解器可快速求解并分析结果。

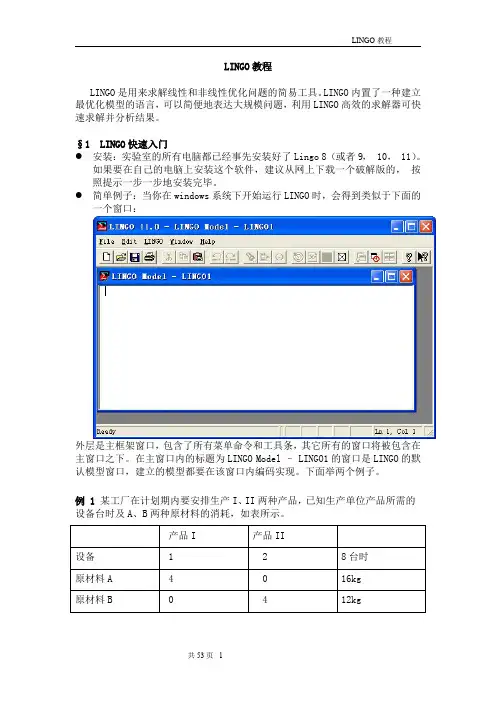
§1 LINGO 快速⼊门当你在windows 下开始运⾏LINGO 系统时，会得到类似下⾯的⼀个窗⼝：外层是主框架窗⼝，包含了所有菜单命令和⼯具条，其它所有的窗⼝将被包含在主窗⼝之下。

在主窗⼝内的标题为LINGO Model – LINGO1的窗⼝是LINGO 的默认模型窗⼝，建⽴的模型都都要在该窗⼝内编码实现。

下⾯举两个例⼦。

例1.1 如何在LINGO 中求解如下的LP 问题：,6002100350..32min 2121121213￡+33++x x x x x x x t s x x在模型窗⼝中输⼊如下代码： min =2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击⼯具条上的按钮即可。

例1.2 使⽤LINGO 软件计算6个发点8个收点的最⼩费⽤运输问题。

产销单位运价如model :!6发点8收点运输问题; sets :warehouses/wh1..wh6/: capacity; vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume; endsets !⽬标函数;min =@sum (links: cost*volume); !需求约束;@for (vendors(J):@sum (warehouses(I): volume(I,J))=demand(J)); !产量约束;@for (warehouses(I):@sum (vendors(J): volume(I,J))<=capacity(I));!这⾥是数据; data :capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38; cost=6 2 6 7 4 2 9 5 4 9 5 3 8 5 8 2 5 2 1 9 7 4 3 3 7 6 7 3 9 2 7 1 2 3 9 5 7 2 6 5 5 5 2 2 8 1 4 3; enddata end然后点击⼯具条上的按钮即可。

外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在 主窗口之下。在主窗口内的标题为 LINGO Model – LINGO1 的窗口是 LINGO 的默 认模型窗口，建立的模型都要在该窗口内编码实现。下面举两个例子。 例 1 某工厂在计划期内要安排生产 I、 II 两种产品， 已知生产单位产品所需的 设备台时及 A、B 两种原材料的消耗，如表所示。 产品 I 设备 原材料 A 原材料 B 1 4 0 产品 II 2 0 4 8 台时 16kg 12kg
目标函数 约束条件
max z=2x_1+3x_2 x_1 + 2x_2 <=8 4x_1 <=16 4x_2 <=12 x_1、x_2 >=0
一般来说，一个优化模型将由以下三部分组成： 1. 目标函数（Objective Function） ：要达到的目标。 2. 决策变量（Decision variables） ：每组决策变量的值代表一种方案。在优化模 型中需要确定决策变量的最优值，优化的目标就是找到决策变量的最优值使 得目标函数取得最优。 3. 约束条件（Constraints） ：对于决策变量的一些约束，它限定决策变量可以取 的值。 在写数学模型时，一般第一行是目标函数，接下来是约束条件，再接着是一些非 负限制等。
设 VOLUME_i_j 为从仓库 i 运送到销售地 j 那里的货物量， 那么我们的目 标函数可以表示为： MIN = 6 * VOLUME_1_1 + 2 * VOLUME_1_2 + 6 * VOLUME_1_3 + 7 * VOLUME_1_4 + 4 * VOLUME_1_5 + . . . 8 * VOLUME_6_5 + VOLUME_6_6 + 4 * VOLUME_6_7 + 3 * VOLUME_6_8; 这里我们只列出了 48 个项中的 9 项，输入这么多的数据非常麻烦，而且容易出 错。而运用 Lingo 提供的模型语言则可以很容易的来描述这个目标函数，而且很 容易扩充模型。

lingo教程Lingo是一个强大且易于学习的编程语言，用于Adobe Director，一个用于创建互动式多媒体应用程序的软件。

在这个Lingo教程中，我们将介绍一些基本的Lingo语法和使用方法。

首先，让我们从Lingo的变量和数据类型开始。

Lingo支持许多数据类型，包括数字，字符串，布尔值和列表。

要声明一个变量，可以使用“variableName = value”的语法。

例如，要声明一个名为“score”的变量，并将其设置为10，可以使用以下代码：```score = 10```要输出变量的值，可以使用“put”命令。

例如：```put score```这将在屏幕上显示变量的值。

Lingo还支持条件语句和循环。

条件语句用于根据条件执行不同的操作。

例如，以下代码将检查“score”变量的值，并根据其值执行不同的操作：if score > 10 thenput "High score!"elseput "Low score."end if```循环用于重复执行一组操作。

例如，以下代码将显示从1到10的所有数字：```repeat with i = 1 to 10put iend repeat```Lingo还支持函数和自定义命令。

函数用于执行特定的操作并返回一个值。

例如，以下代码定义了一个名为“addNumbers”的函数，它将两个数字相加并返回结果：```function addNumbers(num1, num2)return num1 + num2end addNumbers```要使用这个函数，可以使用以下代码：put addNumbers(5, 3)```这将输出结果为8。

自定义命令用于执行一系列的操作，但不返回任何值。

例如，以下代码定义了一个名为“showMessage”的自定义命令，它将显示一个消息框，并将输入的文本作为参数：```on showMessage(text)alert textend showMessage```要使用这个自定义命令，可以使用以下代码：```showMessage("Hello, world!")```这将显示一个消息框，其中包含文本“Hello, world!”。

LINGO 使用教程LINGO 是用来求解线性和非线性优化问题的简易工具。

LINGO 内置了一种建立最优化模型的语言，可以简便地表达大规模问题，利用LINGO 高效的求解器可快速求解并分析结果。

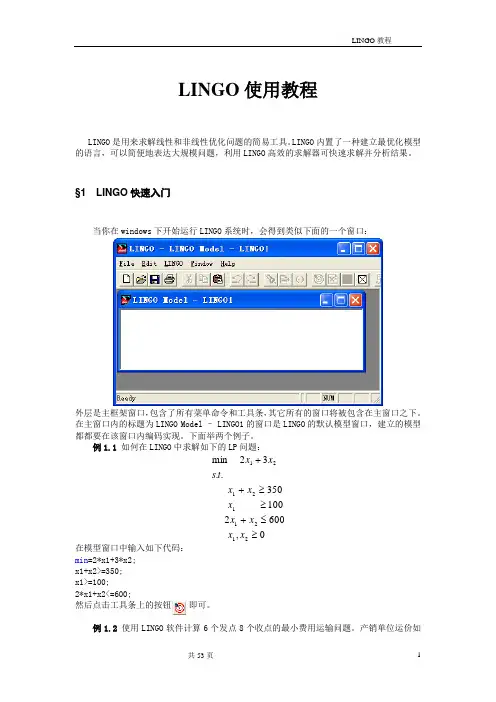
§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时，会得到类似下面的一个窗口：外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在主窗口之下。

在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口，建立的模型都都要在该窗口内编码实现。

下面举两个例子。

例1.1 如何在LINGO 中求解如下的LP 问题：,6002100350..32min212112121≥≤+≥≥++x x x x x x x t s x x 在模型窗口中输入如下代码：min =2*x1+3*x2;x1+x2>=350;x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。

例1.2 使用LINGO 软件计算6个发点8个收点的最小费用运输问题。

产销单位运价如model :!6发点8收点运输问题;sets :warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min =@sum (links: cost*volume);!需求约束;@for (vendors(J):@sum (warehouses(I): volume(I,J))=demand(J));!产量约束;@for (warehouses(I):@sum (vendors(J): volume(I,J))<=capacity(I));!这里是数据;data :capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮 即可。

lingo软件使⽤教程lingo软件使⽤教程⼀般来说，⼀个优化模型将由以下三部分组成：1. ⽬标函数（Objective Function）：要达到的⽬标。

2. 决策变量（Decision variables）：每组决策变量的值代表⼀种⽅案。

在优化模型中需要确定决策变量的最优值，优化的⽬标就是找到决策变量的最优值使得⽬标函数取得最优。

3. 约束条件（Constraints）：对于决策变量的⼀些约束，它限定决策变量可以取的值。

在写数学模型时，⼀般第⼀⾏是⽬标函数，接下来是约束条件，再接着是⼀些⾮负限制等。

在模型窗⼝输⼊如下代码:Max = 2*x1+3*x2;X1+2*x2<=8;4*x1<16;4*x2<12;注意：1.每⼀个lingo表达式最后要跟⼀个分号;2.多数电脑中没有符号，lingo中<=代替；为了⽅便可以⽤<代替⼩于等于，⽤>代替⼤于等于。

3.我们可以添加⼀些注释，增加程序的可读性。

注释以⼀个！（叹号必须在英⽂状态下输⼊，它会⾃动变为绿⾊）开始，以；（分号）结束。

4．Lingo中不区分变量名的⼤⼩写。

变量名必须以字母（A-Z）开头，后⾯的字符可以是字母、数字、下划线。

变量名不能超过32个字符。

Lingo程序的⼀些规则：1. 在Lingo中最开始都是“MAX=”或者“MIN=”开始表⽰求⽬标函数的最⼤或者最⼩值。

2. 变量和它前⾯的系数之间要⽤“*”连接，中间可以有空格。

3. 变量名不区分⼤⼩写，但必须以字母开始，不超过32个字符。

4. 数学表达式结束时要⽤分号“；”表⽰结束。

表达式可以写在多⾏上，但是表达式中间不能⽤分号。

5. 在电脑系统中⼀般没有“⼩于等于”符号，在Lingo采⽤“<=”来表⽰“⼩于等于”，⽤“>=”表⽰“⼤于等于”。

⼩于等于也可以⽤更简单的“<”表⽰，⼤于等于⽤“>”表⽰。

集合段：在我们已经得到的程序⾥有⼀些量没有定义，如WAREHOUSES( I)，DEMAND( J)， LINKS( I, J)。

第十八章LINGO软件的使用18.1 LINGO入门18.1.1 LINGO软件的安装过程点击LINGO9.0 for Windows安装文件，出现点击“Next”按钮，出现此时需要接受安装协议。

系统安装时默认的目录是C:\LINGO9。

安装完成前，会出现下图所示的对话框：这个对话框询问你希望采用的默认的建模（即编程）语言，系统推荐的是采用LINGO语法，也就是选项“LINGO（recommended）”；你也可以选择“LINDO”将LINDO语法作为默认的设置。

当然，安装后你也可以通过“LINGO｜Options｜File Format命令来修改默认的建模（即编程）语言。

在上图中按下“OK”按钮，系统就会完成LINGO的安装过程。

18.1.2 LINGO基础知识LINGO有两种命令格式：一种是常用的Windows模式，通过下拉式菜单命令驱动LINGO 运行，界面是图形式的，使用起来也比较方便；另一种是命令行（Command-Line）模式，仅在命令窗口（Command Window）下操作，通过输入行命令驱动LINGO运行。

由于其使用字符方式输入，初学者往往不太容易掌握。

在这里，我们主要介绍在菜单驱动模式下LINGO的使用方法。

LINGO 9.0软件比以前的版本有了很大的改进，功能大大增强，性能更加稳定，计算的结果更加可靠。

LINGO软件不仅可用于求解非线性规划问题，还可以用以求解非线性整数规划问题；LINGO包含了内置的建模语言，模型中所需的数据可以以一定格式保存在独立的文件中；LINGO允许以简练、直观的方式描述较大规模的优化问题。

注：LIGDO公司目前已将LINDO软件从其产品中删除了。

事实上，LINDO软件的所有功能（包括LINDO语法格式）都在LINGO中得到了支持。

当你在windows下开始运行LINGO系统时，会得到类似下面的一个窗口：外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在主窗口之下。

云南师范大学数学学院
LINGO的基本用法. 点击运行
【目标函数】 max z 200 x1 300 x2
x1 100 x2 120 【约束条件】 x1 2 x2 160 x1 , x2 0
云南师范大学数学学院
运行结果：
目标最优值
决策变量值
云南师范大学数学学院
LINGO的语法规定 ① 求目标函数最大(小）值用MAX=…或MIN=…来表示； ② 每个语句必须以分号“;”结束。 ③ 变量名称必须以字母(A-Z)开头，由字母、数字(0-9) 和下划线“_”组成，不区分大小写； ④ 以“!”开头，以“;”结束的语句是注释语句； ⑤ 默认所有决策变量都非负； ⑥ 程序一般以语句“MODEL:”开头，以“END”结束， 也可以省略。
云南师范大学数学学院
二、了解LINGO的菜单
求 解
云南师范大学数学学院
保存
云南师范大学数学学院
三、 LINGO的常用运算符.
• 算术运算符: + - * / ^ • 数学函数：@abs(x) @sin(x) @cos(x) @tan(x) @exp(x) @log(x) … • 边界限定函数(Lingo默认所有变量都非负)： @bin(x) 限制x为0或1 @gin(x) 限制x为整数 @bnd(L,x,U) 限制L≤x≤U @free(x) x可以取任意实数
云南师范大学数学学院m源自x z 200 x1 300 x2 x1 100 x2 120 x1 2 x2 160 x1 , x2 0
可以编程为以下两种代码：
定义集合和变量
云南师范大学数学学院
四、 LINGO的集合（数组）定义使用.
集合必须在关键字SETS和ENDSETS之间定义，例如: SETS: WH/1..6/; VD/1..8/; LINKS(WH,VD); ENDSETS SETS: WH/1..6/:a; VD/1..8/:b; LINKS(WH,VD):x,c; ENDSETS 定义了下标集合： WH={1 2 3 4 5 6} VD={1 2 3 4 5 6 7 8} LINKS={(i,j) | i∈WH, j∈VD} 定义了变（常）量： a(1)…a(6)或a(i),i∈WH b(1)…b(8)或b(j),j∈VD x(i,j),c(i,j),(i,j)∈LINKS

8小时 每天 50桶牛奶 时间480小时 至多加工100公斤A1 决策变量 目标函数 x1桶牛奶生产A1 获利 24×3x1 x2桶牛奶生产A2 获利 16×4 x2 线性 规划 模型 (LP)
1桶 牛奶 或
12小时
3公斤A1 4公斤A2
获利24元/公斤 获利16元/公斤
每天获利
原料供应 约束条件
注：LINDO中没有数组，只能对每个季度分别定义变量，如正常产 量就要有RP1，RP2，RP3，RP4 4个变量等。写起来就比较麻烦， 尤其是更多(如1000个季度)的时候。 记四个季度组成的集合QUARTERS={1，2，3，4}，它们就是上 面数组的下标集合，而数组DEM,RP,OP, INV对集合QUARTERS中的 每个元素1，2，3，4分别对应于一个值。LINGO正是充分利用了 这种数组及其下标的关系，引入了“集合”及其“属性”的概念， 把QUARTERS={1，2，3，4}称为集合，把DEM,RP,OP, INV称为该集 合的属性(即定义在该集合上的属性)。
最优解不变时目标 系数允许变化范围 (约束条件不变) x1系数范围(64,96) x2系数范围(48,72)
x1系数由243= 72 增加为 3 480.000000 53.333332 80.000000 4 100.000000 INFINITY 40.000000 303= 90，在 允许范围内 不变！ A1获利增加到 30元/千克，应否改变生产计划
6.666667
结果解释
RANGES IN WHICH THE BASIS IS UNCHANGED: OBJ COEFFICIENT RANGES VARIABLE CURRENT ALLOWABLE ALLOWABLE COEF INCREASE DECREASE X1 X2 ROW 2 3 4 72.000000 24.000000 8.000000 64.000000 8.000000 16.000000 RIGHTHAND SIDE RANGES CURRENT ALLOWABLE ALLOWABLE RHS INCREASE DECREASE 50.000000 480.000000 100.000000 10.000000 53.333332 INFINITY 6.666667 80.000000 40.000000

LINGO 是用来求解线性和非线性优化问题的简易工具。

LINGO 内置了一种建立最优化模型的语言，可以简便地表达大规模问题，利用LINGO 高效的求解器可快速求解并分析结果。

§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时，会得到类似下面的一个窗口：外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在主窗口之下。

在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口，建立的模型都都要在该窗口内编码实现。

下面举两个例子。

例1.1 如何在LINGO 中求解如下的LP 问题：0,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码： min =2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。

例1.2 使用LINGO 软件计算6个发点8个收点的最小费用运输问题。

产销model :!6发点8收点运输问题; sets :warehouses/wh1..wh6/: capacity; vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume; endsets !目标函数;min =@sum (links: cost*volume); !需求约束;@for (vendors(J):@sum (warehouses(I): volume(I,J))=demand(J)); !产量约束;@for (warehouses(I):@sum (vendors(J): volume(I,J))<=capacity(I));!这里是数据; data :capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38; cost=6 2 6 7 4 2 9 5 4 9 5 3 8 5 8 2 5 2 1 9 7 4 3 3 7 6 7 3 9 2 7 1 2 3 9 5 7 2 6 5 5 5 2 2 8 1 4 3; enddata end然后点击工具条上的按钮 即可。

第1讲 LINGO 软件入门司守奎烟台市，海军航空大学 Email ：sishoukui@1.1 初识LINGO 程序LINGO 程序书写实际上特别简捷，数学模型怎样描述，LINGO 语言就对应地怎样表达。

首先介绍两个简单的LINGO 程序。

例1.1 求解如下的线性规划问题：121212112max726450,128480,s.t.3100,,0z x x x x x x x x x =++≤⎧⎪+≤⎪⎨≤⎪⎪≥⎩ LINGO 求解程序如下max =72*x1+64*x2; x1+x2<=50;12*x1+8*x2<=480; 3*x1<=100;说明：LINGO 中默认所有的变量都是非负的，在LINGO 中就不需写出对应的约束。

例 1.2 抛物面22y x z+=被平面1=++z y x 截成一椭圆，求原点到这椭圆的最短距离。

该问题可以用拉格朗日乘子法求解。

下面我们把问题归结为数学规划模型，用LINGO 软件求解。

设原点到椭圆上点),,(z y x 的距离最短，建立如下的数学规划模型：⎩⎨⎧+==++++.,1s.t.min22222y x z z y x z y xLINGO 求解程序如下：min =(x^2+y^2+z^2)^(1/2); x+y+z=1; z=x^2+y^2;@free (x); @free (y);说明：LINGO 中默认所有变量都是非负的，这里y x ,的取值是可正可负的，所以使用LINGO 函数free 。

例1.3 求解如下的数学规划模型：⎪⎪⎩⎪⎪⎨⎧==∑∑∑===.,1s.t.min9912100100110012i ii i i ix x x x用LINGO 求解上述数学规划问题，使用集合和函数比较方便，使用集合的目的是为了定义向量，集合使用前，必须先定义；LINGO 程序中的标量不需要定义，直接使用即可。

sets :var/1..100/:x; endsetsmin =@sqrt (@sum (var(i):x(i)^2)); @sum (var(i):x(i))=1;x(100)=@sum (var(i)|i#le#99:x(i)^2); @for (var(i)|i#le#99:@free (x(i)));说明：如果不使用集合和函数，全部使用标量x1,x2,…,x100，最后一个约束就要写99遍，@free(x1); …; @free (x99)。

LINGO 是用来求解线性和非线性优化问题的简易工具。

LINGO 内置了一种建立最优化模型的语言，可以简便地表达大规模问题，利用LINGO 高效的求解器可快速求解并分析结果。

§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时，会得到类似下面的一个窗口：外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在主窗口之下。

在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口，建立的模型都都要在该窗口内编码实现。

下面举两个例子。

例1.1 如何在LINGO 中求解如下的LP 问题：,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码： min =2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。

例1.2 使用LINGO 软件计算6个发点8个收点的最小费用运输问题。

产销单位运价如model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。