昆明理工大学工程力学习题册问题详解

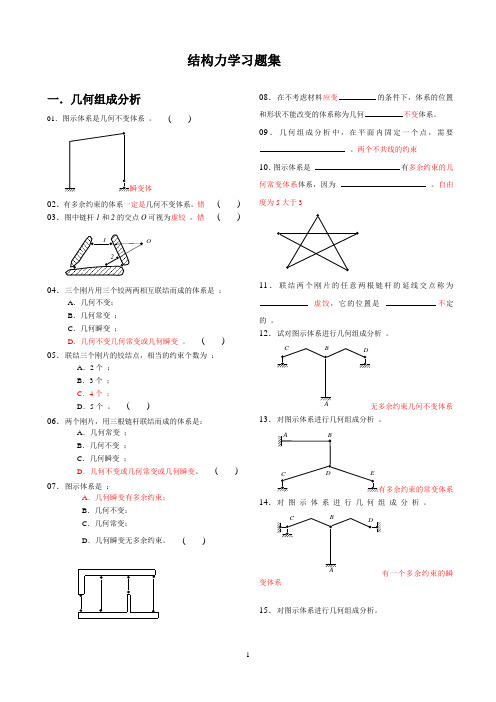
结构力学习题集一．几何组成分析01．图示体系是几何不变体系。

()瞬变体02．有多余约束的体系一定是几何不变体系。

错() 03．图中链杆1和2的交点O可视为虚铰。

错()12O04．三个刚片用三个铰两两相互联结而成的体系是：A．几何不变；B．几何常变；C．几何瞬变；D．几何不变几何常变或几何瞬变。

() 05．联结三个刚片的铰结点，相当的约束个数为：A．2个；B．3个；C．4个；D．5个。

()06．两个刚片，用三根链杆联结而成的体系是：A．几何常变；B．几何不变；C．几何瞬变；D．几何不变或几何常变或几何瞬变。

() 07．图示体系是：A．几何瞬变有多余约束；B．几何不变；C．几何常变；D．几何瞬变无多余约束。

()08．在不考虑材料应变的条件下，体系的位置和形状不能改变的体系称为几何不变体系。

09．几何组成分析中，在平面内固定一个点，需要。

两个不共线的约束10．图示体系是有多余约束的几何常变体系体系，因为。

自由度为5大于311．联结两个刚片的任意两根链杆的延线交点称为虚饺，它的位置是不定的。

12．试对图示体系进行几何组成分析。

AC DB无多余约束几何不变体系13．对图示体系进行几何组成分析。

AC DBE有多余约束的常变体系14．对图示体系进行几何组成分析。

AC DB有一个多余约束的瞬变体系15．对图示体系进行几何组成分析。

AB CDEF无多余约束的几何不变体16．对图示体系进行几何组成分析。

ABCDEF17．对图示体系进行几何组成分析 。

BC DE FA G18．对图示体系进行几何组成分析。

ABCDE19．对图示体系进行几何组成分析 。

ABCDE20．对图示体系进行几何组成分析 。

ABCDGE F21．对图示体系进行几何组成分析。

A BC DE FGHK几何不变体系二．内力分析计算01．静定结构的全部内力及反力，只根据平衡条件求得 ， 且解答是唯一的。

（ 对）02．静定结构受外界因素影响均产生内力。

大小与杆件截 面尺寸无关 。

结构力学习题集一．几何组成分析01．图示体系是几何不变体系。

()瞬变体02．有多余约束的体系一定是几何不变体系。

错() 03．图中链杆1和2的交点O可视为虚铰。

错()O04．三个刚片用三个铰两两相互联结而成的体系是：A．几何不变；B．几何常变；C．几何瞬变；D．几何不变几何常变或几何瞬变。

() 05．联结三个刚片的铰结点，相当的约束个数为：A．2个；B．3个；C．4个；D．5个。

()06．两个刚片，用三根链杆联结而成的体系是：A．几何常变；B．几何不变；C．几何瞬变；D．几何不变或几何常变或几何瞬变。

() 07．图示体系是：A．几何瞬变有多余约束；B．几何不变；C．几何常变；D．几何瞬变无多余约束。

()08．在不考虑材料应变的条件下，体系的位置和形状不能改变的体系称为几何不变体系。

09．几何组成分析中，在平面内固定一个点，需要。

两个不共线的约束10．图示体系是有多余约束的几何常变体系体系，因为。

自由度为5大于311．联结两个刚片的任意两根链杆的延线交点称为虚饺，它的位置是不定的。

12．试对图示体系进行几何组成分析。

AC DB无多余约束几何不变体系13．对图示体系进行几何组成分析。

AC DBE有多余约束的常变体系14．对图示体系进行几何组成分析。

AC D B有一个多余约束的瞬变体系15．对图示体系进行几何组成分析。

ABCDEF无多余约束的几何不变体16．对图示体系进行几何组成分析。

ABCDEF17．对图示体系进行几何组成分析 。

BC DE FA G18．对图示体系进行几何组成分析。

ABCDE19．对图示体系进行几何组成分析 。

ABCDE20．对图示体系进行几何组成分析 。

ABCDGEF21．对图示体系进行几何组成分析。

ABCDEFGHK几何不变体系二．内力分析计算01．静定结构的全部内力及反力，只根据平衡条件求得 ， 且解答是唯一的。

（ 对）02．静定结构受外界因素影响均产生内力。

大小与杆件截 面尺寸无关 。

第三章平面一般力系答案一、填空(将正确的答案填写在横线上)1、作用在物体上的各力的作用线都在同一平面内 ,并呈任意分布的力系,称为平面一般力系。

2、平面一般力系的两个基本问题是平面力系的简化 ,其平面条件的的应用。

3、力的平移定理表明,若将作用在物体某点的力平移到物体上的另一点,而不改变原力对物体的作用效果,则必须附加一力偶,其力偶距等于原来的力对新作用点的距。

4、平面一般力系向已知中心点简化后得到一力和一力偶距。

5平面一般力系的平衡条件为;各力在任意两个相互垂直的坐标轴上的分量的代数和均为零力系中所有的力对平面内任意点的力距的代数和也等零。

6.平面一般力系平衡方程中,两个投影式ΣFix=0 和ΣFiy=0 保证物体不发生移动 ;一个力矩式ΣMo(Fi)=0 保证物体不发生转动。

三个独立的方程,可以求解三个未知量。

7.平面一般力系平衡问题的求解中,固定铰链的约束反力可以分解为相互垂直的两个分力固定端约束反力可以简化为相互垂直的两个分力和一个附加力偶矩。

8.平衡方程ΣMA(Fi)=0、ΣMB(Fi)=0、ΣFiX=0适用于平面一般力系,使其用限制条件为AB连线与X轴不垂直。

9.平衡方程ΣMA(Fi)=0、ΣMB(Fi)=0、ΣMc(Fi)=0的使用限制条约为ABC不在同一直线上。

10.若力系中的各力作用现在同一平面内且相互平行,称为平面平行力系。

它是平面一般力系的特殊情况。

11.平面平行力系有两个独立方程,可以解出两个未知量。

12.平面平行力系的基本平衡方程是：ΣFi X=0，ΣM O(Fi)=0二、判断题（正确的打“√”，错误的打“×”）1.作用于物体上的力,其作用线可在物体上任意平行移动,其作用效果不变。

(×)2.平面一般力系的平衡方程可用于求解各种平面力系的平衡问题。

(√)3.若用平衡方程解出未知力为负值,则表明：(1)该力的真实方向与受力图上假设的方向相反。

(√)(2)该力在坐标轴上的投影一定为负值。

2-1 求下列结构中指定杆内的应力。

已知(a)图中杆的横截面面积A 1=A 2=1150mm 2； 解：（1）分析整体，作示力图∑=0)(i BF M：CB 041088=××−×A F AF N1F N2(c)40kN A F =（2）取部分分析，示力图见（b ）∑=0)(i CF M：02442.22=×+×−×q F F A N2(404402)36.36kN 2.2N F ×−×==3262236.361031.62MPa 115010N F A σ−×===×（3）分析铰E ，示力图见（c ）∑=0ix F ：0sin 12=−βN N F F1240.65kN N N F F == 3161137.961035.3MPa 115010N F A σ−×===×2-2 求下列各杆内的最大正应力。

（3）图(c)为变截面拉杆，上段AB 的横截面积为40mm 2，下段BC 的横截面积为30mm 2，杆材料的ρg =78kN/m 3。

解：1.作轴力图，BC 段最大轴力在B 处6N 120.530107812.0kN B F −=+×××AB 段最大轴力在A 处6N 12(0.5300.540)107812.0kN A F −=+×+×××3N 2612.010400MPa 30mm3010B B F σ−−×===× 3N 2612.010300MPa 40mm 4010AA F σ−−×===×杆件最大正应力为400MPa ，发生在B 截面。

EDF BF AF CxF N2(b)A120B120F NC2-4 一直径为15mm ，标距为200mm 的合金钢杆，比例极限内进行拉伸试验，当轴向荷载从零缓慢地增加58.4kN 时，杆伸长了0.9mm ，直径缩小了0.022mm ，确定材料的弹性模量E 、泊松比µ。

工程力学答案详解1-1试画出以下各题中圆柱或圆盘的受力图。

与其它物体接触处的摩擦力均略去。

解：1-2 试画出以下各题中AB 杆的受力图。

(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。

(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。

(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。

解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D1-5 试画出以下各题中指定物体的受力图。

(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。

解：(a)(d) FC(e)WB (f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2-3 水平力F 作用在刚架的B 点，如图所示。

如不计刚架重量，试求支座A 和D 处的约束力。

解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。

姓名 班级 学号 41第十章 组合变形 11-1悬臂梁各种可能截面如下图所示。今在梁的自由端加有垂直与梁的轴线的集中力，其方向如图中虚线所示。试分析：哪些情况下将发生平面弯曲？如果不是平面弯曲，又将发生什么结果？ 答案： (a)斜弯曲；(b)平面弯曲；(c)对称弯曲；(d)斜弯曲； (e)斜弯曲；(f)平面弯曲+扭转；(g)平面弯曲；(h)斜弯曲。

11-2简支于屋架上的檩条承受均布荷载q=14kN/m，如图所示。檩条跨长为L=4m，采用工字钢，其许用应力[σ]=160MPa，试选择工字钢型号。

答案：№.40C工字钢

11-3 图示悬臂梁在两个不同截面上分别受有水平力P1=800N和铅垂力P2=1650N的作用。试求以下两种情况下， 梁内最大正应力并指出其作用位置。 (1) 梁的截面为矩形，其宽和高分别为b=9cm，h=18cm. (2) 梁为圆截面，其直径d =13cm 。

答案：（1）MPa98.9max=σ，

MPa98.9min=σ（压） （2）MPa7.10max=σ， MPa7.10min=σ（压） 11-4 图示一简支梁，选用了25a号工字钢。已知：作用在跨中的集中力P= 5kN，力P的作用线与截面的竖直主轴间的夹角度α=30ｏ，钢材的弹性模量E=210GPa，许用应力[σ]=160MPa，梁的许用挠度[f]=L/500。试对此梁进行强度和刚度校核。

答案：MPa5.62max=σ，mmf74.5max=

PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn姓名 班级 学号 4211-5 图(a)所示正方形短拄，受轴向压力P的作用。若将短柱中间部分开一槽, 如图(b)所示,开槽所削弱的面积为原截面积的二分之一。 试确定开槽后，柱内最大正应力比未开槽时增加多少倍。

答案：8倍 11-6 图示短柱，材料的弹性模量E = 2.1×10 5MPa ，受偏心压力P作用，在两侧用应变片测得轴向应变εa = –0.4×10 - 3， εb = –1.0×10 - 3 。试求 ：(1)绘横截面上正应力分布图；(2)压力P及偏心距e的值。