人工地震动生成程序
- 格式:pdf
- 大小:68.71 KB
- 文档页数:6



地震动曲线的选取⼀、引⾔地震动曲线是描述地震动特性的重要参数,对于地震⼯程和结构安全评估具有重要意义。
地震动曲线的选取是地震⼯程研究中的⼀项重要任务,对于结构的抗震设计、抗震性能评估以及地震灾害预测等⽅⾯具有关键作⽤。
本⽂将对地震动曲线的选取进⾏全⾯探讨。
⼆、地震动曲线的基本概念地震动曲线,也称为地震加速度曲线或地震反应谱,描述了地震动强度随时间变化的规律。
它通常由两个主要参数构成:峰值加速度和持续时间。
峰值加速度表示地震动过程中最⼤的加速度值,持续时间则表示地震动过程的时⻓。
三、地震动曲线的选取⽅法在地震⼯程中,根据不同的需求和场景,有多种⽅法可以选取地震动曲线。
以下是⼏种常⽤的⽅法:1.基于历史地震数据选取:通过对历史上地震动的记录数据进⾏统计分析,选取具有代表性的地震动曲线。
这种⽅法考虑了实际地震事件的统计特性,具有较⾼的实际意义。
2.⼈⼯合成地震动曲线:根据地震学的理论知识和地震动的统计规律,通过⼈⼯合成⽅法⽣成地震动曲线。
这种⽅法可以根据研究需求定制,便于进⾏理论分析和数值模拟。
3.考虑场地条件的地震动曲线:在选取地震动曲线时,应充分考虑场地的地质构造、⼟层分布、地下⽔位等因素。
不同场地条件下的地震动曲线具有差异性,因此需要根据具体场地进⾏选取。
4.多因素综合选取:在实际应⽤中,应综合考虑多种因素选取地震动曲线,如地震事件的震级、震源深度、地表地质等因素。
通过多因素综合分析,可以更加准确地模拟实际地震事件的地震动效应。
四、地震动曲线的应⽤地震动曲线的选取在多个领域具有⼴泛的应⽤:1.结构抗震设计:在建筑结构的抗震设计中,需要依据地震动曲线进⾏结构分析和设计。
通过对结构物在地震作⽤下的反应进⾏计算和分析,评估其抗震性能,优化抗震设计。
2.基础设施抗震评估:对于桥梁、隧道、⾼速公路等基础设施,通过选取合适的地震动曲线,可以评估其在地震作⽤下的安全性。
这有助于提前发现潜在的⻛险因素,采取相应的加固措施。

peer人工合成地震波的步骤嘿,想知道怎么合成地震波吗?嗯,别急,跟我来,我带你一起探个究竟。
人工合成地震波就是通过一些技术手段,模仿地震波的传播方式,然后“制造”一个地震场景出来。
想象一下,就像是拍电影时用特效制作场景,虽然没有真的地震,但那种震撼感,绝对不容小觑。
合成地震波的步骤并不复杂,学会了,感觉自己就像变成了地震科学家呢。
好了,话不多说,咱们开始吧。
得有个好基础,那就是数据。
没错,合成地震波并不是凭空捏造的,得有原始数据支持。
咱们通常会用到一些历史地震记录,或者类似的地震波资料。
这些数据就像是做饭时的食材,只有选对了,才有可能做出美味佳肴。
所以,第一步就是从真实的地震记录中“挑选”合适的波形。
你想啊,不同的地震波有不同的特性,有的波动大,有的波动小,就像人有胖有瘦一样,得看你的“菜谱”需求。
有了数据之后,接下来就开始了真正的“烹饪”阶段——选择模型和参数。
别看这名字挺简单,里面可是大有文章呢。
你得根据你的目标,选择适合的合成模型。
比如说,想要模拟一个大地震,就得挑一个波形宽、震中强的模型;如果是小震动,那就得选个小巧温柔的模型。
这个就像你做菜时,挑选调料一样,得用对了,味道才正。
这里面的参数得调得精准,有些波形的幅度和频率非常关键,弄错了,可能整个合成的地震波就跑偏了。
咱们来到了计算的环节。
这个过程有点复杂,但你放心,咱们不一定得深刻理解每一根公式,知道“怎么做”就行。
实际上,计算是通过一些复杂的算法,把真实的地震波数据与选择的模型相结合,然后生成出一套新的地震波形。
这一步不亚于你在厨房里加调料和火候,稍微掌握不好,可能会让你的地震波“过火”或者“不到位”,这样可不好!不过,放心,现代的计算机软件都能帮助你快速完成这一步。
好啦,波形合成出来了。
下一步就得看看效果怎么样,是不是符合你要的标准。
要是合成的地震波看起来太平淡,那可不行,得适当调整。
你得根据测试结果,优化波形的频率、振幅,甚至传播速度。

地震安全评估的软件
以下是一些常用的地震安全评估软件:
1. ETABS:熟知的建筑结构分析和设计软件,可用于地震安
全评估和结构设计。
2. SAP2000:广泛用于结构分析和设计的软件,可用于地震安
全评估和结构抗震设计。
3. SeismoSoft:专门用于地震工程的软件套件,包括SeismoStruct、SeismoBuild、SeismoArtif等模块,用于地震分析、结构设计和地震动人工生成等。
4. OpenSees:开放式地震工程模拟平台,可用于地震分析和结构响应模拟,可灵活定制分析算法。
5. SeismoSignal:用于地震记录分析和处理的软件,可以用于
生成和处理地震动输入。
6. SeismoMatch:用于生成匹配目标地震动的人工时程的软件。
7. FEMA P-58:美国联邦紧急管理局(FEMA)开发的软件,
用于评估建筑物的震害、损失和维修成本。
请注意,这些软件的选择应根据具体的需求和专业知识来进行,建议咨询地震工程专业人士或地震工程师以获取最合适的软件和方法。

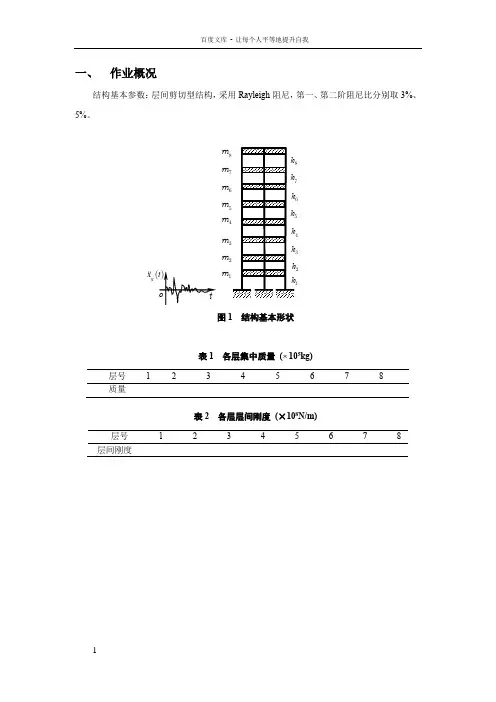
一、 作业概况结构基本参数:层间剪切型结构,采用Rayleigh 阻尼,第一、第二阶阻尼比分别取3%、5%。
图1 结构基本形状表1 各层集中质量 ( 105kg)层号 12345678质量表2 各层层间刚度 (×108N/m)层号 1 2 3 4 5 6 7 8 层间刚度m m m m m m m m ()g x t二、 频率及振型计算根据层间模型的假定,可以建立结构的质量矩阵以及刚度矩阵如下。
12345678000000000000000000000000000000000000000000000000000000003.400000000 3.400000000 3.200000000 3.20000 =0000 2.800000000 2.800000000 2.700000000 2.6m m m m m m m m ⎛⎫ ⎪ ⎪ ⎪ ⎪⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎛⎫ ⎝M 510kg ⎪⎪⎪⎪⎪⨯⎪⎪⎪⎪⎪⎪⎭ 11121314151617182122232425262728313233343536373841424344454647485152535455565758616263646566676871727374757677788182838485868788k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k ⎛ =⎝K 8420000002 3.8 1.8000000 1.8 3.6 1.8000000 1.8 3.6 1.8000 =10/000 1.8 3.6 1.8000000 1.8 3.4 1.6000000 1.6 3.2 1.6000000 1.6 1.6N m ⎫⎪⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎭-⎛⎫ ⎪-- ⎪ ⎪-- ⎪-- ⎪⨯ ⎪-- ⎪-- ⎪ ⎪-- ⎪ ⎪-⎝⎭根据上面求得的质量、刚度矩阵,即可求解特征方程:20K M(1)求解自振频率以及阵型向量已经演变成为典型的求解矩阵特征值以及特征向量的问题,特征值即为圆频率2,特征向量即为振型向量。

姓名:郭 勇 学号:0220020128人工地震波生成程序简介一、 程序设计内容及方法1、程序内容本程序根据特征周期、水平地震波影响系数最大值和地震波幅值等初始条件生成人工地震波,为结构动力分析的时程分析法提供地震波来源。
2、程序设计方法(1) 理论依据本程序采用三角级数法生成人工地震波。
对于给定的功率谱密度函数()x S ω,按照下面的公式可以方便的生成以()x S ω为功率谱密度函数、均值为零的高斯平稳过程()a t 。
1()cos()Nk k k k a t C t ωϕ==+∑ (1)式中:12[4()]()/1()2k x k u l k l C S N k ωωωωωωωω⎫⎪=∆⎪∆=-⎬⎪⎪=+-∆⎭(2)k ϕ为内均匀分(0,2)π布的随机相角;u ω,l ω分别为正域ω内的上、下限值,即认为的有()x S ω效功率在范(,)u l ωω围内,而范围外的()x S ω值可视为零。
为了反映地面运动的非平稳性,采用包络函数乘以平稳()f t 过程()a t ,()()()x t f t a t = (3)(3)式即为人工地震波模型。
()f t 可根据下式确定:2221112()233/01()0c t t t t t t t t t f t e t t t t t T--⎧≤<⎪≤<⎪=⎨≤<⎪⎪<≤⎩ (4)式中:c 为衰减系数,通常取值范围为0.1~1.0,本程序取0.15;1t ,2t 和根据不同3t 实际情况取值,T 为地震波持时,本程序取1t ,2t 分别为4s ,15s ,3t 和均为40T s 。
本程序采用《建筑抗震设计规范》(GB50011-2001)中的反应谱作为目标谱,通过Kau l 提出的平稳过程反应谱与功率谱的近似关系22()[()]/[2ln(ln )]Tx k a k kk dS S p T ξπωωπωω=--(5) 式中:()Ta k S ω为规范反应谱;ξ为阻尼比;d T 为地震动持时;p 为反应不超过反应谱值的概率,本程序取0.85。
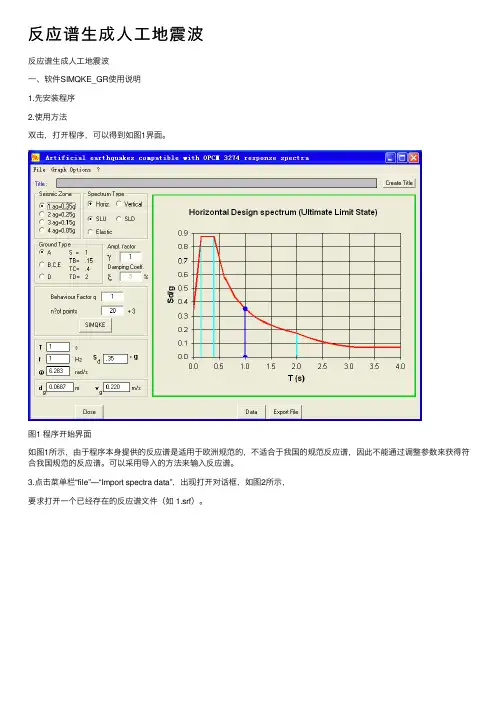
反应谱⽣成⼈⼯地震波反应谱⽣成⼈⼯地震波⼀、软件SIMQKE_GR使⽤说明1.先安装程序2.使⽤⽅法双击,打开程序,可以得到如图1界⾯。
图1 程序开始界⾯如图1所⽰,由于程序本⾝提供的反应谱是适⽤于欧洲规范的,不适合于我国的规范反应谱,因此不能通过调整参数来获得符合我国规范的反应谱。
可以采⽤导⼊的⽅法来输⼊反应谱。
3.点击菜单栏“file”—“Import spectra data”,出现打开对话框,如图2所⽰,要求打开⼀个已经存在的反应谱⽂件(如 1.srf)。
图2 导⼊反应谱⽂件对话框4.⽂件格式如下所⽰(红字部分不能修改,注意反应谱单位为g),下⾯部分可以替换。
response spectrumtime(s) acc(g)0 0.12150.01 0.136350.02 0.15120.03 0.166050.04 0.18090.05 0.195750.06 0.21060.07 0.225450.08 0.24030.09 0.255150.1 0.270.15 0.270.2 0.270.25 0.270.3 0.270.35 0.270.4 0.270.45 0.270.5 0.2430.7 0.173571429 0.8 0.1518750.9 0.1351 0.12151.1 0.110454545 1.2 0.101251.3 0.093461538 1.4 0.086785714 1.5 0.0811.6 0.0759375 1.7 0.071470588 1.8 0.06751.9 0.0639473682 0.060752.1 0.057857143 2.2 0.055227273 2.3 0.052826087 2.4 0.050625 2.5 0.04862.6 0.046730769 2.7 0.0452.8 0.0433928572.9 0.0418965523 0.04053.1 0.039193548 3.2 0.03796875 3.3 0.036818182 3.4 0.035735294 3.5 0.034714286 3.6 0.033753.7 0.032837838 3.8 0.0319736843.9 0.0311538464 0.0303754.1 0.029634146 4.2 0.028928571 4.3 0.028255814 4.4 0.027613636 4.5 0.0274.6 0.026413043 4.7 0.025851064 4.8 0.02531255 0.02435.1 0.023823529 5.2 0.023365385 5.3 0.022924528 5.4 0.02255.5 0.022090909 5.6 0.021696429 5.7 0.021315789 5.8 0.0209482765.9 0.020593226 0.020256.1 0.019918033 6.2 0.019596774 6.3 0.019285714 6.4 0.018984375 6.5 0.018692308 6.6 0.018409091 6.7 0.018134328 6.8 0.0178676476.9 0.0176086967 0.0173571437.1 0.017112676 7.2 0.016875 7.3 0.016643836 7.4 0.016418919 7.5 0.01627.6 0.015986842 7.7 0.015779221 7.8 0.0155769237.9 0.0153797478 0.01518758.1 0.0158.2 0.014817073 8.3 0.014638554 8.4 0.014464286 8.5 0.014294118 8.6 0.014127907 8.7 0.013965517 8.8 0.013806818 8.9 0.0136516859.1 0.013351648 9.2 0.0132065229.4 0.0129255329.5 0.0127894749.6 0.012656259.7 0.0125257739.8 0.0123979599.9 0.01227272710 0.01215选择桌⾯上的“1.srf”⽂件,打开后的程序界⾯如图3所⽰:图3 打开反应谱⽂件1.srf⽂件后的程序界⾯点击图3中的“SIMQKE”按钮,得到如图4所⽰的界⾯。


八层框架的地震响应计算和人工波生成的matlab实现及所需曲线图的自动存储12345678000000000000000000000000000000000000000000000000000000003.400000000 3.400000000 3.200000000 3.20000 =0000 2.800000000 2.800000000 2.700000000 2.6m m m m m m m m ⎛⎫ ⎪ ⎪ ⎪ ⎪⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎛⎫ ⎝M 510kg ⎪⎪⎪⎪⎪⨯⎪⎪⎪⎪⎪⎪⎭11121314151617182122232425262728313233343536373841424344454647485152535455565758616263646566676871727374757677788182838485868788k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k ⎛ =⎝K 8420000002 3.8 1.8000000 1.8 3.6 1.8000000 1.8 3.6 1.8000 =10/000 1.8 3.6 1.8000000 1.8 3.4 1.6000000 1.6 3.2 1.6000000 1.6 1.6N m ⎫⎪⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎭-⎛⎫ ⎪-- ⎪ ⎪-- ⎪-- ⎪⨯ ⎪-- ⎪-- ⎪ ⎪-- ⎪ ⎪-⎝⎭根据上面求得的质量、刚度矩阵,即可求解特征方程:20K M-=w(1)求解自振频率以及阵型向量已经演变成为典型的求解矩阵特征值以及特征向量的问题,特征值即为圆频率2w,特征向量即为振型向量。
根据式(1)利用matlab编程计算,求解矩阵1-M K 的特征值以及特征向量,进而可以得到结构前八阶的自振圆频率、自振频率、自振周期如表2.1所示。
clear
clc
close all hidden %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
fni=input('生成人工地震波-输入数据文件名(20041012):','s');
fid=fopen(fni,'r');
fs=fscanf(fid,'%f',1);%采样频率
tu=fscanf(fid,'%f',1);%上升时间长度
%上升时间包络线线形(1-直线、2-抛物线、3-指数曲线)
iu=fscanf(fid,'%f',1);
%上升时间包络线线形参数(只有指数曲线需要具体参数,其均为1)
cu=fscanf(fid,'%f',1);
ta=fscanf(fid,'%f',1);%持时时间长度
td=fscanf(fid,'%f',1);%下降时间长度
%下降时间包络线线形(1-直线、2-抛物线、3-指数曲线)
id= fscanf(fid,'%f',1);
%下降时间包络线线形(只有抛物线,指数曲线需要具体参数,其余为1)
cd=fscanf(fid,'%f',1);
dp=fscanf(fid,'%f',1);%阴尼比值
p=fscanf(fid,'%f',1);%概率系数(一般可取P=0.85)
nn=fscanf(fid,'%f',1);%迭代次数
fno=fscanf(fid,'%f',1);%输出数据文件名
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %对目标反应谱取值
x=fscanf(fid,'%f',[2,inf]);%反应谱频率和幅值数据
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% tatus=fclose(fid);
%计算生成地震波的数据长度
tl=tu+ta+td;
%计算生成地震波的数据长度
nt=round(fs*tl+1);
%大于并最接近nt的2的幂次方为FFT长度
nfft=2^nestpow2(nt)
%计算频率间隔(Hz)
df=fs/nfft
%定义反应谱的离散频率向量
f=0:df:(nfft/2-1)*df
%计算时间间隔(s)
dt=1/fs;
%定义的离散时间向量
t=0:dt:(nt-1)*dt
%生成0到2PI的随机数为随机相位
g=rand(1,nfft/s)*2*pi;
%建立时间包络线
%建立与地震波长度相同元素为1的向量
en=ones(1,nt);
%上升时间阶段
%确定上升时间段的长度
l=round(tu*fs)+1
%产生上升时间段的包络线数组元素
switch iu
case 1 %直线
en(1:l)=linspace(0,1,1);% y = linspace(a,b,n) generates a row vector y of n points linearly
spaced between and including a and b.
case 2 %抛物线
a=0:l-1;
en(1:l)=(a/(l-1)).^2;
case 3 %指数曲线
a=0:l-1;
en(1:l)=1-exp(-cu*a/(l-1));
end
%持续时间阶段
%确定0时刻到持续时间结束时刻时间段的长度
m=round((tu+ta)*fs)+1;
%下降时间阶段
%产生下降时间段的包络线数组元素
switch id
case 1 %直线
en(m:nt)=linspace(1,0,nt-m+1);
case 2 %抛物线
a=0:nt-m;
en(m:nt)=1-cd*(a/(nt-m)).^2;
case 3 %指数曲线
a=0:nt-m;
en(m:nt)=exp(-cd*a/(nt-m));
end
%按线性插值建立目标反应谱离散数据
%按目标反应谱的长度生成元素为0的向量
a0=zeros(x(1,:));
%取目标反应谱数据的长度
n=length(x(1,:));
%四舍五入取整求反应谱最大频率对应数组元素的下标
nb=round(x(1,n)/df)+1;
for k=1:n-1
%四舍五入取整求反应谱前一个频率数据对应数组元素的下标 l=round(x(1,K)/df)+1;
%四舍五入取整求反应谱后一个频率数据对应数组元素的下标
m=round(x(1,K+1)/df)+1;
%线性插值产生前后两个频率数据间的反应谱数组元素 a0(1:m)=linspace(x(2,k),x(2,k+1),m-l+1)
end
%根据目标反应谱计算对应的近似功率谱
a1=a0;
s=zeros(1,nfft/2);
k=nb:ne;
s(k)=2*dp/(pi.*(a1(k).^2)./f(k)./(-2*log(-log(p)*pi/tl)./f(k)));
%将功率谱转换成傅里叶幅值谱
b1=sqrt(4*df*s)*nfft/2;
%定义元素为0的反谱传递函数矩阵
hf=zeros(ne,nfft);
%计算加速度反应谱传递函数矩阵
for j-0:ne-1
w=2*pi*df*j
wd=w*sqrt(1-dp*dp);
e=exp(-t.*W*dp);
a=t.*wd;
s=sin(a)>*((1-2*dp*dp)/(1-dp*dp));
c=cos(a).*(2*dp/sqrt(1-dp*dp));
%计算加速度反应谱的脉冲响应函数向量
h=wd*e.*(s+c)/fs;
%通过FFT变换求加速度反应谱传递函数向量
hf(j+1,:)=fft(h,nfft);
end
mm=nn
%进行生成人工地震波迭代计算
%100为最大迭代次数
for k=1:100
%将幅值谱和相位谱转化为实部和虚部
c=b1.*exp(i*g);
%将正负圆频率傅里叶谱向量组合成一仙向量
d=[c,c(nfft/2:-1:1)];
%IFFT变换,并取变换结果实部为生成的地震波
e=ifft(d,nfft);
%给生成的地震波加上强度包络线
y=en.*real(e(1:nt));
%计算反应谱
%对生成的地震波进行FFT变换
yf=fft(y,nfft);
for j=1:ne
%用地震波FFT变换结果和反应谱传递函数的乘积的逆变换做卷积运算 d=ifft(yf.*hf(j,:),nfft);
%求各频率对应地震的最大响应
al(j)=max(real(d(1:nt)));
end
%如果达到指定的迭代次数显于图形
if k==mm
subplot(2,1,1);
%m 同时显示生成的地震波的强度包络线
plot(t,y,t,en,t,-en);
xlabel('时间(s)');
ylabel('加速度(g)');
grid on
sublpot(2,1,2);
%同时显示期望反应谱与反应谱计算谱、
l=1:ne
plot(f(l),a0(l),':'f(l),a1(l));
xlabel('频率(Hz)');
ylabel('加速度(g)');
legend('目标谱','计算谱');
grid on;
ig=input('继续迭代次数[取值1-9,否则退出]:');
if ig>0&ig<10 %如果输入数字是1-9
mm=mm+ig
else
break;
end
end
c=bl
%期望谱与计算谱的比值来修改傅里叶值谱
j=nb:ne;
bl(j)=c(j).*a0(j)./a1(j);
end
%打开文件输入人工地震动数据
fid=fopen(fno,'W');
for K=1:nt
%每一行输出两个实型数据,t为时间,y为人工地震动信号值 fprintf(fid,'%f%f\n',t(k),y(k));
end
status=fclose(fid);。