中科大固体物理课程作业答案
- 格式:ppt
- 大小:12.66 MB
- 文档页数:86

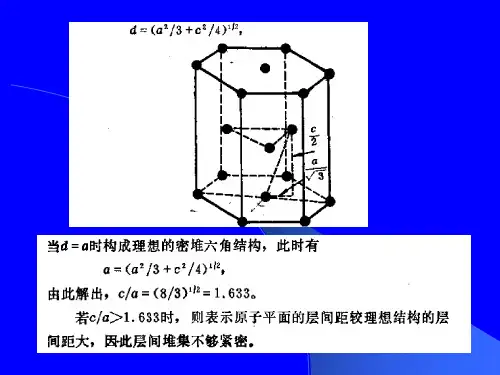
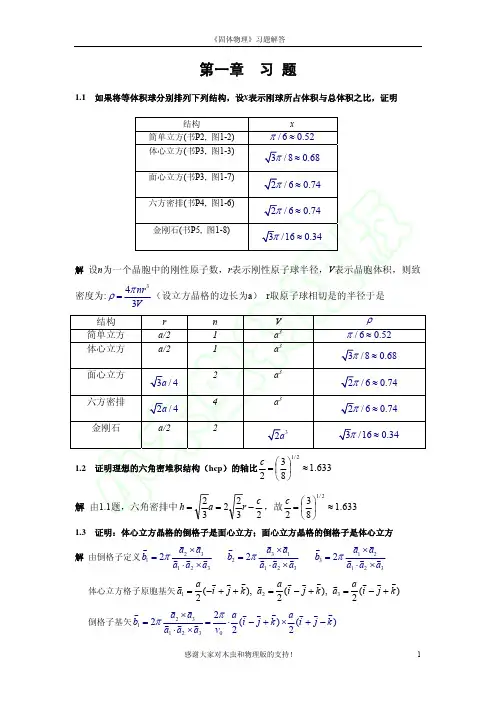
固体物理第一次习题参考答案1.如果将等体积球分别排成下列结构,设x 表示刚球所占体积与总体积之比,证明结构 x简单立方 0.526x π=≈体心立方 30.688x π=≈ 面心立方 20.746x π=≈ 六角密排 20.746x π=≈ 金刚石 30.3416x π=≈解:设钢球半径为r ,立方晶系晶格常数为a ,六角密排晶格常数为a,c 钢球体积为V 1,总体积为V 2(1)简单立方单胞含一个原子,a r =2 52.06343321≈==ππa r V V(2)体心立方取惯用单胞,含两个原子,r a 43= 68.0833423321≈=⋅=ππar V V (3)面心立方取惯用单胞,含4个原子,r a =2 74.0623443321≈=⋅=ππar V V (4)六角密排与面心立方同为密堆积结构,可预期二者具有相同的空间占有率 取图示单胞,含两个原子,a r =2 单胞高度a c 38=(见第2题) 74.062233422321≈=⋅⋅=ππc a r V V (5)金刚石取惯用单胞,含8个原子,r a 2341= 34.01633483321≈=⋅=ππar V V2.试证六方密排密堆积结构中128() 1.6333c a =≈解: 六角密排,如图示,4个原子构成正四面体222)2332(2a a c =⋅+⎪⎭⎫⎝⎛ ⇒ a c 38=3.证明:体心立方晶格的倒格子是面心立方,面心立方的倒格子是体心立方。
证:体心立方基矢取为⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=++-=-+=)(2)(2)(2321k j i a a k j i a a k j i a a其中a 为晶格常数其倒格子基矢,按定义)(2)(21111114212)(223321j i b j i a kj ia a a a b+=+=--⋅=⨯Ω=πππ)(2)(2132k j b a a b +=⨯Ω=π)(2)(2213k i b a a b +=⨯Ω=π可见,体心立方的倒格子是晶格常数为a b π4=的面心立方。

第一章 金属自由电子气体模型习题及答案1. 你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的?[解答] 自由电子论只考虑电子的动能。
在绝对零度时,金属中的自由(价)电子,分布在费米能级及其以下的能级上,即分布在一个费米球内。
在常温下,费米球内部离费米面远的状态全被电子占据,这些电子从格波获取的能量不足以使其跃迁到费米面附近或以外的空状态上,能够发生能态跃迁的仅是费米面附近的少数电子,而绝大多数电子的能态不会改变。
也就是说,常温下电子的平均动能与绝对零度时的平均动能十分相近。
2. 晶体膨胀时,费米能级如何变化?[解答] 费米能级3/222)3(2πn mE o F= , 其中n 单位体积内的价电子数目。
晶体膨胀时,体积变大,电子数目不变,n 变小,费密能级降低。
3. 为什么温度升高,费米能反而降低?[解答] 当K T 0≠时,有一半量子态被电子所占据的能级即是费米能级。
除了晶体膨胀引起费米能级降低外,温度升高,费米面附近的电子从格波获取的能量就越大,跃迁到费米面以外的电子就越多,原来有一半量子态被电子所占据的能级上的电子就少于一半,有一半量子态被电子所占据的能级必定降低,也就是说,温度生高,费米能反而降低。
4. 为什么价电子的浓度越大,价电子的平均动能就越大?[解答] 由于绝对零度时和常温下电子的平均动能十分相近,我们讨论绝对零度时电子的平均动能与电子的浓度的关系。
价电子的浓度越大,价电子的平均动能就越大,这是金属中的价电子遵从费米—狄拉克统计分布的必然结果。
在绝对零度时,电子不可能都处于最低能级上,而是在费米球中均匀分布。
由式3/120)3(πn k F =可知,价电子的浓度越大费米球的半径就越大,高能量的电子就越多,价电子的平均动能就越大。
这一点从3/2220)3(2πn m E F=和3/222)3(10353πn mE E oF ==式看得更清楚。
电子的平均动能E 正比于费米能o F E ,而费米能又正比于电子浓度32l n。

1.1 如果将等体积球分别排列成下列结构,设x 表示钢球所占体积与总体积之比,证明结构x简单立方π/ 6 ≈0.52 体心立方3π/ 8 ≈0.68 面心立方2π/6 ≈0.74六方密排2π/ 6 ≈0.74 金刚石3π/16 ≈0.34解:设钢球半径为r ,根据不同晶体结构原子球的排列,晶格常数a 与r 的关系不同,分别为:简单立方:a = 2r金刚石:根据金刚石结构的特点,因为体对角线四分之一处的原子与角上的原子紧贴,因此有1.3 证明:体心立方晶格的倒格子是面心立方;面心立方晶格的倒格子是体心立方。
证明:体心立方格子的基矢可以写为面心立方格子的基矢可以写为根据定义,体心立方晶格的倒格子基矢为同理与面心立方晶格基矢对比,正是晶格常数为4π / a的面心立方的基矢,说明体心立方晶格的倒格子确实是面心立方。
注意,倒格子不是真实空间的几何分布,因此该面心立方只是形式上的,或者说是倒格子空间中的布拉菲格子。
根据定义,面心立方的倒格子基矢为同理而把以上结果与体心立方基矢比较,这正是晶格常数为4πa的体心立方晶格的基矢。
证明:根据定义,密勒指数为的晶面系中距离原点最近的平面ABC 交于基矢的截距分别为即为平面的法线根据定义,倒格子基矢为则倒格子原胞的体积为1.6 对于简单立方晶格,证明密勒指数为(h, k,l)的晶面系,面间距d 满足其中a 为立方边长。
解:根据倒格子的特点,倒格子与晶面族(h, k,l)的面间距有如下关系因此只要先求出倒格,求出其大小即可。
因为倒格子基矢互相正交,因此其大小为则带入前边的关系式,即得晶面族的面间距。
1.7 写出体心立方和面心立方晶格结构的金属中,最近邻和次近邻的原子数。
若立方边长为a ,写出最近邻和次近邻的原子间距。
答:体心立方晶格的最近邻原子数(配位数)为8,最近邻原子间距等于次近邻原子数为6,次近邻原子间距为a ;面心立方晶格的最近邻原子数(配位数)为12,最近邻原子间距等于次近邻原子数为6,次近邻原子间距为a 。
![《固体物理学》答案[1]](https://uimg.taocdn.com/f8d34b12866fb84ae45c8da9.webp)

固体物理习题参考答案(部分)第一章 晶体结构1.氯化钠:复式格子,基元为Na +,Cl -金刚石:复式格子,基元为两个不等价的碳原子 氯化钠与金刚石的原胞基矢与晶胞基矢如下:原胞基矢)ˆˆ()ˆˆ()ˆˆ(213212211j i a a i k a a k j a a +=+=+= , 晶胞基矢 ka a j a a ia a ˆˆˆ321===2. 解:31A A O ':h:k;l;m==-11:211:11:111:1:-2:1 所以(1 1 2 1) 同样可得1331B B A A :(1 1 2 0); 5522A B B A :(1 1 0 0);654321A A A A A A :(0 0 0 1)3.简立方: 2r=a ,Z=1,()63434r 2r a r 3333πππ===F体心立方:()πππ833r4r 342a r 3422a 3r 4a r 4a 33333=⨯=⨯=∴===F Z ,,则面心立方:()πππ622r 4r 34434442r 4a r 4a 233ar 33=⨯=⨯=∴===F Z ,,则 六角密集:2r=a, 60sin 2c a V C = a c 362=,πππ622336234260sin 34223232=⨯⨯⨯=⨯=⎪⎭⎫ ⎝⎛a a c a r F a金刚石:()πππ163r 38r 348a r 3488Z r 8a 33333=⨯=⨯===F ,, 4. 解:'28109)31arccos(312323)ˆˆˆ()ˆˆˆ(cos )ˆˆˆ()ˆˆˆ(021*******12211=-=-=++-⋅+-=⋅=++-=+-=θθa a k j i a k j i a a a a a kj i a a kj i a a 5.解:对于(110)面:2a 2a a 2S =⋅=所包含的原子个数为2,所以面密度为22a2a22=对于(111)面:2a 2323a 22a 2S =⨯⨯= 所包含的原子个数为2,所以面密度为223a34a 232=8.证明:ABCD 是六角密堆积结构初基晶胞的菱形底面,AD=AB=a 。


《固体物理学》部分习题解答1.3 证明:体心立方晶格的倒格子是面心立方;面心立方晶格的倒格子是体心立方 。
解 由倒格子定义2311232a a b a a a π⨯=⋅⨯ 3121232a a b a a a π⨯=⋅⨯ 1231232a a b a a a π⨯=⋅⨯体心立方格子原胞基矢123(),(),()222a a aa i j k a i j k a i j k =-++=-+=-+ 倒格子基矢231123022()()22a a a ab i j k i j k a a a v ππ⨯==⋅-+⨯+-⋅⨯202()()4a i j k i j k v π=⋅-+⨯+-2()j k a π=+ 同理31212322()a ab i k a a a aππ⨯==+⋅⨯ 32()b i j a π=+ 可见由123,,b b b 为基矢构成的格子为面心立方格子 面心立方格子原胞基矢123()/2()/2()/2a a j k a a k i a a i j =+=+=+ 倒格子基矢2311232a a b a a a π⨯=⋅⨯ 12()b i j k a π=-++ 同理22()b i j k a π=-+ 32()b i j k aπ=-+ 可见由123,,b b b 为基矢构成的格子为体心立方格子1.4 证明倒格子原胞的体积为03(2)v π,其中0v 为正格子原胞体积证 倒格子基矢2311232a a b a a a π⨯=⋅⨯3121232a a b a a a π⨯=⋅⨯1231232a a b a a a π⨯=⋅⨯倒格子体积*0123()v b b b =⋅⨯3*23311230(2)()()()v a a a a a a v π=⨯⋅⨯⨯⨯ 3*00(2)v v π=1.5 证明:倒格子矢量112233G hb h b h b =++垂直于密勒指数为123()hh h 的晶面系。

固体物理学概念和习题答案固体物理学是物理学中的一个分支,主要研究固态物质的性质和行为。
固态物质是由原子和分子组成的,因此它具有一些特殊的性质。
本文将介绍一些固态物理学的概念和习题答案。
固态物质的结构固态物质的结构对其性质和行为有很大的影响。
在固体物理学中,人们通常将固态物质分为晶体和非晶体两类。
晶体晶体是由具有宏观周期性排列的原子或分子组成的固体物质。
晶体的周期性结构可以看作是由几何图形不断重复而成。
晶体中的原子或分子排列方式可以用晶体结构进行描述。
常见的晶体结构包括立方晶系、正交晶系、单斜晶系、三斜晶系、四方晶系和六方晶系。
非晶体非晶体是没有宏观周期性的固体物质,其原子或分子的排列具有无序性。
非晶体的结构一般用玻璃结构来进行描述。
固态物质的性质固态物质具有多种多样的性质。
在这里,我们介绍几种常见的性质。
热导率热导率是指在单位时间内,单位温度梯度下传热量的比率。
固态物质的热导率往往与其结构有关,例如晶体中的结构与热导率之间存在一定的相互关系。
电导率电导率是指在单位电场下,单位长度内电流的比率。
固态物质的导电性往往与其晶体结构有关,不同晶体结构的物质具有截然不同的导电性。
声波速度声波速度是指声波在介质中传播的速度。
固态物质的声波速度往往与其密度、弹性模量和波长等因素有关。
光学性质固态物质的光学性质很常见,包括折射率、吸收系数、透过率和反射率等。
这些光学性质往往与物质的电子结构和晶体结构有关。
固态物理学习题答案下面是一些固态物理学的习题答案。
习题1某个晶体中,某个方向上的原子排列方式为ABABAB…,另一个方向上的原子排列方式为ABCABCABC…,请确定该晶体的晶体结构。
答案:该晶体为六方晶系。
习题2一种固态物质的密度为2.5 g/cm3,它的弹性模量为4.0×1010 N/m2。
请计算该物质的声波速度。
答案:物质的声波速度为3.0×103 m/s。
习题3一种固态物质的热导率为0.1 W/m·K,其密度为2700 kg/m3。

高等计算固体力学作业参考答案 *解答: 设332210)(x a x a x a a x +++=φ, 余量)()(22x Q dxd x R +=φ由边界条件0)0(=φ, 可得00=a ;由10==Lx dxd φ可得010322321=-++L a L a a(1)(a) 配点法: 取x=L/3和2L/3为配点, 要求:0)3/(=L R (2) 0)3/2(=L R(3)解方程组(1)-(3),可得La a L a 21 ,1 ,2/10321=-=+= (b) 子域法: 取2/0L x ≤≤和L x L ≤≤2/为子域, 则0)(2/0=⎰dx x R L (4) 0)(2/=⎰dx x R LL(5)*任何问题请email to: yqhuang@解方程组(1),(4),(5),可得La a L a 31 ,4/3 ,2/10321=-=+= (b) 伽辽金法. 取权函数33221,,x W x W x W ===,则0)10()(101=--=⎰L x Ldx d W dx x R W φ(6) 0)10()(202=--=⎰L x Ldx d W dx x R W φ(7) 0)10()(303=--=⎰Lx Ldx d W dx x R W φ(8)解方程组(6)-(8),可得La a L a 165,32/23 ,321710321=-=+=解答: 微分算子为) ()() () (2222c y x L +∂∂+∂∂=,取任意函数u, v ,dsnvu ds n u v dxdy u vL ds n v u ds n y u v n x u v dxdy cu y u x u v ds n y v u n x v u dxdy cuv y v y u x v x u dxdy cv y v x v u dxdy v uL y x y x ⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰∂∂+∂∂-=∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-⎪⎪⎭⎫ ⎝⎛+∂∂+∂∂=⎪⎪⎭⎫⎝⎛∂∂+∂∂+⎪⎪⎭⎫ ⎝⎛+∂∂∂∂-∂∂∂∂-=⎪⎪⎭⎫⎝⎛+∂∂+∂∂=)()(22222222故算子是自伴随的.原问题等价于: (假设φ已满足1Γ上的边界条件)0212121212121)()(222222222222222=⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛∂∂-⎪⎭⎫ ⎝⎛∂∂-=+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛∂∂-⎪⎭⎫ ⎝⎛∂∂-=+⎪⎪⎭⎫⎝⎛++⎪⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎭⎫ ⎝⎛∂∂∂∂-=⎪⎭⎫⎝⎛-∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛++∂∂∂∂-∂∂∂∂-=⎪⎭⎫⎝⎛-∂∂-⎪⎪⎭⎫ ⎝⎛++∂∂+∂∂⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ΓΓΓΓΓds q dxdy Q c y x ds q dxdy Q c y x ds q dxdy Q c y y x x ds q n ds n dxdy Q c y y x x ds q n dxdy Q c y x φφφφφδδφφφφφδδφδφφδφφδφφδφφδφφδφδφφδφδφφδφφφδφφφφδφ等价的自然变分原理为:()⎰⎰⎰Γ+⎪⎪⎭⎫⎝⎛++⎪⎪⎭⎫ ⎝⎛∂∂-⎪⎭⎫ ⎝⎛∂∂-=∏2222212121ds q dxdy Q c y x φφφφφφ 或()⎰⎰⎰Γ-⎪⎪⎫ ⎛--⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=∏2221222ds q dxdy Q c y x φφφφφφ解答: 此时问题的变分原理简化为()⎰⎰⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=∏dxdy y x φφφφ42122 将近似函数代入可以得到:截面的扭矩⎰⎰2Tφ=dxdy解答:()()()()()()0=Γ⎪⎭⎫⎝⎛∂∂+Γ⎪⎭⎫ ⎝⎛+-∂∂+Ω⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎭⎫ ⎝⎛∂∂∂∂-=Γ--Γ⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+Ω⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫⎝⎛∂∂∂∂-⎪⎭⎫ ⎝⎛∂∂∂∂-=Γ--Ω⎥⎦⎤⎢⎣⎡-∂∂∂∂+∂∂∂∂=Γ--Ω⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂=∏⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰Γ-ΓΓΩΓΓΩΓΩΓΩqq qqq d n k d q n k d Q y k y x k x d q d n y k n x k d Q y k y x k x d q d Q y y k x x k d q d Q y y k x x ky x δφφδφαφφδφφφδφαφδφδφφδφφδφδφφδφφδφαφδφδφδφφδφφδφαφδφδφφδφφδφφδ由变分δφ的任意性,可得相应的欧拉方程和边界条件:0=+⎪⎪⎭⎫⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂Q y k y x k x φφ, Ω内 q Γ上的自然边界条件: 0=+-∂∂q nkαφφq Γ-Γ上的强迫边界条件: 0=δφ,或φφ=解答: 方法1:设A,B 两点的坐标为(x 1,y 1,z 1), (x 2,y 2,z 2), 并设x=x(s),y=y(s),z=z(s), 则dsdxx x ds dy 21--=问题的泛函可以表示为:),()()(11222222z x L ds dsdz ds dx x dz dy dx ds L BAB ABA =+-=++==⎰⎰⎰ 问题转化为求泛函L(x,z)在满足端点条件下的最小值问题。
若是将等体积球别离排列成以下结构,设x 表示钢球所占体积与整体积之比,证明结构x简单立方π/ 6 ≈体心立方3π/ 8 ≈面心立方2π/ 6 ≈六方密排2π/ 6 ≈金刚石3π/16 ≈解:设钢球半径为r ,依照不同晶体结构原子球的排列,晶格常数a 与r 的关系不同,别离为:简单立方:a = 2r金刚石:依照金刚石结构的特点,因为体对角线四分之一处的原子与角上的原子紧贴,因此有证明:体心立方晶格的倒格子是面心立方;面心立方晶格的倒格子是体心立方。
证明:体心立方格子的基矢能够写为面心立方格子的基矢能够写为依照概念,体心立方晶格的倒格子基矢为同理与面心立方晶格基矢对照,正是晶格常数为4π/ a的面心立方的基矢,说明体心立方晶格的倒格子确实是面心立方。
注意,倒格子不是真实空间的几何散布,因此该面心立方只是形式上的,或说是倒格子空间中的布拉菲格子。
依照概念,面心立方的倒格子基矢为同理而把以上结果与体心立方基矢比较,这正是晶格常数为4πa的体心立方晶格的基矢。
证明:依照概念,密勒指数为的晶面系中距离原点最近的平面ABC 交于基矢的截距别离为即为平面的法线依照概念,倒格子基矢为那么倒格子原胞的体积为关于简单立方晶格,证明密勒指数为(h, k,l)的晶面系,面间距d 知足其中a 为立方边长。
解:依照倒格子的特点,倒格子与晶面族(h, k,l)的面间距有如下关系因此只要先求出倒格,求出其大小即可。
因为倒格子基矢相互正交,因此其大小为那么带入前边的关系式,即得晶面族的面间距。
写出体心立方和面心立方晶格结构的金属中,最近邻和次近邻的原子数。
假设立方边长为a ,写出最近邻和次近邻的原子间距。
答:体心立方晶格的最近邻原子数(配位数)为8,最近邻原子间距等于次近邻原子数为6,次近邻原子间距为a ;面心立方晶格的最近邻原子数(配位数)为12,最近邻原子间距等于次近邻原子数为6,次近邻原子间距为a 。
证明两种一价离子组成的一维晶格的马德隆常数为α= 2ln 2证明:设一个由正负两种离子相间等距排列的无穷一维长链,取一负离子作参考离子,用r表示相邻离子间的距离,于是有依照假设,马德隆常数求和中的正负号如此选取,即遇正离子取正号,遇负离子取负号。
第一章 晶体结构1.1、 如果将等体积球分别排成下列结构,设x 表示钢球所占体积与总体积之比,证明:结构 X简单立方52.06=π体心立方68.083≈π 面心立方74.062≈π 六角密排74.062≈π 金刚石34.063≈π解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06834343333====πππrra r x (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)334(3423423333≈=⨯=⨯=πππr r a r x (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)22(3443443333≈=⨯=⨯=πππr r a r x (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062)22(3443443333≈=⨯=⨯=πππr r a r x (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.06333834834833333≈=⨯=⨯=πππr r a r x 1.3、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
11级第一次(作业)请充分利用网络、本校及外校图书馆的相关资料,同时联系相关专业的老师,调查关于固体物理的简史、发展趋势以及当代的热门前沿课题(针对自己感兴趣的某个方面),形成一份报告,阐述自己的看法,要求2000字以上。
(已经在第一次课布置,11月1日前后上交)11级固体物理第2次习题和思考题1.在结晶学中,我们课堂上讲的单胞,也叫元胞,或者叫结晶学原胞,也叫晶胞,试回忆一下晶胞是按晶体的什么特性选取的?答:在结晶学中,晶胞选取的原则是既要考虑晶体结构的周期性又要考虑晶体的宏观对称性。
2.解释Bravais 点阵并画出氯化钠晶体的结点所构成的Bravais 点阵。
答:晶体的内部结构可以概括为由一些相同的结点构成的基元在空间有规则的作周期性的无限分布,这些结点构成点阵,如果基元只由一个结点构成,这种点阵称为Bravais 点阵。
氯化钠晶体的Bravais 点阵可参照书p8的图1-13,点阵的结点由钠离子和氯离子组成。
3.说明金刚石结构是复式点阵的原因。
答:金刚石结构可这样描述:面心立方的体心向顶角引8条对角线,在互不相邻的四条对角线中点,各有一个原子。
以金刚石为例,顶角和面心处的原子周围情况和对角线上的原子周围情况不相同,因而金刚石结构是复式晶格,可看作两套面心立方子晶格沿体对角线移开1/4体对角线长度而成。
Bravais 点阵包含两个原子。
4.体心立方点阵和面心立方点阵互为正、倒格子,试证明之。
答:面心立方的三个基矢为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=)(2)(2)(2321i k a a k j a a j i a a其体积为43a ,根据倒格矢的定义得:⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=⨯⋅⨯=++-=⨯⋅⨯=+-=⨯⋅⨯=)(2)(2)(2)(2)(2)(2321213321132321321k j i a a a a a a b k j i a a a a a a b k j i a a a a a a bππππππ 可见,除了系数不同之外,方向正好是体心立方的晶格基矢。