第03章 构造研究中的应力分析基础

第3章 地质构造分析的力学基础
9
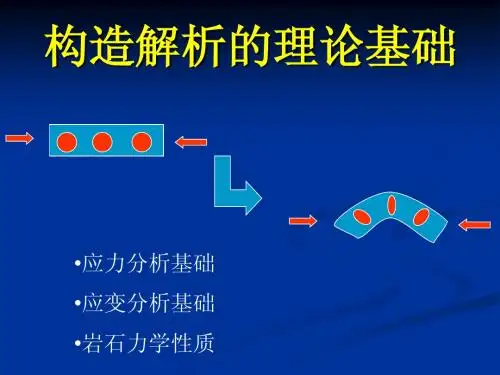
(二) 应力状态和应力椭球
4.常见的几种应力状态：
单轴
压缩：σ1﹥σ2＝σ3＝0 拉伸：σ1＝σ2＝0﹥σ3
双轴
双轴压缩：σ1﹥σ2﹥σ3＝0
压缩—拉伸(平面应力状态):
双轴拉伸σ1
σ1﹥σ2＝0﹥σ3
=0 ＞σ2 ＞ σ3，
三轴：三个主应力都不等于0
（6） 已知应力摩尔圆圆周上一个点, 找出该点在单元体中的对应截面
第3章 地质构造分析的力学基础 23
(三) 二维应力分析―摩尔圆图解法
3. 应力摩尔圆的性质:
从单元体可以看出 ： 1）当在a=0°截面时, 对应的应力摩尔圆圆周上的A点,此时, sa =s1 ， sa =smax, , ta=0 , 即在此截面上有最大主应力而无剪应力 2）当在a=90°截面时, 对应的应力摩尔圆圆周上的B点,此时, sa =s2 , sa =smin ,ta=0 , 即在此截面上有最小主应力而无剪应力., 3）当在a=45°和a=135° 截面时, 对应的应力摩尔圆 圆周上最高和最低点,此时, sa = (s1 + s2)/2 ， ta= (s1 - s2)/2 =tmax 和ta=- (s1 - s2)/2 =tmix,， 即在此截面上有剪应力绝对 值最大。
第3章 地质构造分析的力学基础
12
(三) 二维应力分析―摩尔圆图解法
1. 单轴应力状态的二维应力分析
1) 平面上一矩形物体, 作用于物体上的外力为P1 , 内力为p1, 那么, 垂 直于外力截面A0上的主应力为: 2) s1 =p1/A0 （ 1）
在与内力p1斜交的截面Aa上, 设其正应力为上sa, 剪应力为ta, 合应 sA =p1/Aa （ 2）
1）先求出由p1单独作用在Aa截面上的应力, 由单轴应力 状态的应力分析公式（4） 和（6）,即得p1单独作用形成的 应力 sa= s1(1+cos2 a ) / 2 （4） ta = s1 sin2 a /2 （6） 2） 再求由p2单独作用在Aa截面上的应力: s = s1(1+cos2 ) / 2 （7） t = s1 sin2 /2 （8） ＝ 90+a 代人 （7） 和（8）即得 s =s2(1-cos2a) / 2 t =-s2sin2a / 2
第3章 地质构造分析的力学基础 21
(三) 二维应力分析―摩尔圆图解法
2. 双轴应力状态的二维应力分析
3） 根据叠加原理: s = sa + s t= ta + t 可得 s =(s1 + s2)/2+ (s1 - s2) cos2a /2 （9） t= (s1 - s2) sin2a/2 （10）
第3章 地质构造分析的力学基础
15
(三) 二维应力分析―摩尔圆图解法
1. 单轴应力状态的二维应力分析
τ
O
(σ1, 0)
(σ1/2, 0)
σ2=0
D′
σ
第3章 地质构造分析的力学基础
16
τ
D(σα, τ α)
P1
a
n
a
P1=s1A0
O
α
σ2=0
D′
2α (σ1/2, 0)
(σ1, 0)
σ
A0 A1
第3章 地质构造分析的力学基础 27
(二) 应力场
5. 应力集中
第3章 地质构造分析的力学基础
28
体，其中长轴代表最大主应
力s1, 短轴代表最小主应力 s3, 中间轴代表中间主应力s2
第3章 地质构造分析的力学基础
8
(二) 应力状态和应力椭球
3. 应力椭圆：沿椭球体三个主应力平面切割椭球体, 可得三 个椭圆, 叫应力椭圆, 每一
个应力椭圆中有两个主应
力, 代表二维应力状态. 这 三个应力椭圆分别为: s1与s2椭圆、s1与s3椭圆、 s2与s3椭圆
第3章 地质构造分析的力学基础
14
(三) 二维应力分析―摩尔圆图解法
1. 单轴应力状态的二维应力分析
用倍角公式sin2 a ＝2 cos a sina ta = s1 sin2 a /2 （6） （4）和（6）式为单轴应力状态下，任意切面上主应力s1、正 应力sa及剪应力ta的关系，即： sa= s1(1+cos2 a ) / 2 ta = s1 sin2 a /2 可写成：
第3章 地质构造分析的力学基础 24
(二) 应力场
1. 应力场:
上面讲述的是物体内一点的应力状态, 任一物体和地 壳岩石中都存在一系列点的应力状态，它们构成了物体 或岩石中的空间应力场。也就是说, 物体内一系列点的 瞬时应力状态叫应力场 应力场中各点的应力状态如果都相同或相似, 叫做
均匀应力场。
应力场中各点的应力状态从一点到另一点是不相 同和变化的, 这种应力场叫非均匀应力场。
19
(三) 二维应力分析―摩尔圆图解法
2. 双轴应力状态的二维应力分析
一矩形物体, 在其相互垂直的面上, 分别作用有外力p1和
p2,且p1>p2,。据应力叠加原理，采用两个单轴应力状态的叠 加方法
第3章 地质构造分析的力学基础
20
(三) 二维应力分析―摩尔圆图解法
2. 双轴应力状态的二维应力分析
第3章 地质构造分析的力学基础
6
(二) 应力状态和应力椭球
1) 主平面：S1, S2, S3
2) 主应力：
σ1(最大)，σ2 (中间) ，σ3 (最小).
σ3 σ2 σ1 σ2 σ3
第3章 地质构造分析的力学基础 7
σ1
(二) 应力状态和应力椭球
2. 应力椭球：当物体内一点主应力性质相同，大小不同, 即 s1>s2>s3时, 可以取三个主应 力的矢量为半径, 作一个椭球 体, 该椭球体代表作用于该点 的全应力状态, 称为应力椭球
构造应力场的时间分类
第3章 地质构造分析的力学基础
26
(二) 应力场
3. 应力集中
当物体内部有孔洞, 缺口或裂隙存在时, 就会在这些地方产生局部的应 力集中。 地壳中的岩石中有上述的现象时, 也会产生应力集中, 应力集中 会影响构造应力场中的应力分布状态. 地球的演化经历了漫长的历史, 一个地区发生过多期次的构造运动和 构造变形, 在早期构造变形的部位, 尤其是在断裂的端点, 拐折点, 分枝点 以及两条或两条以上的断裂的交汇处, 都是后期构造应力场的应力集中部 位 有破裂存在的岩石再次受力后, 其应力集中与受力条件有密切关系, 例 如, 张应力作用方向与先存破裂面垂直, 则在破裂面两端产生应力集中区; 当压应力作用方向与先存破裂面垂直时, 则不出现应力集中区. 此外, 应力集中还与岩石的力学性质有关, 当岩石呈韧性时, 虽然岩石 中有断裂存在, 后期构造应力场不会产生应力集中; 而岩石呈脆性状态时, 后期构造应力场则在断裂处容易产生应力集中.
所取空间包含的物质质量有关的非接触力.（重力、磁力）
2. 内力：物体内部质点之间的相互作用力
1) 固有内力：在没有外力作用时物体内质点间的相互作 用力，它保持物体的形状和状态 2) 附加内力：在外力作用下固有内力的改变量，它阻止 物体继续变形并力图恢复原始状态（常称为内力）
外力和内力的相对性——尺度
《构造地质学》
第3章 构造研究中的应 力分析基础
刘重庆 天津城建大学 地质与测绘学院
主要内容
1. 应力 2. 应力场
主要内容
1. 应力 2. 应力场
（一）外力、内力、应力
1. 外力：另一物体所施加的力
1) 面力：作用在物体边界一定面积范围内的接触力. 2) 体力：作用在物体内部每一质点上，与围绕质点邻域
第3章 地质构造分析的力学基础
17

1) a=0, t=0, s最大. 2) a=450, | t |=Max. 3) 任意两个相互垂直面上剪 应力t大小相等，符号相反.
τ
D(τα, σα)
P1
a
n
a
P1=s1A0
O
α
σ2=0
D′
第3章 地质构造分析的力学基础
2α (σ1/2, 0)
(σ1, 0)
第3章 地质构造分析的力学基础
22
(三) 二维应力分析―摩尔圆图解法
3. 应力摩尔圆的性质:
如以s为横坐标，t为纵坐标 （1） 圆心一定在横轴上, 圆 心坐标为 ((s1 + s2)/2, 0) （2） 圆的半径为(s1 - s2) /2 （3） 单元体中截面角a, 应 力圆上为2a （4） 单元体上任何一截面都对应于摩尔应力圆圆周上的的一个点, 该 截面上的一组应力值即为圆周上对应点的一组坐标 （5） 已知单元体上的一个截面, 求该截面在应力摩尔圆圆周上对应点.
-Hale Waihona Puke dTdT+
dA M
dN dP
5
dT
第3章 地质构造分析的力学基础
(二) 应力状态和应力椭球
1. 弹性力学证明：任何受力物体内部总是能够 找到三个相互垂直的面，其上只有正应力而无剪 应力.
主应力：某一截面上只有正应力，没有剪应力时 的正应力 主应力轴：主应力作用的方向线 主应力面（主平面）：垂直于主应力的平面
σ
A0 A1
18
例：已知：物体的σ1＝20 MPa, 求作：
①该受力物体的应力摩尔圆.
②求出法线与σ1成30°交角的斜面上的正应力和剪应
力的值.
③求出与σ1成20°夹角斜面上的正应力和剪应力的值.
τ
P1 a
R=s1/2
60o
n
a
P1=s1A0
σ
A0 A1
第3章 地质构造分析的力学基础