西城区学习探究诊断_期末检测题

北京市西城区级期末测考试题及答案姓名:_____________ 年级:____________ 学号:______________一、选择题（共6题） 1.下列词语中加点字的读音完全正确的一项是A ．蝉蜕（tuì） 毋宁（wú） 冗杂（chén） 燕然勒功（lè）B ．骊歌（lí） 羸弱（yínɡ） 蓦然（mò） 戛然而止（ɡá）C ．菜畦（qí） 行辈（hánɡ） 珊瑚（shān） 叱咤风云（zhà）D ．炽痛（zhì） 怂恿（s ón ɡ） 悲怆（chu àn ɡ） 锲而不舍（q ì）【答案】C [A 冗杂（r ǒn ɡ） B 羸弱（l éi ） 戛然而止（ji á）D 炽痛（ch ì） 怂恿（s ǒn ɡ） 锲而不舍（qi è）]难度：容易 知识点：字音2.下列词语中没有错别字的一项是A ．撺掇 惬意 人声鼎沸 进退维谷B ．亢奋 阴霾 锋芒必露 语无轮次C ．怅然 抽搐 一拍既合 尽态极研D ．庇荫 真谛齐心谐力 来势凶凶【答案】A （B 锋芒毕露 语无伦次 C 一拍即合 尽态极妍 D 齐心协力 来势汹汹）难度：容易 知识点：字形3.下列句子中加点词语运用有误的一项是A ．历史上曾经人来人往的丝绸之路古迹，如今已变成人迹罕至的沙漠。

B ．马布里的篮球技术比中国国内球员略胜一筹，所以他成了球队的绝对核心。

C ．救援队忍冻挨饿，冒着余震的危险，在废墟中救人的事迹真是可歌可泣。

D ．透过十五倍的放大镜，才能看到针孔中的两只大熊猫，微雕艺术令人叹为观止。

【答案】B （马布里的技术比中国队员不是略胜一筹，而是高出一大截）难度：中等知识点：词语4.对下面文段中所使用的修辞方法的判断和分析理解不正确的一项是①__________________。

第十五章．．．．整式．．测试．．1 ．整式的乘法．．．．．学习要求．．．．会进行整式的乘法计算．．．．．．．．．．．．课堂学习检测．．．．．．一、填空题．．．．．1．．．（．1．）单项式相乘，把它们的．．．．．．．．．．．________．．．．．．．．分别相乘，对于只在一个单项式里．．．．．．．．．．．．．．．含有的字母，则．．．．．．．________．．．．．．．．．．（．2．）单项式与多项式相乘，就是用单项式去乘．．．．．．．．．．．．．．．．．．．________．．．．．．．．，再把所得的积．．．．．．．________．．．．．．．．．．（．3．）多项式与多项式相乘，先用．．．．．．．．．．．．．________．．．．．．．．乘以．．________．．．．．．．．，再把所得的积．．．．．．．________．．．．．．．．．． 2．．直接写出结果：．．．．．．．．（．1．）．5．y ．·（－．．4．xy ．．2．）＝．．________．．．．．．．．；（．．2．）（－．．．x ．2．y ．）．3．·（－．．3．xy ．．2．z ．）＝．．________．．．．．．．．；． （．3．）（－．．．2．a ．2．b ．）（．．ab ．．2．－．a ．2．b ．＋．a ．2．）＝．．________．．．．．．．．；．（．4．）．=-⋅-+-)21()864(22x x x ________．．．．．．．．；． （．5．）（．．3．a ．＋．b ．）（．．a ．－．2．b ．）＝．．________．．．．．．．．；（．．6．）（．．x ．＋．5．）（．．x ．－．1．）＝．．________．．．．．．．．．． 二、选择题．．．．．3．．下列算式中正确的是（．．．．．．．．．．． ）．A ．．．3．a ．3．·2．a ．2．＝．6．a ．6．B ．．．2．x ．3．·4．x ．5．＝．8．x ．8．C ．．．3．x ．·3．x ．4．＝．9．x ．4． D ．．．5．y ．7．·5．y ．3．＝．10．．y ．10．． 4．．（－．．．10．．）·（－．．．0．.．3．×．10．．2．）·（．．0．.．4．×．10．．5．）等于（．．．． ）． A ．．．1．.．2．×．10．．8．B ．．．－．0．.．12．．×．10．．7．C ．．．1．.．2．×．10．．7．D ．．．－．0．.．12．．×．10．．8． 5．．下面计算正确的是（．．．．．．．．．． ）．A ．．（．．2．a ．＋．b ．）（．．2．a ．－．b ．）＝．．2．a ．2．－．b ．2．B ．．．（－．．a ．－．b ．）（．．a ．＋．b ．）＝．．a ．2．－．b ．2．C ．．．（．a ．－．3．b ．）（．．3．a ．－．b ．）＝．．3．a ．2．－．10．．ab ．．＋．3．b ．2．D ．．．（．a ．－．b ．）（．．a ．2．－．ab ．．＋．b ．2．）＝．．a ．3．－．b ．3． 6．．已知．．．a ．＋．b ．＝．m ．，．ab ．．＝－．．4．，化简（．．．．a ．－．2．）（．．b ．－．2．）的结果是（．．．．．． ）． A ．．．6． B ．．．2．m ．－．8． C ．．．2．m ．D ．．．－．2．m ．三、计算题．．．．．7．．．)21).(43).(32(222z xy z yz x -- 8．．．[．4．（．a ．－．b ．）．m ．－．1．]．·[．－．3．（．a ．－．b ．）．2．m ．]．9．．．2．（．a ．2．b ．2．－．ab ．．＋．1．）＋．．3．ab ．．（．1．－．ab ．．）． 10．．．．2．a ．2．－．a ．（．2．a ．－．5．b ．）－．．b ．（．5．a ．－．b ．）．11．．．－（－．．．．x ．）．2．·（－．．2．x ．2．y ．）．3．＋．2．x ．2．（．x ．6．y ．3．－．1．）．12．．．．)214)(221(-+x x 13．．．（．．0．.．1．m ．－．0．.．2．n ．）（．．0．.．3．m ．＋．0．.．4．n ．）． 14．．．（．．x ．2．＋．xy ．．＋．y ．2．）（．．x ．－．y ．）．四、解答题．．．．．15．．．先化简，再求值．．．．．．．．．．（．1．）．),43253(4)12(562---+-+--n m m n m m m其中．．m ．＝－．．1．，．n ．＝．2．；． （．2．）（．．3．a ．＋．1．）（．．2．a ．－．3．）－（．．．4．a ．－．5．）（．．a ．－．4．），其中．．．．a ．＝－．．2．.． 16．．．小明同学在长．．．．．．．a ．cm ．．，宽．．cm 43a 的纸上作画，他在纸的四周各留了．．．．．．．．．．．．．．．2cm ．．．的．空白，求小明同学作的画所占的面积．．．．．．．．．．．．．．．．．．综合、运用、诊断．．．．．．．．一、填空题．．．．．17．．．直接写出结果：．．．．．．．．（．1．）．=⨯⨯⨯)1031()103(322______．．．．．．；． （．2．）－．．2．[．（－．．x ．）．2．y ．]．2．·（－．．3．x ．m ．y ．n ．）＝．．______．．．．．．；．（．3．）（－．．．x ．2．y ．m ．）．2．·（．xy ．．）．3．＝．______．．．．．．；（．．4．）（－．．．a ．3．－．a ．3．－．a ．3．）．2．＝．______．．．．．．；．（．5．）（．．x ．＋．a ．）（．．x ．＋．b ．）＝．．______．．．．．．；（．．6．）．=+-)31)(21(n m ______．．．．．．；． （．7．）（－．．．2．y ．）．3．（．4．x ．2．y ．－．2．xy ．．2．）＝．．______．．．．．．；． （．8．）（．．4．xy ．．2．－．2．x ．2．y ．）·（．．3．xy ．．）．2．＝．______．．．．．．．．二、选择题．．．．．18．．．下列各题中，计算正确的是（．．．．．．．．．．．．．． ）．A ．．（－．．．m ．3．）．2．（－．．n ．2．）．3．＝．m ．6．n ．6．B ．．．[．（－．．m ．3．）．2．（－．．n ．2．）．3．]．3．＝－．．m ．18．．n ．18．．C ．．．（－．．m ．2．n ．）．2．（－．．mn ．．2．）．3．＝－．．m ．9．n ．8．D ．．．（－．．m ．2．n ．）．3．（－．．mn ．．2．）．3．＝－．．m ．9．n ．9． 19．．．若（．．．8．×．10．．6．）（．．5．×．10．．2．）（．．2．×．10．．）＝．．M ．×．10．．a ．，则．．M ．、．a ．的值为（．．．． ）．A ．．．M ．＝．8．，．a ．＝．8．B ．．．M ．＝．8．，．a ．＝．10．．C ．．．M ．＝．2．，．a ．＝．9．D ．．．M ．＝．5．，．a ．＝．10．．20．．．设．．M ．＝（．．x ．－．3．）（．．x ．－．7．），．．N ．＝（．．x ．－．2．）（．．x ．－．8．），则．．．M ．与．N ．的关系为．．．．（． ）． A ．．．M ．＜．N ．B ．．．M ．＞．N ．C ．．．M ．＝．N ．D ．．．不能确定．．．．21．．．如果．．．x ．2．与－．．2．y ．2．的和为．．．m ．，．1．＋．y ．2．与－．．2．x ．2．的差为．．．n ．，那么．．．2．m ．－．4．n ．化简后．．．的结果为（．．．．． ）．A ．．－．．6．x ．2．－．8．y ．2．－．4．B ．．．10．．x ．2．－．8．y ．2．－．4．C ．．．－．6．x ．2．－．8．y ．2．＋．4．D ．．．10．．x ．2．－．8．y ．2．＋．4．22．．．如图，用代数式表示阴影部分面积为（．．．．．．．．．．．．．．．．．． ）． A ．．．ac ．．＋．bc ．．B ．．．ac ．．＋（．．b ．－．c ．）．C ．．．ac ．．＋（．．b ．－．c ．）．c ．D ．．．a ．＋．b ．＋．2．c ．（．a ．－．c ．）＋．．（．b ．－．c ．）． 三、计算题．．．．．23．．．－（－．．．．2．x ．3．y ．2．）．2．·（．1．.．5．x ．2．y ．3．）．2 ． 24．．．．)250(241)2)(5(54423x .x x x x -⋅-⋅-- 25．．．．4．a ．－．3．[．a ．－．3．（．4．－．2．a ．）＋．．8．]． 26．．．．)3()]21(2)3([322b a b b a b ab -⋅--- 四、解答题．．．．．27．．．在（．．．x ．2．＋．ax ．．＋．b ．）（．．2．x ．2．－．3．x ．－．1．）的积中，．．．．．x ．3．项的系数是－．．．．．．5．，．x ．2．项的系数．．．．是－．．6．，求．．a ．、．b ．的值．．．．拓展、探究、思考．．．．．．．．28．．．通过对代数式进行适当变形求出代数式的值．．．．．．．．．．．．．．．．．．．．．．（．1．）若．．2．x ．＋．y ．＝．0．，求．．4．x ．3．＋．2．xy ．．（．x ．＋．y ．）＋．．y ．3．的值；．．． （．2．）若．．m ．2．＋．m ．－．1．＝．0．，求．．m ．3．＋．2．m ．2．＋．2008．．．．的值．．．． 29．．．若．．x ．＝．2．m ．＋．1．，．y ．＝．3．＋．4．m ．，请用含．．．．x ．的代数式表示．．．．．．y ．．．测试．．2 ．乘法公式．．．． 学习要求．．．．会用平方差公式、完全平方公式进行计算，巩固乘法公式的使用．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．课堂学习检测．．．．．．一、填空题．．．．． 1．．计算题：．．．．．（．y ．＋．x ．）（．．x ．－．y ．）＝．．______．．．．．．；（．．x ．＋．y ．）（－．．．y ．＋．x ．）＝．．______．．．．．．；．（－．．x ．－．y ．）（－．．．x ．＋．y ．）＝．．______．．．．．．；（－．．．y ．＋．x ．）（－．．．x ．－．y ．）＝．．______．．．．．．；． 2．．直接写出结果：．．．．．．．．（．1．）（．．2．x ．＋．5．y ．）（．．2．x ．－．5．y ．）＝．．________．．．．．．．．；． （．2．）（．．x ．－．ab ．．）（．．x ．＋．ab ．．）．＝．______．．．．．．；．（．3．）（．．12．．＋．b ．2．）（．．b ．2．－．12．．）＝．．________．．．．．．．．；．（．4．）（．．a ．m ．－．b ．n ．）（．．b ．n ．＋．a ．m ．）．＝．______．．．．．．；．（．5．）（．．3．m ．＋．2．n ．）．2．＝．________．．．．．．．．；． （．6．）．=-2)32(b a ______．．．．．．；． （．7．）（．． ）．２．＝．m ．2．＋．8．m ．＋．16．．；．（．8．）．2)325.1(b a -＝．______．．．．．．；． 3．．在括号中填上适当的整式：．．．．．．．．．．．．．（．1．）（．．m ．－．n ．）（．． ）＝．．n ．2．－．m ．2．；． （．2．）（－．．．1．－．3．x ．）（．． ）．＝．1．－．9．x ．2．．．4．．多项式．．．．x ．2．－．8．x ．＋．k ．是一个完全平方式，则．．．．．．．．．．k ．＝．______．．．．．．．．5．．．-+=+222)1(1xx x x ______．．．．．．＝．2)1(x x -＋．______．．．．．．．． 二、选择题．．．．．6．．下列各多项式相乘，可以用平方差公式的有（．．．．．．．．．．．．．．．．．．．．． ）． ①（－．．．2．ab ．．＋．5．x ．）（．．5．x ．＋．2．ab ．．）． ②（．．ax ．．－．y ．）（－．．．ax ．．－．y ．）． ③（－．．．ab ．．－．c ．）（．．ab ．．－．c ．）． ④（．．m ．＋．n ．）（－．．．m ．－．n ．）． A ．．．4．个．B ．．．3．个．C ．．．2．个．D ．．．1．个．7．．下列计算正确的是（．．．．．．．．．． ）．A ．．（．．5．－．m ．）（．．5．＋．m ．）＝．．m ．2．－．25．．B ．．．（．1．－．3．m ．）（．．1．＋．3．m ．）＝．．1．－．3．m ．2．C ．．．（－．．4．－．3．n ．）（－．．．4．＋．3．n ．）＝－．．．9．n ．2．＋．16．．D ．．．（．2．ab ．．－．n ．）（．．2．ab ．．＋．n ．）．＝．2．a ．2．b ．2．－．n ．2．8．．下列等式能够成立的是（．．．．．．．．．．．． ）．A ．．（．．a ．－．b ．）．2．＝（－．．．a ．－．b ．）．2．B ．．．（．x ．－．y ．）．2．＝．x ．2．－．y ．2． C ．．．（．m ．－．n ．）．2．＝（．．n ．－．m ．）．2．D ．．．（．x ．－．y ．）（．．x ．＋．y ．）＝（－．．．．x ．－．y ．）（．．x ．－．y ．）．9．．若．．9．x ．2．＋．4．y ．2．＝（．．3．x ．＋．2．y ．）．2．＋．M ．，则．． M ．为（．． ）．A ．．．6．xy ．．B ．．．－．6．xy ．．C ．．．12．．xy ．．D ．．．－．12．．xy ．．10．．．如图．．．2．－．1．所示的图形面积由以下哪个公式表示（．．．．．．．．．．．．．．．．． ）．A ．．．a ．2．－．b ．2．＝．a ．（．a ．－．b ．）＋．．b ．（．a ．－．b ．）．B ．．（．．a ．－．b ．）．2．＝．a ．2．－．2．ab ．．＋．b ．2．C ．．（．．a ．＋．b ．）．2．＝．a ．2．＋．2．ab ．．＋．b ．2．D ．．．a ．2．－．b ．2．＝．a ．（．a ．＋．b ．）－．．b ．（．a ．＋．b ．）．图．2．－．1．三、计算题．．．．．11．．．（．．x ．n ．－．2．）（．．x ．n ．＋．2．）．12．．．（．．3．x ．＋．0.5．．．）（．．0.5．．．－．3．x ．）．13．．．．)3243)(4332(mn n m +-+14．．．．323.232xy y x +-15．．．（．．3．mn ．．－．5．ab ．．）．2． 16．．．（－．．．4．x ．3．－．7．y ．2．）．2． 17．．．（．．5．a ．2．－．b ．4．）．2． 四、解答题．．．．．18．．．用适当的方法计算．．．．．．．．．．． （．1．）．1.02．．．． ×．0.98．．．．（．2．）．13111321⨯（．3．）．2)2140(（．4．）．2005．．．．2．－．4010．．．．×．2006．．．．＋．2006．．．．2． 19．．．若．．a ．＋．b ．＝．17．．，．ab ．．＝．60．．，求（．．．a ．－．b ．）．2．和．a ．2．＋．b ．2．的值．．．．综合、运用、诊断．．．．．．．．一、填空题．．．．．20．．．（．．a ．＋．2．b ．＋．3．c ．）（．．a ．－．2．b ．－．3．c ．）＝（．．．______．．．．．．）．2．－（．．______．．．．．．）．2．；． （－．．5．a ．－．2．b ．2．）（．．______．．．．．．）＝．．4．b ．4．－．25．．a ．2．．． 21．．．．x ．2．＋．______．．．．．．＋．25．．＝（．．x ．＋．______．．．．．．）．2．；． x ．2．－．10．．x ．＋．______．．．．．．＝．（．______．．．．．．－．5．）．2．；．x ．2．－．x ．＋．______．．．．．．＝（．．x ．－．______．．．．．．）．2．；． 4．x ．2．＋．______．．．．．．＋．9．＝．（．______．．．．．．＋．3．）．2．．．22．．．若．．x ．2．＋．2．ax ．．＋．16．．是一个完全平方式，是．．．．．．．．．．a ．＝．______．．．．．．．．二、选择题．．．．．23．．．下列各式中，能使用平方差公式的是（．．．．．．．．．．．．．．．．．． ）．A ．．（．．x ．2．－．y ．2．）（．．y ．2．＋．x ．2．）．B ．．（．．0.5．．．m ．2．－．0.2．．．n ．3．）（－．．．0.5．．．m ．2．＋．0.2．．．n ．3．）．C ．．（－．．．2．x ．－．3．y ．）（．．2．x ．＋．3．y ．）．D ．．（．．4．x ．－．3．y ．）（－．．．3．y ．＋．4．x ．）． 24．．．下列等式不能恒成立的是（．．．．．．．．．．．．． ）．A ．．（．．3．x ．－．y ．）．2．＝．9．x ．2．－．6．xy ．．＋．y ．2．B ．．（．．a ．＋．b ．－．c ．）．2．＝（．．c ．－．a ．－．b ．）．2．C ．．（．．0.5．．．m ．－．n ．）．2．＝．0.25．．．．m ．2．－．mn ．．＋．n ．2．D ．．（．．x ．－．y ．）（．．x ．＋．y ．）（．．x ．2．－．y ．2．）＝．．x ．4．－．y ．4． 25．．．若．．,51=+a a 则．221a a +的结果是（．．．．． ）．A ．．．23．．B ．．．8．C ．．－．．8．D ．．－．．23．．26．．．（．．a ．＋．3．）（．．a ．2．＋．9．）（．．a ．－．3．）的计算结果是（．．．．．．．． ）． A ．．．a ．4．＋．81．．B ．．－．．a ．4．－．81．．C ．．．a ．4．－．81．．D ．．．81．．－．a ．4． 三、计算题．．．．．27．．．（．．x ．＋．1．）（．．x ．2．＋．1．）（．．x ．－．1．）（．．x ．4．＋．1．）．28．．．（．．2．a ．＋．3．b ．）（．．4．a ．＋．5．b ．）．（．2．a ．－．3．b ．）（．．4．a ．－．5．b ．）．29．．．（．．y ．－．3．）．2．－．2．（．y ．＋．2．）（．．y ．－．2．）．30．．．（．．x ．－．2．y ．）．2．＋．2．（．x ．＋．2．y ．）（．．x ．－．2．y ．）＋（．．．x ．＋．2．y ．）．2．四、计算题．．．．．31．．．当．．a ．＝．1．，．b ．＝－．．2．时，求．．．)212]()21()21[(2222b a b a b a --++的值．．．． 拓展、探究、思考．．．．．．．．32．．．巧算：．．．．).200811()411)(311)(211(2222----ΛΛ33．．．计算：（．．．．．a ．＋．b ．＋．c ．）．2．．．34．．．若．．a ．4．＋．b ．4．＋．a ．2．b ．2．＝．5．，．ab ．．＝．2．，求．．a ．2．＋．b ．2．的值．．．． 35．．．若．．x ．2．－．2．x ．＋．10．．＋．y ．2．＋．6．y ．＝．0．，求（．．．2．x ．＋．y ．）．2．的值．．．．36．．．若△．．．ABC ．．．三边．．a ．、．b ．、．c ．满足．．a ．2．＋．b ．2．＋．c ．2．＝．ab ．．＋．bc ．．＋．ca ．．．试问△．．．．ABC ．．．的三．．边有何关系？．．．．．．测试．．3． 整式的除法．．．．．学习要求．．．．1．．会进行单项式除以单项式的计算．．．．．．．．．．．．．．．．． 2．．会进行多项式除以单项式的计算．．．．．．．．．．．．．．．．．课堂学习检测．．．．．．一、判断题．．．．．1．．．x ．3．n ．÷．x ．n ．＝．x ．3． （． ）．2．．．x xy y x 2121)(2-=÷- （． ）．3．．．2．6．÷．4．2．×．16．．2．＝．512．．． （． ）． 4．．（．．3．ab ．．2．）．3．÷．3．ab ．．3．＝．9．a ．3．b ．3． （． ）．二、填空题．．．．． 5．．直接写出结果：．．．．．．．．（．1．）（．．28．．b ．3．－．14．．b ．2．＋．21．．b ．）÷．．7．b ．＝．______．．．．．．；．（．2．）（．．6．x ．4．y ．3．－．8．x ．3．y ．2．＋．9．x ．2．y ．）÷（－．．．．2．xy ．．）＝．．______．．．．．．；．（．3．）．=-÷-+-)32()32752(32224y y x y x xy y ______．．．．．．．． 6．．已知．．．A ．是关于．．．x ．的四次多项式，且．．．．．．．．A ．÷．x ．＝．B ．，那么．．．B ．是关于．．．x ．的．______．．．．．．次多项式．．．．．． 三、选择题．．．．．7．．．25．．a ．3．b ．2．÷．5．（．ab ．．）．2．的结果是（．．．．． ）．A ．．．a ．B ．．．5．a ．C ．．．5．a ．2．b ．D ．．．5．a ．2． 8．．已知．．．7．x ．5．y ．3．与一个多项式之积是．．．．．．．．．28．．x ．7．y ．3．＋．98．．x ．6．y ．5．－．21．．x ．5．y ．5．，则这个多项式是．．．．．．．．（． ）．A ．．．4．x ．2．－．3．y ．2．B ．．．4．x ．2．y ．－．3．xy ．．2． C ．．．4．x ．2．－．3．y ．2．＋．14．．xy ．．2．D ．．．4．x ．2．－．3．y ．2．＋．7．xy ．．3． 四、计算题．．．．．9．．．3422383ab b a ÷10．．．．22425.0)21(y x y x ÷- 11．．．．)21()52(232434x y a y x a -÷- 12．．．．26)(310)(5y x y x -÷- 13．．．．35433660)905643(ax .ax .x a x a ÷-+- 14．．．．[．2．m ．（．7．n ．3．m ．3．）．2．＋．28．．m ．7．n ．3．－．21．．m ．5．n ．3．]．÷（－．．．7．m ．5．n ．3．）．五、解答题．．．．．15．．．先化简，再求值：．．．．．．．．．[．5．a ．4．·a ．2．－（．．3．a ．6．）．2．÷（．．a ．2．）．3．]．÷（－．．．2．a ．2．）．2．，其中．．．a ．＝－．．5．．．16．．．已知长方形的长是．．．．．．．．．a ．＋．5．，面积是（．．．．．a ．＋．3．）（．．a ．＋．5．），求它的周长．．．．．．．．．17．．．月球质量约．．．．．．5.351．．．．．×．10．．22．．千克，地球质量约．．．．．．．．5.977．．．．．×．10．．24．．千克，问地球质．．．．．．．量约是月球质量的多少倍？（结果保留整数）．．．．．．．．．．．．．．．．．．．．．．综合、运用、诊断．．．．．．．．一、填空题．．．．．18．．．直接写出结果：．．．．．．．．（．1．）．[．（－．．a ．2．）．3．－．a ．2．（－．．a ．2．）．]．÷（－．．．a ．2．）＝．．______．．．．．．．．（．2．）．=-÷-+---++)3()31581(1115n n n n x x x x ______．．．．．．．．19．．．若．．m ．（．a ．－．b ．）．3．＝（．．a ．2．－．b ．2．）．3．，那么整式．．．．．m ．＝．______．．．．．．．．二、选择题．．．．．20．．．．）（yz x z y x 3224214-÷-的结果是（．．．．． ）． A ．．．8．xyz ．．． B ．．－．．8．xyz ．．． C ．．．2．xyz ．．． D ．．．8．xy ．．2．z ．2． 21．．．下列计算中错误的是（．．．．．．．．．．． ）．A ．．．4．a ．5．b ．3．c ．2．÷（－．．．2．a ．2．bc ．．）．2．＝．ab ．．B ．．（－．．．24．．a ．2．b ．3．）÷（－．．．．3．a ．2．b ．）·．2．a ．＝．16．．ab ．．2． C ．．．214)21(4222-=÷-⋅y x y y x D ．．．3658410221)()(a a a a a a =÷÷÷÷ 22．．．当．．43=a 时，代数式（．．．．．．28．．a ．3．－．28．．a ．2．＋．7．a ．）÷．．7．a ．的值是（．．．． ）． A ．．．425B ．．．41C ．．．49-D ．．－．．4．三、计算题．．．．．23．．．．7．m ．2．·（．4．m ．3．p ．4．）÷．．7．m ．5．p ．24．．．（－．．．2．a ．2．）．3．[．－（－．．．a ．）．4．]．2．÷．a ．8．25．．．．)43(]19)38[(23554y x xy z y x -⋅÷- 26．．．．x ．m ．＋．n ．（．3．x ．n ．y ．n ．）÷（－．．．．2．x ．n ．y ．n ．）．27．．．．])(21[)(122+++÷+n n y x y x 28．．．．mmm m )42(372-⨯⨯29．．．．[．（．m ．＋．n ．）（．．m ．－．n ．）－（．．．m ．－．n ．）．2．＋．2．n ．（．m ．－．n ．）．]．÷．4．n ．30．．．．87232232429]31.)3(2)3[(y x y y x x x y x ÷-⋅- 四、解答题．．．．．31．．．求．．1,61=-=y x 时，（．．．3．x ．2．y ．－．7．xy ．．2．）÷．．6．xy ．．－（．．15．．x ．2．－．10．．x ．）÷．．10．．x ．－（．．9．y ．2．＋．3．y ．）÷（－．．．．3．y ．）的值．．．．． 32．．．若．．,72288223b b a b a n m =÷求．m ．、．n ．的值．．．． 拓展、探究、思考．．．．．．．．33．．．已知．．．x ．2．－．5．x ．＋．1．＝．0．，求．．221x x +的值．．．．34．．．已知．．．x ．3．＝．m ．，．x ．5．＝．n ．，试用．．．m ．、．n ．的代数式表示．．．．．．x ．14．．．．35．．．已知除式．．．．．x ．－．y ．，商式．．．x ．＋．y ．，余式为．．．．1．，求被除式．．．．．．．测试．．4 ．提公因式法．．．．．学习要求．．．．能够用提公因式法把多项式进行因式分解．．．．．．．．．．．．．．．．．．．． 一、填空题．．．．．1．．因式分解是把一个．．．．．．．．．______．．．．．．化为．．______．．．．．．的形式．．．．．2．．．ax ．．、．ay ．．、－．．ax ．．的公因式是．．．．．______．．．．．．；．6．mn ．．2．、－．．2．m ．2．n ．3．、．4．mn ．．的公因式是．．．．．______．．．．．．．． 3．．因式分解．．．．．a ．3．－．a ．2．b ．＝．______．．．．．．．．二、选择题．．．．．4．．下列各式变形中，是因式分解的是（．．．．．．．．．．．．．．．．． ）．A ．．．a ．2．－．2．ab ．．＋．b ．2．－．1．＝（．．a ．－．b ．）．2．－．1．Ｂ．．．)11(22222xx x x +=+C ．．（．．x ．＋．2．）（．．x ．－．2．）＝．．x ．2．－．4．D ．．．x ．4．－．1．＝．（．x ．2．＋．1．）（．．x ．＋．1．）（．．x ．－．1．）． 5．．将多项式－．．．．．．6．x ．3．y ．2． ＋．3．x ．2．y ．2．－．12．．x ．2．y ．3．分解因式时，应提取的公因式是（．．．．．．．．．．．．．．． ）．A ．．－．．3．xy ．．B ．．－．．3．x ．2．y ．C ．．－．．3．x ．2．y ．2．D ．．－．．3．x ．3．y ．3． 6．．多项式．．．．a ．n ．－．a ．3．n ．＋．a ．n ．＋．2．分解因式的结果是（．．．．．．．．． ）．A ．．．a ．n ．（．1．－．a ．3．＋．a ．2．）．B ．．．a ．n ．（－．．a ．2．n ．＋．a ．2．）．C ．．．a ．n ．（．1．－．a ．2．n ．＋．a ．2．）．D ．．．a ．n ．（－．．a ．3．＋．a ．n ．）．三、计算题．．．．．7．．．x ．4．－．x ．3．y ．8．．．12．．ab ．．＋．6．b ． 9．．．5．x ．2．y ．＋．10．．xy ．．2．－．15．．xy ．．10．．．．3．x ．（．m ．－．n ．）＋．．2．（．m ．－．n ．）．11．．．．3．（．x ．－．3．）．2．－．6．（．3．－．x ．）． 12．．．．y ．2．（．2．x ．＋．1．）＋．．y ．（．2．x ．＋．1．）．2． 13．．．．y ．（．x ．－．y ．）．2．－（．．y ．－．x ．）．3．14．．．．a ．2．b ．（．a ．－．b ．）＋．．3．ab ．．（．a ．－．b ．）．15．．．－．．2．x ．2．n ．－．4．x ．n ．16．．．．x ．（．a ．－．b ．）．2．n ．＋．xy ．．（．b ．－．a ．）．2．n ．＋．1． 四、解答题．．．．．17．．．应用简便方法计算：．．．．．．．．．．（．1．）．201．．．2．－．201．．．（．2．）．4.3．．．×．199.8．．．．．＋．7.6．．．×．199.8．．．．．－．1.9．．．×．199.8．．．．．（．3．）说明．．．3．200．．．－．4．×．3．199．．．＋．10．．×．3．198．．．能被．．7．整除．．．．综合、运用、诊断．．．．．．．．一、填空题．．．．．18．．．把下列各式因式分解：．．．．．．．．．．．（．1．）－．．16．．a ．2．b ．－．8．ab ．．＝．______．．．．．．；．（．2．）．x ．3．（．x ．－．y ．）．2．－．x ．2．（．y ．－．x ．）．2．＝．______．．．．．．．．19．．．在空白处填出适当的式子：．．．．．．．．．．．．．（．1．）．x ．（．y ．－．1．）－（．．． ）＝（．．．y ．－．1．）（．．x ．＋．1．）；．．（．2．）．=+c b ab 3294278（． ）（．．2．a ．＋．3．bc ．．）．．． 二、选择题．．．．．20．．．下列各式中，分解因式正确的是（．．．．．．．．．．．．．．．． ）．A ．．－．．3．x ．2．y ．2．＋．6．xy ．．2．＝－．．3．xy ．．2．（．x ．＋．2．y ．）．B ．．（．．m ．－．n ．）．3．－．2．x ．（．n ．－．m ．）．3．＝（．．m ．－．n ．）（．．1．－．2．x ．）．C ．．．2．（．a ．－．b ．）．2．－（．．b ．－．a ．）＝（．．．a ．－．b ．）（．．2．a ．－．2．b ．）．D ．．．am ．．3．－．bm ．．2．－．m ．＝．m ．（．am ．．2．－．bm ．．－．1．）．21．．．如果多项式．．．．．．x ．2．＋．mx ．．＋．n ．可因式分解为（．．．．．．．x ．＋．1．）（．．x ．－．2．），则．．．m ．、．n ．的值．．为（．． ）． A ．．．m ．＝．1．，．n ．＝．2． B ．．．m ．＝－．．1．，．n ．＝．2． C ．．．m ．＝．1．，．n ．＝－．．2．D ．．．m ．＝－．．1．，．n ．＝－．．2．22．．．（－．．．2．）．10．．＋（－．．．2．）．11．．等于（．．． ）． A ．．－．．2．10．．B ．．－．．2．11．．C ．．．2．10．．D ．．－．．2．三、解答题．．．．．23．．．已知．．．x ．，．y ．满足．．⎩⎨⎧=-=+,13,62y x y x 求．7．y ．（．x ．－．3．y ．）．2．－．2．（．3．y ．－．x ．）．3．的值．．．．24．．．已知．．．x ．＋．y ．＝．2．，．,21-=xy 求．x ．（．x ．＋．y ．）．2．（．1．－．y ．）－．．x ．（．y ．＋．x ．）．2．的值．． 拓展、探究、思考．．．．．．．．25．．．因式分解：．．．．．．（．1．）．ax ．．＋．ay ．．＋．bx ．．＋．by ．．；．（．2．）．2．ax ．．＋．3．am ．．－．10．．bx ．．－．15．．bm ．．．．测试．．5． 公式法（．．．．1．）．学习要求．．．．能运用平方差公式把简单的多项式进行因式分解．．．．．．．．．．．．．．．．．．．．．．．课堂学习检测．．．．．．一、填空题．．．．．1．．在括号内写出适当的式子：．．．．．．．．．．．．．（．1．）．0.25．．．．m ．4．＝（．． ）．2．；（．．2．）．=n y 294（． ）．2．；（．．3．）．121．．．a ．2．b ．6．＝（．． ）．2．．．2．．因式分解：（．．．．．．．1．）．x ．2．－．y ．2．＝（．． ）（．． ）；．． （．2．）．m ．2．－．16．．＝（．． ）．（． ）；．．（．3．）．49．．a ．2．－．4．＝（．． ）（．． ）．;．（．4．）．2．b ．2．－．2．＝．______．．．．．．（． ）（．． ）．．．二、选择题．．．．．3．．下列各式中，不能用平方差公式分解因式的是（．．．．．．．．．．．．．．．．．．．．．． ）．A ．．．y ．2．－．49．．x ．2． B ．．．4491x - C ．．－．．m ．4．－．n ．2． D ．．．9)(412-+q p4．．．a ．2．－（．．b ．－．c ．）．2．有一个因式是．．．．．．a ．＋．b ．－．c ．，则另一个因式为（．．．．．．．．． ）．A ．．．a ．－．b ．－．c ．B ．．．a ．＋．b ．＋．c ．C ．．．a ．＋．b ．－．c ．D ．．．a ．－．b ．＋．c ．5．．下列因式分解错误的是（．．．．．．．．．．．． ）．A ．．．1．－．16．．a ．2．＝（．．1．＋．4．a ．）（．．1．－．4．a ．）．B ．．．x ．3．－．x ．＝．x ．（．x ．2．－．1．）．C ．．．a ．2．－．b ．2．c ．2．＝（．．a ．＋．bc ．．）（．．a ．－．bc ．．）．D ．．．)l .032)(32l .0(l 0.09422n m m n n m -+=- 三、把下列各式因式分解．．．．．．．．．．．6．．．x ．2．－．25．．7．．．4．a ．2．－．9．b ．2． 8．．（．．a ．＋．b ．）．2．－．64．． 9．．．m ．4．－．81．．n ．4． 10．．．．12．．a ．6．－．3．a ．2．b ．2．11．．．（．．2．a ．－．3．b ．）．2．－（．．b ．＋．a ．）．2． 四、解答题．．．．．12．．．利用公式简算：（．．．．．．．．．1．）．2008．．．．＋．2008．．．．2．－．2009．．．．2．；（．．2．）．3.14．．．．×．51．．2．－．3.14．．．．×．49．．2．．． 13．．．已知．．．x ．＋．2．y ．＝．3．，．x ．2．－．4．y ．2．＝－．．15．．，（．．1．）求．．x ．－．2．y ．的值；（．．．．2．）求．．x ．和．y ．的．值．．．综合、运用、诊断．．．．．．．．一、填空题．．．．．14．．．因式分解下列各式：．．．．．．．．．．（．1．）．m m +-3161＝．______．．．．．．；．（．2．）．x ．4．－．16．．＝．______．．．．．．；．（．3．）．11-+-m m a a ＝．______．．．．．．；．（．4．）．x ．（．x ．2．－．1．）－．．x ．2．＋．1．＝．______．．．．．．．．二、选择题．．．．．15．．．把（．．．3．m ．＋．2．n ．）．2．－（．．3．m ．－．2．n ．）．2．分解因式，结果是（．．．．．．．．． ）．A ．．．0．B ．．．16．．n ．2．C ．．．36．．m ．2．D ．．．24．．mn ．．16．．．下列因式分解正确的是（．．．．．．．．．．．． ）．A ．．－．．a ．2．＋．9．b ．2．＝（．．2．a ．＋．3．b ．）（．．2．a ．－．3．b ．）．B ．．．a ．5．－．81．．ab ．．4．＝．a ．（．a ．2．＋．9．b ．2．）（．．a ．2．－．9．b ．2．）．C ．．．)21)(21(212212a a a -+=- D ．．．x ．2．－．4．y ．2．－．3．x ．－．6．y ．＝（．．x ．－．2．y ．）（．．x ．＋．2．y ．－．3．）．三、把下列各式因式分解．．．．．．．．．．．17．．．．a ．3．－．ab ．．2．18．．．．m ．2．（．x ．－．y ．）＋．．n ．2．（．y ．－．x ．）．19．．．．2．－．2．m ．4．20．．．．3．（．x ．＋．y ．）．2．－．27．．21．．．．a ．2．（．b ．－．1．）＋．．b ．2．－．b ．3．22．．．（．．3．m ．2．－．n ．2．）．2．－（．．m ．2．－．3．n ．2．）．2．四、解答题．．．．．23．．．已知．．．,4425,7522==y x 求（．．x ．＋．y ．）．2．－（．．x ．－．y ．）．2．的值．．．． 拓展、探究、思考．．．．．．．．24．．．分别根据所给条件求出自然数．．．．．．．．．．．．．．x ．和．y ．的值：．．．（．1．）．x ．、．y ．满足．．x ．2．＋．xy ．．＝．35．．；（．．2．）．x ．、．y ．满足．．x ．2．－．y ．2．＝．45．．．．测试．．6． 公式法（．．．．2．）．学习要求．．．．能运用完全平方公式把多项式进行因式分解．．．．．．．．．．．．．．．．．．．．．课堂学习检测．．．．．．一、填空题．．．．．1．．在括号中填入适当的式子，使等式成立：．．．．．．．．．．．．．．．．．．．（．1．）．x ．2．＋．6．x ．＋（．． ）＝（．．． ）．2．；（．．2．）．x ．2．－（．． ）＋．．4．y ．2．＝．（． ）．2．；．（．3．）．a ．2．－．5．a ．＋（．． ）＝（．．． ）．2．；（．．4．）．4．m ．2．－．12．．mn ．．＋（．． ）．＝．（． ）．2．2．．若．．4．x ．2．－．mxy ．．．＋．25．．y ．2．＝（．．2．x ．＋．5．y ．）．2．，则．．m ．＝．______．．．．．．．．二、选择题．．．．．3．．将．．a ．2．＋．24．．a ．＋．144．．．因式分解，结果为（．．．．．．．．． ）．A ．．（．．a ．＋．18．．）（．．a ．＋．8．）．B ．．（．．a ．＋．12．．）（．．a ．－．12．．）．C ．．（．．a ．＋．12．．）．2．D ．．（．．a ．－．12．．）．2．4．．下列各式中，能用完全平方公式分解因式的有（．．．．．．．．．．．．．．．．．．．．．． ）．①．9．a ．2．－．1．；． ②．x ．2．＋．4．x ．＋．4．；． ③．m ．2．－．4．mn ．．＋．n ．2．；． ④－．．a ．2．－．b ．2．＋．2．ab ．．；．⑤．;913222n mn m +- ⑥（．．x ．－．y ．）．2．－．6．z ．（．x ．＋．y ．）＋．．9．z ．2．．． A ．．．2．个． B ．．．3．个． C ．．．4．个． D ．．．5．个．5．．下列因式分解正确的是（．．．．．．．．．．．． ）．A ．．．4．（．m ．－．n ．）．2．－．4．（．m ．－．n ．）＋．．1．＝（．．2．m ．－．2．n ．＋．1．）．2．B ．．．18．．x ．－．9．x ．2．－．9．＝－．．9．（．x ．＋．1．）．2．C ．．．4．（．m ．－．n ．）．2．－．4．（．n ．－．m ．）＋．．1．＝（．．2．m ．－．2．n ．＋．1．）．2．D ．．－．．a ．2．－．2．ab ．．－．b ．2．＝（－．．．a ．－．b ．）．2．三、把下列各式因式分解．．．．．．．．．．．6．．．a ．2．－．16．．a ．＋．64．．7．．－．．x ．2．－．4．y ．2．＋．4．xy ．．8．．（．．a ．－．b ．）．2．－．2．（．a ．－．b ．）（．．a ．＋．b ．）＋（．．．a ．＋．b ．）．2． 9．．．4．x ．3．＋．4．x ．2．＋．x ． 10．．．计算：（．．．．．1．）．297．．．2． （．2．）．10.3．．．．2． 四、解答题．．．．．11．．．若．．a ．2．＋．2．a ．＋．1．＋．b ．2．－．6．b ．＋．9．＝．0．，求．．a ．2．－．b ．2．的值．．．．综合、运用、诊断．．．．．．．．一、填空题．．．．．12．．．把下列各式因式分解：．．．．．．．．．．．（．1．）．49．．x ．2．－．14．．xy ．．＋．y ．2．＝．______．．．．．．；．（．2．）．25．．（．p ．＋．q ．）．2．＋．10．．（．p ．＋．q ．）＋．．1．＝．______．．．．．．；．（．3．）．a ．n ．＋．1．＋．a ．n ．－．1．－．2．a ．n ．＝．______．．．．．．；．（．4．）（．．a ．＋．1．）（．．a ．＋．5．）＋．．4．＝．______．．．．．．．． 二、选择题．．．．．13．．．如果．．．x ．2．＋．kxy ．．．＋．9．y ．2．是一个完全平方公式，那么．．．．．．．．．．．．k ．是（．． ）．A ．．．6．B ．．－．．6．C ．．±．．6．D ．．．18．．14．．．如果．．．a ．2．－．ab ．．－．4．m ．是一个完全平方公式，那么．．．．．．．．．．．．m ．是（．． ）．A ．．．2161b B ．．．2161b - C ．．．281bD ．．．281b -15．．．如果．．．x ．2．＋．2．ax ．．＋．b ．是一个完全平方公式，那么．．．．．．．．．．．．a ．与．b ．满足的关系是（．．．．．．． ）．A ．．．b ．＝．a ．B ．．．a ．＝．2．b ．C ．．．b ．＝．2．a ．D ．．．b ．＝．a ．2． 三、把下列各式因式分解．．．．．．．．．．． 16．．．．x ．（．x ．＋．4．）＋．．4．17．．．．2．mx ．．2．－．4．mxy ．．．＋．2．my ．．2． 18．．．．x ．3．y ．＋．2．x ．2．y ．2．＋．xy ．．3． 19．．．．2341x x x -+四、解答题．．．．．20．．．若．．,31=+x x 求．221x x +的值．．．．21．．．若．．a ．4．＋．b ．4．＋．a ．2．b ．2．＝．5．，．ab ．．＝．2．，求．．a ．2．＋．b ．2．的值．．．．拓展、探究、思考．．．．．．．．22．．．（．．m ．2．＋．n ．2．）．2．－．4．m ．2．n ．2．23．．．．x ．2．＋．2．x ．＋．1．－．y ．2． 24．．．（．．a ．＋．1．）．2．（．2．a ．－．3．）－．．2．（．a ．＋．1．）（．．3．－．2．a ．）＋．．2．a ．－．3． 25．．．．x ．2．－．2．xy ．．＋．y ．2．－．2．x ．＋．2．y ．＋．1．26．．．已知．．．x ．3．＋．y ．3．＝（．．x ．＋．y ．）（．．x ．2．－．xy ．．＋．y ．2．）称为立方和公式，．．．．．．．．．x ．3．－．y ．3．＝（．．x ．－．y ．）．（．x ．2．＋．xy ．．＋．y ．2．）称为立方差公式，据此，试将下列各式因式分解：．．．．．．．．．．．．．．．．．．．．．．． （．1．）．a ．3．＋．8．（．2．）．27．．a ．3．－．1．测试．．7 ．十字相乘法．．．．．学习要求．．．．能运用公式．．．．．x ．2．＋（．．a ．＋．b ．）．x ．＋．ab ．．＝（．．x ．＋．a ．）（．．x ．＋．b ．）把多项式进行因式分．．．．．．．．．．解．．．课堂学习检测．．．．．．一、填空题．．．．．1．．将下列各式因式分解：．．．．．．．．．．．（．1．）．x．2．－．5．x．＋．6．＝．______．．．．．．；．．．．．．．；．（．2．）．x．2．－．5．x．－．6．＝．______（．3．）．x．2．＋．5．x．＋．6．＝．______．．．．．．；．．．．．．．；．（．4．）．x．2．＋．5．x．－．6．＝．______（．5．）．x．2．－．2．x．－．8．＝．______．．．．．．．．．．．．．．；．（．6．）．x．2．＋．14．．xy．．－．32．．y．2．＝．______二、选择题．．．．．2．．将．．．．．．．．．）．．．a．2．＋．10．．a．＋．16．．因式分解，结果是（A．．（．．a．－．8．）．．．a．＋．2．）（．．a．－．2．）（．．a．＋．8．）．B．．（C．．（．．a．－．2．）（．．a．－．8．）．．．a．＋．8．）．D．．（．．a．＋．2．）（3．．因式分解的结果是（．．．．．．．）．．．．．．．．．．．x．－．3．）（．．x．－．4．）的多项式是（A．．．x．2．－．7．x．－．12．．B．．．x．2．－．7．x．＋．12．．C．．．x．2．＋．7．x．＋．12．．D．．．x．2．＋．7．x．－．12．．4．．如果．．．）．．．x．＋．b．），那么．．．．p．等于（．．x．＋．a．）（．．．x．2．－．px．．＋．q．＝（A．．．ab．．B．．．a．＋．b．C．．－．．a．－．b．．．ab．．D．．－5．．若．．．k．的值为（．．．．）．．．x．－．12．．）（．．x．2．＋．kx．．－．36．．＝（．．x．＋．3．），则A．．－．．9．B．．．15．．C．．－．．15．．D．．．9．三、把下列各式因式分解．．．．．．．．．．．6．．．m．2．－．12．．m．＋．20．．7．．．x．2．＋．xy．．－．6．y．2．8．．．10．．－．3．a．－．a．2．9．．．x．2．－．10．．xy．．＋．9．y．2．10．．．（．．36．．11．．．．ma．．2．－．18．．ma．．－．40．．m．．．x．＋．4．）－．．x．－．1．）（12．．．．x．3．－．5．x．2．y．－．24．．xy．．2．四、解答题．．．．．13．．．已知．．．．．．x．＋．y．＝．0．，．x．＋．3．y．＝．1．，求．．3．x．2．＋．12．．xy．．＋．13．．y．2．的值．综合、探究、检测．．．．．．．．一、填空题．．．．．14．．．若．．．a．－．b．＝．______．．．．．．．．．．m．＋．b．），贝．．m．＋．a．）（．．m．2．－．13．．m．＋．36．．＝（15．．．因式分解．．．．．．．．．．．．．x．（．x．－．20．．）＋．．64．．＝．______二、选择题．．．．．16．．．多项式．．．a．、．b．的值为（．．x．－．by．．），则．．．．）．．．．．．x．－．5．y．）（．．．．x．2．－．3．xy．．＋．ay．．2．可分解为（A．．．a．＝．10．．，．b．＝－．．10．．，．b．＝－．．2．．．2．B．．．a．＝－C．．．a．＝．10．．，．b．＝．2．D．．．a．＝－．．10．．，．b．＝．2．17．．．若．．b．的值为（．．．．）．．．a．＋．b．）．x．＋．ab．．＝．x．2．－．x．－．30．．，且．．b．＜．a．，则．．x．2．＋（A．．．5．B．．－．．5．D．．．6．．．6．C．．－18．．．将（．．．．．．．．．）．．．6．因式分解的结果是（．．．x．＋．y．）．2．－．5．（．x．＋．y．）－A．．（．．x．＋．y．＋．3．）．．．x．＋．y．－．2．）（．．x．＋．y．－．3．）．B．．（．．x．＋．y．＋．2．）（C．．（．．x．＋．y．＋．6．）（．．x．＋．y．－．1．）．．．x．＋．y．＋．1．）．D．．（．．x．＋．y．－．6．）（三、把下列各式因式分解．．．．．．．．．．．19．．．（．．x．2．＋．4．x．）．2．－．x．2．－．4．x．－．20．．．．2．20．．．（．．x．2．－．2．）－．．x．2．－．2．）．2．－（拓展、探究、思考．．．．．．．．21．．．因式分解：．．．．．．4．a．2．－．4．ab．．＋．b．2．－．6．a．＋．3．b．－．4．．．22．．．观察下列各式：．．．．．．．．1．×．2．×．3．×．4．＋．1．＝．5．2．；．2．×．3．×．4．×．5．＋．1．＝．11．．2．；．3．×．4．×．5．×．6．＋．1．＝．19．．2．；判断是否任意四个连续正整数之积与．．．．．．．．．．．．．．．．．．．．．．．．．．1．的和都是某个正整数的平方，并说明理由．．．．．．．．．．．。

期末检测题(一)一、选择题(本题共32分，每小题4分)在下列各题的四个各选答案中，只有一个是正确的．1．一元二次方程x 2－9＝0的根为( ) A ．x ＝3 B ．x ＝－3 C ．x 1＝3，x 2＝－3 D ．x 1＝0，x 2＝32．如图，在△ABC 中，DE ∥BC ，DE 分别与AB 、AC 相交于点D 、E ，若AD ＝4，DB＝2，则ECAE的值为( )A ．21 B ．2 C ．32 D ．23 3．已知正六边形的外接圆半径为R ，那么这个正六边形的边长为( ) A ．RB ．R 2C ．2RD ．R 34．已知⊙O 1、⊙O 2的半径分别为2和5，圆心距O 1O 2＝7，则⊙O 1和⊙O 2的位置关系是( ) A ．外切 B ．内切 C ．相交 D ．相离5．盒中装有4只白球5只黑球，从中任取一只球，取出的球是白球的概率是( ) A ．205 B ．95 C ．204 D ．94 6．若将抛物线y ＝3x 2平移，得到抛物线y ＝3(x －2)2－1可采用的办法是( ) A ．向左平移2个单位，再向上平移1个单位 B ．向左平移2个单位，再向下平移1个单位 C ．向右平移2个单位，再向上平移1个单位 D ．向右平移2个单位，再向下平移1个单位7．北京市为迎接2008年奥运会，决定改善城市面貌，绿化环境，计划经过两年时间，绿地面积增加69％，则这两年平均每年绿地面积的增长率是( ) A ．29％ B ．30％ C ．31％ D ．35％8．如果一个圆锥的轴截面是等边三角形，它的边长为4cm ，那么圆锥的全面积是( ) A ．8πcm 2 B ．10πcm 2 C ．12πcm 2 D ．9πcm 2二、填空题(本题共16分，每小题4分)9．学校招收书法班学生，从每5个报名的人中录取3人，如果有200人报名，那么估计有______人被录取．10．关于x 的方程0122=++x k x 有两个不相等的实数根，则k 的取值范围为______． 11．大矩形的周长是与它相似的小矩形周长的2倍，小矩形的面积为5cm 2，大矩形的面积为______cm 2．12．如图，A 点是半圆上一个三等分点，B 点是的中点，P 点是直径MN 上一动点，⊙O 的半径为1，则AP ＋BP 的最小值是______．三、解答题(本题共30分，每小题5分)13．解方程：.020522=-+x x14．从地面竖直向上抛出一个小球．小球的上升高度h (单位：m)与小球运动时间t (单位：s )的关系式是h ＝20t －5t 2．小球运动的时间是多少时，小球最高?小球运动中的最大高度是多少?15．已知：如图，AB ，CD 是⊙O 的直径，∠C ＝∠B ，求证：CF ＝BE ．16．已知：如图，△ABC 中，DE ∥BC ，EF ∥AB ，求证：⋅=ECEFAE AD17．如图，有一表面凸凹不平的圆盘和一把L 型且带有刻度的直角三角尺，尺的两直角边的长度大于圆盘的半径，但小于圆盘的直径，请你设计能计算出圆盘直径的测量方案(请画出图形，并说明测量步骤)．18．小明有红、黄、白、黑四件衬衫，又有米色、蓝色、灰色三条长裤．如果他喜欢穿白色衬衫和米色长裤，那么他在黑暗中随机摸出一套衣裤正是他喜欢的搭配，这种巧合发生的概率是多少，并用列表或树图说明理由．四、解答题(本题共20分，每小题5分)19．如图，⊙O 中，弦AB ，CD 相交于P ，且四边形OEPF 是正方形，连接OP ．若⊙O 的半径为5cm ，cm 23 OP ，求AB 的长．20．已知二次函数图象的顶点坐标为M (3，－2)，且与y 轴交于N (0，25)．(1)求该二次函数的解析式，并用列表、描点画出它的图象；(2)若该图象与x 轴交于A 、B 两点，在对称轴上侧的图象上存在点C ，使得△ABC 的面积等于12，求出C 点的坐标．21．如图，在△ABC中，若AB＝5，AC＝2，∠BAC＝120°．以BC为边作等边三角形BCD，把△ABD绕D点按顺时针方向旋转60°到△ECD的位置．(1)求∠BAD的度数；(2)求AE的长．22．某商店销售一批小家电，平均每天可售出20个，每个盈利50元，为扩大销售，增加盈利，减少库存，商场决定采用适当降价的措施．经调查发现，如果每个小家电每降价1元，商店平均每天可多售出2个，若商场平均每天要盈利1600元，每个小家电应降价多少元商店可达到减少库存的目的．五、解答题(本题共22分，第23题6分，第24题8分，第25题8分)23．如图，AB，AC分别是⊙O的直径和弦，D为劣弧上的一点，DE⊥AB于点H，交⊙O于点E，交AC于点F，P为ED的延长线上的一点．(1)当△PCF满足什么条件时，PC与⊙O相切，用给出的条件证明结论；(2)当点D在劣弧的什么位置时，才能使AD2＝DE·DF，请加以证明．24．如图，直角坐标系内的梯形AOBC(O为原点)中AC∥OB，AO⊥OB，AC＝1，OA ＝2，OB＝5．(1)求经过O，C，B三点的抛物线的解析式；(2)延长AC交抛物线于点D，求线段CD的长；(3)在(2)的条件下，动点P、Q分别从O、D同时出发，都以每秒1个单位的速度运动，其中点P沿OB由O向B运动，点Q沿DC由D由C运动(其中一个点运动到终点后，另一个点运动也随之停止)，过点Q作QM⊥CD交BC于点M，连结PM．设动点运动的时间为t秒，请你探索：当时间t为何值时，△PMB中有一个角是直角．25．如图1，在等腰梯形ABCD中AB∥DC，已知AB＝12，,2BC∠DAB＝45°，4以AB所在直线为x轴，A为坐标原点建立直角坐标系，将等腰梯形AB－CD绕A 点按逆时针方向旋转90°得到等腰梯形OEFG(O、E、F、G分别是A、B、C、D 旋转后的对应点)．图1 图2(1)写出C、F两点的坐标；(2)将等腰梯形ABCD沿x轴的负半轴平行移动，设移动后的OA的长度是x，如图2，等腰梯形ABCD与等腰梯形OEFG重合部分的面积为y，当点D移动到等腰梯形OEFG的内部时，求y与x之间的函数关系式并写出自变量x的取值范围；(3)在直线CD上是否存在点P，使△EFP为等腰三角形，若存在，求出P点的坐标，若不存在，说明理由．答案与提示期末检测题(一)一、选择题(本题共32分，每小题4分)二、填空题(本题共16分，每小题4分)9．120． 10．k >1． 11．20． 12．.2 三、解答题(本题共30分，每小题5分) 13．解：.20,52,1-===c b a0100)20(14)52(422>=-⨯⨯-=-ac b,1210052⨯±-=x.55,5521--=+-=x x14．解：h ＝－5t 2＋20t ＝－5(t 2－4t ＋4)＋20＝－5(t －2)2＋20所以，t ＝2时，h ＝20．答：当t ＝2s 时，小球最高，最大高度是20m ． 另解：h ＝－5t 2＋20t ，a ＝－5，b ＝20，c ＝0．所以，abt 2-=时，h 运动到最大高度，即.2)5(220=-⨯-=t.20)5(4200)5(44422=-⨯-⨯-⨯=-=a b ac h答：当t ＝2s 时，小球最高，最大高度是20m ．15．证明：连结AE ，FD ．∵AB ，CD 是⊙O 的直径．∴∠AEB ＝∠DFC ＝90°，AB ＝CD ． ∵∠C ＝∠B ．∴△ABE ≌△DCF ． ∴FC ＝BE ．另证：连结FO ，OE ∵∠B ＝∠C ，∴∠FOD ＝∠EOA 有＝．∵AB ，CD 是⊙O 的直径， ∴=．∴＝．∴FC ＝BE ．16．解：∵在△ABC 中，DE ∥BC ，EF ∥AB ，∴∠ADE ＝∠B ＝∠EFC ． ∵DE ∥BC ， ∴∠AED ＝∠C ， ∴△ADE ∽△EFC ．⋅=∴ECEFAE AD17．方案：(1)L 型直角尺两直角边紧靠圆盘，如图所示，图中点A 、B 表示圆盘与直角尺两直角边的切点．(2)量出MA 的长度，再乘以2就是圆盘的直径．18．⋅1四、解答题(本题共20分，每小题5分) 19．解：连结OA ．∵四边形OEPF 是正方形，∴OE ⊥AB 且平分AB 有AE ＝EB ．,cm 23=OP∴OE 2＋PE 2＝OP 2有OE ＝3cm ，∵OA ＝5cm ，∴AE 2＝OA 2－OE 2有AE ＝4cm ． ∵AB ＝2AE ，∴AB ＝8cm ．20．(1)由于二次函数图象的顶点是(3，－2)，设所求的二次函数解析式是y ＝a (x －3)2－2．由于所求图象过),25,0(N 可得.2)30(252--=a 解得⋅=21a 所以⋅+-=253212x x y 列表：(2)当0253212=+-x x 时，x 1＝1，x 2＝5． ∴点A (1，0)，点B (5，0)， 则 AB ＝4．∵△ABC 的面积为12． ,12||21=⋅∴h AB ∴|h ｜＝6．∴抛物线顶点是(3，－2)． h 1＝6，h 2＝－6(舍去)．⋅+-=2532162x x 解出，x 1＝7，x 2＝－1． 由于抛物线对称轴是x ＝3，所以x 2＝－1(舍去)．有点c (7，6)．21．解：(1)∵把△ABD 绕D 点按顺时针方向旋转60°，到△ECD 位置，∴∠ADE ＝60°，AD ＝DE ，AB ＝CE ．.60260180=-=∠=∠∴DEA DAE∵∠BAC ＝120°，∴∠BAD ＝120°－60°＝60°．(2)由(1)知CE ＝AB ＝5，AC ＝2，∠BAD ＝60°，有∠DCE ＋∠BCD ＋∠BAC ＝180°， ∴AE ＝7．22．解：设每个小家电应降价x 元，根据题意，得(50－x )(20＋2x )＝1600． 即x 2－40x ＋300＝0． 得，x 1＝30，x 2＝10．因为要尽量减少库存，所以x ＝30． 答：每个小家电应降价30元．五、解答题(本题共22分，第23题6分，第24题8分，第25题8分)23．解：(1)当PC ＝PF (或∠PCF ＝∠PFC ，或△PCF 为等边三角形)时，PC 与⊙O 相切，下面对满足条件PC ＝PF ，进行证明 连结OC ，则∠OCA ＝∠F AO ． ∵DE ⊥AB 于H ，PC ＝PF ， ∴∠AHF ＝90°， ∠PCF ＝∠PFC ． ∵∠AFH ＝∠PFC ．∴∠OCA ＋∠PCF ＝∠F AH ＋∠AFH ＝90°． 即OC ⊥PC ，∴PC 与⊙O 相切．(2)当点D 是劣弧的中点，AD 2＝DE ·DF ．连结AE ， ∵D 点是劣弧的中点，∴＝∴∠DAF ＝∠DEA ． ∵∠ADF ＝∠ADE ， ∴△ADF ∽△EDA ．ADDFDE AD =∴，即AD 2＝DE ·DF ． 24．解：(1)由题意知，O (0，0)，C (1，2)，B (5，0)．设过O 、C 、B 三点的抛物线的解析式为y ＝ax 2＋bx ， 将C 、B 点坐标代入y ＝ax 2＋bx ，得⎩⎨⎧=+=+.0525,2b a b a 可得⎪⎪⎩⎪⎪⎨⎧=-=.25,21b a .25212x x y +-=∴(2)当y ＝2时，则,225212=+-x x解得，x 1＝1，x 2＝4．∴CD ＝4－1＝3．(3)延长QM 交x 轴于点N ，有MN ⊥OB ． ①当点P 与点N 重合时，有MP ⊥OB ，则四边形AOPQ 是矩形． ∴AQ ＝OP 即4－t ＝t ∴t ＝2．②若MP ⊥BM ，则△PNM ∽△MNB ． ∴MN 2＝PN ·BN ． ∵CQ ∥NB ，∴△CQM ∽△BNM ．,CQ BN MQ MN =∴即⋅----=-tt MN MN 14)4(52 则⋅+=21t MN ∵BN ＝1＋t ，PN ＝5－(1＋t )－t ＝4－2t ， ).1)(24()21(2+-=+∴t t t解得，t 1＝－1(舍去)，,352=t 综合①，②知，当t ＝2或35=t 时，△PMB 中有一个角是直角．25．解：(1)过C 作CH ⊥x 轴于点H ．,24=BC ∠CBA ＝∠DAB ＝45°．∴CH ＝HB ＝4．∴C 点坐标为(8，4)．同理可求得F 点坐标为(－4，8)．(2)设AD 、CD 分别与OG 、OE 交于点M 、N ． ∵∠DAB ＝∠GOA ＝45°，.4,2222====∴ON x OA AB OM 连结OD ，则S 四边形MOND ＝S △DMO ＋S △DNO ， 即ON DN MO DM y ⋅+⋅=2121 4)4(2122)2224(21⋅-+⋅-=x x x).84(84412<<-+-=x x x(3)设P 点坐标为(a ，4)． ①若PE ＝PF ，在Rt △PNE 和Rt △PGF 中，由PE 2＝PN 2＋NE 2＝PG 2＋FG 2＝PF 2， 得a 2＋(12－4)2＝(a ＋4)2＋42 解得a ＝4．②若PF ＝EF ．则由PF 2＝PG 2＋FG 2＝EF 2， 得.)24(4)4(222=++a 解得a 1＝0，a 2＝－8(舍去)． ③若PE ＝EF ，则由PE 2＝PN 2＋NE 2＝EF 2， 得.)24()412(222=-+a化简得a 2＋32＝0，方程无解，此时P 点不存在．综合①、②、③知，所求P 点坐标为P 1(4，4)，P 2(0，4)．期末检测题(二)一、选择题(共8个小题，每小题4分，共32分)1．在直角坐标系中，点A (2，－3)关于原点对称的点在( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 2．如果两圆的半径分别是3和5，圆心距是8，那么这两圆的位置关系是( ) A ．相离 B ．外切 C ．相交 D ．内切3．已知△ABC ∽△DEF ，若对应边AB ∶DE ＝1∶2，则它们的周长比等于( ) A ．1∶2 B ．1∶4 C ．2∶1 D ．4∶14．将抛物线y ＝2x 2向左平移1个单位，再向上平移3个单位得到的抛物线表达式是( )A ．y ＝2(x －1)2－3B ．y ＝2(x ＋1)2＋3C ．y ＝2(x －1)2＋3D ．y ＝2(x ＋1)2－3 5．同时投掷两枚硬币每次出现反面都向上的概率为( )A ．41 B ．31C ．21 D ．43 6．抛物线y ＝x 2＋x ＋p (p ≠0)与x 轴相交，其中一个交点的横坐标是p ．那么该抛物线的顶点坐标是( ) A ．(0，－2)B ．)49,21(-C ．)49,21(-D ．)49,21(--7．如图，AB 是圆O 的直径，弦AD ，BC 相交于点P ，∠DPB ＝60°，D 是的中点，则ABAC的值是( )A ．21 B ．2 C ．3D ．33 8．如图，二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象经过点(－1，2)，与y 轴交于(0，2)点，且与x 轴交点的横坐标分别为x 1、x 2，其中－2＜x 1＜－1，0＜x 2＜1，下列结论①4a －2b ＋c ＜0；②2a －b ＜0； ③a ＜－1； ④b 2＋8a ＞4ac ． 其中正确的有( ) A ．1个 B ．2个 C ．3个 D ．4个二、填空题(共4个小题，每小题4分，共16分)9．如果01122=-++++y x y y ，那么xy 的值等于______．10．在平面直角坐标系内，已知A (6，3)，B (6，0)两点，以坐标原点O 为位似中心，相似比为31，把线段AB 缩小后得到线段A ＇B ＇，则A ＇、B ＇的坐标分别是___________．11．已知圆锥的侧面积为10π平方厘米，底面半径为2厘米，则圆锥的母线长为______厘米．12．设等边△ABC 的边长为a ，将△ABC 绕它的外心旋转60°，得到对应的△A ＇B ＇C ＇，则A 、B ＇两点间距离等于____________．三、解答题(本题共25分，每小题5分)13．解方程：.02232=--x x14．如图，△ABC和△CDE都是直角三角形，∠A＝∠DCE＝90°，DE与BC相交于点F，AB＝6，AC＝9，CD＝4，CE＝6，问△EFC是否为等腰三角形?试说明理由．15．已知：如图，割线AC与圆O交于点B、C，割线AD过圆心O．若圆O的半径是5，且∠DAC＝30°，AD＝13．求弦BC的长．16．已知二次函数y＝x2－2x－3．(1)在直角坐标系中，用五点法画出它的图象；(2)当x为何值时，函数值y＝0；(3)当－3<x<3时，观察图象直接写出函数值y的取值范围．17．如图，在大圆中有一个小圆O，现有直尺和圆规．(1)简要说明确定大圆的圆心O′的步骤；(2)作直线l，使其将两圆的面积均二等分．四、解答题(共2题，共10分)18．(本小题满分5分)玩具厂生产一种玩具狗，每天最高产量为40只，每天生产的产品全部卖出．已知生产x只玩具狗的成本为R(元)，售价每只P(元)，且R、P与x的关系式分别为R＝600＋30x，P＝170－2x．当日产量为多少时，每日获得的利润为1650元?19．(本小题满分5分)已知点A(－1，－1)在抛物线y＝(k2－1)x2－2(k－2)x＋1上，点B与点A关于抛物线的对称轴对称．(1)求k的值和点B的坐标；(2)是否存在与此抛物线仅有一个公共点B的直线?如果存在，求出符合条件的直线的解析式；如果不存在，简要说明理由．五、解答题20．(本小题满分5分)当m是什么整数时，关于x的一元二次方程mx2－4x＋4＝0与x2－4mx＋4m2－4m－5＝0的根都是整数．六、解答题(共2题，共10分)21．(本小题满分5分)在一个布口袋中装着只有颜色不同，其它都相同的白、红、黑三种颜色的小球各1只，甲乙两人进行摸球游戏；甲先从袋中摸出一球看清颜色后放回，再由乙从袋中摸出一球．(1)试用树状图(或列表法)表示摸球游戏所有可能的结果；(2)如果规定：乙摸到与甲相同颜色的球为乙胜，否则为负，试求乙在游戏中能获胜的概率．22．(本小题满分5分)设点E、F分别在正方形ABCD的边BC、CD上滑动且保持∠EAF＝45°，AP⊥EF于点P．(1)求证：AP ＝AB ；(2)若AB ＝5，求△ECF 的周长．七、解答题23．(本题满分7分)如图，已知直径与等边△ABC 的高相等的圆O 分别与边AB 、BC 相切于点D 、E ，边AC 过圆心O 且与圆O 相交于点F 、G ．(1)求证：DE ∥AC ；(2)若△ABC 的边长为a ，求△ECG 的面积．八、解答题24．(本题满分7分)抛物线y ＝ax 2＋bx ＋c (a >0)经过点)0,3(),0,33(B A 与y 轴交于点C ，设抛物线的顶点为D ，在△BCD 中，CD 边的高为h ．(1)若c ＝ka ，求系数k 的值；(2)当∠ACB ＝90°时，求a 及h 的值；(3)当∠ACB≥90°时，经过探究、猜想，请你直接写出h的取值范围(不要求书写探究、猜想的过程)．九、解答题25．(本题满分8分)Rt△AOB中，∠AOB＝90°，∠ABO＝30°，BO＝4，分别以OA，OB边所在的直线建立平面直角坐标系，D点为x轴正半轴上的一点，以OD为一边在第一象限内作等边△ODE．(1)如图(1)，当E点恰好落在线段AB上，求E点坐标；(2)在(1)问的条件下，将△ODE在线段OB上向右平移如(2)图，图中是否存在一条与线段OO′始终相等的线段?如果存在，请指出这条线段，并加以证明；如果不存在，请说明理由；(3)若点D从原点出发沿x轴正方向移动，设点D到原点的距离为x，△ODE与△AOB重叠部分的面积为y，请直接写出y与x的函数关系式，并写出自变量x的取值范围．答案与提示期末检测题(二)一、选择题(共8个小题，每小题4分，共32分)二、填空题(共4个小题，每小题4分，共16分)9．－2．10．A (2，1)，B (2，0)或A (－2，－1)，B (－2，0)； 11．5；12．a 33或.332a 三、解答题(本题共25分，每小题5分)13．解：,2,2,3-=-==c b a026)2(34)2(422>=-⨯⨯--=-ac b,322623226)2(⨯±=⨯±--=x x⋅-=+=6262,626221x x14．解：△EFC 是等腰三角形．理由如下：在△ABC 和△CDE 中，∵∴===∠=∠,23,90CD EC AB AC DCE A△ABC ∽△CDE ． 有∠ACB ＝∠CED ，故EF ＝FC ．∴△EFC 是等腰三角形．15．解：作OM ⊥BC 于点M ．∵AD ＝13，OD ＝5，∴AO ＝8． ∵∠DAC ＝30°，∴OM ＝4．在Rt △OCM 中，OM ＝4，OC ＝5， ∴MC ＝3．∴BC ＝2MC ＝6．16．解：(1)2－2x －3＝(x －1)2－4．(2)令x －2x －3＝0时，解得x 1＝－1，x 2＝3． ∴当x ＝－1或3时，函数值y ＝0．(3)观察图象知：－4≤y <12．17．答：(1)任作大圆的两条弦AB 、CD ，分别作AB 和CD 的中垂线l 1与l 2，l 1与l 2的交点O ′就是大圆的圆心． (2)过O ，O ＇作直线EF 可等分两圆的面积．四、解答题(共2个题，共10分)18．解：设每日生产x 只玩具狗，每日获得的利润为1650元，依题意有，(170－2x )x －(600＋30x )＝1650． 整理，得x 2－70x ＋1125＝0， 解得x 1＝25，x 2＝45．因为每天最高产量为40只，所以x 2＝45舍去．答：当日产量为25只时，每日获得的利润为1650元．19．解：(1)根据题意，将x ＝－1，y ＝－1，代入抛物线的解析式，得(k 2－1)×(－1)2－2(k －2)×(－1)＋1＝－1． 解得k 1＝1，k 2＝－3．由于k 2－1≠0，所以k ＝－3．抛物线的解析式是y ＝8x 2＋10x ＋1，对称轴为直线⋅-=85x∵点B 和点A (－1，－1)关于直线85-=x 对称，).1,41(--∴B(2)存在．理由如下：设经过点B 的直线的解析式是y ＝mx ＋n ， 将B 点坐标代入得m －4n ＝4． ①又∵要使直线与抛物线只有一个公共点，只要使方程mx ＋n ＝8x 2＋10x ＋1有两个相等的实数根， 方程mx ＋n ＝8x 2＋10x ＋1整理得， 8x 2＋(10－m )x ＋1－n ＝0，得∆＝(10－m )2－32(1－n )＝0． ② 将①代②，解出，,21,6==n m 它的解析式是⋅+=216x y 又有过点B ，平行于y 轴的直线与抛物线仅有一个公共点， 即⋅-=41x 答：直线的解析式是216+=x y 或⋅-=41x 五、解答题(本题满分5分)20．解：由于两方程都有实数根，所以⎪⎩⎪⎨⎧≥∆≥∆=/00021m 即⎪⎩⎪⎨⎧≥----≥--=/0)544(4)4(016)4(0222m m m m m 解得⎪⎪⎩⎪⎪⎨⎧-≥≤=/4510m m m即，,145≤≤-m 且m ≠0． 又因为m 是整数，所以不等式组的整数解是－1和1． 当m ＝－1时，方程mx 2－4x ＋4＝0即为x 2＋4x －4＝0， 其解不是整数，所以m ＝－1舍去． 当m ＝1时，方程mx 2－4x ＋4＝0即为x 2－4x ＋4＝0，其解为x 1＝x 2＝2； 方程x 2－4mx ＋4m 2－4m －5＝0即为x 2－4x －5＝0，其解为x 1＝5，x 2＝－1． 所以，m ＝1时两方程根都是整数．六、解答题(共2个题，共10分)21．(本小题5分)解：(1)或列表如下(2)乙取胜的概率为⋅=39 22．解：(1)将Rt △ABE 绕点A 按逆时针方向旋转90°，得Rt △ADG ．∵∠B ＝∠ADC ＝∠ADG ＝90°， ∠ADF ＋∠ADG ＝180°， 即F 、D 、G 在一条直线上． ∵AE ＝AG ，AF ＝AF ， ∠EAF ＝∠GAF ＝45°， ∴△AEF ≌△AGF ．∵EF ＝FG ，AP ⊥EF ，AD ⊥FG ， ∴AP ＝AD ＝AB ． 即AP ＝AB ．(2)∵△ABE ≌△ADG ， ∴EF ＝FG ．∵△CEF 的周长＝CE ＋EF ＋CF ＝CE ＋FG ＋CF ，DG ＝BE ， ∴△CEF 的周长＝CE ＋EF ＋CF ＝BC ＋DC ＝5×2＝10．七、解答题(本题满分7分)23．(1)∵△ABC 是等边三角形，∴∠B ＝60°，∠A ＝60°．∵AB 、BC 是圆O 的切线，D 、E 是切点， ∴BD ＝BE ．∴∠BDE ＝60°，∠A ＝60°，有DE ∥AC ．(2)分别连结OD 、OE ，作EH ⊥AC 于点H ．∵AB 、BC 是圆O 的切线，D 、E 是切点，O 是圆心， ∴∠ADO ＝∠OEC ＝90°，OD ＝OE ，AD ＝EC ． ∴△ADO ≌△CEO ，有.21a OC AO == ∵圆O 的直径等于△ABC 的高，得半径,43a OG = .4321a a OG OC CG +=+=∴∵EH ⊥OC ，∠C ＝60°， .83,30a EH COE ==∠∴,83)2143(2121a a a EH CG S ECG ⋅+=⋅=∆.64323323643222a a a S ECG +=+=∴∆八、解答题(本题满分7分)24．解：(1)因为)0,3(),0,33(B A -在抛物线y ＝ax 2＋bx ＋c (a ＞0)上，所以有，),932()3)(33(2-+=-+=x x a x x a y c ＝－9a ，所以k ＝－9．(2)由于∠ACB ＝90°时，∵OC ⊥AB ， ∴∠AOC ＝∠BOC ＝90°． 可得∠ACO ＝∠OBC ． ∴△AOC ∽△COB ．,OBOCOC AO =∴即,93332=⨯=⋅=OB OA OC ∴OC ＝3． ∵C (0，－3)，由(1)知－9a ＝－3，⋅=∴31a 过D 作DE ⊥OC 交y 轴于点E ，延 长DC 交x 轴于点H ，过B 作BF⊥CH 于点F ．即BF 是边DC 的高h ． 因为D 是抛物线的顶点，所以),4,3(--D 故OE ＝4，又OC ＝3，可得.3,1==DE CE易证△HCO ∽△DCE ，有,313===EC CO DE HO 故.32,333=-===OB OH BH DE OH 由于∠COH ＝90°，OC ＝3，,33=OH由勾股定理知CH ＝6，有∠OHC ＝30°．又在Rt △BHF 中，32=BH ，所以3=BF ，即.3=h(3)当∠ACB ≥90°时，猜想.30≤<h九、解答题(本题满分8分)25．解：(1)作EH ⊥OB 于点H ，∵△OED 是等边三角形， ∴∠EOD ＝60°．又∵∠ABO ＝30°，∴∠OEB ＝90°．∵BO ＝4，.221==∴OB OE ∵△OEH 是直角三角形，且∠OEH ＝30°，).3,1(.3,1E EH OH ∴==∴(2)存在线段EF ＝OO ＇．∵∠ABO ＝30°，∠EDO ＝60°，∴∠ABO ＝∠DFB ＝30°，∴DF ＝DB ．∴OO ＇＝4－2－DB ＝2－DB ＝2－DF ＝ED －FD ＝EF⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<<-+-≤<=).4(32)42(323243)20(43)3(22x x x x x x y期末检测题(三)一、选择题(共8道小题，每小题4分，共32分)1．若方程x 2－5x ＝0的一个根是a ，则a 2－5a ＋2的值为( ) A ．－2 B ．0 C ．2 D ．42．如图，⊙O 的半径OA 等于5，半径OC 与弦AB 垂直，垂足为D ，若OD ＝3，则弦AB 的长为( )A ．10B ．8C ．6D ．4 3．将抛物线y ＝2x 2经过怎样的平移可得到抛物线y ＝2(x ＋3)2＋4?( ) A ．先向左平移3个单位，再向上平移4个单位 B ．先向左平移3个单位，再向下平移4个单位 C ．先向右平移3个单位，再向上平移4个单位 D ．先向右平移3个单位，再向下平移4个单位4．小莉站在离一棵树水平距离为a 米的地方，用一块含30°的直角三角板按如图所示的方式测量这棵树的高度，已知小莉的眼睛离地面的高度是1.5米，那么她测得这棵树的高度为( )A ．m )33(aB ．m )3(aC ．m )335.1(a +D ．m )35.1(a +5．如图，以某点为位似中心，将△AOB 进行位似变换得到△CDE ，记△AOB 与△CDE 对应边的比为k ，则位似中心的坐标和k 的值分别为( )A ．(0，0)，2B ．21),2,2( C ．(2，2)，2 D ．(2，2)，36．将抛物线y ＝x 2＋1绕原点O 族转180°，则族转后的抛物线的解析式为：( ) A ．y ＝－x 2 B ．y ＝－x 2＋1 C ．y ＝x 2－1 D ．y ＝－x 2－17．如图，P A 、PB 与⊙O 相切，切点分别为A 、B ，P A ＝3，∠P ＝60°，若AC 为⊙O 的直径，则图中阴影部分的面积为( )A ．2π B ．6π3 C ．3π3D ．π8．已知b >0时，二次函数y ＝ax 2＋bx ＋a 2－1的图象如下列四个图之一所示．根据图分析，a 的值等于．．．．( ) A ．－2 B ．－1 C ．1 D ．2二、填空题(共4道小题，每小题4分，共16分)9．若△ABC ∽△DEF ，且对应边BC 与EF 的比为2∶3，则△ABC 与△DEF 的面积等于______．10．如图，⊙O 的直径是AB ，CD 是⊙O 的弦，基∠D ＝70°，则∠ABC 等于______．11．如图，∠ABC ＝90°，O 为射线BC 上一点，以点O 为圆心，OB 21长为半径作⊙O ，将射线BA 绕点B 按顺时针方向旋转至BA ＇，若BA ＇与⊙O 相切，则旋转的角度α (0°＜α ＜180°)等于______．12．等腰△ABC 中，BC ＝8，若AB 、AC 的长是关于x 的方程x 2－10x ＋m ＝0的根，则m 的值等于______．三、解答题(本题共29分，第13～17题每小题5分，第18题4分)13．解方程：2x 2－6x ＋1＝0．14．计算：o 245sin 45tan 30sin 60cos +︒-︒15．已知：关于x 的方程x 2＋2x ＝3－4k 有两个不相等的实数根(其中k 为实数)．(1)求k 的取值范围；(2)若k 为非负整数，求此时方程的根．16．已知：如图，AB 是⊙O 的直径，BC 是弦，∠B ＝30°，延长BA 到D ，使∠ADC＝30°．(1)求证：DC 是⊙O 的切线； (2)若AB ＝2，求DC 的长．17．已知：如图，△ABC 中，AB ＝2，BC ＝4，D 为BC 边上一点，BD ＝1．(1)求证：△ABD ∽△CBA ；(2)若DE ∥AB 交AC 于点E ，请再写出另一个与△ABD 相似的三角形，并直接写出DE 的长．18．已知：如图，∠MAN ＝45°，B 为AM 上的一个定点．若点P 在射线AN 上，以P为圆心，P A 为半径的圆与射AN 的另一个交点为C ．请确定⊙P 的位置，使BC 恰与⊙P 相切．(1)画出⊙P ；(不要求尺规作图，不要求写画法) (2)连结BC 、BP 并填空： ①∠ABC ＝______°；②比较大小：∠ABP ______∠CBP ．(用“＞”、“＜”或“＝”连接)四、解答题(本题共21分，第19题6分，第20题4分，第21题6分，第22题5分)19．已知抛物线y ＝ax 2＋bx ＋c 经过点A (0，3)、B (4，3)、C (1，0)．(1)填空：抛物线的对称轴为直线x ＝______，抛物线与x 轴的另一个交点D 的坐标为______；(2)求该抛物线的解析式．20．已知：如图，等腰△ABC 中，AB ＝BC ，AE ⊥BC 于E ，EF ⊥AB 于F ，若CE ＝2，54cos =∠AEF ，求EF 的长．21．某水果批发市场经销一种水果，如果每千克盈利10元，每天可售出500千克．经市场调查发现，在进货价不变的情况下，若每千克这种水果在原售价的基础上每涨价1元，日销售量将减少20千克．(1)如果市场某天销售这种水果盈利了6 000元，同时顾客又得到了实惠．．．．．．．．．．，那么每千克这种水果涨了多少元?(2)设每千克这种水果涨价x 元时(0＜x ≤25)，市场每天销售这种水果所获利润为y 元．若不考虑其它因素，单纯从经济角度看，每千克这种水果涨价多少元时，市场每天销售这种水果盈利最多?最多盈利多少元?22．已知：如图，△ABC 中，AB ＝3，∠BAC ＝120°，AC ＝1，D 为AB 延长线上一点，BD ＝1，点P 在∠BAC 的平分线上，且满足△P AD 是等边三角形．(1)求证：BC ＝BP ；(2)求点C 到BP 的距离．五、解答题(本题共22分，第23题7分，第24题7分，第25题8分)23．已知关于x 的方程x 2－2ax －a ＋2b ＝0，其中a 、b 为实数．(1)若此方程有一个根为2a (a ＜0)，判断a 与b 的大小关系并说明理由； (2)若对于任何实数a ，此方程都有实数根，求b 的取值范围．24．已知：如图，⊙O 的内接△ABC 中，∠BAC ＝45°，∠ABC ＝15°，AD ∥OC 并交BC 的延长线于D ，OC 交AB 于E ．(1)求∠D 的度数；(2)求证：AC 2＝AD ·CE ； (3)求CDBC的值．25．已知：抛物线)2(3)1(32322a a x a x y -----=与x 轴交于点A (x 1，0)、B (x 2，0)，且x 1＜1＜x 2．(1)求A 、B 两点的坐标(用a 表示)；(2)设抛物线的顶点为C ，求△ABC 的面积；(3)若a 是整数，P 为线段AB 上的一个动点(P 点与A 、B 两点不重合)，在x 轴上方作等边△APM 和等边△BPN ，记线段MN 的中点为Q ，求抛物线的解析式及线段PQ 的长的取值范围．北京新东方学校个性化学习中心——初中数学组答案与提示期末检测题(三)二、填空题(共4个小题，每小题4分，共16分)三、解答题(本题共29分，第13～17题每小题5分，第18题4分)13．解：因为a ＝2，b ＝－6，c ＝1，1分 所以b 2－4ac ＝(－6)2－4×2×1＝28．2分 代入公式，得aac b b x 242-±-=3分 ⋅±=±=⨯±=273472622286 所以原方程的根为⋅-=+=273,27321x x (每个根各1分)5分14．解：45sin 45tan 30sin 60cos 2+- 2)22(1221+-=4分⋅=21 5分 15．(1)解一：原方程可化为(x ＋1)2＝4－4k ．1分 ∵该方程有两个不相等的实数根， ∴4－4k ＞0． 2分 解得k ＜1．∴k 的取值范围是k ＜1．3分 解二：原方程可化为x 2＋2x ＋4k －3＝0．1分∆＝22－4(4k －3)＝4(4－4k )．以下同解法一．(2)解：∵k 为非负整数，k ＜1，∴k ＝0．4分 此时方程为x 2＋2x ＝3，它的根为x 1＝－3，x 2＝1．5分16．(1)证明：连结OC ．∵OB ＝OC ，∠B ＝30°， ∴∠OCB ＝∠B ＝30°．∴∠COD ＝∠B ＋∠COB ＝60°． 1分 ∵∠BDC ＝30°，∴∠BDC ＋∠COD ＝90°，DC ⊥OC ．2分∴BC 是弦，∴点C 在⊙O 上． ∴DC 是⊙O 的切线．3分(2)解：∵AB ＝2，.12===∴ABOB OC4分∵在Rt △COD 中，∠OCD ＝90°，∠D ＝30°， ∴.33==OC DC5分17．(1)证明：∵AB ＝2，BC ＝4，BD ＝1，⋅=∴BABDCB AB1分 ∵∠ABD ＝∠CBA ， 2分 ∴△ABD ∽△CBA ．3分(2)答：△ABD ∽△CDE ；4分 DE ＝ 1.5 .5分 18．解：(1)图形见下．2分 (2)①∠ABC ＝ 45° ； 3分 ②∠ABP ＜ ∠CBP ．4分四、解答题(本题共21分，第19题6分，第20题4分，第21题6分，第22题5分)19．解：(1)抛物线的对称轴为直线x ＝ 2 ，抛物线与x 轴的另一个交点D 的坐标为(3，0)； 2分 (2)∵抛物线经过点C (1，0)、D (3，0)，∴设抛物线的解析式为y ＝a (x －1)(x －3)． 4分 由抛物线经过点A (0，3)，得a ＝1． 5分 ∴抛物线的解析式为y ＝x 2－4x ＋3． 6分20．解：∵AE ⊥BC ，EF ⊥AB ，∴∠1＋∠2＝90°，∠B ＋∠2＝90°． ∴∠1＝∠B ．1分∴,54cos =∠AEF ∴Rt △ABE 中，⋅==54cos AB BE B2分设BE ＝4k ，则AB ＝BC ＝5k ，EC ＝BC －BE ＝k ＝2． ∴BE ＝8． 3分 ∴Rt △BEF 中，⋅=⨯=⋅=524538sin B BE EF4分21．解：(1)设市场某天销售这种水果盈利了6 000元，同时顾客又得到了实惠时，每千克这种水果涨了x 元．由题意得(10＋x )(500－20x )＝6000． 1分 整理，得x 2－15x ＋50＝0． 解得x 1＝5，x 2＝10． 2分 因为顾客得到了实惠，应取x ＝5． 3分 答：市场某天销售这种水果盈利6 000元，同时顾客又得到了实惠时，每千克这种水果涨了5元．(2)因为每千克这种水果涨价x 元时，市场每天销售这种水果所获利润为y 元，y 关于x 的函数解析式为y ＝(10＋x )(500－20x )(0＜x ≤25)． 4分 而y ＝(10＋x )(500－20x )＝－20x 2＋300x ＋5000＝－20(x －7.5)2＋6125． 所以，当x ＝7．5时(0＜7．5≤25)，y 取得最大值，最大值为6 125． 6分 答：不考虑其他因素，单纯从经济角度看，每千克这种水果涨价7.5元时，市场每天销售这种水果盈利最多，最多盈利6 125元．22．(1)证明：如图1，连结PC ． 1分图1∵AC ＝1，BD ＝1， ∴AC ＝BD ． ∵∠BAC ＝120°，AP 平分∠BAC ，.60211 =∠=∠∴BAC∵△P AD 是等边三角形， ∴P A ＝PD ，∠D ＝60°． ∴∠1＝∠D ．∴△P AC ≌△PDB ． 2分∴PC ＝PB ，∠2＝∠3．∴∠2＋∠4＝∠3＋∠4，∠BPC ＝∠DP A ＝60°． ∴△PBC 是等边三角形，BC ＝BP ．3分证法二：作BM ∥P A 交PD 于M ，证明△PBM ≌△BCA ． (2)解法一：如图2，作CE ⊥PB 于E ，PF ⊥AB 于F ．图2∵AB ＝3，BD ＝1， ∴AD ＝4． ∵△P AD 是等边三角形，PF ⊥AB ，,221==∴AD DF .3260sin =⋅= PD PF∴BF ＝DF －BD ＝1， .1322=+PF BF BP4分 ⋅=⨯=⋅=⋅=∴239231360sin 60sin BP BC CE 5分即点C 到BP 的距离等于⋅239解法二：作BN ⊥DP 于N ，BP BN DN DP NP DN ,23,27,21==-==.1322=+=NP BN以下同解法一．五、解答题(本题共22分，第23题7分，第24题7分，第25题8分)23．解：(1)∵方程x 2－2ax －a ＋2b ＝0有一个根为2a ，∴4a 2－4a 2－a ＋2b ＝0．1分 整理，得⋅=2ab 2分 ∵a ＜0，,2aa <∴即a ＜b ．3分 (2)∆＝4a 2－4(－a ＋2b )＝4a 2＋4a －8b ． 4分 ∵对于任何实数a ，此方程都有实数根．∴对于任何实数a ，都有4a 2＋4a －8b ≥0，即a 2＋a －2b ≥0 5分∴对于任何实数a ，都有⋅+≤22aa b,81)21(21222-+=+a a a当21-=a 时，22a a +有最小值⋅-816分∴b 的取值范围是⋅-≤81b24．(1)解：如图3，连结OB ．1分图3∵⊙O 的内接△ABC 中，∠BAC ＝45°， ∴∠BOC ＝2∠BAC ＝90°． ∵OB ＝OC ，∴∠OBC ＝∠OCB ＝45°． ∵AD ∥OC ，∴∠D ＝∠OCB ＝45°． 2分 (2)证明：∵∠BAC ＝45°，∠D ＝45°，∴∠BAC ＝∠D ． 3分 ∵AD ∥OC ，∴∠ACE ＝∠DAC ．4分∴△ACE ∽△DAC ．⋅=∴ACCEDA AC ∴AC 2＝AD ·CE ．5分(3)解法一：如图4，延长BO 交DA 的延长线于F ，连结OA ．图4∵AD ∥OC ，∴∠F ＝∠BOC ＝90°． ∵∠ABC ＝15°，∴∠OBA ＝∠OBC －∠ABC ＝30°． ∵OA ＝OB ．∴∠FOA ＝∠OBA ＋∠OAB ＝60°，∠OAF ＝30°． ∴OA OF 21=． ∵AD ∥OC ，∴△BOC ∽△BFD ． ⋅=∴BFBOBD BC ,2===∴OFOA OF BO CD BC 即CD BC的值为2． 7分解法二：作OM ⊥BA 于M ，设⊙O 的半径为r ，可得,2,33rOM r BM ==,33,332,6330tan ,30r AE r BE r OM ME MOE ===⋅==∠ 所以.2==EABECD BC 25．解：(1)∵抛物线与x 轴交于点A (x 1，0)、B (x 2，0)，∴x 1、x 2是关于x 的方程0)2(3)1(32322=-----a a x a x 的解． 方程可简化为x 2＋2(a －1)x ＋(a 2－2a )＝0． 解方程，得x ＝－a 或x ＝－a ＋2． 1分∵x 1＜x 2，－a ＜－a ＋2， ∴x 1＝－a ，x 2＝－a ＋2．∴A 、B 两点的坐标分别为A (－a ，0)，B (－a ＋2，0)． 2分 (2)∵AB ＝2，顶点C 的纵坐标为,33分∴△ABC 的面积等于.34分(3)x 1＜1＜x 2， ∴－a ＜1＜－a ＋2． ∴－1＜a ＜1． 5分∵a 是整数，∴a ＝0，所求抛物线的解析式为y ＝.3232x x +-6分解法一：此时顶点C 的坐标为).3,1(C如图5，作CD ⊥AB 于D ，连结CQ ．图5则AD ＝1，.3tan ,3=∠=BAC CD∴∠BAC ＝60°．由抛物线的对称性可知△ABC 是等边三角形．由△APM 和△BPN 是等边三角形，线段MN 的中点为Q 可得，点 M 、N 分别在AC 和BC 边上，四边形PMCN 为平行四边形，C 、Q 、 P 三点共线，且.21PC PQ =7分∵点P 在线段AB 上运动的过程中，P 与A 、B 两点不重合，,2,3,==<≤AC DC AC PC DC.123<≤∴PQ 8分解法二：设点P 的坐标为P (x ，0)(0＜x ＜2)．如图6，作MM 1⊥AB 于M 1，NN 1⊥AB 于N 1．图6∵△APM 和△BPN 是等边三角形，且都在x 轴上方， ∴AM ＝AP ＝x ，BN ＝BP ＝2－x ，∠MAP ＝60°，∠NBP ＝60°．,2cos 1x MAB AM AM =∠⋅=∴ ,23sin 1x MAB AM MM =∠⋅= ,22cos 1xNBP BN BN -=∠⋅= ⋅-=∠⋅=2332sin 1xNBP BN NN ⋅+=--=-=∴2222211xx BN AB AN ∴M 、N 两点的坐标分别为).2332,22(),23,2(x x N x x M -+ 可得线段MN 的中点Q 的坐标为).23,21(+x Q 由勾股定理得.3)1(21)23()21(222+-=++-=x x x PQ 7分∵点P 在线段AB 上运动的过程中，P 与A 、B 两点不重合，0＜x ＜2，,123.43)1(32<≤∴<+-≤∴PQ x 8分。

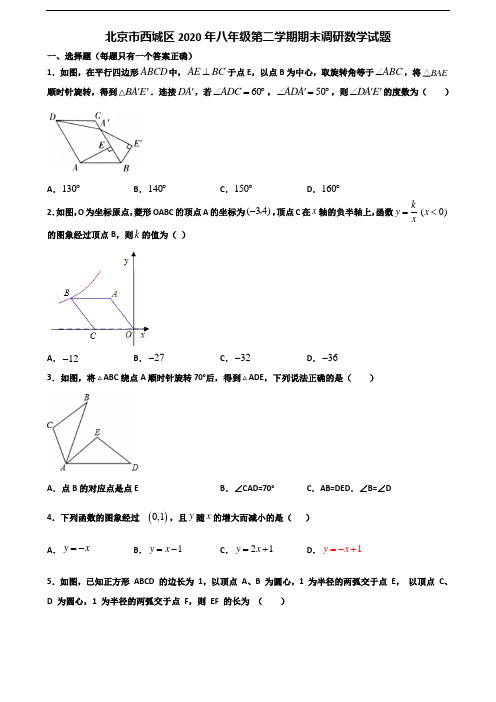
北京市西城区2020年八年级第二学期期末调研数学试题一、选择题（每题只有一个答案正确）1．如图，在平行四边形ABCD 中，AE BC ⊥于点E ，以点B 为中心，取旋转角等于ABC ∠，将BAE △顺时针旋转，得到BA E ''．连接DA '，若60ADC ∠=︒，50ADA ∠'=︒，则DA E ''∠的度数为（ ）A ．130︒B ．140︒C ．150︒D ．160︒2．如图，O 为坐标原点，菱形OABC 的顶点A 的坐标为(34)-，，顶点C 在x 轴的负半轴上，函数(0)ky x x=<的图象经过顶点B ，则k 的值为（ ）A ．12-B ．27-C ．32-D ．36-3．如图，将ABC 绕点A 顺时针旋转70°后，得到ADE ，下列说法正确的是（ ）A ．点B 的对应点是点E B ．∠CAD=70°C ．AB=DED ．∠B=∠D4．下列函数的图象经过()0,1，且y 随x 的增大而减小的是（ ）A ．y x =-B ．1y x =-C ．21y x =+D ．1y x =-+5．如图，已知正方形 ABCD 的边长为 1，以顶点 A 、B 为圆心，1 为半径的两弧交于点 E ， 以顶点 C 、D 为圆心，1 为半径的两弧交于点 F ，则 EF 的长为 （ ）A ．23B ．32C ．23-D ．31-6．对于一次函数y ＝（k ﹣3）x+2，y 随x 的增大而增大，k 的取值范围是（ ） A ．k ＜0B ．k ＞0C ．k ＜3D ．k ＞37．如图，P 是矩形ABCD 的边AD 上一个动点，PE⊥AC 于E ，PF⊥BD 于F ，当P 从A 向D 运动（P 与A ，D 不重合），则PE+PF 的值（ ）A ．增大B ．减小C ．不变D ．先增大再减小8．面试时，某人的基本知识、表达能力、工作态度的得分分别是80分，70分，85分，若依次按30%，30%，40%的比例确定成绩，则这个人的面试成绩是（ ）A ．78.3B ．79C ．235D ．无法确定9．把分式3x yxy-中的x 、y 的值同时扩大为原来的2倍，则分式的值（ ） A ．不变B ．扩大为原来的2倍C ．扩大为原来的4倍D ．缩小为原来的一半10．关于特殊四边形对角线的性质，矩形具备而平行四边形不一定具备的是（ ） A ．对角线互相平分 B ．对角线互相垂直 C ．对角线相等 D ．对角线平分一组对角二、填空题11．如图所示,在直角坐标系中,右边的图案是由左边的图案经过平移得到的,左边图案中左、右眼睛的坐标分别是(-4,2),(-2,2),右边图案中左眼的坐标是(3,4),则右边图案中右眼的坐标是__.12．已知 3a b +=，10ab =，则2222a b ab +=______。

期末检测题(二)一、选择题(共8个小题，每小题4分，共32分)1．在直角坐标系中，点A (2，－3)关于原点对称的点在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．如果两圆的半径分别是3和5，圆心距是8，那么这两圆的位置关系是( )A ．相离B ．外切C ．相交D ．内切3．已知△ABC ∽△DEF ，若对应边AB ∶DE ＝1∶2，则它们的周长比等于( )A ．1∶2B ．1∶4C ．2∶1D ．4∶14．将抛物线y ＝2x 2向左平移1个单位，再向上平移3个单位得到的抛物线表达式是( )A ．y ＝2(x －1)2－3B ．y ＝2(x ＋1)2＋3C ．y ＝2(x －1)2＋3D ．y ＝2(x ＋1)2－35．同时投掷两枚硬币每次出现反面都向上的概率为( )A ．41 B ．31 C ．21 D ．43 6．抛物线y ＝x 2＋x ＋p (p ≠0)与x 轴相交，其中一个交点的横坐标是p ．那么该抛物线的顶点坐标是( ) A ．(0，－2) B ．)49,21(- C ．)49,21(- D ．)49,21(-- 7．如图，AB 是圆O 的直径，弦AD ，BC 相交于点P ，∠DPB ＝60°，D 是的中点，则ABAC 的值是( )A ．21B ．2C ．3D ．33 8．如图，二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象经过点(－1，2)，与y 轴交于(0，2)点，且与x 轴交点的横坐标分别为x 1、x 2，其中－2＜x 1＜－1，0＜x 2＜1，下列结论①4a －2b ＋c ＜0；②2a －b ＜0；③a ＜－1； ④b 2＋8a ＞4ac ．其中正确的有( )A ．1个B ．2个C ．3个D ．4个二、填空题(共4个小题，每小题4分，共16分)9．如果01122=-++++y x y y ，那么xy 的值等于______．10．在平面直角坐标系内，已知A (6，3)，B (6，0)两点，以坐标原点O 为位似中心，相似比为31，把线段AB 缩小后得到线段A ＇B ＇，则A ＇、B ＇的坐标分别是___________． 11．已知圆锥的侧面积为10π平方厘米，底面半径为2厘米，则圆锥的母线长为______厘米．12．设等边△ABC 的边长为a ，将△ABC 绕它的外心旋转60°，得到对应的△A ＇B ＇C ＇，则A 、B ＇两点间距离等于____________．三、解答题(本题共25分，每小题5分)13．解方程：.02232=--x x14．如图，△ABC 和△CDE 都是直角三角形，∠A ＝∠DCE ＝90°，DE 与BC 相交于点F ，AB ＝6，AC ＝9，CD ＝4，CE ＝6，问△EFC 是否为等腰三角形?试说明理由．15．已知：如图，割线AC 与圆O 交于点B 、C ，割线AD 过圆心O ．若圆O 的半径是5，且∠DAC ＝30°，AD ＝13．求弦BC 的长．16．已知二次函数y ＝x 2－2x －3．(1)在直角坐标系中，用五点法画出它的图象；(2)当x为何值时，函数值y＝0；(3)当－3<x<3时，观察图象直接写出函数值y的取值范围．17．如图，在大圆中有一个小圆O，现有直尺和圆规．(1)简要说明确定大圆的圆心O′的步骤；(2)作直线l，使其将两圆的面积均二等分．四、解答题(共2题，共10分)18．(本小题满分5分)玩具厂生产一种玩具狗，每天最高产量为40只，每天生产的产品全部卖出．已知生产x只玩具狗的成本为R(元)，售价每只P(元)，且R、P与x的关系式分别为R＝600＋30x，P＝170－2x．当日产量为多少时，每日获得的利润为1650元?19．(本小题满分5分)已知点A(－1，－1)在抛物线y＝(k2－1)x2－2(k－2)x＋1上，点B与点A关于抛物线的对称轴对称．(1)求k的值和点B的坐标；(2)是否存在与此抛物线仅有一个公共点B的直线?如果存在，求出符合条件的直线的解析式；如果不存在，简要说明理由．五、解答题20．(本小题满分5分)当m是什么整数时，关于x的一元二次方程mx2－4x＋4＝0与x2－4mx＋4m2－4m－5＝0的根都是整数．六、解答题(共2题，共10分)21．(本小题满分5分)在一个布口袋中装着只有颜色不同，其它都相同的白、红、黑三种颜色的小球各1只，甲乙两人进行摸球游戏；甲先从袋中摸出一球看清颜色后放回，再由乙从袋中摸出一球．(1)试用树状图(或列表法)表示摸球游戏所有可能的结果；(2)如果规定：乙摸到与甲相同颜色的球为乙胜，否则为负，试求乙在游戏中能获胜的概率．22．(本小题满分5分)设点E、F分别在正方形ABCD的边BC、CD上滑动且保持∠EAF＝45°，AP⊥EF于点P．(1)求证：AP＝AB；(2)若AB＝5，求△ECF的周长．七、解答题23．(本题满分7分)如图，已知直径与等边△ABC的高相等的圆O分别与边AB、BC相切于点D、E，边AC过圆心O且与圆O相交于点F、G．(1)求证：DE∥AC；(2)若△ABC 的边长为a ，求△ECG 的面积．八、解答题24．(本题满分7分)抛物线y ＝ax 2＋bx ＋c (a >0)经过点)0,3(),0,33(B A 与y 轴交于点C ，设抛物线的顶点为D ，在△BCD 中，CD 边的高为h ．(1)若c ＝ka ，求系数k 的值；(2)当∠ACB ＝90°时，求a 及h 的值；(3)当∠ACB ≥90°时，经过探究、猜想，请你直接写出h 的取值范围(不要求书写探究、猜想的过程)．九、解答题25．(本题满分8分)Rt △AOB 中，∠AOB ＝90°，∠ABO ＝30°，BO ＝4，分别以OA ，OB 边所在的 直线建立平面直角坐标系，D 点为x 轴正半轴上的一点，以OD 为一边在第一象 限内作等边△ODE ．(1)如图(1)，当E 点恰好落在线段AB 上，求E 点坐标；(2)在(1)问的条件下，将△ODE 在线段OB 上向右平移如(2)图，图中是否存在一条与线段OO ′始终相等的线段?如果存在，请指出这条线段，并加以证明；如果不存在，请说明理由；(3)若点D 从原点出发沿x 轴正方向移动，设点D 到原点的距离为x ，△ODE 与△AOB 重叠部分的面积为y ，请直接写出y 与x 的函数关系式，并写出自变量x 的取值范围．答案与提示期末检测题(二)一、选择题(共8个小题，每小题4分，共32分) 题号1 2 3 4 5 6 7 8 答案 B B A B A D A D二、填空题(共4个小题，每小题4分，共16分)9．－2．10．A (2，1)，B (2，0)或A (－2，－1)，B (－2，0)；11．5；12．a 33或.332a 三、解答题(本题共25分，每小题5分)13．解：,2,2,3-=-==c b a026)2(34)2(422>=-⨯⨯--=-ac b,322623226)2(⨯±=⨯±--=x x ⋅-=+=6262,626221x x 14．解：△EFC 是等腰三角形．理由如下：在△ABC 和△CDE 中， ∵∴===∠=∠,23,90CD EC AB AC DCE A △ABC ∽△CDE ． 有∠ACB ＝∠CED ，故EF ＝FC ．∴△EFC 是等腰三角形．15．解：作OM ⊥BC 于点M ．∵AD ＝13，OD ＝5，∴AO ＝8．∵∠DAC ＝30°，∴OM ＝4．在Rt △OCM 中，OM ＝4，OC ＝5，∴MC ＝3．∴BC ＝2MC ＝6．16．解：(1)已知二次函数的解析式是y ＝x 2－2x －3＝(x －1)2－4．x－1 0 1 2 3 y 0 －3 －4 －30 (2)令x 2－2x －3＝0时，解得x 1＝－1，x 2＝3．∴当x ＝－1或3时，函数值y ＝0．(3)观察图象知：－4≤y <12．17．答：(1)任作大圆的两条弦AB 、CD ，分别作AB 和CD 的中垂线l 1与l 2，l 1与l 2的交点O ′就是大圆的圆心．(2)过O ，O ＇作直线EF 可等分两圆的面积．四、解答题(共2个题，共10分)18．解：设每日生产x 只玩具狗，每日获得的利润为1650元，依题意有，(170－2x )x －(600＋30x )＝1650．整理，得x 2－70x ＋1125＝0，解得x 1＝25，x 2＝45．因为每天最高产量为40只，所以x 2＝45舍去．答：当日产量为25只时，每日获得的利润为1650元．19．解：(1)根据题意，将x ＝－1，y ＝－1，代入抛物线的解析式，得(k 2－1)×(－1)2－2(k －2)×(－1)＋1＝－1．解得k 1＝1，k 2＝－3．由于k 2－1≠0，所以k ＝－3．抛物线的解析式是y ＝8x 2＋10x ＋1， 对称轴为直线⋅-=85x ∵点B 和点A (－1，－1)关于直线85-=x 对称， ).1,41(--∴B (2)存在．理由如下：设经过点B 的直线的解析式是y ＝mx ＋n ，将B 点坐标代入得m －4n ＝4． ①又∵要使直线与抛物线只有一个公共点，只要使方程mx ＋n ＝8x 2＋10x ＋1有两个相等的实数根，方程mx ＋n ＝8x 2＋10x ＋1整理得，8x 2＋(10－m )x ＋1－n ＝0，得∆＝(10－m )2－32(1－n )＝0． ② 将①代②，解出，,21,6==n m 它的解析式是⋅+=216x y 又有过点B ，平行于y 轴的直线与抛物线仅有一个公共点， 即⋅-=41x 答：直线的解析式是216+=x y 或⋅-=41x 五、解答题(本题满分5分)20．解：由于两方程都有实数根，所以⎪⎩⎪⎨⎧≥∆≥∆=/00021m 即⎪⎩⎪⎨⎧≥----≥--=/0)544(4)4(016)4(0222m m m m m 解得⎪⎪⎩⎪⎪⎨⎧-≥≤=/4510m m m 即，,145≤≤-m 且m ≠0． 又因为m 是整数，所以不等式组的整数解是－1和1． 当m ＝－1时，方程mx 2－4x ＋4＝0即为x 2＋4x －4＝0， 其解不是整数，所以m ＝－1舍去．当m ＝1时，方程mx 2－4x ＋4＝0即为x 2－4x ＋4＝0，其解为x 1＝x 2＝2；方程x 2－4mx ＋4m 2－4m －5＝0即为x 2－4x －5＝0，其解为x 1＝5，x 2＝－1．所以，m ＝1时两方程根都是整数．六、解答题(共2个题，共10分)21．(本小题5分)解：(1)或列表如下 甲乙 白 红 黑 白白白 红白 黑白 红白红 红红 黑红 黑 白黑 红黑 黑黑(2)乙取胜的概率为⋅=3193 22．解：(1)将Rt △ABE 绕点A 按逆时针方向旋转90°，得Rt △ADG ．∵∠B ＝∠ADC ＝∠ADG ＝90°，∠ADF ＋∠ADG ＝180°，即F 、D 、G 在一条直线上．∵AE ＝AG ，AF ＝AF ，∠EAF ＝∠GAF ＝45°，∴△AEF ≌△AGF ．∵EF ＝FG ，AP ⊥EF ，AD ⊥FG ，∴AP ＝AD ＝AB ．即AP ＝AB ．(2)∵△ABE ≌△ADG ，∴EF ＝FG ．∵△CEF 的周长＝CE ＋EF ＋CF ＝CE ＋FG ＋CF ，DG ＝BE ， ∴△CEF 的周长＝CE ＋EF ＋CF ＝BC ＋DC ＝5×2＝10．七、解答题(本题满分7分)23．(1)∵△ABC 是等边三角形，∴∠B ＝60°，∠A ＝60°．∵AB 、BC 是圆O 的切线，D 、E 是切点，∴BD ＝BE ．∴∠BDE ＝60°，∠A ＝60°，有DE ∥AC ．(2)分别连结OD 、OE ，作EH ⊥AC 于点H ．∵AB 、BC 是圆O 的切线，D 、E 是切点，O 是圆心， ∴∠ADO ＝∠OEC ＝90°，OD ＝OE ，AD ＝EC ．∴△ADO ≌△CEO ，有.21a OC AO == ∵圆O 的直径等于△ABC 的高，得半径,43a OG = .4321a a OG OC CG +=+=∴ ∵EH ⊥OC ，∠C ＝60°， .83,30a EH COE ==∠∴,83)2143(2121a a a EH CG S ECG ⋅+=⋅=∆ .64323323643222a a a S ECG +=+=∴∆ 八、解答题(本题满分7分) 24．解：(1)因为)0,3(),0,33(B A -在抛物线y ＝ax 2＋bx ＋c (a ＞0)上， 所以有，),932()3)(33(2-+=-+=x x a x x a yc ＝－9a ，所以k ＝－9．(2)由于∠ACB ＝90°时，∵OC ⊥AB ，∴∠AOC ＝∠BOC ＝90°．可得∠ACO ＝∠OBC ．∴△AOC ∽△COB ．,OBOC OC AO =∴ 即,93332=⨯=⋅=OB OA OC∴OC ＝3．∵C (0，－3)，由(1)知－9a ＝－3，⋅=∴31a 过D 作DE ⊥OC 交y 轴于点E ，延长DC 交x 轴于点H ，过B 作BF⊥CH 于点F ．即BF 是边DC 的高h ．因为D 是抛物线的顶点，所以),4,3(--D故OE ＝4，又OC ＝3，可得.3,1==DE CE易证△HCO ∽△DCE ，有,313===EC CO DE HO 故.32,333=-===OB OH BH DE OH由于∠COH ＝90°，OC ＝3，,33=OH由勾股定理知CH ＝6，有∠OHC ＝30°．又在Rt △BHF 中，32=BH ，所以3=BF ，即.3=h (3)当∠ACB ≥90°时，猜想.30≤<h九、解答题(本题满分8分)25．解：(1)作EH ⊥OB 于点H ，∵△OED 是等边三角形，∴∠EOD ＝60°．又∵∠ABO ＝30°，∴∠OEB ＝90°．∵BO ＝4，.221==∴OB OE ∵△OEH 是直角三角形，且∠OEH＝30°，).3,1(.3,1E EH OH ∴==∴(2)存在线段EF ＝OO ＇．∵∠ABO ＝30°，∠EDO ＝60°，∴∠ABO ＝∠DFB ＝30°，∴DF ＝DB ．∴OO ＇＝4－2－DB ＝2－DB ＝2－DF ＝ED －FD ＝EF⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<<-+-≤<=).4(32)42(323243)20(43)3(22x x x x x x y。

北京市西城区普通中学2024学年数学高三上期末学业质量监测试题考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设正项等差数列{}n a 的前n 项和为n S ，且满足6322S S -=，则2823a a 的最小值为 A ．8 B ．16 C ．24 D ．362．等比数列{}n a 的前n 项和为n S ，若0n a >，1q >，3520a a +=，2664a a =，则5S =（ ）A ．48B ．36C ．42D ．31 3．已知向量()3,1a =，()3,1b =-，则a 与b 的夹角为（ ） A ．6π B ．3π C ．23π D ．56π 4．已知集合A ={x |–1<x <2}，B ={x |x >1}，则A ∪B =A ．（–1，1）B ．（1，2）C ．（–1，+∞）D ．（1，+∞） 5．复数12i z i=+的共轭复数在复平面内所对应的点位于( ) A ．第一象限B ．第二象限C ．第三象限D ．第四象限 6．已知集合M ＝{y ｜y ＝，x ＞0}，N ＝{x ｜y ＝lg （2x －）}，则M∩N 为（ ）A ．（1，＋∞）B ．（1，2）C ．[2，＋∞）D ．[1，＋∞）7．已知函数f (x )＝223,1ln ,1x x x x x ⎧--+≤⎨>⎩,若关于x 的方程f (x )＝kx －12恰有4个不相等的实数根，则实数k 的取值范围是( )A ．1e 2⎛ ⎝B ．12e ⎡⎢⎣ C ．12e ⎛ ⎝⎦ D ．12e ⎛ ⎝⎭8．三棱柱111ABC A B C -中，底面边长和侧棱长都相等，1160BAA CAA ︒∠=∠=，则异面直线1AB 与1BC 所成角的余弦值为（ ）A ．33B ．66C ．34D ．369．设F 为抛物线24x y =的焦点，A ，B ，C 为抛物线上三点，若0FA FB FC ++=，则|||||FA FB FC ++=（ ）. A ．9 B ．6C ．38D ．316 10．已知点(2,0)M ，点P 在曲线24y x =上运动，点F 为抛物线的焦点，则2||||1PM PF -的最小值为（ ） A ．3B ．2(51)-C ．45D ．411．双曲线﹣y 2=1的渐近线方程是（ ） A ．x±2y=0 B ．2x±y=0 C ．4x±y=0 D ．x±4y=0 12．某四棱锥的三视图如图所示，该几何体的体积是（ ）A ．8B ．83C ．4D ．43二、填空题：本题共4小题，每小题5分，共20分。

2023-2024学年北京市西城区七年级下册数学期末质量检测模拟题（卷一）一.选一选（本大题共10小题，共30.0分）1.下列方程是二元方程的是()A .342x x-= B.35x y= C.20x y += D.223x y y -=2.如图图形中，既是轴对称图形又是对称图形的是()A.B.C.D.3.若方程()3213x x -=的解与关于x 的方程()6223a x -=+的解相同，则ａ的值为()A .2B.2-C.1D.1-4.下列正多边形的组合中，能够铺满地面的是（）A.正六边形和正方形B.正五边形和正八边形C.正六边形和正三角形D.正十边形和正三角形5.如图，直线//a b ，直线c 分别与a ，b 相交于A ，C 两点，AC AB ⊥于点A ，AB 交直线b 于点B ，若140∠=︒，则ABC ∠的度数为()A.52B.50C.45D.40 5.6.若a b >，则下列没有等式中，没有成立的是()A.55a b +>+ B.55a b ->- C.55a b> D.55a b->-7.如图，在长方形ABCD 中，放入六个形状、大小相同的小长方形(即空白的长方形)，若16AB cm =，4EF cm =，则一个小长方形的面积为()A.216cmB.22lcmC.224cm D.322cm 8.若关于x 的没有等式组()322x m x x ->⎧⎨+>+⎩无解，则m 的取值范围为()A.1m ≥- B.1m >- C.1m ≤- D.1m <-9.滴滴快车是一种便捷的出行工具，计价规则如下表：计费项目里程费时长费远途费单价 1.8元/公里0.3元/分钟0.8元/公里注：车费由里程费、时长费、远途费三部分构成，其中里程费按行车的实际里程计算；时长费按行车的实际时间计算；远途费的收取方式为：行车里程7公里以内（含7公里）没有收远途费，超过7公里的，超出部分每公里收0.8元.小王与小张各自乘坐滴滴快车，行车里程分别为6公里与8.5公里，如果下车时两人所付车费相同，那么这两辆滴滴快车的行车时间相差（）A.10分钟B.13分钟C.15分钟D.19分钟10.如图是由●按照一定规律组成的图形，其中第①个图中共有3个●，第②个图中共有8个●，第③个图中共有15个●，第④个图中共有24个⋯⋯●照此规律排列下去，则第⑩个图中●的个数为()A.105B.110C.120D.140二、填空题（本大题共6小题，共18.0分）11.方程226x -+=的解为______．12.已知等腰三角形的两边长是5和12，则它的周长是______________；13.一个多边形的内角和比它的外角和的2倍还大180度，求这个多边形的边数.14.如图，在ABC 中，90B ∠= ，10.AB =将ABC 沿着BC 的方向平移至DEF ，若平移的距离是3，则图中阴影部分的面积为______．15.如图.在长方形ABCD 中，E 为AD 上一点，将边AB 沿BE 折叠，A 点恰好落在CD 边上的点F 处.若6AB BC +=，DEF 的周长为3，则BCF 的周长为______．16.已知关于x 、y 的方程组343x y ax y a +=-⎧-=⎨⎩，其中31a -≤≤，有以下结论：①当2a =-时，x 、y的值互为相反数；②当1a =时，方程组的解也是方程4x y a +=-的解；③若1x ≤，则4.l y ≤≤其中所有正确的结论有______(填序号)三.计算题（本大题共4小题，共24.0分）17.解下列方程(组)：（1）x 22x 1146+--=（2）334214x y x y +=⎧⎨-=⎩18.解没有等式组()22522325131x x x x -+⎧-≤⎪⎨⎪-<+⎩，并把解集在数轴上表示出来．19.已知关于x 、y 的方程组213252x y k x y k +=+⎧-=-⎨⎩的解满足5035x y x y ->⎧-+≥-⎨⎩，求整数k 的值．20.对于任意有理数x ，我们用[]x 表示没有大于x 的整数，则[]1.x x x -<≤如：[]2.72=，[]20182018=，[]3.144-=-，请根据以上信息，回答下列问题()1填空：[]7.4=______，[]5.12-=______；()2若[]324x +=-，求x 的取值范围；()3已知[]13.5122x x +=+，求x 的值．四、解答题（本大题共5小题，共40.0分）21.如图所示的正方形方格（每个小正方形的边长为1个单位）．ABC 的三个顶点均在小方格的顶点上．（1）画出ABC 关于O 点的对称图形111A B C △；（2）画出将111A B C △沿直线l 向上平移5个单位得到的222A B C △；（3）要使222A B C △与12CC C △重合，则222A B C △绕点2C 顺时针方向至少旋转的度数为__________．22.如图，△ABC ≌△DEF ，∠A=33°，∠E=57°，CE=5cm ．（1）求线段BF 的长；（2）试判断DF 与BE 的位置关系，并说明理由．23.如图，在ABC 中，点D 为BC 上一点，将ABD 沿AD 翻折得到AED ，AE 与BC 相交于点F ，若AE 平分CAD ∠，40B ∠= ，35C ∠= ，求1∠的度数．24.2018年暑期临近，学生们也可轻松逛逛商场，选择自己心仪的衣服.安岳上府街一服装店老板打算没有错失这一良机，计划购进甲、乙两种T 恤.已知购进甲T 恤2件和乙T 恤3件共需310元；购进甲T 恤1件和乙T 恤2件共需190元()1求甲、乙两种T 恤每件的进价分别是多少元？()2为满足市场需求，服装店需购进甲、乙两种T 恤共100件，要求购买两种T 恤的总费用没有超过6540元，并且购买甲T 恤的数量应小于购买甲乙两种T 恤总数量的14，请你通过计算，确定服装店购买甲乙两种T 恤的购买．25.将两块三角板按图1摆放，固定三角板ABC ，将三角板CDE 绕点C 按顺时针方向旋转，其中45A ∠=︒，30D ∠=︒，设旋转角为α，(080)a <<︒︒()1当//DE AC 时(如图2)，求α的值；()2当//DE AB 时(如图3).AB 与CE 相交于点F ，求α的值；()3当090α︒<<︒时，连结(AE 如图4)，直线AB 与DE 相交于点F ，试探究123∠+∠+∠的大小是否改变？若没有改变，请求出此定值，若改变，请说明理由．2023-2024学年北京市西城区七年级下册数学期末质量检测模拟题（卷一）一.选一选（本大题共10小题，共30.0分）1.下列方程是二元方程的是()A.342x x -=B.35x y =C.20x y += D.223x y y -=【正确答案】B【分析】直接利用二元方程的定义即可解答．【详解】选项选项A ，342x x -=，是一元方程；选项B ，35x y =，是二元方程；选项C ，20x y +=，是二元二次方程；选项D ，223x y y -=，是二元二次方程.故选B ．本题题主要考查了二元方程的定义，正确把握二元方程的定义是解题关键．2.如图图形中，既是轴对称图形又是对称图形的是()A.B.C.D.【正确答案】A【分析】根据轴对称图形与对称图形的概念解答即可．【详解】选项A 、是轴对称图形，也是对称图形；选项B 、没有是轴对称图形，也没有是对称图形；选项C 、是轴对称图形，没有是对称图形；选项D 、是轴对称图形，没有是对称图形.故选A ．本题考查了对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；对称图形是要寻找对称，旋转180度后与原图重合．3.若方程()3213x x -=的解与关于x 的方程()6223a x -=+的解相同，则ａ的值为()A.2B.2- C.1D.1-【正确答案】D【分析】先解方程3(2x-1)=3x ，得x=1，因为这个解也是方程6-2a=2(x+3)的解，根据方程的解的定义，把x 代入方程6-2a=2(x+3)中求出a 的值即可．【详解】3(2x-1)=3x 解得：x=1．把x=1代入方程6-2a=2(x+3)得：6-2a=2×(1+3)解得：a=-1．故选D ．本题考查了方程的解的定义，解题的关键是熟知能够使方程左右两边相等的未知数的值是方程的解．4.下列正多边形的组合中，能够铺满地面的是（）A.正六边形和正方形B.正五边形和正八边形C.正六边形和正三角形D.正十边形和正三角形【正确答案】C【详解】能够铺满地面的图形，即是能够凑成360°的图形组合．解：A 、正六边形的每个内角是120°，正方形的每个内角是90°，120m+90n=360°，显然n 取任何正整数时，m 没有能得正整数，故没有能铺满；B 、正五边形每个内角是180°-360°÷5=108°，正八边形每个内角为135度，135m+108n=360°，显然n 取任何正整数时，m 没有能得正整数，故没有能铺满；C 、正六边形的每个内角为120°，正三角形的每个内角为60°，一个正六边形和一个正三角形刚好能铺满地面；D 、正三角形每个内角为60度，正十边形每个内角为144度，60m+144n=360°，显然n 取任何正整数时，m 没有能得正整数，故没有能铺满．故选C ．掌握好平铺的条件，算出每个图形内角和即可．5.如图，直线//a b ，直线c 分别与a ，b 相交于A ，C 两点，AC AB ⊥于点A ，AB 交直线b 于点B ，若140∠=︒，则ABC ∠的度数为()A.52B.50C.45D.40 5.【正确答案】B【分析】先根据AC AB ⊥，140∠=︒，求得2∠的度数，再根据平行线的性质，即可得到ABC ∠的度数．【详解】如图，AC AB ⊥ ，140∠=︒，2904050∴∠=-=︒︒︒，//a b ，250ABC ∴∠=∠=︒，故选B ．本题主要考查了平行线的性质，解题的关键是掌握：两直线平行，内错角相等．6.若a b >，则下列没有等式中，没有成立的是()A.55a b +>+B.55a b ->- C.55a b> D.55a b->-【正确答案】D【详解】A.B.没有等式的两边都加或都减同一个整式，没有等号的方向没有变，故A.B 正确；C.没有等式的两边都乘以同一个正数没有等号的方向没有变，故C 正确；D.没有等式的两边都乘以同一个负数没有等号的方向改变，故D 错误；故选D.点睛:此题考查了没有等式的基本性质,属于基础题.7.如图，在长方形ABCD 中，放入六个形状、大小相同的小长方形(即空白的长方形)，若16AB cm =，4EF cm =，则一个小长方形的面积为()A.216cmB.22lcmC.224cm D.322cm 【正确答案】B【分析】设长方形的长和宽为未数，根据图示可得两个量关系：①小长方形的1个长3+个宽16cm =，②小长方形的1个长1-个宽4cm =，进而可得到关于x 、y 的两个方程，可求得解，从而可得到小长方形的面积．【详解】设小长方形的长为x ，宽为y ，如图可知，3164x y x y +=⎧-=⎨⎩，解得：{73x y ==．所以小长方形的面积()23721.cm =⨯=故选B ．本题考查了二元方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．8.若关于x 的没有等式组()0322x m x x ->⎧⎨+>+⎩无解，则m 的取值范围为()A.1m ≥-B.1m >- C.1m ≤- D.1m <-【正确答案】A【分析】解两个没有等式，再根据没有等式组的解集确定方法“小小找没有着”可得m 的取值范围．【详解】解没有等式0x m ->，得：x m >，解没有等式()322x x +>+，得：1x <-，没有等式组无解，1m ∴≥-，故选A ．本题主要考查了解没有等式组，根据求没有等式的无解，遵循“小小解没有了”原则是解题关键．9.滴滴快车是一种便捷的出行工具，计价规则如下表：计费项目里程费时长费远途费单价 1.8元/公里0.3元/分钟0.8元/公里注：车费由里程费、时长费、远途费三部分构成，其中里程费按行车的实际里程计算；时长费按行车的实际时间计算；远途费的收取方式为：行车里程7公里以内（含7公里）没有收远途费，超过7公里的，超出部分每公里收0.8元.小王与小张各自乘坐滴滴快车，行车里程分别为6公里与8.5公里，如果下车时两人所付车费相同，那么这两辆滴滴快车的行车时间相差（）A.10分钟B.13分钟C.15分钟D.19分钟【正确答案】D【分析】设小王的行车时间为x分钟，小张的行车时间为y分钟，根据计价规则计算出小王的车费和小张的车费，建立方程求解.【详解】设小王的行车时间为x分钟，小张的行车时间为y分钟，依题可得：1.8×6+0.3x=1.8×8.5+0.3y+0.8×（8.5-7）,10.8+0.3x=16.5+0.3y,0.3（x-y）=5.7,x-y=19,故答案为D.本题考查列方程解应用题，读懂表格中的计价规则是解题的关键.10.如图是由●按照一定规律组成的图形，其中第①个图中共有3个●，第②个图中共有8个●，●照此规律排列下去，则第⑩个图中●的第③个图中共有15个●，第④个图中共有24个⋯⋯个数为()A.105B.110C.120D.140【正确答案】Cn n+，把n=10代入【分析】观察图形，根据图形中蕴含的规律得出第n个图中●的个数为()2即可求解．=⨯个，【详解】 第①个图中●有313=⨯个，第②个图中●有824=⨯个，第③个图中●有1535=⨯个，第④个图中●有2446……∴第⑩个图中●的个数为1012120⨯=个，故选C．本题主要考查图形的变化规律，解题的关键是根据题意得出第n 个图中●的个数为()2n n +．二、填空题（本大题共6小题，共18.0分）11.方程226x -+=的解为______．【正确答案】x=-2【分析】方程移项合并同类项后，把x 系数化为1，即可求解．【详解】方程226x -+=，移项合并得：24x -=，解得：2x =-，故答案为2x =-本题考查了解一元方程，解方程移项时注意要变号．12.已知等腰三角形的两边长是5和12，则它的周长是______________；【正确答案】29【分析】没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【详解】解：当5为腰长时，∵5+5<12，故没有能组成三角形，当12为腰长时，边长分别为：5，12，12，∵5+12>12，故能组成三角形，故周长为：5+12+12=29；故29．本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，同时需要验证各种情况是否能构成三角形进行解答．13.一个多边形的内角和比它的外角和的2倍还大180度，求这个多边形的边数.【正确答案】这个多边形的边数是7．【分析】设这个多边形的边数为n ，根据多边形的内角和公式（n ﹣2）•180°与外角和定理列出方程，求解即可．【详解】设这个多边形的边数为n ，根据题意，得（n ﹣2）×180°=2×360°+180°，解得n =7．故这个多边形的边数是7．14.如图，在ABC 中，90B ∠= ，10.AB =将ABC 沿着BC 的方向平移至DEF ，若平移的距离是3，则图中阴影部分的面积为______．【正确答案】30【分析】先根据平移的性质得AC DF =，3AD CF ==，再可判断四边形ACFD 为平行四边形，然后根据平行四边形的面积公式计算即可．【详解】 直角ABC 沿BC 边平移3个单位得到直角DEF ，AC DF ∴=，3AD CF ==，∴四边形ACFD 为平行四边形，31030ACFD S CF AB ∴=⋅=⨯=平行四边形，即阴影部分的面积为30．故答案为30．本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点.连接各组对应点的线段平行且相等.15.如图.在长方形ABCD 中，E 为AD 上一点，将边AB 沿BE 折叠，A 点恰好落在CD 边上的点F 处.若6AB BC +=，DEF 的周长为3，则BCF 的周长为______．【正确答案】9【分析】根据折叠的性质可得AE EF =，AB BF =，从而DEF 的周长可转化为：3AD DF +=，求出CF ，再由FCB 的周长，即可解决问题．【详解】由折叠得：AE EF =，AB BF =，DEF 的周长为3，3DE EF DF DE AE DF AD DF ∴++=++=+=，6AB BC AD DF CF +=++= ，633CF ∴=-=，BCF ∴ 的周长为：639BC BF CF AB BC CF ++=++=+=，故答案为9本题主要考查了翻折变换的性质、矩形的性质等几何知识点；根据折叠的性质将DEF 的周长进行转化是解决问题的关键．16.已知关于x 、y 的方程组343x y a x y a +=-⎧-=⎨⎩，其中31a -≤≤，有以下结论：①当2a =-时，x 、y 的值互为相反数；②当1a =时，方程组的解也是方程4x y a +=-的解；③若1x ≤，则4.l y ≤≤其中所有正确的结论有______(填序号)【正确答案】①②③【分析】解方程组得出x 、y 的表达式，根据a 的取值范围确定x 、y 的取值范围，再逐一判断即可．【详解】解方程组343x y ax y a +=-⎧-=⎨⎩，得{121x a y a =+=-，31a -≤≤ ，53x ∴-≤≤，04y ≤≤，①当2a =-时，123x a =+=-，13y a =-=，x ，y 的值互为相反数，结论正确；②当1a =时，23x y a +=+=，43a -=，方程4x y a +=-两边相等，结论正确；③当1x ≤时，121a +≤，解得0a ≤，且31a -≤≤，30a ∴-≤≤，114a ∴≤-≤，14y ∴≤≤结论正确，故答案为①②③．本题考查了二元方程组的解，解一元没有等式组.关键是根据条件，求出x 、y 的表达式及x 、y 的取值范围．三.计算题（本大题共4小题，共24.0分）17.解下列方程(组)：（1）x 22x 1146+--=（2）334214x y x y +=⎧⎨-=⎩【正确答案】(1)x=-4;(2)23x y =⎧⎨=-⎩.【分析】()1方程去分母，去括号，移项合并，把x 系数化为1，即可求出解；()2方程组利用加减消元法求出解即可．【详解】解：（1）去分母得：364212x x +-+=，移项合并得：4x -=，解得：4x =-；（2）3327x y x y +=⎧⎨-=⎩①②，①+②得：510x =，解得：2x =，把2x =代入②得：3y =-，则方程组的解为23x y =⎧⎨=-⎩．本题考查了解二元方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．18.解没有等式组()22522325131x x x x -+⎧-≤⎪⎨⎪-<+⎩，并把解集在数轴上表示出来．【正确答案】-2≤x<2【分析】分别求出各没有等式的解集，再求出两个没有等式解集的公共部分即可得没有等式组的解集，并在数轴上表示出来即可．【详解】解没有等式2252232x x -+-≤，得：2x ≥-，解没有等式()5131x x -<+，得：2x <，则没有等式组的解集为22x -≤<，将没有等式组的解集表示在数轴上如下：本题考查的是解一元没有等式组，熟知“同大取大；同小取小；大小小大中间找；小小找没有到”的原则是解答此题的关键．19.已知关于x 、y 的方程组213252x y k x y k +=+⎧-=-⎨⎩的解满足5035x y x y ->⎧-+≥-⎨⎩，求整数k 的值．【正确答案】1、2【分析】两方程分别相加和相减可得561343x y k x y k -=-⎧-+=-+⎨⎩，由已知没有等式组得出关于k 的没有等式组，解没有等式组即可．【详解】两方程分别相加和相减可得561343x y k x y k -=-⎧-+=-+⎨⎩，{610435k k ->∴-+≥-，解得126k <≤，∴整数k 的值为1、2．本题考查了二元方程组的解与解一元没有等式组，方程组的解即为能使方程组中两方程成立的未知数的值，解决本题的关键是求出方程组的解，列出没有等式组．20.对于任意有理数x ，我们用[]x 表示没有大于x 的整数，则[]1.x x x -<≤如：[]2.72=，[]20182018=，[]3.144-=-，请根据以上信息，回答下列问题()1填空：[]7.4=______，[]5.12-=______；()2若[]324x +=-，求x 的取值范围；()3已知[]13.5122x x +=+，求x 的值．【正确答案】(1)7,-6;(2)5 23x -≤<-;(3)1 4x =±.【分析】()1根据整数的定义即可求解；()2根据整数的定义即可得到一个关于x 的没有等式组，即可求得x 的范围．()3根据新定义列出关于x 的没有等式组，解之求得x 的范围及122x +的范围，再根据122x +为整数可得122x +的值，解之可得．【详解】()[] 17.47=，[]5.126-=-，故答案为7、6-；()[]21x x x -<≤ ，321432x x ∴+-<-≤+，解得：523x -≤<-；()[]31x x x -<≤ ，13.5112 3.512x x x ∴+-<+≤+，解得1133x -≤<，1172626x ∴-≤+<，122x + 为整数，1202x ∴+=或1，14x ∴=±．本题考查了解一元没有等式组，能得出关于x 的没有等式组是解此题的关键．四、解答题（本大题共5小题，共40.0分）21.如图所示的正方形方格（每个小正方形的边长为1个单位）．ABC 的三个顶点均在小方格的顶点上．（1）画出ABC 关于O 点的对称图形111A B C △；（2）画出将111A B C △沿直线l 向上平移5个单位得到的222A B C △；（3）要使222A B C △与12CC C △重合，则222A B C △绕点2C 顺时针方向至少旋转的度数为__________．【正确答案】90°【分析】（1）找出点,,A B C 关于原点O 的对应点111A B C ，，，顺次连接即可.（2）将111A B C ，，按照平移条件找出它们的对应点222A B C ，，，顺次连接即可.（3）观察一对对应点的位置关系即可求出答案.【详解】（1）如图，111A B C 即为所求．（2）如图，222A B C 即为所求．（3）由题可得，要使222A B C 与12CC C 重合，则222A B C 绕点2C 顺时针方向至少旋转的度数为90︒．故答案为90︒．考查旋转以及平移作图，都需要找到各关键点的对应点，然后顺次连接即可.22.如图，△ABC ≌△DEF ，∠A=33°，∠E=57°，CE=5cm ．（1）求线段BF 的长；（2）试判断DF 与BE 的位置关系，并说明理由．【正确答案】(1)5cm;(2)见解析.【分析】(1)根据全等三角形的性质得出BC=EF ，求出EC=BF 即可；(2)根据全等三角形的性质可得∠A=∠D=33°，根据三角形内角和定理求出∠DFE 的度数，即可得出答案．【详解】() 1ABC ≌DEF ，BC EF ∴=，BC CF EF CF ∴+=+，即5BF CE cm ==；()2ABC ≌DEF ，33A ∠=︒，33A D ∴∠=∠=︒，180D E DFE ∠+∠+∠=︒ ，57E ∠=︒，180573390DFE ︒︒∴--︒∠==︒，DF BE ∴⊥．本题考查了全等三角形的性质和三角形内角和定理，能灵活运用全等三角形的性质进行推理是解此题的关键．23.如图，在ABC 中，点D 为BC 上一点，将ABD 沿AD 翻折得到AED ，AE 与BC 相交于点F ，若AE 平分CAD ∠，40B ∠= ，35C ∠= ，求1∠的度数．【正确答案】30°【分析】根据三角形内角和定理可求出∠BAC 的值，根据角平分线的性质折叠的性质可得出∠BAD=∠DAE=∠CAE=35°、∠B=∠E=40°，再利用三角形的外角的性质可求出∠AFD 及∠1的度数．【详解】解：180B C BAC ∠+∠+∠= ，40B ∠= ，35C ∠= ，105BAC ∴∠= ．又AE 平分CAD ∠，CAE DAE ∴∠=∠．由翻折得：BAD DAE ∠=∠，40B E ∠=∠= ，35BAD DAE CAE ∴∠=∠=∠= ，70AFD CAE C ∴∠=∠+∠= ．又1AFD E ∠=∠+∠ ，1704030∴∠=-= ．本题考查了三角形内角和定理、三角形的外角性质、角平分线的性质以及折叠的性质，利用角平分线的性质、折叠的性质及三角形的外角性质找出各角之间的关系是解题的关键．24.2018年暑期临近，学生们也可轻松逛逛商场，选择自己心仪的衣服.安岳上府街一服装店老板打算没有错失这一良机，计划购进甲、乙两种T 恤.已知购进甲T 恤2件和乙T 恤3件共需310元；购进甲T 恤1件和乙T 恤2件共需190元()1求甲、乙两种T 恤每件的进价分别是多少元？()2为满足市场需求，服装店需购进甲、乙两种T 恤共100件，要求购买两种T 恤的总费用没有超过6540元，并且购买甲T 恤的数量应小于购买甲乙两种T 恤总数量的14，请你通过计算，确定服装店购买甲乙两种T 恤的购买．【正确答案】(1)甲种T 恤每件进价为50元，乙种T 恤每件进价为70元;(2)见解析.【分析】(1)设甲种商品每件的进价为x 元，乙种商品每件的进价为y 元，根据“购进甲商品2件和乙商品3件共需270元；购进甲商品3件和乙商品2件共需230元”可列出关于x 、y 的二元方程组，解方程组即可得出两种商品的单价；(2)设商场购进甲种T 恤a 件，则购进乙种T 恤为(100-a)件.根据“购买两种T 恤的总费用没有超过6540元，并且购买甲T 恤的数量应小于购买甲乙两种T 恤总数量的14”列出没有等式组并解答．【详解】()1设甲种T 恤每件进价为x 元，乙种T 恤每件进价为y 元.由题意得233102190x y x y +=⎧⎨+=⎩解得5070x y =⎧⎨=⎩．答：甲种T 恤每件进价为50元，乙种T 恤每件进价为70元．()2设商场购进甲种T 恤a 件，则购进乙种T 恤为()100a -件．根据题意得：()5070100654011004a a a ⎧+-≤⎪⎨<⨯⎪⎩解得2325a ≤<a 为整数，a ∴为23或24∴当23a =时，10077a -=；当24a =时，10076a -=∴有两种购买，一：购买甲种T 恤23件，购买乙种T 恤77件，二：购买甲种T 恤24件，购买乙种T 恤76件．本题考查了二元方程组的应用、解一元没有等式，解题的关键是：(1)根据数量关系列出关于x 、y 的二元方程组；（2）解决该题型题目时，根据数量关系列出方程(方程组、没有等式或函数关系式)是关键．25.将两块三角板按图1摆放，固定三角板ABC ，将三角板CDE 绕点C 按顺时针方向旋转，其中45A ∠=︒，30D ∠=︒，设旋转角为α，(080)a <<︒︒()1当//DE AC 时(如图2)，求α的值；()2当//DE AB 时(如图3).AB 与CE 相交于点F ，求α的值；()3当090α︒<<︒时，连结(AE 如图4)，直线AB 与DE 相交于点F ，试探究123∠+∠+∠的大小是否改变？若没有改变，请求出此定值，若改变，请说明理由．【正确答案】(1)60°;(2)105°;(3)没有改变，105°.【分析】()1由//DE AC 可得30DCA D ∠=∠=︒，则可求60DCB α∠=∠=︒；()2由//DE AB 可得60E AFC ∠=∠=︒，根据三角形内角和可求75FCA ∠=︒即可求15ACD =︒∠，由此即可求得α∠；()3根据三角形内角和和外角等于没有相邻的两个内角和，列出1∠，2∠，3∠关系式可求123∠+∠+∠的值【详解】() 1//DE AC ，30D ACD ∴∠=∠=︒，又90BCA ∠=︒ ，60BCD BCA ACD ∴∠=∠-∠=︒，即60α=︒()2//DE AB ，60E CFA ∴∠=∠=︒，∵45A ∠=︒，∴75FCA ∠=︒，∴15ACD =︒∠，105BCD ACB ACD ∴∠=∠+∠=︒，即105α=︒；() 3大小没有变，其值为105︒．ACD CAB D AFD ∠+∠=∠+∠ ，45CAB ∠=︒，30D ∠=︒，15AFD ACD ∴∠-∠=︒，又12AFD ∠+∠=∠ ，390ACD ∠=-∠︒，123909015105AFD ACD ∴∠+∠+∠=∠+-+︒︒∠==︒︒.本题考查了旋转的性质，平行线的性质，灵活运用这些性质是解决问题的关键．2023-2024学年北京市西城区七年级下册数学期末质量检测模拟题（卷二）一、选一选（本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中只有项是符合要求的，请把正确选项的字母代号写在下表内）1.25的算数平方根是A.B.±5C. D.52.在2273.14159π，0.中，无理数有（）个．A.2B.3C.4D.53.在下列四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（）A. B. C. D.4.下列中，适合采用全面（普查）方式的是（）A.对邕江水质情况的B.对端午节期间市场上粽子质量情况的C.对某班50名同学体重情况的D.对我国居民日平均用水量的5.下列计算正确的是（）A.23= B.3= C.4=± D.3=-6.如图，用没有等式表示数轴上所示的解集，正确的是（）A.x ＞﹣2B.x ≥﹣2C.x ＜﹣2D.x ≤﹣27.点N(-1，3)可以看作由点M(-1，-1)()A.向上平移4个单位长度所得到的B.向左平移4个单位长度所得到的C.向下平移4个单位长度所得到的D.向右平移4个单位长度所得到的8.方程2x +y =8的正整数解的个数是（）A.4B.3C.2D.19.如图，BE 是AB 的延长线，下面说确的是（）A .由∠1=∠2，可得到AB ∥CDB.由∠2=∠C ，可得到AD ∥BCC.由∠1=∠C ，可得到AD ∥BCD.由∠1=∠C ，可得到AB ∥CD10.如图所示的象棋盘上，若“帅”位于(1,2)-，“相”位于(3,2)-，则“炮”位于（）A.(1,1)-B.(1,2)-C.(2,1)- D.(2,2)-二、填空题（本大题共6个小题，每小题3分，共18分）11.剧院里5排2号可用（5，2）表示，则（7，4）表示_____．12.如图，将直线l 1沿着AB 的方向平移得到直线l 2，若∠1=50°，则∠2=_____．13.﹣5的相反数是_____．14.用“＞”或“＜”填空：若﹣2a+1＜﹣2b+1，则a_____b ．15.若关于x ，y 的二元方程组3+1+33x y ax y =⎧⎨+=⎩的解满足2x y +＜，则a 的取值范围为______．16.已知点A (a ，0)和点B (0，5)两点，且直线AB 与坐标轴围成的三角形的面积等于10，则a 的值是______.三、解答题（共52分）17.计算和求x 的值：（1）+|1|（2）x 2﹣5=5，求x ．18.解方程组.52253415x y x y +=⎧⎨+=⎩19.解没有等式组：201213x x x +≥⎧⎪+⎨>-⎪⎩，并把解集在数轴上表示出来．20.已知：如图，点A、B、C在一条直线上，AD∥BE，∠1＝∠2，求证：∠A＝∠E．21.如图，△ABC在直角坐标系中．（1）若把△ABC向上平移2个单位，再向左平移1个单位得到△A1B1C1，画出△A1B1C1，并写出点A1，B1，C1的坐标；（2）求△ABC的面积．22.有大小两种货车，2辆大货车与3辆小货车可以运货17吨，5辆大货车与6辆小货车可以运货38吨．求一辆大货车和一辆小货车每次分别可以运货多少吨？23.家庭过期药品属于“国家危险废物”，处理没有当将污染环境，危害健康．某校学生杨杨和舟舟为了解市民家庭处理过期药品的方式，决定对全市家庭作简单随机抽样．（1）下列选取样本的方法最合理的一种是____．（只需填上正确答案的序号）①在市某个居民区以家庭为单位随机抽取；②在全市医务工作者中以家庭为单位随机抽取；③在全市常住人口中以家庭为单位随机抽取．（2）本次抽样发现，接受的家庭都有过期药品，现将有关数据呈现如图：①m=____；n=____；②补全条形统计图；③根据数据，你认为该市市民家庭处理过期药品最常见的方式是____；④家庭过期药品的正确处理方式是送回收站点，若该市有180万户家庭，请估计大约有多少户家庭处理过期药品的方式是送回收站点．24.甲、乙两个厂家生产的办公桌和办公椅的质量、价格一致，每张办公桌800元，每张椅子80元．甲、乙两个厂家推出各自的优惠，甲厂家：买一张桌子送三张椅子；乙厂家：桌子和椅子全部按原价8折优惠．现某公司要购买3张办公桌和若干张椅子，若购买的椅子数为x张（x≥9）．（1）分别用含x的式子表示甲、乙两个厂家购买桌椅所需的金额；（2）购买的椅子至少多少张时，到乙厂家购买更.2023-2024学年北京市西城区七年级下册数学期末质量检测模拟题（卷二）一、选一选（本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中只有项是符合要求的，请把正确选项的字母代号写在下表内）1.25的算数平方根是A. B.±5 C. D.5【正确答案】D【分析】一个正数的平方根有2个，且这两个互为相反数，而算数平方根只有一个且必须是正数，特别地，我们规定0的算术平方根是0负数没有算术平方根，但i的平方是－1，i是一个虚数，是复数的基本单位.5=，∴25的算术平方根是：5.故答案为5.本题考查了算术平方根，熟练掌握该知识点是本题解题的关键.。

2024届北京市西城区第十三中学语文八下期末学业质量监测试题注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．一、语文基础知识（12分）1．（2分）将下列句子组成语意连贯的一段话语序排列正确的一项是( )①就是要让收藏在禁宫里的文物陈列在广阔大地上的遗产、书写在古籍里的文字都活起来②历史文物并不只是历史的沉淀、岁月的陈酿，不是一个静止的存在③让人们触摸中华文化脉络感受中华文化魅力、汲取中华文化精髓④而是寄托着文化血脉的传承,与人们的生活和我们所处的时代息息相关⑤博物馆善用优质文化资源,以丰富的活动接续传统A．⑤③②④①B．②④⑤①③C．③⑤④②①D．②①⑤④③2．（2分）下列词语书写及加点的字注音完全正确．．的一项是（）A．撺．掇（cuàn）殆．慢（dài）恬．静（tián）嘎．然而止（jiá）B．嘱．咐（zhǔ）晦．暗（huì）羁绊．（bàn）销声匿．迹（nì）C．冗．杂（rǒng）缄．默（jiàn）蓦．然（mù）草长．鹰飞（zhǎng）D．儒．家（yú）虔．诚（qiǎn）俯瞰．（kàn）接踵．而至（zhǒng）3．（2分）下列词语中加点的字，每对读音都不相同的一项是（）A．阡．陌/迁．徙行．辈/行．走狡辩．/明辨．是非惟妙惟肖．/销．声匿迹B．追溯．/塑．造抉．择/秘诀．摄．影/蹑．手蹑脚目眩．神迷/自我炫．耀C．缅．怀/腼．腆蠕．动/懦．弱强．制/强．词夺理悄．怆幽邃/峭．壁林立D．卑．鄙/女婢．襁褓．/褒．扬衰竭．/怒不可遏．分崩．离析/欢蹦．乱跳4．（2分）下列关于《名人传》的叙述不正确的一项是（）A．《名人传》的作者是罗曼·罗兰，他是20世纪享誉国际文坛的法国现实主义作家。

2023-2024学年北京市西城区高三生物第一学期期末调研模拟试题考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、选择题(本大题共7小题,每小题6分,共42分。

)1．据《细胞报告》最近报道，我国科学家成功将小鼠的颗粒细胞（卵泡中卵母细胞周围的细胞）转化为GV卵母细胞，进而恢复减数分裂并顺利培育出健康后代（如下图）。

有关叙述错误的是（）A．过程①的实质是基因选择性表达B．X细胞应处于减数第二次分裂中期C．过程③中受精的实质是雌雄原核融合D．过程③选择原肠胚进行胚胎移植2．经下列实验处理后，取样，用不同试剂检测，实验结果正确的一组是（）组别参与反应的物质反应条件检测实验现象A 米汤2mL+唾液1．5mL充分混合反应24h 碘液蓝色B 牛奶2mL+唾液1．5mL 斐林试剂砖红色C 牛奶2mL+肝脏研磨液1．5mL 碘液紫色D 米汤2mL+汗液1．5mL 斐林试剂蓝色A．A B．B C．C D．D3．2019年底武汉出现由新型冠状病毒（SARS- CoV-2）感染引起的肺炎疫情，该病患者肺功能受损引起血氧饱和度下降，主要表现为发热、咳嗽、乏力、浑身酸痛等症状。

SARS-CoV-2主要由蛋白质外壳和内部的RNA组成。

下列相关叙述错误的是（）A．患者血氧饱和度下降导致呼吸急促，以补偿机体缺氧B．患者治愈后，机体产生并在一段时间内保持有对SARS-CoV-2免疫的能力C．体积分数为70%的酒精能使SARS-CoV-2的蛋白质外壳变性，从而失去感染力D．患者发热时机体产热增多、散热减少引起内环境稳态失衡4．下列有关HIV病毒和艾滋病的叙述，错误的是（）A．每个HIV病毒含有2条RNA分子B．HIV感染人群比健康人群更易患甲型H1N1流感C．HIV侵入人体后可以识别并结合脑细胞表面的受体D．没有感染过HIV的人，体内不存在与之相匹配的受体5．人们利用某些微生物制作食品时，需要分析微生物的特点，控制微生物的发酵条件。

2024届北京市西城区北师大附属实验中学物理八年级下册期末学业质量监测模拟试题注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题（每题1.5分，共30题，45分）1．下列有关大气压的叙述，错误的是A．马德堡半球实验有力地证明了大气压的存在B．晴天、阴雨天等天气的变化也会影响大气压C．大气压的大小与大气的密度有关，离地面越高的地方，大气压也越大D．标准大气压的数值约为1.01×l05 Pa2．物理学中引入比热容概念，是为了比较( )A．不同质量的相同物质，升高相同的温度，吸收的热量不同。

B．相同质量的不同物质，升高相同的温度，吸收的热量不同。

C．不同质量的相同物质，吸收相同的热量，升高的温度不同。

D．以上说法都不对。

3．用水平风吹图中的四个模型，受到的压强差向下的是A．B．C．D．4．如图所示的生活实例中，力对物体做功的是A．运动员举着杠铃静止不动B．提着滑板在水平路面上前行C．小车在推力的作用下,向前运动了一段距离D．用尽全力搬石头,搬而未起5．下列四种情况下，物质比热容会发生变化的是A．一瓶酒精倒去一半B．水凝结成冰C．一块铁锻打成宝刀D．铜块降温20℃6．小华同学在科技馆观摩自行车走钢丝表演后回家做了一个模型，如图所示，下列说法正确的是（）A．自行车的重力与钢丝对自行车的支持力是一对平衡力B．自行车和所挂物体总重力与钢丝对自行车的支持力是一对平衡力C．自行车对钢丝的压力与钢丝对自行车的支持力是一对平衡力D．自行车对绳的拉力与钩码的重力是一对平衡力7．在第十七届“渝洽会”上，重庆造恩斯特龙408型直升机（如图所示）签下了20架大订单。