有限元计算结果的应力分类

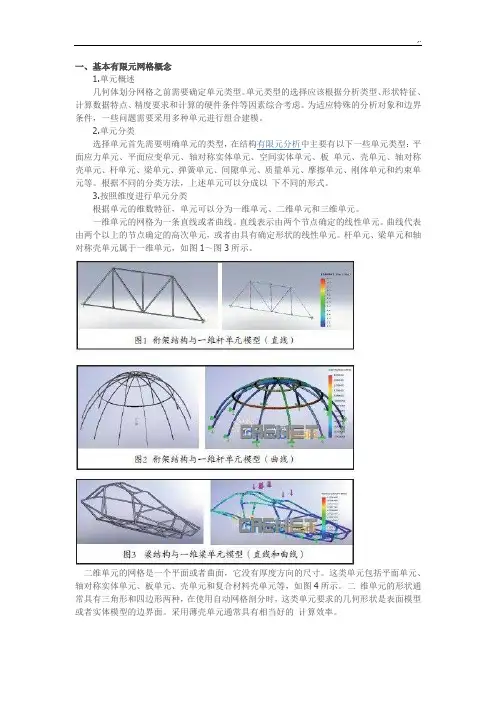
一、基本有限元网格概念1.单元概述几何体划分网格之前需要确定单元类型。

单元类型的选择应该根据分析类型、形状特征、计算数据特点、精度要求和计算的硬件条件等因素综合考虑。

为适应特殊的分析对象和边界条件，一些问题需要采用多种单元进行组合建模。

2.单元分类选择单元首先需要明确单元的类型，在结构有限元分析中主要有以下一些单元类型：平面应力单元、平面应变单元、轴对称实体单元、空间实体单元、板单元、壳单元、轴对称壳单元、杆单元、梁单元、弹簧单元、间隙单元、质量单元、摩擦单元、刚体单元和约束单元等。

根据不同的分类方法，上述单元可以分成以下不同的形式。

3.按照维度进行单元分类根据单元的维数特征，单元可以分为一维单元、二维单元和三维单元。

一维单元的网格为一条直线或者曲线。

直线表示由两个节点确定的线性单元。

曲线代表由两个以上的节点确定的高次单元，或者由具有确定形状的线性单元。

杆单元、梁单元和轴对称壳单元属于一维单元，如图1～图3所示。

二维单元的网格是一个平面或者曲面，它没有厚度方向的尺寸。

这类单元包括平面单元、轴对称实体单元、板单元、壳单元和复合材料壳单元等，如图4所示。

二维单元的形状通常具有三角形和四边形两种，在使用自动网格剖分时，这类单元要求的几何形状是表面模型或者实体模型的边界面。

采用薄壳单元通常具有相当好的计算效率。

三维单元的网格具有空间三个方向的尺寸，其形状具有四面体、五面体和六面体，这类单元包括空间实体单元和厚壳单元，如图5所示。

在自动网格划分时，它要求的是几何模型是实体模型(厚壳单元是曲面也可以)。

4.按照插值函数进行单元分类根据单元插值函数多项式的最高阶数多少，单元可以分为线性单元、二次单元、三次单元和更高次的单元。

线性单元具有线性形式的插值函数，其网格通常只具有角节点而无边节点，网格边界为直线或者平面。

这类单元的优点是节点数量少，在精度要求不高或者结果数据梯度不太大的情况下，采用线性单元可以得到较小的模型规模。

吊耳有限元分析作者：渠建华来源：《中国科技博览》2018年第34期中图分类号：TD557 文献标识码：A 文章编号：1009-914X（2018）34-0041-011 前言在船厂生产过程中，无论是船舶建造过程中的分段吊装、设备安装，还是船舶下水过程中的拖拉、牵引，吊耳的使用都是非常广泛的。

吊耳使用过程中，吊耳承压面上应力分布非常复杂，它直接关系到运输和起吊的安全，一旦出现问题将造成很大的损失。

对吊耳强度的校核显得尤为重要，本文采用有限元方法对吊耳的强度进行校核。

本文使用ABAQUS软件，此软件是一套功能强大的基于有限元法的工程模拟软件，其解决问题的范围从相对简单的线性分析到最富有挑战性的非线性模拟。

ABAQUS具备十分丰富的，可模拟任意实际形状的单元库，并与之对应拥有各类型的材料模型库，可以模拟大多数典型工程材料的性能。

2 吊耳有限元计算2.1 计算对象的选择及计算条件本文将用三维实体单元模拟30T的吊耳，此规格吊耳在我厂使用频率较高。

计算条件的设定：1）吊耳固定采用较常见的对接，未采用搭接形式；2）在模型中不考虑复杂的吊耳-卡环相互作用，只是在眼环的下半环作用一个分布压力对吊耳施加载荷；3）忽略眼环环向压力大小的变化，采用均匀压力；4）设定吊耳承受荷载重量为30T（约294KN），计算吊耳在1.5倍允许负荷下的状态；5）所施加的均匀压力的大小取近似180MPa[294KN/（0.064mx0.025m）=183.75MPa]。

2.2 建立模型1）创建部件：在Module/Part项中按照尺寸绘制轮廓图，完成轮廓拉伸，生成模型。

2）定义材料和截面属性。

在Module/Property项中，给出单个线弹性材料属性，其弹性模量E=200GPa，泊松比ν=0.3。

分别在Section/Create中定义截面为实体、均匀截面。

并在Module/Assembly项中将装配件定义为实体。

3）定义分析步及指定输出结果。

有限元分析中应力集中的处理方法理论上可以证明，如果插值函数使用了“协调和完整的位移函数”，则当网格尺寸逐渐减小而单元数量增加时，解就会单调收敛。

而且，当单元数目增加时，得到的刚度会降低，并收敛于真实刚度；这就意味着，当单元增加时，得到的位移增加，而收敛于精确位移解。

其图形如下：这里所说的“协调和完整位移函数”，是指：1.近似函数式一般是多项式。

2.近似函数在单元内要保持连续。

3.近似函数应提供单元间的连续性，包括离散单元每一个节点所有自由度都应该是连续的，二维单元和三维单元沿着公共边界线和公共面必须是连续的。

既能够保证单元内的连续，又能够保证单元间的连续的形函数称为协调函数。

4.近似函数应考虑刚体位移和单元内的常应变状态。

即有常数项保证刚体运动（无应变的运动），而有一次项保证有常应变状态发生。

这是形函数的完整性问题。

例如，对于一维单元而言，若取形函数则同时满足上面四个条件，称为协调且完整的位移函数。

一般来说，我们所用的单元使用的位移函数都满足上述四个条件，所以从理论上来说，只要网格加密，就可以收敛于真实解。

为了验证上述理论的真实性，我们选用了一个材料力学中的例子来做仿真。

该例子如下使用材料力学的理论进行求解，简要过程如下使用ANSYS进行分析，使用BEAM188单元，首先创建如图所示的几何模型然后分别对各段直线加密网格划分，得到的结果如下上表中，第一列是划分的单元数，第二列是最大的压应力，第三列是最大的拉应力。

可以看到，随着单元数目的增加，最大拉伸，压缩应力的绝对值都在增加。

从材料力学得到的精确解，最大的压应力是-46.2MPa, 最大的拉应力是28. 8MPa。

这样，当单元数增加到64个时，压应力的误差是（46.2-45.7）/46.2 = 1.1%; 拉应力的精度是（28.8-28.6)/28.8=0.7%.此时精度已经相当高了。

可以明显的看出，随着单元数目的增加，应力解的确是在逐渐逼近真实解。

有限元分析报告1. 引言有限元分析（Finite Element Analysis）是一种数值计算方法，用于求解工程和科学领域中的复杂问题。

它利用离散化技术将连续问题转化为离散问题，并应用数值算法进行求解。

本报告将主要介绍有限元分析的基本原理、应用和分析结果。

2. 有限元分析基本原理有限元分析的基本原理是将求解区域划分为互不重叠的有限个小单元，并将问题转化为在每个小单元内求解。

这些小单元通常为简单的几何形状，如三角形或四边形。

然后，在每个小单元内应用适当的数学模型和力学方程，得到相应的微分方程。

接着，通过对每个小单元的微分方程进行积分，并利用边界条件和连续性条件，得到整个求解区域的离散形式。

最后，通过求解离散形式的方程组，得到整个系统的解。

3. 有限元分析应用有限元分析在工程领域有着广泛的应用。

以下是几个典型的应用案例：3.1 结构分析有限元分析在结构分析中的应用非常广泛，可以用于确定结构的强度和刚度，评估结构的安全性，并进行结构优化设计。

通过对结构施加正确的边界条件和加载条件，可以得到结构的应力、应变和变形等重要信息。

3.2 流体力学分析有限元分析在流体力学分析中的应用可以用于模拟流体的流动和传热过程，例如气体和液体的流动、传热设备的设计优化等。

通过分析流体系统的流速、压力和温度等参数，可以对流体系统的性能和行为进行合理评估。

3.3 热力学分析有限元分析在热力学分析中的应用可以用于分析和优化热传导、热辐射和热对流等热问题。

通过模拟物体的温度分布和热流动，可以评估物体的热性能和热耗散效果。

4. 有限元分析结果有限元分析的计算结果可以提供丰富的信息，帮助工程师和科学家理解和优化系统的行为和性能。

以下是一些常见的有限元分析结果：4.1 应力分布通过有限元分析，可以得到结构或部件内的应力分布情况。

这对于评估结构的强度和安全性非常重要，并可以指导优化设计。

4.2 变形分析有限元分析可以给出结构或部件的变形情况。

第十一章 有限元分析方法概述1、基本概念有限元分析方法是随着电子计算机的发展而迅速发展起来的一种现代没计计算方法。

它是20世纪50年代首先在连续体力学领域—飞机结构静、动态特性分析中应用的一种有效的数值分析方法，随后很快就广泛地应用于求解热传导、电磁场、流体力学等连续性问题。

在工程分析和科学研究中，常常会遇到大量的由常微分方程、偏微分方程及相应的边界条件描述的场问题，如位移场、应力场和温度场等问题。

求解这类场问题的方法主要有两种：用解析法求得精确解；用数值解法求其近似解。

应该指出，能用解析法求出精确解的只是方程性质比较简单且几何边界相当规则的少数问题。

而对于绝大多数问题，则很少能得出解析解。

这就需要研究它的数值解法，以求出近似解。

目前工程中实用的数值解法主要有三种：有限差分法、有限元法和边界元法。

其中，以有限元法通用性最好，解题效率高，目前在工程中的应用最为广泛。

下面通过一个具体例子，分别采用解析法和数值解法进行求解，从而体会一下有限元分析方法的含义及其相关的一些基本概念。

如下图所示为一变横截面杆，杆的一端固定，另一端承受负荷P ，试求杆沿长度方向任一截面的变形大小。

其中，杆的上边宽度为1w ，下边宽度为2w ，厚度为t ，长度为L ，杆的材料弹性模量为E 。

已知P ＝4450N ，1w ＝50mm ，2w =25mm ，t =3mm ，L =250mm ，E =72GPa 。

① 采用解析法精确求解假设杆任一横截面面积为)(y A ，其上平均应力为σ，应变为ε。

根据静力平衡条件有：0)(=-y A P σ根据虎克定律有：εσE =而任一横截面面积为：t y L w w w y A )()(121-+= 任一横截面产生的应变为：dydu=ε将上述方程代入静力平衡条件，进行变换后有：dy y EA Pdu )(=沿杆的长度方向对上式两边进行积分，可得：⎰⎰⎰-+==y yudy y Lw w w Et P dy y EA P du 01210)()(将)(y A 表达式代入上式，并对两边进行积分，得杆沿长度方向任一横截面的变形量：]ln )[ln()()(112112w y Lw w w w w Et PL y u --+-=当y 分别取0、62.5、125、187.5、250值时，变截面杆相应横截面处的沿杆长方向的变形量分别为：m u m u m u m u m u 6564636211080.142 ;1083.96 ;1027.59 ;1051.27 ;0----⨯=⨯=⨯=⨯==② 采用数值解法近似求解将变横截面杆沿长度方向分成独立的4小段，每一小段采用等截面直杆近似，等截面直杆的横截面面积为相应的变截面杆横截面面积的平均面积表示，每一小段称为一个单元，小段之间通过节点连接起来。

应力集中系数的计算应力集中系数（Stress Concentration Factor，SCF）是指实际零件受力时，应力场的非均匀性程度。

当零件周围存在几何不连续性、孔洞或裂纹等应力集中因素时，这些因素会导致局部应力显著增加，从而导致零件更容易发生破坏。

要计算应力集中系数，通常需要进行有限元分析或使用解析方法。

下面将介绍几种常用的计算方法。

1. 平均法（Average Stress Method）：平均法是应力集中系数计算中最简单的方法之一、它假设零件在受力时，应力在截面上是均匀分布的，忽略了应力集中的影响。

通过比较零件在应力集中位置和无应力集中位置的应力值，计算平均法系数（Kavg）。

该系数一般取平均应力与未集中应力之比。

2. 直接法（Direct Stress Method）：直接法是一种比较精确的计算方法，它通过在应力集中位置附近布置不同几何形状的有限元模型，通过有限元分析得到实际的应力分布。

直接法可以考虑几何不连续性、孔洞或裂纹等因素对应力集中的影响，并计算出准确的应力集中系数。

3. 极限法（Limit Load Method）：极限法是一种适用于计算裂纹局部应力集中系数的方法。

它首先确定零件的极限载荷，然后在应力集中位置附近布置不同几何形状的有限元模型，使用有限元分析计算出该载荷下的应力分布。

然后，将计算出的应力与零件的极限强度进行比较，得到极限应力集中系数。

实际工程中，除了上述方法外，还有一些经验公式和图表可以用来估算应力集中系数。

这些经验公式和图表通常基于实验数据的统计分析，并可以在设计初期提供快速估算应力集中系数的方法。

在进行应力集中系数的计算时，需要注意以下几点：1.根据具体的几何形状和应力集中位置选择合适的计算方法，以得到准确的应力集中系数。

2.在进行有限元分析时，需要注意选择合适的网格密度和边界条件，以保证计算结果的准确性。

3.应力集中系数通常是根据理想化的条件计算得出的，实际零件的行为可能会受到其他因素的影响，如材料的非线性、温度变化等。