七年级数学 平行线的判定与性质单元练习

平行线的判定与性质的综合应用 一、应用题 1．如图所示，已知∠1+∠2= 180°．∠DEF= ∠A. (1)试判断DE与AC的位置关系，并说明理由； (2)若∠A= 60°，∠ACD= 35°，求∠1的度数．

2．如图所示，点B、C在线段AD的异侧，点E、F分别是线段AB、CD上的点，已知∠AEG= ∠AGE，∠DCG= ∠DGC. (1)求证：AB∥CD； (2)若∠AGE+∠AHF= 180°，且∠BFC-30°= 2∠C，求∠B的度数，

3.如图所示，AB∥CD，直线EF分别与AB、CD相交于M、N，∠AME= 60°． (1)求∠DNF的度数； (2)若∠P= 90°，∠2= ∠6=60°，求证：MP平分∠BMN． 4．如图所示，B、C、E三点在同一条直线上，A、F、E三点在同一条直线上，AB∥CD，∠1=∠2，∠3= ∠4. (1)试判断AD与BE是否平行，说说你的理由； (2)若∠1= 46°，∠4= 75°，求∠ABC的度数．

5．如图所示，已知∠1= ∠BDC．∠2+∠3=180°. (1)请你判断AD与EC的位置关系，并说明理由； (2)若DA平分∠BDC，CE⊥FA交FA的延长线于E，∠1= 70°，试求∠FAB的度数．

6.已知，如图所示，四边形ABCD中，∠B=∠D=90°，AE平分∠DAB，AE∥CF. (1)求证：CE平分∠BCD； (2)作△ADE的高DM，若AD=8，DE=6,AE=10，求DM的长.

7．如图所示，AD∥BC，∠EAD=∠C． (1)试判断AE与CD的位置关系，并说明理由； (2)若∠FEC= ∠BAE，∠EFC= 50°，求∠B的度数．

8.【问题情境】 我们知道“两条平行线被第三条直线所截，同位角相等，内错角相等，同旁内角互补”，所以在某些探究性问题中通过“构造平行线”可以起到转化的作用． 已知三角板ABC中，∠BAC= 60°，∠B= 30°，∠BCA= 90°，长方形DEFG中，DE∥GF. 【问题初探】 (1)如图①所示，若将三角板ABC的顶点A放在长方形的边GF上，BC与DE相交于点M，AB⊥DE于点M，求∠EMC的度数． 分析：过点C作CH∥GF，则CH∥DE∥GF，从而得∠CAF= ∠HCA，∠EMC= ∠BCH，从而可以求得∠EMC的度数， 根据分析，请你直接写出：∠CAF的度数为 ，∠EMC的度数为 ； 【类比再探】 (2)若将三角板ABC按图②所示的方式摆放（AB与DE不垂直），请你猜想∠CAF与∠EMC的数量关系，并说明理由.

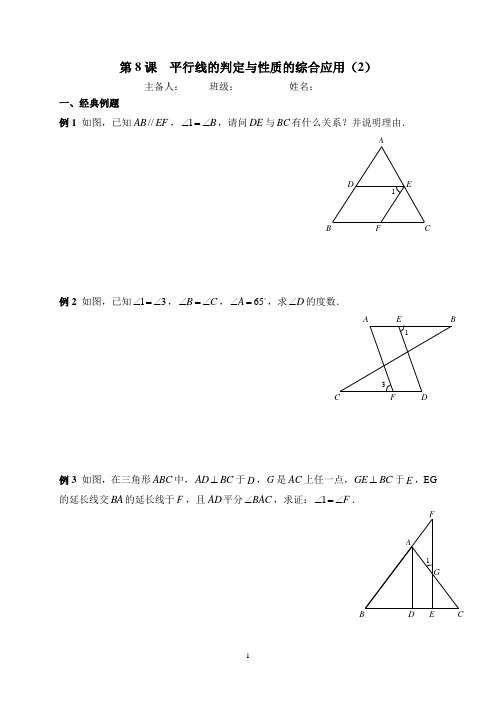
第8课 平行线的判定与性质的综合应用（2）主备人： 班级：________ 姓名：_________一、经典例题例1 如图，已知//AB EF ，1B ∠=∠，请问DE 与BC 有什么关系？并说明理由．例2 如图，已知13∠=∠，B C ∠=∠，65A ∠=，求D ∠的度数．例3 如图，在三角形ABC 中，AD BC ⊥于D ，G 是AC 上任一点，GE BC ⊥于E ，EG 的延长线交BA 的延长线于F ，且AD 平分BAC ∠，求证：1F ∠=∠．F EDCB A13F EDC BA 1GF E D CB A1三、课外练习1、如图，已知170∠=，270∠=，360∠=，求∠4的度数。

2、（画图） 如图，//AB CD ，直线EF 分别交AB 、CD 于E 、F ，EG 平分BEF ∠．若176∠=，求2∠的度数．3、如图，已知12∠=∠，370∠=，EG 平分FEH ∠，求∠FEG 的度数dcba4321G2F EDCBA 1HG32F EDCBA15、如图，BD 平分ABC ∠，且2D ∠=∠，求证：A ACD ∠=∠．6、如图，已知//AB CE ，1C ∠=∠，375∠=，求4∠的度数．2EDC B A1432FED C BA17、如图，在四边形ABCD 中，AD//BC ，点P 是DC 上一点，点P 在DC 上移动时，是否总是有∠DAP+APD=∠C ，为什么？★ 预习新知：P21—P22 §5.4 《命题、定理、证明》1、如图，直线a 、b 被直线c 所截，若要//a b ，需增加条件_____________________． （填一个即可）第1题图 第2题图2、填写推理过程和推理根据：如图，（1）若12∠=∠，则_____//_____（______________________________________） 若180A ABC ∠+∠=，则_____//_____（______________________________________） （2）若_____//_____，则180C ABC ∠+∠=（___________________________________） 若_____//_____，则3C ∠=∠（___________________________________）cba 4321D CBA321。

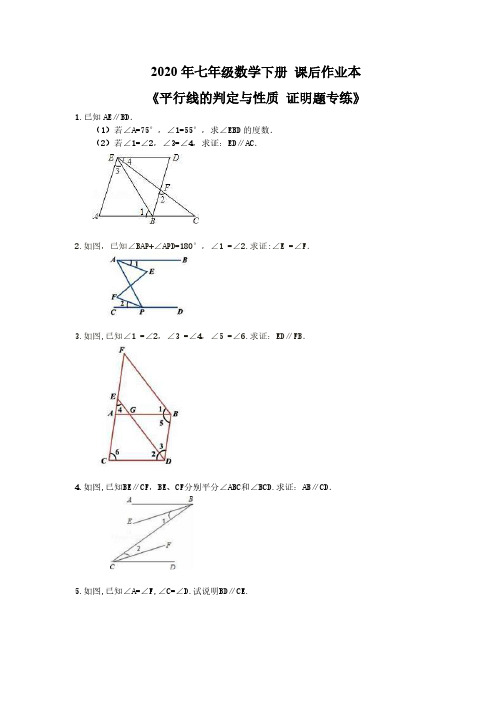
2020年七年级数学下册 课后作业本《平行线的判定与性质 证明题专练》1.已知AE∥BD．（1）若∠A=75°，∠1=55°，求∠EBD的度数．（2）若∠1=∠2，∠3=∠4，求证：ED∥AC．

2.如图，已知∠BAP+∠APD=180°，∠1 =∠2.求证:∠E =∠F．

3.如图,已知∠1 =∠2，∠3 =∠4，∠5 =∠6.求证：ED∥FB．

4.如图,已知BE∥CF，BE、CF分别平分∠ABC和∠BCD.求证：AB∥CD．

5.如图,已知∠A=∠F,∠C=∠D.试说明BD∥CE. 6.如图,已知∠1=250,∠2=450, ∠3=300，∠4=100.求证:AB//CD.7.如图，已知AB∥CD，∠ABE和∠CDE的平分线相交于F，∠E = 140º，求∠BFD的度数.

8.如图,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC．求∠PAG的度数．

9.如图1，AB∥CD，EOF是直线AB、CD间的一条折线.（1）说明：∠O=∠BEO+∠DFO. （2）如果将折一次改为折二次，如图-2，则∠BEO、∠O、∠P、∠PFC会满足怎样的关系，证明你的结论.

10.（1）如图1，已知任意三角形ABC，过点C作DE∥AB，求证：∠DCA=∠A；（2）如图1，求证：三角形ABC的三个内角（即∠A，∠B，∠ACB）之和等于180°；（3）如图2，求证：∠AGF=∠AEF＋∠F；（4）如图3，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=150°，求∠F的度数.参考答案1.（1）解：∵AE∥BD，∴∠A+∠1+∠EBD=180°，∵∠A=75°，∠1=55°，∴∠EBD=50°；（2）证明：∵AE∥BD，∴∠3=∠EBD，∵∠1=∠2，∠2=∠EBD+∠BAF，∠3=∠4，∴∠1=∠DEB，∴ED∥AC．

2.证明：∵ ∠BAP+∠APD = 180°，∴ AB∥CD.∴ ∠BAP =∠APC. 又∵ ∠1 =∠2,∴ ∠BAP-∠1 =∠APC-∠2. 即∠EAP =∠APF.∴ AE∥FP.∴ ∠E =∠F.

七上数学每日一练：平行线的判定与性质练习题及答案_2020年压轴题版答案解析答案解析2020年七上数学：图形的性质_相交线与平行线_平行线的判定与性质练习题1.(2020洛宁.七上期末) 如图，在△ABC 中，点E 、H 在BC 上，EF ⊥AB ，HD ⊥AB ，垂足分别是F 、D ，点G 在AC 上，∠AGD＝∠ACB ，试说明∠1+∠2＝180°.考点： 垂线;平行线的判定与性质;2.(2020南召.七上期末) 问题情景：如图1，AB ∥CD ，∠PAB=130°，∠PCD=120°，求∠APC 的度数．（1） 数学活动小组经过讨论形成下列推理，请你补全推理依据．如图2，过点P 作PE ∥AB ，∵PE ∥AB(作图知)又∵AB ∥CD ，∴PE ∥CD ．∴∠A+∠APE=180°．∠C+∠CPE=180°．∵∠PAB=130°，∠PCD=120°，∴∠APE=50°，∠CPE=60°∴∠APC=∠APE+∠CPE=110°．（2） 如图3，AD ∥BC ，当点P 在A 、B 两点之间运动时，∠ADP=α，∠BCP=β，求∠CPD 与α、β之间有何数量关系？请说明理由．（3） 在（2）的条件下，如果点P 在A 、B 两点外侧运动时（点P 与点A 、B 、O 三点不重合），请你直接写出∠CPD 与α、β之间的数量关系．考点： 平行线的判定与性质;3.(2019南岗.七上期末) 已知：点A 在射线CE 上，∠C ＝∠D ．给出了这道题的解题过程，请完成下面的解题过程，并填空（理由或数学式）：E EF AB（2）（探究）当点E在如图②的位置时，其他条件不变，试说明∠（3）（应用）点E、F、G在直线答案解析答案解析若∠EFG ＝36°，则∠BAE+∠AEF+∠FGC+∠DCG ＝°．考点： 平行线的判定与性质;5.(2018商水.七上期末) 如图，CD ∥AB ，∠DCB=70°，∠CBF=20°，∠EFB=130°，（1） 问直线EF 与AB 有怎样的位置关系？加以证明；（2） 若∠CEF=70°，求∠ACB 的度数．考点： 平行线的判定与性质;2020年七上数学：图形的性质_相交线与平行线_平行线的判定与性质练习题答案1.答案：2.答案：3.答案：4.答案：5.答案：。