小学六年级数学公式大全教学提纲

学习整理收集于网络，仅供参考小学六年级数学公式大全整理小学六年级数学公式大全涵盖了多个方面，包括几何图形的周长、面积和体积计算，单位换算，以及基本的数量关系等。

以下是一些主要公式和概念的整理：一、几何图形相关公式1. 长方形周长：C = (a + b) × 2面积：S = a × b其中，a为长，b为宽。

2. 正方形周长：C = 4a面积：S = a^2其中，a为边长。

3. 三角形周长：三条边之和面积：S = (底×高) ÷ 2内角和：180度4. 平行四边形面积：S = 底×高5. 梯形面积：S = (上底 + 下底) ×高÷ 26. 圆直径：d = 2r半径：r = d ÷ 2周长（圆周）：C = πd = 2πr面积：S = πr^27. 长方体底面积：长×宽表面积：(长×宽 + 长×高 + 宽×高) × 2体积：V = 长×宽×高8. 正方体棱长总和：12a表面积：6a^2体积：V = a^39. 圆柱体侧面积：底面周长×高 = 2πrh表面积：侧面积 + 2个底面面积 = 2πrh + 2πr^2体积：V = 底面积×高 = πr^2h10. 圆锥体体积：V = (1/3) ×底面积×高 = (1/3)πr^2h二、单位换算1、长度单位：1公里 = 1千米 = 1000米，1米 = 10分米 = 100厘米 = 1000毫米2、面积单位：1平方米 = 100平方分米 = 10000平方厘米 = 1000000平方毫米，1公顷 = 10000平方米3、体积单位：1立方米 = 1000立方分米 = 1000000立方厘米 = 1000000000立方毫米，1升 = 1立方分米 = 1000毫升4、重量单位：1吨 = 1000千克 = 1000000克 = 1000公斤 = 2000市斤5、时间单位：1世纪 = 100年，1年 = 12月，1日 = 24小时，1小时 = 60分钟 = 3600秒6、货币单位：1元 = 10角 = 100分三、数量关系速度、时间、路程：速度×时间 = 路程单价、数量、总价：单价×数量 = 总价工作效率、工作时间、工作总量：工作效率×工作时间 = 工作总量四、其他常用公式利息：利息 = 本金×利率×时间利润：利润 = 售价 - 成本利润率：利润率 = (利润÷成本) × 100%这些公式和概念是小学六年级数学学习中的重要内容，掌握它们对于解决实际问题具有重要意义。

六年级数学常用公式大全一、几何图形相关公式1. 长方形-周长=（长+ 宽）×2，即C = 2×(a + b)，其中C 表示周长，a 表示长，b 表示宽。

-面积= 长×宽，即S = a×b。

2. 正方形-周长= 边长×4，即C = 4a，其中C 表示周长，a 表示边长。

-面积= 边长×边长，即S = a×a = a²。

3. 三角形-面积= 底×高÷2，即S = a×h÷2，其中S 表示面积，a 表示底，h 表示高。

-三角形内角和为180°。

4. 平行四边形-面积= 底×高，即S = a×h，其中S 表示面积，a 表示底，h 表示高。

5. 梯形-面积=（上底+ 下底）×高÷2，即S = (a + b)×h÷2，其中S 表示面积，a表示上底，b 表示下底，h 表示高。

6. 圆-周长= 2×π×半径，即C = 2πr，其中C 表示周长，r 表示半径，π通常取3.14。

-面积= π×半径×半径，即S = πr²。

二、立体图形相关公式1. 长方体-表面积=（长×宽+ 长×高+ 宽×高）×2，即S = 2×(ab + ah + bh)，其中S 表示表面积，a 表示长，b 表示宽，h 表示高。

-体积= 长×宽×高，即V = a×b×h。

2. 正方体-表面积= 边长×边长×6，即S = 6a²，其中S 表示表面积，a 表示边长。

-体积= 边长×边长×边长，即V = a³。

3. 圆柱-侧面积= 底面圆周长×高，即S_{侧}= 2πrh，其中S_{侧}表示侧面积，r 表示底面半径，h 表示高。

小学6年级数学教学大纲第一篇：小学6年级数学教学大纲小学六年级数学教学大纲教学内容(每周5课时)(一)数与计算(1)分数的乘法和除法。

分数乘法的意义。

分数乘法。

乘法的运算定律推广到分数。

倒数。

分数除法的意义。

分数除法。

(2)分数四则混合运算。

分数四则混合运算。

(3)百分数。

百分数的意义和写法。

百分数和分数、小数的互化。

(二)比和比例比的意义和性质。

比例的意义和基本性质。

解比例。

成正比例的量和成反比例的量。

(三)几何初步知识圆的认识。

圆周率。

画圆。

圆的周长和面积。

*扇形的认识。

轴对称图形的初步认识。

圆柱的认识。

圆柱的表面积和体积。

圆锥的认识。

圆锥的体积。

球和球的半径、直径的初步认识。

(四)统计初步知识统计表。

条形统计图，折线统计图，*扇形统计图。

(五)应用题分数四则应用题(包括工程问题)。

百分数的实际应用(包括发芽率、合格率、利率、税率等的计算)。

比例尺。

按比例分配。

(六)实践活动联系学生所接触到的社会情况组织活动。

例如就家中的卧室，画一个平面图。

(七)整理和复习教学要求1.理解分数乘、除法的意义。

掌握分数乘、除法的计算法则。

会计算分数乘、除法。

会口算简单的分数乘、除法。

会进行分数四则混合运算（不超过三步）。

2.理解百分数的意义。

知道百分数在实际中的应用。

会进行有关百分数的计算。

3.理解比的意义和性质。

会求比值和化简比。

理解比例的意义和基本性质。

会解比例。

理解正、反比例的意义。

会判断两个量是否成正比例或反比例。

通过比例的教学，使学生进一步受到辩证唯物主义观点的启蒙教育。

4.认识圆。

会画圆。

掌握圆的周长和圆面积的计算公式。

通过介绍圆周率的史料，使学生受到爱国主义教育。

5.认识圆柱和圆锥。

会计算圆柱的表面积和圆柱、圆锥的体积。

6.会制作简单的统计表，利用作图纸绘制简单的统计图。

会对统计图表进行一些简单的分析，使学生受到国情教育。

绘制统计图表要注意整洁、美观。

7.会解答分数、百分数应用题(最多不超过两步)。

小学六年级数学上册知识点汇总贵州省台江县城关二小 熊 黎第一单元：位置1、用数对确定物体的位置要用到两个数据，第一个数表示列，第二个数表示行。

例如：(3，5)表示(第三列，第五行)2、确定一个点的位置，应该先看下边的数字，再看左边的数字，中间用逗号隔开。

第二单元 分数乘法一、分数乘法的意义和小数乘法一样也有两种：1、分数乘整数的意义（与整数乘法的意义相同）都是求几个相同加数的和的简便运算。

例如：43×5表示求5个43的和是多少? 或 43的5倍是多少？）2、一个数乘分数的意义 一个数乘分数是求一个数的几分之几是多少。

例如：5×43表示求5的43是多少。

二、分数乘法的计算法则：1、分数乘整数：分母不变，分子与整数相乘的积做分子。

(能约分的拿整数和分母约分)2、分数乘分数：用分子相乘的积做分子，分母相乘的积做分母。

（为了计算简便，能约分的要先约分，再计算。

）注意：有带分数时，要先把带分数化成假分数再进行计算。

有小数时，要先把小数化成最简分数再进行计算。

四、整数乘法的交换律、结合律和分配律，对于分数乘法也同样适用。

乘法交换律： a × b = b × a 乘法结合律： ( a × b )×c = a × ( b × c ) 乘法分配律： ( a + b )×c = a×c + b×c 或 a×c + b×c =( a + b )×c三、倒数1、倒数的意义： 乘积是1的两个数互为倒数。

1的倒数是1; 0没有倒数。

注意：互为倒数是指：倒数是两个数的关系，它们互相依存，倒数不能单独存在。

(要说清谁是谁的倒数)。

2、求一个数的倒数的方法：(1)、求分数的倒数：直接交换分子分母的位置。

(2)、求整数的倒数：把整数看做分母是1的分数，再交换分子分母的位置。

(3)、求带分数的倒数：把带分数化为假分数，再交换分子分母的位置。

小学六年级上册数学公式详细整理汇总一、用字母表示运算定律或性质加法交换律: a+b=b+a加法结合律: (a+b)+c=a+(b+c)乘法交换律: ab=ba乘法结合律:(ab)c=a(bc)乘法分配律:a(b+c)=ab+ac二、几何图形计算公式(1)周长:即围绕物体一周的长度。

①长方形周长=(长+宽)×2 C=(a+b)×2②正方形周长=边长×4 C=4a③圆的周长=圆周率×直径=圆周率×半径×2 C=πd C =2πr(2)面积:即物体的表面或封闭图形的大小①长方形的面积=长×宽S=ab②正方形的面积=边长×边长S=a?a=a2③平行四边形的面积=底×高S=ah④三角形的面积=底×高÷2 S=ah÷2⑤梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷2⑥圆的面积=圆周率×半径S=πr2⑦直径d=2r 半径=直径÷2 r= d÷2⑧环形面积=外圆面积-内圆面积S环=S外-S内【相互联系】平面图形的面积公式是以长方形面积计算公式为基础的。

如两个完全相同的三角形、梯形可拼成一个平行四边形。

圆拼成长方形的长时1/2C,宽是R.(3)表面积:立体图形的所有面的面积之和叫做它的表面积①长方体的表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)②正方体的表面积=棱长×棱长×6 S=a×a×6 =6a2③圆柱体的侧面积=底面周长×高S=Ch =2πrh④圆柱体的表面积=侧面积+底面积×2 S= Ch+2πr2 = 2πrh+2πr2 注意:圆柱的底面周长与高相等时侧面展开是正方形，C=h 2πr=h(4)体积:物体所占空间的大小叫体积①长方体的体积=长×宽×高V=abh②正方体的体积=棱长×棱长×棱长V=a×a×a=a3③圆柱的体积=底面积×高V=sh=πr2h④圆锥的体积=底面积×高÷3 V=1/3sh= 1/3πr2h 【相互联系】长方体、正方体和圆柱体的体积公式可统一成:V=sh即底面积×高.。

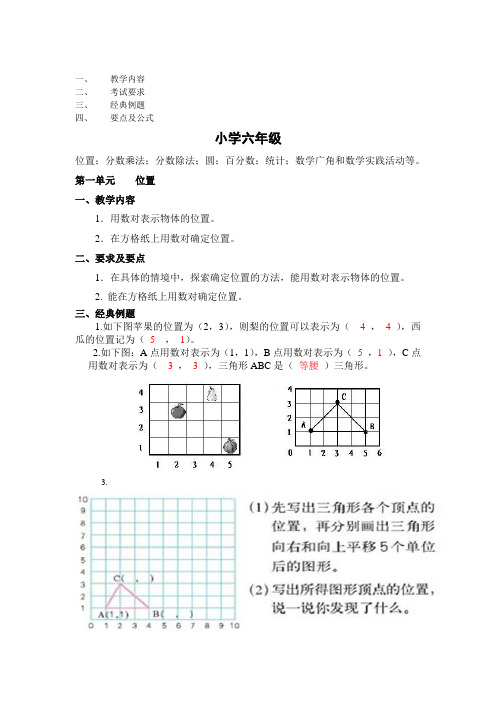
一、教学内容二、考试要求三、经典例题四、要点及公式小学六年级位置；分数乘法；分数除法；圆；百分数；统计；数学广角和数学实践活动等。

第一单元位置一、教学内容1．用数对表示物体的位置。

2．在方格纸上用数对确定位置。

二、要求及要点1．在具体的情境中，探索确定位置的方法，能用数对表示物体的位置。

2. 能在方格纸上用数对确定位置。

三、经典例题1.如下图苹果的位置为（2，3），则梨的位置可以表示为（ 4 ，4 ），西瓜的位置记为（ 5 ，1）。

2.如下图：A点用数对表示为（1，1），B点用数对表示为（5，1），C点用数对表示为（3，3），三角形ABC是（等腰）三角形。

3.第二单元 分数乘法一、 教学内容掌握分数乘法的意义；分数乘法；乘法的运算定律推广到分数；倒数；分数乘法、解决问题和倒数。

二、考试要求1．理解并掌握分数乘法的计算法则，会进行分数乘法的计算。

2．理解乘法运算定律对于分数乘法同样适用，并会应用这些运算定律进行一些简便计算。

3．理解倒数的意义，掌握求倒数的方法。

4．会运用分数乘法解决一些简单的实际问题，体会数学与日常生活的联系。

三、经典例题1.今年妈妈36岁，小明年龄是妈妈的31。

小明今年多少岁？ 答：单位1为：小明妈妈的年龄36岁小明年龄为：36×31=12（岁） 难题： 1.某班有45人，在一次语文数学双科测试中，每人至少有一科得优，已知语文得优的占全班同学的五分之三数学得优的占全班同学的三分之二，双科都得优的有多少人？答： 45×（3/5+2/3-1）=12人2.某车间计划一个月生产农具1200件，上半个月完成计划的三分之二，下半个月再生产多少件就超产计划的五分之一？？？答： 1200×（1+1/5-2/3）=640（件）3.商店运来一批服装，分为男装、女装和童装，公450套，其中3分之1是女装，剩下的五分之一是男装，那么运进童装有多少套？？？答： 女装有450×1/3=150（套）男装有（450-150）×1/5=60（套）运进的童装 450-150-60=240（套）4.一本故事书有140页，小红第一天读了全书的七分之一，第二天读了余下的六分之一，第三天因从第几页读起？答： 第一天读了 140×1/7=20页第二天读了 （140-20）×1/6=20页第三天从41页读起。

一、方程1、数量关系小强的年龄×3 + 4 岁 = 小强爸爸的年龄小瓶的容量×4 - 0.9升 = 大瓶的容量三角形的面积=底×高÷2长方形的周长=（长+宽）×2梯形的面积=（上底+下底）×高÷2速度和×相遇时间=总路程小华走的路程 + 小明走的路程 = 甲、乙两地之间的路程3个排球的价钱+营业员找回的钱=付给营业员的钱华氏温度（°F ）=摄氏温度(°C )×1.8+32二、长方体和正方体1、两个面相交的线叫做棱，三条棱相交的点叫做顶点。

2、长方体相交于同一顶点的三条棱的长度，分别叫做它的长、宽、高。

长方体的12条棱有3组，每组的四条棱长度相等。

长方体的棱长总和=长×4+宽×4+高×4=（长+宽+高）×4长方体放桌面上，最多只能看到3个面。

3、正方体的展开1）．“141型”，中间一行4个图：作侧面，上下两个各作为上下底面，•共有6种基本图形。

2）．“231型”，中间3个作侧面，共3种基本图形。

见上图3）．“222”型，两行只能有1个正方形相连。

4）．“33”型，两行只能有1个正方形相连。

4、长方体的表面积就是长方体六个面的总面积。

由于相对的面完全相同，所以可以先求出前面、后面和下面三个面的面积，再乘以2，就可以求出表面积了。

长方体的表面积= 长×宽×2+长×高×2+宽×高×2=（长×宽+长×高+宽×高）×2正方体的六个面完全相同，所以计算时只要算出其中的一个面，再乘6就可以了。

正方体的表面积= 棱长×棱长×65、在解决一些问题时，要充分考虑实际情况，想清楚要算几个面。

在解答时，可以把这几个面的面积分别算出来，再相加，也可以先算出六个面的面积总和，再减去不需要的那个（些）面。

小学六年级数学毕业总复习公式大全一、图形计算公式1、正方形 C：周长 S：面积 a：边长周长＝边长×4 C=4a面积=边长×边长S=a×a2、长方形 C：周长 S：面积 a：边长周长=长+宽×2 C=2a+b长=周长÷2－宽 a= C÷2－b面积=长×宽 S=ab长=面积÷宽 a= S÷b3、三角形 S：面积 a：底 h：高面积=底×高÷2 S=ah÷2三角形高=面积×2÷底 h= S×2÷a三角形底=面积×2÷高 a =S×2÷h三角形内角和：180度4、平行四边形 S：面积 a：底 h：高面积=底×高 S=ah底=面积÷高 a= S÷h5、梯形 S：面积 a：上底 b：下底 h：高面积=上底+下底×高÷2 s=a+b× h÷2高=面积×2÷上底+下底 h =S×2÷a+b上底=面积×2÷高－下底 a=S×2÷h- b6、圆形 S：面积 C：周长л d=直径 r=半径1周长=直径×π=2×π×半径C=πd=2πr 2面积=半径×半径×π S=πr27、正方体 V:体积 a:棱长表面积=棱长×棱长×6 S表= 6a2体积=棱长×棱长×棱长 V=a38、长方体V:体积 S:表面积 a:长 b: 宽 h:高1表面积长×宽+长×高+宽×高×2S=2ab+ah+bh2体积=长×宽×高 V=abh9、圆柱体 v:体积 h:高 S：面积r:底面半径 C:底面周长1侧面积=底面周长×高 S侧=Ch=2πr=πd2底面积=半径×半径×π S底=πr23表面积=侧面积+底面积×2S表= S侧+2S底=2πr+2πr24体积=底面积×高 V=S h h= V÷S S= V÷h5体积＝侧面积÷2×半径 V= S侧÷2×r 10、圆锥体 v:体积 h:高 s：底面积 r:底面半径体积=底面积×高×错误!V=Sh×错误! h= V×3÷S S= V×3÷h二、数量关系式1、加法加数＋加数＝和和－一个加数＝另一个加数2、减法被减数－减数＝差被减数－差＝减数差＋减数＝被减数3、乘法因数×因数＝积积÷一个因数＝另一个因数4、除法被除数÷除数＝商被除数÷商＝除数商×除数＝被除数5、份数每份数×份数＝总数总数÷每份数＝份数总数÷份数＝每份数6、倍数1倍数×倍数＝几倍数几倍数÷1倍数＝倍数几倍数÷倍数＝1倍数7、平均数问题：总数÷总份数＝平均数8、和差问题：和＋差÷2＝大数和－差÷2＝小数9、和倍问题：和÷倍数＋1＝1份数 1份数×倍数＝几份数10、差倍问题：差÷倍数－1＝1份数 1份数×倍数＝几份数11、行程问题：速度×时间＝路程路程÷速度＝时间路程÷时间＝速度12、相遇问题相遇路程＝速度和×相遇时间相遇时间＝相遇路程÷速度和速度和＝相遇路程÷相遇时间13、追及问题追及距离＝速度差×追及时间追及时间＝追及距离÷速度差速度差＝追及距离÷追及时间14、价钱问题：单价×数量＝总价总价÷单价＝数量总价÷数量＝单价15、工作问题：工作效率×工作时间＝工作总量工作总量÷工作效率＝工作时间工作总量÷工作时间＝工作效率16、工程问题：错误!=工作效率 1÷工作效率=工作时间17、年龄问题：年龄差永远不变18、植树问题：⑴两端都要植树棵数＝全长÷棵距＋1⑵一端植树及封闭线路上植树棵数＝全长÷棵距⑶两端都不植树棵数＝全长÷棵距－119、盈亏问题盈＋亏÷两次分配量之差＝参加分配的份数大盈－小盈÷两次分配量之差＝参加分配的份数大亏－小亏÷两次分配量之差＝参加分配的份数20、浓度问题溶质的重量＋溶剂的重量＝溶液的重量溶质的重量÷溶液的重量×100%＝浓度溶液的重量×浓度＝溶质的重量溶质的重量÷浓度＝溶液的重量21、利润与折扣问题利润＝售出价－成本利润率＝利润÷成本×100%＝售出价÷成本－1×100% 涨跌金额＝本金×涨跌百分比利息＝本金×利率×时间税后利息＝本金×利率×时间×1－20%22、百分率问题：部分量÷总量×100%=百分率三、常用单位换算1、长度单位：1公里=1千米 1千米=1000米1米=10分米 1分米=10厘米 1厘米=10毫米2、面积单位：1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米3、体积单位1立方米=1000立方分米1立方分米=1000立方厘米1立方厘米=1000立方毫米1升=1立方分米=1000毫升1毫升=1立方厘米4、重量单位1吨=1000千克1千克= 1000克= 1公斤= 2市斤5、人民币单位1元=10角 1角=10分 1元=100分6、时间单位1世纪=100年 1年=12月大月31天有:1\3\5\7\8\10\12月小月30天的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时 1时=60分1分=60秒 1时=3600秒四、运算定律及运算性质1、加法交换律：a + b = b + a2、加法结合律：a + b+c = a + b +c3、乘法交换律：a × b = b × a4、乘法结合律：a × b × c = a ×b × c5、乘法分配律：a × b + a × c = a ×b + c6、减法的性质：a - b - c = a -b＋ c6、除法的性质：a ÷ b ÷ c = a ÷b × c五、100以内的质数表100以内的质数有：2、3、5、7、11、13、17、19、 23、29、 31、37、41、43、47、 53、59、 61、67、71、73、79、 83、89、 97;六、π倍表。

精心整理小学数学六年级上册知识点及复习提纲第一单元分数乘法1.分数乘整数（第2页例1）分数乘整数的意义：分数乘整数表示求几个相同加数的和的简便×表示求的是多少？反之：的是多少？就用：×；×表示求的是多少？反之：2.8的是多少？就用：×。

3.分数乘分数的计算方法：分数乘分数，用分子乘分子的积作分子，用分母乘分母的积作分母。

4.分数乘法的简便计算（第5页例4）为了计算简便，可以先约分再乘。

5.分数乘小数（第8页例5）分数乘小数，可以把分数化成小数再乘，也可以把小数化成分数再乘，但一般采用把小数化成分数再乘，因为有些分数化不成有限小数。

6.分数混合运算（第8页例6）8.连续求一个数的几分之几是多少（连乘）（第13页例8）如：我班有36人，的同学喜欢打篮球，喜欢打乒乓球的人数是喜欢打篮球人数的。

我班有多少名同学喜欢打乒乓球？9.求比一个数多（或少）几分之几的数是多少（第14页例9）如：乙数是10，甲数比乙数多，甲数是多少？分析：把比字后面的乙数看成单位1，那甲数就是乙数的1+=，也就是甲数比乙数多可以理解为甲数是乙数的，根据求一个数的几分之几用乘法，得出关系式：甲数=乙数×，把乙数换成10，得甲数=10×。

25度，距离是400米。

一般情况下，“在”字左面是要确定的点，“在”字右面是观察点。

方向包括“东偏北，北偏东；南偏东，南偏西；西偏北，西偏南；北偏东，北偏西”八个“偏”，几度要看夹角，一般不超过45度。

当超过45度时，就要用90度减去这个度数，再把方向颠倒过来，如：北偏东，就要改成东偏北。

通常用小于45度的度数来描述。

距离要看比例尺，1厘米代表多长，有几个这样的长度，就用“段数×比例尺代表的长度=距离”。

2.根据方向和距离的描述，在图上确定某个点的位置（第20页三步法来画路线图。

第三单元分数除法1.倒数的认识:（第28页例1）乘积是1的两个数互为倒数。

小学数学图形计算公式1、正方形（C：周长S：面积a：边长）周长＝边长×4 C=4a 面积=边长×边长S=a×a2、正方体（V:体积a:棱长）表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长V=a×a×a3、长方形（C：周长S：面积a：边长）周长=(长+宽)×2 C=2(a+b) 面积=长×宽S=ab4、长方体（V:体积s:面积a:长b: 宽h:高）(1)表面积(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh) (2)体积=长×宽×高V=abh5、三角形（s：面积a：底h：高）面积=底×高÷2 s=ah÷2 三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形（s：面积a：底h：高）面积=底×高s=ah7、梯形（s：面积a：上底b：下底h：高）面积=(上底+下底)×高÷2 s=(a+b)× h÷28、圆形（S：面积C：周长л d=直径r=半径）(1)周长=直径×л=2×л×半径C=лd=2лr (2)面积=半径×半径×л9、圆柱体（v:体积h:高s：底面积r:底面半径c:底面周长）(1)侧面积=底面周长×高=ch(2лr或лd) (2)表面积=侧面积+底面积×2(3)体积=底面积×高（4）体积＝侧面积÷2×半径10、圆锥体（v:体积h:高s：底面积r:底面半径）体积=底面积×高÷311、总数÷总份数＝平均数12、和差问题的公式：(和＋差)÷2＝大数(和－差)÷2＝小数13、和倍问题：和÷(倍数－1)＝小数小数×倍数＝大数(或者和－小数＝大数)14、差倍问题：差÷(倍数－1)＝小数小数×倍数＝大数(或小数＋差＝大数)15、相遇问题相遇路程＝速度和×相遇时间；相遇时间＝相遇路程÷速度和；速度和＝相遇路程÷相遇时间16、浓度问题溶质的重量＋溶剂的重量＝溶液的重量溶质的重量÷溶液的重量×100%＝浓度溶液的重量×浓度＝溶质的重量溶质的重量÷浓度＝溶液的重量17、利润与折扣问题利润＝售出价－成本；利润率＝利润÷成本×100%＝(售出价÷成本－1)×100%涨跌金额＝本金×涨跌百分比；利息＝本金×利率×时间；税后利息＝本金×利率×时间×(1－20%)常用的数量关系式1、每份数×份数＝总数总数÷每份数＝份数总数÷份数＝每份数2、1倍数×倍数＝几倍数几倍数÷1倍数＝倍数几倍数÷倍数＝1倍数3、速度×时间＝路程路程÷速度＝时间路程÷时间＝速度4、单价×数量＝总价总价÷单价＝数量总价÷数量＝单价5、工作效率×工作时间＝工作总量工作总量÷工作效率＝工作时间工作总量÷工作时间＝工作效率6、加数＋加数＝和和－一个加数＝另一个加数7、被减数－减数＝差被减数－差＝减数差＋减数＝被减数8、因数×因数＝积积÷一个因数＝另一个因数9、被除数÷除数＝商被除数÷商＝除数商×除数＝被除数常用单位换算长度单位换算1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米面积单位换算：1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米体(容)积单位换算：1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升重量单位换算：1吨=1000 千克1千克=1000克1千克=1公斤人民币单位换算：1元=10角1角=10分1元=100分时间单位换算：1世纪=100年1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒基本概念第一章数和数的运算一概念（一）整数1 整数的意义：自然数和0都是整数。