最新人教版高中数学选修4-1《弦切角的性质》课后训练

【全程复习方略】2013-2014学年高中数学第二讲四弦切角的性质课时作业（含解析）新人教A版选修4-11．P在⊙O外，PM切⊙O于C，PAB交⊙O于A、B，则( )A．∠MCB＝∠B B．∠PAC＝∠PC．∠PCA＝∠B D．∠PAC＝∠BCA解析：选C.由弦切角定理知∠PCA＝∠B.2．已知AB为⊙O的直径，CD切⊙O于D，AB延长线交CD于点C，若∠CAD＝25°，则∠C 等于( )A．45° B．40°C．35° D．30°解析：选B.如图，连接BD，∵∠BDA＝90°.又∵CD为⊙O的切线，切点为D，由弦切角定理知∠BDC＝∠CAD＝25°.∴∠CDA＝90°＋25°＝115°.在△ACD中，∠C＝180°－∠A－∠CDA＝180°－25°－115°＝40°.3．如图，已知AB、AC与⊙O相切于B、C，∠A＝50°，点P是⊙O上异于B、C的一动点，则∠BPC的度数是( )A．65° B．115°C．65°或115° D．130°或50°4．如图，在圆内接四边形ABCD中，AC平分∠BAD，EF切⊙O于C点，那么图中与∠DCF相等的角的个数是( )A ．4B ．5C ．6D ．7解析：选B.∵EF 切⊙O 于点C ，∴∠DCF ＝∠CAD ＝∠CBD ，∠BCE ＝∠BAC ＝∠BDC.∵AC 平分∠BAD ，∴∠BAC ＝∠CAD.∴∠DCF ＝∠CAD ＝∠CBD ＝∠BCE ＝∠BAC ＝∠BDC.∴图中与∠DCF 相等的角有5个．5．如图，AB 是⊙O 的直径，EF 切⊙O 于C ，AD ⊥EF 于D ，AD ＝2，AB ＝6，则AC 的长为()A ．2B ．3C ．2 3D ．4解析：选C.连接BC ，则∠ACB ＝90°.∵AD ⊥EF ，∴∠ADC ＝90°. ∵EF 为⊙O 的切线，∴∠B ＝∠ACD.∴△ADC ∽△ACB.∴AD AC ＝ACAB ，即AC2＝AD·AB＝2×6＝12.∴AC ＝2 3.答案：45°135°45°90°7．已知AB是⊙O的直径，PB，PE分别切⊙O于B，C，若∠ACE＝40°，则∠P＝________.解析：连接BC.∵AB是⊙O的直径，PB切⊙O于B，∴∠ACB＝90°，∠ABP＝90°.又∠ACE＝40°，可求得∠PCB＝∠PBC＝50°，∴∠P＝80°.答案：80°8．如图，点P在圆O直径AB的延长线上，且PB＝OB＝2，PC切圆O于C点，CD⊥AB于D 点，则CD＝________.解析：连接OC.∵PC切⊙O于C点，∴OC⊥PC.∵PB＝OB＝2，OC＝2.∴PC＝2 3.∵OC·PC＝OP·CD，∴CD＝2×234＝ 3.答案： 39．如图，圆O 和圆O′相交于A ，B 两点，AC 是圆O′的切线，AD 是圆O 的切线，若BC ＝2，AB ＝4，求BD.解：∵AB 是弦，且AC 与圆O′相切于点A ，∴∠CAB ＝∠D ，∵AB 是弦，且AD 与圆O 相切于点A ，∴∠DAB ＝∠C ，∴△ABC ∽△DBA. ∴AB BD ＝BC AB ，∴BD ＝AB2BC ＝422＝8.10．如图，AB 是⊙O 的弦，CD 是经过⊙O 上的点M 的切线．求证：(1)如果AB ∥CD ，那么AM ＝MB ；(2)如果AM ＝BM ，那么AB ∥CD.证明：(1)CD 切⊙O 于M 点，∴∠DMB ＝∠A ，∠CMA ＝∠B.∵AB ∥CD ，∴∠CMA ＝∠A.∴∠A ＝∠B.∴AM ＝MB.(2)∵AM ＝BM ，∴∠A ＝∠B.∵CD 切⊙O 于M 点，∴∠CMA ＝∠B.∴∠CMA ＝∠A ，∴AB ∥CD.11．如图，已知AB 是⊙O 的直径，直线CD 与⊙O 相切于点C ，AC 平分∠DAB.(1)求证：AD ⊥CD ；(2)若AD ＝2，AC ＝5，求AB 的长．解：(1)证明：如图，连接BC.∵直线CD 与⊙O 相切于点C ，∴∠DCA ＝∠B.∵AC 平分∠DAB ，∴∠DAC ＝∠CAB.∴∠ADC ＝∠ACB.∵AB 为⊙O 的直径，∴∠ACB ＝90°.∴∠ADC ＝90°，即AD ⊥CD.(2)∵∠DCA ＝∠B ，∠DAC ＝∠CAB ，∴△ADC ∽△ACB.∴AD AC ＝AC AB， ∴AC2＝AD·AB.∵AD ＝2，AC ＝5，∴AB ＝52.。

课堂导学三点剖析一、弦切角定理【例】如图、切⊙于、,∠°,则∠等于()图°°°°思路分析：连结,∠与∠分别处于两个三角形,它们之间的联系途径就是弦切角. 解:连结.∵是弦、切圆于、,∴∠∠,∠∠.∴∠∠.在△中,∠(°∠)°,∴∠∠°.答案二、弦切角定理综合运用【例】如图切⊙于是⊙的割线,在上截取,求证:∠∠.图证明：∵,∴∠∠.∵∠∠∠,∠∠∠,∴∠∠∠∠.又∵切⊙于为弦,∴∠∠.∴∠∠.三、本节数学思想选讲【例】如图,已知为⊙直径为延长线上一动点,过点作⊙的切线,设切点为.()请你连结,作∠的平分线,交于点,测量∠的度数.()当在延长线上运动时,∠的度数作何变化?请你猜想,并证明.图解析:()作图,并测量,∠°.()∠不随在延长线上的位置变化而变化,即∠°是一个定值.证明:连结交于,∵∠是△的外角,∴∠∠∠.同理,∠∠∠.但∠∠.又∵是弦与⊙切于,∴∠∠.∴∠∠.∴.∵是直径,∴∠°.∴△是等腰直角三角形.∴∠°.各个击破类题演练如图,△为⊙的内接三角形为直径为延长线上一点切⊙于点,∠°,则∠等于()图°°°°解析:∵是直径,∴∠°.∴∠∠°,∠∠°.∵是切线为弦,∴∠∠.∴∠∠°.答案类题演练如图⊥直径为⊙切线为切点,求证:∠∠.图证明:连结,∵是直径,∴∠°.∴∠∠°.∵⊥,∴∠°.∴∠∠°.∴∠∠.又∵切⊙于是弦,∴∠∠.∴∠∠.类题演练在△中,∠的平分线与△的外接圆相交于,过作圆的切线.求证∥.。

1．P在⊙O外，PM切⊙O于C，PAB交⊙O于A、B，则( )A．∠MCB＝∠B B．∠PAC＝∠PC．∠PCA＝∠B D．∠PAC＝∠BCA解析：选C.由弦切角定理知∠PCA＝∠B.2．已知AB为⊙O的直径，CD切⊙O于D，AB延长线交CD于点C，若∠CAD＝25°，则∠C等于( )A．45°B．40°C．35°D．30°解析：选B.如图，连接BD，∵∠BDA＝90°.又∵CD为⊙O的切线，切点为D，由弦切角定理知∠BDC＝∠CAD＝25°.∴∠CDA＝90°＋25°＝115°.在△ACD中，∠C＝180°－∠A－∠CDA＝180°－25°－115°＝40°.3．如图，已知AB、AC与⊙O相切于B、C，∠A＝50°，点P是⊙O上异于B、C的一动点，则∠BPC的度数是( )A．65°B．115°C．65°或115°D．130°或50°4．如图，在圆内接四边形ABCD中，AC平分∠BAD，EF切⊙O于C点，那么图中与∠DCF 相等的角的个数是( )A．4 B．5C．6 D．7解析：选B.∵EF切⊙O于点C，∴∠DCF＝∠CAD＝∠CBD，∠BCE＝∠BAC＝∠BDC.∵AC平分∠BAD，∴∠BAC＝∠CAD.∴∠DCF＝∠CAD＝∠CBD＝∠BCE＝∠BAC＝∠BDC.∴图中与∠DCF相等的角有5个．5．如图，AB是⊙O的直径，EF切⊙O于C，AD⊥EF于D，AD＝2，AB＝6，则AC的长为( )A．2 B．3 C．2 3 D．4解析：选C.连接BC，则∠ACB＝90°. ∵AD⊥EF，∴∠ADC＝90°.∵EF为⊙O的切线，∴∠B＝∠ACD.∴△ADC∽△ACB.∴ADAC＝ACAB，即AC2＝AD·AB＝2×6＝12. ∴AC＝2 3.答案：45°135°45°90°7．已知AB是⊙O的直径，PB，PE分别切⊙O于B，C，若∠ACE＝40°，则∠P＝________.解析：连接BC.∵AB是⊙O的直径，PB切⊙O于B，∴∠ACB＝90°，∠ABP＝90°.又∠ACE＝40°，可求得∠PCB＝∠PBC＝50°，∴∠P＝80°.答案：80°8．如图，点P在圆O直径AB的延长线上，且PB＝OB＝2，PC切圆O于C点，CD⊥AB 于D点，则CD＝________.解析：连接OC.∵PC切⊙O于C点，∴OC⊥PC.∵PB＝OB＝2，OC＝2.∴PC＝2 3.∵OC·PC＝OP·CD，∴CD＝2×234＝ 3.答案： 39．如图，圆O和圆O′相交于A，B两点，AC是圆O′的切线，AD是圆O的切线，若BC＝2，AB＝4，求BD.解：∵AB是弦，且AC与圆O′相切于点A，∴∠CAB＝∠D，∵AB是弦，且AD与圆O相切于点A，∴∠DAB＝∠C，∴△ABC∽△DBA.∴ABBD＝BCAB，∴BD＝AB2BC＝422＝8.10．如图，AB是⊙O的弦，CD是经过⊙O上的点M的切线．求证：(1)如果AB∥CD，那么AM＝MB；(2)如果AM＝BM，那么AB∥CD.证明：(1)CD切⊙O于M点，∴∠DMB＝∠A，∠CMA＝∠B.∵AB∥CD，∴∠CMA＝∠A.∴∠A＝∠B.∴AM＝MB.(2)∵AM＝BM，∴∠A＝∠B.∵CD切⊙O于M点，∴∠CMA＝∠B.∴∠CMA＝∠A，∴AB∥CD.11．如图，已知AB 是⊙O 的直径，直线CD 与⊙O 相切于点C ，AC 平分∠DAB . (1)求证：AD ⊥CD ；(2)若AD ＝2，AC ＝5，求AB 的长． 解：(1)证明：如图，连接BC .∵直线CD 与⊙O 相切于点C ， ∴∠DCA ＝∠B .∵AC 平分∠DAB ，∴∠DAC ＝∠CAB . ∴∠ADC ＝∠ACB .∵AB 为⊙O 的直径，∴∠ACB ＝90°. ∴∠ADC ＝90°，即AD ⊥CD .(2)∵∠DCA ＝∠B ，∠DAC ＝∠CAB ， ∴△ADC ∽△ACB .∴AD AC ＝AC AB ，∴AC 2＝AD ·AB .∵AD ＝2，AC ＝5，∴AB ＝52.。

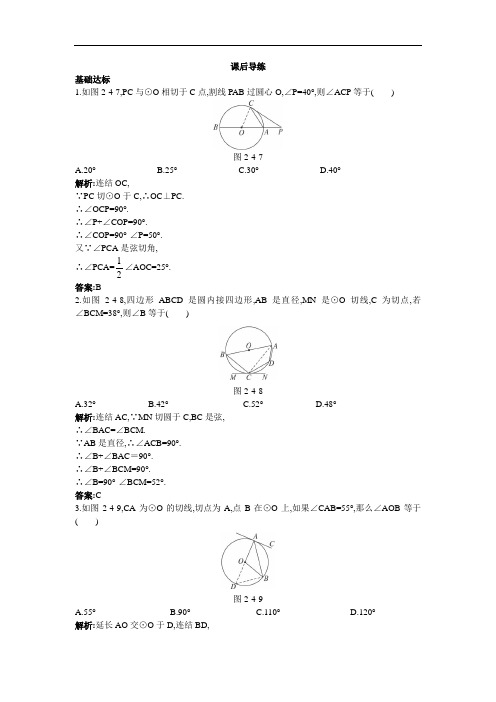
课后导练基础达标1.如图2-4-7,PC 与⊙O 相切于C 点,割线PAB 过圆心O,∠P=40°,则∠ACP 等于( )图2-4-7 A.20° B.25° C.30° D.40° 解析:连结OC,∵PC 切⊙O 于C,∴OC ⊥PC. ∴∠OCP=90°.∴∠P+∠COP=90°. ∴∠COP=90°-∠P=50°. 又∵∠PCA 是弦切角, ∴∠PCA=21∠AOC=25°. 答案:B2.如图2-4-8,四边形ABCD 是圆内接四边形,AB 是直径,MN 是⊙O 切线,C 为切点,若∠BCM=38°,则∠B 等于( )图2-4-8 A.32° B.42° C.52° D.48° 解析:连结AC,∵MN 切圆于C,BC 是弦, ∴∠BAC=∠BCM.∵AB 是直径,∴∠ACB=90°. ∴∠B+∠BAC ＝90°. ∴∠B+∠BCM=90°. ∴∠B=90°-∠BCM=52°. 答案:C3.如图2-4-9,CA 为⊙O 的切线,切点为A,点B 在⊙O 上,如果∠CAB=55°,那么∠AOB 等于( )图2-4-9A.55°B.90°C.110°D.120° 解析:延长AO 交⊙O 于D,连结BD,∵AC 切⊙O 于A,AB 是弦, ∴∠D=∠CAB. 又∵∠D=21∠AOB, ∴∠AOB=2∠CAB=110°. 答案:C4.如图2-4-10,∠ABC=90°,O 是AB 上一点,⊙O 切AC 于D,交AB 于E,连结DB 、DE 、OC,则图中与∠CBD 相等的角共有( )图2-4-10A.1个B.2个C.3个D.4个 解析:∵AB ⊥BC,∴BC 与⊙O 相切,BD 为弦. ∴∠CBD=∠BED. 同理,∠CDB=∠BED. ∴∠CBD=∠CDB. 又OC ⊥BD,DE ⊥BD, ∴DE ∥OC.∴∠BED=∠BOC. ∴∠CBD=∠BOC. ∴共3个. 答案:C5.如图2-4-11,AB 、AC 与⊙O 相切于B 、C,∠A=50°,点P 是圆上异于B 、C 的一动点,则∠BPC 的度数是( )图2-4-11A.65°B.115°C.65°或115°D.130°或50° 解析:点P 可能位置有两种情况,点P 在优弧上或在劣弧上.图2-4-12(1)如图2-4-12,在优弧上, ∵AB 、AC 是切线,∴∠ABC=∠P 1,∠ACB=∠P 1,∠ABC=21(180°-∠A)=65°. (2)如图2-4-13,在劣弧上,可在优弧上任取一点Q,图2-4-13由(1)知∠Q=65°,∵四边形BP 2CQ 内接于圆O, ∴∠BP 2C+∠Q=180°. ∴∠BP 2C=180°-∠Q=115°. 综上,∠BPC=65°或115°. 答案:C 温馨提示本题运用了运动变化思想、分类思想和化归思想. 综合运用6.如图2-4-14,AD 是圆内接△ABC 的∠A 的平分线,交圆于D,E 为BC 中点,BF 为圆的切线,DF ⊥BF. 求证:DE=DF.图2-4-14证明:连结BD,∵BF 是切线,BD 是弦, ∴∠DBF=∠BAD. ∵=,∴∠DBC=∠DAC.又∵AD 是∠BAC 的平分线,∴∠BAD=∠DAC.∴∠DBF=∠DBE, 即BD 是∠EBF 的平分线. ∵∠BAD=∠DAC,∴=,即D 是中点.∵E 是BC 中点,∴DE ⊥BC. ∴DE=DF.7.如图2-4-15,梯形ABCD 中,AB ∥DC,AD=BC,以AD 为直径的⊙O 交AB 于点E,⊙O 的切线EF 交BC 于F,求证:EF ⊥BC.图2-4-15证明:∵AD是直径,∴∠AED=90°.∴∠DEF+∠BEF=90°.∵EF切⊙O于点E,DE是弦,∴∠DEF=∠A.∴∠A+∠BEF=90°.∵AD=BC,AB∥DC,∴∠B=∠A.∴∠B+∠BEF=90°.∴∠BFE=90°.∴EF⊥BC.8.两圆内切于点P,大圆的弦AD交小圆于点B、C.求证:∠APB=∠CPD.图2-4-16证明:过P作两圆的公切线MN.∵PB是小圆弦,MN是切线,∴∠BPM=∠BCP.∵PA是大圆弦,MN是切线,∴∠APM=∠D.∴∠BPM-∠APM=∠BCP-∠D.又∠BCP=∠D+∠CPD,∴∠BCP-∠D=∠CPD.∴∠APB=∠CPD.9.如图2-4-17,AB是⊙O的弦,CD是经过⊙O上一点M的切线.图2-4-17求证:(1)AB∥CD时,AM=MB.(2)AM=MB时,AB∥CD.证明:(1)∵AB∥CD,∴∠A=∠AMC.∵CD切⊙O于M,AM是弦,∴∠AMC=∠B.∴∠A=∠B.∴AM=BM.(2)∵AM=MB,∴∠A=∠B.又∵CD切⊙O于M,AM是弦,∴∠AMC=∠B.∴∠AMC=∠A.∴AB∥CD.拓展探究10.如图2-4-18,AB是半圆O的直径,点M是半径OA的中点,点P在线段AM上运动(不与点M重合),点Q在半圆O上运动且总保持PQ=PO,过Q作⊙O的切线交BA的延长线于点C.图2-4-18(1)当∠QPA=60°时,请你对△QCP的形状作出猜想,并证明;(2)当QP⊥AO时,△QCP的形状是___________三角形.(3)由(1)、(2)得出的结论,请你进一步猜想,当点P在线段AM上运动到任何位置时△QCP一定是___________三角形.解析:(1)△QCP是等边三角形,证明:连结OQ,则CQ⊥OQ.∵PQ=PO,∠QPC=60°,∴∠POQ=∠PQO=30°.∴∠C=∠CQO-∠POQ=60°.∴∠CQP=∠C=∠QPC=60°.∴△QPC是等边三角形.(2)等腰直角(解析:略)(3)等腰(解析:略)备选习题11.如图2-4-19,BC为⊙O直径,DE切⊙O于A点,BD⊥DE于D,若∠ABD=50°,则的度数为_________________.图2-4-19解析:∵BD⊥DE,∴∠BDA=90°.∴∠ABD+∠BAD=90°.∴∠BAD=90°-50°=40°.∵AB是弦,AD是切线,∴∠C=∠BAD=40°.∴BC是直径.∴∠BAC=90°.∴∠C+∠ABC=90°.∴∠ABC=90°-∠C=50°.∴的度数为100°.答案:100°12.如图2-4-20,AB为⊙O的直径,DA、DE为⊙O两切线,A、C为切点,A、B、E共线,若的度数为60°,则∠CAD的度数为____________,∠E的度数为_____________.图2-4-20解析:∵度数为60°,∴∠BAC=30°,∠BCE=30°.∵AD为切线,∴BA⊥AD.∴∠BAC+∠CAD=90°.∴∠CAD=90°-∠BAC=60°.∵AB为直径,∴∠ACB=90°.∴∠ABC=90°-∠BAC=30°.∴∠E=∠ABC-∠BCE=30°.答案:60°30°13.两圆内切于点P,大圆的弦AB切小圆于C，求证：∠APC＝∠CPB.图2-4-21证明:过P作两圆公切线MN,设PB交小圆于D,连结CD.∵PC是小圆弦,MN切小圆于P,∴∠MPC=∠PDC.∵PA是大圆弦,MN切大圆于P,∴∠MPA=∠B.∴∠MPC-∠MPA=∠PDC-∠B.∵∠PDC=∠B+∠BCD,∴∠PDC-∠B=∠BCD.∴∠APC=∠BCD.又AB切小圆于C，CD是小圆弦,∴∠BCD=∠CPB.∴∠APC=∠CPB.14.如图2-4-22,△ABC中,过A与BC相切于D的圆分别交AB、AC于E、F,且EF∥BC. 求证:AD平分∠A.图2-4-22证明:连结DF,∵BC 切圆于D,DF 是弦, ∴∠3=∠2.∵EF ∥BC,∴∠3=∠4. 又∠1=∠4,∴∠1=∠2,即AD 平分∠BAC.15.如图2-4-12(1),OA 和OB 是⊙O 的半径,且OA ⊥OB,P 是OA 上任一点,BP 的延长线交⊙O 于Q,过Q 的⊙O 的切线交OA 的延长线于R,易证RP=RQ(不要求证明). (1)现将PA 向上平移至图2-4-23(2)位置,结论还成立吗?若成立,请证明.(2)若将PA 向上平移至⊙O 外,结论还成立吗?如图2-4-23(3),若成立,请证明.(1) (2) (3)图2-4-23解析:(1)成立.证明:连结OQ,则QR ⊥OQ. ∴∠PQR+∠BQO=90°.∵∠RPQ=∠1,∠1+∠B=90°, ∴∠RPQ+∠B=90°.又OB=OQ,∴∠B=∠BQO. ∴∠PQR=∠RPQ.∴RP=RQ. (2)结论仍然成立.证明:连结OQ,则OQ ⊥RQ. ∴∠RQO=90°.∴∠RQP+∠BQO=90°.∵OA ⊥PA,∴∠P+∠ABP=90°. 又∠PBA=∠OBQ,∵OB=OQ, ∴∠OBQ=∠OQB.∴∠P=∠PQR.∴RP=RQ.。

四弦切角的性质课时过关·能力提升基础巩固1如图,已知AB是半圆O的直径,C,D是半圆上的两点,半圆O的切线PC交AB的延长线于点P,∠PCB=25°,则∠ADC为()A.105°B.115°C.120°D.125°,连接BD.∵PC与☉O相切,∴∠BDC=∠BCP=25°.∵AB是直径,∴∠ADB=90°.∴∠ADC=∠ADB+∠BDC=90°+25°=115°.2如图,PQ为☉O的切线,A是切点,若∠BAQ=55°,则∠ADB=()A.55°B.110°C.125°D.155°PQ是切线,∴∠C=∠BAQ=55°.∵四边形ADBC内接于圆,∴∠ADB=180°-∠C=180°-55°=125°.3如图,△ABC内接于☉O,EC切☉O于点C.若∠BOC=76°,则∠BCE等于()A.14°B.38°C.52°D.76°EC为☉O的切线,∴∠BCE=∠BAC=1∠BOC=38°.24如图,四边形ABCD是圆内接四边形,AB是直径,MN是☉O的切线,C为切点,若∠BCM=38°,则∠B等于()A.32°B.42°C.52°D.48°AC,如图.∵MN切☉O于点C,BC是弦,∴∠BAC=∠BCM.∵AB是直径,∴∠ACB=90°.∴∠B+∠BAC=90°.∴∠B+∠BCM=90°,∴∠B=90°-∠BCM=52°.5如图,AD切☉O于点F,FB,FC为☉O的两弦,请列出图中所有的弦切角.AFB,∠AFC,∠DFC,∠DFB6如图,AB是☉O的直径,直线CE与☉O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则☉O的面积是.DE是切线,∴∠ACD=∠ABC=30°.又AD⊥CD,∴AC=2AD=2.∵AB是直径,∴∠ACB=90°.又∠ABC=30°,∴AB=2AC=4,AB=2.∴OA=12∴☉O的面积为S=π·OA2=4π.π7如图,AB是☉O的弦,CD是经过☉O上的点M的切线.求证:(1)如果AB∥CD,那么AM=MB;(2)如果AM=BM,那么AB∥CD.∵CD切☉O于点M,∴∠DMB=∠A,∠CMA=∠B.∵AB∥CD,∴∠CMA=∠A,∴∠A=∠B,∴AM=MB.(2)∵AM=BM,∴∠A=∠B.∵CD切☉O于点M,∴∠CMA=∠B.∴∠CMA=∠A.∴AB∥CD.8如图,四边形ABED内接于☉O,AB∥DE,AC切☉O于点A,交ED延长线于点C.求证:AD∶AB=DC∶BE.ACD和△ABE中,所以只要证明△ACD∽△AEB即可.四边形ABED内接于☉O,∴∠ADC=∠ABE.∵AC是☉O的切线,∴∠CAD=∠AED.∵AB∥DE,∴∠BAE=∠AED.∴∠CAD=∠BAE,∴△ACD∽△AEB.∴AD∶AB=DC∶BE.9如图,已知圆上的,过点C的圆的切线与BA的延长线交于点E.求证:(1)∠ACE=∠BCD;(2)BC2=BE·CD.证明这两个角都等于∠ABC;(2)转化为证明△BDC∽△ECB.∵,∴∠BCD=∠ABC.∵EC与圆相切于点C,∴∠ACE=∠ABC.∴∠ACE=∠BCD.(2)∵∠ECB=∠CDB,∠EBC=∠BCD,∴△BDC∽△ECB.∴,即BC2=BE·CD.10如图,AB是半圆O的直径,C是圆周上异于点A,B的一点,过点C作圆O的切线l,过点A作直线l的垂线AD,垂足为点D,AD交半圆于点E.求证:CB=CE.CBE=∠CEB.方法一)连接BE,如图.因为AB是半圆O的直径,点E为圆周上一点,所以∠AEB=90°,即BE⊥AD.又因为AD⊥l,所以BE∥l.所以∠DCE=∠CEB.因为直线l是圆O的切线,所以∠DCE=∠CBE.所以∠CBE=∠CEB,故CE=CB.(方法二)连接AC,BE,在DC延长线上取一点F,如图.因为AB是半圆O的直径,C为圆周上一点,所以∠ACB=90°,即∠BCF+∠ACD=90°.因为AD⊥l,所以∠DAC+∠ACD=90°,所以∠BCF=∠DAC.因为直线l是圆O的切线,所以∠CEB=∠BCF.又∠DAC=∠CBE,所以∠CBE=∠CEB.所以CE=CB.能力提升1如图,AB是☉O的直径,EF切☉O于点C,AD⊥EF于点D,若AD=2,AB=6,则AC的长为()A.2B.3C.23D.4BC,如图.∵EF是☉O的切线,∴∠ACD=∠ABC.又AB是☉O的直径,∴∠ACB=90°.又AD⊥EF,∴∠ACB=∠ADC.∴△ADC∽△ACB.∴.∴AC2=AD·AB=2×6=12,∴AC=23.★2如图,已知∠ABC=90°,O是AB上一点,☉O切AC于点D,交AB于点E,B,连接DB,DE,OC,则图中与∠CBD相等的角共有()A.1个B.2个C.3个D.4个AB⊥BC,∴BC与☉O相切,BD为弦.∴∠CBD=∠BED.同理可得∠CDB=∠BED,∴∠CBD=∠CDB.连接OD.∵OD=OB,OC=OC,∴Rt△COD≌Rt△COB.∴CB=CD,∠DCO=∠BCO.∴OC⊥BD.又DE⊥BD,∴DE∥OC.∴∠BED=∠BOC,∴∠CBD=∠BOC.∴与∠CBD相等的角共有3个.3如图,AB是☉O的直径,PB,PE分别切☉O于点B,C,若∠ACE=40°,则∠P=.,连接BC,则∠ACE=∠ABC,∠ACB=90°.又∠ACE=40°,则∠ABC=40°.所以∠BAC=90°-∠ABC=90°-40°=50°,∠ACP=180°-∠ACE=140°.又AB是☉O的直径,则∠ABP=90°.又四边形ABPC的内角和等于360°,所以∠P+∠BAC+∠ACP+∠ABP=360°.所以∠P=80°.4如图,已知圆O的直径AB=6,C为圆周上一点,BC=3,过点C作圆的切线l,过点A作l的垂线AD,垂足为点D,则线段CD的长为.直线l是圆O的切线,∴∠ACD=∠ABC.又AB是直径,∴AC⊥BC.∵BC=3,AB=6,∴∠ABC=60°.∴AC=33.又∠ACD=∠ABC,∴∠ACD=60°..又AD⊥l,∴CD=AC cos60°=3325如图,☉O和☉O'相交于A,B两点,过点A作两圆的切线,分别交两圆于C,D两点,若BC=2,BD=4,则AB的长为.AC,AD分别是两圆的切线,∴∠C=∠BAD,∠D=∠BAC.∴△ACB∽△DAB.∴.∴AB2=BC·DB=2×4=8.∴AB=22(负值舍去).26如图,BA是☉O的直径,AD是☉O的切线,切点为A,BF,BD分别交AD于点F,D,交☉O于点E,C,连接CE.求证:BE·BF=BC·BD.BE·BF=BC·BD,只需证,即证明△BEC∽△BDF.由∠DBF为公共角,只需再找一组角相等,为此,过点B作☉O的切线,构造弦切角.,过点B作☉O的切线BG,则AB⊥BG.又AD是☉O的切线,∴AD⊥AB,∴BG∥AD,∴∠GBC=∠BDF.∵∠GBC=∠BEC,∴∠BEC=∠BDF.又∠CBE=∠DBF,∴△BEC∽△BDF.∴.∴BE·BF=BC·BD.7如图,△ABC内接于☉O,AB=AC,直线MN切☉O于点C,弦BD∥MN,AC与BD相交于点E.求证:(1)△ABE≌△ACD;(2)BE=BC.由已知,得∠ABE=∠ACD,只需证明∠BAE=∠CAD,转化为证明∠BAE=∠CDB,∠CDB=∠DCN,∠DCN=∠CAD.(2)转化为证明∠BEC=∠ECB.∵BD∥MN,∴∠CDB=∠DCN.又∠BAE=∠CDB,∴∠BAE=∠DCN.又直线MN是☉O的切线,∴∠DCN=∠CAD.∴∠BAE=∠CAD.又∠ABE=∠ACD,AB=AC,∴△ABE≌△ACD.(2)∵∠EBC=∠BCM,∠BCM=∠BDC,∴∠EBC=∠BDC.∴CB=CD.∵∠BEC=∠EDC+∠ECD,∠ECD=∠ABE,∴∠BEC=∠EBC+∠ABE=∠ABC.又AB=AC,∴∠ABC=∠ECB.∴∠BEC=∠ECB.∴BE=BC.★8如图,已知点P在☉O外,PC是☉O的切线,切点为C,直线PO与☉O相交于点A,B.(1)试探索∠BCP与∠P的数量关系.(2)若∠A=30°,则PB与PA有什么关系?(3)∠A可能等于45°吗?为什么?∵PC是切线,∴∠BCP=∠A.∵AB是直径,∴∠ACB=90°.在△ACP中,∠A+∠P+∠ACP=180°,∴∠BCP+∠P+∠ACB+∠BCP=180°.∴2∠BCP+∠P+90°=180°.∴∠P=90°-2∠BCP.(2)若∠A=30°,则∠BCP=∠A=30°,∠ABC=60°.∴∠P=30°,∴PB=BC,BC=1AB.2∴PB=1PA,即PA=3PB.3(3)∠A不可能等于45°.理由如下:设∠A=45°,则∠ABC=45°,∠BCP=45°,∴CP∥AB,与题干中PC与AB交于点P矛盾, ∴∠A不可能等于45°.。

课后训练1．如图，O 的半径为2 cm,O 切AC 于D ，切BE 于E ，∠ACB ＝60°,则CE 的长为（ ）．A ．3cmB ．23cm 3C ．3cm 3D ．23cm2．如图,AB 是O 的直径,直线EF 切O 于B ，C 、D 为O 上的点，∠CBE ＝40°，AD CD =,则∠BCD 的度数是( )．A ．110°B ．115°C ．120°D ．135°3．如图，在圆的内接四边形ABCD 中，AC 平分∠BAD ，EF 切O 于C 点，那么图中与∠DCF 相等的角的个数是( )．A ．4B ．5C ．6D ．74．如图，BD 为O 的直径，AB 、AE 切O 于B 、C ，∠BDC ＝65°,则∠BAC ＝________。

5．如图，已知AB 与O 相切于点M ，MC MD =，且MC 、MD 为14圆周长,则∠AMC ＝__________。

6．已知,如图，△ABC内接于O,DC切O于C点，BC平分∠ACD，则△ABC为________．7．如图，AB是O的直径，CD是O的切线，C为切点，AC 平分∠BAD．求证：AD⊥CD．8．如图，P是O的半径OA上的一点，D在O上，且PD＝PO.过点D作O的切线交OA的延长线于点C，延长DP交O于K，连接KO，OD．(1）证明：PC＝PD；(2)若该圆的半径为5，CD∥KO，求出OC的长．如图,BC为O的直径,AB AD=，过点A的切线与CD的延长线交于点E.(1）试猜想∠AED是否等于90°？为什么？（2）若25AD=，ED∶EA＝1∶2，求O的半径．(3）在（2）的条件下求∠CAD的正弦值．参考答案1.答案：B解析：∵CD、CE是O的切线，∴OC平分∠ECD．∴∠OCE＝12∠ECD＝12(180°－∠ACB)＝12(180°－60°）＝60°.∴CE＝OE cot60°＝323233⨯=(cm）．2。

【课堂新坐标】高中数学 2.4 弦切角的性质课后知能检测 新人教A版选修4-1一、选择题1．如图2－4－12所示，AB 是⊙O 的直径，MN 与⊙O 切于点C ，AC ＝12BC ，则sin ∠MCA＝( )图2－4－12A.12 B.22 C.32D.55【解析】 由弦切角定理，得 ∠MCA ＝∠ABC .∵sin ∠ABC ＝AC AB ＝AC AC 2＋BC 2＝AC 5AC ＝55，故选D. 【答案】 D图2－4－132．如图2－4－13所示，AB 是⊙O 的直径，EF 切⊙O 于C ，AD ⊥EF 于D ，AD ＝2，AB ＝6，则AC 的长为( )A ．2B ．3C ．2 3D ．4【解析】 连接BC .∵AB 是⊙O 的直径， ∴AC ⊥BC ，由弦切角定理可知， ∠ACD ＝∠ABC ，∴△ABC ∽△ACD ， ∴AC AD ＝AB AC，∴AC 2＝AB ·AD ＝6×2＝12， ∴AC ＝23，故选C. 【答案】 C3．如图2－4－14，PC 与⊙O 相切于C 点，割线PAB 过圆心O ，∠P ＝40°，则∠ACP 等于( )图2－4－14A ．20°B ．25°C ．30°D ．40°【解析】 如图，连接OC ， ∵PC 切⊙O 于C 点， ∴OC ⊥PC ，∵∠P ＝40°， ∴∠POC ＝50°， 连接BC ，∵OC ＝OB ， ∴∠B ＝12∠POC ＝25°，∴∠ACP ＝∠B ＝25°.【答案】 B4．如图2－4－15所示，已知AB 、AC 与⊙O 相切于B 、C ，∠A ＝50°，点P 是⊙O 上异于B 、C 的一动点，则∠BPC 的度数是( )A．65°B．115°C．65°或115°D．130°或50°图2－4－15【解析】当点P在优弧BC上时，由∠A＝50°，得∠ABC＝∠ACB＝65°.∵AB是⊙O的切线，∴∠ABC＝∠BPC＝65°.当P点在劣弧BC上时，∠BPC＝115°.故选C.【答案】 C二、填空题5．(2012·广东高考)如图2－4－16所示，直线PB与圆O相切于点B，D是弦AC上的点，∠PBA＝∠DBA.若AD＝m，AC＝n，则AB＝________.图2－4－16【解析】利用弦切角定理及相似三角形求解．∵PB切⊙O于点B，∴∠PBA＝∠ACB.又∠PBA＝∠DBA，∴∠DBA＝∠ACB，∴△ABD∽△ACB.∴AB AC ＝AD AB，∴AB 2＝AD ·AC ＝mn ， ∴AB ＝mn . 【答案】mn6. 如图2－4－17，点P 在圆O 直径AB 的延长线上，且PB ＝OB ＝2，PC 切圆O 于C 点，CD ⊥AB 于D 点，则CD ＝__________.图2－4－17【解析】 连接OC ，∵PC 切⊙O 于点C ， ∴OC ⊥PC ，∵PB ＝OB ＝2，OC ＝2，∴PC ＝23，∵OC ·PC ＝OP ·CD ， ∴CD ＝2×234＝ 3.【答案】 3三、解答题7．如图2－4－18所示，△ABT 内接于⊙O ，过点T 的切线交AB 的延长线于点P ，∠APT 的平分线交BT 、AT 于C 、D .求证：△CTD 为等腰三角形．图2－4－18【证明】 ∵PD 是∠APT 的平分线， ∴∠APD ＝∠DPT .又∵PT 是圆的切线，∴∠BTP ＝∠A .又∵∠TDC ＝∠A ＋∠APD ， ∠TCD ＝∠BTP ＋∠DPT ， ∴∠TDC ＝∠TCD ， ∴△CTD 为等腰三角形．8．(2012·辽宁高考)如图2－4－19，⊙O 和⊙O ′相交于A ，B 两点，过A 作两圆的切线分别交两圆于C ，D 两点，连接DB 并延长交⊙O 于点E .证明：图2－4－19(1)AC ·BD ＝AD ·AB ； (2)AC ＝AE .【证明】 (1)由AC 与⊙O ′相切于A ，得∠CAB ＝∠ADB ，同理∠ACB ＝∠DAB ，所以△ACB ∽△DAB .从而AC AD ＝AB BD，即AC ·BD ＝AD ·AB .(2)由AD 与⊙O 相切于A ，得∠AED ＝∠BAD . 又∠ADE ＝∠BDA ，得△EAD ∽△ABD . 从而AE AB ＝AD BD，即AE ·BD ＝AD ·AB . 综合(1)的结论知，AC ＝AE .9．(2013·辽宁高考)如图2－4－20，AB 为⊙O 的直径，直线CD 与⊙O 相切于E ，AD 垂直CD 于D ，BC 垂直CD 于C ，EF 垂直AB 于F ，连接AE ，BE .图2－4－20证明：(1)∠FEB ＝∠CEB ； (2)EF 2＝AD ·BC .【证明】 (1)由直线CD 与⊙O 相切，得∠CEB ＝∠EAB . 由AB 为⊙O 的直径，得AE ⊥EB ，从而∠EAB ＋∠EBF ＝π2；又EF ⊥AB ，得∠FEB ＋∠EBF ＝π2.从而∠FEB ＝∠EAB .故∠FEB ＝∠CEB .(2)由BC ⊥CE ，EF ⊥AB ，∠FEB ＝∠CEB ，BE 是公共边，得Rt△BCE ≌Rt△BFE ，所以BC ＝BF .类似可证Rt△ADE ≌Rt△AFE ，得AD ＝AF . 又在Rt△AEB 中，EF ⊥AB ，故EF 2＝AF ·BF ， 所以EF 2＝AD ·BC .10．如图，△ABC 内接于圆O ，AB ＝AC ，直线MN 切圆O 于点C ，弦BD ∥MN ，AC 与BD 相交于点E .(1)求证：△ABE ≌△ACD ； (2)若AB ＝6，BC ＝4，求AE .【解】 (1)证明：由已知得∠ABE ＝∠ACD ，∠BAE ＝∠EDC ， 又∵BD ∥MN ，∴∠DCN ＝∠EDC ， ∴∠BAE ＝∠DCN . 又直线MN 切圆O 于点C ， ∴∠CAD ＝∠DCN . ∴∠CAD ＝∠BAE .又AB ＝AC ，∴△ABE ≌△ACD . (2)由于△ABE ≌△ACD ，则BE ＝CD ， 由(1)得∠CAD ＝∠BAE ， ∴BC ＝CD .∴BE ＝CD ＝4. 在△ABE 和△CDE 中，∠BAE ＝∠EDC ，∠EBA ＝∠ECD ， ∴△ABE ∽△DCE .∴BE CE ＝AB CD. ∴BE AC －AE ＝ABCD. ∴46－AE ＝64，10 3.解得AE＝。

人教新课标A版选修4-1数学2.4弦切角的性质同步检测A卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分）如图，经过⊙O上的点 A的切线和弦 BC的延长线相交于点 P，若∠CAP=40°，∠ACP=100°，则∠BAC所对的弧的度数为（）A . 40°B . 100°C . 120°D . 30°2. （2分）如图，在⊙O中，AB是弦，AC是⊙O的切线，A是切点，过 B作BD⊥AC于D，BD交⊙O于E点，若AE平分∠BAD，则∠BAD=（）A . 30°B . 45°C . 50°D . 60°3. （2分）(2016·天津模拟) 如图，圆O的直径AB长度为10，CD是点C处的切线，AD⊥CD，若BC=8，则CD=（）A .B .C .D .4. （2分） PT切⊙O于T，割线PAB经过O点交⊙O于A、B，若PT=4，PA=2，则cos∠BPT=（）A .B .C .D .5. （2分）若图中，PA切⊙O于点A，PCB交⊙O于C、B两点，且PCB过点O，AE⊥BP交⊙O于E，则图中与∠CAP相等的角的个数是（）A . 1B . 2C . 3D . 46. （2分） (2017高一下·河北期末) 如图所示，在圆的内接四边形中，平分，切于点，那么图中与相等的角的个数是（）A . 4B . 5C . 6D . 77. （2分）如图，直线BC切⊙O于B，AB=AC，AD=BD，则∠A=（）A . 35°B . 36°C . 40°D . 50°8. （2分） (2017高二上·信阳期末) 如图，已知四边形ABCD是圆内接四边形，且∠BCD=120°，AD=2，AB=BC=1，现有以下结论：①B，D两点间的距离为；②AD是该圆的一条直径；③CD= ；④四边形ABCD的面积S= ．其中正确结论的个数为（）A . 1B . 2C . 3D . 49. （2分）如图⊙O中，弦AB与弦CD相交于点P，∠B=38°，∠APD=80°，则∠A等于（）A . 38°B . 42°C . 80°D . 118°10. （2分） (2016高二下·五指山期末) 如图，四边形ABCD是⊙O的内接四边形，延长BC到E，已知∠BCD：∠ECD=3：2，那么∠BOD等于（）A . 120°B . 136°C . 144°D . 150°二、填空题 (共5题；共5分)11. （1分）如图，圆O是△ABC的外接圆，过点C的切线交AB的延长线于点D，CD=， AB=BC=3．AC 的长为________ ．12. （1分）如图，已知点D在圆O直径AB的延长线上，过D作圆O的切线，切点为C．若CD=， BD=1，则圆O的面积为________ ．13. （1分）如图，从圆O外一点P作圆O的割线PAB、PCD，AB是圆O的直径，若PA=4，PC=5，CD=3，则∠CBD=________ ．14. （1分）如图，AB的延长线上任取一点C，过C作圆的切线CD，切点为D，∠ACD的平分线交AD于E，则∠CED=________15. （1分）如图，AB、AC是⊙O的两条切线，切点分别为B、C．若∠BAC=60°，BC=6，则⊙O的半径为________ ．三、解答题 (共10题；共70分)16. （10分） (2015高三上·苏州期末) 如图，四边形么BDC内接于圆，BD=CD，过C点的圆的切线与AB的延长线交于E点．（1）求证：∠EAC=2∠DCE；（2）若BD⊥AB，BC=BE，AE=2，求AB的长．17. （5分）(2016·城中模拟) 如图，在△ABC和△ACD中，∠ACB=∠ADC=90°，∠BAC=∠CAD，⊙O是以AB 为直径的圆，DC的延长线与AB的延长线交于点E．（Ⅰ）求证：DC是⊙O的切线；（Ⅱ）若EB=6，EC=6 ，求BC的长．18. （5分）如图，四边形ABCD内接于⊙O，BD是⊙O的直径，过点A作⊙O的切线AE，与CD的延长线交于E，AE⊥CD，垂足为点E．（Ⅰ）证明：DA平分∠BDE；（Ⅱ）如果AB=4，AE=2，求对角线CA的长．19. （5分）如图，∠PAQ是直角，圆O与射线AP相切于点T，与射线AQ相交于两点B，C．求证：BT平分∠OBA．20. （10分）(2016·大连模拟) 如图所示，已知圆O1与圆O2相交于A，B两点，过点A作圆O1的切线交圆O2于点C，过点B作两圆的割线，分别交圆O1 ，圆O2于点D，E，DE与AC相交于点P．（1）求证：AD∥EC；（2）若AD是圆O2的切线，且PA=3，PC=1，AD=6，求DB的长．21. （10分）(2017·白山模拟) 如图，A，B，C，D四点在同一圆上，BC与AD的延长线交于点E，点F在BA 的延长线上．（1）若 = ， =1，求的值；（2）若EF2=FA•FB，证明：EF∥CD．22. （5分）(2017·镇江模拟) 如图，圆O的直径AB=6，C为圆周上一点，BC=3，过C作圆的切线l，过A 作l的垂线AD，AD分别与直线l、圆交于点D、E．求∠DAC的度数与线段AE的长．23. （5分）(2017·唐山模拟) 如图，A、B、C为⊙O上三点，B为的中点，P为AC延长线上一点，PQ 与⊙O相切于点Q，BQ与AC相交于点D．（Ⅰ）证明：△DPQ为等腰三角形；（Ⅱ）若PC=1，AD=PD，求BD•QD的值．24. （10分）如图，AB切O于点D，直线AD交O于D，E两点，BC⊥DE，垂足为C．（1）证明：CBD=DBA；（2）若AD=3DC，BC=，求O的直径．25. （5分）(2017·榆林模拟) 如图，已知PA与圆O相切于点A，经过点O的割线PBC交圆O于点B，C，∠APC 的平分线分别交AB，AC于点D，E．（Ⅰ）证明：∠ADE=∠AED；（Ⅱ）若AC=AP，求的值．参考答案一、选择题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共5题；共5分)11-1、12-1、13-1、14-1、15-1、三、解答题 (共10题；共70分) 16-1、16-2、17-1、18-1、19-1、20-1、20-2、21-1、21-2、22-1、23-1、24-1、24-2、25-1、。

温馨提示：此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。

知能巩固提升(九)/课后巩固作业(九)（时间：45分钟满分：100分）一、选择题(每小题6分，共36分)1.如图，PC与⊙O相切于C点，割线PAB过圆心O，∠P=40°，则∠ACP等于( )(A)20° (B)25°(C)30° (D)40°2.如图，四边形ABCD是圆的内接四边形，AB是直径，MN是切圆于C点的切线，若∠BCM=38°,则∠B=( )(A)32° (B)42°(C)52° (D)48°3.已知如图，PA切⊙O于点A，PCB交⊙O于C，B两点，且PCB过点O，AE ⊥BP交⊙O于E，则图中与∠CAP相等的角的个数是( )(A)1 (B)2 (C)3 (D)44.已知PA是⊙O的切线，切点为A，PA=2，AC是⊙O的直径，PC 交⊙O 于点B ，∠PAB ＝30°，则⊙O 的半径为( ) (A)1 (B)2(()C D 5.如图所示，AB 是⊙O 的直径，MN 与⊙O 切于点C ，AC=BC ，则sin ∠MCA=( )()()()()1A B C D 22256.(易错题)如图，已知AB ，AC 与⊙O 分别相切于B ，C ，∠A=50°，点P 是⊙O 上异于B ，C 的一动点，则∠BPC 的度数是( )(A)65° (B)115° (C)65°或115° (D)130°或50° 二、填空题(每小题6分，共18分)7.(2012·广东高考)如图所示，直线PB 与圆O 相切于点B,D 是弦AC 上的点，∠PBA=∠DBA,若AD=m,AC=n,则AB=______.8.如图，AB是⊙O的直径，PB，PE分别切⊙O于B，C，若∠ACE=40°，则∠P=____.9.如图，△ABC是圆O的内接三角形，圆O的半径r=1,AB=1,BC=EC是圆O 的切线，则∠ACE=______.三、解答题(每小题14分，共28分)10.如图，△ABC内接于⊙O，AB=AC，直线MN切⊙O于点C，弦BD∥MN，AC 与BD相交于点E.求证:△ABE≌△ACD.11.如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.(1)求证:AD⊥CD;(2)若AD=2,AC=求AB的长.【挑战能力】(18分)如图，AB是⊙O的弦，M是上任一点，过点M的切线与分别以A、B 为垂足的直线AD、BC交于D、C两点，过M点作NM⊥CD交AB于点N，求证：MN2=AD·BC.答案解析1.【解析】选B.连接OC，∵PC切⊙O于点C，∴OC⊥PC.∴∠OCP=90°，∴∠P+∠COP=90°，∴∠COP=90°-∠P=50°.又∵∠PCA是弦切角，∴∠PCA=∠AOC=25°.2.【解析】选C.连接AC.∵∠BCM=38°，MN是⊙O的切线，∴∠BAC=38°，∵AB为⊙O的直径，∴∠B=90°-38°=52°.3.【解析】选C.其中∠B，∠AEC都与∠CAP相等，连接OA，OE，则△AOE为等腰三角形.∵OC⊥AE，∴OC垂直平分AE，∴△ACE为等腰三角形，∴∠EAC=∠AEC=∠CAP.4. 【解析】选C.∵AB 是弦，且PA 与⊙O 相切于点A ， ∴∠C=∠PAB ＝30°， 又∵AC 是⊙O 的直径， ∴AC ⊥AP ， ∴在Rt △PAC 中，AP 2AC tan C tan30===︒∴⊙O 的半径为5. 【解析】选D.由弦切角定理，得∠MCA=∠ABC.∵AC sin ABC AB 5∠====故选D. 【误区警示】本题易错选A.错因是由AC=BC ，易错误得出∠B=30°，故得出sin ∠MCA=sin B=sin 30°=. 6. 【解析】选C.当点P 在优弧上时， 由∠A=50°，得∠ABC=∠ACB=65°， ∵AB 是⊙O 的切线， ∴∠ABC=∠BPC=65°.当P 点在劣弧上时，∠BPC=115°.故选C.【误区警示】本题容易错选A.容易忽视点P 在劣弧上的情况而导致漏解. 7.【解题指南】本题要注意利用圆的几何性质，判断出∠PBA=∠ACB=∠ABD,从而证出△ABD ∽△ACB ，这是解答此题的关键. 【解析】由题意知∠PBA=∠ACB=∠ABD ， 所以△ABD ∽△ACB ， 所以AD ABAB AB AC===，所以答案：8.【解析】如图所示，连接BC，则∠ACE=∠ABC，∠ACB=90°.又∠ACE=40°，∴∠ABC=40°.∴∠BAC=90°-∠ABC=90°-40°=50°，∠ACP=180°-∠ACE=140°.又∵AB是⊙O的直径，则∠ABP=90°.又∵四边形ABPC的内角和等于360°，所以∠P+∠BAC+∠ACP+∠ABP=360°.所以∠P=80°.答案：80°9.【解析】连接OA,OB,OC,∵OA=OB=1,AB=1,∴△AOB为等边三角形,∴∠AOB=60°.∵OB=OC=1,BC=∴∠BOC=90°,∴∠AOC=30°,∵EC是圆O的切线,∴∠ACE=∠AOC=15°.答案：15°10.【证明】在△ABE和△ACD中,AB=AC,∠ABE=∠ACD,∠BAE=∠EDC, ∵BD∥MN,∴∠EDC=∠DCN,∵直线MN是圆的切线,∴∠DCN=∠CAD,∴∠BAE=∠CAD,∴△ABE≌△ACD.【方法技巧】如何证明两个三角形全等(1)依据：①SAS;②ASA;③AAS;④SSS;⑤直角三角形HL.(2)思路:①首先分析两个要证全等的三角形中已经给出的条件.②在已有条件的基础上找出或证出与它们搭配的其他条件.③对“SAS”定理，应用时不要出现用“SSA”的错误.11.【解析】(1)如图,连接BC.∵直线CD与⊙O相切于点C,∴∠DCA=∠B.∵AC平分∠DAB,∴∠DAC=∠CAB.∴∠ADC=∠ACB.∵AB为⊙O的直径,∴∠ACB=90°.∴∠ADC=90°,即AD⊥CD.(2)∵∠DCA=∠B,∠DAC=∠CAB,∴△ADC∽△ACB.∴∴AC2=AD·AB.∵AD=2, 【挑战能力】【解题指南】本题首先需根据条件证明△ADM ∽△MNB,然后再证明进而得到所证的结果.【证明】连接AM 、MB ，∵DA ⊥AB ，MN ⊥CD ， ∴∠MDA+∠MNA=180°， 又∵∠MNA+∠MNB=180°， ∴∠MDA=∠BNM ，又∵CD 为⊙O 的切线，∴∠1=∠2， ∴△ADM ∽△MNB,∴AD AM MN AM,MN BM BC BM==同理：，∴即有MN 2=AD ·BC.。

高中数学选修4-1切线长定理及弦切角练习题（一）填空1．已知：如图7－143，直线BC切⊙O于B点，AB=AC，AD=BD，那么∠A=____．2．已知：如图7－144，直线DC与⊙O相切于点C，AB为⊙O直径，AD⊥DC 于D，∠DAC=28°侧∠CAB=____ ．3．已知：直线AB与圆O切于B点，割线ACD与⊙O交于C和D4．已知：如图7－145，PA切⊙O于点A，割线PBC交⊙O于B和C两点，∠P=15°，∠ABC=47°，则∠C= ____．5．已知：如图7－146，三角形ABC的∠C=90°，内切圆O与△ABC的三边分别切于D，E，F三点，∠DFE=56°，那么∠B=____．6．已知：如图 7－147，△ABC内接于⊙O，DC切⊙O于C点，∠1=∠2，则△ABC为____ 三角形．7．已知：如图7－148，圆O为△ABC外接圆，AB为直径，DC切⊙O于C点，∠A=36°，那么∠ACD=____．（二）选择8．已知：△ABC内接于⊙O，∠ABC=25°，∠ACB= 75°，过A点作⊙O的切线交BC的延长线于P，则∠APB等于[ ]A．62.5°；B．55°；C．50°；D．40°．9．已知：如图 7－149，PA，PB切⊙O于A，B两点，AC为直径，则图中与∠PAB相等的角的个数为[ ]A．1 个；B．2个；C．4个；D．5个．10．已知如图7－150，四边形ABCD为圆内接四边形，AB是直径，MN切⊙O 于C点，∠BCM=38°，那么∠ABC的度数是[ ]A．38°；B．52°；C．68°；D．42°．11．已知如图7－151，PA切⊙O于点A，PCB交⊙O于C，B两点，且 PCB 过点 O，AE⊥BP交⊙O于E，则图中与∠CAP相等的角的个数是[ ]A．1个；B．2个；C．3个；D．4个．（三）计算12．已知：如图7－152，PT与⊙O切于C，AB为直径，∠BAC=60°，AD为⊙O一弦．求∠ADC与∠PCA的度数．13．已知：如图7－153，PA切⊙O于A，PO交⊙O于B，C，PD平分∠APC．求∠ADP的度数．14．已知：如图7－154，⊙O的半径OA⊥OB，过A点的直线交OB于P，交⊙O于Q，过Q引⊙O的切线交OB延长线于C，且PQ=QC．求∠A的度数．15．已知：如图7－155，⊙O内接四边形ABCD，MN切⊙O于C，∠BCM=38°，AB为⊙O直径．求∠ADC的度数．16．已知：如图7－156，PA，PC切⊙O于A，C两点，B点17．已知：如图 7－157，AC为⊙O的弦，PA切⊙O于点A，PC过O点与⊙O 交于B，∠C=33°．求∠P的度数．18．已知：如图7－158，四边形ABCD内接于⊙O，EF切⊙O19．已知 BA是⊙O的弦，TA切⊙O于点A，∠BAT= 100°，点M在圆周上但与A，B不重合，求∠AMB的度数．20．已知：如图7－159，PA切圆于A，BC为圆直径，∠BAD=∠P，PA=15cm，PB=5cm．求 BD的长．21．已知：如图7－160，AC是⊙O直径，PA⊥AC于A，PB切⊙O于B，BE ⊥AC于E．若AE=6cm，EC=2cm，求BD的长．22．已知：如图7－161所示，P为⊙O外一点，PA切⊙O于A，从PA中点M 引⊙O割线MNB，∠PNA=138°．求∠PBA的度数．23．已知：如图7－162，DC切⊙O于C，DA交⊙O于P和B两点，AC交⊙O 于Q，PQ为⊙O直径交BC于E，∠BAC=17°，∠D=45°．求∠PQC与∠PEC的度数．24．已知：如图 7－163，QA切⊙O于点A，QB交⊙O于B25．已知：如图7－164，QA切⊙O于A，QB交⊙O于B和C26．已知：在图7－165中，PA切⊙O于A，AD平分∠BAC，PE平分∠APB，AD=4cm，PA=6cm．求EP的长．27．已知；如图7－166，PA为△ABC外接圆的切线，A 为切点，DE∥AC，PE=PD．AB=7cm，AD=2cm．求DE的长．28．已知：如图 7－167，BC是⊙O的直径，DA切⊙O于A，DA=DE．求∠BAE 的度数．29．已知：如图 7－168，AB为⊙O直径，CD切⊙O于CAE∠CD于E，交BC 于F，AF=BF．求∠A的度数．30．已知：如图7－169，PA，PB分别切⊙O于A，B，PCD为割线交⊙O于C，D．若 AC=3cm，AD=5cm，BC= 2cm，求DB的长．ABCD的顶点A，D，C在圆O上，AB的延长线31．已知：如图7－170，与⊙O交于M，CB的延长线与⊙O交于点N，PD切⊙O于D，∠ADP=35°，∠ADC=108°．求∠M的度数．32．已知：如图7－171，PQ为⊙O直径，DC切⊙O于C，DP交⊙O于B，交CQ延长线于A，∠D=45°，∠PEC=39°．求∠A的度数．33．已知：如图 7－172，△ABC内接于⊙O，EA切⊙O于A，过B作BD∥AE 交AC延长线于D．若AC=4cm，CD= 3cm，求AB的长．34．已知：如图7－173，△ABC内接于圆，FB切圆于B，CF⊥BF于F交圆于 E，∠1=∠2．求∠1的度数．35．已知：如图7－174，PC为⊙O直径，MN切⊙O于A，PB⊥MN于B．若PC=5cm，PA=2cm．求PB的长．36．已知：如图7－175，AD为⊙O直径，CBE，CD分别切⊙37．已知：如图7－176，圆内接四边形ABCD的AB边经过圆心，AD，BC的延长线相交于E，过C点的切线CF⊥AE于F．求证：（1）△ABE为等腰三角形；（2）若 BC=1cm，AB=3cm，求EF的长．38．已知：如图7－177，AB，AC切⊙O于B，C，OA交⊙O于F，E，交BC 于D．（1）求证：E为△ABC内心；（2）若∠BAC=60°，AB=a，求OB与OD的长．（四）证明39．已知：在△ABC中，∠C=90°，以C为圆心作圆切AB边于F点，AD，BC分别与⊙C切于D，E两点．求证：AD∥BE．40．已知：PA，PB与⊙O分别切于A，B两点，延长OB到C，41．已知：⊙O与∠A的两边分别相切于D，E．在线段AD，AE（或在它们的延长线）上各取一点B，C，使DB=EC．求证：OA⊥BC．⊥EC于H，AO交BC于D．求证：BC·AH=AD·CE．*43．已知：如图7－178，MN切⊙O于A，弦BC交OA于E，过C点引BC的垂线交MN于D．求：AB∥DE．44．已知：如图7－179，OA是⊙O半径，B是OA延长线上一点，BC切⊙O 于C，CD⊥OA于D．求证：CA平分∠BCD．45．已知：如图7－180，BC是⊙O直径，EF切⊙O于A点，AD⊥BC于D．求证：AB平分∠DAE，AC平分∠DAF．46．已知：如图7－181，在△ABC中，AB=AC，∠C= 2∠A，以 AB为弦的圆O与 BC切干点 B，与 AC交于 D点．求证：AD=DB=BC．47．已知：如图7－182，过△ADG的顶点A作直线与DG的延长线相交于C，过G作△ADG的外接圆的切线二等分线段AC于E．求证：AG2=DG·CG．48．已知：如图7－183，PA，PB分别切⊙O于A，B两点，PCD为割线．求证：AC·BD=BC·AD．BC=BA，连结AC交圆于点E．求证：四边形ABDE是平行四边形．50．已知：如图7－185，∠1=∠2，⊙O过A，D两点且交AB，AC于E，F，BC切⊙O于D．求证：EF∥BC．51．已知：如图7－186，AB是半圆直径，EC切半圆于点C，BE⊥CE交AC 于F．求证：AB=BF．52．已知：如图7－187，AB为半圆直径，PA⊥AB，PC切半圆于C点，CD⊥AB于D交PB于M．求证：CM=MD．（五）作图53．求作以已知线段AB为弦，所含圆周角为已知锐角∠α（见图7－188）的弧（不写作法，写出已知、求作，答出所求）．54．求作一个以α为一边，所对角为∠α，此边上高为h的三角形．55．求作一个以a为一边，m为此边上中线，所对角为∠α的三角形（不写作法，答出所求）．切线长定理及弦切角练习题(答案)（一）填空1．36° 2．28° 3．50° 4．32°5．22° 6．等腰 7．54°（二）选择8．C 9．D 10．B 11．C（三）计算12．30°，30°．13．45°．提示：连接AB交PD于E．只需证明∠ADE=∠AED，证明时利用三角形外角定理及弦切角定理．14．30°．提示：因为PQ=QC，所以∠QCP=∠QPC．连接OQ，则知∠POQ与∠QCP互余．又∠OAQ=∠OQA与∠QPC互余，所以∠POQ=∠OAQ=∠OQA．而它们的和为90°（因为∠AOC=90°）．所以∠OAQ=30°16．67.5°．提示：解法一连接AC，则∠PAC=∠PCA．又∠P=45°，所以∠PAC=∠PCA=67.5°．从而∠B=∠PAC=67.5°．解法二连接OA，OC，则∠AOC=180°－∠P=135°，所以17．24°．提示：连接OA，则∠POA=66°．18．60°．提示：连接BD，则∠ADB=40°，∠DBC=20°．设∠ABD=∠BDC（因为AB//CD）=x°，则因∠B+∠D=180°，所以2x°+60°=180°，x°=60°，从而∠ADE=∠ABD=60°．19．100°或80°．提示： M可在弦AB对的两弧的每一个上．从而22．42°．提示：∠ABM=∠NAM．于是显然△ABM∽△NAM，NMP，所以△PMB∽△NMP，从而∠PBM=∠NPM．再由∠ABM=∠NAM，就有∠PBA=∠PBM+∠NAM=∠NPM+∠NAM=180°－∠PNA=42°．23．28°，39°．提示：连接PC．24．41°．提示：求出∠QAC和∠ACB的度数．25．100°．以DB=9．因为2DP2=2×9，由此得DP2=9．又DP＞0，所以DP=3，从而，DE=2×3=6（cm）．28．45°．提示：连接AC．由于DA=DE，所以∠ABE+∠BAE=∠AED=∠EAD=∠CAD+∠CAE，但∠ABE=∠CAD，所以∠BAE=∠CAE．由于∠BAE+∠CAE=90°，所以∠BAE=45°．29．60°．提示：解法一连接AC，则AC⊥BC．又AF⊥CE，所以∠ACE=∠F．又DC切⊙O于C，所以∠ACE=∠B．所以∠F=∠B．因为AF=BF，所以∠BAF=∠B=∠F．所以∠BAF=60°．31．37°．提示：连接AC，则∠M=∠ACN=∠CAD．32．17°．提示：连接PC，则∠QPC+∠PBC=90°．45°=∠D=（∠BPQ+∠QPC）∠DCP=（∠BPQ+∠QPC）－∠PBC=[∠BPQ+（90°－∠PBC）]－∠PBC．所以2∠PBC－∠BPQ=45°．（1）又∠PBC+∠BPQ=39°，（2）从而∠PBC=28°，∠BPQ=11°．于是∠A=∠PBC－∠BPQ=17°．34．30°．提示：连接BE，由∠1=∠2，可推出∠EBF=∠ECB=∠EBC，而这三个角的和为90°，所以每个角为30°．36．60°．提示：连接OB，则OB⊥CE，从而∠C=∠BOE= 60°．37．（1）提示：连接OC，则∠E=∠OCB=∠OBC=∠CDE，所以△ABE为等腰三角形．38．（1）提示：连接BE．只需证明∠ABE=∠DBE．（四）证明39．提示：AC，BC各平分∠A，∠B．设法证出∠A+∠B=180°．40．提示：连接OP，设法证出∠BPC=∠BPO．42．提示：在△BCE和△DAH中，∠BCE=∠DAH（它们都与∠DCH互补）．又A，D，C，H共圆，所以∠CEB=∠ACB=∠AHD，从而△BCE∽△DAH．这就得所要证明的比例式．43．提示：连接AC．先证明A，E，C，D四点共圆．由此得∠ADE=（∠ACE=）∠MAB，所以AB//DE．44．提示：证法一延长AO交⊙O于点E，连接EC，则∠BCA=∠E，且∠ACD=∠E．所以∠BCA=∠ACD．证法二连接OA，则∠BCA与∠OCA互余；又∠ACD与∠OAC互余，而∠OCA=∠OAC，所以∠BCA=∠ACD．46．提示：由已知得∠A=36°，∠B=∠C=72°，∠DBC=∠A=36°，所以∠ABD=36°，从而AD=BD．又∠C=∠CDB=72°，所以BD=BC．47．提示：过A作CD的平行线交BC于H，则AH=CG．然后证AG2=DG·AH=DG·CG．49．提示：因为BC=BA，所以∠A=（∠C=）∠D；又∠CED=∠DBF（BF是AB 的延长线），所以它们的补角∠DEA=∠ABD．从而四边形ABDE是平行四边形．50．提示：连接DE，则∠BDE=∠1=∠2=∠FED．所以EF//BC．51．提示：连接BC，则∠ACB=90°=∠FCB．因为CE⊥BE，所以∠F=∠ECB．因为EC切半圆于C，所以∠ECB=∠A，所以∠A=∠F，因此AB=BF．52．提示：连接AC，BC并延长BC交AP延长线于点N．首先所以CM=MD．。