齿轮机构的齿廓啮合基本规律、特点和类型
- 格式:ppt
- 大小:3.01 MB
- 文档页数:39

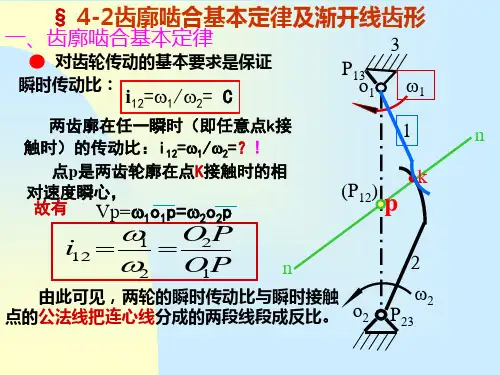
齿轮机构的齿廓啮合基本规律、特点和类型齿轮机构的齿廓啮合基本规律、特点和类型第一节齿轮机构的齿廓啮合基本规律,特点和类型平行轴垂直轴交错轴返回齿轮机构的齿廓啮合基本规律、特点和类型一,齿轮机构的特点和类型(一)平行轴线齿轮传动返回齿轮机构的齿廓啮合基本规律、特点和类型齿轮机构的齿廓啮合基本规律、特点和类型(二)空间齿轮传动5返回齿轮机构的齿廓啮合基本规律、特点和类型齿轮传动的基本要求传动准确和平稳(任意瞬时传动比恒定) 传动准确和平稳(任意瞬时传动比恒定)------由齿由齿轮轮廓和制造精度决定. 轮轮廓和制造精度决定. 传动比ω1 i12 = ω2承载能力强(足够强度,刚度,耐磨) 承载能力强(足够强度,刚度,耐磨)--------由齿由齿轮尺寸,材料和工艺决定. 轮尺寸,材料和工艺决定.返回齿轮机构的齿廓啮合基本规律、特点和类型二,齿廓啮合基本定律保证两齿廓在公法线n-n 保证两齿廓在公法线方向不发生分离或相互嵌接触点k的线速度在公入,接触点的线速度在公法线上的投影应相等. 法线上的投影应相等.即Cυk1 cosαk1 =υk 2 cosαk 2ω1 O2 N 2 O2 P i12 = = = ω 2 O1 N1 O1 P 返回齿轮机构的齿廓啮合基本规律、特点和类型齿廓啮合基本定律:相互啮合传动的一对齿廓,在齿廓啮合基本定律:相互啮合传动的一对齿廓,任意瞬时的传动比, 任意瞬时的传动比,必等于该瞬时两轮连心线被齿廓接触点公法线所分割的两线段长度的反比. 接触点公法线所分割的两线段长度的反比. C—节点,节圆半径分别为节点, 节点r ,r/ 1/ 2O1r’1一对齿轮传动, 一对齿轮传动,可视为上述两节圆作纯滚动的摩擦轮传动. 作纯滚动的摩擦轮传动.cO2 r’2ω1 O2 N 2 O2C r2 ‘i12 = = = = ω2 O1 N1 O1C r1 ‘返回齿轮机构的齿廓啮合基本规律、特点和类型第二节渐开线齿廓渐开线的形成----一条直线在圆周上作纯滚动时, 渐开线的形成一条直线在圆周上作纯滚动时,该一条直线在圆周上作纯滚动时直线上任意一点的轨迹称该圆的渐开线. 直线上任意一点的轨迹称该圆的渐开线.返回齿轮机构的齿廓啮合基本规律、特点和类型一,渐开线的形成和特性 (1) NK = NA线长是K点的曲率半径 (2)NK线长是点的曲率半径, ) 线长是点的曲率半径, N点为曲率中心.靠近基圆的渐点为曲率中心. 点为曲率中心开线曲率半径小,曲率大. 开线曲率半径小,曲率大. NK 线是K点的法线点的法线. 点的速度垂线是点的法线. K点的速度垂直于NK. 直于 . (3)渐开线形状取决于基圆 ) 的大小; rb →∞,渐开线趋近的大小; , 直线(齿条). 直线(齿条). (4)基圆内无渐开线. )基圆内无渐开线.返回齿轮机构的齿廓啮合基本规律、特点和类型的压力角---渐开线齿廓上 (5)渐开线齿廓上任意点的压力角渐开线齿廓上 )渐开线齿廓上任意点K的压力角 K点的法线与齿廓上该点速度方向线之间的夹角k. 点的法线与齿廓上该点速度方向线之间的夹角α 点的法线与齿廓上该点速度方向线之间的夹角cos αk =ON/OK= rb/r k返回齿轮机构的齿廓啮合基本规律、特点和类型二,渐开线齿廓啮合特点r’1 O1 rb1 N1(一)中心距可分性渐开线齿廓两基圆内公切线只有一条, 渐开线齿廓两基圆内公切线只有一条, 因而与中心线只有一个交点. 因而与中心线只有一个交点.CN2 rb2 r’2 O2ω1 rb 2 r2 ‘i12 = = = ω 2 rb1 r1 ‘中心距具有可分性---中心距变化, 点中心距具有可分性中心距变化,P点中心距变化位置变化, 变化, 位置变化,则r’1,r’2变化,但因基圆半径固定不变,所以传动比不变. 径固定不变,所以传动比不变.返回齿轮机构的齿廓啮合基本规律、特点和类型(二)啮合线为直线啮合线----齿轮传动时, 啮合线齿轮传动时,一对齿啮齿轮传动时合点所走过的轨迹. 合点所走过的轨迹.对于渐开线齿轮,啮合线是一条不变的直线, 齿轮,啮合线是一条不变的直线, 即两基圆的内公切线N 即两基圆的内公切线 1N2.返回齿轮机构的齿廓啮合基本规律、特点和类型啮合角----啮合线啮合角啮合线N1N2与两节圆过啮合线节点P的公切线所夹锐角α’的公切线tt所夹锐角节点的公切线所夹锐角 .该角在啮合过程中保持不变. 角在啮合过程中保持不变.cos α’ =rb1/r1’= rb2/r2’返回齿轮机构的齿廓啮合基本规律、特点和类型第三节渐开线标准齿轮几何尺寸返回齿轮机构的齿廓啮合基本规律、特点和类型1,齿数Z ,齿数 2,齿顶圆直径:da=d+2ha=m(z+2) ,齿顶圆直径: 3,齿根圆直径:df=d-2hf=m(z-2.5) ,齿根圆直径: 4,齿厚sk,齿槽宽 k ,齿厚齿槽宽e 齿距P 齿距k= sk+ ek= π dk/Z, , dk= Z Pk/ π5,分度圆---圆周上的P/ π =m(模数)为标准值 ,分度圆圆周上的 (模数) GB1357-87,压力角亦为标准值的圆. 亦为标准值的圆. ,压力角α亦为标准值的圆 d=m Z,α=200,标准齿轮P=s+e,s=e= π m/2 , ,返回齿轮机构的齿廓啮合基本规律、特点和类型6,全齿高h= ha+ hf ,全齿高齿顶高h 齿顶高 a=ha_m=m, , 齿根高h 齿根高f=(ha_+c_)m=1.25m, , 其中:c= c_m顶隙作用是避免轮齿顶撞,贮存润滑油. 顶隙作用是避免轮齿顶撞, 其中顶隙作用是避免轮齿顶撞贮存润滑油. m≥1时,ha_=1, c_=0.25 时 , m_lt;1时, ha_=1, c_=0.35 _lt; 时 , 7,标准直齿圆柱齿轮的分度圆半径, r=rb/cos α,db=d cos α=mZ cos α ,返回齿轮机构的齿廓啮合基本规律、特点和类型第四节渐开线标准直齿圆柱齿轮的啮合传动一,正确啮合条件---一对齿相正确啮合条件一对齿相邻两齿同侧齿廓间在啮合线上的法线距离相等, 的法线距离相等,pn1=pn2 . 渐开线的特性即p 渐开线的特性即 b1=pb2 推导: 推导: π db1/z1= π db2/z2 m1cos α1= m2cosα2 结论: 结论:m1= m2=m, α1=α2=200 ,二,标准中心距 a=(d2+d1)/2=m(z2+z1)/2 标准安装, (标准安装,s1=e2,侧隙为零) ,侧隙为零)返回齿轮机构的齿廓啮合基本规律、特点和类型三,连续传动条件连续传动条件---前一对齿轮即将脱离连续传动条件前一对齿轮即将脱离啮合时,后一对齿轮刚好进入啮合. 啮合时,后一对齿轮刚好进入啮合. 重合度: ε=B2B1/pb= [Z1(tgαa1-tg α’)+ Z2(tgαa2-tg α’)] ≥1ha_=1, α=200时,εma_≈1.982 , 标准齿轮恒有1_lt;ε_lt;2,不必校核标准齿轮恒有 , 但要理解其物理含义. 但要理解其物理含义.返回齿轮机构的齿廓啮合基本规律、特点和类型第五节渐开线齿廓的根切现象一,齿轮加工方法(一)仿形(成型)法仿形(成型)返回齿轮机构的齿廓啮合基本规律、特点和类型(二)范成法返回齿轮机构的齿廓啮合基本规律、特点和类型二,根切现象和最少齿数避免根切的条件: 避免根切的条件: PB2≤PN 而:PB2= ha_m/sin α PN=PO sin α =mz/2sinα 有:Z≥2 ha_/sin2α ha_ =1,a=200时 , Zmin=17返回。



齿轮机构的齿廓啮合基本规律特点和类型齿轮机构是一种重要的传动机构,用于将转动的运动和转矩传递的机械元件。
齿轮的齿廓啮合是齿轮机构工作的核心部分,其基本规律、特点和类型对于齿轮机构的设计和应用具有重要的参考价值。
一、基本规律1.齿廓规律:齿廓规律描述了齿轮齿廓线的几何形状。
常见的齿廓规律有圆弧齿廓、渐开线齿廓和非渐开线齿廓等。
(1)圆弧齿廓:圆弧齿廓是通过圆弧曲线来描述齿槽的齿轮齿廓。
圆弧齿廓的优点是简单,易于加工,但啮合时存在齿间间隙和传动误差。
(2)渐开线齿廓:渐开线齿廓是常用的齿廓规律,可以在齿轮齿廓上实现圆顶啮合,具有传动平稳、效率高、传动误差小等优点。
常见的渐开线齿廓包括标准渐开线、修形渐开线和端面渐开线等。
(3)非渐开线齿廓:非渐开线齿廓是指不能用一个等角参数来描述的齿廓,例如双曲线齿廓和伞齿轮齿廓等。
非渐开线齿廓的优点是能够实现更大的传动比和更平滑的啮合过程。
2.齿廓规律的选择:选择合适的齿廓规律可以提高齿轮机构的传动效率和运动平稳性。
在选择齿廓规律时,需要考虑以下因素:(1)传动要求:根据齿轮机构的传动要求,选择适合的齿廓规律。
例如,要求传动平稳和效率高的应选用渐开线齿廓,要求传动比大且运动平稳的应选用非渐开线齿廓。
(2)制造和加工因素:考虑齿轮的加工工艺和精度要求,选择适合加工的齿廓规律。
例如,圆弧齿廓适合用铣床加工,而渐开线齿廓适合用滚齿机加工。
二、特点1.几何特点:齿廓啮合过程中,齿轮的齿廓线和花键的啮合点始终保持一定的关系,包括齿廓的曲率半径和齿廓线与法线的夹角等特征。
这些几何特点决定了齿轮的啮合性能和传动特性。
2.运动特点:齿轮机构的齿廓啮合过程中,齿轮的运动特点包括啮合速度、传动比和传动误差等。
齿轮的啮合速度是指齿轮工作时齿廓线移动的速度,而传动比是指输入轴和输出轴的转速之比。
传动误差则是齿轮啮合过程中由于齿廓不完美造成的传动误差,会导致振动和噪声。
三、类型1.直齿轮:直齿轮是最常见的齿轮类型,其齿廓线是直线,适用于输送大扭矩或平稳传动的场合。





什么是齿廓啮合基本定律齿廓啮合基本定律是指在齿轮啮合过程中,两齿轮齿廓曲线的几何关系的基本规律。
它是研究齿轮啮合的重要理论基础,对于齿轮传动的设计和分析具有重要的指导作用。
齿廓啮合基本定律分为两个方面,即齿轮的齿廓形状和齿轮的啮合条件。
首先是齿轮的齿廓形状。
齿轮的齿廓形状决定了齿轮的传动性能和运动特性。
齿廓形状通常由齿廓曲线来描述,包括圆弧齿廓和直线齿廓两种类型。
圆弧齿廓适用于传统的齿轮传动,其齿廓曲线为圆弧形状,具有平稳的传动特性;而直线齿廓适用于高速和高精度传动,其齿廓曲线为直线形状,具有更高的传动效率和更小的传动误差。
其次是齿轮的啮合条件。
齿轮的啮合条件是指在齿轮传动中,齿轮齿廓曲线的几何关系必须满足一定的条件,才能保证传动的可靠性和稳定性。
齿轮的啮合条件包括啮合比、啮合角和啮合线等。
啮合比是指两个齿轮的齿数之比,它决定了齿轮的传动比;啮合角是指齿轮齿廓曲线的夹角,它决定了齿轮的啮合位置和啮合效果;啮合线是两个齿轮齿廓曲线的公共切线,它决定了齿轮的传动方向和传动效率。
齿廓啮合基本定律的应用可以通过齿轮的设计和分析来实现。
在齿轮设计中,通过选择合适的齿廓形状和齿廓参数,可以满足不同传动要求的齿轮传动。
在齿轮分析中,通过对齿轮的齿廓曲线进行分析和计算,可以评估齿轮的传动性能和运动特性,进而优化齿轮的设计方案。
齿廓啮合基本定律是齿轮传动的重要理论基础,它指导着齿轮的设计和分析。
通过遵循齿廓啮合基本定律,可以实现齿轮传动的可靠性、稳定性和高效性。
在齿轮传动领域的应用中,齿廓啮合基本定律是必须要遵循的原则,它为齿轮传动的发展和应用提供了重要的理论基础。