立体几何随堂测试

立体几何测试题一、选择题（每题3分，共15分）1. 在正方体ABCD-EFGH中，点M是棱AB的中点，点N是棱AD的中点，点P是棱CD上的点，且DP:PC=1:2。

求线段MN与MP所成角的余弦值。

A. 1/3B. √2/3C. √3/3D. 2/32. 已知圆锥的底面半径为r，高为h，求圆锥的侧面展开图的扇形半径。

A. rB. hC. √(r² + h²)D. 2πr3. 一个球的体积为V，求该球的表面积。

A. 3VB. 4πVC. 6VD. 4π(3V/π)^(2/3)4. 已知三棱锥P-ABC的四个顶点均在同一个球面上，且PA=PB=PC=4，AB=6，AC=BC=2√3，求球的半径。

A. 2B. 4C. 2√3D. 35. 一个正四面体的顶点都在一个球面上，且正四面体的边长为a，求球的半径。

A. a/√2B. a/2C. √3a/4D. a/√3二、填空题（每题4分，共20分）6. 若一个长方体的长、宽、高分别为l、w、h，则其对角线的长度为_________。

7. 已知一个圆柱的底面半径为r，高为h，求圆柱的体积，其体积为_________。

8. 若一个圆锥的底面半径为r，高为h，求圆锥的体积，其体积为_________。

9. 已知一个球的直径为d，求球的表面积，其表面积为_________。

10. 若一个正三棱柱的底面边长为a，高为h，求其体积，其体积为_________。

三、简答题（每题10分，共30分）11. 描述如何使用向量法证明两个平面的垂直性。

12. 给出一个球面上四点构成的四面体的体积公式。

13. 解释何为“内接球”和“外接球”，并给出一个几何体的内接球和外接球的半径计算方法。

四、计算题（每题15分，共30分）14. 已知一个正十二面体的边长为a，求其体积。

15. 已知一个圆锥的底面半径为r，高为h，求圆锥的内接球的半径。

五、证明题（15分）16. 证明：在一个正四面体中，从一个顶点出发的三条棱的中点，这四个点构成一个正四面体。

立体测试题及答案一、单项选择题（每题2分，共10题）1. 下列哪个选项是立体几何中的基本元素？A. 点B. 线C. 面D. 体答案：D2. 空间中两条直线的位置关系有几种？A. 1种B. 2种C. 3种D. 4种答案：C3. 一个立方体有多少个顶点？A. 6B. 8C. 12D. 14答案：B4. 一个正四面体有多少条棱？A. 6B. 8C. 12D. 16答案：A5. 空间直角坐标系中，点(1,2,3)到原点的距离是多少？A. 1B. 2C. 3D. √14答案：D6. 一个球体的表面积公式是？A. 4πr²B. 2πr²C. πr²D. 4πr³答案：A7. 空间中两个平面的位置关系有哪些？A. 平行B. 相交C. 重合D. 以上都是答案：D8. 一个圆柱体的体积公式是？A. πr²hB. 2πrhC. πr²D. πr³答案：A9. 空间中一个点到一个平面的距离公式是？A. |Ax + By + Cz + D| / √(A² + B² + C²)B. |Ax + By + Cz - D| / √(A² + B² + C²)C. |Ax + By + Cz + D| / √(A² + B²)D. |Ax + By + Cz - D| / √(A² + B²)答案：B10. 空间中一个点到一条直线的距离公式是？A. |Ax + By + Cz + D| / √(A² + B² + C²)B. |Ax + By + Cz - D| / √(A² + B² + C²)C. |(Ax + By + Cz + D) / (A² + B² + C²)| * √(A² + B²)D. |(Ax + By + Cz - D) / (A² + B² + C²)| * √(A² + B²)答案：D二、多项选择题（每题3分，共5题）1. 空间中两个平面相交，它们的交线是？A. 直线B. 曲线C. 点D. 面答案：A2. 空间中一个点到一个平面的距离公式中，A、B、C、D分别代表什么？A. 平面方程的系数B. 平面方程的常数项C. 点的坐标D. 点到平面的距离答案：A, B3. 空间直角坐标系中，点(1,2,3)到点(4,5,6)的距离公式是？A. √((4-1)² + (5-2)² + (6-3)²)B. √((1-4)² + (2-5)² + (3-6)²)C. √((4-1)² + (5-2)² + (6-3)²)D. √((1-4)² + (2-5)² + (3-6)²)答案：A, B4. 空间中一个点到一条直线的距离公式中，A、B、C、D分别代表什么？A. 直线方程的系数B. 直线方程的常数项C. 点的坐标D. 点到直线的距离答案：A, C5. 空间中一个平面的方程可以表示为？A. Ax + By + Cz + D = 0B. Ax + By + Cz = DC. Ax + By + Cz + D = ED. Ax + By + Cz = 0答案：A, D结束语：以上是立体测试题及答案的全部内容，希望对你有所帮助。

《立体几何》测试及答案（时间：120分钟满分：150分）一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有 一项是符合题目要求的.1 .已知平而。

内的一条直线1及平而£,则'3_L £”是“ a_L £”的（）A.充分必要条件B.充分不必要条件C.必要不充分条件 D,既不充分也不必要条件 解析根据直线与平面垂直的判定定理，由lu "”可证得“a_L £”，即充分性是 成立的.反之由“ a 工B,k a”不一定得到“AL £”，即必要性不成立.所以是 “。

J_ £ ”的充分不必要条件.故选B.答案B72 .已知圆锥的顶点为凡母线州，所所成角的余弦值为石，以与圆锥底面所成角为45° ,若 O △为5的面积为5仃，则该圆锥的侧面积为（） A. 40（72 +1） nB. 40^2 HC.8（4i5 + 5） nD. 8710 n解析设。

为圆锥底而圆的圆心，设底而圆的半径为r.以与圆锥底而所成角为45° ,即/80=45°.所以以=小厂7 7母线闩1,所所成角的余弦值为5即cosN 川沙=小 o o 由 S^=^PA • j^sinZJj^=|x2?X^^=5J15. A?=40, ， 2 o v故 S 秘侧=n r • PA — n r • \[2r=y[2 n y = 4(h/2 n .答案B3 .如图，在正四棱柱物/一儿RG 〃中，底而边长为2,直线。

乙与平而月以所成角的正弦值 为今则该正四棱柱的高为（）贝I] sinN 川哈、= 7、J15 S 8A. 2B. 3C. 4D. 5解析以〃为坐标系原点，DA, DC 、弧所在直线分别为x, y, z 轴建立空间直角坐标系。

一 xyz,如图所示，设正四棱柱的高为方，则。

（0, 0，0）,月（2, 0, 0）,。

（0, 2, 0）, 〃（0, 0, 血，4（0, 2,a ），五=（0, 0,方），赤=（-2, 2, 0）,遨=（0, -2,方）.设平而月曲的法n • m —2乂+2%=0,向量为〃=（%，必，％）,则j —令二=2,则必=方，&=方，A=（/b h,.n •速=-2%+方冬=0, 2）为平面月四的一个法向量.又直线CG 与平面月8所成角的正弦值为所以cos " CG ）答案C4 .设三棱柱 四。

立几测001试一、选择题：1．a 、b 是两条异面直线，下列结论正确的是（ ）A ．过不在a 、b 上的任一点，可作一个平面与a 、b 都平行B ．过不在a 、b 上的任一点，可作一条直线与a 、b 都相交C ．过不在a 、b 上的任一点，可作一条直线与a 、b 都平行D ．过a 可以且只可以作一个平面与b 平行2．空间不共线的四点，可以确定平面的个数为 ( )Ａ．0 Ｂ．1 Ｃ．1或4 Ｄ．无法确定3．在正方体1111ABCD A B C D -中，M 、N 分别为棱1AA 、1BB 的中点，则异面直线CM 和1D N 所成角的正弦值为 ( ) Ａ．19 Ｂ．2345 254．已知平面α⊥平面β，m 是α内的一直线，n 是β内的一直线，且m n ⊥，则：①m β⊥；②n α⊥；③m β⊥或n α⊥；④m β⊥且n α⊥。

这四个结论中，不正确．．．的三个是 ( )Ａ．①②③ Ｂ．①②④ Ｃ．①③④ Ｄ．②③④5.一个简单多面体的各个面都是三角形，它有6个顶点，则这个简单多面体的面数是( ) A. 4 B. 5 C. 6 D. 86. 在北纬45°的纬度圈上有甲、乙两地，两地经度差为90°，则甲、乙两地最短距离为（设地球半径为R ）( ) A.R π42 B. R 3π C. R 2π D. 3R7. 直线l ⊥平面α，直线m ⊂平面β，有下列四个命题(1)m l ⊥⇒βα// (2)m l //⇒⊥βα (3)βα⊥⇒m l // (4)βα//⇒⊥m l 其中正确的命题是( )A. (1)与(2)B. (2)与(4)C. (1)与(3)D. (3)与(4)8. 正三棱锥的侧面均为直角三角形，侧面与底面所成角为α，则下列不等式成立的是( ) A. 60πα<< B.46παπ<< C.34παπ<< D.23παπ<<9．ABC ∆中，9AB =，15AC =，120BAC ∠=︒，ABC ∆所在平面α外一点P 到点A 、B 、C 的距离都是14，则P 到平面α的距离为( )Ａ．7 Ｂ．9 Ｃ．11 Ｄ．1310．在一个45︒的二面角的一个平面内有一条直线与二面角的棱成角45︒，则此直线与二面角的另一个平面所成角的大小为 ( )Ａ．30︒ Ｂ．45︒ Ｃ．60︒ Ｄ．90︒11. 如图,E, F 分别是正方形SD 1DD 2的边D 1D,DD 2的中点, 沿SE,SF,EF 将其折成一个几何体,使D 1,D,D 2重合,记作 D.给出下列位置关系:①SD ⊥面DEF; ②SE ⊥面DEF;③DF ⊥SE; ④EF ⊥面SED,其中成立的有: ( )Ａ. ①与② B. ①与③ C. ②与③ D. ③与④12. 某地球仪的北纬60度圈的周长为6πcm,则地球仪的表面积为( )A. 24πcm 2B. 48πcm 2C. 144πcm 2D. 288πcm 2二、填空题（本大题共4小题，每小题4分，共16分） 13. 直二面角α—MN —β中，等腰直角三角形ABC 的斜边BC ⊂α，一直角边AC ⊂β，BC 与β所成角的正弦值是46，则AB 与β所成角大小为__________。

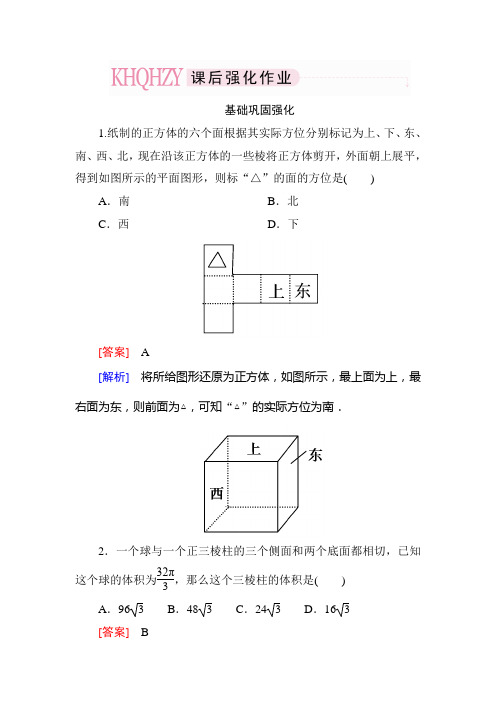
基础巩固强化1.纸制的正方体的六个面根据其实际方位分别标记为上、下、东、南、西、北，现在沿该正方体的一些棱将正方体剪开，外面朝上展平，得到如图所示的平面图形，则标“△”的面的方位是( )A ．南B ．北C ．西D ．下[答案] A[解析] 将所给图形还原为正方体，如图所示，最上面为上，最右面为东，则前面为△，可知“△”的实际方位为南．2．一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积为32π3，那么这个三棱柱的体积是( )A ．963B ．483C ．243D ．16 3 [答案] B[解析] 已知正三棱柱的高为球的直径，底面正三角形的内切圆是球的大圆．设底面正三角形的边长为a ，球的半径为R ，则a ＝23R ，又43πR 3＝32π3，∴R ＝2，a ＝43，于是V ＝34a 2·2R ＝48 3.3．(2012·新课标全国，7)如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为( )A ．6B ．9C ．12D ．18[答案] B[解析] 由三视图知，该几何体是一个三棱锥，由俯视图知三棱锥的底面是等腰三角形，底边长为6，底边上的高为3，面积S ＝12×6×3＝9，由正视图和侧视图可知棱锥的高为3，∴体积V ＝13×9×3＝9.4．(文)若某空间几何体的三视图如图所示，则该几何体的体积是( )A ．2B ．1 C.23 D.13[答案] B[解析] 由几何体的三视图可知，该几何体是直三棱柱，其直观图如图所示，其体积为V ＝12×2×1×2＝1.(理)(2011·潍坊二检)如图是一个长方体截去一个角后所得多面体的三视图，则该多面体的体积为( )A.1423B.2843C.2803D.1403[答案] B [解析]截去一角在正视图中位于左侧上部，在侧视图中位于右侧上部，结合俯视图可知，截去的一角应位于几何体的上部左前方，可画出多面体的形状如图．这个多面体是由长方体截去一个正三棱锥而得到的，所以所求多面体的体积V ＝V 长方体－V 正三棱锥＝4×4×6－13×(12×2×2)×2＝2843.5．(文)一空间几何体的三视图如图所示，则该几何体的体积为( )A ．2π＋2 3B ．4π＋2 3C ．2π＋233 D ．4π＋233[答案] C[解析] 由几何体的三视图可知，该几何体是由一个底面直径和高都是2的圆柱和一个底面边长为2，侧棱长为2的正四棱锥叠放而成．故该几何体的体积为V ＝π×12×2＋13×(2)2×3＝2π＋233，故选C.[点评] 由三视图想象几何体的形状时，一要注意常见柱、锥、台的三视图结构特征，二要注意方位，三要注意细节．本题中正视图与侧视图都不变，若俯视图中把外部的圆改为正方形，则几何体就是上部为正四棱锥，下部为正四棱柱的组合体．(理)(2011·湖南文，4)设下图是某几何体的三视图，则该几何体的体积为( )A ．9π＋42B ．36π＋18 C.92π＋12 D.92π＋18[答案] D[解析] 由三视图可知，该几何体是一个球体和一个长方体的组合体．其中，V 球＝43π·(32)3＝9π2，V 长方体＝2×3×3＝18.所以V 总＝92π＋18.6.(2012·山西高考联合模拟)一个几何体是由若干个相同的正方体组成的，其正视图和侧视图如图所示，则这个几何体最多可由这样的正方体组成的个数为( )A ．12个B ．13个C ．14个D ．18个[答案] B[解析] 由正视图知该几何体有三列，左右两排都存在2层的情形，中间一排，只有一层，由侧视图知，该几何体有三行，前后两排都存在2层的情形，中间一排只有一层，因此此几何体最多可由13个小正方体组成，你能求出最少可由多少个小正方体构成吗？7．圆台的上、下底半径分别为2和4，母线长为4，则截得此圆台的圆锥侧面展开图的中心角为________．[答案] π[解析] 如图，设PD ＝x ，则24＝x x ＋4，∴x ＝4，∴θ＝48×2π＝π.8．一个底面半径为1，高为6的圆柱被一个平面截下一部分，如图(1)所示，截下部分的母线最大长度为2，最小长度为1，则截下部分的体积是________．[答案] 3π2[解析] 根据对称性把它补成如图(2)所示的圆柱，这个圆柱的高是3，体积是所求几何体体积的2倍，故所求的几何体的体积是12×π×12×3＝3π2.故填3π2.9．圆柱内切球的表面积为4π，则圆柱的表面积为________． [答案] 6π[解析] 设球半径为R (R >0)，则圆柱的底面半径为R ，高为2R ，由条件知，4πR 2＝4π，∴R ＝1.∴圆柱的表面积S ＝2π·R 2＋2πR ·2R ＝6πR 2＝6π.10．已知P 在矩形ABCD 的边DC 上，AB ＝2，BC ＝1，F 在AB 上且DF ⊥AP ，垂足为E ，将△ADP 沿AP 折起，使点D 位于D ′位置，连接D ′B 、D ′C 得四棱锥D ′－ABCP .(1)求证：D ′F ⊥AP ；(2)若PD ＝1，且平面D ′AP ⊥平面ABCP ，求四棱锥D ′－ABCP 的体积．[解析] (1)∵AP ⊥D ′E ，AP ⊥EF ，D ′E ∩EF ＝E ， ∴AP ⊥平面D ′EF ，∴AP ⊥D ′F .(2)∵PD ＝1，∴四边形ADPF 是边长为1的正方形， ∴D ′E ＝DE ＝EF ＝22，∵平面D ′AP ⊥平面ABCP ，D ′E ⊥AP ，∴D ′E ⊥平面ABCP ， ∵S 梯形ABCP ＝12×(1＋2)×1＝32，∴V D ′－ABCP ＝13×D ′E ×S 梯形ABCP ＝24.能力拓展提升11.如图，正方体ABCD －A 1B 1C 1D 1的棱长为2.动点E ，F 在棱A 1B 1上，点Q 是棱CD 的中点，动点P 在棱AD 上．若EF ＝1，DP ＝x ，A 1E ＝y (x ，y 大于零)，则三棱锥P －EFQ 的体积( )A ．与x ，y 都有关B ．与x ，y 都无关C ．与x 有关，与y 无关D ．与y 有关，与x 无关[答案] C[解析] 设P 到平面EFQ 的距离为h ，则V P －EFQ ＝13×S △EFQ ·h ，由于Q 为CD 的中点，∴点Q 到直线EF 的距离为定值2，又EF ＝1，∴S △EFQ 为定值，而P 点到平面EFQ 的距离，即P 点到平面A 1B 1CD 的距离，显然与x 有关与y 无关，故选C.12．(2011·陕西文，5)某几何体的三视图如图所示，则它的体积为( )A ．8－2π3B ．8－π3C ．8－2πD.2π3[答案] A[解析] 由三视图知，原几何体为如图所示一正方体挖去一个与正方体等高底面是正方形的内切圆的圆锥，则其体积为V ＝23－13π×12×2＝8－2π3.故选A. 13．(2011·东北三校)一个几何体的三视图及部分数据如图所示，侧视图为等腰三角形，俯视图为正方形，则这个几何体的体积等于( )A.13B.23C.156D.6224[答案] A[解析] 由三视图知，这是一个四棱锥，其底面为正方形，一条侧棱垂直于底面其长度为2，底面正方形对角线长为1，∴边长为22，体积V ＝13×(22)2×2＝13.14．(文)一等边圆柱(轴截面是正方形的圆柱)的表面积为24π，一圆锥与此圆柱一个底面重合，顶点在另一个底面上，则此圆锥的表面积为________．[答案] 4(5＋1)π[解析] 设圆柱底半径为R ，则2πR 2＋2πR ·2R ＝24π，∴R ＝2， ∴圆锥的底半径为R ＝2，高为4，母线长l ＝22＋42＝25，∴圆锥的表面积S ＝πR 2＋πRl ＝4π＋45π＝4(5＋1)π.(理)圆锥的高为4，侧面积为15π，其内切球的表面积为________．[答案] 9π[解析]设圆锥底面半径为r (r >0)，则母线长l ＝16＋r 2，由πrl ＝15π得r ·16＋r 2＝15，解之得r ＝3，∴l ＝5.设内切球半径为R ，作出圆锥的轴截面如图，则BD ＝BO 1＝3，PD ＝5－3＝2，PO ＝4－R ，∵OD ⊥PB ，∴R 2＋4＝(4－R )2，∴R ＝32， ∴球的表面积S ＝4πR 2＝9π.15．(文)(2011·安徽省淮南市模拟)如图是以正方形ABCD为底面的正四棱柱被一平面所截得的几何体，四边形EFGH为截面，且AB＝BC＝2，AE＝1，BF＝DH＝2，CG＝3.(1)证明：截面四边形EFGH是菱形；(2)求几何体C－EFGH的体积．[解析](1)证明：因为平面ABFE∥平面CDHG，且平面EFGH分别交平面ABFE、平面CDHG于直线EF、GH，所以EF∥GH.同理，FG∥EH.因此，四边形EFGH为平行四边形．因为BD⊥AC，而AC为EG在底面ABCD上的射影，所以EG⊥BD.因为BF綊DH，所以FH∥BD.因此，FH⊥EG.所以四边形EFGH是菱形．(2)解：连接CE、CF、CH、CA，则V C－EFGH＝V－V C－ABFE－V C－ADHE，其中V是几何体的体积，∵AE＝1，BF＝DH＝2，CG＝3且几何体是以正方形ABCD为底面的正四棱柱的一部分，所以该几何体的体积为V＝(2)2×2＝4，V C－ABFE＝13×S四边形ABFE×BC＝13×12(AE＋BF)×AB×BC＝16×(1＋2)×2×2＝1.同理，得V C－ADHE＝1，所以，V C－EFGH＝V－V C－ABFE－V C－ADHE＝4－1－1＝2，即几何体C－EFGH的体积为2.(理)(2011·江西文)如图在△ABC中，∠B＝π2，AB＝BC＝2，P为AB边上一动点，PD∥BC交AC于点D，现将△PDA沿PD翻折至△PDA ′，使平面PDA ′⊥平面PBCD .(1)当棱锥A ′－PBCD 的体积最大时，求P A 的长；(2)若点P 为AB 的中点，E 为A ′C 的中点，求证：A ′B ⊥DE .[解析] (1)令P A ＝x (0<x <2)，则A ′P ＝PD ＝x ，BP ＝2－x ，因为A ′P ⊥PD 且平面A ′PD ⊥平面PBCD ，故A ′P ⊥平面PBCD .所以V A ′－PBCD ＝13Sh ＝16(2－x )(2＋x )x ＝16(4x－x 3)．令f (x )＝16(4x －x 3)，由f ′(x )＝16(4－3x 2)＝0，得x ＝23 3.当x ∈(0，233)时，f ′(x )>0，f (x )单调递增；当x ∈(233，2)时，f ′(x )<0，f (x )单调递减．所以，当x ＝233时，f (x )取得最大值，即当V A ′－PBCD 最大时，P A ＝233.(2)设F 为A ′B 的中点，连接PF ，FE ，则有EF 綊12BC ，PD 綊12BC ，∴EF 綊PD ，∴四边形EFPD 为平行四边形，∴DE ∥PF .又A ′P ＝PB ，所以PF ⊥A ′B ，故DE ⊥A ′B .16．(2012·新课标全国文，19)如图，在三棱柱ABC －A 1B 1C 1中，侧棱垂直于底面，∠ACB ＝90°，AC ＝BC ＝12AA 1，D 是棱AA 1的中点．(1)证明：平面BDC 1⊥平面BDC ；(2)平面BDC 1分此棱柱为两部分，求这两部分体积的比．[分析] (1)证两个平面垂直，可转化为在其中一个平面内找到一条直线与另一个平面垂直；(2)平面BDC1分棱柱成两部分，下面部分B－ADC1C为四棱锥，可直接求体积，上面部分可用间接法求得体积，从而确定两部分体积之比．[解析](1)由题设知BC⊥CC1，BC⊥AC，CC1∩AC＝C，所以BC⊥平面ACC1A1.又DC1⊂平面ACC1A1，所以DC1⊥BC.由题设知∠A1DC1＝∠ADC＝45°，所以∠CDC1＝90°，即DC1⊥DC.又DC∩BC＝C，所以DC1⊥平面BDC.又DC1⊂平面BDC1，故平面BDC1⊥平面BDC.(2)设棱锥B－DACC1的体积为V1，AC＝1.由题意得，V1＝13×1＋22×1×1＝12.又三棱柱ABC－A1B1C1的体积V＝1，所以(V－V1) V1＝1 1.故平面BDC1分此棱柱所得两部分体积的比为1 1.[点评]本题考查线面的位置关系及几何体体积的求法．求解几何体的体积时，若遇不规则的几何体时，经常采用割补法和间接法求其体积．1．用单位正方体搭几何体，使它的正视图和俯视图如图所示，则符合条件的几何体体积的最小值与最大值分别是()A．9,13 B．7,16C．10,15 D．10,16[答案] D[解析]由俯视图知底层有七个小正方体，结合正视图知，最左边一列，最多都是三层，最少只有一行是三层，故左边一列最多9个、最少5个；中间一列最多都是二层有6个，最少只有一行二层，共4个；右边一列只一层一行，故最多9＋6＋1＝16个，最少5＋4＋1＝10个．2．一个几何体的三视图如图，该几何体的表面积为()A．280 B．292C．360 D．372[答案] C[解析]由三视图知该几何体是两个长方体的组合体，上面的长方体的表面积为(6×8)×2＋(8×2)×2＋6×2＝140.下面的长方体的表面积为(10×8)×2＋(10×2)×2＋(8×2)×2－6×2＝220.故表面积为140＋220＝360.选C.3．如图，已知在多面体ABC－DEFG中，AB、AC、AD两两互相垂直，平面ABC∥平面DEFG，平面BEF∥平面ADGC，AB＝AD ＝DG＝2，AC＝EF＝1，则该多面体的体积为()A．2B．4C．6D．8[答案] B[解析] 补成长方体ABMC －DEFN 并连接CF ，易知三棱锥F －BCM 与三棱锥C －FGN 的体积相等，故几何体体积等于长方体的体积4.故选B.[点评] 1.也可以用平面BCE 将此几何体分割为两部分，设平面BCE 与DG 的交点为H ，则ABC －DEH 为一个直三棱柱，由条件易证EH 綊FG 綊BC ，平面BEF ∥平面CHG ，且△BEF △CHG ，∴几何体BEF －CHG 是一个斜三棱柱，这两个三棱柱的底面都是直角边长为2和1的直角三角形，高都是2，∴体积为4.2．如图(2)，几何体ABC －DEFG 也可看作棱长为2的正方体中，取棱AN 、EK 的中点C 、F ，作平面BCGF 将正方体切割成两部分，易证这两部分形状相同，体积相等，∴V ABC －DEFG ＝12×23＝4.4．在一个倒置的正三棱锥容器内放入一个钢球，钢球恰与棱锥的四个面都接触，过棱锥的一条侧棱和高作截面，正确的截面图形是( )[答案] B[解析]球与正三棱锥底面的切点为底面正三角形的中心，故在截面图中，此切点将截面三角形的这一条边(底面正三角形的高)分为1 2两部分，截面过三棱锥的高和一条侧棱，故截面图中球大圆与侧棱外离且圆心在三角形的高(即棱锥的高)上，这条高应是顶点与底面中心的连线段，故选B.5．四棱锥P－ABCD的底面为正方形，侧面P AD为等边三角形，且侧面P AD⊥底面ABCD，点M在底面正方形ABCD内(含边界)运动，且满足MP＝MC，则点M在正方形ABCD内的轨迹一定是()[答案] B[解析]由满足条件MP＝MC，可知点M应在线段PC的所有中垂线构成的平面α内，又点M在正方形ABCD内，所以点M的轨迹平面α与平面ABCD的交线，则必为直线，故D不正确．又BP不等于BC，故A不正确．由题意知PD＝DC，所以D点在M的轨迹上．设E、F分别为AB、AD的中点，连接PF、EF，则PF⊥EF.设AB＝2，则PF＝3，EF＝2，所以PE＝ 5.在Rt△CBE中，BC＝2，BE＝1，则CE＝5＝EP，所以AB边中点E也在点M的轨迹上，则点M的轨迹为线段DE.6．(2012·吉林省实验中学模拟)一个几何体的三视图如图所示，其中俯视图与侧视图均为半径是 1 的圆，则这个几何体的体积是( )A.4π3B ．π C.2π3D.π3[答案] B[解析] 由三视图知，该几何体是半径为1的球去掉了半球的一半，故几何体是34个球，体积V ＝34×(43π·13)＝π.7．(2012·河南六市联考)如图，已知四棱锥P－ABCD中，底面ABCD是直角梯形，AB∥DC，∠ABC＝45°，DC＝1，AB＝2，P A⊥平面ABCD，P A＝1.(1)求证：AB∥平面PCD；(2)求证：BC⊥平面P AC；(3)若M是PC的中点，求三棱锥M－ACD的体积．[解析](1)由已知底面ABCD是直角梯形，AB∥DC，又AB⊄平面PCD，CD⊂平面PCD，∴AB∥平面PCD.(2)在直角梯形ABCD中，过C作CE⊥AB于点E，则四边形ADCE 为矩形，∴AE＝DC＝1又AB＝2，∴BE＝1，在Rt△BEC中，∠ABC＝45°，∴CE＝BE＝1，CB＝2，∴AD＝CE＝1，则AC＝AD2＋CD2＝2，AC2＋BC2＝AB2，∴BC⊥AC.又P A⊥平面ABCD，∴P A⊥BC，又P A∩AC＝A，∴BC⊥平面P AC.(2)∵M是PC中点，∴M到平面ADC的距离是P到平面ADC距离的一半．∴V M－ACD＝13S△ACD·(12P A)＝13×(12×1×1)×12＝112.。

高一数学下册人教A版必修2随堂小练1.1空间几何体的结构一、选择题1.设集合M={正四棱柱},N={长方体},P={直四棱柱},Q={正方体},这些集合间的关系是( )A. Q N M P⊇⊇⊇B. Q M N P⊇⊇⊇C. P M N Q⊇⊇⊇D. P N M Q⊇⊇⊇2.下列图形所表示的几何体中,不是棱锥的为( )A. B. C. D.3.下列命题正确的是( )A.棱柱的底面一定是平行四边形B.棱锥的底面一定是三角形C.棱台的底面是两个相似的正方形D.棱台的侧棱延长后必交于一点4.以下命题中真命题的序号是( )①若棱柱被一平面所截,则分成的两部分不一定是棱柱；②有两个面平行,其余各面都是梯形的几何体叫棱台；③用一个平面去截圆锥,底面和截面之间的部分组成的几何体叫圆台；④有两个面平行,其余各面都是平行四边形的几何体叫棱柱．A. ③④B.①④C. ①②④D. ①5.一个直角三角形绕斜边所在直线旋转360°形成的空间几何体为( )A.一个圆锥B.一个圆锥和一个圆柱C.两个圆锥D.一个圆锥和一个圆台6.有下面三组定义：①有两个面平行，其余各面都是四边形，且相邻四边形的公共边都互相平行的几何体叫棱柱；②用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台；③有一个面是多边形，其余各面都是三角形的几何体是棱锥．其中正确定义的个数是()A．0 B．1 C．2 D．37.下列几何体中是棱柱的有( )A．1个B．2个C．3个D．4个8.绕直线l旋转一周,可以得到如图所示的几何体的是( )A. B. C. D.9.如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥不可能是( )A.正三棱锥B.正四棱锥C.正五棱锥D.正六棱锥10.3、下列命题中正确的是( )A. 用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台B. 平行四边形的直观图是平行四边形C. 有两个面平行，其余各面都是平行四边行的几何体叫棱柱D. 正方形的直观图是正方形11.给出下列命题:①在圆柱的上、下两底面的圆周上各取一点,则这两点的连线是圆柱的母线;② 圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线;③ 在圆台上、下两底面的圆周上各取一点,则这两点的连线是圆台的母线;④ 圆柱的任意两条母线相互平行.其中正确的是( )A.①②B.②③C.①③D.②④12.如图,根据下列条件能推断出这个几何体可能是三棱台的是( )A. 11112,3,3,4A B AB B C BC ====B. 1111111,2, 1.5,3,2,3A B AB B C BC AC AC ======C. 1111111,2, 1.5,3,2,4A B AB B C BC AC AC ======D. 111111,,AB A B BC B C CA C A ===二、填空题13.下列说法正确的是__________.①圆台可以由任意一个梯形绕其一边所在直线旋转形成;②在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线;③圆柱的任意两条母线平行,圆锥的任意两条母线相交,圆台的任意两条母线延长后相交.14.不在同一平面上的两个顶点的连线叫做棱柱的体对角线,则六棱柱有__________条体对角线.三、解答题15.将下列平面图形绕直线AB 旋转一周,所得的几何体分别是什么?参考答案1.答案：D正方体是侧棱长等于底面边长的正四棱拄,正四棱柱的上、下两个底面都是正方形,其余各面都是矩形,因此正四棱柱一定是长方体,长方体的侧棱和上、下两底面垂直,因此长方体一定是直四棱柱,故,,,M N P Q 的关系为P N M Q ⊇⊇⊇,因此选D.2.答案：AA 是两个四棱锥的组合.3.答案：D棱台的侧棱延长后必交于一点.4.答案：D解:①若棱柱被一平面所截,则分成的两部分不一定是棱柱;正确,当平面与棱柱的所有平面不平行时,截出的两个几何体不是棱柱.②有两个面平行,其余各面都是梯形的几何体叫棱台;不正确,不满足棱台的定义.③用一个平面去截圆锥,底面和截面之间的部分组成的几何体叫圆台;不正确,当平面与底面平行时,底面和截面之间的部分组成的几何体叫圆台.④有两个面平行,其余各面都是平行四边形的几何体叫棱柱.不正确,不满足棱柱的定义.如下图:故选D.5.答案：C6.答案：B由棱柱的定义可知只有①正确，②中截面必须平行于底面,③中其余各三角形应有一个公共顶点，所以②③都不正确.故选B.7.答案：C观察图形得：“有两个面互相平行，其余各面都是四边形，”的几何体有：①③⑤，只有它们是棱柱，故答案为：①③⑤。

2014高中数学第一章立体几何初步章末综合检测随堂自测和课后作业苏教版必修2(时间：120分钟；满分：160分)一、填空题(本大题共14小题，每小题5分，共70分，请把答案填在题中横线上)1.有下列四个结论，其中正确结论的个数为________．①互相垂直的两直线，有且只有一个公共点；②经过一点有且只有一条直线垂直于已知直线；③垂直于同一条直线的两条直线平行；④两平行线之一垂直于一条直线，则另一条也垂直于此直线．解析：①错误，异面直线也可能垂直．②错误，应有无数条．③错误，可能平行，相交或异面．④正确．答案：12.下列几何体中既能使截面是长方形，又能使截面是圆的是________．①圆锥；②棱柱；③圆柱；④球．解析：③平行于轴的截面是长方形，垂直于轴的截面是圆．答案：③3.下列给出4个“平面α与β重合”的条件，其中正确的一个是________(填序号)．①有两个公共点；②有无数个公共点；③有不共线的三个公共点；④有一条公共直线．答案：③4.在正方体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是________(写出所有正确结论的编号)．①矩形；②不是矩形的平行四边形；③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；④每个面都是等边三角形的四面体；⑤每个面都是直角三角形的四面体．解析：在正方体ABCD－A1B1C1D1中，若所取四点共面，则只能是正方体的表面或对角面，即正方形或长方形，∴①正确，②错误；棱锥A－BDA1符合③，∴③正确；棱锥A1－BDC1符合④，∴④正确；棱锥A1－ABC符合⑤，∴⑤正确．答案：①③④⑤5.如图甲，在正方形SG1G2G3中，E、F分别是边G1G2、G2G3的中点，D是EF的中点，现沿SE、SF及EF把这个正方形折成一个几何体(图乙)，使G1、G2、G3三点重合于点G，这样，下面结论成立的是________．①SG ⊥平面EFG ；②SD ⊥平面EFG ； ③GF ⊥平面SEF ；④GD ⊥平面SEF .解析：在图甲中，SG 1⊥G 1E ，SG 3⊥G 3F ； 在图乙中，SG ⊥GE ，SG ⊥GF ， ∴SG ⊥平面EFG . 答案：①6.正方体的表面积是a 2，它的顶点都在球面上，这个球的表面积是________． 解析：设正方体棱长为b ，则3b ＝2R ，S 球＝4πR 2＝4π·(32b ) 2＝3πb 2，又a 2＝6b 2，∴S 球＝π2a 2.答案：π2a 27.四面体S －ABC 的三组对棱分别相等，且长度依次为25，13，5，则该四面体的体积为________．解析：由已知对棱相等，将四面体“补”成如图所示的长方体，使四面体的对棱分别为长方体相对面的对角线．设长方体的三棱长分别为x ，y ，z ，则⎩⎨⎧x 2＋y 2＝（25）2，y 2＋z 2＝（13）2，x 2＋z 2＝52，解得⎩⎪⎨⎪⎧x ＝4，y ＝2，z ＝3.那么V 四面体＝V 长方体－4V D －SAB ＝V 长方体－4×16V 长方体＝13V 长方体＝8.答案：88.在正三棱锥P －ABC 中，D ，E 分别是AB ，BC 的中点，有下列三个论断：①AC ⊥PB ；②AC ∥平面PDE ；③AB ⊥平面PDE .其中正确论断的序号为________．解析：由P －ABC 为正三棱锥知，PB ⊥AC ，又由DE ∥AC 得，AC ∥平面PDE . 答案：①②9.如果底面直径和高相等的圆柱的侧面积是S ，那么圆柱的体积等于________． 解析：设底面半径为r ，则2πr ·2r ＝S ，故r ＝S4π，所以V ＝πr 2·2r ＝S 4Sπ.答案：S4Sπ10.若一圆锥的轴截面面积为43cm 2，侧面积为83πcm 2，则它的体积等于________cm 3.解析：设圆锥的底面半径为r ，高为h ，母线长为l ，则有12·2r ·h ＝43，12·2πr ·l ＝83π，又h 2＋r 2＝l 2，因此可得r ＝2 3 cm ，h ＝2 cm ，l ＝4 cm ，∴V 圆锥＝13πr 2h ＝8π cm 3.答案：8π11.圆柱形容器内部盛有高度为8 cm 的水，若放入三个相同的球(球的半径与圆柱的底面半径相同)后，水恰好淹没最上面的球(如图所示)，则球的半径是________ cm. 解析：设球的半径为r cm ，则πr 2×8＋43πr 3×3＝πr 2×6r ，解得r ＝4.答案：412.如图所示，正方体ABCD －A 1B 1C 1D 1中，三棱锥D 1－AB 1C 的表面积与正方体的表面积的比为________．解析：设正方体的棱长为a ，则S 正方体＝6a 2，正四面体D 1－AB 1C 的棱长为2a ，S 正四面体＝4×34×(2a )2＝23a 2， 所以S 四面体S 正方体＝236＝33. 答案：3313.在正三棱柱ABC －A 1B 1C 1中，AB ＝1，若二面角C －AB －C 1的大小为60°，则点C 到平面ABC 1的距离为________． 解析：如图，取AB 中点为O ，连结C 1O 和CO . ∵三棱柱ABC －A 1B 1C 1是正三棱柱， ∴CO ⊥AB .∵AC 1＝BC 1，∴C 1O ⊥AB ，则∠C 1OC 即为二面角C －AB －C 1的平面角．又AB ＝1，∴CO ＝32，C 1C ＝32，OC 1＝ 3.下面用等体积法求距离． VC 1－ABC ＝VC －ABC 1， ∴13S △ABC ·CC 1＝13S △ABC 1·d ， 即34×32＝12×1×3×d .∴d ＝34. 答案：3414.已知Rt △ABC 的斜边在平面α内，直角顶点C 是α外一点，AC 、BC 与α所成角分别为30°和45°，则平面ABC 与α所成锐角为________．解析：如图所示，过点C 作垂直于α的直线CO ，交α于点O . ∴∠CAO ＝30°，∠CBO ＝45°.设CO ＝a ，∴Rt △ACO 中，AC ＝2a ， 在Rt △BCO 中，BC ＝2a .过C 点在平面ABC 内作CD ⊥AB ，连结OD ，则∠CDO 为平面ABC 与α所成的锐角，AB ＝6a ，∴CD ＝23a ，∴在Rt △CDO 中，sin ∠CDO ＝a 2a 3＝32，∴∠CDO ＝60°答案：60°二、解答题(本大题共6小题，共计90分，解答时应写出必要的文字说明、证明过程或演算步骤) 15.(本小题满分12分)如图，已知正三棱柱ABC ­A 1B 1C 1的底面边长为2，侧棱长为32，点E 在侧棱AA 1上，点F 在侧棱BB 1上，且AE ＝22，BF ＝ 2. 求证：CF ⊥C 1E .证明：由已知可得CC 1＝32，CE ＝C 1F ＝22＋()222＝23，EF 2＝AB 2＋()AE －BF 2，EF ＝C 1E ＝22＋()22＝6，于是有EF 2＋C 1E 2＝C 1F 2， CE 2＋C 1E 2＝CC 21， 所以C 1E ⊥EF ，C 1E ⊥CE .又EF ∩CE ＝E ，所以C 1E ⊥平面CEF . 又CF ⊂平面CEF ，故CF ⊥C 1E .16.(本小题满分14分)如图，四棱锥P －ABCD 的底面是矩形，PA ⊥平面ABCD ，E ，F 分别是AB ，PD 的中点，且二面角P －CD －B 为45°.求证： (1)AF ∥平面PEC ；(2)平面PEC ⊥平面PCD .证明：(1)如图，取PC 的中点G ，连结EG ，FG ，因为F 是PD 的中点，所以FG ∥CD ，且FG ＝12CD ，而AE ∥CD ，且AE ＝12CD ，所以EA ∥GF ，且EA ＝GF ，故四边形EGFA 是平行四边形，从而EG ∥AF ，又AF ⊄平面PEC ，EG⊂平面PEC ，所以AF ∥平面PEC .(2)因为PA ⊥平面ABCD ，所以PA ⊥CD ，又CD ⊥AD ，所以CD ⊥平面PAD ，所以CD ⊥PD ，则∠PDA 就是二面角P －CD －B 的平面角，所以∠PDA ＝45°，则AF ⊥PD .又AF ⊥CD ，PD ∩CD ＝D ，所以AF ⊥平面PCD ，由(1)知，EG ∥AF ，所以EG ⊥平面PCD ，而EG ⊂平面PEC ，所以平面PEC ⊥平面PCD .17.(本小题满分14分)将圆心角为120°，面积为3π的扇形，作为圆锥的侧面，求圆锥的表面积和体积．解：设扇形的半径和圆锥的母线都为l ，圆锥的半径为r ，则120°360°πl 2＝3π，∴l ＝3.又∵2π3×3＝2πr ，∴r ＝1.∴h ＝l 2－r 2＝2 2.∴S 表面积＝S 侧面＋S 底面＝πrl ＋πr 2＝4π， V ＝13Sh ＝13×π×12×22＝223π.18.(本小题满分16分)如图，在斜三棱柱ABC －A 1B 1C 1中，AA 1＝AC ＝BC ＝a ，∠A 1AC ＝∠C 1CB ＝60°，二面角A －CC 1－B 的大小为90°，求此斜三棱柱的侧面积．解：易知∠A 1C 1C ＋∠CC 1B 1＝180°，可将侧面AC 1与侧面BC 1展开在一个平面内(如图)，连结A 1B ，在△ABA 1内，∠A 1AB ＝60°，AA 1＝a ，AB ＝AC ＋BC ＝2a ，∴∠AA 1B ＝90°，即A 1B ⊥AA 1.∵AC ＝CB ，A 1C 1＝C 1B 1，∴CC 1∥AA 1，∴A 1B ⊥CC 1，设A 1B 与CC 1交于D ，则D 为CC 1的中点，且A 1D ⊥CC 1，BD ⊥CC 1.回到立体图中，取CC 1中点D ，连结A 1D ，BD ，则A 1D ⊥CC 1，BD ⊥CC 1，∴CC 1⊥平面A 1BD ，即平面A 1BD 为斜三棱柱ABC －A 1B 1C 1的直截面，且∠A 1DB 为二面角A －CC 1－B 的平面角，即有∠A 1DB ＝90°.易求得A 1D ＝BD ＝32a ，A 1B ＝62a .∴三棱柱的侧面积S 侧＝(32a ＋32a ＋62a )a ＝12(6＋23)a 2.19.(本小题满分16分)如图，圆锥的轴截面为等腰直角三角形SAB ，Q 为底面圆周上一点． (1)如果QB 的中点为C ，OH ⊥SC ，求证：OH ∥平面SBQ ；(2)如果∠AOQ ＝60°，QB＝ 23，求圆锥的体积．解：(1)证明：连结OC ，∵OH ⊥SC ，SO ⊥OH ，SO ∩SC ＝S ， ∴OH ⊥平面SOC ，∴OH ⊥OC .∵QB 的中点为C ， ∴OC ⊥QB .∵QB 、OC 、OH在同一平面内， ∴OH ∥QB ，QB ⊂平面SBQ ，OH ⊄平面SBQ ， ∴OH ∥平面SBQ .(2)∵∠AOQ ＝60°，AO ＝QO ，∴∠BAQ ＝60°.在Rt △ABQ 中，AB ＝BQ sin 60°＝2332＝4.∵圆锥的轴截面是等腰直角三角形，∴圆锥的高SO ＝12AB ＝2.∴V 圆锥＝13π(AB 2)2·SO ＝13π·4·2＝83π.20.(本小题满分16分)如图，在四棱锥P －ABCD 中，底面ABCD 是正方形，PD ⊥底面ABCD ，M ，N 分别是PA ，BC 的中点，且PD ＝AD ＝1. (1)求证：MN ∥平面PCD ；(2)求证：平面PAC ⊥平面PBD ； (3)求三棱锥P －ABC 的体积． 解：(1)证明：如图，取AD 中点E ，连结ME ，NE ，由已知M ，N 分别是PA ，BC 的中点，所以ME ∥PD ，NE ∥CD ，又ME ，NE ⊂平面MNE ，ME ∩NE ＝E ， PD ∩CD ＝D ，PD ，CD ⊂平面PCD .所以平面MNE ∥平面PCD ， 所以MN ∥平面PCD .(2)证明：因为ABCD 为正方形， 所以AC ⊥BD ，又PD ⊥平面ABCD ，所以PD ⊥AC ，所以AC ⊥平面PBD ，又AC ⊂平面PAC ， 所以平面PAC ⊥平面PBD .(3)PD ⊥平面ABCD ，所以PD 为三棱锥P －ABC 的高，三角形ABC 为等腰直角三角形，所以三棱锥P －ABC 的体积V ＝13S △ABC ·PD ＝16.。

DB D ABBCAD立体几何测试题班级 姓名一．选择题（每小题5分，共60分） 1.如图1，在空间四边形ABCD 中，点E,F 分别是边AB,CD 的中点，F ,G 分别是边BC,CD 上的点，且CF CB ＝CG CD ＝23，则（ ） （A ）EF 与GH 互相平行 （B ）EF 与GH 异面（C ）EF 与GH 的交点M 可能在直线AC 上，也可能不在直线AC 上 （D ）EF 与GH 的交点M 一定在直线AC 上 2.下列说法正确的是( )（A ）直线a 平行于平面M ,则a 平行于M 内的任意一条直线; （B ）直线a 与平面M 相交,则a 不平行于M 内的任意一条直线; （C ）直线a 不垂直于平面M ,则a 不垂直于M 内的任意一条直线; （D ）直线a 不垂直于平面M ,则过a 的平面不垂直于M .3．三棱锥P ABC -中，M 为BC 的中点，以PA ，PB ，PC 为基底，则AM 可表示为（ ） （A ）AM PA PB PC =-- （B ）AM PB PC PA =+- （C ）1122AM PA PB PC =-- （D ）1122AM PB PC PA =+- 4．向量,a b 满足：4,3π===a b a,b ，则-=a b ( )（A ）4 （B ）8 （C ）37 （D ）135．平面α外一点P 到平面α内的四边形的四条边的距离都相等，且P 在α内的射影在四边形内部，则四边形是（ ）（A ）梯形 （B ）圆外切四边形 （C ）圆内接四边形 （D ）任意四边形 6. 已知,m n 为不重合的直线, ,αβ为不重合的平面,有下列命题中真命题个数是( ) ① 若m α⊂,n α，则mn ； ②若m α,m β,则αβ；③若n αβ=,m n ,则mα且m β；④m α⊥,m β⊥,则αβ；（A ） 0 （B ） 1 （C ） 2 （D ）3图7．在空间四边形ABCD 中，己知AB AD =，则BC CD =是AC BD ⊥的（ ）（A ）充分条件 （B ）必要不充分条件 （C ）充要条件 （D ）既不充分又不必要条件 8．已知,,a b c 是直线，β是平面，给出下列命题中，真命题的个数是（ ）①若c a c b b a //,,则⊥⊥； ②若//,,a b b c ⊥则a c ⊥；③若//,a b ββ⊂，则//a b ； ④若a b 、异面，且//,a β则b β与相交；⑤若a b 、异面，则至多有一条直线与a b 、都垂直. （A ）1 （B ）2 （C ）3（D ）49．长方体1111ABCD A BC D -中，12AA AB ==，1AD =，点E F G 、、分别 11DD AB CC 、、的中点，则异面直线1A E GF 、所成的角是（ ）（A ）515arccos（B ）4π （C ）510arccos（D ）2π10.A 是平面BCD 外一点，E,F ,G 分别是BD,DC,CA 的中点，设过这三点的平面为α，则在直线AB,AC,AD,BC,BD,DC 中，与平面α平行的直线有（ ）（A ）0 （B ）1条 （C ）2条 （D ）3条11.如图：正方体1111ABCD A BC D -中，点P 在侧面11BCC B 及其边界上运动，在运动过程中，保持1AP BD ⊥，则动点P 的轨迹是（ C ） （A ）1BB 中点与1CC 中点连成的线段 （B ）BC 中点与11C B 中点连成的线段 （C ）线段1B C （D ）线段1BC12、若正方体1111ABCD A BC D -的棱长为1，P 为对角线1AC 上的一点，Q 是棱1BB 上一点，则PQ 的取值范围是（ B ）A 、122≤≤PQB 、222≤≤PQC PQ ≤≤、31≤≤PQ二、填空题：（每小题6分，共24分）13.如图，PA ABC ⊥平面，90ACB ∠=PA AC BC a ===且， 则异面直线PB 与AC 所成的角的正切值等于 ．14.空间四边形ABCD ，AB BC ⊥，BC CD ⊥，异面直线AB 与CD 所成的角为45，且1AB BC ==，CD =AD 的长为 .15.正方体1111ABCD A BC D -中，E,F 分别是正方形11ADD A 和ABCD 的中心，G 是1CC 的中点，设1GF,C E 与AB 所成的角分别为βα,，则=+βα .16.在正方形''''D C B A ABCD -中，过对角线'BD 的一个平面交'AA 于E ，交'CC 于F ，① 四边形E BFD '一定是平行四边形 ② 四边形E BFD '有可能是正方形③ 四边形E BFD '在底面ABCD 内的投影一定是正方形④ EF 有可能垂直于平面D BB '你认为正确的命题的所有序号有 . 三．解答题（共66分）17.(16分)如图所示，平面α//平面β，点A ,C αα∈∈,点B ,D ββ∈∈，点E,F 分别在线段AB,CD 上，AB,CD 所在直线异面,且AE :EB CF :FD = （Ⅰ）求证：EF //β;（Ⅱ）若E,F 分别是AB,CD 的中点，46AC ,BD ==，且AC,BD 所成的角为︒60，求EF 的长. 7或19EF =ABC D A'B 'C 'D '18.（16分）如图，在五棱锥S ABCDE -中，SA ⊥底面ABCDE ，2SA AB AE ,BC DE ====,120BAE BCD CDE ∠=∠=∠=︒（Ⅰ）求异面直线CD 与SB 所成的角（用反三角函数值表示）； （Ⅱ）证明BC ⊥平面SAB ；19.（16分）已知平行六面体1111ABCD A BC D -中，底面ABCD 是边长为a 的正方形，侧棱1AA 的长为b ，o 11A AB =A AD =120∠∠.（Ⅰ）求对角线1AC 的长.（Ⅱ）求直线1BD 和AC 的夹角. (答案见教材复习参考题91页B 组第4题)20.（18分）如图，ABC ∆是以AC 为斜边的等腰直角三角形，,,E F O 分别为PA ，PB ，AC 的中点，16AC =，10PA PC ==．ABC PO 面⊥（I ）设G 是OC 的中点，证明：//FG 平面BOE ；（II ）证明：在ABO ∆内存在一点M ，使FM ⊥平面BOE ，并求点M 到OA ，OB 的 距离．αFEDBCAA 1D1C 1B 1A DCBβ立体几何文科试题一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的． 1、设有直线m 、n 和平面α、β.下列四个命题中，正确的是( )A.若m ∥α,n ∥α,则m ∥nB.若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βC.若α⊥β，m ⊂α,则m ⊥βD.若α⊥β，m ⊥β，m ⊄α,则m ∥α 2、已知直线,l m 与平面αβγ，，满足//l l m βγαα=⊂，，和m γ⊥，则有A ．αγ⊥且l m ⊥B ．αγ⊥且//m βC ．//m β且l m ⊥D ．//αβ且αγ⊥3.若()0,1,1a =-，()1,1,0b =，且()a b a λ+⊥，则实数λ的值是（ ） A .－1 B.0 C.1 D.－24、已知平面α⊥平面β，α∩β= l ，点A ∈α，A ∉l ，直线AB ∥l ，直线AC ⊥l ，直线m ∥α，m ∥β，则下列四种位置关系中，不一定．．．成立的是（ ） A. AB ∥mB. AC ⊥mC.AB ∥β D. AC ⊥β5一个几何体的三视图及长度数据如图，则几何体的表面积与体积分别为()3,27+A ()328，+B()2327，+C ()23,28+D6、已知长方体的表面积是224cm ，过同一顶点的三条棱长之和是6cm ，则它的对角线长是（ ）B. 4cmC.D.7、已知圆锥的母线长5l cm =，高4h cm =，则该圆锥的体积是____________3cmA. 12π B 8π C. 13π D. 16π8、某几何体的三视图如图所示，当b a +取最大值时，这个几何体的体积为 （ ）A ．61 B ．31C ．32D ．21 9、已知,,,A B C D 在同一个球面上,,AB BCD ⊥平面,BC CD ⊥若6,AB=AC =8AD =,则,B C 两点间的球面距离是 （ ） A. 3πB. 43πC. 23πD. 53π10、四面体ABCD 的外接球球心在CD 上，且2CD =，3=AB ，在外接球面上A B ，两点间的球面距离是（ ） A ．π6B ．π3C ．2π3D ．5π611、半径为2cm 的半圆纸片做成圆锥放在桌面上，一阵风吹倒它，它的最高处距桌面（ ） A ．4cmB ．2cmC ．cm 32D ．cm 312、 有一正方体，六个面上分别写有数字1、2、3、4、5、6，有三个人从不同的角度观察的结果如图所示.如果记3的对面的数字为m ，4的对面的数字为n ，那么m+n 的值为（ ） A ．3 B ．7 C ．8 D ．11二．填空题：本大题共4个小题。

高一数学必修二立体几何随堂训练41．如图，四棱锥ABCD P -的底面是正方形，侧棱PD ⊥平面ABCD ，M 、N 分别是AB 、PC 的中点．（1）求证：//MN 平面PAD ；（2）求证：PCD PBC ⊥平面平面.2．如图，已知O PA 圆⊥所在的平面，AB 是O 圆的直径，2=AB ,O C 是圆上的一点，且BC AC =,角所在的平面成与圆 45O PC ，PC E 是中点，PB F 为的中点．（1）求证：EF //面ABC ；（2）求证：PAC EF 面⊥；（3）求三棱锥PAC B -的体积3．已知正方体1111D C B A ABCD -，求证：（１）//BD 1C 面面11D AB ；（2 ）C A 1⊥平面11D AB ；PD C BA N4．正三棱柱111ABC A B C -中,点D 是BC 的中点,12,BC BB ==（1）求证:1//AC 平面1AB D ；（2）求证:1BC ⊥平面1AB D .5．如图，在四面体ABCD 中，CB CD AD BD =⊥，，点E F ，分别是AB BD ，的中点．求证：（1）直线//EF 面ACD ；平面EFC ⊥面BCD ．6.如图，在三棱柱111C B A ABC -中，1AA ⊥底面ABC ，且△ABC 为正三角形，61==AB AA ，D 为AC 的中点． (1)求证:直线1AB ∥平面D BC 1；(2)求证:平面D BC 1⊥平面11A ACC ；(3)求三棱锥D BC C 1-的体积．111A16．（1）证明见解析；（2）证明见解析【解析】试题分析：（1）证明线面平行常用方法：一是利用线面平行的判定定理，二是利用面面平行的性质定理，三是利用面面平行的性质，注意把证明的条件写齐全；(2)要证平面与平面垂直，需要证明直线与平面垂直，证明线面垂直的方法：一是线面垂直的判定定理；二是利用面面垂直的性质定理；三是平行线法（若两条平行线中的一条垂直于这个平面，则另一条也垂直于这个平面.解题时，注意线线、线面与面面关系的相互转化. 试题解析：解：（1)取PD 的中点F ，连接FN AF ,点N 是PC 的中点DC FN //∴，且DC FN 21= 又 四边形ABCD 是正方形，且点M 是AB 的中点DC AM //∴，且DC AM 21=AM FN //∴，且AM FN =∴四边形FNMA 是平行四边形，FA MN //∴又⊄MN 平面PAD ，⊂FA 平面PAD//MN ∴平面PAD⊥PD 平面ABCD ，且⊂BC 平面ABCDBC PD ⊥∴四边形ABCD 是正方形，CD BC ⊥∴又D CD PD =⊥∴BC 平面PCD又⊂BC 平面PBC∴平面PCD ⊥平面PBC . 考点：1、直线与平面平行的判定；2、平面与平面垂直的判定.17．（1）见解析;（2）见解析;（3）111()(332B PAC PAC V S BC -∆∴=⨯==【解析】试题分析：（1）证明线面平行常用方法：一是利用线面平行的判定定理，二是利用面面平行的性质定理，三是利用面面平行的性质；（2）证明线面垂直的方法：一是线面垂直的判定定理；二是利用面面垂直的性质定理；三是平行线法（若两条平行线中的一条垂直于这个平面，则另一条也垂直于这个平面．解题时，注意线线、线面与面面关系的相互转化．（3） 利用棱锥的体积公式Sh V 31=求体积．在求三棱柱体积时，选择适当的底作为底面，这样体积容易计算．试题解析：（1）证明：在PBC ∆中，EF 为中位线，所以//EF BC ，又EF ⊄平面ABC ，BC ⊂平面ABC ，所以//EF 平面ABC ． 4分（2） AB 是圆O 的直径，BC CA ∴⊥；PA ⊥平面ACB ，BC ⊂平面ACB ，PA BC ∴⊥；又BC CA C =，BC ∴⊥平面PAC ，又//BC EF ，EF ∴⊥平面PAC ． 8分（3）由第2问知BC ⊥平面PAC ，BC ∴是三棱锥B PAC -的高；AC BC PA ===，111()(332B PAC PAC V S BC -∆∴=⨯== 13分 考点：（1）直线与平面平行的判定；（2）直线与平面平行的判定；（3）三棱锥的体积公式18．（1）证明：//BD 1C 面面11D AB ；（2）证明：C A 1⊥平面11D AB ．【解析】试题分析：（1）证明//BD 1C 面面11D AB ，关键是要在一个面内找到两条与另外一个平面平行的相交直线，而找与面平行的直线，又需要通过线线平行去找，而在正方体中知： BD ∥B 1D 1 , AD 1∥BC 1；（2）证明C A 1⊥平面11D AB ，关键是要在平面11D AB 找到两条相交直线与C A 1垂直，而找线线垂直，又可以通过线面垂直来证明．试题解析：（1）在正方体中由 BD ∥B 1D 1知 B 1D 1∥面C 1BD ，同理，由AD 1∥BC 1知AD 1∥面C 1BD ，而AD 1与B 1D 1是面AB 1D 1内两条相交直线，∴面AB 1D 1∥面C 1BD ．（2）如上图，在正方体ABCD-A 1B 1C 1D 1中，∵BD ⊥AC ，且由AA 1⊥面ABCD 知∴BD ⊥AA 1．∴BD ⊥面ACC 1A 1，又A 1C 面ACC 1A 1，∴A 1C ⊥BD ．同理A 1C ⊥C 1D ，∴A 1C ⊥面C 1BD ．因为//BD 1C 面面11D AB 所以C A 1⊥平面11D AB ． 考点： 1、线面平行的判定定理和性质定理；2、线面垂直的判定定理和性质定理．19． 见解析.【解析】试题分析：（1）证明线面平行，要找线线平行，在平面1AB D 内找一直线与1AC 平行即可.连1A B 交1AB于O,连OD ,则OD||1AC 即证.（2）依题意可得AD ⊥平面11BCC B ,故AD ⊥1BC .在矩形11BCC B 中，由条件可证111BDB BB C ∆∆,从而得11BC DB ⊥,故可得1BC ⊥平面1AB D . 试题解析：（1）连接11,A B AB O OD ⋂=连接1111//,,AC OD OD AB D AC AB D ⊂⊄面面 11//AC AB D 面 6分（漏线不在面内扣2分）（2）设D 为BC 中点，∴AD ⊥BC ，正三棱柱中，11BB ABC AD ABC AD BB ⊥⊂∴⊥面，面，,1111,BC BB B BC BB BCC B =⊂，平面111111,,AD BCC B BC BCC B AD BC ∴⊥⊂∴⊥平面平面 9分设11B D BC F =111DBB BB C 直角和直角中，111111BB BD DBB BB C BB B C ===∴111,90,90BDF C BB CBB FBD BDF FBD ∴∠=∠∠+∠=∴∠+∠=又 11BC B D ∴⊥ 13分又1111,,,BC AD AD B D D AD B D AB D ⊥=⊂平面11BC AB D ∴⊥平面 16分考点：线面平行，线面垂直的判定与性质20．（1）见解析 （2）见解析【解析】试题分析：（1）利用线面平行的判断定理证明线面平行，首先说明线线平行，然后再说明线面平行.（2）证明面面垂直的方法是利用线面垂直的判定定理首先说明线面垂直，然后再说明平面经过这条直线即可证明面面垂直解题时，注意线线、线面与面面关系的相互转化. 试题解析：（1）∵E F ，分别是AB BD ，的中点．∴EF 是ABD ∆的中位线，∴AD EF //，∵//EF ⊄面ACD ，AD ⊂面ACD ，∴直线//EF 面ACD ；（2）∵BD AD ⊥，AD EF //，∴BD EF ⊥，∵CD CB =，F 是BD 的中点，∴BD CF ⊥又F CF EF =⋂, ∴BD ⊥面EFC ，∵BD ⊂面BCD ，∴面EFC ⊥面BCD考点：平面与平面垂直的判定；直线与平面平行的判定．21．（1）证明：见解析；（2）证明：见解析；（3）．【解析】试题分析：（1）证明思路：连接B 1C 交BC 1于点O ，连接OD ，则点O 为B 1C 的中点． 知DO 为C AB 1∆中位线，得到OD B A //1．（2）证明思路：由⊥1AA 底面ABC ，得到BD AA ⊥1，又底面ABC 正三角形，D 是AC 的中点，可得BD AC ⊥；（3）由（2）知ABC △中，603BD AC BD BCsin ⊥=︒=，计算得BCD S ∆ == ，又1CC 是底面BCD 上的高，计算得到BD C C D BC C V V 11--=.试题解析：（1）证明：连接B 1C 交BC 1于点O ，连接OD ，则点O 为B 1C 的中点． 1分∵D 为AC 中点，得DO 为C AB 1∆中位线，∴OD B A //1． 2分 C AB B A C AB OD 111,平面平面⊄⊂ ∴直线1AB ∥平面1BC D 4分（2）证明：∵⊥1AA 底面ABC ，∴BD AA ⊥1 5分 ∵底面ABC 正三角形，D 是AC 的中点 ∴BD AC ⊥ 6分 ∵A AC AA =⋂1，∴BD ⊥平面ACC 1A 1 7分D BC BD 1平面⊂ ,111A ACC D BC 平面平面⊥∴ 8分（3）由（2）知ABC △中，603BD AC BD BCsin ⊥=︒=，∴BCD S ∆ == 10分 又1CC 是底面BCD 上的高 11分∴BD C C D BC C V V 11--==••69= 13分考点：1.垂直关系；2.平行关系；3.几何体的体积，“等体积法”.。

高2012级立体几何测试题考试时间：90分钟命题：朱老师 审题：朱老师班级 姓名一．选择题（每小题5分，共60分） 1.如图1，在空间四边形ABCD 中，点E,F 分别是边AB,CD 的中点，F ,G 分别是边BC,CD 上的点，且CF CB ＝CG CD ＝23，则（ D ） （A ）EF 与GH 互相平行 （B ）EF 与GH 异面 （C ）EF 与GH 的交点M 可能在直线AC 上，也可能不在直线AC 上 （D ）EF 与GH 的交点M 一定在直线AC 上 2.下列说法正确的是( B )（A ）直线a 平行于平面M ,则a 平行于M 内的任意一条直线; （B ）直线a 与平面M 相交,则a 不平行于M 内的任意一条直线; （C ）直线a 不垂直于平面M ,则a 不垂直于M 内的任意一条直线; （D ）直线a 不垂直于平面M ,则过a 的平面不垂直于M .3．三棱锥P ABC -中，M 为BC 的中点，以PA ，PB ，PC 为基底，则AM 可表示为（ D ） （A ）AM PA PB PC =-- （B ）AM PB PC PA =+- （C ）1122AM PA PB PC =-- （D ）1122AM PB PC PA =+- 4．向量,a b 满足：4,3π===a b a,b ，则-=a b ( A )（A ）4 （B ）8 （C ）37 （D ）135．平面α外一点P 到平面α内的四边形的四条边的距离都相等，且P 在α内的射影在四边形内部，则四边形是（ B ）（A ）梯形 （B ）圆外切四边形 （C ）圆内接四边形 （D ）任意四边形 6. 已知,m n 为不重合的直线, ,αβ为不重合的平面,有下列命题中真命题个数是( B ) ① 若m α⊂,n α，则mn ； ②若m α,m β,则αβ；③若n αβ=,m n ,则mα且m β；④m α⊥,m β⊥,则αβ；图（A ） 0 （B ） 1 （C ） 2 （D ） 37．在空间四边形ABCD 中，己知AB AD =，则BC CD =是AC BD ⊥的（ C ）（A ）充分条件 （B ）必要不充分条件 （C ）充要条件 （D ）既不充分又不必要条件 8．已知,,a b c 是直线，β是平面，给出下列命题中，真命题的个数是（ A ） ①若c a c b b a //,,则⊥⊥； ②若//,,a b b c ⊥则a c ⊥；③若//,a b ββ⊂，则//a b ； ④若a b 、异面，且//,a β则b β与相交；⑤若a b 、异面，则至多有一条直线与a b 、都垂直. （A ）1 （B ）2 （C ）3（D ）49．长方体1111ABCD A B C D -中，12AA AB ==，1AD =，点E F G 、、分别 11DD AB CC 、、的中点，则异面直线1A E GF 、所成的角是（ D ）（A ）515arccos（B ）4π （C ）510arccos（D ）2π10.A 是平面BCD 外一点，E,F ,G 分别是BD,DC,CA 的中点，设过这三点的平面为α，则在直线AB,AC,AD,BC,BD,DC 中，与平面α平行的直线有（ ）（A ）0 （B ）1条 （C ）2条 （D ）3条11.如图：正方体1111ABCD A B C D -中，点P 在侧面11BCC B 及其边界上运动，在运动过程中，保持1AP BD ⊥，则动点P 的轨迹是（ C ） （A ）1BB 中点与1CC 中点连成的线段 （B ）BC 中点与11C B 中点连成的线段 （C ）线段1B C （D ）线段1BC12、若正方体1111ABCD A B C D -的棱长为1，P 为对角线1AC 上的一点，Q 是棱1BB 上一点，则PQ 的取值范围是（ B ）A 、122≤≤PQ B 、222≤≤PQ C PQ ≤≤、31≤≤PQ高2012级立体几何(9.1-9.6)测试题(答题卷) 班级姓名二、填空题：（每小题6分，共24分）13.如图，PA ABC⊥平面，90ACB∠=PA AC BC a===且，则异面直线PB与AC14.空间四边形ABCD，AB BC⊥，BC CD⊥，异面直线AB与CD所成的角为45，且1AB BC==，CD=AD15.正方体1111ABCD A B C D-中，E,F分别是正方形11ADD A和ABCD的中心，G是1CC的中点，设1GF,C E与AB所成的角分别为βα,，则=+βα︒90 .16.在正方形''''DCBAABCD-中，过对角线'BD的一个平面交'AA于E，交'CC于F，①四边形EBFD'一定是平行四边形②四边形EBFD'有可能是正方形③四边形EBFD'在底面ABCD内的投影一定是正方形④EF有可能垂直于平面DBB'你认为正确的命题的所有序号有①③④ .三．解答题（共66分）17.(16分)如图所示，平面α//平面β，点A,Cαα∈∈,点B,Dββ∈∈，点E,F分别在线段AB,CD上，AB,CD所在直线异面,且AE:EB CF:FD=（Ⅰ）求证：EF//β; （Ⅱ）若E,F分别是AB,CD的中点，46AC,BD==，且A BCDA'B'C'D'AC,BD 所成的角为︒60，求EF 的长. 7或19EF =18.（16分）如图，在五棱锥S ABCDE -中，SA ⊥底面ABCDE ，2SA AB AE ,BC DE =====,120BAE BCD CDE∠=∠=∠=︒（Ⅰ）求异面直线CD 与SB 所成的角（用反三角函数值表示）； （Ⅱ）证明BC ⊥平面SAB ；(1) 连结BE ，延长BC 、ED 交于点F ，则060=∠=∠CDF DCF ，.DF CF ，CDF =∴∆∴为正三角形又BC=DE ， EF BF =∴，因此，BFE ∆为正三角形，因为ABE ∆是等腰三角形,且0090,120=∠∴=∠ABC BAE以A 为原点，AB 、AS 边所在的直线分别为x 轴、z 轴，以平面ABC 内垂直于AB 的直线为y 轴，建立空间直角坐标系（如图） A （0，0，0）， B （2，0，0） S （0，0，2），且 D()0,233,21,于是,2(),,23,23(-=-=BS O CD 则,462233,cos =⋅=>=< .46arccos,>=∴< 所以异面直线CD 与SB 所成的角为：.46arccosαFEDBCAβEFy(2))2,0,0(),0,0,2(),0,3,0(-=== ,,0)0,0,2()0,3,0(=⋅=⋅∴,0)2,0,0()0,3,0(=-⋅=⋅ .,SA BC AB BC ⊥⊥∴ ,A SA AB =⋂ SAB 。