空间立体几何基础练习题
- 格式:doc
- 大小:195.12 KB
- 文档页数:2

立体测试题及答案一、单项选择题(每题2分,共10题)1. 下列哪个选项是立体几何中的基本元素?A. 点B. 线C. 面D. 体答案:D2. 空间中两条直线的位置关系有几种?A. 1种B. 2种C. 3种D. 4种答案:C3. 一个立方体有多少个顶点?A. 6B. 8C. 12D. 14答案:B4. 一个正四面体有多少条棱?A. 6B. 8C. 12D. 16答案:A5. 空间直角坐标系中,点(1,2,3)到原点的距离是多少?A. 1B. 2C. 3D. √14答案:D6. 一个球体的表面积公式是?A. 4πr²B. 2πr²C. πr²D. 4πr³答案:A7. 空间中两个平面的位置关系有哪些?A. 平行B. 相交C. 重合D. 以上都是答案:D8. 一个圆柱体的体积公式是?A. πr²hB. 2πrhC. πr²D. πr³答案:A9. 空间中一个点到一个平面的距离公式是?A. |Ax + By + Cz + D| / √(A² + B² + C²)B. |Ax + By + Cz - D| / √(A² + B² + C²)C. |Ax + By + Cz + D| / √(A² + B²)D. |Ax + By + Cz - D| / √(A² + B²)答案:B10. 空间中一个点到一条直线的距离公式是?A. |Ax + By + Cz + D| / √(A² + B² + C²)B. |Ax + By + Cz - D| / √(A² + B² + C²)C. |(Ax + By + Cz + D) / (A² + B² + C²)| * √(A² + B²)D. |(Ax + By + Cz - D) / (A² + B² + C²)| * √(A² + B²)答案:D二、多项选择题(每题3分,共5题)1. 空间中两个平面相交,它们的交线是?A. 直线B. 曲线C. 点D. 面答案:A2. 空间中一个点到一个平面的距离公式中,A、B、C、D分别代表什么?A. 平面方程的系数B. 平面方程的常数项C. 点的坐标D. 点到平面的距离答案:A, B3. 空间直角坐标系中,点(1,2,3)到点(4,5,6)的距离公式是?A. √((4-1)² + (5-2)² + (6-3)²)B. √((1-4)² + (2-5)² + (3-6)²)C. √((4-1)² + (5-2)² + (6-3)²)D. √((1-4)² + (2-5)² + (3-6)²)答案:A, B4. 空间中一个点到一条直线的距离公式中,A、B、C、D分别代表什么?A. 直线方程的系数B. 直线方程的常数项C. 点的坐标D. 点到直线的距离答案:A, C5. 空间中一个平面的方程可以表示为?A. Ax + By + Cz + D = 0B. Ax + By + Cz = DC. Ax + By + Cz + D = ED. Ax + By + Cz = 0答案:A, D结束语:以上是立体测试题及答案的全部内容,希望对你有所帮助。
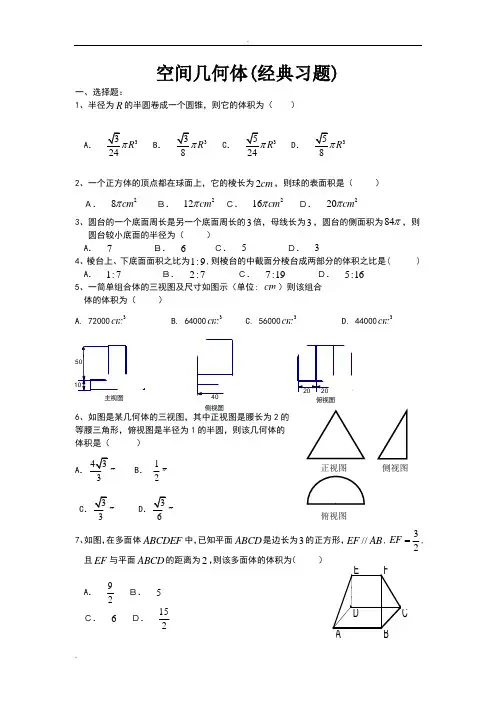
正视图 俯视图侧视图空间几何体(经典习题)一、选择题:1、半径为R 的半圆卷成一个圆锥,则它的体积为( )A .3R B .3R C .3R D .3R 2、一个正方体的顶点都在球面上,它的棱长为2cm ,则球的表面积是( ) A. 28cm π B. 212cmπC. 216cmπD. 220cm π3、圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则 圆台较小底面的半径为( )A . 7 B. 6 C. 5 D. 34、棱台上、下底面面积之比为1:9,则棱台的中截面分棱台成两部分的体积之比是( ) A . 1:7 B. 2:7 C. 7:19 D. 5:165、一简单组合体的三视图及尺寸如图示(单位: cm )则该组合 体的体积为( )A. 720003cmB. 640003cmC. 560003cmD. 440003cm62的等腰三角形,俯视图是半径为1的半圆,则该几何体的 体积是( )A. C 7、如图,在多面体ABCDEF 中,已知平面ABCD 是边长为3的正方形,//EF AB ,32EF =,且EF 与平面ABCD 的距离为2,则该多面体的体积为( )A .92B. 5 C. 6 D. 152侧视图俯视图8、一个棱锥的三视图如图,则该棱锥的体积是( ) C.4 D.89、如图是一个空间几何体的三视图,则该几何体的侧面积为( )第8题 第9题10、如图为一平面图形的直观图,则此平面图形可能是选项中的( )11、棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8 个三棱锥后,剩下的凸多面体的体积是( )A、23 B 、76 C 、45 D 、5612、在一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞D 、E 、F ,且知SD :DA=SE :EB=CF :FS=2:1,若仍用这个容器盛水,则最多可盛原来水的( )A 、2923 B 、2719 C 、3130 D 、2723 13、 一空间几何体的三视图如图所示,A.2π+B. 4π+C. 23π+D. 43π+俯视图14、一个棱锥的三视图如图,则该棱锥的全面积(单位:c 2m )为( ).(A )(B )(C )(D )15、正六棱锥P-ABCDEF 中,G 为PB 的中点,则三棱锥D-GAC 与三棱锥P-GAC 体积之比为( )(A )1:1 (B) 1:2 (C) 2:1 (D) 3:216、如右图,某几何体的正视图与侧视图都是边长为1的正方形, 且体积为12。
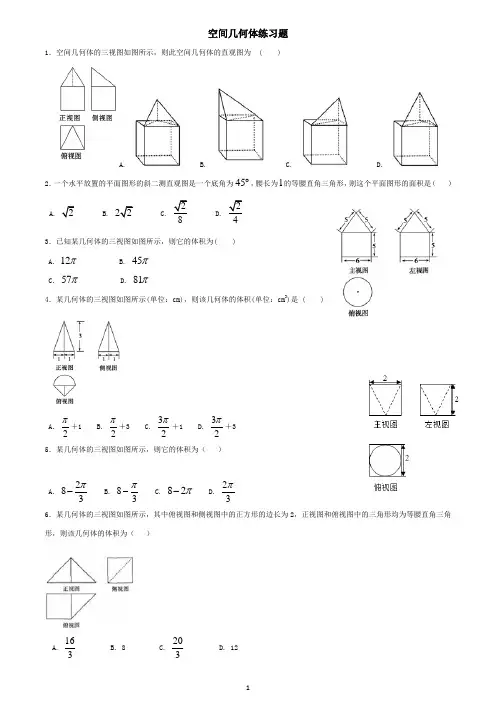
空间几何体练习题1.空间几何体的三视图如图所示,则此空间几何体的直观图为 ( )A. B. C. D.2.一个水平放置的平面图形的斜二测直观图是一个底角为45︒,腰长为1的等腰直角三角形,则这个平面图形的面积是( ) A. 2 B. 22 C. 28 D. 243.已知某几何体的三视图如图所示,则它的体积为( )A. 12πB. 45πC. 57πD. 81π4.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是 ( )A. 2π+1B. 2π+3C. 32π+1D. 32π+35.某几何体的三视图如图所示,则它的体积为( )A. 283π- B. 83π- C. 82π- D. 23π6.某几何体的三视图如图所示,其中俯视图和侧视图中的正方形的边长为2,正视图和俯视图中的三角形均为等腰直角三角形,则该几何体的体积为( )A. 163B. 8C. 203D. 127.某空间几何体的三视图如图所示,则该几何体的体积为()A. 16+2πB. 16+πC. 8+πD. 8+2π8.某空间几何体的三视图如图所示,则该几何体的体积为()A. 4B. 6C. 8D. 169.将棱长为2的正方体削成一个体积最大的球,则这个球的体积为( )A. 163π B.43πC.323π D. 4π10.如图是三棱锥D ABC-的三视图,则该三棱锥的外接球体积为( )A. 92πB.33πC. 62πD.23π11.某空间几何体的正视图是三角形,则该几何体不可能是( )A. 圆锥B. 圆柱C. 四面体D. 三棱锥12.若一个正三棱柱的三视图如下图所示,则这个正三棱柱的高和底面边长分别为().A. 2,22B. 2,4C. 23,2D. 4,313.某几何体的三视图如图所示,则该几何体的表面积是()A.322++ B.5322++ C.332++ D.7322++14.一个球的内接正方体的表面积为54,则球的表面积为( )A. 27πB. 18πC. 19πD. 54π15.将一个直角边长为1的等腰直角三角形绕其一条直角边旋转一周所形成几何体的侧面积为( )A. 4πB. 22πC. 2πD. 2π16.把球的表面积扩大到原来的2倍,那么体积扩大到原来的( )A. 2倍B. 22倍C. 2倍D. 32倍17.如果一个几何体的主视图与左视图是全等的长方形,边长分别是4,2,如图所示,俯视图是一个边长为4的正方形.(1)求该几何体的表面积;(2)求该几何体的外接球的体积.18.如图是一建筑物的三视图(单位:m),现需将其外壁用油漆粉刷一遍,已知每平方米用漆0.2kg,问需要油漆多少千克?(无需求近似值)cm. 19.一个棱柱的侧面展开图是三个全等的矩形,矩形的长和宽分别为6cm,4cm,则该棱柱的侧面积为________2 20.一个几何体的三视图如图所示,则该几何体的体积为______.21.一个几何体的三视图如图所示,则该几何体的表面积为_______.22.体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是________.23.已知正三棱锥的高为1,底面边长为26,则该三棱锥的表面积为________.-的所有棱长都为2,则该三棱锥的外接球的表面积为________.24.已知三棱锥A BCD25.若正三棱锥的底面边长为3,侧棱长为2,则其外接球的表面积为__________.26.已知高与底面直径之比为2:1的圆柱内接于球,且圆柱的体积为500π,则球的体积为________.cm).27.某几何体的三视图如图所示(单位:cm),则该几何体的体积是_____(单位:3参考答案1.A2.A3.C4.A5.A6.C7.D8.C9.B10.A11.B12.B13.D14.A15.C16.B17.(1)64;(2)36π.18.()()4.87.8kg π+19.7220.2π321.5π22.5423.24.3π25.4π26π+27.12。

空间向量和立体几何练习题与答案
1.若把空间平行于同一平面且长度相等的所有非零向量的始点放置在同一点,则这些向量的终点构成的图形就是( )
A.一个圆
B.一个点
C.半圆
D.平行四边形
答案:A
2.在长方体 ABCD-A₁B ₁C ₁D ₁中,下列关于AC₁的表达中错误的 一个就是( )
A. AA₁+A ₁B ₁+A ₁D ₁
B. AB+DD₁
+D ₁C ₁
C. AD+CC₁+D ₁C ₁
D.12(AB 1+CD 1)+A 1C 1
答案:B
3.若a ,b ,c 为任意向量,m ∈R ,下列等式不一定成立的就是( )
A.(a+b)+c=a+(b+c)
B.(a+b)•c=a•c+b•c
C. m(a+b)=ma+mb
D.(a·b)·c=a·(b·c)
答案:D
4.若三点A, B, C 共线,P 为空间任意一点,且PA+αPB=βPC,则α-β的值为( )
A.1
B.-1
C.12
D.-2
答案:B
5.设a=(x,4,3), b=(3,2, z),且a ∥b,则xz 等于( )
A.-4
B.9
C.-9
D.649
答案:B
6.已知非零向量 e ,e₂不共线,如果AB=e₁+e ₂ A C=2e ₂ 8e ₂AD=3e ₁3 ,则四点 A. B C (
) A.一定共圆
B.恰就是空间四边形的四个顶点心
C.一定共面
D.肯定不共面
答案:C。

1.(本题满分15分)如图,在三棱锥D -ABC 中,DA =DB =DC ,D 在底面ABC 上的射影为E ,AB ⊥BC ,DF ⊥AB 于F .(Ⅰ)求证:平面ABD ⊥平面DEF ;(Ⅱ)若AD ⊥DC ,AC =4,∠BAC =60°,求直线BE 与平面DAB 所成的角的正弦值.答案及解析:1.(Ⅰ)如图,由题意知⊥DE 平面ABC所以DE AB ⊥,又DFAB ⊥所以⊥AB 平面DEF ,………………3分又⊂AB 平面ABD 所以平面⊥ABD 平面DEF…………………6分(Ⅱ)解法一:由DC DB DA ==知ECEB EA ==所以E 是ABC ∆的外心又BC AB ⊥所以E 为AC 的中点…………………………………9分过E 作DF EH ⊥于H ,则由(Ⅰ)知⊥EH 平面DAB所以EBH ∠即为BE 与平面DAB 所成的角…………………………………12分由4=AC , 60=∠BAC 得2=DE ,3=EF 所以7=DF ,732=EH 所以721sin ==∠BE EH EBH …………………………………15分解法二:如图建系,则)0,2,0(-A ,)2,0,0(D ,)0,1,3(-B 所以)2,2,0(--=DA ,)2,1,3(--=DB ……………………………………9分设平面DAB 的法向量为),,(z y x n =由⎪⎩⎪⎨⎧=⋅=⋅00DB n DA n 得⎩⎨⎧=--=--023022z y x z y ,取)1,1,33(-=n ………………12分设EB 与n 的夹角为θ所以7213722||||cos ==⋅=n EB nEB θ所以BE 与平面DAB 所成的角的正弦值为721………………………………15分2.如图,在直三棱柱ABC ﹣A 1B 1C 1中,AA 1=AC=2AB=2,且BC 1⊥A 1C .(1)求证:平面ABC 1⊥平面A 1ACC 1;(2)设D是线段BB1的中点,求三棱锥D﹣ABC1的体积.答案及解析:2.【考点】棱柱、棱锥、棱台的体积;平面与平面垂直的判定.【专题】综合题;转化思想;综合法;立体几何.【分析】(1)证明A1C⊥面ABC1,即可证明:平面ABC1⊥平面A1ACC1;(2)证明AC⊥面ABB1A1,利用等体积转换,即可求三棱锥D﹣ABC1的体积.【解答】(1)证明:在直三棱锥ABC﹣A1B1C1中,有A1A⊥面ABC,而AB⊂面ABC,∴A1A⊥AB,∵A1A=AC,∴A1C⊥AC1,又BC1⊥A1C,BC1⊂面ABC1,AC1⊂面ABC1,BC1∩AC1=C1∴A1C⊥面ABC1,而A1C⊂面A1ACC1,则面ABC1⊥面A1ACC1…(2)解:由(1)知A1A⊥AB,A1C⊥面ABC1,A1C⊥AB,故AB⊥面A1ACC1,∴AB⊥AC,则有AC⊥面ABB1A1,∵D是线段BB1的中点,∴.…【点评】本题考查线面垂直、平面与平面垂直的判定,考查三棱锥D﹣ABC1的体积,考查学生分析解决问题的能力,正确运用定理是关键.3.如图所示,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点.(1)求证:CD⊥PD;(2)求证:EF∥平面PAD.答案及解析:3.【考点】空间中直线与直线之间的位置关系;直线与平面平行的判定.【分析】本题是高考的重要内容,几乎年年考,次次有:(1)的关键是找出直角三角形,也就是找出图中的线线垂直.(2)的关键是找出平面PAD中可能与EF平行的直线.【解答】解:(1)证明:∵PA⊥平面ABCD,而CD⊂平面ABCD,∴PA⊥CD,又CD⊥AD,AD∩PA=A,∴CD⊥平面PAD,∴CD⊥PD、(2)取CD的中点G,连接EG、FG.∵E、F分别是AB、PC的中点,∴EG∥AD,FG∥PD,∴平面EFG∥平面PAD,又∵EF⊂平面EFG,∴EF∥平面PAD.【点评】线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a∥α,b⊂α,a∥b⇒a∥α);③利用面面平行的性质定理(α∥β,a⊂α⇒a∥β);④利用面面平行的性质(α∥β,a⊄β,a∥α⇒a∥β).4.如图,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.(1)求证:AC⊥BC1;(2)求证:AC1∥平面CDB1.答案及解析:4.【考点】直线与平面垂直的性质;直线与平面平行的判定.【专题】综合题;空间位置关系与距离.【分析】(1)利用勾股定理的逆定理可得AC⊥BC.利用线面垂直的性质定理可得CC1⊥AC,再利用线面垂直的判定定理即可证明结论;(2)利用直三棱柱的性质、正方形的性质、三角形的中位线定理即可得出ED∥AC1,再利用线面平行的判定定理即可证明结论【解答】证明:(1)因为三棱柱ABC﹣A1B1C1为直三棱柱,所以C1C⊥平面ABC,所以C1C⊥AC.又因为AC=3,BC=4,AB=5,所以AC2+BC2=AB2,所以AC⊥BC.又C1C∩BC=C,所以AC⊥平面CC1B1B,所以AC⊥BC1.(2)连结C1B交CB1于E,再连结DE,由已知可得E为C1B的中点,又∵D为AB的中点,∴DE为△BAC1的中位线.∴AC1∥DE又∵DE⊂平面CDB1,AC1⊄平面CDB1∴AC1∥平面CDB1.【点评】熟练掌握勾股定理的逆定理、线面垂直的判定和性质定理、直三棱柱的性质、正方形的性质、三角形的中位线定理、线面平行的判定定理是解题的关键.5.已知在三棱锥S﹣ABC中,∠ACB=90°,又SA⊥平面ABC,AD⊥SC于D,求证:AD⊥平面SBC.答案及解析:5.【考点】直线与平面垂直的判定.【专题】证明题.【分析】要证明AD⊥平面SBC,只要证明AD⊥SC(已知),AD⊥BC,而结合已知∠ACB=90°,又SA⊥平面ABC,及线面垂直的判定定理及性质即可证明【解答】证明:∵SA⊥面ABC,∴BC⊥SA;∵∠ACB=90°,即AC⊥BC,且AC、SA是面SAC内的两相交线,∴BC⊥面SAC;又AD⊂面SAC,∴BC⊥AD,又∵SC⊥AD,且BC、SC是面SBC内两相交线,∴AD⊥面SBC.【点评】本题主要考查了直线与平面垂直,平面与平面垂直的相互转化,线面垂直的判定定理的应用,属于基础试题6.如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥底面ABCD,AP=AB=,点E 是棱PB的中点.(Ⅰ)证明:AE⊥平面PBC;(Ⅱ)若AD=1,求二面角B﹣EC﹣D的平面角的余弦值.答案及解析:6.【考点】二面角的平面角及求法;直线与平面垂直的判定.【专题】空间位置关系与距离;空间角.【分析】(Ⅰ)由PA⊥底面ABCD,得PA⊥AB.又PA=AB,从而AE⊥PB.由三垂线定理得BC⊥PB,从而BC⊥平面PAB,由此能证明AE⊥平面PBC.(Ⅱ)由BC⊥平面PAB,AD⊥AE.取CE的中点F,连结DF,连结BF,则∠BFD为所求的二面角的平面角,由此能求出二面角B﹣EC﹣D的平面角的余弦值.【解答】(Ⅰ)证明:如图1,由PA⊥底面ABCD,得PA⊥AB.又PA=AB,故△PAB为等腰直角三角形,而点E是棱PB的中点,所以AE⊥PB.由题意知BC⊥AB,又AB是PB在面ABCD内的射影,由三垂线定理得BC⊥PB,从而BC⊥平面PAB,故BC⊥AE.因为AE⊥PB,AE⊥BC,所以AE⊥平面PBC.(Ⅱ)解:由(Ⅰ)知BC⊥平面PAB,又AD∥BC,得AD⊥平面PAB,故AD⊥AE.在Rt△PAB中,PA=AB=,AE=PB==1.从而在Rt△DAE中,DE==.在Rt△CBE中,CE==,又CD=,所以△CED为等边三角形,取CE的中点F,连结DF,则DF⊥CE,∵BE=BC=1,且BC⊥BE,则△EBC为等腰直角三角形,连结BF,则BF⊥CE,所以∠BFD为所求的二面角的平面角,连结BD,在△BFD中,DF=CD=,BF=,BD==,所以cos∠BFD==﹣,∴二面角B﹣EC﹣D的平面角的余弦值为﹣.【点评】本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.7.如图所示,四棱锥P ABCD的底面ABCD是平行四边形,BA=BD=,AD=2,PA=PD=,E,F分别是棱AD,PC的中点,二面角PADB为60°.(1)证明:平面PBC⊥平面ABCD;(2)求直线EF与平面PBC所成角的正弦值.答案及解析:7.证明:(1)连接PE,BE,∵PA=PD,BA=BD,而E为AD中点,∴PE⊥AD,BE⊥AD,∴∠PEB为二面角P﹣AD﹣B的平面角.在△PAD中,由PA=PD=,AD=2,解得PE=2.在△ABD中,由BA=BD=,AD=2,解得BE=1.在△PEB中,PE=2,BE=1,∠PEB=60˚,由余弦定理,解得PB==,∴∠PBE=90˚,即BE⊥PB.又BC∥AD,BE⊥AD,∴BE⊥BC,∴BE⊥平面PBC.又BE⊂平面ABCD,∴平面PBC⊥平面ABCD.解:(2)连接BF,由(1)知,BE⊥平面PBC,∴∠EFB为直线EF与平面PBC所成的角.∵PB=,∠ABP为直角,MB=PB=,∴AM=,∴EF=.又BE=1,∴在直角三角形EBF中,sin∠EFB==.∴直线EF与平面PBC所成角的正弦值为.考点:直线与平面所成的角;平面与平面垂直的判定.专题:证明题;转化思想;综合法;空间位置关系与距离;空间角.分析:(1)连接PE,BE,由已知推导出∠PEB为二面角P﹣AD﹣B的平面角,推导出BE⊥PB,BE⊥BC,由此能证明平面PBC⊥平面ABCD.(2)连接BF,由BE⊥平面PBC,得∠EFB为直线EF与平面PBC所成的角,由此能求出直线EF与平面PBC所成角的正弦值.解答:证明:(1)连接PE,BE,∵PA=PD,BA=BD,而E为AD中点,∴PE⊥AD,BE⊥AD,∴∠PEB为二面角P﹣AD﹣B的平面角.在△PAD中,由PA=PD=,AD=2,解得PE=2.在△ABD中,由BA=BD=,AD=2,解得BE=1.在△PEB中,PE=2,BE=1,∠PEB=60˚,由余弦定理,解得PB==,∴∠PBE=90˚,即BE⊥PB.又BC∥AD,BE⊥AD,∴BE⊥BC,∴BE⊥平面PBC.又BE⊂平面ABCD,∴平面PBC⊥平面ABCD.解:(2)连接BF,由(1)知,BE⊥平面PBC,∴∠EFB为直线EF与平面PBC所成的角.∵PB=,∠ABP为直角,MB=PB=,∴AM=,∴EF=.又BE=1,∴在直角三角形EBF中,sin∠EFB==.∴直线EF与平面PBC所成角的正弦值为.点评:本题考查面面垂直的证明,考查线面角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养8.(15分)(2010秋•杭州校级期末)如图,已知△BCD中,∠BCD=90°,AB⊥平面BCD,BC=CD=1,分别为AC、AD的中点.(1)求证:平面BEF⊥平面ABC;(2)求直线AD与平面BEF所成角的正弦值.答案及解析:8.【考点】平面与平面垂直的判定;直线与平面所成的角.【专题】计算题;证明题.【分析】(1)通过证明CD⊥平面ABC,CD∥EF,说明EF⊂平面BEF,即可证明平面BEF⊥平面ABC;(2)过A作AH⊥BE于H,连接HF,可得AH⊥平面BEF,推出∠AFH为直线AD与平面BEF所成角.在Rt△AFH中,求直线AD与平面BEF所成角的正弦值.【解答】解:(1)证明:∵AB⊥平面BCD,∴AB⊥CD.又∵CD⊥BC,∴CD⊥平面ABC.∵E、F分别为AC、AD的中点,∴EF∥CD.∴EF⊥平面ABC,∵EF⊂平面BEF,∴平面BEF⊥平面ABC.(2)过A作AH⊥BE于H,连接HF,由(1)可得AH⊥平面BEF,∴∠AFH为直线AD与平面BEF所成角.在Rt△ABC中,为AC中点,∴∠ABE=30°,∴.在Rt△BCD中,BC=CD=1,∴.∴在Rt△ABD中,∴.∴在Rt△AFH中,,∴AD与平面BEF所成角的正弦值为.【点评】证明两个平面垂直,关键在一个面内找到一条直线和另一个平面垂直;利用三垂线定理找出二面角的平面角,解三角形求出此角,是常用方法.9.答案及解析:9.10.(12分)(2015秋•拉萨校级期末)如图,边长为2的正方形ABCD中,(1)点E是AB的中点,点F是BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.求证:A′D⊥EF(2)当BE=BF=BC时,求三棱锥A′﹣EFD的体积.答案及解析:10.【考点】直线与平面垂直的性质;棱柱、棱锥、棱台的体积.【专题】空间位置关系与距离.【分析】(1)由正方形ABCD知∠DCF=∠DAE=90°,得A'D⊥A'F且A'D⊥A'E,所以A'D⊥平面A'EF.结合EF⊂平面A'EF,得A'D⊥EF;(2)由勾股定理的逆定理,得△A'EF是以EF为斜边的直角三角形,而A'D是三棱锥D﹣A'EF的高线,可以算出三棱锥D﹣A'EF的体积,即为三棱锥A'﹣DEF的体积.【解答】解:(1)由正方形ABCD知,∠DCF=∠DAE=90°,∴A'D⊥A'F,A'D⊥A'E,∵A'E∩A'F=A',A'E、A'F⊆平面A'EF.∴A'D⊥平面A'EF.又∵EF⊂平面A'EF,∴A'D⊥EF.(2)由四边形ABCD为边长为2的正方形故折叠后A′D=2,A′E=A′F=,EF=则cos∠EA′F==则sin∠EA′F==•A′E•A′F•sin∠EA′F=故△EA′F的面积S△EA′F由(1)中A′D⊥平面A′EF可得三棱锥A'﹣EFD的体积V=××2=.【点评】本题以正方形的翻折为载体,证明两直线异面垂直并且求三棱锥的体积,着重考查空间垂直关系的证明和锥体体积公式等知识,属于中档题.11.(12分)(2015秋•沧州月考)如图,在△ABC中,AO⊥BC于O,OB=2OA=2OC=4,点D,E,F分别为OA,OB,OC的中点,BD与AE相交于H,CD与AF相交于G,将△ABO 沿OA折起,使二面角B﹣OA﹣C为直二面角.(Ⅰ)在底面△BOC的边BC上是否存在一点P,使得OP⊥GH,若存在,请计算BP的长度;若不存在,请说明理由;(Ⅱ)求二面角A﹣GH﹣D的余弦值.答案及解析:11.【考点】用空间向量求平面间的夹角;直线与平面垂直的性质;二面角的平面角及求法.【专题】数形结合;向量法;空间位置关系与距离;空间角;空间向量及应用.【分析】(Ⅰ)根据条件便知H,G分别为△AOB,△AOC的重心,从而有GH∥EF∥BC,并可说明∠BOC为直角,过O作OP⊥BC,从而有OP⊥GH,而根据摄影定理便有,这样即可求出BP的长度;(Ⅱ)根据上面知OB,OC,OA三直线两两垂直,分别以这三直线为x,y,z轴,建立空间直角坐标系,从而可以根据条件求出图形上一些点的坐标,从而可以得到向量的坐标,可设平面AGH的法向量为,而根据即可求出,同样的方法可以求出平面DGH的一个法向量,根据cos=即可得出二面角A﹣GH﹣D的余弦值.【解答】解:(Ⅰ)H,G分别为△AOB和△AOC的重心;∴;连接EF,则GH∥EF;由已知,EF∥BC,∴GH∥BC;∵OA⊥OB,OA⊥OC,二面角B﹣OA﹣C为直二面角;∴∠BOC为直角;∴在Rt△BOC中,过O作BC的垂线,垂足为P,OP⊥BC,又BC∥GH;∴OP⊥GH,则由摄影定理得:OB2=BP•BC;∴;(Ⅱ)分别以OB,OC,OA为x,y,z轴,建立如图所示空间直角坐标系,则:O(0,0,0),A(0,0,2),D(0,0,1),B(4,0,0),C(0,2,0),H(),;∴,;设为平面AGH的法向量,则:;取x1=1,则y1=2,z1=1,∴;设为平面DGH的法向量,则:;取x2=1,则;∴;∴由图可知二面角A﹣GH﹣D为锐角,∴该二面角的余弦值为.【点评】考查三角形重心的概念及其性质,平行线分线段成比例,三角形中位线的性质,以及二面角的平面角的定义,直角三角形的摄影定理的内容,建立空间直角坐标系,利用空间向量解决二面角问题的方法,平面的法向量的概念及求法,能求空间点的坐标,根据点的坐标求向量的坐标,向量垂直的充要条件,以及向量夹角的余弦公式,清楚两平面所成二面角的大小和两平面的法向量夹角的关系.12.(12分)(2014•芜湖模拟)如图,E是以AB为直径的半圆上异于A、B的点,矩形ABCD 所在的平面垂直于该半圆所在的平面,且AB=2AD=2.(1)求证:EA⊥EC;(2)设平面ECD与半圆弧的另一个交点为F.①试证:EF∥AB;②若EF=1,求三棱锥E﹣ADF的体积.答案及解析:12.【考点】直线与平面垂直的性质;棱柱、棱锥、棱台的体积;直线与平面平行的性质.【专题】空间位置关系与距离.【分析】(1)利用面面垂直的性质,可得BC⊥平面ABE,再利用线面垂直的判定证明AE⊥面BCE,即可证得结论;(2)①先证明AB∥面CED,再利用线面平行的性质,即可证得结论;②取AB中点O,EF的中点O′,证明AD⊥平面ABE,利用等体积,即可得到结论.【解答】(1)证明:∵平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,BC⊥AB,BC⊂平面ABCD∴BC⊥平面ABE∵AE⊂平面ABE,∴BC⊥AE∵E在以AB为直径的半圆上,∴AE⊥BE∵BE∩BC=B,BC,BE⊂面BCE∴AE⊥面BCE∵CE⊂面BCE,∴EA⊥EC;(2)①证明:设面ABE∩面CED=EF∵AB∥CD,AB⊄面CED,CD⊂面CED,∴AB∥面CED,∵AB⊂面ABE,面ABE∩面CED=EF∴AB∥EF;②取AB中点O,EF的中点O′,在Rt△OO′F中,OF=1,O′F=,∴OO′=∵BC⊥面ABE,AD∥BC∴AD⊥平面ABE∴V E﹣ADF =V D﹣AEF===【点评】本题考查面面垂直的性质,线面垂直的判定与性质,考查线面垂直,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.13.(12分)(2014•浙江模拟)如图,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.(1)求证:AC⊥BC1;(2)求证:AC1∥平面CDB1.答案及解析:13.【考点】直线与平面垂直的性质;直线与平面平行的判定.【专题】综合题;空间位置关系与距离.【分析】(1)利用勾股定理的逆定理可得AC⊥BC.利用线面垂直的性质定理可得CC1⊥AC,再利用线面垂直的判定定理即可证明结论;(2)利用直三棱柱的性质、正方形的性质、三角形的中位线定理即可得出ED∥AC1,再利用线面平行的判定定理即可证明结论【解答】证明:(1)因为三棱柱ABC﹣A1B1C1为直三棱柱,所以C1C⊥平面ABC,所以C1C⊥AC.又因为AC=3,BC=4,AB=5,所以AC2+BC2=AB2,所以AC⊥BC.又C1C∩BC=C,所以AC⊥平面CC1B1B,所以AC⊥BC1.(2)连结C1B交CB1于E,再连结DE,由已知可得E为C1B的中点,又∵D为AB的中点,∴DE为△BAC1的中位线.∴AC1∥DE又∵DE⊂平面CDB1,AC1⊄平面CDB1∴AC1∥平面CDB1.【点评】熟练掌握勾股定理的逆定理、线面垂直的判定和性质定理、直三棱柱的性质、正方形的性质、三角形的中位线定理、线面平行的判定定理是解题的关键.14.如图,在三棱锥S﹣ABC中,SB⊥底面ABC,且SB=AB=2,BC=,D、E 分别是SA、SC的中点.(I)求证:平面ACD⊥平面BCD;(II)求二面角S﹣BD﹣E的平面角的大小.答案及解析:14.【考点】用空间向量求平面间的夹角;平面与平面垂直的判定.【专题】空间位置关系与距离;空间角.【分析】(Ⅰ)根据面面垂直的判定定理证明AD⊥平面BCD即可证明平面ACD⊥平面BCD.(Ⅱ)建立空间直角坐标系,利用向量法即可求二面角S﹣BD﹣E的余弦值.【解答】证明:(I)∵∠ABC=,∴BA⊥BC,建立如图所示的坐标系,则C(0,,0),A(2,0,0),D(1,0,1),E(0,,1),S(0,0,2),则=(﹣1,0,1),=(0,,0),=(1,0,1),则•=(﹣1,0,1)•(0,,0)=0,•=(﹣1,0,1)•(1,0,1)=﹣1+1=0,则⊥,⊥,即AD⊥BC,AD⊥BD,∵BC∩BD=B,∴AD⊥平面BCD;∵AD⊂平面BCD;∴平面ACD⊥平面BCD;(II)=(0,,1),则设平面BDE的法向量=(x,y,1),则,即,解得x=﹣1,y=,即=(﹣1,,1),又平面SBD的法向量=(0,,0),∴cos<,>==,则<,>=,即二面角S﹣BD﹣E的平面角的大小为.【点评】本题主要考查空间面面垂直的判定,以及二面角的求解,利用向量法是解决二面角的常用方法.15.如图,在四棱锥P﹣ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD,(Ⅰ)求证:平面PED⊥平面PAC;(Ⅱ)若直线PE与平面PAC所成的角的正弦值为,求二面角A﹣PC﹣D的平面角的余弦值.答案及解析:15.【考点】用空间向量求平面间的夹角;平面与平面垂直的判定;二面角的平面角及求法.【专题】计算题;空间位置关系与距离;空间角.【分析】(I)由面面垂直的性质定理证出PA⊥平面ABCD,从而得到AB、AD、AP两两垂直,因此以AB、AD、AP为x轴、y轴、z轴,建立坐标系o﹣xyz,得A、D、E、C、P的坐标,进而得到、、的坐标.由数量积的坐标运算公式算出且,从而证出DE⊥AC且DE⊥AP,结合线面垂直判定定理证出ED⊥平面PAC,从而得到平面PED⊥平面PAC;(II)由(Ⅰ)得平面PAC的一个法向量是,算出、夹角的余弦,即可得到直线PE与平面PAC所成的角θ的正弦值,由此建立关于θ的方程并解之即可得到λ=2.利用垂直向量数量积为零的方法,建立方程组算出=(1,﹣1,﹣1)是平面平面PCD的一个法向量,结合平面PAC的法向量,算出、的夹角余弦,再结合图形加以观察即可得到二面角A﹣PC﹣D的平面角的余弦值.【解答】解:(Ⅰ)∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,AB⊥PA∴PA⊥平面ABCD结合AB⊥AD,可得分别以AB、AD、AP为x轴、y轴、z轴,建立空间直角坐标系o﹣xyz,如图所示…(2分)可得A(0,0,0)D(0,2,0),E(2,1,0),C(2,4,0),P(0,0,λ)(λ>0)∴,,得,,∴DE⊥AC且DE⊥AP,∵AC、AP是平面PAC内的相交直线,∴ED⊥平面PAC.(4分)∵ED⊂平面PED∴平面PED⊥平面PAC(6分)(Ⅱ)由(Ⅰ)得平面PAC的一个法向量是,设直线PE与平面PAC所成的角为θ,则,解之得λ=±2∵λ>0,∴λ=2,可得P的坐标为(0,0,2)(8分)设平面PCD的一个法向量为=(x0,y0,z0),,由,,得到,令x0=1,可得y0=z0=﹣1,得=(1,﹣1,﹣1)(10分)∴cos<,(11分)由图形可得二面角A﹣PC﹣D的平面角是锐角,∴二面角A﹣PC﹣D的平面角的余弦值为.(12分)【点评】本题在四棱锥中证明面面垂直,并且在线面所成角的正弦情况下求二面角A﹣PC ﹣D的余弦值.着重考查了线面垂直、面面垂直的判定定理和利用空间向量研究直线与平面所成角和二面角大小的方法,属于中档题.16.如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.(Ⅰ)证明:PA⊥BD;(Ⅱ)若PD=AD,求二面角A﹣PB﹣C的余弦值.答案及解析:16.(Ⅰ)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD=,从而BD2+AD2=AB2,故BD⊥AD又PD⊥底面ABCD,可得BD⊥PD所以BD⊥平面PAD.故PA⊥BD(Ⅱ)如图,以D为坐标原点,AD的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz,则A(1,0,0),B(0,,0),C(﹣1,,0),P(0,0,1).=(﹣1,,0),=(0,,﹣1),=(﹣1,0,0),设平面PAB的法向量为=(x,y,z),则即,因此可取=(,1,)设平面PBC的法向量为=(x,y,z),则,即:可取=(0,1,),cos<>==故二面角A﹣PB﹣C的余弦值为:﹣.考点:直线与平面垂直的性质;用空间向量求平面间的夹角.专题:计算题;证明题;综合题;数形结合;转化思想.分析:(Ⅰ)因为∠DAB=60°,AB=2AD,由余弦定理得BD=,利用勾股定理证明BD⊥AD,根据PD⊥底面ABCD,易证BD⊥PD,根据线面垂直的判定定理和性质定理,可证PA⊥BD;(Ⅱ)建立空间直角坐标系,写出点A,B,C,P的坐标,求出向量,和平面PAB的法向量,平面PBC的法向量,求出这两个向量的夹角的余弦值即可.解答:(Ⅰ)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD=,从而BD2+AD2=AB2,故BD⊥AD又PD⊥底面ABCD,可得BD⊥PD所以BD⊥平面PAD.故PA⊥BD(Ⅱ)如图,以D为坐标原点,AD的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz,则A(1,0,0),B(0,,0),C(﹣1,,0),P(0,0,1).=(﹣1,,0),=(0,,﹣1),=(﹣1,0,0),设平面PAB的法向量为=(x,y,z),则即,因此可取=(,1,)设平面PBC的法向量为=(x,y,z),则,即:可取=(0,1,),cos<>==故二面角A﹣PB﹣C的余弦值为:﹣.点评:此题是个中档题.考查线面垂直的性质定理和判定定理,以及应用空间向量求空间角问题,查了同学们观察、推理以及创造性地分析问题、解决问题能力.17.如图,在三棱锥P﹣ABC中,∠ABC=90°,PA⊥平面ABC,E,F分别为PB,PC的中点.(1)求证:EF∥平面ABC;(2)求证:平面AEF⊥平面PAB.答案及解析:17.【考点】平面与平面垂直的判定;直线与平面平行的判定.【专题】空间位置关系与距离.【分析】(1)根据三角形中位线定理可得EF∥BC,进而根据线面平行的判定定理可得EF∥平面ABC;(2)根据PA⊥平面ABC,可得PA⊥BC,结合∠ABC=90°,及线面垂直的判定定理可得BC⊥平面PAB,进而由线面垂直的第二判定定理可得EF平面PAB,最后由面面垂直的判定定理可得平面AEF⊥平面PAB.【解答】证明:(1)∵E,F分别为PB,PC的中点.∴EF∥BC,又∵BC⊂平面ABC,EF⊄平面ABC,∴EF∥平面ABC;(2)∵PA⊥平面ABC,BC⊂平面ABC,∴PA⊥BC,又∵∠ABC=90°,∴AB⊥BC,又∵PA∩AB=A,PA,AB⊂平面PAB,∴BC⊥平面PAB,由(1)中EF∥BC,∴EF⊥平面PAB,又∵EF⊂平面AEF,∴平面AEF⊥平面PAB.【点评】本题考查的知识点是线面平行的判定定理,线面垂直的判定定理,面面垂直的判定定理,是空间线面关系的简单综合应用,难度中档.18.(14分)如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.(Ⅰ)求证:AC⊥平面BCE;(Ⅱ)求三棱锥A﹣CDE的体积;(Ⅲ)线段EF上是否存在一点M,使得BM⊥CE?若存在,确定M点的位置;若不存在,请说明理由.答案及解析:18.【考点】棱柱、棱锥、棱台的体积;直线与平面垂直的判定.【专题】空间位置关系与距离.【分析】(I)如图所示,取AB的中点N,连接CN,可得四边形ADCN是正方形,可得NA=NB=NC,可得AC⊥CB,利用AF⊥平面ABCD,AF∥BE,可得BE⊥平面ABCD,即可证明.=V三棱锥E﹣ACD=即可得出.(II)利用V三棱锥A﹣CDE(III)线段EF上存在一点M为线段EF的中点,使得BM⊥CE.连接MN,BM,EN,则四边形BEMN为正方形,可得BM⊥EN,利用线面面面垂直的判定与性质定理可得:CN⊥平面ABEF,可得CN⊥BM,又BM⊥CE.即可证明BM⊥平面CEN.【解答】(I)证明:如图所示,取AB的中点N,连接CN,则四边形ADCN是正方形,可得NA=NB=NC,∴AC⊥CB,∵AF⊥平面ABCD,AF∥BE,∴BE⊥平面ABCD,∴BE⊥AC,又BE∩BC=B,∴AC⊥平面BCE.=V三棱锥E﹣ACD===.(II)解:V三棱锥A﹣CDE(III)解:线段EF上存在一点M为线段EF的中点,使得BM⊥CE.连接MN,BM,EN,则四边形BEMN为正方形,∴BM⊥EN,∵CN⊥AB,平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB,∴CN⊥平面ABEF,∴CN⊥BM,又CN∩EN=N,∴BM⊥平面CEN,∴BM⊥CE.【点评】本题考查了线面面面垂直的判定与性质定理、正方形的判定与性质定理、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.19.(13分)如图,在正方体A1B1C1D1﹣ABCD中,(1)在正方体的12条棱中,与棱AA1是异面直线的有几条(只要写出结果)(2)证明:AC∥平面A1BC1;(3)证明:AC⊥平面BDD1B1.答案及解析:19.【考点】直线与平面垂直的判定;直线与平面平行的判定.【专题】证明题;数形结合;数形结合法;空间位置关系与距离.【分析】(1)画出正方体ABCD﹣A1B1C1D1,根据异面直线的概念即可找出与棱AA1异面的棱.(2)连接AC,A1C1,则A1C1∥AC,利用线面平行的判定定理即可证明;(3)由DD1⊥面AC,知DD1⊥AC,由DD1⊥BD,能够证明AC⊥平面BDD1B1.【解答】解:(1)与棱AA1异面的棱为:CD,C1D1,BC,B1C1,共4条.(2)证明:连接AC,A1C1,则A1C1∥AC,∵AC⊄平面A1BC1,A1C1⊂平面A1BC1,∴AC∥平面A1BC1;(3)证明:∵DD1⊥面AC,AC⊂平面AC,∴DD1⊥AC,∵AC⊥BD,DD1∩BD=D,BD⊂平面BDD1B1,DD1⊂平面BDD1B1∴AC⊥平面BDD1B1.【点评】考查异面直线的概念,直线与平面垂直的证明,直线与平面平行的判定,解题时要认真审题,仔细解答,注意合理地进行等价转化,属于中档题.20.如图,在正方体ABCD﹣A1B1C1D1中,(1)证明:BC1⊥面A1B1CD;(2)求直线A1B和平面A1B1CD所成的角.答案及解析:20.【考点】直线与平面所成的角;直线与平面垂直的判定.【分析】(1)要证BC1⊥面A1B1CD;应通过证明A1B1⊥BC1.BC1⊥B1C两个关系来实现,两关系容易证明.(2)因为BC1⊥平面A1B1CD,所以A1O为斜线A1B在平面A1B1CD内的射影,所以∠BA1O 为A1B与平面A1B1CD所成的角.在RT△A1BO中求解即可.【解答】解:(1)连接B1C交BC1于点O,连接A1O.在正方体ABCD﹣A1B1C1D1中因为A1B1⊥平面BCC1B1.所以A1B1⊥BC1.又∵BC1⊥B1C,又BC1∩B1C=O∴BC1⊥平面A1B1CD(2)因为BC1⊥平面A1B1CD,所以A1O为斜线A1B在平面A1B1CD内的射影,所以∠BA1O 为A1B与平面A1B1CD所成的角.设正方体的棱长为a在RT△A1BO中,A1B=a,BO=a,所以BO=A1B,∠BA1O=30°,即直线A1B和平面A1B1CD所成的角为30°.【点评】本题考查空间直线与平面垂直关系的判断,线面角大小求解,考查空间想象能力、推理论证、计算、转化能力.21.如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点.(1)证明:PA∥平面EDB;(2)证明:平面PAC⊥平面PDB.答案及解析:21.【考点】平面与平面垂直的判定;直线与平面平行的判定.【专题】证明题;转化思想;综合法;空间位置关系与距离.【分析】(1)欲证PA∥平面EDB,根据直线与平面平行的判定定理可知只需证PA与平面EDB内一直线平行,连接AC,交BD于O,连接EO,根据中位线定理可知EO∥PA,PA⊄平面EDB,EO⊂平面EDB,满足定理所需条件;(2)证明AC⊥平面PBD,即可证明平面PAC⊥平面PDB.【解答】证明:(1)设AC与BD相交于点O,则O为AC的中点.∵E是P的中点,∴EO∥PA又∵EO⊂平面EDB,PA⊄平面EDB,∴PA∥平面EDB;(2)∵PO⊥平面ABCD,∴PD⊥AC又∵四边形ABCD为正方形,∴AC⊥BD从而AC⊥平面PBD,∴平面PAC⊥平面PBD.【点评】本题考查直线与平面平行的判定,以及平面与平面垂直的判定,考查空间想象能力,逻辑思维能力,计算能力,是中档题.22.如图,在直三棱柱ABC=A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.(1)求证:BC⊥A1B;(2)若AD=,AB=BC=2,P为AC的中点,求二面角P﹣A1B﹣C的平面角的余弦值.答案及解析:22.【考点】用空间向量求平面间的夹角;空间中直线与直线之间的位置关系.【专题】空间位置关系与距离;空间角.【分析】(Ⅰ)由已知得A1A⊥平面ABC,A1A⊥BC,AD⊥BC.由此能证明BC⊥A1B.(Ⅱ)由(Ⅰ)知BC⊥平面A1AB,从而BC⊥AB,以B为原点建立空间直角坐标系B﹣xyz,利用向量法能求出二面角P﹣A1B﹣C的平面角的余弦值.【解答】(Ⅰ)证明:∵三棱柱ABC﹣A1B1C1为直三棱柱,∴A1A⊥平面ABC,又BC⊂平面ABC,∴A1A⊥BC,∵AD⊥平面A1BC,且BC⊂平面A1BC,∴AD⊥BC.又AA1⊂平面A1AB,AD⊂平面A1AB,A1A∩AD=A,∴BC⊥平面A1AB,又A1B⊂平面A1BC,∴BC⊥A1B.(Ⅱ)解:由(Ⅰ)知BC⊥平面A1AB,AB⊂平面A1AB,从而BC⊥AB,如图,以B为原点建立空间直角坐标系B﹣xyz∵AD⊥平面A1BC,其垂足D落在直线A1B上,∴AD⊥A1B.在Rt△ABD中,AD=,AB=2,sin∠ABD==,∠ABD=60°,在直三棱柱ABC﹣A1B1C1中,A1A⊥AB.在Rt△ABA1中,AA1=AB•tan60°=2,则B(0,0,0),A(0,2,0),C(2,0,0),P(1,1,0),A 1(0,2,2),,=(0,2,2),,设平面PA1B的一个法向量,则,即,得,设平面CA1B的一个法向量,则,即,得,,∴二面角P﹣A1B﹣C平面角的余弦值是.…【点评】本题考查异面直线垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.23.(16分)如图,在正方体ABCD﹣A1B1C1D1的棱长为a,E为棱AB上的一动点.(1)若E为棱AB的中点,①求四棱锥B1﹣BCDE的体积②求证:面B1DC⊥面B1DE(2)若BC1∥面B1DE,求证:E为棱AB的中点.答案及解析:23.【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定;平面与平面垂直的判定.【专题】数形结合;数形结合法;空间位置关系与距离.【分析】(1)①四棱锥B1﹣BCDE的底面为直角梯形BEDC,棱锥的高为B1B,代入体积公式即可;②面B1DC∩面B1DE=B1D,故只需在平面B1DE找到垂直于交线B1D的直线即可,由DE=B1E=a可易知所找直线为等腰△EB1D底边中线;(2)辅助线同上,由中位线定理可得OF∥DC,且OF=DC,从而得出OF∥EB,由BC1∥面B1DE可得EO∥B1C,故四边形OEBF是平行四边形,得出结论.【解答】证明:(1)①∵正方体ABCD﹣A1B1C1D1∴B1B平面BEDC,•B1B=•(a+)•a•a=.∴V=•S梯形BCDE②取B1D的中点O,设BC1∩B1C=F,连接OF,∵O,F分别是B1D与B1C的中点,∴OF∥DC,且OF=DC,又∵E为AB中点,∴EB∥DC,且EB=DC,∴OF∥EB,OF=EB,即四边形OEBF是平行四边形,∴OE∥BF,∵DC⊥平面BCC1B1,BC1⊂平面BCC1B1,∴BC1⊥DC,∴OE⊥DC.又BC1⊥B1C,∴OE⊥B1C,又∵DC⊂平面B1DC,B1C⊂平面B1DC,DC∩B1C=C,∴OE⊥平面B1DC,。
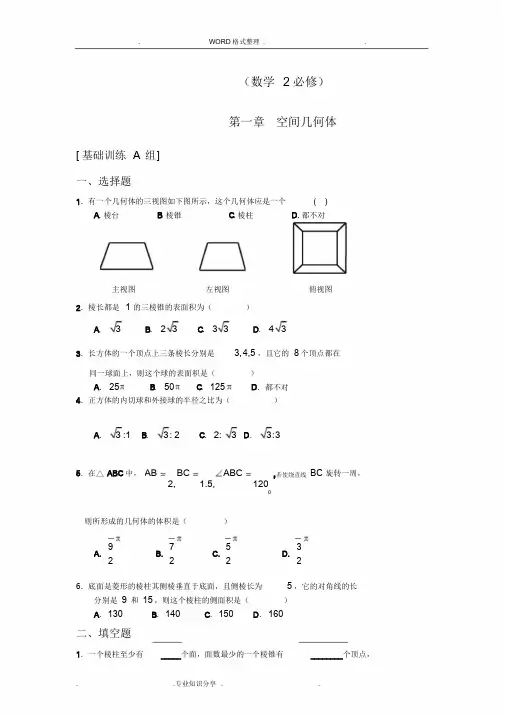
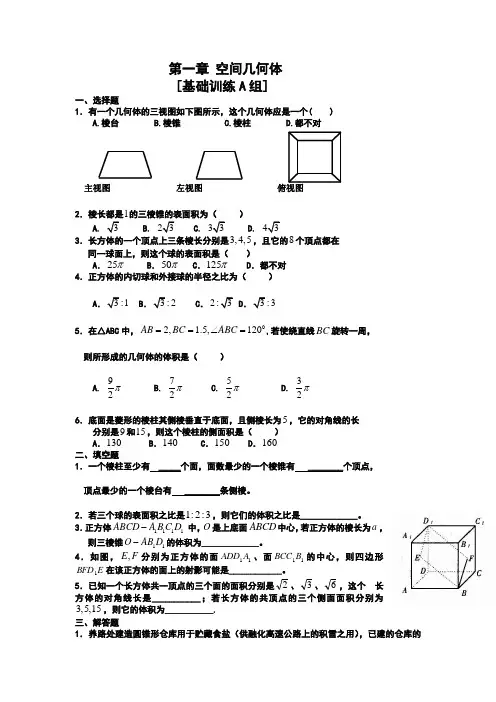
(数学 2 必修)第一章空间几何体[ 基础训练A组]一、选择题1.有一个几何体的三视图如下图所示,这个几何体应是一个( )A. 棱台B. 棱锥C. 棱柱D. 都不对主视图左视图俯视图2.棱长都是1的三棱锥的表面积为()A. 3B. 2 3C. 3 3D. 4 33.长方体的一个顶点上三条棱长分别是3, 4,5 ,且它的8 个顶点都在同一球面上,则这个球的表面积是()A.25 B.50 C.125 D.都不对4.正方体的内切球和外接球的半径之比为()A. 3 :1 B.3: 2 C.2: 3 D.3:35.在△ABC中,AB BC ABC ,若使绕直线BC 旋转一周,2, 1.5, 120则所形成的几何体的体积是()A. 92B.72C.52D.326.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为 5 ,它的对角线的长分别是9和15 ,则这个棱柱的侧面积是()A.130 B.140 C.150 D.160二、填空题1.一个棱柱至少有_____个面,面数最少的一个棱锥有________个顶点,. .专业知识分享. .顶点最少的一个棱台有________条侧棱。
2.若三个球的表面积之比是1: 2 :3,则它们的体积之比是_____________。
3.正方体ABCD A1B1C1D1 中,O是上底面ABCD 中心,若正方体的棱长为a,则三棱锥O AB D 的体积为_____________。
1 14.如图,E,F 分别为正方体的面ADD1 A1 、面BCC1B1 的中心,则四边形B F D1E 在该正方体的面上的射影可能是____________ 。
5.已知一个长方体共一顶点的三个面的面积分别是 2 、 3 、 6 ,这个长方体的对角线长是___________;若长方体的共顶点的三个侧面面积分别为3,5,15 ,则它的体积为___________.三、解答题1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12M ,高4M ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4M (高不变);二是高度增加4M (底面直径不变)。

立几测001试一、选择题:1.a 、b 是两条异面直线,下列结论正确的是( )A .过不在a 、b 上的任一点,可作一个平面与a 、b 都平行B .过不在a 、b 上的任一点,可作一条直线与a 、b 都相交C .过不在a 、b 上的任一点,可作一条直线与a 、b 都平行D .过a 可以且只可以作一个平面与b 平行2.空间不共线的四点,可以确定平面的个数为 ( )A.0 B.1 C.1或4 D.无法确定3.在正方体1111ABCD A B C D -中,M 、N 分别为棱1AA 、1BB 的中点,则异面直线CM 和1D N 所成角的正弦值为 ( ) A.19 B.2345 254.已知平面α⊥平面β,m 是α内的一直线,n 是β内的一直线,且m n ⊥,则:①m β⊥;②n α⊥;③m β⊥或n α⊥;④m β⊥且n α⊥。
这四个结论中,不正确...的三个是 ( )A.①②③ B.①②④ C.①③④ D.②③④5.一个简单多面体的各个面都是三角形,它有6个顶点,则这个简单多面体的面数是( ) A. 4 B. 5 C. 6 D. 86. 在北纬45°的纬度圈上有甲、乙两地,两地经度差为90°,则甲、乙两地最短距离为(设地球半径为R )( ) A.R π42 B. R 3π C. R 2π D. 3R7. 直线l ⊥平面α,直线m ⊂平面β,有下列四个命题(1)m l ⊥⇒βα// (2)m l //⇒⊥βα (3)βα⊥⇒m l // (4)βα//⇒⊥m l 其中正确的命题是( )A. (1)与(2)B. (2)与(4)C. (1)与(3)D. (3)与(4)8. 正三棱锥的侧面均为直角三角形,侧面与底面所成角为α,则下列不等式成立的是( ) A. 60πα<< B.46παπ<< C.34παπ<< D.23παπ<<9.ABC ∆中,9AB =,15AC =,120BAC ∠=︒,ABC ∆所在平面α外一点P 到点A 、B 、C 的距离都是14,则P 到平面α的距离为( )A.7 B.9 C.11 D.1310.在一个45︒的二面角的一个平面内有一条直线与二面角的棱成角45︒,则此直线与二面角的另一个平面所成角的大小为 ( )A.30︒ B.45︒ C.60︒ D.90︒11. 如图,E, F 分别是正方形SD 1DD 2的边D 1D,DD 2的中点, 沿SE,SF,EF 将其折成一个几何体,使D 1,D,D 2重合,记作 D.给出下列位置关系:①SD ⊥面DEF; ②SE ⊥面DEF;③DF ⊥SE; ④EF ⊥面SED,其中成立的有: ( )A. ①与② B. ①与③ C. ②与③ D. ③与④12. 某地球仪的北纬60度圈的周长为6πcm,则地球仪的表面积为( )A. 24πcm 2B. 48πcm 2C. 144πcm 2D. 288πcm 2二、填空题(本大题共4小题,每小题4分,共16分) 13. 直二面角α—MN —β中,等腰直角三角形ABC 的斜边BC ⊂α,一直角边AC ⊂β,BC 与β所成角的正弦值是46,则AB 与β所成角大小为__________。

空间几何体的结构选择(基础题)1.下列各组几何体中全是多面体的一组是()A.三棱柱四棱台球圆锥B.三棱柱四棱台正方体圆台C.三棱柱四棱台正方体六棱锥D.圆锥圆台球半球解:选项A中的球和圆锥是旋转体,A不正确;B中的圆台是旋转体,所以B不正确;D中的四个几何体全是旋转体,所以D不正确;只有C中的四个几何体符合多面体概念.故选C.2.若正四棱台的上底边长为2,下底边长为8,高为4则它的表面积为()A.50 B.100C.248 D.以上答案都不对解:∵上底的边心距为1,下底的边心距为4,高是4,∴斜高为=5,故侧面积等于4××5=100.它的表面积为S=100+22+82=168.故选:D.3.某四面体的三视图如图所示.该四面体的六条棱的长度中,最大的是()A.2B.2C.2D.4解:由三视图可知原几何体为三棱锥,其中底面△ABC为俯视图中的钝角三角形,∠BCA为钝角,其中BC=2,BC边上的高为2,PC⊥底面ABC,且PC=2,由以上条件可知,∠PCA为直角,最长的棱为PA或AB,在直角三角形PAC中,由勾股定理得,PA===2,又在钝角三角形ABC中,AB==.故选C.4.下列四种说法中:①有两个面平行,其余各面都是平行四边形的几何体叫棱柱②相等的线段在直观图中仍然相等③一个直角三角形绕其一边旋转一周所形成的封闭图形叫圆锥④用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台正确的个数是( )A.0 B.1 C.2 D.3解:有两个面平行,其余各面都是平行四边形,并且相邻的两个平行四边形的公共边都相互平行,这些面围成的几何体叫棱柱,故①错误.②相等的线段在直观图中仍然相等,不一定相等,不正确;③根据一个直角三角形绕其一个直角边边旋转一周所形成的封闭图形叫圆锥,可得不正确;④用平行于底面的平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台,不正确.故选A.5.下列命题中,正确的是()A.底面是正方形的四棱柱是正方体B.棱锥的高线可能在几何体之外C.有两个面互相平行,其余各面是平行四边形的几何体是棱柱D.有一个面是多边形,其余各面都是三角形的几何体是棱锥解:底面是正方形的四棱柱不一定是正方体,故A错误;斜棱锥的高线有可能在几何体之外,故B正确;根据棱柱的定义可得,有两个面互相平行,其余各面是平行四边形的几何体不一定是棱柱,故C错误;有一个面是多边形,其余各面是有公共顶点的三角形的几何体是棱锥,故D错误.故选:B.6.下列说法正确的是()A.圆锥的侧面展开图是一个等腰三角形B.棱柱的两个底面全等且其余各面都是矩形C.任何一个棱台的侧棱必交于同一点D.过圆台侧面上一点有无数条母线解:在A中,圆锥的侧面展开后是一个扇形,不是等腰三角形,故A错误;在B中,棱柱的两个底面全等且其余各面都是平行四边形,故B错误;在C中,由棱台的定义得任何一个棱台的侧棱必交于同一点,故C正确;在D中,过圆台侧面上一点有且只有1数条母线,故D错误.故选:C.7.下列结论,其中正确的个数是( )①梯形的直观图可能是平行四边形②三棱锥中,四个面都可以是直角三角形③如果一个棱锥的各个侧面都是等边三角形,这个棱锥不可能是六棱锥④底面是矩形的平行六面体是长方体.A.1 B.2 C.3 D.4解:①梯形的直观图可能是平行四边形;不正确,因为平行x轴的线段长度不变;②三棱锥中,四个面都可以是直角三角形;正确,一条棱长垂直底面直角三角形的一个锐角,即可满足题意.③如果一个棱锥的各个侧面都是等边三角形,这个棱锥不可能是六棱锥;错误,满足条件,结果是正六边形.④底面是矩形的平行六面体是长方体.棱长不垂直底面,不正确.故选A.8.下列几何体是组合体的是()A.B.C.D.解:选项A是圆锥体,B是圆柱体,C是球体,D是圆台与圆锥体的组合体.故选:D.9.在空间中有下列四个命题:①有两组对边相等的四边形是平行四边形;②四边相等的四边形是菱形;③两组对边分别平行的四边形是平行四边形;④连接空间四边形各边中点的四边形一定是梯形.其中正确命题的个数为( )A.1 B.2 C.3 D.4解:四边相等和两组对边相等的四边形可以是空间四边形,故①②错误,连接空间四边形各边中点的四边形一定是平行四边形,故④错误,两组对边分别平行的四边形是平行四边形,正确,故正确命题的个数为1个,故选:A10.以下说法正确的是()A.球的截面中过球心的截面面积未必最大B.圆锥截去一个小圆锥后剩下来的部分是圆台C.棱锥截去一个小棱锥后剩下来的部分是棱台D.用两个平行平面去截圆柱,截得的中间部分还是圆柱解:在A中,球的截面中过球心的截面面积最大,故A错误;在B中,圆锥截去一个小圆锥后剩下来的部分是圆台,由圆台的定义知B正确;在C中,棱锥截去一个小棱锥后剩下来的部分有可是棱台,有可能不是棱台,故C错误;在D中,用两个平行平面去截圆柱,如果沿纵切面方向截得的中间部分不是圆柱,故D错误.故选:B.12.如图几何体中不是柱体的有()A.1个 B.2个 C.3个 D.4个解:①是三棱柱,②的上下两个平面不平行,不是三棱柱,③是四棱柱,④是圆柱,⑤是四棱柱,⑥是四棱台,⑦三棱锥;∴不是柱体的为②⑥⑦,共3个.故选C.14.下列说法正确的是( )A.以直角三角形一边为轴旋转所得的旋转体是圆锥B.用一个平面去截圆锥,得到一个圆锥和一个圆台C.正棱锥的棱长都相等D.棱柱的侧棱都相等,侧面是平行四边形解:对于A,以直角三角形的一直角边为轴旋转所得的旋转体是圆锥,斜边为轴旋转所得的旋转体是组合体,故A错误.对于B,用平行与底面的平面去截圆锥,得到一个圆锥和一个圆台,否则不是,故B错误;对于C,正棱锥的侧棱长都相等,底边棱长不一定相等,故C错误;对于D,棱柱的侧棱都相等,侧面是平行四边形,D正确.故选:D.15.下列命题中正确的是()A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台B.有两个面平行,其他面都是平行四边形的几何体叫棱柱C.棱台的底面是两个相似的正方形D.棱台的侧棱延长后必交于一点解:在A中,用一个平行于底面的平面去截棱锥,棱锥底面和截面之间的部分是棱台,故A不正确;在B中,两个底面平行且相似,其余各面都是梯形的多面体是棱台,侧棱不一定相交于一点,故B不正确.在C中,棱台的底面是两个相似的多边形,故C错误;在D中,由棱台的性质得棱台的侧棱延长后必交于一点,故D正确.故选:D.16.下列结论正确的是()A.圆锥的顶点与底面圆周上的任意一点的连线都是母线B.以三角形的一条边所在直线为旋转轴,其余两边绕旋转轴旋转形成的曲面所围成的几何体叫圆锥C.棱锥的侧棱长与底面多边形的边长都相等,则该棱锥可能是六棱锥D.各个面都是三角形的几何体是三棱锥解:在A中,由圆锥的定义知:圆锥的顶点与底面圆周上的任意一点的连线都是母线,故A正确;在B中,如图,若△ABC不是直角三角形,或△ABC是直角三角形但旋转轴不是直角边,所得的几何体都不是圆锥,故B错误;在C中,若该棱锥是六棱锥,由题设知,它是正六棱锥,正六棱锥的侧棱长必大于底面边长,这与题设矛盾,故C错误;在D中,三棱锥每个面都是三角形,但是每个面都是三角形的几何体不一定是三棱锥,2个一样的三棱锥上下拼接成一个六面体,它每个面都是三角形,故D错误.故选:A.17.若一个长方体共顶点的三个面的对角线长分别是a,b,c,则长方体的对角线长是()A.B.C.D.解:设同一顶点的三条棱分别为x,y,z,则x2+y2=a2,y2+z2=b2,x2+z2=c2得x2+y2+z2=(a2+b2+c2),则对角线长为.故选:B.18.如图是正方体的表面展开图,则图中的直线AB,CD在原正方体中是()A.平行B.相交成60°角C.异面成60°角D.异面垂直解:把正方体的表面展开图变形为正方体,B与D重合,此时AB=AC=BC,∴△ABC为等边三角形,即∠ABC=60°,则图中的直线AB,CD在原正方体中是相交成60°角,故选:B.19.在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为的正方形,AA1=3,E是AA1的中点,过C1作C1F⊥平面BDE 与平面ABB1A1交于点F,则等于()A.B.C.D.解:连结AC、BD,交于点O,∵四边形ABCD是正方形,AA1⊥底面ABCD,∴BD⊥平面ACC1A1,则当C1F与EO垂直时,C1F⊥平面BDE,∵F∈平面ABB1A1,∴F∈AA1,在矩形ACC1A1中,△C1A1F∽△EAO,则=,∵A1C1=2AO=,AE=,∴A1F=,∴AF=,∴=.故选:C.20.下面没有体对角线的一种几何体是( )A.三棱柱B.四棱柱C.五棱柱D.六棱柱解:三棱柱,四棱锥,五棱柱,六棱柱,底面分别为三角形,四边形,五边形,六边形,三角形没有对角线,所以三棱柱没有对角线.故选:A.22.如图所示是正方体的平面展开图,在这个正方体中()①BM与ED平行②CN与BE是异面直线;③CN与BM成60°角;④DM与BN垂直.A.①②③B.②④C.③④D.②③④解:由题意画出正方体的图形如图:显然①②不正确;③CN与BM成60°角,即∠ANC=60°正确;④DM⊥平面BCN,所以④正确;故选C.23.有下列三种说法①侧棱垂直于底面的棱柱是直棱柱②底面是正多边形的棱柱是正棱柱③棱柱的侧面都是平行四边形.其中正确说法的个数是()A.0 B.1 C.2 D.3解:①侧棱垂直于底面的棱柱是直棱柱,正确;②底面是正多边形的直棱柱是正棱柱,不正确;③棱柱的侧面都是平行四边形,正确,故选:C.24.如图所示,是一个正方体的表面展开图,则图中“2”所对的面是()A.1 B.7 C.快D.乐解:由已知中的正方体表面展开图可得:2和7对面,0和快对面,1和乐对面,故选:B25.如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是()A.平行B.相交成60° C.相交且垂直D.异面直线解:将正方体还原得到A,B,C,D的位置如图因为几何体是正方体,所以连接AC,得到三角形ABC是等边三角形,所以∠ABC=60°;故选:B.26.半径为R的半圆卷成底面最大的圆锥,所得圆锥的高为()A.B.C.D.解:半径为R的半圆弧长为πR,圆锥的底面圆的周长为πR,圆锥的底面半径为:,所以圆锥的高:=.故选:B.27.若圆锥的侧面展开图是圆心角为120°、半径为l的扇形,则这个圆锥的表面积与侧面积的比是()A.4:3 B.2:1 C.5:3 D.3:2解:圆锥的侧面积=π×12×=圆锥的底面半径=2π×1×÷2π=,圆锥的底面积==,圆锥的表面积=侧面积+底面积=,∴这个圆锥的表面积与侧面积的比=4:3.故选A28.在正四棱锥V﹣ABCD中(底面是正方形,侧棱均相等),AB=2,VA=,且该四棱锥可绕着AB任意旋转,旋转过程中CD∥平面α,则正四棱锥V﹣ABCD在平面α内的正投影的面积的取值范围是()A.[2,4] B.(2,4] C.[,4] D.[2,2]解:由题意,侧面上的高为=,∴侧面的面积为=2,又由于底面的面积为2×2=4,当正四棱锥的高平行于面时面积最小是2,∴正四棱锥V﹣ABCD在面α内的投影面积的取值范围是[2,4],故选:A.29.观察如图所示几何体,其中判断正确的是()A.①是棱台B.②是圆台C.③是棱锥D.④不是棱柱解:图形①,不满足棱台的定义,所以①不正确;图形②,不满足圆台的定义,所以②不正确;图形③满足棱锥的定义,所以③正确;图形④是棱柱,所以④的判断不正确.故选:C.30.正四棱锥的侧棱长是底面长的k倍,则k的取值范围是()A.(0,+∞)B.(,+∞}) C.(,+∞) D.(,+∞)解:如图所示,设正四棱锥V﹣ABCD底面中心为O,BC=a,则VB=ka,易知OB=a;在Rt△VOB中,cos∠VBO==,∵∠VBO∈(0,),∴0<<1,∴,解得k>;∴k的取值范围是(,+∞).32.用一个平面去截四棱锥,不可能得到()A.棱锥B.棱柱C.棱台D.四面体解:∵棱柱的上下底面是相同的,∴用一个平面去截四棱锥,不可能得到棱柱.故选:B.33.正四面体的内切球球心到一个面的距离等于这个正四面体高的()A.B.C.D.解:球心到正四面体一个面的距离即球的半径r,连接球心与正四面体的四个顶点.把正四面体分成四个高为r的三棱锥,所以4×S•r=•S•h,r=h.(其中S为正四面体一个面的面积,h为正四面体的高)答案:C.35.如图所示,观察四个几何体,其中判断正确的是( )A.①是棱台B.②是圆台C.③是棱锥D.④不是棱柱解:图①不是由棱锥截来的,所以①不是棱台;图②上、下两个面不平行,所以②不是圆台;图③是棱锥.图④前、后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以④是棱柱.故选C.37.下列说法中不正确的是()A.棱柱的各个侧面都是平行四边形B.棱锥的侧面都是三角形C.棱台的所有侧棱都相等D.圆柱的任意两条母线互相平行解:棱柱的侧面是平行四边形,正确;棱锥的侧面是有公共顶点的三角形,正确棱台的各条棱不一定都相等,不正确,圆柱的任意两条母线互相平行,正确,故选:C.38.下列关于棱锥、棱台的说法,其中不正确的是()A.棱台的侧面一定不会是平行四边形B.棱锥的侧面只能是三角形C.由四个面围成的封闭图形只能是三棱锥D.棱锥被平面截成的两部分不可能都是棱锥解:在A中,棱台的侧面是梯形,故A正确;在B中,由棱锥的定义得棱锥的侧面只能是三角形,故B正确;在C中,由棱锥的定义得四个面围成的封闭图形只能是三棱锥,故C正确;在D中,棱锥被平面截成的两部分有可能都是棱锥,故D错误.故选:D.42.如图是由哪个平面图形旋转得到的()A.B.C.D.解:图中所给的几何体是由上部的圆锥和下部的圆台组合而成的,故轴截面的上部是直角三角形,下部为直角梯形构成,故选 D.43.将半径为1的圆分割成面积之比为1:2:3的三个扇形作为三个圆锥的侧面,设这三个圆锥底面半径依次为r1,r2,r3,那么r1+r2+r3的值为( )A.B.2 C.D.1解:∵2πr1=,∴r1=,同理,∴r1+r2+r3=1,故选:D.45.一个底面半径为2cm的圆柱形容器内盛有高度为6cm的水,现将一个母线长为cm的圆锥形物体完全浸入水中,容器里水的高度上升到7cm,则该圆锥的高为( )A.1cm B.2cm C.3cm D.cm解:圆锥的体积V=π×22×1=4π,设圆锥的高为h,则圆锥的底面半径r=,∴V==4π,解得h=1或h=3.当h=1时,r==2>2,不符合题意.故选:C.47.如图,已知半径为2的半圆中,BC为直径,O为圆心,点A在半圆弧上,且AB=AC,则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为()A.B.C.16πD.32π解:半圆绕BC旋转一周所得球体的体积V球==.三角形ABC绕BC旋转一周所得几何体体积V′==.∴阴影部分绕BC旋转一周所得几何体体积V=V球﹣V′=.故选:A.48.若一个圆锥的轴截面是等边三角形,则该圆锥的侧面积与底面积的比等于()A.3 B.2 C.D.解:设圆锥的底面半径为r,则母线l=2r,∴S侧=πrl=2πr2,S底=πr2,∴=2.故选:B.49.将直角三角形绕它的一个直角边所在的直线旋转一周,形成的几何体一定是( )A.圆锥B.圆柱C.圆台D.以上均不正确解:由旋转体的定义,将直角三角形绕它的一个直角边所在的直线旋转一周,形成的几何体为圆锥故选A50.一竖立在地面上的圆锥形物体的母线长为4m,侧面展开图的圆心角为,则这个圆锥的体积等于( )A.πm3B.πm3C.πm3D.πm3解:设圆锥的底面半径为r,圆锥形物体的母线长l=4m,侧面展开图的圆心角为,故2πr=l,解得:r=m,故圆锥的高h==m,故圆锥的体积V==πm3,故选:D。
第一章 空间几何体 [基础训练A 组]一、选择题1.有一个几何体的三视图如下图所示,这个几何体应是一个( )A.棱台B.棱锥C.棱柱D.都不对2.棱长都是1的三棱锥的表面积为( )3.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在 同一球面上,则这个球的表面积是( )A .25πB .50πC .125πD .都不对 4.正方体的内切球和外接球的半径之比为( )AB2 C.5.在△ABC 中,02, 1.5,120AB BC ABC ==∠=,若使绕直线BC 旋转一周, 则所形成的几何体的体积是( )A.92π B. 72π C. 52π D. 32π 6.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长 分别是9和15,则这个棱柱的侧面积是( ) A .130 B .140 C .150 D .160 二、填空题1.一个棱柱至少有 _____个面,面数最少的一个棱锥有 ________个顶点, 顶点最少的一个棱台有 ________条侧棱。
2.若三个球的表面积之比是1:2:3,则它们的体积之比是_____________。
3.正方体1111ABCD A BC D - 中,O 是上底面ABCD 中心,若正方体的棱长为a , 则三棱锥11O AB D -的体积为_____________。
4.如图,,E F 分别为正方体的面11A ADD 、面11B BCC 的中心,则四边形E BFD 1在该正方体的面上的射影可能是____________。
5.已知一个长方体共一顶点的三个面的面积分别是2、3、6,这个 长方体的对角线长是___________;若长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为___________. 三、解答题1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的主视图 左视图 俯视图C 底面直径为12M ,高4M ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4M (高不变);二是高度增加4M (底面直径不变)。
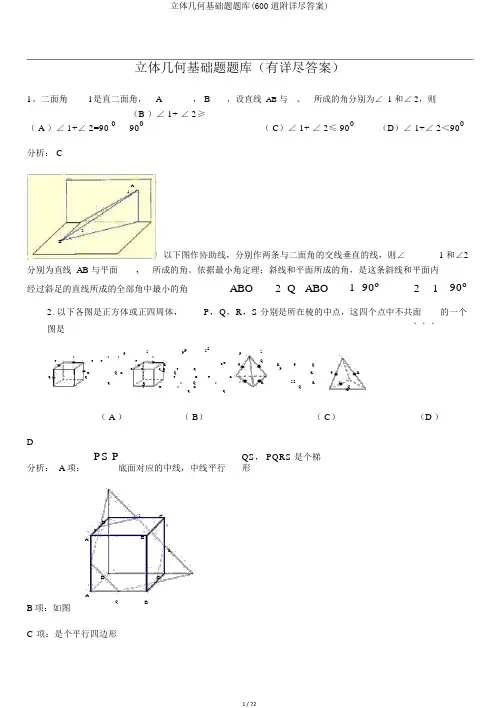
立体几何基础题题库(有详尽答案)1、二面角 l 是直二面角, A, B ,设直线 AB 与 、 所成的角分别为∠ 1 和∠ 2,则( A )∠ 1+∠ 2=90 0 (B )∠ 1+ ∠ 2≥900( C )∠ 1+ ∠ 2≤ 900(D )∠ 1+∠ 2<900分析: CA 12B,以下图作协助线,分别作两条与二面角的交线垂直的线,则∠ 1和∠2分别为直线 AB 与平面所成的角。
依据最小角定理:斜线和平面所成的角,是这条斜线和平面内经过斜足的直线所成的全部角中最小的角ABO2 Q ABO1 90o2 1 90o2. 以下各图是正方体或正四周体,P ,Q ,R ,S 分别是所在棱的中点,这四个点中不共面 的一个...图是PSPPSSPSSSSPSPQPPRRR PPQRR Q RRPQ RP QPRPRQPQQPR RS SSQQ R SQSSQRRQS SR QQQ( A )( B )( C )(D )D分析: A 项:PS PQS , PQRS 是个梯形底面对应的中线,中线平行D'SC 'PA'DAQB 项:如图B'RCBC 项:是个平行四边形D项:是异面直线。
3. 有三个平面,β,γ ,以下命题中正确的选项是( A )若,β,γ 两两订交,则有三条交线(B)若⊥ β,⊥ γ,则β∥γ( C)若⊥ γ,β∩=a,β∩γ=b,则 a⊥ b(D)若∥ β,β∩γ=,则∩γ=D分析: A 项:如正方体的一个角,三个平面订交,只有一条交线。
B项:如正方体的一个角,三个平面相互垂直,却两两订交。
C项:如图4.以下图,在正方体 ABCD -A1B1C1D1的侧面 AB 1内有一动点 P 到直线 AB 与直线 B1C1的距离相等,则动点 P 所在曲线的形状为A B A B A B A B D CO O O A BPP P PP D1C1A 1B 1 A 1 B 1 A 1 B 1 A 1 B1A 1 B1CD' C'A' B'PD C分析: B1C1 平面 AB1B1C1 A P 点到定点 B 的距离与到定直线AB 的PB,,如图:B距离相等,成立坐标系绘图时能够以点B1B 的中点为原点成立坐标系。
立体几何基础题题库(240道附详细解析)361. 有一个三棱锥和一个四棱锥,棱长都相等,将它们一个侧面重叠后,还有几个暴露面? 解析:有5个暴露面.如下图,过V 作VS ′∥AB ,那么四边形S ′ABV 为平行四边形,有∠S ′VA=∠VAB=60°,从而ΔS ′VA 为等边三角形,同理ΔS ′VD 也是等边三角形,从而ΔS ′AD 也是等边三角形,得到以ΔVAD 为底,以S ′与S 重合.这说明ΔVAB 与ΔVSA 共面,ΔVCD 与ΔVSD 共面,故共有5个暴露面. 362. 假设四面体各棱长是1或2,且该四面体不是正四面体,那么其体积的值是 .(只须写出一个可能的值)解析: 该题的显著特点是结论发散而不惟一.此题表面上是考查锥体求积公式那个知识点,实际上要紧考查由所给条件构造一个四面体的能力,首先得考虑每个面的三条棱是如何构成的.排除{1,1,2},可得{1,1,1},{1,2,2},{2,2,2},然后由这三类面在空间构造满足条件的一个四面体,再求其体积.由平时所见的题目,至少可构造出二类满足条件的四面体,五条边为2,另一边为1,对棱相等的四面体.关于五条边为2,另一边为1的四面体,参看图1所示,设AD=1,取AD 的中点为M ,平面BCM 把三棱锥分成两个三棱锥,由对称性可知AD ⊥面BCM ,且V A —BCM =V D —BCM ,因此V ABCD =31S ΔBCM ·AD. CM=22DM CD -=22)21(2-=215.设N 是BC 的中点,那么MN ⊥BC ,MN=22CN CM -=1415-=211,从而S ΔBCM =21×2×211=211, 故V ABCD =31×211×1=611.关于对棱相等的四面体,可参见图2.其体积的计算可先将其置于一个长方体之中,再用长方体的体积减去四个小三棱锥的体积来进行.亦可套公式V=122·)b a c )(a c b )(c b a (222222222-+-+-+, 不妨令a=b=2,c=1,那么V=122·)441)(414)(144(-+-+-+ =122·7=1214. 363. 湖结冰时,一个球漂在其上,取出后(未弄破冰),冰面上留下了一个直径为24cm,深为8cm 的空穴,求该球的半径.解析:设球的半径为R ,依题意知截面圆的半径r =12,球心与截面的距离为d =R-8,由截面性质得:r 2+d 2=R 2,即122+(R-8)2=R 2. 得R =13 ∴该球半径为13cm.364. 在有阳光时,一根长为3米的旗轩垂直于水平地面,它的影长为3米,同时将一个半径为3米的球放在这块水平地面上,如下图,求球的阴影部分的面积(结果用无理数表示).解析:由题意知,光线与地面成60°角,设球的阴影部分面积为S ,垂直于光线的大圆面积为S ′,那么Scos30°=S ′,同时S ′=9π,因此S =63π(米2)365. 设棱锥M —ABCD 的底面是正方形,且MA =MD ,MA ⊥AB ,假如ΔAMD 的面积为1,试求能够放入那个棱锥的最大球的半径.解析: ∵AB ⊥AD ,AB ⊥MA , ∴AB ⊥平面MAD ,由此,面MAD ⊥面AC. 记E 是AD 的中点, 从而ME ⊥AD.∴ME ⊥平面AC , ME ⊥EF设球O 是与平面MAD 、AC 、平面MBC 都相切的球. 不妨设O ∈平面MEF ,因此O 是ΔMEF 的内心. 设球O 的半径为r ,那么r =MFEM EF S MEF++△2设AD =EF =a,∵S ΔAMD =1. ∴ME =a2.MF =22)2(a a +,r =22)2(22aa a a +++≤2222+=2-1当且仅当a =a2,即a =2时,等号成立. ∴当AD =ME =2时,满足条件的球最大半径为2-1. 366. 在正方体ABCD —A 1B 1C 1D 1中,期棱长为a. (1)求证BD ⊥截面AB 1C ;(2)求点B 到截面AB 1C 的距离;(3)求BB 1与截面AB 1C 所成的角的余弦值。
空间几何体部分1、假如一个水平搁置的图形的斜二测直观图是一个底面为45o,腰和上底均为1的等腰梯形,那么原平面图形的面积是()A. 2 2B. 1 2C. 2 2D. 1 22 22、半径为 R的半圆卷成一个圆锥,则它的体积为()A. 3 R3B. 3 R3C. 5 R3D. 5 R324 8 24 83、一个棱柱是正四棱柱的条件是A 、底面是正方形,有两个侧面是矩形B 、底面是正方形,有两个侧面垂直于底面C、底面是菱形,且有一个极点处的三条棱两两垂直D、每个侧面都是全等矩形的四棱柱4.有一个几何体的三视图以下列图所示,这个几何体应是一个A、棱台 B 、棱锥 C 、棱柱 D 、都不对5.在棱长为 1 的正方体上,分别用过共极点的三条棱中点的平面截该正方形,则截去8 个三棱锥后,剩下的几何体的体积是()A. 2B. 7C. 4D. 53 6 5 66.长方体的一个极点上三条棱长分别是 3、4、5,且它的 8 个极点都在同一球面上,则这个球的表面积是A、25 B 、 50 C 、125 D、都不对7. 正方体的内切球和外接球的半径之比为()A. 3 :1B. 3 : 2C. 2 : 3D. 3 : 3o8. 在△ ABC中,AB=2,BC=,∠ABC=120, 若使绕直线 BC旋转一周,则所形成的几何体的体积是A. 9B. 7C. 5D. 322 2 29、圆台的一个底面周长是另一个底面周长的 3 倍,母线长C 为 3,圆台的侧面积为84,则圆台较小底面的半径为A、7 B 、6 C、5 D、310. 直三棱柱 ABC—A1B1C1的体积为 V,点 P、Q分别在V侧棱 AA 和 CC上, AP=CQ,则四棱锥 B—APQC的体积 ED1 1 1FA CPB为A 、VB 、 VC 、 VD 、V234511、如图,在多面体 ABCDEF 中, 已知平面 ABCD 是边长为 3 的正方形 ,EF ∥AB, EF 3 ,且 EF 与平面 的距离为 2, 则该多面体的体2 ABCD积为 ( )A 、9、5 C 、6 D 、152212、如右图所示,正三棱锥V-ABC中,D,E,F分别是 VC ,VA,AC 的中点,P为VB上随意一点,则直线DE与P F 所成的角的大小是()ABCD 随P点的变化而623变化。
立体几何基础A 组题一、选择题:1.下列命题中正确命题的个数是 ( ) ⑴ 三点确定一个平面⑵ 若点P 不在平面α内,A 、B 、C 三点都在平面α内,则P 、A 、B 、C 四点不在同一平面内 ⑶ 两两相交的三条直线在同一平面内⑷ 两组对边分别相等的四边形是平行四边形A.0B.1C.2D.3答案:A2.已知异面直线a 和b 所成的角为︒50,P 为空间一定点,则过点P 且与a 、b 所成的角都是︒30的直线条数有且仅有 ( ) A.1条 B.2条 C.3条 D.4条答案:B 3.已知直线⊥l 平面α,直线⊂m 平面β,下列四个命题中正确的是 ( ) (1) 若βα//,则m l ⊥ (2) 若βα⊥,则m l // (3) 若m l //,则βα⊥ (4) 若 m l ⊥,则βα//A.(3)与(4)B.(1)与(3)C.(2)与(4)D.(1)与(2)答案:B4.已知m 、n 为异面直线,⊂m 平面α,⊂n 平面β,l =βα ,则l ( ) A.与m 、n 都相交 B.与m 、n 中至少一条相交 C.与m 、n 都不相交 D.至多与m 、n 中的一条相交答案:B5.设集合A={直线},B={平面},B A C =,若A a ∈,B b ∈,C c ∈,则下列命题中的真命题是 ( )A. c a b a b c ⊥⇒⎭⎬⎫⊥// B.c a c b b a //⇒⎭⎬⎫⊥⊥ C.c a b c b a //////⇒⎭⎬⎫ D. c a b c b a ⊥⇒⎭⎬⎫⊥//答案:A6.已知a 、b 为异面直线,点A 、B 在直线a 上,点C 、D 在直线b 上,且AC=AD ,BC=BD ,则直线a 、b 所成的角为 ( ) A. ︒90 B. ︒60 C. ︒45 D. ︒30答案:A7.下列四个命题中正确命题的个数是 ( ) 有四个相邻侧面互相垂直的棱柱是直棱柱 各侧面都是正方形的四棱柱是正方体底面是正三角形,各侧面都是等腰三角形的三棱锥是正三棱锥A.1个B.2个C.3个D.0个答案:D8.设M={正四棱柱},N={长方体},P={直四棱柱},Q={正方体},则这些集合之间关系是 ( ) A.Q M N P B.Q M N P C.Q N M P D.Q N M P答案:B9.正四棱锥P —ABCD 中,高PO 的长是底面长的21,且它的体积等于334cm ,则棱AB 与侧面PCD 之间的距离是 ( ) A.cm 2 B. cm 2 C. cm 1 D.cm 22答案:A10.纬度为α的纬圈上有A 、B 两点,弧在纬圈上,弧AB 的长为απcos R (R 为球半径),则A 、B 两点间的球面距离为 ( )A. R πB. R )(απ-C. R )2(απ-D. R )2(απ-答案:D11.长方体三边的和为14,对角线长为8,那么 ( ) A.它的全面积是66 B.它的全面积是132C.它的全面积不能确定D.这样的长方体不存在答案:D12.正四棱锥P —ABCD 的所有棱长都相等,E 为PC 的中点,那么异面直线BE 与PA 所成角的余弦值等于( )A.21B. 22C. 32D. 33答案:D13.用一个过正四棱柱底面一边的平面去截正四棱柱,截面是 ( )A.正方形B.矩形C.菱形D.一般平行四边形答案:B二、填空题:14.正方体1111D C B A ABCD -中,E 、F 、G 分别为AB 、BC 、CC 1的重点,则EF 与BG 所成角的余弦值为________________________答案:510 15.二面角βα--a 内一点P 到两个半平面所在平面的距离分别为22和4,到棱a 的距离为24,则这个二面角的大小为__________________答案:︒︒16575或16.四边形ABCD 是边长为a 的菱形,︒=∠60BAD ,沿对角线BD 折成︒120的二面角A —BD —C 后,AC 与BD 的距离为_________________________答案:a 43 17.P 为︒120的二面角βα--a 内一点,P 到α、β的距离为10,则P 到棱a 的距离是_________________答案:3320 18.如图:正方形ABCD 所在平面与正方形ABEF 所在平面成︒60的二面角,则异面直线AD 与BF 所成角的余弦值是______________________答案:4219.已知三棱锥P —ABC 中,三侧棱PA 、PB 、PC 两两互相垂直,三侧面与底面所成二面角的大小分别为γβα,,,则=++γβα222cos cos cos _______________答案:1 20.若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积的值是_____________(只需写出一个可能的值)。
高中数学 第一章《空间几何体》练习(基础版) 新人教A版必修2一、选择题(共12小题,每小题 5分,共60分)1.下图几何体是由选项中的哪个平面图旋转而得到的( )A B C D 2.下列关于直观图的说法中正确的是( )A .正方形的直观图可能是梯形B .相等的线段在直观图中仍然相等C .平行四边形的直观图是平行四边形D .垂直线段在直观图中仍然垂直 3.若圆柱与圆锥的底面积相等,高也相等,它们的体积分别为1V和2V ,则1V :2V =( ) A 3:2 B .2:1 C .3:1 D .1:1 4.一个球的外切正方体的全面积等于26cm ,则此球的体积为( ) A π343cm Bπ863cm C π66 3cm D π61 3cm 5.如图是一个几何体的三视图,根据图中数据, 可得该几何体的表面积为( )A π8B π12C π16D π326.圆柱的轴截面是正方形,面积是S ,则圆柱的侧面积是 ( ) A .S π1B .S πC .S π2D .S π47.下面三视图的实物图形的名称是( ) A 四棱台 B 四棱锥 C 三棱柱 D 三棱锥俯视图8.可得几何体的表面积是( )A 244+πB 324+πC π22D π129.右图中三棱柱的正视图为 ( )A B C D10.棱长为1正方体1111D C B A ABCD -中截去三棱锥111BC A B -,剩下几何体的体积为( ) A .32 B .65 C .43 D .21 11.一枚骰子的每一面有一个数字,右图 是从3种不同角度看同一骰子的情况, 则数字1对面的数字是( )A .3B .4C .5D .6 12.纸质的正方体的六个面根据其方位分别标记为 上、下、东、南、西、北 现在沿该正方体的一 些棱将正方体剪开、外面朝上展平,得到右侧的 平面图形,则标“△”的面的方位是( )A 南B 北C 西D 下 二、填空题(共4小题,每小题5分,共20分)13.球的面积扩大为原来的4倍,它的体积扩大为原来的_______倍. 14.底边和侧棱长均为3的三棱锥的表面积为__________.15.已知一个正方体的顶点都在同一球面上,若球的半径为3,则该正方体的表面积为 __________.16.如右图所示,一个空间几何体的主视图和左视图俯视图1 2334 561 5△上东正视图侧视图都是上、下底分别为2和4,腰为2的等腰梯 形,俯视图是两个同心圆,那么这个几何体的体 积为________.三、解答题(共6小题,其中第17小题10分,其他各题12分,共70分)17.( 10分) 一个几何体的三视图如图所示,其中正视图与侧视图都是边长为2的正三角形, 求这个几何体的表面积.18.( 12分) 圆柱的侧面展开图是长12 cm ,宽8 cm 的矩形,求这个圆柱的体积.19.( 12分) 如图所示,已知三棱锥BCD A -的底面是等边三角形,三条侧棱长都等于1, 且 20=∠BAC ,M 、N 分别在棱AC 和AD 上,求NB MN BM ++的最小值.20.(12分) 如图,在三角形ABC 中,若3=AC ,4=BC ,5=AB ,以AB 所在直线为 轴,将此三角形旋转一周, 求所得旋转体的表面积.ACOB侧视图正视图俯视图俯视图21.( 12分)(1) 写出这个几何体的名称;(2) 求此几何体的体积.22.( 12分) 将圆心角为120、面积为 3的扇形,作为一个圆锥的侧面,求此圆锥的体积.正视图侧视图俯视图10 104 45。
空间几何体的结构选择(基础题)1.下列各组几何体中全是多面体的一组是()A.三棱柱四棱台球圆锥B.三棱柱四棱台正方体圆台C.三棱柱四棱台正方体六棱锥D.圆锥圆台球半球解:选项A中的球和圆锥是旋转体,A不正确;B中的圆台是旋转体,所以B不正确;D中的四个几何体全是旋转体,所以D不正确;只有C中的四个几何体符合多面体概念.故选C.2.若正四棱台的上底边长为2,下底边长为8,高为4则它的表面积为()A.50 B.100C.248 D.以上答案都不对解:∵上底的边心距为1,下底的边心距为4,高是4,∴斜高为=5,故侧面积等于4××5=100.它的表面积为S=100+22+82=168.故选:D.3.某四面体的三视图如图所示.该四面体的六条棱的长度中,最大的是()A.2 B.2 C.2 D.4解:由三视图可知原几何体为三棱锥,其中底面△ABC为俯视图中的钝角三角形,∠BCA为钝角,其中BC=2,BC边上的高为2,PC⊥底面ABC,且PC=2,由以上条件可知,∠PCA为直角,最长的棱为PA或AB,在直角三角形PAC中,由勾股定理得,PA===2,又在钝角三角形ABC中,AB==.故选C.4.下列四种说法中:①有两个面平行,其余各面都是平行四边形的几何体叫棱柱②相等的线段在直观图中仍然相等③一个直角三角形绕其一边旋转一周所形成的封闭图形叫圆锥④用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台正确的个数是()A.0 B.1 C.2 D.3解:有两个面平行,其余各面都是平行四边形,并且相邻的两个平行四边形的公共边都相互平行,这些面围成的几何体叫棱柱,故①错误.②相等的线段在直观图中仍然相等,不一定相等,不正确;③根据一个直角三角形绕其一个直角边边旋转一周所形成的封闭图形叫圆锥,可得不正确;④用平行于底面的平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台,不正确.故选A.5.下列命题中,正确的是()A.底面是正方形的四棱柱是正方体B.棱锥的高线可能在几何体之外C.有两个面互相平行,其余各面是平行四边形的几何体是棱柱D.有一个面是多边形,其余各面都是三角形的几何体是棱锥解:底面是正方形的四棱柱不一定是正方体,故A错误;斜棱锥的高线有可能在几何体之外,故B正确;根据棱柱的定义可得,有两个面互相平行,其余各面是平行四边形的几何体不一定是棱柱,故C错误;有一个面是多边形,其余各面是有公共顶点的三角形的几何体是棱锥,故D错误.故选:B.6.下列说法正确的是()A.圆锥的侧面展开图是一个等腰三角形B.棱柱的两个底面全等且其余各面都是矩形C.任何一个棱台的侧棱必交于同一点D.过圆台侧面上一点有无数条母线解:在A中,圆锥的侧面展开后是一个扇形,不是等腰三角形,故A错误;在B中,棱柱的两个底面全等且其余各面都是平行四边形,故B错误;在C中,由棱台的定义得任何一个棱台的侧棱必交于同一点,故C正确;在D中,过圆台侧面上一点有且只有1数条母线,故D错误.故选:C.7.下列结论,其中正确的个数是()①梯形的直观图可能是平行四边形②三棱锥中,四个面都可以是直角三角形③如果一个棱锥的各个侧面都是等边三角形,这个棱锥不可能是六棱锥④底面是矩形的平行六面体是长方体.A.1 B.2 C.3 D.4解:①梯形的直观图可能是平行四边形;不正确,因为平行x轴的线段长度不变;②三棱锥中,四个面都可以是直角三角形;正确,一条棱长垂直底面直角三角形的一个锐角,即可满足题意.③如果一个棱锥的各个侧面都是等边三角形,这个棱锥不可能是六棱锥;错误,满足条件,结果是正六边形.④底面是矩形的平行六面体是长方体.棱长不垂直底面,不正确.故选A.8.下列几何体是组合体的是()A.B.C.D.解:选项A是圆锥体,B是圆柱体,C是球体,D是圆台与圆锥体的组合体.故选:D.9.在空间中有下列四个命题:①有两组对边相等的四边形是平行四边形;②四边相等的四边形是菱形;③两组对边分别平行的四边形是平行四边形;④连接空间四边形各边中点的四边形一定是梯形.其中正确命题的个数为()A.1 B.2 C.3 D.4解:四边相等和两组对边相等的四边形可以是空间四边形,故①②错误,连接空间四边形各边中点的四边形一定是平行四边形,故④错误,两组对边分别平行的四边形是平行四边形,正确,故正确命题的个数为1个,故选:A10.以下说法正确的是()A.球的截面中过球心的截面面积未必最大B.圆锥截去一个小圆锥后剩下来的部分是圆台C.棱锥截去一个小棱锥后剩下来的部分是棱台D.用两个平行平面去截圆柱,截得的中间部分还是圆柱解:在A中,球的截面中过球心的截面面积最大,故A错误;在B中,圆锥截去一个小圆锥后剩下来的部分是圆台,由圆台的定义知B正确;在C中,棱锥截去一个小棱锥后剩下来的部分有可是棱台,有可能不是棱台,故C错误;在D中,用两个平行平面去截圆柱,如果沿纵切面方向截得的中间部分不是圆柱,故D错误.故选:B.12.如图几何体中不是柱体的有()A.1个B.2个C.3个D.4个解:①是三棱柱,②的上下两个平面不平行,不是三棱柱,③是四棱柱,④是圆柱,⑤是四棱柱,⑥是四棱台,⑦三棱锥;∴不是柱体的为②⑥⑦,共3个.故选C.14.下列说法正确的是()A.以直角三角形一边为轴旋转所得的旋转体是圆锥B.用一个平面去截圆锥,得到一个圆锥和一个圆台C.正棱锥的棱长都相等D.棱柱的侧棱都相等,侧面是平行四边形解:对于A,以直角三角形的一直角边为轴旋转所得的旋转体是圆锥,斜边为轴旋转所得的旋转体是组合体,故A错误.对于B,用平行与底面的平面去截圆锥,得到一个圆锥和一个圆台,否则不是,故B错误;对于C,正棱锥的侧棱长都相等,底边棱长不一定相等,故C错误;对于D,棱柱的侧棱都相等,侧面是平行四边形,D正确.故选:D.15.下列命题中正确的是()A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台B.有两个面平行,其他面都是平行四边形的几何体叫棱柱C.棱台的底面是两个相似的正方形D.棱台的侧棱延长后必交于一点解:在A中,用一个平行于底面的平面去截棱锥,棱锥底面和截面之间的部分是棱台,故A 不正确;在B中,两个底面平行且相似,其余各面都是梯形的多面体是棱台,侧棱不一定相交于一点,故B不正确.在C中,棱台的底面是两个相似的多边形,故C错误;在D中,由棱台的性质得棱台的侧棱延长后必交于一点,故D正确.故选:D.16.下列结论正确的是()A.圆锥的顶点与底面圆周上的任意一点的连线都是母线B.以三角形的一条边所在直线为旋转轴,其余两边绕旋转轴旋转形成的曲面所围成的几何体叫圆锥C.棱锥的侧棱长与底面多边形的边长都相等,则该棱锥可能是六棱锥D.各个面都是三角形的几何体是三棱锥解:在A中,由圆锥的定义知:圆锥的顶点与底面圆周上的任意一点的连线都是母线,故A 正确;在B中,如图,若△ABC不是直角三角形,或△ABC是直角三角形但旋转轴不是直角边,所得的几何体都不是圆锥,故B错误;在C中,若该棱锥是六棱锥,由题设知,它是正六棱锥,正六棱锥的侧棱长必大于底面边长,这与题设矛盾,故C错误;在D中,三棱锥每个面都是三角形,但是每个面都是三角形的几何体不一定是三棱锥,2个一样的三棱锥上下拼接成一个六面体,它每个面都是三角形,故D错误.故选:A.17.若一个长方体共顶点的三个面的对角线长分别是a,b,c,则长方体的对角线长是()A.B.C.D.解:设同一顶点的三条棱分别为x,y,z,则x2+y2=a2,y2+z2=b2,x2+z2=c2得x2+y2+z2=(a2+b2+c2),则对角线长为.故选:B.18.如图是正方体的表面展开图,则图中的直线AB,CD在原正方体中是()A.平行 B.相交成60°角C.异面成60°角D.异面垂直解:把正方体的表面展开图变形为正方体,B与D重合,此时AB=AC=BC,∴△ABC为等边三角形,即∠ABC=60°,则图中的直线AB,CD在原正方体中是相交成60°角,故选:B.19.在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为的正方形,AA1=3,E是AA1的中点,过C1作C1F⊥平面BDE与平面ABB1A1交于点F,则等于()A.B.C.D.解:连结AC、BD,交于点O,∵四边形ABCD是正方形,AA1⊥底面ABCD,∴BD⊥平面ACC1A1,则当C1F与EO垂直时,C1F⊥平面BDE,∵F∈平面ABB1A1,∴F∈AA1,在矩形ACC1A1中,△C1A1F∽△EAO,则=,∵A1C1=2AO=,AE=,∴A1F=,∴AF=,∴=.故选:C.20.下面没有体对角线的一种几何体是()A.三棱柱B.四棱柱C.五棱柱D.六棱柱解:三棱柱,四棱锥,五棱柱,六棱柱,底面分别为三角形,四边形,五边形,六边形,三角形没有对角线,所以三棱柱没有对角线.故选:A.22.如图所示是正方体的平面展开图,在这个正方体中()①BM与ED平行②CN与BE是异面直线;③CN与BM成60°角;④DM与BN垂直.A.①②③B.②④ C.③④ D.②③④解:由题意画出正方体的图形如图:显然①②不正确;③CN与BM成60°角,即∠ANC=60°正确;④DM⊥平面BCN,所以④正确;故选C.23.有下列三种说法①侧棱垂直于底面的棱柱是直棱柱②底面是正多边形的棱柱是正棱柱③棱柱的侧面都是平行四边形.其中正确说法的个数是()A.0 B.1 C.2 D.3解:①侧棱垂直于底面的棱柱是直棱柱,正确;②底面是正多边形的直棱柱是正棱柱,不正确;③棱柱的侧面都是平行四边形,正确,故选:C.24.如图所示,是一个正方体的表面展开图,则图中“2”所对的面是()A.1 B.7 C.快D.乐解:由已知中的正方体表面展开图可得:2和7对面,0和快对面,1和乐对面,故选:B25.如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是()A.平行 B.相交成60°C.相交且垂直D.异面直线解:将正方体还原得到A,B,C,D的位置如图因为几何体是正方体,所以连接AC,得到三角形ABC是等边三角形,所以∠ABC=60°;故选:B.26.半径为R的半圆卷成底面最大的圆锥,所得圆锥的高为()A.B.C.D.解:半径为R的半圆弧长为πR,圆锥的底面圆的周长为πR,圆锥的底面半径为:,所以圆锥的高:=.故选:B.27.若圆锥的侧面展开图是圆心角为120°、半径为l的扇形,则这个圆锥的表面积与侧面积的比是()A.4:3 B.2:1 C.5:3 D.3:2解:圆锥的侧面积=π×12×=圆锥的底面半径=2π×1×÷2π=,圆锥的底面积==,圆锥的表面积=侧面积+底面积=,∴这个圆锥的表面积与侧面积的比=4:3.故选A28.在正四棱锥V﹣ABCD中(底面是正方形,侧棱均相等),AB=2,VA=,且该四棱锥可绕着AB任意旋转,旋转过程中CD∥平面α,则正四棱锥V﹣ABCD在平面α内的正投影的面积的取值范围是()A.[2,4] B.(2,4] C.[,4] D.[2,2]解:由题意,侧面上的高为=,∴侧面的面积为=2,又由于底面的面积为2×2=4,当正四棱锥的高平行于面时面积最小是2,∴正四棱锥V﹣ABCD在面α内的投影面积的取值范围是[2,4],故选:A.29.观察如图所示几何体,其中判断正确的是()A.①是棱台 B.②是圆台 C.③是棱锥 D.④不是棱柱解:图形①,不满足棱台的定义,所以①不正确;图形②,不满足圆台的定义,所以②不正确;图形③满足棱锥的定义,所以③正确;图形④是棱柱,所以④的判断不正确.故选:C.30.正四棱锥的侧棱长是底面长的k倍,则k的取值范围是()A.(0,+∞)B.(,+∞})C.(,+∞)D.(,+∞)解:如图所示,设正四棱锥V﹣ABCD底面中心为O,BC=a,则VB=ka,易知OB=a;在Rt△VOB中,cos∠VBO==,∵∠VBO∈(0,),∴0<<1,∴,解得k>;∴k的取值范围是(,+∞).32.用一个平面去截四棱锥,不可能得到()A.棱锥 B.棱柱 C.棱台 D.四面体解:∵棱柱的上下底面是相同的,∴用一个平面去截四棱锥,不可能得到棱柱.故选:B.33.正四面体的内切球球心到一个面的距离等于这个正四面体高的()A.B.C.D.解:球心到正四面体一个面的距离即球的半径r,连接球心与正四面体的四个顶点.把正四面体分成四个高为r的三棱锥,所以4×S•r=•S•h,r=h.(其中S为正四面体一个面的面积,h为正四面体的高)答案:C.35.如图所示,观察四个几何体,其中判断正确的是()A.①是棱台 B.②是圆台 C.③是棱锥 D.④不是棱柱解:图①不是由棱锥截来的,所以①不是棱台;图②上、下两个面不平行,所以②不是圆台;图③是棱锥.图④前、后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以④是棱柱.故选C.37.下列说法中不正确的是()A.棱柱的各个侧面都是平行四边形B.棱锥的侧面都是三角形C.棱台的所有侧棱都相等D.圆柱的任意两条母线互相平行解:棱柱的侧面是平行四边形,正确;棱锥的侧面是有公共顶点的三角形,正确棱台的各条棱不一定都相等,不正确,圆柱的任意两条母线互相平行,正确,故选:C.38.下列关于棱锥、棱台的说法,其中不正确的是()A.棱台的侧面一定不会是平行四边形B.棱锥的侧面只能是三角形C.由四个面围成的封闭图形只能是三棱锥D.棱锥被平面截成的两部分不可能都是棱锥解:在A中,棱台的侧面是梯形,故A正确;在B中,由棱锥的定义得棱锥的侧面只能是三角形,故B正确;在C中,由棱锥的定义得四个面围成的封闭图形只能是三棱锥,故C正确;在D中,棱锥被平面截成的两部分有可能都是棱锥,故D错误.故选:D.42.如图是由哪个平面图形旋转得到的()A.B.C.D.解:图中所给的几何体是由上部的圆锥和下部的圆台组合而成的,故轴截面的上部是直角三角形,下部为直角梯形构成,故选 D.43.将半径为1的圆分割成面积之比为1:2:3的三个扇形作为三个圆锥的侧面,设这三个圆锥底面半径依次为r1,r2,r3,那么r1+r2+r3的值为()A.B.2 C.D.1解:∵2πr1=,∴r1=,同理,∴r1+r2+r3=1,故选:D.45.一个底面半径为2cm的圆柱形容器内盛有高度为6cm的水,现将一个母线长为cm 的圆锥形物体完全浸入水中,容器里水的高度上升到7cm,则该圆锥的高为()A.1cm B.2cm C.3cm D.cm解:圆锥的体积V=π×22×1=4π,设圆锥的高为h,则圆锥的底面半径r=,∴V==4π,解得h=1或h=3.当h=1时,r==2>2,不符合题意.故选:C.47.如图,已知半径为2的半圆中,BC为直径,O为圆心,点A在半圆弧上,且AB=AC,则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为()A.B.C.16π D.32π解:半圆绕BC旋转一周所得球体的体积V球==.三角形ABC绕BC旋转一周所得几何体体积V′==.∴阴影部分绕BC旋转一周所得几何体体积V=V球﹣V′=.故选:A.48.若一个圆锥的轴截面是等边三角形,则该圆锥的侧面积与底面积的比等于()A.3 B.2 C.D.解:设圆锥的底面半径为r,则母线l=2r,∴S侧=πrl=2πr2,S底=πr2,∴=2.故选:B.49.将直角三角形绕它的一个直角边所在的直线旋转一周,形成的几何体一定是()A.圆锥 B.圆柱 C.圆台 D.以上均不正确解:由旋转体的定义,将直角三角形绕它的一个直角边所在的直线旋转一周,形成的几何体为圆锥故选A50.一竖立在地面上的圆锥形物体的母线长为4m,侧面展开图的圆心角为,则这个圆锥的体积等于()A.πm3 B.πm3C.πm3D.πm3解:设圆锥的底面半径为r,圆锥形物体的母线长l=4m,侧面展开图的圆心角为,故2πr=l,解得:r=m,故圆锥的高h==m,故圆锥的体积V==πm3,故选:D。
《空间几何体》基础达标测试一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若一个几何体的三视图都是等腰三角形,则这个几何体可能是( ) A .圆锥 B .正四棱锥 C .正三棱锥D .正三棱台2.如图,是一个物体的三视图,则此物体的直观图是( )3.一个几何体的三视图如图,其中正视图是边长为2的正三角形,俯视图是正方形,那么该几何体的侧视图的面积是( )A .23B .3C .4D .24.已知圆台的上下底面半径分别为1和2,高为1,则该圆台的全面积为( ) A .32π B .(5+32)π C.5+323πD .5+22π5.某几何体三视图如图所示,则该几何体的体积为( )A.13+2π B .13π6C.7π3D .5π26.已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为( ) A .120° B .150° C .180°D .240°7.一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A.18 B .17C.16D .158.一个圆台的上、下底面面积分别为1,49,一个平行于底面的截面面积为25,则这个截面与上、下两个底面的距离之比为( )A .2∶1B .3∶1 C.2∶1D .3∶19.长方体ABCD -A 1B 1C 1D 1的三条棱长分别是AA 1=1,AB =2,AD =4,则从A 点出发,沿长方体的表面到C 1的最短距离是( )A .5B .7 C.29D.3710.如图所示,在三棱柱ABC -A 1B 1C 1中,侧棱垂直于底面,AB =AC =13,BB 1=BC =6,E ,F 为侧棱AA 1上的两点,且EF =3,则多面体BB 1C 1CEF 的体积为( )A.30 B.18C.15 D.12二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)11.底面直径和高都是4 cm的圆柱的侧面面积为______ cm2.12.如果圆锥的侧面展开图是半圆,那么这个圆锥的顶角(圆锥轴截面中两条母线的夹角)是________.13.一个棱锥的三视图如图,则该棱锥的全面积为______________cm2.14.一个底面直径是32 cm的圆柱形水桶装入一些水,将一个球放入桶内完全淹没,水面上升了9 cm,则这个球的表面积是________ cm2.三、解答题(本大题共2小题,共20分.解答应写出文字说明、证明过程或演算步骤)15.(本小题12分)如图所示,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=22,AD=2,求四边形ABCD绕AD旋转一周所形成几何体的表面积和体积.16.(本小题满分18分)如图,如果一个几何体的正视图与侧视图都是全等的长方形,边长分别是4 cm与2 cm,俯视图是一个边长为4 cm的正方形.(1)求该几何体的全面积;(2)求该几何体的外接球的体积.详细参考答案:一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.解析:圆锥的俯视图是一个圆,正四棱锥的俯视图是正方形和它的两条对角线,三棱台的正视图与侧视图是梯形,故只有C 正确.答案:C2.解析:由三视图知几何体为圆锥与圆柱的组合体如图.故选D.答案:D3.解析:由题意可知侧视图与正视图形状完全一样,是正三角形,面积S =34×22= 3. 答案:B4.解析:由已知可求得,圆台的母线长为2,∴圆台的全面积为π×(12+22)+π·2×(1+2)=(5+32)π.故选B. 答案:B5.解析:由三视图可知:原几何体左侧是半圆锥,右侧是圆柱,∴V =V 半圆锥+V 圆柱=12×13·π(1)2×1+π(1)2×1=136π. 答案:B6.解析:设圆锥底面半径为r ,母线为l ,则πrl +πr 2=3πr 2,得l =2r ,∴展开图扇形半径为2r ,弧长为2πr .∴展开图是半圆.∴扇形的圆心角为180°.故选C. 答案:C7.解析:如图所示,在正方体ABCD -A 1B 1C 1D 1中,截掉三棱锥A 1-AB 1D 1.设正方体的棱长为a ,则VA 1-AB 1D 1=13×12a 3=16a 3,故剩余几何体的体积为a 3-16a 3=56a 3,所以比值为15,故选D.答案:D8.解析:如图,设上底面、下底面、平行平面的半径分别为r ,R ,r 0,从圆台轴截面计算,还原为圆锥, 则有r R =17,r r 0=15,所以SO 1SO 2=15,SO 1SO =17.所以SO 1O 1O 2=14,SO 1O 2O =12.所以O 1O 2O 2O =21.答案:A9.解析:两点之间线段最短,在长方体展开图中,由A 到C 1的路线有三条,如下图,三条路线长分别为l 1=12+(2+4)2=37,l 2=42+(1+2)2=5, l 3=22+(1+4)2=29.所以最短距离为5. 答案:A10.解析:VBB 1C 1CEF =VABC -A 1B 1C 1-VF -A 1B 1C 1-V E -ABC =S △ABC ·6-13S △ABC ·A 1F -13S △ABC ·AE=S △ABC ·⎣⎡⎦⎤6-13(A 1F +AE )=5S △ABC , ∵AC =AB =13,BC =6, ∴S △ABC =12×6×(13)2-32=6.所以VBB 1C 1CEF =5×6=30. 答案:A二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 11.解析:圆柱的底面半径为r =12×4=2 cm ,故S 侧=2π·2×4=16π cm 2. 答案:16π12.解析:如图,∵半圆弧长为πl ,圆锥的底面圆周长为2πr ,∴πl =2πr .∴r =12l .∴在Rt △PBO 中,∠BPO =30°.∴∠APB =60°. 答案:60°13.解析:如图所示三棱锥.AO ⊥底面BCD ,O 是BD 中点,BC =CD =6,BC ⊥CD ,AO =4,AB =AD . S △BCD =12×6×6=18,S △ABD =12×62×4=12 2.取BC 中点E ,连接AE ,OE . 可得BC ⊥AE ,AE =AO 2+OE 2=5,∴S △ABC =S △ACD =12×6×5=15.∴S 全=18+122+15+15=48+12 2. 答案:48+12 214.解析:球的体积等于底面半径为16 cm ,高为9 cm 的圆柱的体积,设球的半径为R cm ,所以43πR 3=π·162×9,解得R =12.所以S 球=4πR 2=576π cm 2. 答案:576π三、解答题(本大题共2小题,共30分.解答应写出文字说明、证明过程或演算步骤) 15.解:S 表面=S 圆台底面+S 圆台侧面+S 圆锥侧面 =π·52+π·(2+5)×5+π·2×22=60π+42π. V =V 圆台-V 圆锥=13π(r 21+r 1r 2+r 22)h 圆台-13πr 21h 圆锥=1483π. 16. 解:(1)由题意可知,该几何体是长方体, 底面是正方形,边长是4 cm ,高是2 cm ,因此该几何体的全面积是2×4×4+4×4×2=64 (cm 2),即该几何体的全面积是64 cm 2.(2)由长方体与球的性质可得,长方体的体对角线是其外接球的直径,设长方体的体对角线为d cm ,外接球的半径为r cm ,则d =16+16+4=36=6 (cm),所以外接球的半径为r =3 (cm).所以外接球的体积V =43πr 3=43×27π=36π(cm 3).。
空间立体几何基础练习题
1、如图,平行四边形ABCD 中,CD BD ⊥,正方形ADEF 所在的平面和平面ABCD 垂直,H 是BE 的中点,G 是,AE DF 的交点.
⑴求证: //GH 平面CDE ;⑵求证: BD ⊥平面CDE .
2、如图,四棱锥S ABCD -的底面是正方形,SD ⊥平面ABCD ,E 是SD 的中点.
(Ⅰ)求证://SB 平面EAC ;(Ⅱ)求证:AC BE ⊥.
3、长方体1111ABCD A B C D -中11,2AB AA AD ===.点E 为AB中点.
(I)求三棱锥1A ADE -的体积;(II)求证:1A D ⊥平面11ABC D ;(III )求证:1BD // 平面1A DE .
4、如图,矩形ABCD 中,ABE AD 平面⊥,2===BC EB AE ,F 为CE 上的点,
且ACE BF 平面⊥.(Ⅰ)求证:BCE AE 平面⊥;(Ⅱ)求证;BFD AE 平面//;(Ⅲ)求三棱锥BGF C -的体积.
5、如图,在四棱锥P-ABCD 中,底面ABCD 是正方形,PD ⊥底面ABCD ,M 、N 分别为PA 、BC 的中 点,且PD=AD=2。
(1)求证:MN ∥平面PCD ; (2)求证:平面PAC ⊥平面PBD ;(3)求三棱锥P-ABC 的体积。
6、四棱锥A BCDE -中,底面BCDE 为矩形,AB AC =, 1,2==CD BC .并且侧面ABC ⊥底面
BCDE ,
(Ⅰ)取CD 的中点为F ,AE 的中点为G ,证明:FG ∥面ABC ;
(Ⅱ)若M 为BC 中点,求证:DM AE ⊥.
A B C D
E F G A B C D E M G F。