材料力学习题册(1)

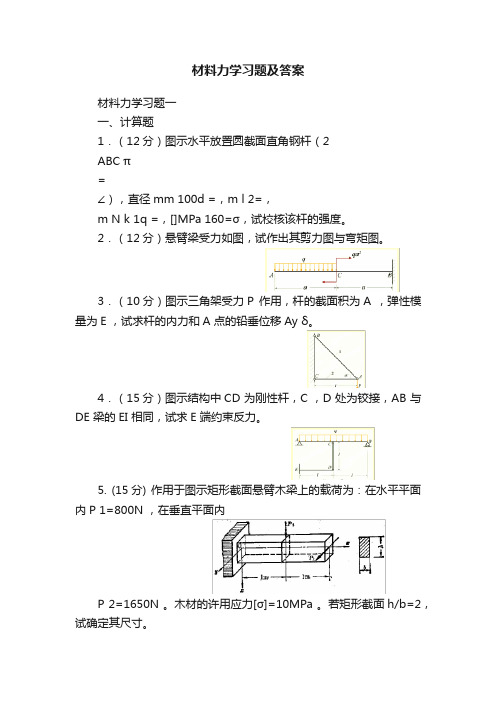
材料力学习题及答案材料力学习题一一、计算题1．（12分）图示水平放置圆截面直角钢杆（2ABC π=∠），直径mm 100d =，m l 2=，m N k 1q =，[]MPa 160=σ，试校核该杆的强度。

2．（12分）悬臂梁受力如图，试作出其剪力图与弯矩图。

3．（10分）图示三角架受力P 作用，杆的截面积为A ，弹性模量为E ，试求杆的内力和A 点的铅垂位移Ay δ。

4．（15分）图示结构中CD 为刚性杆，C ，D 处为铰接，AB 与DE 梁的EI 相同，试求E 端约束反力。

5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为：在水平平面内P 1=800N ，在垂直平面内P 2=1650N 。

木材的许用应力[σ]=10MPa 。

若矩形截面h/b=2，试确定其尺寸。

三．填空题（23分）1．（4分）设单元体的主应力为321σσσ、、，则单元体只有体积改变而无形状改变的条件是＿＿＿＿＿＿＿＿＿＿；单元体只有形状改变而无体积改变的条件是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

2．（6分）杆件的基本变形一般有＿＿＿＿＿＿、＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿四种；而应变只有＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿两种。

3．（6分）影响实际构件持久极限的因素通常有＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿，它们分别用＿＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿＿＿＿＿＿来加以修正。

4.（5分）平面弯曲的定义为＿＿＿＿＿＿＿＿＿＿＿＿_＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿_。

5.（2分）低碳钢圆截面试件受扭时，沿＿＿＿＿＿＿＿＿＿＿＿＿截面破坏；铸铁圆截面试件受扭时，沿＿＿＿＿＿＿＿＿＿＿＿＿面破坏。

四、选择题（共2题，9分）2．（5分）图示四根压杆的材料与横截面均相同，试判断哪一根最容易失稳。

答案：（）材料力学习题二二、选择题：（每小题3分，共24分）1、危险截面是______所在的截面。

材料力学习题册参考答案材料力学习题册参考答案（无计算题）第1章：轴向拉伸与压缩一：1（ABE ）2（ABD ）3（DE ）4（AEB ）5（C ）6（ＣＥ）７（ABD ）8（C ）9（BD ）10（ADE ）11（ACE ）12（D ）13（CE ）14（D ）15（ＡＢ）１６（BE ）17（D ）二：1对2错3错4错5对6对7错8错9错10错11错12错13对14错15错三：1：钢铸铁 2：比例极限p σ 弹性极限e σ 屈服极限s σ 强度极限b σ3.横截面 45度斜截面4. εσE =， EAFl l =5.强度，刚度，稳定性；6.轴向拉伸（或压缩）；7. llb b ?μ?=8. 1MPa=106 N/m 2 =1012 N/mm 2 9. 抵抗伸缩弹性变形，加载方式 10. 正正、剪 11.极限应力 12. >5% <5% 13. 破坏s σ b σ 14.强度校核截面设计荷载设计15. 线弹性变形弹性变形 16.拉应力 45度 17.无明显屈服阶段的塑性材料力学性能参考答案：1. A 2. C 3. C 4. C 5. C 6. 5d ; 10d 7. 弹塑8. s2s 9. 0.1 10. 压缩11. b 0.4σ 12. <；< 剪切挤压答案：一：1.（C ），2.（B ），3.（A ），二：1. 2bh db 2. b(d+a) bc 3. 4a δ a 2 4. F第2章：扭转一：1.（B ） 2.（C D ） 3.（C D ） 4. （C ） 5. （A E ） 6. （A ）7. （D ）8. （B D ） 9.（C ） 10. （B ） 11.（D ） 12.（C ）13.（B ）14.（A ） 15.（A E ）二：1错 2对 3对 4错 5错 6 对三：1. 垂直 2. 扭矩剪应力 3.最外缘为零4. p ττ< 抗扭刚度材料抵抗扭转变形的能力5. 不变不变增大一倍6. 1.5879τ7.实心空心圆8. 3241)(α- 9. m ax m in αττ= 10. 长边的中点中心角点 11.形成回路（剪力流）第3章：平面图形的几何性质一：1.（C ），2.（A ），3.（C ），4.（C ），5.（A ），6.（C ），7.（C ），8.（A ），9.（D ）二：1）. 1；无穷多；2）4)4/5(a ； 3），84p R I π=p 4z y I 16R I I ===π4）12/312bh I I z z ==；5）)/(/H 6bh 6BH W 32z -= 6）12/)(2211h b bh I I I I z y z y +=+=+；7）各分部图形对同一轴静矩8）两轴交点的极惯性矩；9）距形心最近的；10）惯性主轴；11）图形对其惯性积为零三：1：64/πd 114； 2.（0 , 14.09cm ）(a 22，a 62)3： 4447.9cm 4， 4：0.00686d 4 ，5: 77500 mm 4 ;6: 64640039.110 23.410C C C C y y z z I I mm I I mm ==?==?第4章：弯曲内力一：1.（A B ）2.（D ）3.（B ）4.（A B E ）5.（A B D ）6.（ACE ） 7.（ABDE ） 8.（ABE ）9. （D ） 10. （D ） 11.（ACBE ） 12.（D ） 13.（ABCDE ）二：1错 2错 3错 4对 5错 6对 7对三：1. 以弯曲变形 2.集中力 3. KNm 2512M .max =4. m KN 2q = 向下 KN 9P = 向上5.中性轴6.荷载支撑力7. 小8. 悬臂简支外伸9. 零第5章：弯曲应力一：1（ＡＢＤ）２．（C ）3.（BE ）4.（A ）5.（C ）6.（C ）7.（B ）8.（C ）9.（BC ）二：1对 2错 3错 4 对 5 错 6错 7 对三：1.满足强度要求更经济、更省料2. 变成曲面，既不伸长也不缩短3.中性轴4.形心主轴5.最大正应力6.剪力方向7.相等8.平面弯曲发生在最大弯矩处9.平面弯曲第6章：弯曲变形一：1（B ），2（B ），3（A ），4（D ），5（C ），6（A ），7（C ），8（B ），9（A ）10（B ），11（A ）二：1对2错3错4错5错6对7错8错9错10对11错12对三：1.（转角小量:θθtan ≈）（未考虑高阶小量对曲率的影响）2. 挠曲线采用近似微分方程导致的。

练习1 绪论及基本概念1-1 是非题（1）材料力学是研究构件承载能力的一门学科。

（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。

（是 ）（3）构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。

（ 是 ） （4）应力是内力分布集度。

（是 ）（5）材料力学主要研究构件弹性范围内的小变形问题。

（是 ） （6）若物体产生位移，则必定同时产生变形。

（非 ） （7）各向同性假设认为，材料沿各个方向具有相同的变形。

（F ）（8）均匀性假设认为，材料内部各点的力学性质是相同的。

（是）（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。

（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。

（非 ）1-2 填空题（1）根据材料的主要性质对材料作如下三个基本假设：连续性假设 、均匀性假设 、 各向同性假设 。

（2）工程中的 强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。

（3）保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性 三个方面。

（4）图示构件中，杆1发生 拉伸 变形，杆2发生 压缩 变形， 杆3发生 弯曲 变形。

（5）认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设 。

根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。

（6）图示结构中，杆1发生 弯曲 变形，构件2发生 剪切 变形，杆件3发生 弯曲与轴向压缩组合。

变形。

（7）解除外力后，能完全消失的变形称为 弹性变形 ，不能消失而残余的的那部分变形称为 塑性变形 。

（8）根据 小变形 条件，可以认为构件的变形远 小于 其原始尺寸。

1-3 选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。

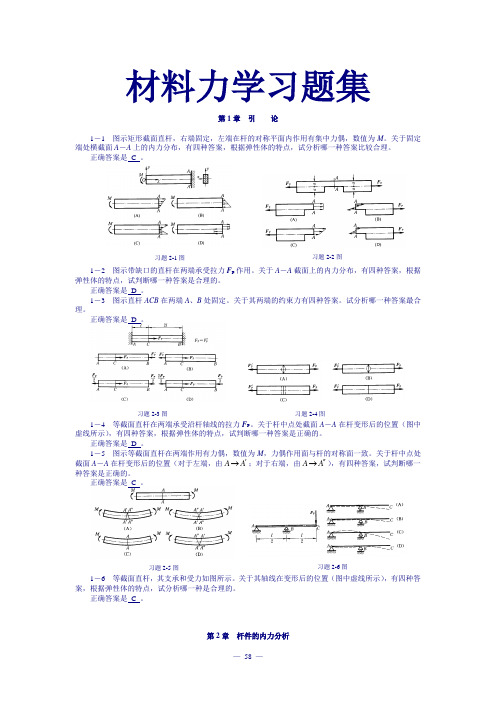
习题2-1图 习题2-2图习题2-3图 习题2-4图 习题2-5图 习题2-6图 材料力学习题集第1章 引 论1－1 图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M 。

关于固定端处横截面A －A 上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。

正确答案是 C 。

1－2 图示带缺口的直杆在两端承受拉力F P 作用。

关于A －A 截面上的内力分布，有四种答案，根据弹性体的特点，试判断哪一种答案是合理的。

正确答案是 D 。

1－3 图示直杆ACB 在两端A 、B 处固定。

关于其两端的约束力有四种答案。

试分析哪一种答案最合理。

正确答案是 D 。

1－4 等截面直杆在两端承受沿杆轴线的拉力F P 。

关于杆中点处截面A －A 在杆变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试判断哪一种答案是正确的。

正确答案是 D 。

1－5 图示等截面直杆在两端作用有力偶，数值为M ，力偶作用面与杆的对称面一致。

关于杆中点处截面A －A 在杆变形后的位置（对于左端，由A A '→；对于右端，由A A ''→），有四种答案，试判断哪一种答案是正确的。

正确答案是 C 。

1－6 等截面直杆，其支承和受力如图所示。

关于其轴线在变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试分析哪一种是合理的。

正确答案是 C 。

第2章 杆件的内力分析习题2-1图习题2-2图习题2-3图习题2-4图2－1 平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。

试分析下列平衡微分方程中哪一个是正确的。

（A d Q F d M（B （C （D 2－2 对于图示承受均布载荷q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四种答案中。

2－3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ，如图所示。

为确定b M 、M ，现有下列四种答案，试分析哪一种 （A （B （C （D 之间剪力图的面积，以此类推。

第一章 绪论1-1矩形平板变形后为平行四边形，水平轴线在四边形AC 边保持不变。

求(1)沿AB边的平均线应变； (2)平板A 点的剪应变。

（答案：εAB =7.93×10-3 γXY =-1.21×10-2rad ）第二章 拉伸、压缩与剪切2-1 试画图示各杆的轴力图，并指出轴力的最大值。

2-2 一空心圆截面杆，内径d=30mm ，外径D=40mm ，承受轴向拉力F=KN 作用，试求横截面上的正应力。

（答案：MPa 7.72=σ）2-3 题2－1 c 所示杆，若该杆的横截面面积A=502m m ，试计算杆内的最大拉应力与最大压应力（答案：MPa t 60max ,=σ MPa c 40max ,=σ）2.4图示轴向受拉等截面杆，横截面面积A=5002m m ，载荷F=50KN 。

试求图示截面m-m 上的正应力与切应力，以及杆内的最大正应力与最大切应力。

（答案：MPa MPa MPa MPa 50 ; 100 ; 24.49 ; 32.41max max ==-==τστσαα）2.5如图所示，杆件受轴向载荷F 作用。

该杆由两根木杆粘接而成，若欲使粘接面上的正应力为其切应力的二倍，则粘接面的方位角θ应为何值（答案： 6.26=θ）2.6 等直杆受力如图所示，试求各杆段中截面上的轴力，并绘出轴力图。

2.7某材料的应力－应变曲线如图所示，图中还同时画出了低应变去区的详图，试确定材料的弹性模量E 、屈服极限s σ、强度极限b σ、与伸长率δ，并判断该材料属于何种类型（塑性或脆性材料）。

2.8某材料的应力－应变曲线如图所示，试根据该曲线确定： （1）材料的弹性模量E 、比例极限P σ与屈服极限2.0σ; （2）当应力增加到MPa 350=σ时，材料的正应变ε， 以及相应的弹性应变e ε与塑性应变p ε2.9图示桁架，杆1与杆2的横截面均为圆形，直径分别为d1=30mm 与d2＝20mm ，两杆材料相同，许用应力[]σ＝160MPa ，该桁架在节点A 处承受铅垂方向的载荷F=80KN 作用。

习题2-1图 习题2-2图习题2-3图 习题2-4图 习题2-5图 习题2-6图 材料力学习题第1章 引 论1－1 图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M 。

关于固定端处横截面A －A 上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。

正确答案是 C1－2 图示带缺口的直杆在两端承受拉力F P 作用。

关于A －A 截面上的内力分布，有四种答案，根据弹性体的特点，试判断哪一种答案是合理的。

正确答案是 D1－3 图示直杆ACB 在两端A 、B 处固定。

关于其两端的约束力有四种答案。

试分析哪一种答案最合理。

正确答案是 D1－4 等截面直杆在两端承受沿杆轴线的拉力F P 。

关于杆中点处截面A －A 在杆变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试判断哪一种答案是正确的。

正确答案是 D 。

1－5 图示等截面直杆在两端作用有力偶，数值为M ，力偶作用面与杆的对称面一致。

关于杆中点处截面A －A 在杆变形后的位置（对于左端，由A A '→；对于右端，由A A ''→），有四种答案，试判断哪一种答案是正确的。

正确答案是 C 。

1－6 等截面直杆，其支承和受力如图所示。

关于其轴线在变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试分析哪一种是合理的。

正确答案是 C 。

第2章 杆件的内力分析习题2-1图习题2-2图习题2-3图习题2-4图2－1 平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。

试分析下列平衡微分方程中哪一个是正确的。

（A d Q F d M（B （C （D 2－2 对于图示承受均布载荷q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四种答案中。

2－3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ，如图所示。

为确定b M 、M ，现有下列四种答案，试分析哪一种 （A （B （C （D 之间剪力图的面积，以此类推。

材料力学性能课后习题第一章1.解释下列名词①滞弹性：金属材料在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象称为滞弹性，也就是应变落后于应力的现象。

②弹性比功：金属材料吸收弹性变形功的能力，一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。

③循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。

④包申格效应：金属材料经过预先加载产生少量塑性变形，卸载后再同向加载，规定残余伸长应力增加；反向加载，规定残余伸长应力降低的现象。

⑤塑性：金属材料断裂前发生不可逆永久（塑性）变形的能力。

⑥韧性：指金属材料断裂前吸收塑性变形功和断裂功的能力。

⑦加工硬化：金属材料在再结晶温度以下塑性变形时,由于晶粒发生滑移,出现位错的缠结,使晶粒拉长、破碎和纤维化,使金属的强度和硬度升高,塑性和韧性降低的现象。

⑧解理断裂：解理断裂是在正应力达到一定的数值后沿一定的晶体学平面产生的晶体学断裂。

2.解释下列力学性能指标的意义（1）E( 弹性模量）；（2）σp（规定非比例伸长应力）、σe（弹性极限）、σs（屈服强度）、σ0.2（规定残余伸长率为0.2%的应力）；（3）σb（抗拉强度）；（4）n（加工硬化指数）;（5）δ（断后伸长率）、ψ（断面收缩率）3.金属的弹性模量取决于什么？为什么说他是一个对结构不敏感的力学性能？取决于金属原子本性和晶格类型。

因为合金化、热处理、冷塑性变形对弹性模量的影响较小。

4.常用的标准试样有5倍和10倍，其延伸率分别用δ5和δ10表示，说明为什么δ5>δ10。

答：对于韧性金属材料，它的塑性变形量大于均匀塑性变形量，所以对于它的式样的比例，尺寸越短，它的断后伸长率越大。

5.某汽车弹簧，在未装满时已变形到最大位置，卸载后可完全恢复到原来状态；另一汽车弹簧，使用一段时间后，发现弹簧弓形越来越小，即产生了塑性变形，而且塑性变形量越来越大。

试分析这两种故障的本质及改变措施。

F12312练习 1 绪论及基本概念1-1 是非题（1） 材料力学是研究构件承载能力的一门学科。

（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。

（是）（3） 构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。

（ 是 ） （4） 应力是内力分布集度。

（是 ）（5） 材料力学主要研究构件弹性范围内的小变形问题。

（是 ） （6） 若物体产生位移，则必定同时产生变形。

（非 ） （7） 各向同性假设认为，材料沿各个方向具有相同的变形。

（F ） （8） 均匀性假设认为，材料内部各点的力学性质是相同的。

（是）（9） 根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。

（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。

（非 ）1-2 填空题（1） 根据材料的主要性质对材料作如下三个基本假设：连续性假设、均匀性假设 、各向同性假设 。

（2） 工程中的强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。

（3） 保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性三个方面。

3（4） 图示构件中，杆 1 发生 拉伸 变形，杆 2 发生 压缩 变形，杆 3 发生 弯曲 变形。

（5） 认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设。

根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。

（6） 图示结构中，杆 1 发生 弯曲变形，构件 2发生 剪切 变形，杆件 3 发生 弯曲与轴向压缩组合。

变形。

（7） 解除外力后，能完全消失的变形称为 弹性变形，不能消失而残余的的那部分变形称为 塑性变形 。

（8） 根据 小变形 条件，可以认为构件的变形远 小于 其原始尺寸。

1-3选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。

材料力学习题册（1）学院专业学号教师学生姓名第一章绪论一、选择题1．根据均匀性假设，可认为构件的（）在各处相同。

A．应力B．应变C．材料的弹性系数D．位移2．构件的强度是指（），刚度是指（），稳定性是指（）。

A．在外力作用下构件抵抗变形的能力B．在外力作用下构件保持原有平衡状态的能力C．在外力作用下构件抵抗强度破坏的能力3．单元体变形后的形状如下图虚线所示，则A点剪应变依次为图(a) （），图(b) （），图(c) （）。

A．0B．r2C．r D．1.5r4.下列结论中( )是正确的。

A．内力是应力的代数和；B．应力是内力的平均值；C．应力是内力的集度；D．内力必大于应力；5. 两根截面面积相等但截面形状和材料不同的拉杆受同样大小的轴向拉力，它们的应力是否相等（）。

A．不相等；B．相等；C．不能确定；6．为把变形固体抽象为力学模型，材料力学课程对变形固体作出一些假设，其中均匀性假设是指（）。

A. 认为组成固体的物质不留空隙地充满了固体的体积；B. 认为沿任何方向固体的力学性能都是相同的；C. 认为在固体内到处都有相同的力学性能；D. 认为固体内到处的应力都是相同的。

二、填空题1.材料力学对变形固体的基本假设是。

2．材料力学的任务是满足的要求下，为设计经济安全的构件提供必要的理论基础和计算方法。

3．外力按其作用的方式可以分为和，按载荷随时间的变化情况可以分为和。

4．度量一点处变形程度的两个基本量是和。

三、判断题1．因为构件是变形固体，在研究构件平衡时，应按变形后的尺寸进行计算。

（）2．外力就是构件所承受的载荷。

（）3．用截面法求内力时，可以保留截开后构件的任一部分进行平衡计算。

（）4．应力是横截面上的平均内力。

（）5．杆件的基本变形只是拉(压)、剪、扭和弯四种，如果还有另一种变形，必定是这四种变形的某种组合。

（）6．材料力学只限于研究等截面杆。

（）四、计算题1．图示三角形薄板因受外力作用而变形，角点B垂直向上的位移为0.03mm，但AB和BC 仍保持为直线。

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。

( × ) 1.2 力只作用在杆件截面的形心处。

( × ) 1.3 杆件某截面上的力是该截面上应力的代数和。

( × ) 1.4 确定截面力的截面法，适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。

( ∨ ) 1.5 根据各向同性假设，可认为材料的弹性常数在各方向都相同。

( ∨ ) 1.6 根据均匀性假设，可认为构件的弹性常数在各点处都相同。

( ∨ ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。

( ∨ ) 1.8 同一截面上各点的正应力σ必定大小相等，方向相同。

( × ) 1.9 同一截面上各点的切应力τ必相互平行。

( × ) 1.10 应变分为正应变ε和切应变γ。

( ∨ ) 1.11 应变为无量纲量。

( ∨ ) 1.12 若物体各部分均无变形，则物体各点的应变均为零。

( ∨ ) 1.13 若物体各点的应变均为零，则物体无位移。

( × ) 1.14 平衡状态弹性体的任意部分的力都与外力保持平衡。

( ∨ ) 1.15 题1.15图所示结构中，AD 杆发生的变形为弯曲与压缩的组合变形。

( ∨ )1.16 题1.16图所示结构中，AB 杆将发生弯曲与压缩的组合变形。

( × )二、填空题1.1 材料力学主要研究 受力后发生的以及由此产生1.2 拉伸或压缩的受力特征是 ，变形特征是 。

1.3 剪切的受力特征是 ，变形特征B题1.15图题1.16图外力的合力作用线通过杆轴线 杆件 沿杆轴线伸长或缩短 受一对等值，反向，作用线距离很近的力的作用 沿剪切面发生相对错动是 。

1.4 扭转的受力特征是 ，变形特征是 。

1.5 弯曲的受力特征是 ，变形特征是 。

1.6 组合受力与变形是指 。

1.7 构件的承载能力包括 ， 和 三个方面。