北师大版八上§1.3蚂蚁怎样走最近
- 格式:ppt
- 大小:209.00 KB
- 文档页数:10

北师大版数学八年级上册3《蚂蚁怎样走最近》教学设计1一. 教材分析《蚂蚁怎样走最近》是北师大版数学八年级上册第三章的内容。
本节课主要通过蚂蚁走最近的问题,引导学生学习图形的运动和变换,培养学生的空间想象能力和逻辑思维能力。
教材通过生活实例引入,激发学生的学习兴趣,接着引导学生通过观察、操作、思考、交流等过程,自主探索蚂蚁走最近的路径,最后总结出图形的运动和变换的规律。
二. 学情分析学生在七年级时已经学习了图形的运动和变换,对平移、旋转等概念有了一定的了解。
但部分学生对图形的运动和变换的应用和实际意义的理解还不够深入。
因此,在教学过程中,要注重引导学生通过实际问题,理解图形的运动和变换的规律。
三. 教学目标1.理解图形的运动和变换的概念,掌握图形的运动和变换的规律。
2.能够运用图形的运动和变换解决实际问题,培养学生的空间想象能力和逻辑思维能力。
3.通过小组合作学习,培养学生的合作意识和团队精神。
四. 教学重难点1.教学重点:图形的运动和变换的概念及规律。
2.教学难点:如何运用图形的运动和变换解决实际问题。
五. 教学方法1.采用问题驱动法,引导学生通过实际问题,探索图形的运动和变换的规律。
2.运用小组合作学习,让学生在讨论和交流中,共同解决问题,培养学生的合作意识和团队精神。
3.利用多媒体辅助教学,直观展示图形的运动和变换的过程,提高学生的空间想象能力。
六. 教学准备1.准备相关的多媒体课件和教学素材。
2.准备练习题和拓展题,以便学生在课后进行巩固和拓展。
七. 教学过程1.导入(5分钟)通过一个实际问题,如“一只蚂蚁从A点出发,如何走才能最快到达B点?”引发学生的思考,激发学生的学习兴趣。
2.呈现(10分钟)呈现教材中的案例,引导学生观察蚂蚁走的过程,让学生说一说蚂蚁是如何走的。
通过观察和交流,让学生初步感知图形的运动和变换。
3.操练(10分钟)让学生通过实际操作,尝试用图形运动和变换的规律来解决问题。

北师版八年级数学蚂蚁怎样走最近
教案
§1.3蚂蚁怎样走最近
--北师大版八(上)1.3
教师:徐飞彦
单位:鸡泽县实验中学
课题《蚂蚁怎样走最近》
--北师大版八(上)1.3
教学目的:
1、知识目标:运用勾股定理及直角三角形的判别条件解决简单的实际问题。
2、能力目标:培养学生运用所学知识解决实际问题的意识,增强学生的数学应用能力。
通过与同伴交流,培养协作与交流的意识。
3、情感目标:通过创设问题情境让学生主动参与,激发学生学习数学的热情和兴趣。
增强学数学的自信心。
教学重点:
经历勾股定理解决实际问题的过程;增强学生的数学应用能力。
教学难点:
勾股定理的灵活运用。
教学方法与教学手段:
1、情境探究、师生互动。
2、自主探索、分层推进。
3、教具演示、直观形象。

北师大版数学八年级上册3《蚂蚁怎样走最近》教案3一. 教材分析《蚂蚁怎样走最近》是人教版初中数学八年级上册的一章内容,主要介绍蚂蚁的行走方式以及如何计算蚂蚁走的最近距离。
这一章节是在学生学习了平面几何的基础知识之后进行的,对学生进一步理解几何图形的性质和计算方法有重要的意义。
二. 学情分析学生在学习这一章节之前,已经掌握了平面几何的基础知识,如点、线、面的基本性质和运算方法,对几何图形有一定的理解。
但是,对于蚂蚁的行走方式和计算最近距离的方法可能比较陌生,需要通过实例和操作来理解和掌握。
三. 教学目标1.让学生理解蚂蚁的行走方式,并能够运用到实际问题中。
2.让学生掌握计算蚂蚁走的最近距离的方法。
3.培养学生的空间想象能力和解决问题的能力。
四. 教学重难点1.蚂蚁的行走方式的的理解和应用。
2.计算蚂蚁走的最近距离的方法的掌握。
五. 教学方法1.实例教学法:通过具体的例子,让学生理解和掌握蚂蚁的行走方式和计算最近距离的方法。
2.问题驱动法:通过提出问题,引导学生思考和探索,激发学生的学习兴趣和解决问题的能力。
3.小组合作学习法:让学生分组讨论和解决问题,培养学生的团队合作能力和沟通能力。
六. 教学准备1.PPT课件:制作相关的PPT课件,用于展示实例和讲解知识点。
2.教学素材:准备相关的实例和问题,用于引导学生思考和探索。
3.教学工具:准备白板和板书笔,用于板书和讲解。
七. 教学过程1.导入(5分钟)利用PPT课件展示蚂蚁的行走方式,引导学生关注蚂蚁的行走特点,激发学生的学习兴趣。
2.呈现(10分钟)呈现实例,让学生观察和分析蚂蚁行走的路径,引导学生思考如何计算蚂蚁走的最近距离。
3.操练(15分钟)让学生分组讨论和解决问题,教师巡回指导,引导学生运用蚂蚁的行走方式来计算最近距离。
4.巩固(10分钟)让学生回答问题,检验学生对蚂蚁行走方式和计算最近距离方法的掌握程度。
5.拓展(10分钟)提出更深层次的问题,引导学生思考和探索,激发学生的学习兴趣和解决问题的能力。


1.3蚂蚁怎样走近教学设计:本节课体现了以教师为主导,以学生为主体,以知识为载体,以培养学生的思维能力,动手能力,探究能力为重点的教学思想。
在课堂教学中,尽量为学生提供“做中学”的时空,小组合作,探究交流得到了真正体现。
数学源于生活,并运用于生活是整节课的一条暗线贯穿其中,真正体现了新课标的理念。
教学反思:客观的讲,这是一节很普通的常规课,如何把这节课进行的生动而不失规范是我设计时考虑的主要出发点。
而ZJZ提供了这样的一个平台,丰富了我的教学。
教学目标:1、能运用勾股定理及直角三角形的判别条件(即勾股定理的逆定理)解决简单的实际问题。
2、能在实际问题中构造直角三角形,提高建模能力,进一步深化对构造法和代数计算法和理解。
3、在解决实际问题的过程中,体验空间图形展开成平面图形时,对应的点,线的位置关系,从中培养空间观念。
4、在解决实际问题的过程中,进一步培养从“形”到“数”和从“数”到“形”的转化,培养学生的转化、推理能力。
5、通过研究勾股定理的历史,了解中华民族文化的发展对数学发展的贡献,激发学生的爱国热情和学习数学的兴趣。
6、培养学生从空间到平面的想象能力,运用数学方法解决实际问题的创新能力及探究意识。
教学重、难点:如何将立体图形展开成平面图形,利用平面几何相关知识如对称、线段公理、点到直线的距离等求最短路径问题。
教学方法:探究学习、合作学习教学用具:“ Z+Z”智能教育平台教学过程:一、情景引入,知识回顾:1、问:李老师家装修。
这一天,下班后老师抽空去了一趟现场,工人们正在做门窗,老师很想检验一下工程的质量如何,可对工程质量的好坏,老师只知道可以通过检验门窗相邻两框是否互相垂直的方法来完成,但老师随身只带了一把卷尺(长为一米的简易卷尺)和一个计算器,你能想办法利用这两种工具帮老师检验一下工程的质量吗?(视频显示:工程现场的情景,一筹莫展的老师。
)处理方式:1)以小组讨论的方式确定行动方案。
2)以教室里的门窗为例验证方案的可行性。
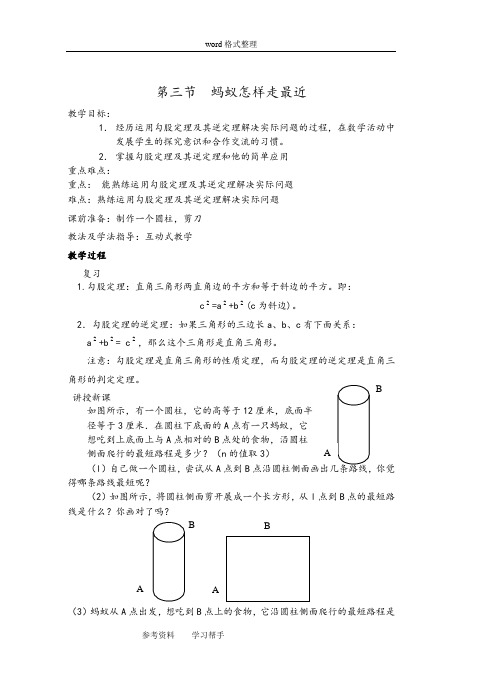
第三节 蚂蚁怎样走最近教学目标:1. 经历运用勾股定理及其逆定理解决实际问题的过程,在数学活动中发展学生的探究意识和合作交流的习惯。
2. 掌握勾股定理及其逆定理和他的简单应用重点难点:重点: 能熟练运用勾股定理及其逆定理解决实际问题难点:熟练运用勾股定理及其逆定理解决实际问题课前准备:制作一个圆柱,剪刀教法及学法指导:互动式教学教学过程复习1.勾股定理:直角三角形两直角边的平方和等于斜边的平方。
即:c 2=a 2+b 2(c 为斜边)。
2.勾股定理的逆定理:如果三角形的三边长a 、b 、c 有下面关系:a 2+b 2=c 2,那么这个三角形是直角三角形。
注意:勾股定理是直角三角形的性质定理,而勾股定理的逆定理是直角三角形的判定定理。
讲授新课如图所示,有一个圆柱,它的高等于12厘米,底面半径等于3厘米.在圆柱下底面的A 点有一只蚂蚁,它想吃到上底面上与A 点相对的B 点处的食物,沿圆柱侧面爬行的最短路程是多少?(n 的值取3)(l )自己做一个圆柱,尝试从A 点到B 你觉得哪条路线最短呢?(2)如图所示,将圆柱侧面剪开展成一个长方形,从l 点到B 点的最短路线是什么?你画对了吗?(3)蚂蚁从A 点出发,想吃到B 点上的食物,它沿圆柱侧面爬行的最短路程是B BB多少?做一做李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但池随身只带了卷尺.(l)你能替他想办法完成任务吗?(2)李叔叔量得 AD长是 30厘米,AB长是40厘米,BD长是50厘米. AD 边垂直于AB边吗?(3)小明随身只有一个长度为20厘米的刻度尺,他能有办法检验AD边是否垂直干AB边吗? BC边与AB边呢?课堂练习1.甲、乙两位探险者到沙漠进行探险.某日里晏 8:00甲先出发,他以6千米”时的速度向东行走.1时后乙出发.他以5千米/时的速度向北行进.上午10:00,甲、乙二人相距多远!2.如果梯子的底端离建筑物9米,那么15米长的梯子可以到达建筑物的高度是多少?课堂小结1.勾股定理:直角三角形两直角边的平方和等于斜边的平方。
1.3 勾股定理的应用引言勾股定理是数学中的一个重要定理,它是我们学习数学的基础。
在八年级数学上册的第一章中,我们学习了勾股定理以及它的应用。
在本文档中,我们将重点讨论勾股定理的应用之一:蚂蚁怎样走最近。
蚂蚁怎样走最近在我们的日常生活中,我们经常会遇到类似的问题:蚂蚁在平面上的两个点之间移动,它应该选择怎样的路径才能够走得最近呢?这个问题可以通过勾股定理来解决。
假设蚂蚁需要从点A到达点B,我们可以将平面上的点A和点B连接起来,形成一条直线。
根据勾股定理,直角三角形的斜边的长度等于两个直角边长度的平方和的平方根。
因此,我们可以通过计算直线AB的长度,再结合其他已知条件,来确定蚂蚁应该走的最短路径。
解决问题的步骤在解决蚂蚁怎样走最近的问题时,我们可以按照以下步骤进行:1.确定两点的坐标:首先,我们需要确定点A和点B的坐标。
假设点A的坐标为(x1, y1),点B的坐标为(x2, y2)。
2.计算直线AB的长度:根据勾股定理,直线AB的长度可以通过以下公式计算:AB = √((x2-x1)^2 + (y2-y1)^2)。
3.根据其他条件确定最短路径:除了直线AB的长度,我们还需要根据其他条件来确定最短路径,例如是否存在障碍物等。
示例接下来,我们通过一个示例来演示蚂蚁怎样走最近的问题。
假设蚂蚁需要从点A(1, 2)到达点B(4, 6),我们需要确定蚂蚁应该走的最短路径。
首先,我们可以计算直线AB的长度:AB = √((4-1)^2 + (6-2)^2) = √(3^2 + 4^2) = √(9 + 16) = √25 = 5因此,直线AB的长度为5。
接下来,我们需要根据其他条件确定最短路径。
假设在点C(2, 4)处存在一个障碍物,蚂蚁不能穿过障碍物。
根据直线AB的长度为5,我们可以尝试绘制一条与直线AB等长的线段CD,并且使得线段CD与直线AB垂直相交。
请注意,我们可以使用勾股定理来计算线段CD的长度。
假设线段CD的长度为d,则有:d^2 + 4^2 = 5^2解方程,我们可以得到:d^2 + 16 = 25d^2 = 9d = 3因此,线段CD的长度为3。
北师大版数学八年级上册3《蚂蚁怎样走最近》教学设计1一. 教材分析《蚂蚁怎样走最近》是北师大版数学八年级上册第3课的内容。
本节课主要通过探究蚂蚁走最近的问题,引入图形的运动,让学生理解平移和旋转的性质,以及它们在实际问题中的应用。
教材通过丰富的图片和实际问题,激发学生的学习兴趣,培养学生解决实际问题的能力。
二. 学情分析学生在七年级已经学习了图形的运动,对平移和旋转有了初步的认识。
但他们对平移和旋转的性质和应用还不够深入。
因此,在教学过程中,教师需要引导学生通过观察、操作、思考、交流等方式,进一步理解平移和旋转的性质,提高解决实际问题的能力。
三. 教学目标1.知识与技能:理解平移和旋转的性质,能运用平移和旋转解决实际问题。
2.过程与方法:培养学生的观察能力、操作能力和思考能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养他们解决实际问题的能力。
四. 教学重难点1.教学重点:平移和旋转的性质。
2.教学难点:如何运用平移和旋转解决实际问题。
五. 教学方法1.情境教学法:通过丰富的图片和实际问题,激发学生的学习兴趣。
2.启发式教学法:引导学生通过观察、操作、思考、交流等方式,自主探究平移和旋转的性质。
3.小组合作学习:培养学生的团队协作能力和沟通能力。
六. 教学准备1.教学课件:制作精美的课件,展示图片和实际问题。
2.教学素材:准备相关的图片和实际问题,用于引导学生探究。
3.学生活动材料:准备纸张、彩笔等,让学生动手操作。
七. 教学过程1.导入(5分钟)利用课件展示蚂蚁走最近的图片,引导学生观察并思考:蚂蚁是如何走最近的?激发学生的学习兴趣。
2.呈现(10分钟)呈现相关的实际问题,如:如何在地图上找到两个城市的最短路线?引导学生思考并讨论。
3.操练(10分钟)让学生分组进行讨论,每组选择一个实际问题,运用平移和旋转的性质,找出解决问题的方法。
教师巡回指导,给予学生必要的帮助。
4.巩固(10分钟)邀请几组学生分享他们的解题过程和答案,让其他学生进行评价和讨论。