下载文档原格式
2011年第26卷 第5期南昌教育学院学报 高等教育收稿日期：2011-04-28作者简介：刘小红（1977-），女，湖南邵东人，从事基础教学方向的研究。
数学期望简称期望，又称均值，是概率统计中一项重要的数字特征，它代表了随机变量取值的平均水平。
在实际应用中，其实许多问题都可以直接或间接的转化为数学期望问题来反映。
本文主要解析了数学期望在日常生活中的应用，如求职决策问题、投资问题、彩票问题等，从而不断激发学生学习数学的积极性和主动性，让学生在兴趣中学习探索，并应用于生活，让数学改变生活。
一、求职决策问题设想某大学生甲在求职过程中收到了三个公司的面试结果，如果按照面试时间的顺序来划分，我们将其标记为A公司，B公司，C公司。
假定这三个公司每个公司有三种不同的职位：极好，好以及一般。
估计能得到这些职位的概率为0.2、0.3、0.4，被拒绝的可能性为0.1，按规定，双方在面试后要立即作出决定提供、接受或拒绝某种职位，那么应遵循什么策略应答呢？三家公司的工资承诺如下表：我们的方案是采取期望受益最大的原则。
按照面试顺序的规则来看，我们先从A公司开始面试，这样甲在面试A公司时必然会权衡考虑B、C公司的机会和待遇。
同样道理，在选择面试B公司时自然也会考虑C公司的机会和待遇。
通过三个公司机会和待遇的横向和纵向比较，从而选择一个效益最大化的公司。
一般来说，从第三次面试的期望值来看，也就说从C公司来看，其工资的期望值表现为：2700元(=4000×0.2+3000×0.3+2500×0.4)。
而B公司的职位工资是2500元，这样经过横向比较，往往会选择去C公司。
而第二次面试的期望值可由以下数据求知：极好的职位工资3900元，好的职位工资2950元，接受第三次面试期望工资2700元。
所以在最后考虑A公司时，只有极好的职位工资超过3015元，甲才会接受。
这样，对于三次面试应采取的决策是：A公司只接受极好的职位，否则去B公司，在B公司可接受极好的和好的职位，否则去C公司，在C公司可接受任何可能提供的职位。
浅谈数学期望在生活中的应用浅谈数学期望在生活中的应用一、数学期望的定义引例某射手在一次射击比赛中共发射了10发子弹,其中有一发中7环,有二发中8环,有三发中9环,有4发中10环,求该射手在此次射击比赛中每发子弹击中的平均环数. 解平均环数这里的平均环数并不是这10发子弹击中的4个值的简单平均,而是以取这些值的次数与射击总次数的比值为权重的加权平均.在某种程度上说,这个加权平均可以用来衡量该射手的射击水平.二、数学期望的应用1.数学期望在疾病普查中的应用在一个人数为N的人群中普查某种疾病,为此要抽验N个人的血,如果将每个人的血分别检验,那么共需检验N次,为了能减少工作量,一位统计学家提出一种方法:按k个人一组进行分组,把同组k个人的血样混合检验,如果这混合血样呈阴性反响,就说明此k个人的血都呈阴性反响,此k个人都无此疾病,因而这k个人只需要检验一次就够了,相当于每个人检验1/k次,检验的工作量明显的减少了.如这混合血样呈阳性反响,就说明此k个人中至少有一个人的血呈阳性反响,那么在对这k个人的血样分别进行检验,因而这k个人的血要检验1+k次,相当于每个人检验1+1/k 次,此时增加了检验次数,假设该疾病的发病率为р且得此病相互独立,试问此种方法能否减少平均检验次数? 分析看能否减少平均检验次数,可以求出每个人检验次数的数学期望,根据数学期望大小再判断.解设以k个人为一组时,组内每个人检验次数为x,那么x是一个随机变量,其分布规律为所以每人平均检验次数为 .由此可知,只要选择k使就可减少验血次数,而且也可以通过不同的发病率р计算出最正确分组人数,此外,也得知:发病率越小,分组检验的效益越大.在二战期间,美国对新兵验血就是使用这种方法来减少工作量的.2.数学期望在揭开赌场骗局中的应用在我国南方流行一种称为“捉水鸡〞的押宝,其规那么如下:由庄家摸出一只棋子放在密闭的盒中,这只棋子可以是红的或黑的将、士、象、车、马、炮之一.赌客把钱押在一块写有上述12个字(六个红字,六个黑字)的台面的某一个字上,押定后,庄家揭开盒子露出原来的棋子,凡押中者(字和颜色都对)以一比十得奖金,不中者其押金归庄家,此押宝赌博对谁有利? 分析这道题的思想简单,与0-1分布一样.解不妨设一个赌徒押了10元,而收回奖金X元,假设押中,X=100;假设不中,X=0.X的概率分布列为因此数学期望元.由于支付10元,和期望收入8.33元不等.因此这是不公平的赌博,明显对庄家有利,事实上,当赌徒进入赌场,他面临的都是这种不公平的赌博,否那么赌场的巨额开支业主的高额利润从何而来.3.数学期望在通信中的应用设无线电台发出的呼唤信号被另一电台收到的概率为0.2,信号每隔5秒钟拍发一次,直到收到对方的答复为止.假设发出信号到收到对方答复信号之间至少要经过16秒时间,求在双方建立联系之前已经拍发的呼唤信号的平均次数.分析明显,此题是考查几何分布数学期望的求法,但是又隐藏陷阱“假设发出信号到收到对方答复信号之间至少要经过16秒时间〞,意味随机变量X最小取值为4.×0.8k-4,k=4,5,... X的期望为因此在双方建立联系之前已经拍发的呼唤信号的平均次数为8次.这个例题虽是很简单的一个求数学期望的问题,但是“假设发出的信号到收到对方答复信号之间至少要经过16秒时间〞这个条件极易被忽略.上面这几题都是关于离散型随机变量数学期望一些性质应用的例子,接下来的4、5两个例子都是关于连续型随机变量数学期望一些性质,还要注意函数是分段函数. 4.数学期望在交通上的应用地铁列车到达某一站时刻为每个整点的第5分,25分,45分,设某一乘客在早上8点到9点之间随时到站候车,求他的平均候车时间.分析此题主要考查分段函数求期望的方法,必须先求出分段函数的表达式及X的密度函数.解设他到达地铁站的时刻为X,他候车时间为Y,那么由题意知X～U(0,60),那么有又知Y是变量X的函数, 由期望的性质知利用此例题可准确地对乘客的平均等待时间进行了预测,可以更好地指导实际,为人民群众效劳. 5.数学期望在决策中的应用设某种商品每周需求量是区间[10,30]上的均匀分布随机变量,而经销商店进货数量为区间[10,30]中的某一整数,商店每销售一单位商品可获利500元,假设供大于求时那么削价处理,每处理一单位商品亏损100元,假设供不应求时,可从外部调剂供给,此时每一单位商品获利300元,为使商品获利润值不少于9280元,试确定最少进货多少?分析此题主要考查分段函数数学期望的求法,但是此处应注意分段函数的求法及均匀分布的密度函数的表达式. 解设进货数量为a,利润为g(X),那么 X的密度函数为得21≤a≤26.故所获利润期望值不少于9280元,最少进货为21单位. 接下来继续看6、7两个应用随机变量的和式分解这个性质解题的例子.这种方法可以解决用期望的定义不能直接求,甚至无法求解的题目,大大降低了求期望的难度,即使随机变量不是同分布也可以运用这一性质. 6.数学期望在电梯运行中的应用一架电梯载有8位乘客,从一楼上升,每位乘客在20层的每一层都可以下电梯,如果没人下,那一层电梯就不停.设每位乘客在各层楼下电梯是等可能的,且各乘客是否下电梯是相互独立的.以X表示电梯停下的次数,求E(X).分析显然X是一个离散型的随机变量,X=1,2,…,20,直接不易求出.不妨转换思想,假设电梯在i层停,那么Xi=1,否那么Xi=0,那么 .现在用数学期望的性质易求出E(X). 解设随机变量那么即xi(i=1,2,...,20)的分布规律为由此可知本例将随机变量分解为多个相互独立的随机变量之和的形式,再利用数学期望的性质.这个处理方法在实际应用中具有普遍意义.如果不用和式分解法几乎无从着手. [。
数学期望应用毕业论文(2)数学期望应用毕业论文篇三【摘要】数学期望是随机变量最重要的特征数之一，它是消除随机性的主要手段.本文通过对数学期望的概念、性质以及应用性的举例，阐述了数学期望在随机事件中的重要地位和很强的应用性.【关键词】数学期望;概率;随机事件引言在17世纪中叶，以为赌徒向法国数学家帕斯卡提出一个使他苦恼长久的份赌本问题：甲、乙两赌徒赌技不相上下，各出赌注50法郎，每局中无平局.他们约定，谁先赢三局，则得到全部的赌本100法郎.当甲赢二局、乙赢了一局时，因故(国王召见)要中止赌博，现在要分这100法郎.1654年帕斯卡提出了分法，在其解法里面也首次出现了“数学期望”.本文通过借鉴诗松的《概率论与数理统计》、中山大学数力系翻译的P.L.Meyer的《概率引论及统计应用》和石庆东发表在中国科技信息上的例谈数学期望这篇文章，对数学期望的相关性质以及应用做了进一步的探讨.1.数学期望的定义由于随机变量分为离散随机变量和连续随机变量，所以在定义数学期望式分两种情况.1.1 离散随机变量的数学期望设离散随机变量X的分布列为：这里例题所求运用了期望的定理1，对随机变量所得函数进行了期望计算.3.2 数学期望在实际生活中的应用3.2.1 数学期望在商店进货问题中应用例2 设某商店销售某种商品，该商品每周的需求量ξ是一个服从区间[100，300] 上的均匀分布的随机变量.正常情况下，每销售一单位商品可获利500元.若供大于求，则削价处理，每处理一单位剩余商品亏损100元;若供不应求，可以外部调剂供应，此时一单位商品获利300元.问该商店进货量应该为多少，可使平均每周的利润达到最大?y实际上为变量，对y求导得0，得到y=23.33.又因为E L ″ y=-15<0.所以当y=23.33时，利润的数学期望E L 取得最大值.3.2.2 数学期望在法律纠纷中的应用在民事纠纷案件中，受害人如果将案件提交法院诉讼，其不仅需要考虑诉讼胜利的可能性，还应该考虑承担诉讼的费用问题.如果对案件进行理性思考，一般人往往会选择私下解决而不通过法院.现在以一个民事纠纷案件来说明.例3 某施工单位A在施工过程中由于某种原因致使居民B受伤，使居民受伤并使其遭受了20万元的经济损失.若将该案件提交诉讼，则诉讼费共需要0.8万元，并按所负责任的比例双方共同承担.而根据案件发生的情形以及外部因素的影响，法院最后的判决可能有三种情况：(1)施工单位A承担事故100 % 责任，要向受害人B支付20万元的赔偿费，并支付诉讼费0.8万元;(2)施工单位A承担70 % 的责任，要向受害人B支付14万元的赔偿费，并支付诉讼费0.56万元，另外0.24万元诉讼费由受害人支付;(3)施工单位A承担50 % 的责任，要向受害人B支付10万元的赔偿费，并支付诉讼费0.4万元，另外0.4万元诉讼费由受害人支付.居民B估计法院三种判决的可能性分别为0.2，0.6，02，如果施工单位A想私下和解而免于诉讼，至少应向受害人B赔偿多少数额的赔偿费，才能使受害居民B从经济利益考虑而选择私下和解?首先从受害人B的角度来看受害人通过法院诉讼所获得的期望赔偿.设受害人B上诉可获赔偿为：(万元)，则ξ的分布列：由上述分析和求解可以看出，若从经济利益角度来看，私下和解赔偿给受害人B的数额应该不超过14.976万元，否则，私下和解对于施工单位A便失去了意义.结束语本论文主要涉及了数学期望的概念，性质，定理并通过商品进货，法律问题方面的举例来说明数学期望在实际生活中的应用.整体是由数学期望的理论转向其在实际生活中的应用.从上述众多性质和所列举的例子中可以体会到数学期望的奇妙之处和应用的广泛性，它是减少随机性的重要手段，在涉及概率统计和决策时，往往会利用数学期望理论，但数学期望只是一种平均值，在实际问题中往往要结合其他的数字特征才能更好的解决问题.。
数学期望在实际生活中的应用研究作者：滕子来源：《中国科技博览》2018年第12期[摘要]数学起源于人类早期的生产活动，在人类历史发展和社会生活中，数学具有重要作用。
现在数学已经包括多个分支，被应用于多个不同领域，包括科学、工程、医学和经济学等。
数学期望属于概率论和统计学，它是最基本的数学特征之一，反映随机变量取值的平均大小。
本文对数学期望在实际生活中的应用进行了研究。
[关键词]数学期望；实际生活；应用中图分类号：S211 文献标识码：A 文章编号：1009-914X（2018）12-0280-011.数学期望数学期望起源于17世纪，有一个赌徒向法国著名数学家帕斯卡发出挑战，提出了一个数学难题，两个人进行赌博，称之为甲方、乙方。
综合各项因素，甲乙双方每局获胜机率都一样，甲方获胜的机率为百分之五十，乙方获胜的机率也为百分之五十。
比赛规定先胜三局者为赢家，赢家可以拿走巨额金钱奖励。
前三局，甲方赢了两局，乙方赢了一局，两人都没有满足游戏获胜的规则，但是由于某些因素比赛不能继续进行，因此甲乙双方为如何分配奖金产生了争执。
甲方赢了两局，乙方赢了一局，那么甲方分得奖金的三分之二，乙方获得奖金的三分之一吗？这不符合游戏规则，赢家获得全部奖金。
甲方、乙方平分奖金？甲方赢了两局，乙方只赢了一局，很显然甲方的赢的概率更大，并不公平。
那么如何分配奖金才合理？数学期望这个概念就此产生，数学期望是每次试验可能结果的概率乘积。
根据数学期望，甲方获胜的机率为1/2+（1/2）*（1/2）=3/4，而乙方获胜的机率为（1/2）*（1/2）=1/4。
因此甲方获得奖金的四分之三，乙方获得的奖金为四分之一。
2.数学期望在实际生活中的应用研究2.1风险决策问题某商城决定开展促销活动，活动有两种实施方案场内和场外，如果天气良好就在场外举行，天气下雨就在场内举行。
根据以往的销售情况，估计商城内促销活动可以带来两万元的效益，天气好可获得十万元的效益，但是天气不好将会损失四万元。
![[整理版]数学期望在实际生活中的应用](https://img.taocdn.com/s1/m/0482266e1611cc7931b765ce05087632311274fa.png)
摘要在现代快速发展的社会中，数学期望作为一门重要的数学学科，它是随机变量的重要数字特征之一，也是随机变量最基本的特征之一。
通过几个例子，阐述数学期望在实际生活中的应用包括经济决策、彩票抽奖、求职决策、医疗、体育比赛等方面的一些实例，体现出数学期望在实际生活中颇有价值的应用。
通过探讨数学期望在实际生活中的应用，以起到让大家了解知识与人类实践紧密联系的丰富底蕴，切身体会到“数学的确有用”。
所谓的求数学期望其实就是去求随机变量的以概率为权数的加权平均值，而平均值这一概念又是我们在实际应用中最常用的一个指标,在预测中使用是很具有科学性的。
关键词：数学期望随机变量性质实际应用AbstractIn the rapid development of modern society, the mathematical expectation as an important mathematical subject, it is one of the important digital features of random variables, is also one of the basic characteristics of random variables. Through several examples, in this paper, the mathematical expectation in the practical application of life including economic decision-making, lottery tickets, job, health, sports, etc. In some instances, manifests the mathematical expectation valuable application in real life. Through discuss the application of mathematical expectation in real life to play let everybody understand the knowledge and practice closely linked human rich background, personal experience "mathematics really useful". So-called mathematical expectation is to actually ask for random variables of the probability weighted average of the weight, and mean value in actual application of this concept is our one of the most commonly used indicators, used in the forecast, it is very scientific.Key words: Mathematical Expectation; Stochastic V ariable; quality; Practical Application目录摘要 (1)Abstract (2)第一章绪论 (4)1.1数学期望的起源及定义 (4)1.2数学期望的意义 (5)第二章数学期望前瞻 (5)2.1离散型 (5)2.2连续型 (6)2.3随机变量的数学期望值 (7)2.4单独数据的数学期望的算法 (8)2.5数学期望的基本性质 (8)第三章数学期望在实际中的应用 (9)3.1 经济决策中的应用 (9)3.2 彩票、抽奖问题 (10)3.2.1彩票问题 (10)3.2.2抽奖问题 (11)3.3 求职决策问题 (12)3.4医疗问题 (13)3.5体育比赛问题 (15)结论 (16)参考文献 (16)致谢 (18)第一章 绪论1.1数学期望的起源及定义早在17世纪，有一个赌徒向法国著名数学家帕斯卡挑战，给他出了一道题目：甲乙两个人赌博，他们两人获胜的机率相等，比赛规则是先胜三局者为赢家，赢家可以获得100法郎的奖励。
谈数学期望在现实生活中的应用【摘要】概率统计是研究随机现象与统计规律的科学，数学期望是随机变量的重要特征之一.概率问题与我们的生活紧密联系，数学期望则更是在我们的生活中发挥着巨大的作用.本文介绍了有关数学期望的知识，并列举了一些实例，说明数学期望在现实生活中的应用.【关键词】概率统计;数学期望;应用;统计规律;随机变量一、关于离散型和连续型随机变量数学期望的定义1.对于离散型随机变量x，设其分布律为p{x=x k}=p k,（k=1,2,…），若级数 ∑∞[]k=1 x kp k绝对收敛，则称该级数为随机变量x的数学期望（简称期望或均值），记为e(x)，即e(x)= ∑∞[]k=1 x kp k.2.设连续型随机变量x的概率密度函数为f(x),若积分 ∫ +∞ -∞ xf(x)dx绝对收敛，则称该积分为随机变量x的数学期望，记作：e(x),即e(x)= ∫ +∞ -∞ xf(x)dx.二、数学期望在现实生活中的一些应用1.配对问题一把钥匙开一把锁，每把锁都有各自对应的钥匙与其配对.同样，不同的信应装入不同的信封.而我们如果在每个信封内都随意地装一封信，又能有几封信恰好落入与其相对应的信封呢？这时我们便可以利用数学期望求出信与信封对应的个数.这样我们可以得到一个科学合理的解释，事实并不像想象中的那样巧合.例1 某人先写了n封投向不同地址的信，再写了这n个地址的信封，然后在每个信封内随意地装入一封信，求信与地址配成对的个数x的期望.解首先定义n个随机变量如下：x i=1 第i封信配对成功0 第i封信配对不成功（i=1,2,…,n)，则 x= ∑n[]i=1 xi(i=1,2,…,n)．配对试验的样本空间的样本总点数=n·（n-1)· …· 2·1=n!（第1封信有n种配法，第2封信就剩下n-1种配法……最后一封信就只有1种配法），而事件{x i=1}={第i封信配对成功，而其他n-1封信随意配}的样本总点数=(n-1)!(因为第i封信已配成对，所以其余的 n- 1封信只能与余下的n-1个信封配）.所以p{x i=1}=1[]n,p{x i=0}=1-1[]n.从而e(x i)=1[]n，因此e(x)=e( ∑n[]i=1 x i)= ∑n[]i=1 e(x i)= n× 1[]n=1.2.获奖问题买彩票、摸奖、有奖销售中的高额大奖刺激人心，每个人都期望自己拥有那份幸运，然而事实真如我们期望的那样吗？通过下面计算期望值可以看出，这一切活动我们都应少参加，三思而后行.例2 某银行开展定期定额的有奖储蓄，定期一年，定额60元.按规定10000个户头中，头等奖一个，奖金500元；二等奖10个，各奖100元；三等奖100个，各奖10元；四等奖1000个，各奖2元.某人买了五个户头，他期望得奖多少元？解因为任何一个户头得奖都是等可能的，我们先计算一个户头的得奖金数x的期望.依题意，x的分布列为:即买５个户头的期望得奖数为e(5x)=5e(x)=5×0.45=2.25(元）.从上述计算结果我们可以看出得奖的金额是很小的.3.保险问题购买保险是我们日常生活中非常重要的一件事情，高额的赔偿金是我们选择各类保险的一个重要理由，通过本题的计算，我们可改变一下平时的看法，我们并不是保险的最大受益者.例3 据统计，在一年内健康的人死亡率为2‰，保险公司开展保险业务，参加者每年支付20元保险金，若一年内死亡，公司赔偿a 元(a>20)，问a应为多少，才能使保险公司获益？解设随机变量ξ为保险公司从每一个参加保险者处获得的净收益，ξ的概率分布为：ξ[]20-a[]20p{ξ=x k}[]0.002[]0.998e(ξ)=(20-a)×0.002+20×0.998=20-0.002a.要使e（ξ）>0，得到20期望获益.从上面的例子可以看出，数学期望与我们的日常生活有着紧密的联系，通过它我们可以更好地解决生活中的许多问题，作出科学准确的决策.当然除了上述的例子外，还有很多实际例子，需要我们在以后的日常生活中去发现.。
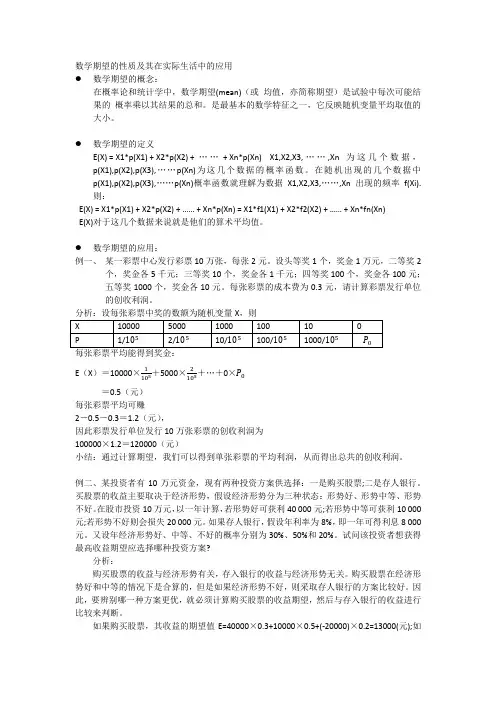
数学期望的性质及其在实际生活中的应用●数学期望的概念：在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和。
是最基本的数学特征之一，它反映随机变量平均取值的大小。
●数学期望的定义E(X) = X1*p(X1) + X2*p(X2) + …… + Xn*p(Xn) X1,X2,X3,……,Xn为这几个数据，p(X1),p(X2),p(X3),……p(Xn)为这几个数据的概率函数。
在随机出现的几个数据中p(X1),p(X2),p(X3),……p(Xn)概率函数就理解为数据X1,X2,X3,……,Xn出现的频率f(Xi).则：E(X) = X1*p(X1) + X2*p(X2) + …… + Xn*p(Xn) = X1*f1(X1) + X2*f2(X2) + …… + Xn*fn(Xn)E(X)对于这几个数据来说就是他们的算术平均值。
●数学期望的应用：例一、某一彩票中心发行彩票10万张，每张2元。
设头等奖1个，奖金1万元，二等奖2个，奖金各5千元；三等奖10个，奖金各1千元；四等奖100个，奖金各100元；五等奖1000个，奖金各10元。
每张彩票的成本费为0.3元，请计算彩票发行单位的创收利润。
E（X）＝10000×＋5000×＋ 0＝0.5（元）每张彩票平均可赚2－0.5－0.3＝1.2（元），因此彩票发行单位发行10万张彩票的创收利润为100000×1.2＝120000（元）小结：通过计算期望，我们可以得到单张彩票的平均利润，从而得出总共的创收利润。
例二、某投资者有10万元资金，现有两种投资方案供选择：一是购买股票;二是存人银行。
买股票的收益主要取决于经济形势，假设经济形势分为三种状态：形势好、形势中等、形势不好。
在股市投资10万元，以一年计算，若形势好可获利40 000元;若形势中等可获利10 000元;若形势不好则会损失20 000元。
一、数学期望的定义及性质（一）数学期望分为离散型和连续型1、离散型离散型随机变量的一切可能的取值Xi与对应的概率Pi(=Xi)之积的和称为该离散型随机变量的数学期望（设级数绝对收敛），记为E（X）。
数学期望是最基本的数学特征之一。
它反映随机变量平均取值的大小。
又称期望或均值。
如果随机变量只取得有限个值，称之为离散型随机变量的数学期望。
它是简单算术平均的一种推广，类似加权平均。
E(X) = X1*P(X1）+ X2*P(X2)+…… + Xn*P(Xn)。
X1,X2,X3，……，Xn 为这几个数据，P(X1）,P(X2）,P(X3），……，P(Xn)为这几个数据的概率函数。
在随机出现的几个数据中，P(X1）,P(X2）,P(X3），……，P(Xn)概率函数就理解为数据X1,X2,X3，……，Xn出现的频率f(Xi),则：E(X) = X1*P(X1）+ X2*P(X2）+ …… + Xn*P(Xn) = X1*f1(X1）+ X2*f2(X2）+ …… + Xn*fn(Xn)。
2、连续型连续型则是：设连续性随机变量X的概率密度函数为f（X），若积分绝对收敛，则称积分的值为随机变量的数学期望，记为E(X)。
若随机变量X的分布函数F(X)可表示成一个非负可积函数f(X)的积分，则称X为连续随机变量，f(X)称为X的概率密度函数（分布密度函数）。
能按一定次序一一列出，其值域为一个或若干个有限或无限区间，这样的随机变量称为连续型随机变量。
（二）数学期望的常用性质1.设X是随机变量，C是常数，则E（CX）=CE（X）；2.设X，Y是任意两个随机变量，则有E（X+Y）=E（X）+E（Y）；3.设X,Y是相互独立的随机变量，则有E（XY）=E（X）E（Y）。
对于第一条性质，假设E（X）你的考试成绩，C为你们全班人数，则你们全班总分的期望等于全班人数乘以个人的期望，这很好理解。
对于第二条性质，E（X）为你的考试成绩，E(Y)是小明的考试成绩，你和他成绩总和的期望当然等于你和他的期望值和。
对于第三条性质，我们一再强调是独立的，也就是相互没有关联，有关联是肯定是不是不等的。
二、数学期望在生活中的运用（一）经济决策问题假设某一超市出售的某种商品，每周的需求量X在10至30范围内等可能取值，该商品的进货量也在10至30范围内等可能取值（每周只进一次货）超市每销售一单位商品可获利500元，若供大于求，则削价处理，每处理一单位商品亏损100元；若供不应求，可从其他超市调拨，此时超市商品可获利300元。
试计算进货量多少时，超市可获得最佳利润？并求出最大利润的期望值。
分析：由于该商品的需求量（销售量）X 是一个随机变量，它在区间[10,30]上均匀分布，而销售该商品的利润值Y 也是随机变量，它是X 的函数，称为随机变量的函数。
题中所涉及的最佳利润只能是利润的数学期望（即平均利润的最大值）。
因此，本问题的解算过程是先确定Y 与X 的函数关系，再求出Y 的期望E （Y ），最后利用极值法求出E （Y ）的极大值点及最大值。
先假设每周的进货量为a ，则 Y=500300(),500100(),a x a x ax a x x a+-≥⎧⎨--<⎩=200300,600100,a x x a x a x a+≥⎧⎨-<⎩利润Y 的数学期望为：EY=1(600100)1020a x a dx -⎰+301(300200)20x a dx a+⎰=-7.52a 2+350a+5250da dEY=-15a+350=0 a=35015≈23.33 EY 的最大值max EY=-7.5×270()3+350×703+5250≈9333.3元根据结果可知，周最佳进货量为23.33（单位），最大利润的期望值为9333.3元。
在经济活动中，不论是厂家的生产还是商家的销售，总是追求利润的最大化，供大于求或供不应求都不利于获得最大利润。
但供应量和需求量又不是预先知道的。
理性的厂家或商家往往根据过去的数据(概率），用数学期望结合微积分的有关知识，制定最佳的生产或销售策略。
（二）投资方案问题假设某人用10万元进行为期一年的投资，有两种投资方案：一是购买股票;二是存入银行获取利息。
买股票的收益取决于经济形势，若经济形势好可获利4万元，形势中等可获利1万元，形势不好要损失2万元。
如果存入银行，假设利率为8%，可得利息8000元，又设经济形势好、中、差的概率分别为30%、50%、20%。
试问应选择哪一种方案可使投资的效益较大？比较两种投资方案获利的期望大小：购买股票的获利期望是E(A1)=4×0.3+1×0.5+(-2)×0.2=1.3(万元）,存入银行的获利期望是E(A2)=0.8（万元），由于E(A1)>E(A2)，所以购买股票的期望收益比存入银行的期望收益大，应采用购买股票的方案。
在这里，投资方案有两种，但经济形势是一个不确定因素,做出选择的根据必须是数学期望高的方案。
（三）体育比赛问题我国的羽毛球在世界上处于领先水平，技术风格是“快速、凶狠、准确、灵活”；指导思想是“以我为主，以快为主，以攻为主”。
现以羽毛球比赛的安排提出一个问题：假设马来西亚队和中国队比赛。
赛制有两种，一种是双方各出3人, 三局两胜制, 一种是双方各出5人，五局三胜制, 哪一种赛制对中国队更有利？下面,我们利用数学期望解答这个问题。
由于中国队在这项比赛中的优势，我们不妨设中国队中每一位队员对马来西亚队员的胜率都为60%。
根据前面的分析，下面我们只需要比较两个队对应的数学期望即可。
在五局三胜制中，中国队要取得胜利, 获胜的场数有3、4、5三种结果。
我们计算三种结果对应的概率。
应用二项式定理可知，恰好获胜三场(即其中两场失利)对应的概率：；恰好获胜四场对应的概率为：；五场全部获胜的概率为： 。
设随机变量为x 为为该赛制下中国队在比赛中获胜的场数，则可建立x 分布律：3456.0)6.01()6.0(2335=-c2592.0)6.01()6.0(1445c =-07776.0)6.01()6.0(0555c =-计算随机变量X 的数学期望:E(X) = 3⨯0. 346 5 + 4⨯0. 259 2 + 5⨯0. 077 76= 2.465 1； 在三场两胜制中，中国队取得胜利，获胜的场数有2、3两种结果。
对应的概率分别为：恰好获胜两场(其中有一场失利)对应的概率：432.0)6.01()6.0(223=-c ；三场全部获胜的概率为：。
设随机变量Y 为该赛制下中国队在比赛中获胜的场数, 则可建立Y 的分布律：计算随机变量Y 的数学期望: E(Y) = 2×0. 432+3×0. 216=1. 512。
比较两个期望值得：E(X)> E(Y)。
所以我们可以得出结论，五局三胜制对中国队更有利。
（四）抽奖问题假设某百货超市现有一批快到期的日用产品急需处理，超市老板设计了免费抽奖活动来处理掉了这些商品。
纸箱中装有大小216.0)6.01()6.0(0333c =-相同的20个球，10个10分，10个5分，从中摸出10个球，摸出的10个球的分数之和即为中奖分数，获奖如下：一等奖100分，空调一个，价值2500元；二等奖50分，微波炉一个，价值1000元；三等奖95分，沐浴露6瓶，价值178元；四等奖55分，沐浴露3瓶，价值88元；五等奖60分，沐浴露1瓶，价值44元；六等奖65分，洗面奶一瓶，价值8元；七等奖70分，洗衣粉一袋，价值5元；八等奖85分，香皂一块，价值3元；九等奖90分，牙刷一把，价值2元；十等奖75分与80分为优惠奖，只收成本价22元，将获得洗发露一瓶；解析：表面上看整个活动对顾客都是有利的，一等奖到就等奖都是白得的，只有十等奖才收取一点成本价。
但经过分析可以知道商家真的就亏损了吗？顾客就真能从中获得抽取大奖的机会吗？用以上方法分析一下并求得其期望值真相就可大白了。
摸出10个球的分值只有11种情况，用X 表示摸奖者获得的奖励金额数，一等奖等分100分，其对应事件101010101020(2500)c c X c ==，X 的取值为250010001768844853222-、、、、、、、、、，概率可以类似求出，其概率分布为：()1E 10.098i i i X x p ∞===-∑表明商家在平均每一次的抽奖中将获得10.098元，而平均每个抽奖者将花10.098元来享受这种免费的抽奖。
从而可以看出顾客根本没有占到什么便宜。
相反，商家采用这种方法不仅把快要到期的商品处理出去了，而且还为超市大量集聚了人气，为一举多得的手法。
此百货超市老板运用数学期望估计出了他不会亏损而做了这个免费抽奖活动，最后一举多得，从中也看出了数学期望这一科学的方法在经济决策中的重要性。
（五）彩票问题随着社会生活的丰富，人们购买彩票，谈论彩票中奖的热潮正在兴起。
报纸上不时发表谈论彩票的文章，有时也谈到摸彩与数学的关系。
但众所纷纭，也说不详，论也不确。
众所周知，彩票抽奖属于“独立随机事件”，彩票预测违背科学。
但从总体上来说，中奖号码有服从于某些统计规律。
为了研究彩票中的概率统计问题，我们选取了体育彩票和七乐彩及一些简单的模拟实验来帮助我们研究，例如：我们进行了模红白球的实验，先进性简单的概率计算问题，我们又以体育彩票和七乐彩为辅助实验并根据。
由此我们计算出体彩的中奖概率如下（以一注为单位）特等奖P0=1/10000000；一等奖P1=1/1000000；二等奖P2=20/1000000；三等奖P3=300/1000000；四等奖P4=4000/1000000；五等奖P5=50000/1000000；P=P0+P1+P2+P3+P4+P5=0.0543211。
这就是说每1000注彩票约有54注中奖，经过公式计算我们计算出了七乐彩的中奖概率：一等奖：C30~1/2035；二等奖：P1=1/290829；三等奖：P2=1/13219；四等奖：P3=1/4406；五等奖：P4=1/420；六等奖：P5=1/252；七等奖：P6=1/38。
一般来说，各类彩票各奖级的中奖几率总和在4%-5%左右。
如果要中奖金数目大的最高奖，概率一般为几十万至几百万分之一，难度更为大，是可遇而不可求的。
对于购买题材只能是本着对中国体育事业支持的想法，而不能对回报有过高的期望。
彩票的中奖概率与数学里的数理统计学有着密切的关系，通过统计概率，我们可以更好的发现数理统计学与生活的密切关系。
在彩票市场异常火爆的今天，我们要作一个理性的彩迷，对彩票持有正确的认识，买彩票是彩民的一个爱好，一种自愿的活动，理智的彩民不该抱着赌博的心态，孤注一掷，投入极大的资金，应量力而出以平常健康重在参与的心态买彩票。
