当前位置：文档之家 › 高中数学正态分布ppt课件

高中数学正态分布ppt课件

  • 格式：ppt
  • 大小：1.58 MB
  • 文档页数：57

下载文档原格式

  / 57

合集下载

2025届高中数学一轮复习课件《正态分布》ppt

2025届高中数学一轮复习课件《正态分布》ppt

高考一轮总复习•数学
A．甲工厂生产的零件尺寸的平均值等于乙工厂生产的零件尺寸的平均值 由正态曲线的对称轴相等可知． B．甲工厂生产的零件尺寸的平均值小于乙工厂生产的零件尺寸的平均值 C．甲工厂生产的零件尺寸的稳定性高于乙 甲的正态曲线瘦高，即稳定性高于乙． 工厂生产的零件尺寸的稳定性 D．甲工厂生产的零件尺寸的稳定性低于乙工厂生产的零件尺寸的稳定性
(2)由已知得 E(ξ)＝3，D(ξ)＝4，故 E(2ξ＋1)＝2E(ξ)＋1＝7，D(2ξ＋1)＝4D(ξ)＝16.故选 D．
解析
高考一轮总复习•数学
第21页
题型
服从正态分布的概率计算
典例 2 (1)(2024·陕西西安模拟)陕西洛川苹果享誉国内外，据统计，陕西洛川苹果(把
苹果近似看成球体)的直径 X(单位：mm)服从正态分布 N(70,52)，则直径在(80,85]内的概率
高考一轮总复习•数学
第27页
135 分的为特别优秀，那么本次数学考试成 μ＋2σ 绩特别优秀的大约有________人．(若 X～N(μ，σ2)，则 P(μ－σ≤X≤μ＋σ)≈0.68，P(μ －2σ≤X≤μ＋2σ)≈0.95) (2)(2024·河北张家口统考)某校举办乒乓球颠球比赛，现从高一年级 1 000 名学生中随机 选出 40 名学生统计成绩(单位：个)，其中 24 名女生的平均成绩 x 女＝70，标准差 s 女＝4；16 名男生的平均成绩 y 男＝80，标准差 s 男＝6.
σ ＝ 9. 因 为
μ
－ 2σ
＝
110
－
2×9
＝ 92
，
P(ξ≥90)>P(ξ≥92) ＝
P(ξ≥μ －
2σ)
＝
1 2

正态分布完整ppt课件

正态分布完整ppt课件
正态性检验
使用如Shapiro-Wilk检验、Kolmogorov-Smirnov检验等方法，对 误差项进行正态性检验，以验证其是否符合正态分布。
方差分析中F分布应用
01 02
F分布的定义
F分布是一种连续型概率分布，常用于方差分析中的假设检验。在方差 分析中，通过比较不同组间的方差与组内方差，判断各因素对结果的影 响是否显著。
筛选方法
包括单变量分析和多变量分析等，结合临床 意义和统计学显著性进行生物标志物的筛选 。
社会科学调查数据分析
社会科学调查数据特点
大量、复杂、多维度的数据，往往需要进行统计分析和数据挖掘。
正态分布在社会科学调查数据分析中的应用
通过对调查数据进行正态性检验，选择合适的数据处理和分析方法，如参数检验、回归分析等。
有对称性和单峰性。
性质
对称性：正态分布曲线关于均值对称 。
单峰性：正态分布曲线只有一个峰值 ，位于均值处。
均值、中位数和众数相等。
概率密度函数在均值两侧呈指数下降 。
正态曲线特点
01
02
03
04
形状
钟形曲线，中间高，两边低。
对称性
关于均值对称，即左右两侧形 状相同。
峰值
位于均值处，且峰值高度由标 准差决定。
05
正态分布在金融学领域应用
风险评估及资产组合优化
风险评估
正态分布用于描述金融资产的收益和风险分布，通过计算均值和标准差来评估投资组合 的风险水平。
资产组合优化
基于正态分布假设，利用马科维茨投资组合理论等方法，构建最优资产组合以降低风险 并提高收益。
VaR（Value at Risk）计算
正态分布用于计算投资组合在一定置信水平下的最大可能损失（VaR），以衡量潜在风 险。

北师大版高中数学选择性必修1第6章5.正态分布课件

北师大版高中数学选择性必修1第6章5.正态分布课件
(6)当μ一定时，曲线的形状由σ确定 .
σ越大，曲线越矮胖，表示总体的散布越分散；
σ越小，曲线越瘦高，表示总体的散布越集中.
课堂小结
4.正态散布的3 原则
课后作业
1、已知一次考试共有60名同学参加，考生的成绩X~N(100,52 )，
据此估计，大约应有57人的分数在下列哪个区间内？（
）
A.(90,110] B. (95,125] C. (100,120] D.(105,115]
（2）曲线是单峰的,它关于直线x=μ对称.1
（3）曲线在x=μ处到达峰值(最高点) σ 2π
X=μ
σ=1
σ=2
-3
-2
-1
0
1
2
3
x
（4）当 x<μ时,曲线上升;当x>μ时,曲线降落.并且当曲线向左、
右两边无限延伸时,以x轴为渐近线,曲线与x轴之间的面积为1.
(5)当σ一定时，曲线的位置由μ确定，曲线随着μ的变化而沿x轴平移
抽象概括
正态散布是最常见、最重要的连续型随机变量的散布，是刻画误
差散布的重要模型，因此也称为误差模型.
如果一个随机变量X服从正态散布，那么对于任何实数a,b(a<b),
随机变量X在区间(a,b]的概率可以用P(a<X≤b)来表示.它的几何意义就
是随机变量X的散布密度曲线在区间(a,b]对应的曲边梯形面积的值如
的特征以及区分 .
性质探究
正
态
曲
线
的
性
质
y
y
μ=1
μ=0
σ=1
-3 -2 -1 0
1 2 3 x
σ=
-3 -2 -1
0
1

正态分布及其应用--ppt课件

正态分布及其应用--ppt课件
➢ 有两个参数：位置参数 和变异度参数 。 一定， 越大，数据越分散，曲线越平坦； 一
定， 增大，曲线沿 X 轴向右平移。因此，不
同的 ，不同的 ，对应不同的正态分布。
PPT课件
5
不同均值正态分布示意图
PPT课件
6
1.5 1
不同标准差的正态分布示意图
PPT课件
7
➢ 正态曲线下面积的分布规律
➢估计频数分布。
➢制定医学参考值范围。
➢正态分布是许多统计方法的理论基础。
今后要讨论到的 分布t 、 分布F 与
分布 2等都是在正态分布的基础上推导 出来的。
ቤተ መጻሕፍቲ ባይዱPPT课件
9
第二节 标准正态分布及其应用
只要变量 X ~ N(, 2 ) ，就可经下式 转换为 0、 1的标准正态分布，记 作 u ~ N(0,1) 。此变换也称为标准化变换，
通过对密度函数积分我们可以知道正态曲线下， 横轴上所夹的面积为1。理论上：
范围内曲线下的面积占总面积的68.27%； 1.645 范围内曲线下的面积占总面积的90%； 1.96 范围内曲线下的面积占总面积的95%；
2.58 范围内曲线下的面积占总面积的99%。
PPT课件
8
➢四、正态分布的应用
正态分布及其应用
(normal distribution)
PPT课件
1
第一节 正态分布的概念和特征
➢一.概念 正态分布又称高斯（Gauss）分布，
是最常见、最重要的一种连续型分布， 医学资料中有许多指标的频数分布都呈 正态分布，如身高、体重、脉搏、血红 蛋白、血清总胆固醇等。
PPT课件
2
➢二．图形 正态分布密度函数
PPT课件

《正态分布》ppt课件

《正态分布》ppt课件
《正态分布》ppt课件
目录
CONTENTS
• 正态分布基本概念 • 正态分布在统计学中应用 • 正态分布在自然科学领域应用 • 正态分布在社会科学领域应用 • 正态分布计算方法及工具介绍 • 正态分布在实际问题中案例分析
01 正态分布基本概念
CHAPTER
定义与性质
定义
对称性
正态分布是一种连续型概率分布，描述了许 多自然现象的概率分布情况。在统计学中， 正态分布又被称为高斯分布。
系统误差与随机误差
正态分布可以帮助区分系统误差和随机误差。系统误差是由于实验装置或方法本身的缺陷引 起的，而随机误差则是由于各种不可控因素引起的。通过正态分布分析，可以对这两类误差 进行识别和纠正。
化学中浓度分布规律研究
01
溶液浓度的正态分布
在化学实验中，溶液的浓度分布往往符合正态分布。通过测量不同位置
利用SPSS的图形功能，可以绘制多种统计图表，包括频率分布直 方图、正态分布曲线图等。
SPSS提供了丰富的统计分析方法，如参数估计、假设检验、方差 分析等，可以根据研究需求选择合适的方法进行分析。
06 正态分布在实际问题中案例分析
CHAPTER
质量控制过程中产品合格率评估
质量控制图
利用正态分布原理，通过绘制质 量控制图，可以直观地展示产品 质量的波动情况，从而及时发现 并处理异常波动，确保产品合格
数据输入与整理
在Excel中输入数据，并进行必要的整理，如删除重复值、处理缺失 值等。
使用内置函数计算均值和标准差
Excel提供了丰富的内置函数，可以直接计算数据集的均值 （AVERAGE函数）和标准差（STDEV函数）。
绘制图表
利用Excel的图表功能，可以根据数据快速生成频率分布直方图和正 态分布曲线图。

正态分布 课件

正态分布 课件

；
• 特别地有：P(μ－σ<X≤μ＋σ)＝ 0.6862 ；
• P(μ－2σ<X≤μ＋2σ)＝ 0.9544 ；
• P(μ－3σ<X≤μ＋3σ)＝ 0.9974 .
[答案] B
[解析] 仔细对照正态分布密度函数：f(x)＝ 21πσe－
(x－μ)2
2σ2 (x∈R)，注意指数 σ 和系数的分母上的 σ 要一致，以及
正态分布
• 1．当样本容量无限增大时，它的频率分 布直方图 无限接近于 一条总体密度曲 线，在总体所在系统相对稳定的情况下， 总体密度曲线就是或近似地是以下函数的 图象：
• 其中μ和σ(σ>0)为参数．我们称φμ，σ(x)的图 象为 正态分布密度曲线，简称 正态曲线 ．
• (4)曲线与x轴之间的面积为 1 ；
• (5) 当 σ 一 定 时 ， 曲 线 随 μ 的 变 化而沿 x 轴 平移；
• (6)当μ一定时，曲线的形状由σ确定：σ越小，
曲线越“
瘦高”，表示总体的分布越
集中 ；σ越大，曲线越“
矮胖 ”，表示
总体的分布越 分散 ．
• 4．若X～N(μ，σ2)，则对任何实数a>0，概
率P(μ－a<X≤μ＋a)＝
称 性 得 P(3<X≤4) ＝ P(6<X≤7) ， 所 以
P(6<X≤7)＝
＝0.1359.
• [点评] 解此类题首先由题意求出μ及σ的
值，然后根据三个特殊区间上的概率值及
正态曲线的特点(如对称性，与x轴围成的 面积是1等)进行求解．
• [例5] 某年级的一次信息技术测验成绩近 似服从正态分布N(70,102)，如果规定低于 60分为不及格，求：

人教版高中数学选择性必修3《正态分布》PPT课件

人教版高中数学选择性必修3《正态分布》PPT课件

P(μ-2σ≤X≤μ+2σ)≈0.954 5,
P(μ-3σ≤X≤μ+3σ)≈0.997 3.
2.3σ原则
在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取[μ3σ,μ+3σ]中的值,这在统计学中称为3σ原则.
名师点析 对于正态分布N(μ,σ2)而言,随机变量X在[μ-3σ,μ+3σ]之外取值几
第七章
7.5 正态分布
内
容
索
引
01
课前篇 自主预习
02
课堂篇 探究学习
课标阐释
1.利用实际问题的直方图,了解正态分
布密度曲线的特点及曲线所表示的意
义.(直观想象)
2.了解变量落在区间[μ-σ,μ+σ],[μ2σ,μ+2σ],[μ-3σ,μ+3σ]的概率大小.(数学
运算)
3.会用正态分布去解决实际问题.(逻辑
变量X的分布比较集中;当σ较大时,峰值低,曲线“矮胖”,表示随机变量X的分
布比较分散,如图②.
微练习
(多选)已知三个正态密度函数φi(x)=
所示,则下列结论正确的是(
A.σ1=σ2 B.μ1>μ3
C.μ1=μ2 D.σ2<σ3
)
1
2π
(- )2
2
e 2
(x∈R,i=1,2,3)的图象如图
乎不可能发生,它在产品检查、质量检验中起着重要的作用.
微练习
设X~N(1,22),试求:
(1)P(-1≤X≤3);
(2)P(3≤X≤5);
(3)P(X≥5).
解 ∵X~N(1,22),
∴μ=1,σ=2.
(1)P(-1≤X≤3)=P(1-2≤X≤1+2)≈0.682 7.

正态分布的种类PPT课件

正态分布的种类PPT课件

用几台机器生产时, 因特定机器的故障 等发生的分布
一般的双重峰
极端的双重峰
4
斜型(Skewness)的解释
如柱型图,斜型分布是平均的分布从分布的中心偏向左或右,是左右 非对称的 Skewness表示数据偏移的程度
正态分布时 Skewness为0, 右边斜型分布是(+),左边斜型 分布是(-)值. 在左边图中Skewness值为2.186, 是(+)值,因此是右边斜型分布
6
3. 非正态分布的原因
非对称或非正态分布的问题是在现场经常出现的问题,其潜在的原因 如下
1) 具有自然界限的数据 2) 筛选检查时不良品的选别 3) 分布的混合 4) 输入变量与输出变量间的非线性关系 5) 输入变量间的交互作用 • 按照时间的工程变化 • 缺乏独立性或周期的变化 • 测定器精密度问题 • 具有异常点(Outliers)的数据
5
尖度(Skewness)的解释
急尖或平尖分布的平均的分布在中心,但左,右两边的尾巴比正态分布 短或长. Kurtosis称为尖度,表示分布形态的平或尖的程度
正态分布时 Kurtosis为0, 急尖分布时(+),平尖分布时(-) 值. 在左图中Kurtosis值为3.082, 是(+)值,可以看出是平尖分布
35
输 30 出
25
收率的分布 (右边斜型)
80% 相对粘性
粘性的分布 (正态分布)
输入
30% 相对粘性
50도
75도
输入
温度的分布
(正态分布)
12
6) 按时间工程变化时
按时间作业条件变化,因此制品品质变化时,有可能带来右边斜型 或左边斜型的结果
30

《高中数学正态分布》课件

《高中数学正态分布》课件

正态分布的实例分析
1 案例一：商品售价的概率分布
探讨商品售价符合正态分布时的概率分布情况，为合理定价提供依据。
2 案例二：身高的概率分布
分析人类身高在不同群体中的分布，理解身高的统计特征和差异。
3 案例三：考试成绩的分布
研究考试成绩的正态分布特征，评估学生的相对表现和优势科目。
总结与思考
正态分布在数学与实践中的重要 性
3
应用示例
通过标准化后的数据，可以进行正态分布的统计估计、抽样与推论，并用于描述 实际情况。
正态分布的应用
统计估计
正态分布在估计总体参数和进行 置信区间估计时非常有用。
抽样与推论
正态分布可用于抽样分布的建立 和统计推断的进行。
实际情况分析
通过近似描述实际情况，例如商 品售价、身高和考试成绩的分布。
《高中数学正态分布》 PPT课件
引言
正态分布的定义
正态分布是一种连续型概率分布，具有钟形曲线，以均值μ和标准差σ来描述。
正态分布的性质
正态分布的均值、中位数和众数相等；左右对称；68%的数据落在一个标准差内；95%的数 据落在两个标准差内。
概率密度函数
密度函数的输入和输出，函数图 像
密度函数接受一个输入值x并给出对应的概率密度 值。函数图像呈现出正态分布的钟形曲线。
正态分布是统计学中最重要的概率分布之一，在自 然科学、社会科学和经济金融等领域有广泛应用。
对于其他分布的启示
正态分布的性质和应用可以启发我们研究和理解其 他概率分布。
参考文献
• 统计学与实际 • 十二年高等数学 • 数学建模及其应用 • 离散数学及其应用
均值和标准差对函数图像的影响
均值决定函数图像的中心位置，标准差影响函数图 像的分散程度。正态分布的Fra bibliotek准化1

高二数学理正态分布(共10张PPT)

高二数学理正态分布(共10张PPT)
高二数学理正态分布 课件
样本的频率如何估计总体频率。
研读教材P -P72： 探究2：利用教材P73图2.
探究2：利用教材P73图2.
70 某地区数学考试的成绩X服从正态分布, 其密度函
数曲线图形如图,
成绩X位于区间
1. 高尔顿板与正态曲线的联系 (52, 68]的概率
是多少？ 样本的频率如何估计总体频率。
4-5, 结合
的解析式, 请谈谈 对正态曲线图象的影响。
高尔顿板与正态曲线的联系
4. 正态分布的基本判断方法和实际例子。 2.
正态分布的基本判断方法和实际例子。 4
A组T1、T2 B组T2.
探究1：利用教材P71图2.4-3与图
2.4-4, 结合 , (x)的解析式及概率的
性质, 请你说说正态曲线的特点。
对正态曲线,图象
的影响。 4-5, 结合
的解析式, 请谈谈 对正态曲线图象的影响。
4-5, 结合
的解析式, 请谈谈 对正态曲线图象的影响。
正态分布的基本判断方法和实际例子。
4
A组T1、T2 B组T2.
正态分布的基本判断方法和实际例子。
样本的频率如何估计总体频率。
正态分布的基本判断方法和实际例子。
正态分布的基本判断方法和实际例子。
4-5, 结合
的解析式, 请谈谈 对正态曲线图象的影响。
4-4, 结合
的解析式及概率的
2. 正态曲线的函数表达式及其图象； 性质, 请你说说正态曲线的特点。
探究教材P71图2.
例1.
3. 正态分布的概念； 正态分布的基本判断方法和实际例子。
研读教材P70-P72： 1.
x
0 40 50 60 70 80

新人教版高中数学必修第三册-7-5 正态分布【课件】

新人教版高中数学必修第三册-7-5 正态分布【课件】
(6)当 σ 一定时，曲线随着 μ 的变化而沿 x 轴平移，如图 1 所示．
(7)当 μ 一定时，曲线的形状由 σ 确定．σ 越小，曲线越“瘦高”，表示随机变 量 X 的分布越集中；σ 越大，曲线越“矮胖”，表示随机变量 X 的分布越分散，如 图 2 所示．
4．3σ 原则 (1)正态分布在三个特殊区间内取值的概率： P(μ－σ≤X≤μ＋σ)≈____0_._6_8_2_7________， P(μ－2σ≤X≤μ＋2σ)≈___0_._9_5_4_5_________， P(μ－3σ≤X≤μ＋3σ)≈____0_._9_9_7_3________. (2)通常认为服从于正态分布 N(μ，σ2)的随机变量 X 只取[μ－3σ，μ＋3σ]之间的 值，这在统计学中称为 3σ 原则．
__μ_＝__0___，标准差为 σ＝ 2π.
4.如图是当 σ 取三个不同值 σ1，σ2，σ3 时的三种正态曲线，那么 σ1，σ2，σ3 的 大小关系是什么？
提示：0<σ1<σ2＝1<σ3.
二、练一练 1．设 X～N(μ，σ2)，则众数，中位数，平均数满足( D ) A．众数＝σ2，中位数＝平均数＝μ B．平均数＝μ，众数＝中位数＝σ2 C．中位数＝μ，众数＝平均数＝σ2 D．众数＝中位数＝平均数＝μ 解析：利用众数、中位数、平均数的定义同频率分布直方图的关系．
第七章 随机变量及其分布
7．5 正态分布
[课标解读]1.通过误差模型，了解服从正态分布的随机变量.2.通过具体实例、 借助频率分布直方图的几何直观，了解正态分布的特征.3.了解正态分布的均值、方 差及其含义．
[素养目标] 水平一：利用实际问题的直方图，了解正态曲线的特征和正态曲 线所表示的意义．(逻辑推理)
，x∈R，则称随机变

正态分布ppt精品课件

正态分布ppt精品课件
结果解释
根据检验结果，解释两组数据 是否存在显著差异，并结合实
际背景进行讨论。
06
正态分布在生活中的应用举例
质量控制领域应用举例
01
产品规格设定
在制造业中，正态分布用于设定产品规格。通过对产品特性进行统计分
析，可以确定产品特性的均值和标准差，进而设定合理的上下规格限。
02 03
过程能力分析
正态分布也用于评估生产过程的能力。通过计算过程能力指数（如Cp 和Cpk），可以了解生产过程是否稳定，并确定是否需要采取改进措施 。
多元方差分析（MANOVA）与多元回归分析（ Multiple Regression Analysis）：当涉及多个自 变量或多个因变量时，可以使用多元方差分析或 多元回归分析来探究它们之间的关系。
回归分析（Regression Analysis）：用于探究自 变量与因变量之间的线性或非线性关系，通过拟 合回归方程来预测因变量的取值。
概率密度函数性质 f(x)≥0，对于所有x∈R。
02
正态分布在统计学中应用
描述性统计量计算
均值（Mean）：表示数据的“中心 ”或“平均”水平，计算方法是所有 数值之和除以数值个数。
偏度（Skewness）：描述数据分布 形态的偏斜程度，正偏态表示数据向 右偏，负偏态表示数据向左偏。
标准差（Standard Deviation）：衡 量数据分布的离散程度，即数据偏离 均值的程度，计算方法是方差的平方 根。
实例分析：两组数据是否存在显著差异
数据描述
给出两组数据的描述性统计量， 如均值、标准差等。
假设检验步骤
按照上述假设检验步骤，对两组 数据进行假设检验。
结果解释
根据检验结果，判断两组数据是 否存在显著差异，并给出相应的
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

底部建立一个水平坐标
轴 ,其刻度单位为球槽的
宽度 ,用 X 表示落下的小
球 第 1次 与 高 尔 顿 板 底 部
o
图2.44
x
接触时的坐标 ,则 X是一
个随机变量 .X 落在区间 a,b 的概率为
P a
即
Xb
由
正 a,b过 φ态 μ,σ x点 曲 a,d0x和 线点 b,0的
两x轴 条的,垂
及 x轴 所 围 成 的面 平(积 图 面 2.4图 4中 形阴 的影
分 的)面 就 , 积 X 是 落 在a 区 ,b的 间概 率 的 . 近
.
12
一 般 地,如果对于任何实 a 数b,随 机 变 量 X满 足
Pa Xb bφμ,σxdx, a
则 称X的 分 布 为 正态分布 (normadl istribuotin).正
态 分 布 完 全 由 参μ和数σ 确 定,因 此 正 态 分 布 常
标,频可 率 以画出频率分布图直图方 2.42.
0.35 0.30 0.25 0.20 0.15 0.10 0.05
O 1 2 3 4 5 6 7 8 9 10 11 槽的编号
图2.4. 2
10
随 着 重 复 次 数,这 的个 增频 加率 直 方 图 的
会 越 来 越 像 一 条 线图 钟2.4形3曲 .
.
14
在 现 实 生 活,很中多 随 机 变 量 都 服近从似或地 服 从 正 态 分 布.例 如 长 度 测 量 误 ;某差一 地 区 同 年 龄 人身群 的 高 、 体 重 、 肺 活;量 一等 定 条 件 下 生 长 的的小株麦高 、 穗 长 、 单 位 面 积 产;正 量常 等生 产 条 件 下 各品种(如产 零 件 的 尺 寸 、 纤的维纤 度 、 电器容的 电 容 量 、 电 管 的 使 用 寿 命);某 等地 每 年 七 月 份 的气平温均、 平 均 湿 度 、 降 雨 量.一等般 都 服 从 正 态.分 布
.
15
早 在 173年 3,法 国 数 学 家 棣n莫 !的弗 近就 似用 公 式 到 了 正 态.之分后 ,德 布国 数 学 家 高测 斯量 在误 研差 究 时 从 另 一 个 角它 度,并导研出究了了 它,因 的此 ,性 人质 们 也 称 正 态 分分 布布 .为 高 斯
所以 ,正态分布广泛存 然在 现于 象自 、生产和 际之。中正态分布在概率 中和 占统 有计 重要 。地
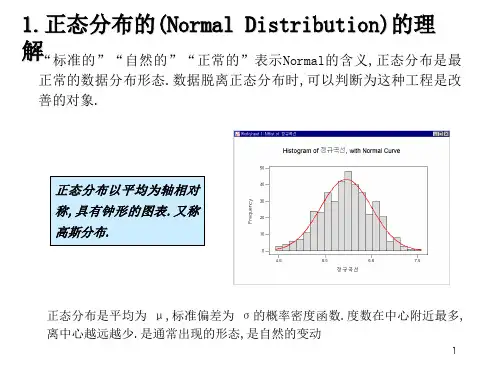
图.在一块木板上钉上若干排相
互平行但相互错开的圆柱 形小
木块,小木块之间留有适当的空
隙作为通道,前面挡有一块玻璃.
让一个小球从高尔顿板 上方的
通道口落下,小球在下落过 程中
图2.41
与层层小木块碰撞,最后掉入高尔顿板下方的某一球槽内.
如果把球槽,就 编可 号以考察到底第是几落号在球槽
中.重复进行高尔顿,随板着试试验验次数,的 掉增 入加
4曲 线x轴 与之 间 的1.面
.
17
信息技术应用
用 计 算 机 研 究 正 态 曲 线随 着μ和σ变 化 而 变 化 的 特 点
.
18
y
μ 1 μ 0 μ 1
σ0.5
.
16
y
思考 观 察 图 2 .4 4 ,结
合 φ μ ,σ x 的
解析式及概 率的性质 , 你 能说 说正态 曲线 的特点 吗?
o
x
图2.44
可以发现 ,正态曲线有如下特: 点
1 曲线 x 轴 位 ,上 与 x 于 轴 方 不 ;
2曲 线 是,它 单关 峰于 的 x直 μ
对;称
3曲线 x在 μ处达到 ; 峰
2.4 正态分布
.1ຫໍສະໝຸດ 温故知新：1．在频率分布直方图中，纵坐标的含义是 频率 _组__距__，用小矩形的_面__积_表示数据落在该组中 的频率，在折线图中，随着分组越来越多，
其越来越接近于一条__光__滑__的__曲__线．
.
2
2．若函数 f(x)＞0，则bf(x)dx 的几何意义 a
是 y＝f(x)的图象与 x＝a，x＝b 及 x 轴所围 成的曲边梯形的面积．
各个球槽内的小数球就越 的来 个越,堆 多积的高度
会越来越 .各高个球 槽的堆积高度反球映掉了入小各
球槽的个数?多少 .
8
N=500, P=0.5 M=10
.
9
为了更好地考察随验着次试数的增,落加在在各 个球槽内的小球分况布,我情们进一步从频率的 角度探究一下小球布的规分律.以球槽的编号为 横坐标 ,以小球落 入各个球槽内的频为率纵值坐
频率 组距
25.235 25.295 25.355
25.415
.
产品 尺寸 （mm)
25.475 25.535
5
6.
样本容量增大时 频率分布直方图
频率 组距
总体密度曲 线
产品 尺寸 (mm)
.
6
7.
总体密度曲 线
产品 尺寸 (mm)
.
7
新知传授：
你见过高尔顿板吗 ? 图2. 4 1
所示的就是一块高尔顿板示意
3．对于X～B(η，p)，则E(X)＝___n，p D(X)＝ ____n_p_(1_－_，p)当n＝1时，是___两_分点布．
.
3
4.
100个产品尺寸的频率分布直方图
频率 组距
25.235 25.295 25.355
25.415
.
产品 尺寸 （mm)
25.475 25.535
4
5.
200个产品尺寸的频率分布直方图
记 作Nμ,σ2.如果随机变X量 服从正态分,则 布记 为X ~ Nμ,σ2 .
参数 μ是反映随机变平 量的 取特 值,征 可 水数 以
用样本均值;σ去 是估 衡计 量随机变动 量大 总体
小的特,征 可数 以用样本标计 准. 差去估
.
13
经验表明 ,一个随机变量如果是众 多的、互 不相干的、不分主 次的偶 然因素作用结果 之和 ,它就服从或近似服从正 态分布 .例如高 尔顿板试 验中 ,小球下落过程中要与众 多小 木板碰撞 , 每次碰撞的结果使得小 球随机地 向左或向右下落 ,因此小球第 1 次与高尔顿板 底部接触时的坐标 X 是众多随机碰 撞的结 果,所以它近似服从正态分 布.
y
O
图2.43
x
这条曲线 (或 就近 是似 )下地 列函数的 : 图象
φμ,σx 1 ex 2 σ μ 22,x , ,
2π σ
其中 μ 和 σ σ 实 0 为 数 .我 参φ 们 μ 数 ,σ x 的 称
图正象 态分布密为 度曲线 .
,简 正态称 曲线 .
11
如果去掉高尔顿板试验
y
中最下边的球槽 ,并沿其