下载文档原格式
matlab使⽤经验模式分解emd对信号进⾏去噪:对于这个例⼦，考虑由具有明显频率变化的正弦波组成的⾮平稳连续信号。
⼿提钻的振动或烟花声是⾮平稳连续信号的例⼦。
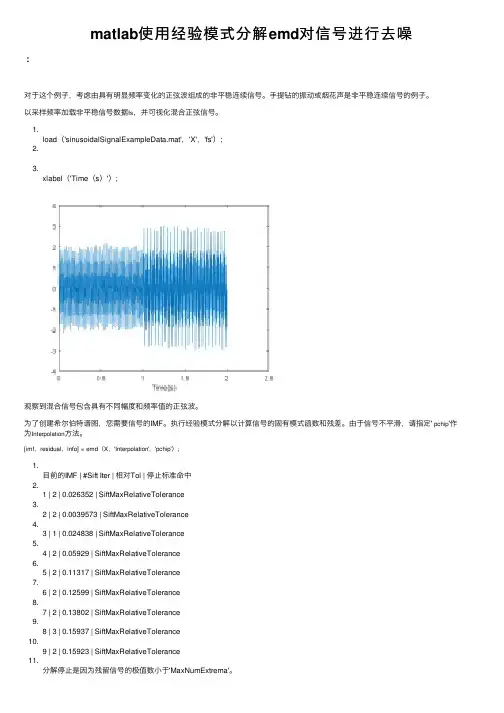
以采样频率加载⾮平稳信号数据fs，并可视化混合正弦信号。
1.load（'sinusoidalSignalExampleData.mat'，'X'，'fs'）;2.3.xlabel（'Time（s）'）;观察到混合信号包含具有不同幅度和频率值的正弦波。
为了创建希尔伯特谱图，您需要信号的IMF。
执⾏经验模式分解以计算信号的固有模式函数和残差。
由于信号不平滑，请指定' pchip'作为Interpolation⽅法。
[imf，residual，info] = emd（X，'Interpolation'，'pchip'）;1.⽬前的IMF | #Sift Iter | 相对Tol | 停⽌标准命中2.1 |2 | 0.026352 | SiftMaxRelativeTolerance3.2 | 2 | 0.0039573 | SiftMaxRelativeTolerance4.3 | 1 | 0.024838 | SiftMaxRelativeTolerance5.4 | 2 | 0.05929 | SiftMaxRelativeTolerance6.5 | 2 | 0.11317 | SiftMaxRelativeTolerance7.6 | 2 | 0.12599 | SiftMaxRelativeTolerance8.7 | 2 | 0.13802 | SiftMaxRelativeTolerance9.8 | 3 | 0.15937 | SiftMaxRelativeTolerance10.9 | 2 | 0.15923 | SiftMaxRelativeTolerance11.分解停⽌是因为残留信号的极值数⼩于'MaxNumExtrema'。
基于经验模式分解的心肺耦合技术在睡眠分析中的应用刘冬冬;张玲;杨晓文;张博;武文芳【摘要】Objective To explore application of the EMD (Empirical Mode Decomposition)-based CPC (Cardio-Pulmonary Coupling) technique in sleep analysis. Methods Through analysis of 30 cases of thoracic ECG signals recorded by PSG (Poly-Somno-Graphy), the instantaneous frequency and instantaneous phase were obtained with deployment of EMD so as to construct a CPC map. Then, CAP (Cyclic Alternating Pattern) was utilized to divide sleep into three stages: CAP Stage, Non-CAP Stage and Wake/REM (Rapid Eyes Movement) Stage. The waving degree of the maximum CPC peak was measured by ZCR (Zero Crossing Rate), which reflected the severity of OSAHS (Obstructive Sleep Apnea-Hypopnea Syndrome). Results The frequency band of OSAHS patients’ map was distributed centralizedly in the low-frequency areas with small waving changes of the maximum peak at each time. Comparisons were made between manual staging and automatic staging, which revealed that EMD-based CPC could differentiate accurately between the different sleep statuses. Significant differences existed between the waving principles of the maximum peak in OSAHS Patient Group and Healthy Volunteer Group. ZCR values were significantly different between Slight/Middle OSAHS Patient Group and Healthy Volunteer Group (P<0.001), and between Slight/Middle OSAHS Patient Group and Severe OSAHS Patient Group (P<0.001). Therefore, the maximum coupling peak value and apnea-hypopnea Index could be used as indexes to identify the different severity of OSAHS patients. Moreover, strong negative correlation was seen between the two indexes (r=-0.77,P=5.8×10-18).Conclusion Combinationof EMD and the CPC technique had proven its easy-to-operate features in data acquisition so as to provide reliable micro-structure and disorder information of sleep, which had huge development potentials in the ifelds of wearable health management and clinically-aided diagnosis.%目的：探讨基于经验模式分解的心肺耦合技术在睡眠分析中的应用。
HHT变换1.1简介传统的信号处理方法，如傅立叶分析是一种纯频域的分析方法。
它用频率不同的各复正弦分量的叠加来拟合原函数，也即用()ωF在有限频域上的信息不足以确定在任意小f。
而()ωF来分辨()ω范围内的函数()ωf，特别是非平稳信号在时间轴上的任何突变，其频谱将散布在整个频率轴上。
而且，非平稳动态信号的统计特性与时间有关，对非平稳信号的处理需要进行时频分析，希望得到时域和频域中非平稳信号的全貌和局域化结果。
在傅立叶变换中，人们若想得到信号的时域信息，就得不到频域信息。
反之亦然。
后来出现的小波（Wavelet）变换通过一种可伸缩和平移的小波对信号变换，从而达到时频局域化分析的目的。
但这种变换实际上没有完全摆脱傅立叶变换的局限，它是一种窗口可调的傅立叶变换，其窗内的信号必须是平稳的。
另外，小波变换是非适应性的，小波基一旦选定，在整个信号分析过程中就只能使用这一个小波基了。
HHT（Hilbert-Huang Transform）技术是(1998年由NASA的Norden E Huang 等提出的新的信号处理方法。
该方法适用于非线性非平稳的信号分析，被认为是近年来对以傅立叶变换为基础的线性和稳态谱分析的一个重大突破。
目前HHT技术已用于地球物理学和生物医学等领域的研究，并取得了较好的结果。
存在的问题尽管HHT技术在处理非线性、非稳态信号方面有很大的优势，但是这个方法本身还是有许多的问题有待进一步研究。
正如Huang 在文章中指出的那样，对于这种新的信号处理方法，其基的完备性还需要严密的证明。
另外，在做Hilbert变换时出现的边界效应也需要更好的方法来解决。
但是，HHT技术中最严重，也是现今研究的最多的是EMD 分解中的包络过程。
从对EMD分解方法的介绍可以看出，包络线的构造影响着整个分解的结果，也决定了后面的Hilbert变换。
Huang 采用的三次样条插值来拟和包络线。
在实际应用中，发现这样做会产生严重的边界效应，污染了原始数据。
经验模式分解（Empirical Mode Decomposition, EMD）是一种用于处理非线性、非平稳信号的适应性数据分析方法。
它可以将一个复杂的信号分解为一系列固有模态函数（Intrinsic Mode Functions, IMFs）。
在C语言中实现EMD算法需要一些数学和信号处理的基础知识。
以下是一个简单的EMD算法的C语言实现步骤：定义信号和分解的IMFs数量。
初始化残差和IMFs数组。
对信号进行经验模式分解，得到IMFs数组。
将IMFs数组中的元素相加得到残差。
将残差与原始信号进行比较，如果残差小于某个阈值，则停止分解；否则返回步骤3继续分解。
咨询QQ：3025393450有问题百度搜索“”就可以了欢迎登陆官网：/datablogmatlab使用经验模式分解emd 对信号进行去噪数据分析报告来源：大数据部落| 有问题百度一下“”就可以了对于这个例子，考虑由具有明显频率变化的正弦波组成的非平稳连续信号。
手提钻的振动或烟花声是非平稳连续信号的例子。
以采样频率加载非平稳信号数据fs，并可视化混合正弦信号。
load（'sinusoidalSignalExampleData.mat'，'X'，'fs'）;xlabel（'Time（s）'）;咨询QQ：3025393450有问题百度搜索“”就可以了欢迎登陆官网：/datablog观察到混合信号包含具有不同幅度和频率值的正弦波。
为了创建希尔伯特谱图，您需要信号的IMF。
执行经验模式分解以计算信号的固有模式函数和残差。
由于信号不平滑，请指定' pchip'作为Interpolation方法。
[imf，residual，info] = emd（X，'Interpolation'，'pchip'）;目前的IMF | #Sift Iter | 相对Tol | 停止标准命中1 |2 | 0.026352 | SiftMaxRelativeTolerance2 | 2 | 0.0039573 | SiftMaxRelativeTolerance3 | 1 | 0.024838 | SiftMaxRelativeTolerance4 | 2 | 0.05929 | SiftMaxRelativeTolerance5 | 2 | 0.11317 | SiftMaxRelativeTolerance6 | 2 | 0.12599 | SiftMaxRelativeTolerance7 | 2 | 0.13802 | SiftMaxRelativeTolerance咨询QQ：3025393450有问题百度搜索“”就可以了欢迎登陆官网：/datablog8 | 3 | 0.15937 | SiftMaxRelativeTolerance9 | 2 | 0.15923 | SiftMaxRelativeTolerance分解停止是因为残留信号的极值数小于'MaxNumExtrema'。
经验模式分解摘要近些年来,随着计算机技术的高速发展与信号处理技术的不断提高,人们对图像的分析结构的要求也越来越高。
目前图像处理已经发展出很多分支,包括图像分割、边缘检测、纹理分析、图像压缩等。
经验模式分解(EMD)是希尔伯特-黄变换(Hilbert-HuangTransform)中的一部分,它是一种新的信号处理方法,并且在非线性、非平稳信号处理中取得了重大进步,表现出了强大的优势与独特的分析特点。
该方法主要是将复杂的非平稳信号分解成若干不同尺度的单分量平稳信号与一个趋势残余项,所以具有自适应性、平稳化、局部性等优点。
鉴于EMD方法在各领域的成功应用以及进一步的发展,国内外很多学者开始将其扩展到了二维信号分析领域中,并且也取得的一定的进展。
但是由于二维信号不同于一种信号,限于信号的复杂性和二维数据的一些处理方法的有限性,二维经验模式分解(BEMD)在信号分析和处理精度上还存在一些问题,这也是本文要研究和改善的重点。
关键词：图像处理；信号分解；BEMDIn recent years, with the rapid development of computer technology and the continuous improvement of signal processing technology, the demand for the analysis structure of the image is becoming more and more high. At present, many branches have been developed in image processing, including image segmentation, edge detection, texture analysis, image compression and so on. Empirical mode decomposition (EMD) is a part of Hilbert Huang transform (Hilbert-HuangTransform). It is a new signal processing method, and has made significant progress in nonlinear and non-stationary signal processing, showing strong advantages and unique analysis points. This method mainly decomposes the complex non-stationary signals into several single scale stationary signals with different scales and a trend residual term, so it has the advantages of adaptability, stationarity and locality. In view of the successful application and further development of EMD method in many fields, many scholars at home and abroad have expanded it to the two-dimensional signal analysis field, and have made some progress. However, because two dimensional signal is different from one signal, it is limited to the complexity of signal and the processing methods of two-dimensional data. Two-dimensional empirical mode decomposition (BEMD) still has some problems in the accuracy of signal analysis and processing, which is also the important point of research and improvement in this paper.Key words: image processing; signal decomposition; BEMD摘要 (1)第一章概况 (4)2.EMD方法原理 (5)2.1 本征模函数 (5)2.2 .EMD分解过程 (5)2.3.分解举例： (6)3. BEMD分解原理 (8)3.1 图像极值点的选取： (8)3.2 Delaunay 三角剖分 (9)3.3 基于三角网络的曲面插值 (11)3.4 分解方法 (11)3.5 BEMD 分解停止准则 (12)4 二维经验模态分解在图像处理中的应用.................................... 错误!未定义书签。
4.1图像分解实例............................................................... 错误!未定义书签。
4.2图像降噪 ..................................................................... 错误!未定义书签。
5总结...................................................................................... 错误!未定义书签。
参考文献.................................................................................. 错误!未定义书签。
第一章概况随着计算机技术的不断发展和其应用领域的不断扩展，数字图像处理技术得到了迅猛的发展，涉及信息科学、计算机科学、数学、物理学以及生物学等学科，因此数理及相关的边缘学科对图像处理科学的发展有越来越大的影响。
近年来，数字图像处理技术日趋成熟，它广泛应用于空间探测、遥感、生物医学、人工智能以及工业检测等许多领域，并促使这些学科产生了新的发展。
数字图像处理就是利用计算机对图像进行处理，其任务是将原图像的灰度分布作某种变换，使图像中的某部分信息更加突出，以使其适应于某种特殊的需求。
目前数字图像处理已经发展出很多分支，包括图像分割、边缘检测、纹理分析、机器视觉等领域。
多分辨率多尺度是人类视觉高效、准确工作的重要特征之一。
自然产生的图像大多包含大量不同尺度的信息，这些信息在一幅图像中同时出现。
而对图像的应用研究往往仅限于某一尺度或某些尺度上的现象，或者只需要某些尺度的信息；其他尺度的信息往往会对处理结果有不良影响，或者增大了处理的难度和复杂性。
所以把图像信息按尺度进行分离非常必要。
多尺度图像分解可以消除其他无用尺度信息对处理结果的影响，也简化了处理的难度和复杂性；也是图像目标识别和边缘检测等处理过程的预处理方法之一。
图像可以看作二维的随机信号，因此也可以通过对一维随机信号处理方法的二维扩展实现。
经典的信号处理方法是傅立叶谱分析法，其必须对信号进行全局分析，不具备局部性，只适合线形和平稳信号分析。
为了分析非平稳与非线性信号，人们发展了信号的时频分析法，如短时傅立叶变换、Wigner-Ville 分布以及小波变换等。
由于所有的这些时频分析方法都是以 Fourier 变换为最终理论依据，故有一定难以克服的局限性，难以在时频分析的方法中取得突破。
为了克服这些弊端，1998 年, Huang[1]等人提出了一种具有自适应时频分辨能力的信号分析方法——经验模式分解（EMD，Empirical Mode Decomposition）。
鉴于经验模式分解在一维信号处理方面已经获得巨大的成功，将其推广到二维情况，将图像按尺度从小到大进行分离，小尺度信息包含了图像的细节信息，剩余的大尺度信息表达了图像的基本趋势和结构，将会给图像处理领域提供一种新的有效的数据处理手段。
2.EMD方法原理大多数的工程实际信号都是由多频分量组成的,这种模式下的信号性质很复杂不容易分析。
而单分量的信号在任一时间只有一个频率或一个频率窄带的信号,对人们来说分析起来即直观又明了,同时很容易进行进一步的深入处理。
所以将多分量信号分解成若干个单分量的信号形式就是信号处理领域需解决的重点EMD的分解过程就是将复杂信号单分量化,也就是说,对原始数据序列通过EMD分解成若干个本征模函数(IMF)和一个残余分量。
2.1 本征模函数在物理上,一个函数的瞬时频率有意义,那么这个函数序列必须是对称的、局部均值为零、具有相同的过零点和极值点数目。
在这样的条件下,N.E.Huang等人提出了本征模函数(Intrinsic Mode Function,简称IMF)的概念[2]。
假设任何信号都是由若干本征模函数组成,一个信号都可以包含若干个本征模函数,如果本征模函数之间相互重叠,便形成复合信号。
EMD分解的目的就是为了获取本征模函数。
本征模函数形成条件有以下两个:1.函数在整个时间范围内,局部极值点和过零点的数目必须相等或最多相差一个;2.在任意时刻点,局部最大值的包络(上包络线)和局部最小值的包络(下包络线)平均值必须为零。
2.2 .EMD分解过程EMD分解方法进行是需要一定条件(1)整个信号中至少存在一个极大值点和一个极小值点。
(2)两个相邻的极大值点或者是两个相邻的极小值点间的时间间隔作为EMD分解的尺度特征。
(3)如果信号中不存在任何极值点,但是有拐点,可以通过一阶或者多阶微分求得极值点,最后再对分量求积分获得结果。
如果信号满足以上3个条件,则这个信号就可以进行EMD的分解。
具体的实现过程是：设原数据序列为f(t)，首先对f(t)选取局部极值(包括极小值和极大值)，所有的极大值的插值曲线连接作为包络的上界，所有的极小值的插值曲线连接作为包络的下界，包络的上下界将覆盖所有的数据，得到极大值包络数据E max(t)和极小值包络数据E min(t)。
由这两条包络得到一个均值函数e1,即：e1=E max(t)+E min(t)2e1与原始信号 f(t)的差量定义为分量d1，即d1=f(t)−e1考察d1是否为 IMF 函数。
