新疆英吉沙县实验中学2015届九年级上期中考试数学试卷

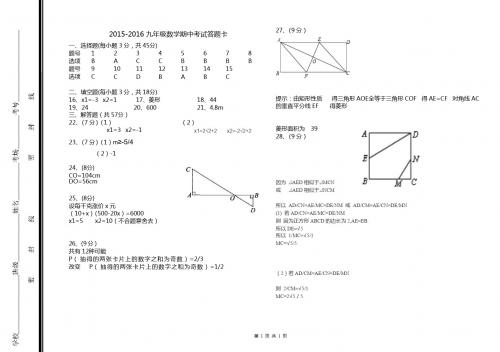
2015—2016学年度第一学期期中调考九年级数学参考答案一、选择题（共10小题，每小题3分，共30分）C B CD A B C D B A二、填空题（共6小题，每小题3分，共18分）11、-3； 12、1000； 13、k>34且k ≠1； 14、80°或120°； 15、2(+2)2y x =+ ； 16、2441三、解答题（共8小题，共72分） 17题（本题8分）解：∵1,2,1a b c ==-=-，………………3分∴2480b ac ∆=-=>………………5分∴22=22x ±±=……………………7分1x =2x =………8分18题（本题8分）（1）（4,4）（2）（-2，-2），（3，112） 19题（本题8分）解：设正中央的矩形长为2xm ，则其宽为xm ，-------1分 依题意得2x ×x=20×10×(1-1625)，-------4分 解得x 1=6 ,x 2=-6(不符合题意，舍去) -------6分∴正中央的矩形宽为6m ∴左、右边衬的宽为10-62=2m -------8分 20题（本题8分）⑴由已知条件可得:其对称轴为：x=1, ∵AB=4∴A(-1，0) ,B(3，0) ∵ OC=OB, ∴C （0，3) ------2分代之得：a=-1 c=3 ------3分∴此二次函数的解析式为y=223x x -++----------4分（2）（1， 4）；（3，0）和（-1,0）------6分（3）（4，-5）------------------8分21、（本题8分）（1）画图………………2′ （0，-3）…………………3′（2）画图………5′（-3，-2）……………6′ （3）53………………8′ 22（本题10分）解：（1）如图所示：△ABE ′即为所求；………2′（2）作∠EAE ′的平分线交BC 于点F ，则△CFE 的周长等于正方形ABCD 的周长的一半， 在△AEF 和△AE ′F 中：∵AE=AE′ ∠EAF=∠E′AF AF=AF ，∴△AEF ≌△AE ′F （SAS ），∴EF=E ′F=BF+DE ，∴EF+EC+FC=BC+CD ．………6′（3）作BM ⊥BD,BM=PD,连AM,易证△ADP ≌△ABM （SAS ）∴AM=AP ∠BAM =∠DAP ∵∠PAQ=45°∴∠DAP+∠BAQ=∠BAM+∠BAQ =45°即∠MAQ=45°易证△MAQ ≌△PAQ （SAS ）∴MQ=PQ∴MQ 2= BM 2 +BQ 2∴PQ 2= PD 2 +BQ 2………10′23、（本题10分）（1）=y ()()22501202215030452++-=--+x x x x （1≤x ＜40且为整数）=y ()()825011021503085+-=--x x （40≤x ≤70且为整数）……… 4分（2）当1≤x ＜40 x=30 y max =4050元当40≤x ≤70时，x=40 y max =3850元∴ 第30天时，y max =4050元………8分（3）共有36天………10分24. （本题12分）解：（1）21)4y a x =-+（可得其顶点D 坐标为（1，4）,C(0，a+4) ∴CE=1, 由勾股定理得DE=1DE=DM-EM=4-(a+4)=1 ∴a=-1∴抛物线的解析式; 223y x x =-++………3分 （2）设P （x ，-x+3），则M （x ，-x 2+2x+3），∴PM=（-x 2+2x+3）-（-x+3）=-x 2+3x ，M Q P E D C A∴S △BCM =S △PMC +S △PMB =12PM •NO+12PM •NB=12PM （NO+BN ）=12PM •BO =32PM ， ∴S △BCM =32（-x 2+3x ）=-32（x-32）2+278， ∴当x=32时，△BCM 的面积最大， ∴N （32，0）；………7分解法2：因为BC 长为定值，所以BC 上高要最大，将BC 平移至与抛物线相切时高最大 BC 的解析式y=-x+3，设ME 的解析式y=-x+b代入223y x x =-++得2330x x b -+-=∴24940b ac ∆=-=-=（b-3），b=214 当b=214时，代入2330x x b -+-=得唯一交点横坐标为32 ∴N （32，0） （3）作抛物线的对称轴EP ， CN ⊥EP 于N, HM ⊥EP 于M,由（1）中得△DNC 为等腰直角三角形，∴△DHE 也为等腰直角三角形∴EM=DM=HM=12m ∴H(1+12m,4+ 12m ) ∵点H 在抛物线21)4+y x m =--+（上 ∴4+12m 21+1)4+2m m =--+（1 ∴21142m m = ∴m=2或m=0(舍去)∴m 的值为m=2. ………12分。

2014-2015学年九年级英语上册期中综合检测☆（总分为100分，时间：120分钟）第Ⅰ卷(共55分)Ⅰ. 单项选择(15分)1. I study English ______ making flashcards.A. ofB. byC. inD. On2. Great changes in our hometown in the last ten years.A. have happenedB. have been taken placeC. have been happenedD. have taken place3. —Do you know the meaning of these new words?—Sorry, I don’t. Let’s in the dictionary.A. look after themB. look up themC. look them afterD. look them up4. It’s too. I don’t think you can g et to school on time, you take a taxi.A. late; unlessB. late; ifC. early; unlessD. early; if5. The thief often things from this factory.A. stealsB. treatsC. punishesD. spreads6. _____ you _____ to go to the park when they were children?A. Did, useB. Did, usedC. Do, usedD. Do, use7. The Dragon Boat Festival is a festival China.A. tradition; ofB. traditional; ofC. tradition; atD. traditional; at8. I Linda will get good grades because she has worked hard for a long time.A. ask thatB. ask ifC. believe thatD. believe whether9. ______ fine weather today! Why not go out for a walk?A. What aB. WhatC. HowD. How a10. Can you tell me to the post office?A. where getB. where to getC. how getD. how to get11. Please tell me to improve my English.A. what I can doB. what can I doC. how I can doD. how can I do12. Mr. Wang used to dinner in the restaurant, but now he is used to every meal with his family at home.A. have; eatB. have; eatingC. having; eatD. having; eating13. Mary is very shy. She goes out and she has few friends.A. oftenB. alwaysC. seldomD. usually14. A lot of water in Shanghai every year. It’s a big problem.A. wastesB. is wastedC. have been wastedD. is wasting15. No matter, you must follow the school rules.A. where are youB. what do you doC. who are youD. who you areⅡ. 完形填空(10分)How do the students in our class study English? We do a survey and this is 1we learn. Most students say they learn English by2it. Some students have more specific3. Tom says that he learns English by working4 a group. He has some good friends. They study together every day. They can learn 5each other and talk in English. Tom says he can learn a lot that way. Linda learns English by listening to6. She often listens to English in the morning, sometimes in the evening. She reads English well and gets the pronunciation right. Lin Tao says that7the English club is the best way to learn English. In the club, he can get lots of conversation practice and they have fun8English. As for learning grammar, some students say they don’t learn grammar, 9 some say it’s necessary10grammar. If you learn grammar well, you can make the perfect sentences and get good grades.()1. A. when B. what C. where D. how()2. A. use B. to use C. using D. used()3. A. suggest B. suggestion C. advice D. advices()4. A. with B. without C. to D. at()5. A. to B. from C. with D. in()6. A. TV B. music C. tape D. tapes()7. A. join B. joining C. take part in D. taking part in()8. A. to learn B. learning C. learn D. learned()9. A. but B. and C. or D. because()10. A. to learn B. learning C. learn D. learnedⅢ. 阅读理解(30分)ADo you want to do well in exams? Sometimes your knowledge is not enough, you also need good strategies. Here are some for you:Before you answer the questions, if you feel a little nervous, take a few deep breaths to help you relax.Always read the question carefully and make sure that you understand it. Read it a few times if possible.Find out how much each question is worth or how many points you need.If it asks to give one answer, only write one.If there is a difficult question, don’t worry. Go on to the next question and come back to it if you have time later.Try not to leave questions unanswered when you finish the test. Sometimes a guess may get your points.When you finish, go back and check your answers. You will need to check your writing or spelling mistakes.1. From the passage, we know we can to help ourselves relax if we feel a little nervous.A. tell ourselves not to be nervousB. ask the teacher for helpC. go out for a walkD. take a few deep breaths2. To make sure we understand the question, we had better.A. read it fastB. read it till we finish itC. read it a few times if possibleD. read it slowly3. When we finish answering all the questions, we need to.A. hand in at onceB. check spelling mistakesC. worry about our pointsD. check with classmates4. The underlined word “strategies” in the passage means.A. 策略B. 思维C. 途径D. 智慧5. Which of the following is NOT true according to the passage?A. Find out how many points we need or how much each question is worth.B. Try not to leave questions unanswered when we finish the test.C. If it asks to give one answer, we’d better write more.D. Sometimes we should guess the answers to get points.BThere is no quick and easy way to learn English. But there is a simple and good way. Speak English as much as you can. Speak only English with your teacher and your classmates. Speak English while you are either in class or after class. Listen to English as much as you can in class. Listen to your classmates when they speak English after class. Listen to the radio and watch some English programs on TV.Speak, listen and read English as much as you can. Don’t just read the textbooks that you use in class. Go to the library or to a bookshop and read easier English books.Speak, listen, read and write English as much as you can. Buy a small notebook and write on it every day. Write about the things that you do during the day. Write about what you learn in class.These things are not hard, but they are the work you should do. If you do them, with the help of your teacher, you’ll learn English well.根据短文内容, 判断下列句子正误(T/F)。

一、选择题（本大题共10小题，每小题4分，共40分）每题的选项中只有一项符合题目要求，请在答题卡的相应位置填涂正确选项．1．（4分）﹣2的倒数是（ ）A ．﹣2B ．12-C ．12D ．2 2．（4分）如图，直线a ∥b ，∠1=108°，则∠2的度数是（ ）A ．72°B ．82°C ．92°D ．108°3．（4分）下列计算正确的是（ ）A ．32a a a -=B ．326a a a ⋅=C ．32a a a ÷=D ．325()a a = 4．（4分）在下列的四个几何体中，其主视图与俯视图相同的是（ ）5．（4分）在某次射击训练中，甲、乙、丙、丁4人各射击10次，平均成绩相同，方差分别是S 甲2=，S 乙2=，S 丙2=，S 丁2=，这4人中成绩发挥最稳定的是（ ）A ．甲B ．乙C ．丙D ．丁6．（4分）圆锥的侧面展开图是一个弧长为12π的扇形，则这个圆锥底面积的半径是（ ）A ．24B ．12C ．6D ．37．（4分）如图，△ABC 的面积等于6，边AC =3，现将△ABC 沿AB 所在直线翻折，使点C 落在直线AD 上的C ′处，点P 在直线AD 上，则线段BP 的长不可能是（ ）A ．3B ．4C ．5D ．68．（4分）九年级学生去距学校10km 的博物馆参观，一部分学生骑自行车先走，过了20min 后，其余学生乘汽车出发，结果他们同时到达．已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度．设骑车学生的速度为xkm /h ，则所列方程正确的是（ ）A ．1010123x x =-B ．1010202x x =-C ．1010123x x =+D ．1010202x x=+ 9．（4分）如图，将斜边长为4的直角三角板放在直角坐标系xOy 中，两条直角边分别与坐标轴重合，P 为斜边的中点．现将此三角板绕点O 顺时针旋转120°后点P 的对应点的坐标是（ ）A ．（3，1）B ．（1，3-）C ．（23，﹣2）D ．（2，23-）10．（4分）如图，在直角坐标系xOy 中，点A ，B 分别在x 轴和y 轴，34OA OB =．∠AOB 的角平分线与OA 的垂直平分线交于点C ，与AB 交于点D ，反比例函数k y x =的图象过点C ．当以CD 为边的正方形的面积为27时，k 的值是（ ）A ．2B ．3C ．5D ．7二、填空题（本大题共5小题，每小题4分，共20分）把答案直接填在答题卡的相应位置处．11．（4分）不等式组2213x x -<⎧⎨+<⎩的解集为 ． 12．（4分）等腰三角形的一个外角是60°，则它的顶角的度数是 ． 13．（4分）掷一枚质地均匀的正方体骰子（六个面上分别刻有1到6的点数），向上一面出现的点数大于2且小于5的概率为 ．14．（4分）若菱形的周长为8，相邻两内角之比为3：1，则菱形的高是 ．15．（4分）如图，抛物线2y ax bx c =++的对称轴是1x =-．且过点（12，0），有下列结论：①abc ＞0；②a ﹣2b +4c =0；③25a ﹣10b +4c =0；④3b +2c ＞0；⑤a ﹣b ≥m （am ﹣b ）；其中所有正确的结论是 ．（填写正确结论的序号）三、解答题（本大题包括Ⅰ-Ⅴ题，共2小题，共90分）解答时应在答题卡的相应位置处写出文字说明、证明过程或演算过程．Ⅰ．（本题满分16分，第16，17题每题8分）16．（8分）计算：23(2)2127-+--．17．（8分）先化简，再求值：22214()244a a a a a a a a+--+÷--+，其中a 满足2410a a --=． 18．（10分）某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映：每降价1元，每星期可多卖出20件．已知商品的进价为每件40元，在顾客得实惠的前提下，商家还想获得6080元的利润，应将销售单价定为多少元？19．（10分）如图，▱ABCD 中，点E ，F 在直线AC 上（点E 在F 左侧），BE ∥DF ．（1）求证：四边形BEDF 是平行四边形；（2）若AB ⊥AC ，AB =4，BC =13BEDF 为矩形时，求线段AE 的长．20．（10分）如图，小俊在A 处利用高为米的测角仪AB 测得楼EF 顶部E 的仰角为30°，然后前进12米到达C 处，又测得楼顶E 的仰角为60°，求楼EF 的高度．（结果精确到米）21．（12分）将九年级部分男生掷实心球的成绩进行整理，分成5个小组（x 表示成绩，单位：米）．A 组：≤x ＜；B 组：≤x ＜；C 组：≤x ＜；D 组：≤x ＜；E 组：≤x ＜，并绘制出扇形统计图和频数分布直方图（不完整）．规定x ≥为合格，x ≥为优秀．（1）这部分男生有多少人？其中成绩合格的有多少人？（2）这部分男生成绩的中位数落在哪一组？扇形统计图中D 组对应的圆心角是多少度？（3）要从成绩优秀的学生中，随机选出2人介绍经验，已知甲、乙两位同学的成绩均为优秀，求他俩至少有1人被选中的概率．22．（10分）如图，AB 是⊙O 的直径，CD 与⊙O 相切于点C ，与AB 的延长线交于点D ，DE ⊥AD 且与AC 的延长线交于点E ．（1）求证：DC =DE ；（2）若tan ∠CAB =12，AB =3，求BD 的长． 23．（10分）一辆货车和一辆小轿车同时从甲地出发，货车匀速行驶至乙地，小轿车中途停车休整后提速行驶至乙地．货车的路程1y （km ），小轿车的路程2y （km ）与时间x （h ）的对应关系如图所示．（1）甲乙两地相距多远？小轿车中途停留了多长时间？ （2）①写出1y 与x 的函数关系式；②当x ≥5时，求2y 与x 的函数解析式；（3）货车出发多长时间与小轿车首次相遇？相遇时与甲地的距离是多少？24．（12分）抛物线213242y x x =-+与x 轴交于A ，B 两点（OA ＜OB ），与y 轴交于点C ． （1）求点A ，B ，C 的坐标；（2）点P 从点O 出发，以每秒2个单位长度的速度向点B 运动，同时点E 也从点O 出发，以每秒1个单位长度的速度向点C 运动，设点P 的运动时间为t 秒（0＜t ＜2）．①过点E 作x 轴的平行线，与BC 相交于点D （如图所示），当t 为何值时，11OP ED+的值最小，求出这个最小值并写出此时点E ，P 的坐标；②在满足①的条件下，抛物线的对称轴上是否存在点F ，使△EFP 为直角三角形？若存在，请直接写出点F 的坐标；若不存在，请说明理由． 一、选择题（本大题共10小题，每小题4分，共40分）每题的选项中只有一项符合题目要求，请在答题卡的相应位置填涂正确选项．1．（4分）﹣2的倒数是（ ）A ．﹣2B ．12-C ．12D ．2 【答案】B ．考点：倒数．2．（4分）如图，直线a ∥b ，∠1=108°，则∠2的度数是（ ）A ．72°B ．82°C ．92°D ．108°【答案】A ．考点：平行线的性质．3．（4分）下列计算正确的是（ ）A ．32a a a -=B ．326a a a ⋅=C ．32a a a ÷=D ．325()a a = 【答案】C ．【解析】考点：1．同底数幂的除法；2．合并同类项；3．同底数幂的乘法；4．幂的乘方与积的乘方．4．（4分）在下列的四个几何体中，其主视图与俯视图相同的是（ ）【答案】D ．考点：简单几何体的三视图．5．（4分）在某次射击训练中，甲、乙、丙、丁4人各射击10次，平均成绩相同，方差分别是S 甲2=，S 乙2=，S 丙2=，S 丁2=，这4人中成绩发挥最稳定的是（ ）A ．甲B ．乙C ．丙D ．丁【答案】B ．考点：方差．6．（4分）圆锥的侧面展开图是一个弧长为12π的扇形，则这个圆锥底面积的半径是（ ）A ．24B ．12C ．6D ．3【答案】C ．考点：圆锥的计算．7．（4分）如图，△ABC 的面积等于6，边AC =3，现将△ABC 沿AB 所在直线翻折，使点C 落在直线AD 上的C ′处，点P 在直线AD 上，则线段BP 的长不可能是（ ）A ．3B ．4C ．5D ．6【答案】A ．考点：翻折变换（折叠问题）．8．（4分）九年级学生去距学校10km 的博物馆参观，一部分学生骑自行车先走，过了20min 后，其余学生乘汽车出发，结果他们同时到达．已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度．设骑车学生的速度为xkm /h ，则所列方程正确的是（ ）A ．1010123x x =-B ．1010202x x =-C ．1010123x x =+D ．1010202x x=+ 【答案】C ．考点：由实际问题抽象出分式方程．9．（4分）如图，将斜边长为4的直角三角板放在直角坐标系xOy 中，两条直角边分别与坐标轴重合，P 为斜边的中点．现将此三角板绕点O 顺时针旋转120°后点P 的对应点的坐标是（ ）A ．（3，1）B ．（1，3-）C ．（23，﹣2）D ．（2，23-）【答案】B ．考点：坐标与图形变化-旋转．10．（4分）如图，在直角坐标系xOy 中，点A ，B 分别在x 轴和y 轴，34OA OB =．∠AOB 的角平分线与OA 的垂直平分线交于点C ，与AB 交于点D ，反比例函数k y x =的图象过点C ．当以CD 为边的正方形的面积为27时，k 的值是（ ） A ．2 B ．3 C ．5 D ．7【答案】D ．考点：1．反比例函数综合题；2．综合题；3．压轴题．二、填空题（本大题共5小题，每小题4分，共20分）把答案直接填在答题卡的相应位置处．11．（4分）不等式组2213xx-<⎧⎨+<⎩的解集为．【答案】﹣2＜x＜1．考点：解一元一次不等式组．12．（4分）等腰三角形的一个外角是60°，则它的顶角的度数是．【答案】120°．考点：等腰三角形的性质．13．（4分）掷一枚质地均匀的正方体骰子（六个面上分别刻有1到6的点数），向上一面出现的点数大于2且小于5的概率为 ．【答案】13． 考点：概率公式．14．（4分）若菱形的周长为8，相邻两内角之比为3：1，则菱形的高是 ．【答案】2．考点：菱形的性质．15．（4分）如图，抛物线2y ax bx c =++的对称轴是1x =-．且过点（12，0），有下列结论：①abc ＞0；②a ﹣2b +4c =0；③25a ﹣10b +4c =0；④3b +2c ＞0；⑤a ﹣b ≥m （am ﹣b ）；其中所有正确的结论是 ．（填写正确结论的序号）【答案】①③⑤．考点：二次函数图象与系数的关系．三、解答题（本大题包括Ⅰ-Ⅴ题，共2小题，共90分）解答时应在答题卡的相应位置处写出文字说明、证明过程或演算过程．Ⅰ．（本题满分16分，第16，17题每题8分）16．（8分）计算：23(2)2127- 2．考点：实数的运算．17．（8分）先化简，再求值：22214()244a a a a a a a a+--+÷--+，其中a 满足2410a a --=． 【答案】21(2)a -，15． 考点：分式的化简求值．18．（10分）某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映：每降价1元，每星期可多卖出20件．已知商品的进价为每件40元，在顾客得实惠的前提下，商家还想获得6080元的利润，应将销售单价定为多少元？【答案】56．考点：1．一元二次方程的应用；2．销售问题．19．（10分）如图，▱ABCD中，点E，F在直线AC上（点E在F左侧），BE∥DF．（1）求证：四边形BEDF是平行四边形；（2）若AB⊥AC，AB=4，BC=213，当四边形BEDF为矩形时，求线段AE的长．【答案】（1）证明见试题解析；（2）2．考点：1．平行四边形的判定与性质；2．全等三角形的判定与性质；3．矩形的性质．20．（10分）如图，小俊在A处利用高为米的测角仪AB测得楼EF顶部E的仰角为30°，然后前进12米到达C处，又测得楼顶E的仰角为60°，求楼EF的高度．（结果精确到米）【答案】．EF=EG+GF=63+≈．答：楼EF的高度约为米．考点：解直角三角形的应用-仰角俯角问题．21．（12分）将九年级部分男生掷实心球的成绩进行整理，分成5个小组（x表示成绩，单位：米）．A组：≤x＜；B组：≤x＜；C组：≤x＜；D组：≤x＜；E组：≤x＜，并绘制出扇形统计图和频数分布直方图（不完整）．规定x≥为合格，x≥为优秀．（1）这部分男生有多少人？其中成绩合格的有多少人？（2）这部分男生成绩的中位数落在哪一组？扇形统计图中D组对应的圆心角是多少度？（3）要从成绩优秀的学生中，随机选出2人介绍经验，已知甲、乙两位同学的成绩均为优秀，求他俩至少有1人被选中的概率．【答案】（1）50，45；（2）C组，108°；（3）7 10．考点：1．列表法与树状图法；2．频数（率）分布直方图；3．扇形统计图；4．中位数．22．（10分）如图，AB 是⊙O 的直径，CD 与⊙O 相切于点C ，与AB 的延长线交于点D ，DE ⊥AD 且与AC 的延长线交于点E ．（1）求证：DC =DE ；（2）若tan ∠CAB =12，AB =3，求BD 的长． 【答案】（1）证明见试题解析；（2）1．考点：1．切线的性质；2．勾股定理；3．解直角三角形；4．综合题．23．（10分）一辆货车和一辆小轿车同时从甲地出发，货车匀速行驶至乙地，小轿车中途停车休整后提速行驶至乙地．货车的路程1y （km ），小轿车的路程2y （km ）与时间x （h ）的对应关系如图所示．（1）甲乙两地相距多远？小轿车中途停留了多长时间？（2）①写出1y 与x 的函数关系式；②当x ≥5时，求2y 与x 的函数解析式；（3）货车出发多长时间与小轿车首次相遇？相遇时与甲地的距离是多少？【答案】（1）420，2；（2）①160y x =（0≤x ≤7）；②2100230y x =-（x ≥5）；（3）货车出发小时后首次与小轿车相遇，距离甲地270km ．考点：1．一次函数的应用；2．综合题．24．（12分）抛物线213242y x x =-+与x 轴交于A ，B 两点（OA ＜OB ），与y 轴交于点C ． （1）求点A ，B ，C 的坐标；（2）点P 从点O 出发，以每秒2个单位长度的速度向点B 运动，同时点E 也从点O 出发，以每秒1个单位长度的速度向点C 运动，设点P 的运动时间为t 秒（0＜t ＜2）．①过点E 作x 轴的平行线，与BC 相交于点D （如图所示），当t 为何值时，11OP ED +的值最小，求出这个最小值并写出此时点E ，P 的坐标；②在满足①的条件下，抛物线的对称轴上是否存在点F ，使△EFP 为直角三角形？若存在，请直接写出点F 的坐标；若不存在，请说明理由．【答案】(1) A （2，0），B （4，0），C （0，2）；(2)①t =1时，11OP ED+有最小值1，此时OP =2，OE =1，∴E （0，1），P （2，0）；②F （3，2），（3，7）．【解析】试题分析：（1）在抛物线的解析式中，令y =0，令x =0，解方程即可得到结果；考点：1．二次函数综合题；2．动点型；3．最值问题；4．二次函数的最值；5．分类讨论；6．压轴题．。

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分（每空xx 分，共xx分）试题1:已知x=2是一元二次方程x2﹣mx+2=0的一个解，则m的值是（）A．﹣3 B．3 C．0 D．0或3试题2:如图，晚上小亮在路灯下散步，在小亮由A处走到B处这一过程中，他在地上的影子（）A．逐渐变短 B．逐渐变长 C．先变短后变长 D．先变长后变短试题3:如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM+CN=9，则线段MN 的长为（）A．6 B．7 C．8 D．9试题4:已知实数x，y满足，则以x，y的值为两边长的等腰三角形的周长是（）A．20或16 B．20C．16 D．以上答案均不对试题5:用配方法解关于x的一元二次方程x2﹣2x﹣3=0，配方后的方程可以是（）A．（x﹣1）2=4 B．（x+1）2=4 C．（x﹣1）2=16 D．（x+1）2=16试题6:在反比例函数的图象上有两点（﹣1，y1），，则y1﹣y2的值是（）A．负数 B．非正数 C．正数 D．不能确定试题7:已知等腰△ABC中，AD⊥BC于点D，且AD=BC，则△ABC底角的度数为（）A．45° B．75°C．45°或15°或75° D．60°试题8:如图，在菱形ABCD中，∠A=60°，E、F分别是AB，AD的中点，DE、BF相交于点G，连接BD，CG．有下列结论：①∠BGD=120°；②BG+DG=CG；③△BDF≌△CGB；④S△ABD=AB2其中正确的结论有（）A．1个 B．2个 C．3个 D．4个试题9:方程x2﹣9=0的解是．试题10:一元二次方程x2+2x+a=0有实根，则a的取值范围是．试题11:平行四边形ABCD中，∠A+∠C=100°，则∠B= 度．试题12:如图，在△ABC中，AB=AD=DC，∠BAD=20°，则∠C= ．试题13:如图，正方形ABOC的边长为2，反比例函数y=过点A，则k的值是．试题14:如图，已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm，AE⊥BC于点E，则AE的长是．试题15:如图，边长12的正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在AB、BC、FD上．若BF=3，则小正方形的边长为．试题16:2（x﹣3）=3x（x﹣3）；试题17:x2﹣2x=2x+1．试题18:如图，在△ABC中，AB=AC，∠ABC=72°．（1）用直尺和圆规作∠ABC的平分线BD交AC于点D（保留作图痕迹，不要求写作法）；（2）在（1）中作出∠ABC的平分线BD后，求∠BDC的度数．试题19:如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．求证：（1）BC=AD；（2）△OAB是等腰三角形．试题20:如图，路灯下一墙墩（用线段AB表示）的影子是BC，小明（用线段DE表示）的影子是EF，在M处有一颗大树，它的影子是MN．（1）指定路灯的位置（用点P表示）；（2）在图中画出表示大树高的线段；（3）若小明的眼睛近似地看成是点D，试画图分析小明能否看见大树．试题21:如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BC相交于点N，连接BM，DN．（1）求证：四边形BMDN是菱形；（2）若AB=4，AD=8，求MD的长．试题22:山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：（1）每千克核桃应降价多少元？（2）在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？试题23:一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动：将△MNK的直角顶点M放在△ABC的斜边AB的中点处，设AC=BC=a．（1）如图1，两个三角尺的重叠部分为△ACM，则重叠部分的面积为，周长为；（2）将图1中的△MNK绕顶点M逆时针旋转45°，得到图2，此时重叠部分的面积为，周长为；（3）如果将△MNK绕M旋转到不同于图1，图2的位置，如图3所示，猜想此时重叠部分的面积为多少？并试着加以验证．试题24:如图，已知反比例函数的图象经过第二象限内的点A（﹣1，m），AB⊥x轴于点B，△AOB的面积为2．若直线y=ax+b经过点A，并且经过反比例函数的图象上另一点C（n，一2）．（1）求直线y=ax+b的解析式；（2）设直线y=ax+b与x轴交于点M，求AM的长．试题1答案:B【考点】一元二次方程的解．【分析】一元二次方程的解，就是能够使方程左右两边相等的未知数的值，即用这个数代替未知数所得式子仍然成立．【解答】解：把x=2代入方程x2﹣mx+2=0，可得4﹣2m+2=0，得m=3，故本题选B．【点评】本题考查的是一元二次方程的解的定义．试题2答案:C【考点】中心投影．【分析】根据中心投影的特点：等高的物体垂直地面放置时，在灯光下，离点光源近的物体它的影子短，离点光源远的物体它的影子长．进行判断即可．【解答】解：因为小亮由A处走到B处这一过程中离光源是由远到近再到远的过程，所以他在地上的影子先变短后变长．故选C．【点评】本题综合考查了中心投影的特点和规律．中心投影的特点是：①等高的物体垂直地面放置时，在灯光下，离点光源近的物体它的影子短，离点光源远的物体它的影子长；②等长的物体平行于地面放置时，在灯光下，离点光源越近，影子越长；离点光源越远，影子越短，但不会比物体本身的长度还短．试题3答案:D【考点】等腰三角形的判定与性质；平行线的性质．【分析】由∠ABC、∠ACB的平分线相交于点E，∠MBE=∠EBC，∠ECN=∠ECB，利用两直线平行，内错角相等，利用等量代换可∠MBE=∠MEB，∠NEC=∠ECN，然后即可求得结论．【解答】解：∵∠ABC、∠ACB的平分线相交于点E，∴∠MBE=∠EBC，∠ECN=∠ECB，∵MN∥BC，∴∠EBC=∠MEB，∠NEC=∠ECB，∴∠MBE=∠MEB，∠NEC=∠ECN，∴BM=ME，EN=CN，∴MN=ME+EN，即MN=BM+CN．∵BM+CN=9∴MN=9，故选：D．【点评】此题考查学生对等腰三角形的判定与性质和平行线性质的理解与掌握．此题关键是证明△BME△CNE是等腰三角形．试题4答案:B【考点】等腰三角形的性质；非负数的性质：绝对值；非负数的性质：算术平方根；三角形三边关系．【分析】根据非负数的意义列出关于x、y的方程并求出x、y的值，再根据x是腰长和底边长两种情况讨论求解．【解答】解：根据题意得，解得，（1）若4是腰长，则三角形的三边长为：4、4、8，不能组成三角形；（2）若4是底边长，则三角形的三边长为：4、8、8，能组成三角形，周长为4+8+8=20．故选B．【点评】本题考查了等腰三角形的性质、非负数的性质及三角形三边关系；解题主要利用了非负数的性质，分情况讨论求解时要注意利用三角形的三边关系对三边能否组成三角形做出判断．根据题意列出方程是正确解答本题的关键．试题5答案:A【考点】解一元二次方程-配方法．【分析】在本题中，把常数项﹣3移项后，应该在左右两边同时加上一次项系数﹣2的一半的平方．【解答】解：把方程x2﹣2x﹣3=0的常数项移到等号的右边，得到x2﹣2x=3，方程两边同时加上一次项系数一半的平方，得到x2﹣2x+1=3+1，配方得（x﹣1）2=4．故选A．【点评】本题考查了配方法的一般步骤：（1）把常数项移到等号的右边；（2）把二次项的系数化为1；（3）等式两边同时加上一次项系数一半的平方．选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．试题6答案:A【考点】反比例函数图象上点的坐标特征．【分析】反比例函数：当k＜0时，该函数图象位于第二、四象限，且在每一象限内，y随x的增大而增大．【解答】解：∵反比例函数中的k＜0，∴函数图象位于第二、四象限，且在每一象限内，y随x的增大而增大；又∵点（﹣1，y1）和均位于第二象限，﹣1＜﹣，∴y1＜y2，∴y1﹣y2＜0，即y1﹣y2的值是负数，故选A．【点评】本题考查了反比例函数图象上点的坐标特征．注意：反比例函数的增减性只指在同一象限内．试题7答案:C【考点】含30度角的直角三角形；等腰三角形的性质；等腰直角三角形．【分析】作出图形，分①点A是顶点时，根据等腰三角形三线合一的性质可得BD=CD，从而得到AD=BD=CD，再利用等边对等角的性质可得∠B=∠BAD，然后利用直角三角形两锐角互余求解即可；②点A是底角顶点时，再分AD在△ABC外部时，根据直角三角形30°角所对的直角边等于斜边的一半求出∠ACD=30°，再根据三角形的一个外角等于与它不相邻的两个内角的和求解即可得到底角是15°，AD在△ABC内部时，根据直角三角形30°角所对的直角边等于斜边的一半求出∠C=30°，然后再根据等腰三角形两底角相等求解即可．【解答】解：①如图1，点A是顶点时，∵AB=AC，AD⊥BC，∴BD=CD，∵AD=BC，∴AD=BD=CD，在Rt△ABD中，∠B=∠BAD=（180°﹣90°）=45°；②如图2，点A是底角顶点，且AD在△ABC外部时，∵AD=BC，AC=BC，∴AD=AC，∴∠ACD=30°，∴∠BAC=∠ABC=×30°=15°；③如图3，点A是底角顶点，且AD在△ABC内部时，∵AD=BC，AC=BC，∴AD=AC，∴∠C=30°，∴∠BAC=∠ABC=（180°﹣30°）=75°；综上所述，△ABC底角的度数为45°或15°或75°．故选C．【点评】本题考查了30°角所对的直角边等于斜边的一半的性质，等腰三角形的两底角相等的性质，以及三角形的一个外角等于与它不相邻的两个内角的和的性质，难点在于要分情况讨论求解．试题8答案:C【考点】菱形的性质；全等三角形的判定与性质；等边三角形的判定与性质．【分析】先判断出△ABD、BDC是等边三角形，然后根据等边三角形的三心（重心、内心、垂心）合一的性质，结合菱形对角线平分一组对角，三角形的判定定理可分别进行各项的判断．【解答】解：①由菱形的性质可得△ABD、BDC是等边三角形，∠DGB=∠GBE+∠GEB=30°+90°=120°，故①正确；②∵∠DCG=∠BCG=30°，DE⊥AB，∴可得DG=CG（30°角所对直角边等于斜边一半）、BG=CG，故可得出BG+DG=CG，即②也正确；③首先可得对应边BG≠FD，因为BG=DG，DG＞FD，故可得△BDF不全等△CGB，即③错误；④S△ABD=AB•DE=AB•BE=AB•AB=AB2，即④正确．综上可得①②④正确，共3个．故选C．【点评】此题考查了菱形的性质、全等三角形的判定与性质及等边三角形的判定与性质，综合的知识点较多，注意各知识点的融会贯通，难度一般．试题9答案:x=±3 ．【考点】解一元二次方程-因式分解法．【分析】这个式子左边是一个平方差公式，直接分解因式即可，然后求出x．【解答】解：x2﹣9=0即（x+3）（x﹣3）=0，所以x=3或x=﹣3．故答案为：x=±3．【点评】此题主要考查了平方差公式在因式分解中的应用，比较简单．试题10答案:a≤1 ．【考点】根的判别式；解一元一次不等式．【分析】由方程有实数根可以得出△=22﹣4a≥0，解不等式即可得出结论．【解答】解：∵一元二次方程x2+2x+a=0有实根，∴△=22﹣4a≥0，解得：a≤1．故答案为：a≤1．【点评】本题考查了根的判别式以及解一元一次不等式，解题的关键是由方程有实数根得出关于a的一元一次不等式．本题属于基础题，难度不大，解决该题型题目时，根据方程解得个数结合根的判别式得出不等式（或方程）是关键．试题11答案:130 度．【考点】平行四边形的性质．【分析】根据平行四边形的性质可得∠A=∠C，又有∠A+∠C=100°，可求∠A=∠C=50°．又因为平行四边形的邻角互补，所以，∠B+∠A=180°，可求∠B．【解答】解：∵四边形ABCD为平行四边形，∴∠A=∠C，又∠A+∠C=100°，∴∠A=∠C=50°，又∵AD∥BC，∴∠B=180°﹣∠A=180°﹣50°=130°．【点评】此题主要考查：平行四边形的两组对角分别相等，平行四边形的邻角互补．试题12答案:40°．【考点】三角形的外角性质；三角形内角和定理．【分析】先根据等腰三角形的性质及三角形内角和定理可求出∠B的度数，再根据三角形外角的性质可求出∠ADC的度数，再由三角形内角和定理解答即可．【解答】解：∵AB=AD，∠BAD=20°，∴∠B===80°，∵∠ADC是△ABD的外角，∴∠ADC=∠B+∠BAD=80°+20°=100°，∵AD=DC，∴∠C===40°．【点评】本题涉及到三角形的内角和定理、三角形外角的性质及等腰三角形的性质，属较简单题目．试题13答案:﹣4 ．【考点】反比例函数系数k的几何意义．【分析】因为过双曲线上任意一点引x轴、y轴垂线，所得正方形的面积S是个定值，即S=|k|．【解答】解：根据题意，知|k|=22=4，k=±4，又∵k＜0，∴k=﹣4．故答案为：﹣4．【点评】主要考查了反比例函数中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．试题14答案:cm ．【考点】菱形的性质．【分析】根据菱形的性质得出BO、CO的长，在RT△BOC中求出BC，利用菱形面积等于对角线乘积的一半，也等于BC×AE，可得出AE的长度．【解答】解：∵四边形ABCD是菱形，∴CO=AC=3cm，BO=BD=4cm，AO⊥BO，∴BC==5cm，∴S菱形ABCD==×6×8=24cm2，∵S菱形ABCD=BC×AE，∴BC×AE=24，∴AE==cm．故答案为：cm．【点评】此题考查了菱形的性质，也涉及了勾股定理，要求我们掌握菱形的面积的两种表示方法，及菱形的对角线互相垂直且平分．试题15答案:．【考点】相似三角形的判定与性质；正方形的性质．【分析】先根据相似三角形的判定定理得出△BEF∽△CFD，再根据勾股定理求出DF的长，再由相似三角形的对应边成比例即可得出结论．【解答】解：在△BEF与△CFD中∵∠1+∠2=∠2+∠3=90°，∴∠1=∠3，∵∠B=∠C=90°，∴△BEF∽△CFD，∵BF=3，BC=12，∴CF=BC﹣BF=12﹣3=9，又∵DF===15，∴=，即=，∴EF=，故答案为：．【点评】本题考查的是相似三角形的判定与性质及勾股定理，根据题意得出△BEF∽△CFD是解答此题的关键．试题16答案:2（x﹣3）=3x（x﹣3）移项，得2（x﹣3）﹣3x（x﹣3）=0整理，得（x﹣3）（2﹣3x）=0∴x﹣3=0或2﹣3x=0解得：x1=3，x2=；试题17答案:原方程化为：x2﹣4x=1配方，得x2﹣4x+4=1+4整理，得（x﹣2）2=5∴x﹣2=，即x1=2，x2=2．试题18答案:【考点】作图—基本作图；等腰三角形的性质．【分析】（1）根据角平分线的作法利用直尺和圆规作出∠ABC的平分线即可；（2）先根据等腰三角形的性质及三角形内角和定理求出∠A的度数，再由角平分线的定义得出∠ABD的度数，再根据三角形外角的性质得出∠BDC的度数即可．【解答】解：（1）①一点B为圆心，以任意长长为半径画弧，分别交AB、BC于点E、F；②分别以点E、F为圆心，以大于EF为半径画圆，两圆相交于点G，连接BG角AC于点D即可．（2）∵在△ABC中，AB=AC，∠ABC=72°，∴∠A=180°﹣2∠ABC=180°﹣144°=36°，∵BD是∠ABC的平分线，∴∠ABD=∠ABC=×72°=36°，∵∠BDC是△ABD的外角，∴∠BDC=∠A+∠ABD=36°+36°=72°．【点评】本题考查的是基本作图及等腰三角形的性质，熟知角平分线的作法是解答此题的关键．试题19答案:【考点】全等三角形的判定与性质；等腰三角形的判定．【分析】（1）根据AC⊥BC，BD⊥AD，得出△ABC与△BAD是直角三角形，再根据AC=BD，AB=BA，得出Rt△ABC≌Rt△BAD，即可证出BC=AD，（2）根据Rt△ABC≌Rt△BAD，得出∠CAB=∠DBA，从而证出OA=OB，△OAB是等腰三角形．【解答】证明：（1）∵AC⊥BC，BD⊥AD，∴∠ADB=∠ACB=90°，在Rt△ABC和Rt△BAD中，∵，∴Rt△ABC≌Rt△BAD（HL），∴BC=AD，（2）∵Rt△ABC≌Rt△BAD，∴∠CAB=∠DBA，∴OA=OB，∴△OAB是等腰三角形．【点评】本题考查了全等三角形的判定及性质；用到的知识点是全等三角形的判定及性质、等腰三角形的判定等，全等三角形的判定是重点，本题是道基础题，是对全等三角形的判定的训练．试题20答案:【考点】中心投影．【分析】根据中心投影的特点可知，连接物体和它影子的顶端所形成的直线必定经过点光源．所以分别把AB和DE的顶端和影子的顶端连接并延长可交于一点，即点光源的位置，再由点光源出发连接MN顶部N的直线与地面相交即可找到MN影子的顶端．线段GM是大树的高．若小明的眼睛近似地看成是点D，则看不到大树，GM处于视点的盲区．【解答】解：（1）点P是灯泡的位置；（2）线段MG是大树的高．（3）视点D看不到大树，GM处于视点的盲区．【点评】本题考查中心投影的作图，难度不大，体现了学数学要注重基础知识的新课标理念．解题的关键是要知道：连接物体和它影子的顶端所形成的直线必定经过点光源．试题21答案:【考点】矩形的性质；线段垂直平分线的性质；勾股定理；平行四边形的判定；菱形的性质；菱形的判定．【分析】（1）根据矩形性质求出AD∥BC，推出∠MDO=∠NBO，∠DMO=∠BNO，证△DMO≌△BNO，推出OM=ON，得出平行四边形BMDN，推出菱形BMDN；（2）根据菱形性质求出DM=BM，在Rt△AMB中，根据勾股定理得出BM2=AM2+AB2，推出x2=x2﹣16x+64+16，求出即可．【解答】（1）证明：∵四边形ABCD是矩形，∴AD∥BC，∠A=90°，∴∠MDO=∠NBO，∠DMO=∠BNO，∵在△DMO和△BNO中，，∴△DMO≌△BNO（AAS），∴OM=ON，∵OB=OD，∴四边形BMDN是平行四边形，∵MN⊥BD，∴平行四边形BMDN是菱形．（2）解：∵四边形BMDN是菱形，∴MB=MD，设MD长为x，则MB=DM=x，在Rt△AMB中，BM2=AM2+AB2即x2=（8﹣x）2+42，解得：x=5，所以MD长为5．【点评】本题考查了矩形性质，平行四边形的判定，菱形的判定和性质，勾股定理等知识点的应用，对角线互相平分的四边形是平行四边形，对角线互相垂直的平行四边形是菱形．试题22答案:【考点】一元二次方程的应用．【分析】（1）设每千克核桃降价x元，利用销售量×每件利润=2240元列出方程求解即可；（2）为了让利于顾客因此应下降6元，求出此时的销售单价即可确定几折．【解答】（1）解：设每千克核桃应降价x元．…1分根据题意，得（60﹣x﹣40）（100+×20）=2240．…4分化简，得 x2﹣10x+24=0 解得x1=4，x2=6．…6分答：每千克核桃应降价4元或6元．…7分（2）解：由（1）可知每千克核桃可降价4元或6元．因为要尽可能让利于顾客，所以每千克核桃应降价6元．此时，售价为：60﹣6=54（元），．…9分答：该店应按原售价的九折出售．…10分【点评】本题考查了一元二次方程的应用，解题的关键是根据题目中的等量关系列出方程．试题23答案:【考点】等腰直角三角形；全等三角形的判定与性质；直角三角形斜边上的中线；正方形的性质．【分析】（1）由等腰直角三角形的性质：底边上的中线与底边上的高重合，得到△AMC是等腰直角三角形，AM=MC=AC=a，则重叠部分的面积是△ACB的面积的一半，为a2，周长为（1+）a．（2）易得重叠部分是正方形，边长为a，面积为a2，周长为2a．（3）过点M分别作AC、BC的垂线MH、MG，垂足为H、G．求得Rt△MHE≌Rt△MGF，则阴影部分的面积等于正方形CGMH 的面积．【解答】解：（1）∵AM=MC=AC=a，则∴重叠部分的面积是△ACB的面积的一半为a2，周长为（1+）a．（2）∵重叠部分是正方形∴边长为a，面积为a2，周长为2a．（3）猜想：重叠部分的面积为．理由如下：过点M分别作AC、BC的垂线MH、MG，垂足为H、G设MN与AC的交点为E，MK与BC的交点为F∵M是△ABC斜边AB的中点，AC=BC=a∴MH=MG=又∵∠HME+∠HMF=∠GMF+∠HMF，∴∠HME=∠GMF，∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形CGMH的面积∵正方形CGMH的面积是MG•MH=×=∴阴影部分的面积是．。

新疆哈密地区九年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分）现定义运算“★”，对于任意实数a、b，都有a★b=a2-3a+b，如：4★5=42-3×4+5，若x★2=6，则实数x的值是（）A . -4或-1B . 4或-1C . 4或-2D . -4或22. （2分） (2017九上·灯塔期中) 某校九年级共有1、2、3、4四个班，现从这四个班中随机抽取两个班进行一场篮球比赛，则恰好抽到1班和2班的概率是（）A .B .C .D .3. （2分） (2019九上·兰州期末) 在同一时刻，身高1.6m的小强在阳光下的影长为0.8m，一棵大树的影长为4.8m，则树的高度为（）A . 4.8mB . 6.4mC . 9.6mD . 10m4. （2分）下列命题：①若a+b+c=0，则b2-4ac＜0；②若b=2a+3c，则一元二次方程ax2+bx+c=0有两个不相等的实数根；③若b2-4ac＞0，则二次函数y=ax2+bc+c的图象与坐标轴的公共点的个数是2或3；④若b＞a+c，则一元二次方程ax2+bx+c=0有两个不相等的实数根。

其中正确的是（）A . ②④B . ①③C . ②③D . ③④5. （2分）已知x=1是方程的一个根，则方程的另一个根是（）A . 1B . 2C . -1D . -26. （2分） (2018九上·防城港期中) 设x1 ， x2是一元二次方程x2-2x-3=0的两根，则x1+x2=（）A . -2B . 2C . 3D . -37. （2分）如图，已知D为△ABC边AB上一点，AD=2BD，DE∥BC交AC于E，AE=6，则EC=（）A . 1B . 2C . 3D . 48. （2分） (2018九上·恩阳期中) 某地年投入教育经费万元，预计年投入元．设这两年投入教育经费的年平均增长率为，则下列方程正确的是（）A .B .C .D .9. （2分）(2016·深圳) 如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB：S四边形CBFG=1：2；③∠ABC=∠ABF；④AD2=FQ•AC，其中正确的结论的个数是（）A . 1B . 2C . 3D . 410. （2分）(2019·宝鸡模拟) 如图，矩形ABCD中，AB=8，BC=6，对角线AC，BD交于点O，过点O作OG⊥AB 于点G.延长AB至E，使BE= AB，连接OE交BC于点F，则BF的长为（）A .B . 1C .D . 2二、填空题 (共6题；共7分)11. （2分）方程（x﹣1）2=4的根是________；方程x2=x的根是________．12. （1分）如图，在菱形ABCD中，DE⊥AB，cosA=，则tan∠BDE的值是________13. （1分） (2019九上·江阴期中) A城市的新区建设规划图上，新城区的南北长为120cm，而该新城区的实际南北长为6km，则新区建设规划图所采用的比例尺是________.14. （1分）“奔跑吧，兄弟！”节目组预设计一个新游戏：“奔跑”路线A，B，C，D四地，如图A，B，C 三地在同一直线上，D在A北偏东30°方向，在C北偏西45°方向，C在A北偏东75°方向，且BD=BC=40m，从A 地到D地的距离是________m．15. （1分）关于x的一元二次方程x2+mx+n=0有两个相等的实数根，则2m3﹣8mn+2015的值为________ ．16. （1分）如图，在△ABC中，∠C=90°，BC=6，D、E分别在AB、AC上，将△A BC沿DE折叠，使点A落在点A′处，若A′为CE的中点，则折痕DE的长为________ .三、解答题 (共9题；共70分)17. （5分）解下列方程（1）x(2x-5)=2(2x-5) （2）2x2-3x -1=0（用配方法）18. （5分） (2019九上·辽源期末) 用公式法解方程： .19. （5分）如图所示，在四边形ABCD中，AB=CD，BC=AD，E，F为对角线AC上的点，且AE=CF，求证：BE=DF．20. （5分）已知菱形的边长是5cm，一条对角线的一半长是方程x2﹣3x﹣4=0的根，你能求出这个菱形的面积吗？21. （5分） (2017八下·怀柔期末) 某花圃用花盆培育某种花苗，经过实验发现每盆的盈利与每盆的株数构成一定的关系．每盆植入3株时，平均单株盈利3元；以同样的栽培条件，若每盆增加1株，平均单株盈利就减少0.5元．要使每盆的盈利达到10元，每盆应该植多少株？22. （10分）(2012·朝阳) 在不透明的箱子里放有4个乒乓球，每个乒乓球上分别写有数字1、2、3、4，从箱中摸出一个球记下数字后放回箱中，摇匀后再摸出一个记下数字．若将第一次摸出的球上的数字记为点的横坐标，第二次摸出球上的数字记为点的纵坐标．（1）请用列表法或树状图法写出两次摸球后所有可能的结果．（2）求这样的点落在如图所示的圆内的概率（注：图中圆心在直角坐标系中的第一象限内，并且分别于x轴、y轴切于点（2，0）和（0，2）两点）．23. （15分）(2018·深圳模拟) 已知矩形纸片ABCD中，AB=2，BC=3．操作：将矩形纸片沿EF折叠，使点B落在边CD上．探究：（1）如图1，若点B与点D重合，你认为△EDA1和△FDC全等吗？如果全等，请给出证明，如果不全等，请说明理由；（2）如图2，若点B与CD的中点重合，请你判断△FCB1、△B1DG和△EA1G之间的关系，如果全等，只需写出结果，如果相似，请写出结果和相应的相似比；（3）如图2，请你探索，当点B落在CD边上何处，即B1C的长度为多少时，△FCB1与△B1DG全等．24. （10分）已知：如图，在中，D是AC上一点，联结BD，且∠ABD =∠ACB.（1）求证：△ABD∽△ACB；（2）若AD=5，AB= 7，求AC的长.25. （10分） (2018八上·惠山期中) 如图，长方形ABCD中，AB＝9，AD＝4.E为CD边上一点，CE＝6.点P 从点B出发，以每秒1个单位的速度沿着边BA向终点A运动，连接PE．设点P运动的时间为t秒．（1）当t为何值时，△PAE为直角三角形？（2）是否存在这样的t，使EA恰好平分∠PED，若存在，求出t的值；若不存在，请说明理由．参考答案一、单选题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题；共7分)11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共9题；共70分)17-1、18-1、19-1、20-1、21-1、22-1、22-2、23-1、23-2、23-3、24-1、24-2、25-1、25-2、第11 页共11 页。

2023-2024学年新疆喀什地区英吉沙县九年级（上）期末数学试卷一、选择题：本题共8小题，每小题4分，共32分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知是一元二次方程的一个解，则m的值是()A.3B.C.0D.2.下列函数中是二次函数的是()A. B.C. D.3.下列说法正确的是()A.平移不改变图形的形状和大小，而旋转改变图形的形状和大小B.在平面直角坐标系中，一个点向右平移2个单位，则纵坐标加2C.在成中心对称的两个图形中，连接对称点的线段都被对称中心平分D.在平移和旋转图形中，对应角相等，对应线段相等且平行4.车轮转动一周所行的路程是车轮的()A.半径B.直径C.周长D.面积5.下列事件中，是必然事件的是()A.任意抛掷两枚质地均匀的硬币，正面朝上B.明天一定会下大雨C.装有1个蓝球3个红球的袋子中任取2个球，则至少有一个是红球D.投掷一枚普通骰子，朝上一面的点数是26.不透明口袋中有2个红球、3个黑球、4个白球，这些球除颜色外无其他差别，从中随机摸出1个球，是红球的概率为()A. B. C. D.7.二次函数的图象的对称轴是()A.直线B.直线C.直线D.直线8.如图，AB是的直径，点C、D在上，，则的度数为()A.B.C.D.二、填空题：本题共6小题，每小题3分，共18分。

9.已知关于x的方程的根为，，则的值为______.10.如图，小明对自己某次实心球训练的录像进行分析，发现实心球飞行高度米与水平距离米之间的关系为：，则小明此次实心球训练的成绩为______米.11.点与关于原点对称，则______.12.如图，AB是的弦，AB长为8，P是上一个动点不与A、B重合，过点O作于点C，于点D，则CD的长为_____.13.已知一个圆锥的侧面展开图是圆心角为，半径为3cm的扇形，则这个圆锥的底面圆半径是______14.在一个不透明的袋子中装有6个红球和若干个白球，这些球除颜色外都相同，将球搅匀后随机摸出一个球，记下颜色后放回，不断重复这一过程，共摸球100次，发现有20次摸到红球，估计袋子中白球的个数约为______.三、解答题：本题共8小题，共50分。

2015-2016学年新疆克拉玛依三中九年级（上）期中数学试卷一、填空题（）1．（3分）已知反比例函数y=的图象在第象限．2．（3分）反比例函数y=﹣的图象如图所示，点M是该函数图象上一点，MN 垂直于x轴，垂足是点N，则△MON的面积为．3．（3分）如果点（2，3）和（﹣3，a）都在反比例函数y=的图象上，则a=．4．（3分）若反比例函数y=﹣的图象上有两点A（x1，y1），B（x2，y2），若x1＞x2＞0，则y1，y2的大小关系是．5．（3分）已知关于x的一元二次方程x2+x+m2﹣9=0的一个根是0，则m的值是．6．（3分）不解方程，判别方程2x2﹣3x+5=0的根的情况是．7．（3分）已知关于x的方程（m﹣1）x2﹣8x+16=0有两个不相等的实数根，则m的取值范围是．8．（3分）把二次函数y=x2﹣6x﹣3化为顶点式为．9．（3分）把二次函数y=﹣9x2的图象向左平移3个单位，再向下平移2个单位得到的解析式为．10．（3分）若点（﹣3，y1）和（﹣1，y2）在函数y=的图象上，则y1y2．（填＜；＞；=）11．（3分）二次函数y=2x2﹣4x+m的最小值是1，则m的值为．12．（3分）二次函数y=ax2+bx+c（a≠0）的图象如图，则函数值y＞0时，x的取值范围是．13．（3分）矩形的面积为20，则长y与宽x的函数关系式为．14．（3分）参加一次足球联赛，若进行单循环比赛，共比赛56场，共有多少队参加比赛？设共有x队参加比赛，则所列方程为．15．（3分）如图是二次函数y=ax2+bx+c的图象，下列结论：（1）abc＜0；（2）2a+b=0；（3）a+b+c＞0；（4）b2＜4ac；（5）当﹣1＜x＜3时，y＞0．你认为其中不正确的是（填序号）．二、解方程（）16．（10分）用适当的方法解下列方程：（1）4x2﹣8x=1（2）3y（y﹣2）=4y﹣8．17．（5分）用配方法解方程：2x2﹣8x﹣198=0．三、解答题（共60分）：18．（8分）如图，已知A（﹣4，2）、B（n，﹣4）是一次函数y=kx+b的图象与反比例函数的图象的两个交点．（1）求此反比例函数和一次函数的解析式；（2）根据图象写出不等式kx+b＜的解集为；（3）求△AOB的面积．19．（5分）已知二次函数的图象经过（3，0），（2，﹣3）点，对称轴x=1，求这个函数的解析式．20．（10分）已知二次函数y=﹣x2﹣2x+3（1）求出与x轴和y轴交点坐标，画出大致图象；（2）观察图象，写出﹣x2﹣2x+3≥0的解集；（3）求抛物线与x轴的两个交点与顶点所构成的三角形的面积．21．（7分）某中心城市有一楼盘，开发商准备以每平方米7000元的价格出售，由于国家出台了有关调控房地产的政策，开发商经过两次下调销售价格后，决定以每平方米5670元的价格销售．求平均每次下调的百分率．四、Ⅰ、学区班、内初班学生做（实验班学生不做）（共3小题，满分30分）22．（8分）某经销单位将进货单价为40元的商品按50元售出时，一个月能卖出500个．已知这种商品每涨价1元，其销量就减少10个．为了赚得8000元的利润，销量又不超过300个，售价应定为多少？这时应进货多少个？23．（10分）为了改善小区环境，某小区决定要在一块一边靠墙（墙长25m）的空地上修建一个矩形绿化带ABCD，绿化带一边靠墙，另三边用总长为40m的栅栏围住（如图）．若设绿化带的BC边长为xm，绿化带的面积为ym2．（1）求y与x之间的函数关系式，并写出自变量x的取值范围；（2）当x为何值时，满足条件的绿化带的面积最大．24．（12分）如图，排球运动员站在点O处练习发球，将球从点O正上方2米的点A处发出把球看成点，其运行的高度y（米）与运行的水平距离x（米）满足关系式y=a（x﹣6）2+2.6，已知球网与点O的水平距离为9米，高度为2.43米，球场的边界距点O的水平距离为18米．（1）求y与x的函数关系式；（2）球能否越过球网？（3）球会不会出界？请说明理由．（）五、Ⅱ、实验班学生做（学区班、内初班学生不做）（共3小题，满分30分）25．（8分）某商店如果将进货价格为8元的商品按每件10元售出，每天可销售2000件，现采取提高售价，减少进货量的方法，增加利润，已知这种商品每涨价0.5元，其销售量就减少100件，问应将售价定为多少元时可赚利润6400元？这时应进货多少个？26．（10分）如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度a为10 米），围成一个长方形的花圃．设花圃的宽AB为x米，面积为S平方米．（1）求S与x的函数关系式；写出自变量x的取值范围．（2）怎样围才能使长方形花圃的面积最大？最大值为多少？27．（12分）如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m 的A处正对球门踢出（点A在y轴上），足球的飞行高度y（单位：m）与飞行时间t（单位：s）之间满足函数关系y=at2+5t+c，已知足球飞行0.8s时，离地面的高度为3.5m．（1）足球飞行的时间是多少时，足球离地面最高？最大高度是多少？（2）若足球飞行的水平距离x（单位：m）与飞行时间t（单位：s）之间具有函数关系x=10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？2015-2016学年新疆克拉玛依三中九年级（上）期中数学试卷参考答案与试题解析一、填空题（）1．（3分）已知反比例函数y=的图象在第一，三象限．【解答】解：∵k=8＞0，∴函数图象在第一，三象限．故答案为：一，三．2．（3分）反比例函数y=﹣的图象如图所示，点M是该函数图象上一点，MN 垂直于x轴，垂足是点N，则△MON的面积为2．【解答】解：如右图，设M的坐标是（a，b），那么b=，∴ab=k=﹣4，=ON•MN=×|ab|=×4=2，∴S△MON故答案是：2．3．（3分）如果点（2，3）和（﹣3，a）都在反比例函数y=的图象上，则a=﹣2．【解答】解：∵点（2，3）和（﹣3，a）都在反比例函数y=的图象上，把（2，3）代入上式得k=6，则反比例函数为y=，把（﹣3，a）代入得a=﹣2．故答案为﹣2．4．（3分）若反比例函数y=﹣的图象上有两点A（x1，y1），B（x2，y2），若x1＞x2＞0，则y1，y2的大小关系是y1＞y2．【解答】解：∵反比例函数y=﹣，∴k=﹣5＜0，∴在图象的每一支上，y随x的增大而增大，∵x1＞x2＞0，∴y1＞y2，故答案为：y1＞y2．5．（3分）已知关于x的一元二次方程x2+x+m2﹣9=0的一个根是0，则m的值是m=±3．【解答】解：把x=0代入方程程x2+x+m2﹣9=0得到m2﹣9=0，解得：m=±3，故答案为：m=±3．6．（3分）不解方程，判别方程2x2﹣3x+5=0的根的情况是方程没有实数根．【解答】解：∵△=（﹣3）2﹣4×2×5=9﹣40=﹣31＜0，∴方程没有实数根，故答案为：方程没有实数根．7．（3分）已知关于x的方程（m﹣1）x2﹣8x+16=0有两个不相等的实数根，则m的取值范围是m＜2且m≠1．【解答】解：∵关于x的方程（m﹣1）x2﹣8x+16=0有两个不相等的实数根，∴m﹣1≠0，且△＞0，即64﹣64（m﹣1）＞0，解得m＜2，∴m的取值范围是：m＜2且m≠1．故答案为：m＜2且m≠1．8．（3分）把二次函数y=x2﹣6x﹣3化为顶点式为y=（x﹣3）2﹣12．【解答】解：y=x2﹣6x﹣3=x2﹣6x+9﹣9﹣3=（x﹣3）2﹣12，故答案为：y=（x﹣3）2﹣12．9．（3分）把二次函数y=﹣9x2的图象向左平移3个单位，再向下平移2个单位得到的解析式为y=﹣9（x+3）2﹣2．【解答】解：根据“上加下减，左加右减”的原则可知，二次函数y=﹣9x2的图象向左平移3个单位，再向下平移2个单位得到的图象表达式为：y=﹣9（x+3）2﹣2．故答案为：y=﹣9（x+3）2﹣2．10．（3分）若点（﹣3，y1）和（﹣1，y2）在函数y=的图象上，则y1＞y2．（填＜；＞；=）【解答】解：∵y=，∴抛物线对称轴为x=﹣1，开口向上，∴当x＜﹣1时，y随x增大而减小，∵﹣2＜﹣1＜1，∴y1＞y2．故答案为：＞．11．（3分）二次函数y=2x2﹣4x+m的最小值是1，则m的值为3．【解答】解：根据题意得=1，解得m=3．故答案为3．12．（3分）二次函数y=ax2+bx+c（a≠0）的图象如图，则函数值y＞0时，x的取值范围是x＜﹣1或x＞3．【解答】解：由函数图象位于x轴上方的部分，得x＜﹣1或x＞3，故答案为：x＜﹣1或x＞3．13．（3分）矩形的面积为20，则长y与宽x的函数关系式为y=．【解答】解：由题意得：xy=20，y=，故答案为：y=．14．（3分）参加一次足球联赛，若进行单循环比赛，共比赛56场，共有多少队参加比赛？设共有x队参加比赛，则所列方程为x（x﹣1）=56．【解答】解：设有x个队参赛，x（x﹣1）=56．故答案为：x（x﹣1）=56．15．（3分）如图是二次函数y=ax2+bx+c的图象，下列结论：（1）abc＜0；（2）2a+b=0；（3）a+b+c＞0；（4）b2＜4ac；（5）当﹣1＜x＜3时，y＞0．你认为其中不正确的是（填序号）④．【解答】解：∵图象开口向下，∴a＜0，∵x=﹣=1，∴b=﹣2a，∴b＞0，2a+b=0，∵抛物线交y轴正半轴，∴c＞0，∴abc＜0，故①②正确；∵当x=1时，y＞0，∴a+b+c＞0，故③正确；∵图象和x轴交于两点，∴b2﹣4ac＞0，∴b2＞4ac，故④错误；由图象可知，当﹣1＜x＜3时，y＞0，故⑤正确；所以错误的序号是④故答案为④．二、解方程（）16．（10分）用适当的方法解下列方程：（1）4x2﹣8x=1（2）3y（y﹣2）=4y﹣8．【解答】解：（1）4x2﹣8x=1x2﹣2x=（x﹣1）2=，解得：x1=1+，x2=1﹣；（2）3y（y﹣2）=4y﹣83y（y﹣2）﹣4（y﹣2）=0，（y﹣2）（3y﹣4）=0，解得：y1=2，y2=．17．（5分）用配方法解方程：2x2﹣8x﹣198=0．【解答】解：原方程变形为x2﹣4x=99，∴（x﹣2）2=99+4∴x﹣2=±∴x1=2+，x2=2﹣．三、解答题（共60分）：18．（8分）如图，已知A（﹣4，2）、B（n，﹣4）是一次函数y=kx+b的图象与反比例函数的图象的两个交点．（1）求此反比例函数和一次函数的解析式；（2）根据图象写出不等式kx+b＜的解集为x＞2或﹣4＜x＜0；（3）求△AOB的面积．【解答】解：（1）∵点A（﹣4，2）和点B（n，﹣4）都在反比例函数y=的图象上，∴，解得．又由点A（﹣4，2）和点B（2，﹣4）都在一次函数y=kx+b的图象上，∴，解得．∴反比例函数的解析式为，一次函数的解析式为y=﹣x﹣2．（2）由图象，得x的取值范围是x＞2或﹣4＜x＜0．（3）一次函数与x轴的交点为C，=S△AOC+S△BOC则S△AOB=×2×2+×2×4=6．19．（5分）已知二次函数的图象经过（3，0），（2，﹣3）点，对称轴x=1，求这个函数的解析式．【解答】解：∵二次函数的图象经过（3，0）点，对称轴x=1，∴抛物线与x轴的另一交点坐标为（﹣1，0），故设该抛物线的解析式为y=a（x﹣3）（x+1）（a是常数，a≠0）．∵二次函数的图象经过（2，﹣3）点，∴﹣3=a（2﹣3）（2+1），解得a=1．∴该函数解析式为：y=（x﹣3）（x+1）（或y=x2﹣2x﹣3）．20．（10分）已知二次函数y=﹣x2﹣2x+3（1）求出与x轴和y轴交点坐标，画出大致图象；（2）观察图象，写出﹣x2﹣2x+3≥0的解集；（3）求抛物线与x轴的两个交点与顶点所构成的三角形的面积．【解答】解：（1）∵y=﹣x2﹣2x+3，∴y=﹣（x﹣1）（x+3），∴抛物线与x轴的交点为（1，0），（﹣3，0）．∵令x=0，则y=3，∴抛物线与x轴的交点为（0，3）．其函数图象如图所示：（2）由函数图象可知，当﹣3≤x≤1时，﹣x2﹣2x+3≥0；（3）∵由图可知，抛物线的顶点坐标为（﹣1，4），∴抛物线与x轴的两个交点与顶点所构成的三角形的面积=×（1+3）×4=8．21．（7分）某中心城市有一楼盘，开发商准备以每平方米7000元的价格出售，由于国家出台了有关调控房地产的政策，开发商经过两次下调销售价格后，决定以每平方米5670元的价格销售．求平均每次下调的百分率．【解答】解：设平均每次下调的百分率是x，根据题意列方程得，7000（1﹣x）2=5670，解得：x 1=10%，x2=190%（不合题意，舍去）．答：平均每次下调的百分率为10%．四、Ⅰ、学区班、内初班学生做（实验班学生不做）（共3小题，满分30分）22．（8分）某经销单位将进货单价为40元的商品按50元售出时，一个月能卖出500个．已知这种商品每涨价1元，其销量就减少10个．为了赚得8000元的利润，销量又不超过300个，售价应定为多少？这时应进货多少个？【解答】解：设售价为每个x元，依题意，得（x﹣40）[500﹣10（x﹣50）]=8000，整理得x2﹣140x+4800=0解得：x1=60，x2=80，当x=60时，销售量500﹣10（x﹣50）=400＞300，当x=80时，成本=500﹣10（x﹣50）=200＜300，答：售价为80元，应进货200个．23．（10分）为了改善小区环境，某小区决定要在一块一边靠墙（墙长25m）的空地上修建一个矩形绿化带ABCD，绿化带一边靠墙，另三边用总长为40m的栅栏围住（如图）．若设绿化带的BC边长为xm，绿化带的面积为ym2．（1）求y与x之间的函数关系式，并写出自变量x的取值范围；（2）当x为何值时，满足条件的绿化带的面积最大．【解答】解：（1）由题意得：x2+20x（3分）自变量x的取值范围是0＜x≤25（4分）（2）y=﹣x2+20x=﹣（x﹣20）2+200（6分）∵20＜25，∴当x=20时，y有最大值200平方米即当x=20时，满足条件的绿化带面积最大．（8分）24．（12分）如图，排球运动员站在点O处练习发球，将球从点O正上方2米的点A处发出把球看成点，其运行的高度y（米）与运行的水平距离x（米）满足关系式y=a（x﹣6）2+2.6，已知球网与点O的水平距离为9米，高度为2.43米，球场的边界距点O的水平距离为18米．（1）求y与x的函数关系式；（2）球能否越过球网？（3）球会不会出界？请说明理由．（）【解答】解：（1）把点A（0，2）代入关系式得：2=a（﹣6）2+2.6，解得：a=﹣，则y与x的关系式为：y=﹣（x﹣6）2+2.6；（2）∵当x=9时，y=﹣（9﹣6）2+2.6=2.45＞2.43，∴球能越过球网；（3）∵当x=18时，y=﹣（18﹣6）2+2.6=0.2＞0，∴球会出界．五、Ⅱ、实验班学生做（学区班、内初班学生不做）（共3小题，满分30分）25．（8分）某商店如果将进货价格为8元的商品按每件10元售出，每天可销售2000件，现采取提高售价，减少进货量的方法，增加利润，已知这种商品每涨价0.5元，其销售量就减少100件，问应将售价定为多少元时可赚利润6400元？这时应进货多少个？【解答】解：设每件售价定为x元时，才能使每天利润为6400元，（x﹣8）[2000﹣200（x﹣10）]=6400，解得：x1=12，x2=16，∵采取提高售价，减少进货量的方法，增加利润，∴x取16．答：应将每件售价定为16元时，能使每天利润为6400元．26．（10分）如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度a为10 米），围成一个长方形的花圃．设花圃的宽AB为x米，面积为S平方米．（1）求S与x的函数关系式；写出自变量x的取值范围．（2）怎样围才能使长方形花圃的面积最大？最大值为多少？【解答】解：（1）设花圃的宽AB为x米，则长BC=（24﹣2x）米．由矩形的面积公式可知：S=x（24﹣2x），∴S=﹣2x2+24x．∵墙的最大可用长度a为10米，∴0＜24﹣2x≤10．解得：7≤x＜12．（2）∵a=﹣2，b=24，∴x=﹣==6．∵7≤x＜12，a＜0，∴S随x的增大而减小．∵当x=7时24﹣2x=10，即长为10米，宽为7米时面积最大，∴长方形花圃的最大面积=70平方米．27．（12分）如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m 的A处正对球门踢出（点A在y轴上），足球的飞行高度y（单位：m）与飞行时间t（单位：s）之间满足函数关系y=at2+5t+c，已知足球飞行0.8s时，离地面的高度为3.5m．（1）足球飞行的时间是多少时，足球离地面最高？最大高度是多少？（2）若足球飞行的水平距离x（单位：m）与飞行时间t（单位：s）之间具有函数关系x=10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？【解答】解：（1）由题意得：函数y=at2+5t+c的图象经过（0，0.5）（0.8，3.5），∴，解得：，∴抛物线的解析式为：y=﹣t2+5t+，∴当t=时，y=4.5；最大（2）把x=28代入x=10t得t=2.8，∴当t=2.8时，y=﹣×2.82+5×2.8+=2.25＜2.44，∴他能将球直接射入球门．第21页（共21页）。

2015年新疆、生产建设兵团中考数学试卷一、选择题，共9小题，每小题5分，共45分）×=3．（5分）（2015•新疆）如图所示，某同学的家在A处，星期日他到书店去买书，想尽快赶到书店，请你帮助他选择一条最近的路线（）4．（5分）（2015•新疆）已知，AC∥ED，∠C=26°，∠CBE=37°，则∠BED的度数是（）6．（5分）（2015•新疆）不等式组的解在数轴上表示为（）C28．（5分）（2015•新疆）如图，小红居住的小区内有一条笔直的小路，小路的正中间有一路灯，晚上小红由A处径直走到B处，她在灯光照射下的影长l与行走的路程S之间的变化关系用图象刻画出来，大致图象是（）C9．（5分）（2015•新疆）如图，在矩形ABCD 中，CD=1，∠DBC=30°．若将BD 绕点B 旋转后，点D 落在DC 延长线上的点E 处，点D 经过的路径，则图中阴影部分的面积是（ ）﹣﹣C﹣﹣二、填空题，共6小题，每小题5分，共30分10．（5分）（2015•新疆）分解因式：a 2﹣4b 2= ．11．（5分）（2015•新疆）已知k ＞0，且关于x 的方程3kx 2+12x+k+1=0有两个相等的实数根，那么k 的值等于 ． 12．（5分）（2015•新疆）如图，将周长为8的△ABC 沿BC 方向向右平移1个单位得到△DEF ，则四边形ABFD 的周长为 ．13．（5分）（2015•新疆）若点P 1（﹣1，m ），P 2（﹣2，n ）在反比例函数y=（k ＜0）的图象上，则mn （填“＞”，“＜”或“=”） 14．（5分）（2015•新疆）甲、乙两台机器分别灌装每瓶质量为500克的酸奶，从甲、乙灌装的酸奶中分别随机抽取了30瓶，测得它们实际质量的方差是：S 甲2=4.8，S 乙2=3.6，那么 （填“甲”或“乙”）机器灌装的酸奶质量较稳定． 15．（5分）（2015•新疆）如图，李明打网球时，球恰好打过网，且落在离网4m 的位置上，则网球的击球的高度h 为 ．三、解答题（一）本大题，共4小题，共30分 16．（6分）（2015•新疆）计算：（﹣）2+﹣2sin45°﹣|1﹣|．17．（7分）（2015•新疆）先化简，再求值：﹣，其中a=1．18．（8分）（2015•新疆）如图1，一个圆球放置在V型架中．图2是它的平面示意图，CA、CB都是⊙O 的切线，切点分别是A、B，如果⊙O的半径为cm，且AB=6cm，求∠ACB．19．（9分）（2015•新疆）某超市预购进A、B两种品牌的T恤共200件，已知两种T恤的进价如表所示，恤全部卖出，获得的总利润为W元．品牌进价/（元/件）售价/（元/件）A 50 80B 40 65（2）如果购进两种T恤的总费用不超过9500元，那么超市如何进货才能获得最大利润？并求出最大利润．（提示：利润=售价﹣进价）四、解答题（二）本大题，共4小题，共45分20．（10分）（2015•新疆）为鼓励大学生创业，政府制定了小型企业的优惠政策，许多小型企业应运而生．某市统计了该市2015年1﹣5月新注册小型企业的数量，并将结果绘制成如图两种不完整的统计图：（1）某市2015年1﹣5月份新注册小型企业一共家，请将折线统计图补充完整．（2）该市2015年3月新注册小型企业中，只有2家是养殖企业，现从3月新注册的小型企业中随机抽取2家企业了解其经营情况．请以列表或画树状图的方法求出所抽取的2家企业恰好都是养殖企业的概率．21．（11分）（2015•新疆）如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标（4，2），过点D（0，3）和E（6，0）的直线分别于AB，BC交于点M，N．（1）求直线DE的解析式和点M的坐标；（2）若反比例函数y=（x＞0）的图象经过点M，求该反比函数的解析式，并通过计算判断点N是否在该函数的图象上．22．（11分）（2015•新疆）如图，四边形ABCD为菱形，点E为对角线AC上的一个动点，连结DE并延长交AB于点F，连结BE．（1）如果①：求证∠AFD=∠EBC；（2）如图②，若DE=EC且BE⊥AF，求∠DAB的度数；（3）若∠DAB=90°且当△BEF为等腰三角形时，求∠EFB的度数（只写出条件与对应的结果）23．（13分）（2015•新疆）如图，直线y=﹣3x+3与x轴、y轴分别交于点A、B．抛物线y=a（x﹣2）2+k 经过A、B，并与x轴交于另一点C，其顶点为P，（1）求a，k的值；（2）在图中求一点Q，A、B、C为顶点的四边形是平行四边形，请直接写出相应的点Q的坐标；（3）抛物线的对称轴上是否存在一点M，使△ABM的周长最小？若存在，求△ABM的周长；若不存在，请说明理由；（4）抛物线的对称轴是上是否存在一点N，使△ABN是以AB为斜边的直角三角形？若存在，求出N点的坐标，若不存在，请说明理由．2015年新疆、生产建设兵团中考数学试卷参考答案与试题解析一、选择题，共9小题，每小题5分，共45分解答：解：是无理数，﹣2，0，都是有理数．）×=解答：解：A、﹣（﹣）=，正确，不合题意；、×=3．（5分）（2015•新疆）如图所示，某同学的家在A处，星期日他到书店去买书，想尽快赶到书店，请你帮助他选择一条最近的路线（）4．（5分）（2015•新疆）已知，AC∥ED，∠C=26°，∠CBE=37°，则∠BED的度数是（）A．53°B．63°C．73°D．83°考点：平行线的性质．分析：因为AC∥ED，所以∠BED=∠EAC，而∠EAC是△ABC的外角，所以∠BED=∠EAC=∠CBE+∠C．解答：解：∵在△ABC中，∠C=26°，∠CBE=37°，∴∠CAE=∠C+∠CBE=26°+37°=63°，∵AC∥ED，∴∠BED=∠CAE=63°．故选B点评：本题考查的是两直线平行的性质，关键是根据三角形外角与内角的关系及两直线平行的性质分析．5．（5分）（2015•新疆）估算﹣2的值（）A．在1到2之间B．在2到3之间C．在3到4之间D．在4到5之间考点：估算无理数的大小．分析：先估计的整数部分，然后即可判断﹣2的近似值．解答：解：∵5＜＜6，∴3＜﹣2＜4．故选C．点评：此题主要考查了无理数的估算能力，现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．6．（5分）（2015•新疆）不等式组的解在数轴上表示为（）A．B．C．D．考点：在数轴上表示不等式的解集；解一元一次不等式组．分析：分析：先求出不等式组中每一个不等式的解集，再求出它们的公共部分，然后把不等式的解集表示在数轴上即可．解不等式组得：，再分别表示在数轴上即可得解．解答：解：由x+1＞2，得x＞1；由3﹣x≥1，得x≤2，不等式组的解集是1＜x≤2，故选：C．点评：本题考查了在数轴上表示不等式的解集，把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．7．（5分）（2015•新疆）抛物线y=（x﹣1）2+2的顶点坐标是（）8．（5分）（2015•新疆）如图，小红居住的小区内有一条笔直的小路，小路的正中间有一路灯，晚上小红由A处径直走到B处，她在灯光照射下的影长l与行走的路程S之间的变化关系用图象刻画出来，大致图象是（）C9．（5分）（2015•新疆）如图，在矩形ABCD中，CD=1，∠DBC=30°．若将BD绕点B旋转后，点D落在DC延长线上的点E处，点D经过的路径，则图中阴影部分的面积是（）﹣﹣C﹣﹣，然后由旋转的性质可得：=，=，•=﹣．二、填空题，共6小题，每小题5分，共30分10．（5分）（2015•新疆）分解因式：a2﹣4b2=（a+2b）（a﹣2b）．11．（5分）（2015•新疆）已知k＞0，且关于x的方程3kx2+12x+k+1=0有两个相等的实数根，那么k的值等于3．12．（5分）（2015•新疆）如图，将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为10．13．（5分）（2015•新疆）若点P1（﹣1，m），P2（﹣2，n）在反比例函数y=（k＜0）的图象上，则m＞n（填“＞”，“＜”或“=”）分析：由于比例系数小于0，两点在同一象限，根据反比例函数的图象的性质作答即可．∴反比例函数y=（k＜0）在第二象限内，y随x的增大而增大；故答案为：＞．点评：考查反比例函数y=的图象的性质．用到的知识点为：当k＜0，双曲线的两支分别位14．（5分）（2015•新疆）甲、乙两台机器分别灌装每瓶质量为500克的酸奶，从甲、乙灌装的酸奶中分别随机抽取了30瓶，测得它们实际质量的方差是：S甲2=4.8，S乙2=3.6，那么乙（填“甲”或“乙”）机器灌装的酸奶质量较稳定．15．（5分）（2015•新疆）如图，李明打网球时，球恰好打过网，且落在离网4m的位置上，则网球的击球的高度h为 1.4．分析：判断出△ABC和△AED相似，再根据相似三角形对应边成比例列式计算即可得解．=，即=，三、解答题（一）本大题，共4小题，共30分16．（6分）（2015•新疆）计算：（﹣）2+﹣2sin45°﹣|1﹣|．+2﹣×﹣+1=17．（7分）（2015•新疆）先化简，再求值：﹣，其中a=1．分析：先根据分式混合运算的法则把原式进行化简，再把a=1代入进行计算即可．﹣=﹣，﹣=．18．（8分）（2015•新疆）如图1，一个圆球放置在V型架中．图2是它的平面示意图，CA、CB都是⊙O 的切线，切点分别是A、B，如果⊙O的半径为cm，且AB=6cm，求∠ACB．BOD=19．（9分）（2015•新疆）某超市预购进A、B两种品牌的T恤共200件，已知两种T恤的进价如表所示，恤全部卖出，获得的总利润为W元．（2）如果购进两种T恤的总费用不超过9500元，那么超市如何进货才能获得最大利润？并求出最大利润．（提示：利润=售价﹣进价）四、解答题（二）本大题，共4小题，共45分20．（10分）（2015•新疆）为鼓励大学生创业，政府制定了小型企业的优惠政策，许多小型企业应运而生．某市统计了该市2015年1﹣5月新注册小型企业的数量，并将结果绘制成如图两种不完整的统计图：（1）某市2015年1﹣5月份新注册小型企业一共16家，请将折线统计图补充完整．（2）该市2015年3月新注册小型企业中，只有2家是养殖企业，现从3月新注册的小型企业中随机抽取2家企业了解其经营情况．请以列表或画树状图的方法求出所抽取的2家企业恰好都是养殖企业的概率．故答案为：16；（2）设该镇今年3月新注册的小型企业为甲、乙、丙、丁，其中甲、乙为养殖企业．画树状图得：∵共有12种等可能的结果，甲、乙2家企业恰好被抽到的有2种，∴所抽取的2家企业恰好都是养殖企业的概率为：．点评：本题考查了折线统计图、扇形统计图和列表法与树状图法，解决本题的关键是从两种统计图中整理出解题的有关信息，在扇形统计图中，每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比．用到的知识点为：概率=所求情况数与总情况数之比．21．（11分）（2015•新疆）如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标（4，2），过点D（0，3）和E（6，0）的直线分别于AB，BC交于点M，N．（1）求直线DE的解析式和点M的坐标；（2）若反比例函数y=（x＞0）的图象经过点M，求该反比函数的解析式，并通过计算判断点N是否在该函数的图象上．考点：反比例函数与一次函数的交点问题．分析：（1）设直线DE的解析式为y=kx+b，将D（0，3），E（6，0）代入，利用待定系数法求出直线DE的解析式；由矩形的性质可得M点与B点纵坐标相等，将y=2代入直线DE的解析式，求出x的值，即可得到M的坐标；（2）将点M（2，2）代入y=，利用待定系数法求出反比函数的解析式，再由直线DE的解析式求出N点坐标，进而即可判断点N是否在该函数的图象上．解答：解：（1）设直线DE的解析式为y=kx+b，∵D（0，3），E（6，0），，解得，∴直线DE的解析式为y=﹣x+3；x+3=2（2）∵反比例函数y=（x＞0）的图象经过点M（2，2），∴该反比函数的解析式是y=；x+3∴当x=4时，y=﹣×4+3=1，的图象上．22．（11分）（2015•新疆）如图，四边形ABCD为菱形，点E为对角线AC上的一个动点，连结DE并延长交AB于点F，连结BE．（1）如果①：求证∠AFD=∠EBC；（2）如图②，若DE=EC且BE⊥AF，求∠DAB的度数；（3）若∠DAB=90°且当△BEF为等腰三角形时，求∠EFB的度数（只写出条件与对应的结果）23．（13分）（2015•新疆）如图，直线y=﹣3x+3与x轴、y轴分别交于点A、B．抛物线y=a（x﹣2）2+k 经过A、B，并与x轴交于另一点C，其顶点为P，（1）求a，k的值；（2）在图中求一点Q，A、B、C为顶点的四边形是平行四边形，请直接写出相应的点Q的坐标；（3）抛物线的对称轴上是否存在一点M，使△ABM的周长最小？若存在，求△ABM的周长；若不存在，请说明理由；（4）抛物线的对称轴是上是否存在一点N，使△ABN是以AB为斜边的直角三角形？若存在，求出N点的坐标，若不存在，请说明理由．，可得，解得，AB=1=BQ2=AC=2，如图1，=AB=BC=33；。

○…………外…………○…………装…………○…………订…………○…………线…………○…………学校：___________姓名：___________班级：___________考号：___________○…………内…………○…………装…………○…………订…………○…………线…………○…………绝密★启用前英吉沙县实验中学2014-2015学年度第二学期数学单元测试七年级数学（第五章）考试范围：第五章；考试时间：90分钟；命题人：司依提江注意事项：1. 答题前填写好自己的姓名、班级、考号等信息2. 请将答案正确填写在答题卡上分卷I分卷I 注释一、 选择题（每小题4分、共40分）1. 已知：如图，l1∥l2，∠1=50°, 则∠2的度数是A ．135°B ．130°C ．50°D ．40°2. 下列图形中由AB ∥CD 能得到∠1=∠2的是3. 如图，已知AB ∥CD, ∠2=2∠1，则∠3= A ．90 ° B ．120° C ．60° D ．154. 如图，已知∠1=∠2，∠3=80°,∠4= A ．80° B ．70° C ．60° D ．50°5. 如果∠A 和∠B 是两平行直线中的同旁内角，且∠A 比∠B 的2倍少30º，则∠B 的度数是 A ．30º B ．70º C ．110º D ．30º或70º○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※○…………内…………○…………装…………○…………订…………○…………线…………○…………6. 如图,AB ∥CD ，若∠2=135°，那么∠1的度数是( )A ．30°B ．45°C ．60°D ．75°7. 若一个角的两边分别平行于另一个角的两边，那么这两个角为 A ．相等 B ．互补 C ．相等或互补 D ．以上结论都不对8. 如图，AB ∥CD ，直线EF 分别交AB 、CD 于E 、F 两点，若∠FEB ＝110°，则∠EFD 等于A 、 50 °B 、60°C 、70°D 、110°9. 下列说法错误的是( ) A ．同位角不一定相等 B ．内错角都相等 C ．同旁内角可能相等 D ．同旁内角互补,两直线平行10. 在同一平面内,两条不重合直线的位置关系可能是( )毛 A ．平行或相交 B ．垂直或相交; C ．垂直或平行 D ．平行、垂直或相交分卷II分卷II 注释二、 每题4分，共32分（填空题）11. 如图，直线a ∥b ，直线c 与直线a 、b 相交，若∠1=47º，则∠2的度数为_______。