基于异质集成学习方法的房价预测
- 格式:pdf
- 大小:1.46 MB
- 文档页数:2

Statistics and Application 统计学与应用, 2019, 8(5), 754-759Published Online October 2019 in Hans. /journal/sahttps:///10.12677/sa.2019.85085Forecast of Housing Price Based on BPNeural Network—Taking Handan as an ExampleXincheng Tang, Zhihai Wang*College of Science, Hebei University of Engineering, Handan HebeiReceived: Oct. 1st, 2019; accepted: Oct. 14th, 2019; published: Oct. 21st, 2019AbstractBP neural network is a network structure model, which is the most widely used currently. It has a strong ability to fit and map the nonlinear relationship between variables. This paper takes the average house price and main factor data of Handan from 2003 to 2016 as the object, and uses BP neural network to construct a house price forecasting model. The experimental result shows that BP neural network can effectively predict the housing prices in Handan in a relatively stable ex-ternal environment.KeywordsBP Neural Network, House Price, Prediction基于BP神经网络的房价预测研究——以邯郸市为例汤新程,王志海*河北工程大学数理科学与工程学院,河北邯郸收稿日期:2019年10月1日;录用日期:2019年10月14日;发布日期:2019年10月21日摘要BP神经网络是截止目前应用最为广泛的一种网络结构模型,其对变量之间的非线性关系有着极强的拟合映*通讯作者。

基于GTWR的武汉市房价预测随着经济的持续发展和城市化进程的加速,房地产市场一直是备受关注的热点话题。
作为中国的第七大城市,武汉市的房地产市场一直备受关注。
随着房价的不断攀升,人们对于房价的预测也格外关注。
本文将基于地理加权回归(GTWR)模型来预测武汉市房价,以期为投资者和政府决策者提供参考。
我们需要了解一下GTWR模型。
地理加权回归是一种空间计量模型,其基本假设是不同地理位置的空间单位之间存在着不同的影响关系。
GTWR模型使用了局部权重矩阵将全局线性回归模型中的空间异质性纳入考虑,预测结果更加准确。
这一模型在预测城市房价时被广泛应用,并取得了较好的预测效果。
接下来,我们需要收集武汉市的相关数据。
数据的选择对于模型的准确性至关重要。
我们需要包括人口密度、交通便利度、学区情况、商业中心分布、医疗资源等多个指标,以全面评估房价的影响因素。
我们还需要收集房价数据,这将是我们模型训练的关键。
在数据收集完成后,我们将对数据进行清洗和预处理。
我们需要对数据进行异常值和缺失值的处理,以确保模型的准确性。
我们需要进行数据标准化处理,将各个指标的数据统一到相同的尺度上,避免指标之间的差异对模型产生影响。
接下来,我们将使用GTWR模型进行训练和预测。
我们将利用已有的数据集进行模型训练,寻找数据之间的潜在关系,并用于后续的预测。
我们将利用模型对未来的房价进行预测,根据各个指标的变化情况,得出未来的房价走势。
值得注意的是,GTWR模型的预测结果受到模型的建立和数据选择的影响。
为了提高模型的准确性,我们还可以在模型建立完成后进行模型验证,评估模型的拟合度和预测能力,并对模型进行调整和优化。
通过以上的步骤,我们可以得到基于GTWR的武汉市房价预测结果。
这一预测结果将为投资者和政府决策者提供重要参考,帮助他们更好地了解房地产市场的走势,做出合理的投资和政策决策。
基于GTWR的武汉市房价预测是一项重要的研究工作,它将为城市的经济发展和房地产市场的稳定提供重要支持。

基于机器学习的房价预测技术研究及应用随着人工智能技术的不断发展,机器学习在众多领域展现出了强大的预测和决策能力。
其中,在房地产领域,基于机器学习的房价预测技术可成为为房地产行业分析市场走向的重要依据,为投资者做出更准确的决策,成为房地产领域中备受关注的技术之一。
一、机器学习的基础机器学习是一种人工智能的分支,可以使用算法对大规模数据进行分析和预测。
它可以生动地描述这样一个场景:给定一组数据,它可以通过计算出一些规律并对未知数据进行预测。
基于机器学习的模型可以处理基于数字和文本的数据,并能够自动调整和优化模型的参数,从而改善其表现。
而机器学习的基础通常分为三个主要步骤:数据准备,模型训练和预测。
在这些步骤中,数据准备通常是最重要的一步。
要建立一个高质量的模型,需要大量的数据才能产生高精度的结果。
模型训练是机器学习过程中第二个关键步骤,可以使用不同的算法来训练一个机器学习模型。
最后,预测是这个过程中的最后一个关键步骤,可以使用训练好的模型来预测未传入数据的结果。
二、机器学习在房价预测中的应用对于房地产行业来说,房价预测是一项非常重要的问题。
房地产市场日新月异,而且房价是主要交易因素,因此对未来价格的正确预测将直接影响买卖双方的决策。
而基于机器学习的房价预测技术恰好可以解决这个问题。
基于机器学习的房价预测技术可以通过模型训练来学习有关房地产市场的信息和数据,并使用这些信息来预测未来的房价。
训练机器学习模型的算法可以分为两类:监督算法和非监督算法。
在监督学习中,模型的训练是基于已知信息的,这些信息是由人类专家预测实现的。
在房价预测模型中,为了预测一个地区的房价,模型需要多个变量,如房屋数、平方尺寸、物业税等。
监督学习技术可以用来训练模型来预测这些变量的影响,进而得出房价预测。
非监督学习是一种数据挖掘技术,它可以从数据中自动发现有用的信息并对其加以解释。
房地产市场数据是一个极大的数据集,非监督学习可以通过对该数据进行聚类或降维,来找到这个数据集中有用的视角或特征。
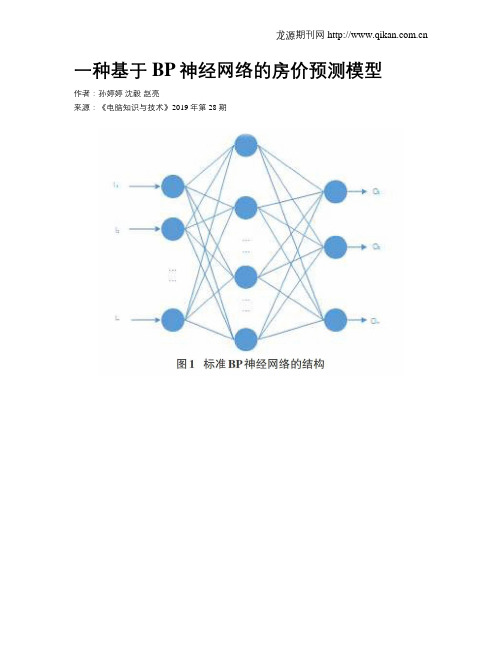
一种基于BP神经网络的房价预测模型作者:孙婷婷沈毅赵亮来源:《电脑知识与技术》2019年第28期摘要:房价复杂多变,具有非线性特性,因此利用非线性模型预测房价走势受到学者们的关注。
而在非线性模型中,BP(Back Propagation)神经网络具有较强的非线性映射能力。
因此,该文基于BP神经网络构造房价预测模型。
在模型的具体实现中,首先基于特征选择方法提取影响房价变化的典型经济要素;然后针对房价要素特点构建BP网络模型,通过已有数据对BP神经网络模型进行深度训练、校验,预测今后房屋价格的走势。
理论分析与实验结果表明,本文提出的模型优于现有一些线性和非线性预测模型,能够对房价变化进行有效预测。
关键词:BP神经网络;非线性映射;特征选择;房价预测中图分类号:TP39; ; ; ; 文献标识码:A文章编号:1009-3044(2019)28-0215-04Abstract:The house price is complex and variable, which has nonlinear characteristics. Therefore, the use of nonlinear models to predict the trend of house prices has attracted more researchers' attention. In the nonlinear model, BP (Back Propagation) neural network has strong nonlinear mapping ability. Inspired by this, this paper constructs a house price forecasting model based on BP neural network. In the concrete realization of the model, firstly, based on the featureselection method, the typical economic factors affecting the house price change are extracted. Then, the BP network model is constructed according to the selected factors, and deeply trained and verified through the existing data, which can favorably predict the future house price trend. Theoretical analysis and experimental results show that the proposed model is superior to the existing linear and nonlinear predicting models, and can effectively predict house price changes.Key words:BP Neural Network; Nonlinear Mapping; Feature Extraction; House Price Forecasting随着我国经济的快速发展和国民生活水平的日益提高,我国的房地产业蓬勃发展。

利用机器学习算法预测房价走势方法比较研究机器学习在房价预测方面有广泛的应用,可以采用不同的算法来预测房价走势。
本文将对几种常见的机器学习算法进行比较研究,并介绍它们的优缺点。
1. 线性回归算法线性回归是一种基本的机器学习算法,它通过拟合线性函数来预测房价。
它的优点是简单易懂,计算速度快。
然而,线性回归对于非线性关系的数据拟合效果较差,无法捕捉到数据中的复杂模式。
因此,对于房价预测这样的复杂问题,线性回归算法效果较一般。
2. 决策树算法决策树是一种常用的机器学习算法,它通过构建树形结构来进行决策。
在房价预测中,决策树可以通过属性的排序来决定房价。
决策树算法的优点是易解释、易理解,可以处理非线性和多分类问题。
然而,决策树容易过拟合,需要进行剪枝等处理才能提高泛化能力。
3. 支持向量机算法支持向量机是一种常用的分类和回归算法,在房价预测中也有一定的应用。
支持向量机通过找到一个超平面来预测不同价格段的房价。
支持向量机算法的优点是可以处理高维数据、对异常值敏感度低。
然而,支持向量机可能受到数据集规模和噪声的影响,对于大型数据集预测效果较差。
4. 随机森林算法随机森林是一种集成学习算法,通过组合多个决策树来预测房价。
随机森林算法的优点是可以处理多维度和非线性数据,对于缺失数据具有较好的鲁棒性。
此外,随机森林也可以提供特征的重要性排序。
然而,随机森林算法需要较多的计算资源,且参数设置较为复杂。
5. 神经网络算法神经网络是一种模拟人脑结构的机器学习算法,在房价预测中也有一定的应用。
神经网络可以通过多层的节点来构建模型,从而捕捉数据中的复杂关系。
神经网络算法的优点是对于非线性问题有较好的适应性,可以自动提取特征。
然而,神经网络算法需要大量的数据来进行训练,且模型的解释性较差。
通过对上述几种机器学习算法的比较,可以看出每个算法都有各自的优缺点。
对于房价预测这样的复杂问题,没有一种算法可以完全胜任,选择合适的算法需要根据具体的数据和问题来决定。

基于BP神经网络对房价预测的研究高文;李富星;牛永洁【摘要】搜集西安市1997年~2016年20年七个对房价影响的数据,首先对数据进行预处理,包括数据集成、空白值填写、数据标准化,然后,使用PCA方法对数据进行降维处理,在干净数据的基础上,采用对数函数logsig为激励函数,学习率为0.3,建立BP神经网络的房价预测模型,选择80%的数据作为训练数据,20%的数据作为测试数据.通过MATLAB对数据进行仿真实验,其实验结果表明用该模型仿真的结果其正确率较高,最高达到94.14%,效果较好,具有一定的实用价值.【期刊名称】《延安大学学报(自然科学版)》【年(卷),期】2018(037)003【总页数】4页(P37-40)【关键词】BP神经网络;房价预测;正确率;降维【作者】高文;李富星;牛永洁【作者单位】延安大学数学与计算机科学学院,陕西延安716000;延安大学数学与计算机科学学院,陕西延安716000;延安大学数学与计算机科学学院,陕西延安716000【正文语种】中文【中图分类】TP183随着房地产市场的迅猛发展,房价的走势受到了越来越多人的关注。
房价是由多个因素决定的,比如国家的宏观调控、居民人均可支配收入、房地产开发投资、住宅销售面积等,这些因素都影响着房价的走势[1]。
本文通过BP神经网络对西安房价做预测分析,BP神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最为广泛的神经网络模型之一。
BP神经网络能学习和存储大量的输入-输出模式的映射关系,而无需事前揭示映射关系的数学方程。
它的学习规则是使用梯度最速下降法,通过误差反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小[2]。
1 BP人工神经网络BP神经网络,即Back Propagation神经网络,其本质是一种基于误差反馈传播的神经网络算法。
BP神经网络通过训练使网络具有联想记忆和预测能力,调整各层权值阈值,使得误差达到最小,从训练模式上看,BP神经网络是由一个信息的正向传播过程和一个误差的反向传播过程反复交替进行的网络模式训练过程[3]。
统计学习方法集成算法在提高预测性能中的策略随着信息时代的到来,数据的快速增长和复杂性给预测问题带来了巨大的挑战。
统计学习方法集成算法作为一种强大的预测工具,被广泛应用于各个领域,如金融、医疗和自然语言处理等。
本文将探讨集成算法在提高预测性能中的策略,并介绍一些常见的集成学习方法。
一、简介统计学习方法集成算法是通过将多个预测模型进行结合,从而获得更准确和稳定的结果。
这种方法充分利用了多模型的优点,并通过组合它们的预测结果来弥补各个模型的不足之处。
二、集成算法的策略1. BaggingBagging是一种基于自助采样的集成学习方法。
它通过从原始训练集中有放回地采样生成若干个采样集,然后分别使用这些采样集训练多个基学习器。
最后,将这些基学习器的预测结果进行投票或平均,得到最终的预测结果。
Bagging的主要优点是能够降低模型的方差,提高预测的稳定性。
2. BoostingBoosting是一种迭代的集成学习方法。
它通过训练一系列弱学习器,然后根据前一个模型的结果来调整样本的权重,使得下一个模型更加关注前一个模型预测错误的样本。
最后,将这些弱学习器的预测结果进行加权融合,得到最终的预测结果。
Boosting的主要优点是能够降低模型的偏差,提高预测的准确性。
3. StackingStacking是一种将多个基学习器进行堆叠的集成学习方法。
它通过将原始训练集分成若干个不相交的子集,然后用每个子集训练一个基学习器。
接下来,将这些基学习器应用于另一个未见过的数据集,得到预测结果。
最后,将这些预测结果作为新的训练集,再用一个元学习器进行训练。
Stacking的主要优点是能够提高模型的灵活性和泛化能力,从而提高预测性能。
三、集成算法在提高预测性能中的应用1. 风控预测风控预测是金融领域中非常重要的预测问题之一。
通过利用集成算法,可以更准确地预测借款人的还款能力和违约概率,从而辅助金融机构做出更准确的信贷决策。
2. 医疗诊断集成算法在医疗诊断中的应用也取得了显著的成果。
基于机器学习算法的智能化房价预测分析系统研究智能化的房价预测分析系统在房地产市场中扮演着越来越重要的角色。
这些系统使用机器学习算法,通过大数据的分析,能够准确地预测未来房价的趋势,并帮助房地产公司和房产经纪人做出更加明智的决策。
本文将介绍基于机器学习算法的智能化房价预测分析系统的研究。
一、机器学习算法在房价预测中的应用机器学习算法是一种通过对大量数据进行学习和分析来获得模式并进行预测的计算机技术。
在房价预测中,机器学习算法可以通过对历史数据的学习来预测未来房价的趋势。
这些历史数据可以包括房价、房屋特征、地理位置、经济指标等等。
目前,机器学习算法在房价预测中的应用已经成为热门的话题。
其中,最常用的机器学习算法包括支持向量机、决策树、神经网络等。
这些算法可以有效地分析数据,并预测未来房价的走向。
二、智能化房价预测分析系统的研究基于机器学习算法的智能化房价预测分析系统可以在不断学习的基础上,根据不同地域、不同面积、不同结构、不同装修情况等因素,预测房屋的价格。
目前,这种系统已经在许多国家和地区的房地产市场中得到了广泛应用。
其中,智能化房价预测分析系统的核心是机器学习算法,因此系统需要大量的数据来进行学习和预测。
这些数据可以通过多种途径获取,例如房地产交易数据、政府公开的经济数据、物业管理数据等,通过机器学习算法将这些数据进行整合并学习,生成预测模型。
当预测模型得到了足够的学习数据后,就可以进行房价预测。
三、机器学习算法的应用案例房价预测是一个非常复杂的问题,涉及到许多因素,如房屋地理位置、面积,社区环境、经济指标等等。
接下来,我们将介绍一些机器学习算法在房价预测中的应用案例。
1. 基于神经网络的房价预测神经网络是一种模仿生物神经网络的计算机技术。
通过对大量数据进行学习,神经网络可以进行非线性函数拟合,提高预测准确率。
在房价预测中,神经网络的应用可以通过多层神经元对数据进行学习,从而实现房价预测。
2. 基于支持向量机的房价预测支持向量机是一种分类算法,它可以通过对数据进行分割,从而实现对未来数据的预测。
面向异构数据的集成学习算法研究与优化引言随着大数据时代的到来,异构数据(heterogeneous data)的处理变得越来越重要。
异构数据是指多个源头、结构、性质不同的数据集合。
由于异构数据的复杂性,传统的数据集成算法难以胜任。
因此,研究和优化面向异构数据的集成学习算法成为了迫切的需求。
本文将介绍面向异构数据的集成学习算法的研究进展和优化方法。
一、异构数据集成学习算法的研究现状1.1 异构数据的特点异构数据的特点包括数据的多样性、异质性、不完整性和不确定性。
多样性体现在异构数据可能包含不同的属性、特征和结构;异质性指不同源头的数据可能具有不同的度量单位、分布和属性类型;不完整性指异构数据集合中的某些属性可能缺失或不完整;不确定性指异构数据的不确定性信息,例如数据的噪声、错误等。
1.2 异构数据集成学习算法的分类目前,针对异构数据集成学习已经提出了多种算法。
常见的算法包括基于特征选择的集成学习、基于实例选择的集成学习、基于模型融合的集成学习和基于多标记学习的集成学习等。
这些算法各有优劣,适用于不同的异构数据处理任务。
1.3 异构数据集成学习算法的应用领域异构数据集成学习算法具有广泛的应用领域,包括数据挖掘、社交网络分析、医学诊断、金融预测等。
在这些应用场景中,所面临的数据多样性、异质性、不完整性和不确定性问题都需要特殊的算法来解决。
二、异构数据集成学习算法的优化方法2.1 特征选择特征选择是异构数据集成学习算法的重要环节之一。
通过选择最具代表性的特征,可以提高数据集成的性能。
常见的特征选择方法包括基于过滤的方法、基于包装的方法和基于嵌入的方法等。
这些方法可以通过特征选择的度量标准和搜索策略来进行优化。
2.2 实例选择实例选择是异构数据集成学习算法的另一个关键步骤。
通过选择最具代表性的实例,可以减少数据集成的计算成本,提高算法的性能。
常见的实例选择方法包括基于重采样的方法、基于聚类的方法和基于分类器的方法等。
使用机器学习技术进行房价预测与分析研究引言:近年来,随着经济的不断发展,房地产市场也呈现出蓬勃的发展态势。
对于购房者、投资者以及房地产从业者来说,了解房价趋势并进行房价预测与分析非常重要。
传统方法通过人工经验和统计模型进行预测,但面临着许多限制。
而机器学习技术的兴起使得房价预测与分析更加准确和可靠。
本文将介绍机器学习技术在房价预测与分析研究中的应用,并探讨其优势和局限性。
一、机器学习技术在房价预测中的应用1. 数据收集和准备房价预测的第一步是收集和准备数据。
大量的历史房价数据以及与房价相关的指标(如地理位置、房屋面积、楼层数等)被收集并整理成适合机器学习算法处理的格式。
这些数据将作为训练集和测试集,用于模型的训练和验证。
2. 特征工程特征工程是机器学习过程中的重要步骤。
通过对房价数据的特征进行提取和转换,可以帮助算法更好地理解和预测房价。
特征工程包括但不限于:缺失值处理、数据标准化、特征选择以及特征交互等。
3. 模型选择和训练在特征工程完成后,需要选择适合的机器学习模型对房价进行预测。
常用的模型包括线性回归、决策树、支持向量机以及神经网络等。
根据实际情况选择合适的模型并进行训练,以便使模型能够基于训练数据建立出准确的预测模型。
4. 模型评估和验证模型训练完成后,需要对其进行评估和验证。
常用的指标有均方误差(MSE)、均方根误差(RMSE)以及决定系数(R2)等。
根据评估指标的结果,可以调整模型的参数或者考虑使用其他模型进行预测。
5. 房价预测与分析当模型通过验证后,可以将其应用于实际的房价预测与分析中。
通过输入新的特征数据,模型能够根据历史数据来预测未来的房价变动趋势,并给出相应的结果和分析报告。
这些预测结果可以帮助购房者和投资者作出更加明智的决策。
二、机器学习技术在房价预测中的优势1. 更准确的预测相比传统的统计模型,机器学习技术能够更准确地预测房价。
机器学习算法可以从大量的历史数据中学习并发现数据之间的潜在规律,从而进行更精确的预测。
2018年10月文通过对人脸上识别基本原理进行相关介绍说明,奠定了本文设计算法的核心思想。
同时在设计硬件设计对其详细介绍,对其进行试验验证并获得了良好的效果。
在设计本文设计的同时,本文作者发现了许多的问题与不足,因此需要在今后的学习工作中对于该方向进行深入研究,以提高和改进本设计的性能。
参考文献[1]王国栋.基于MATLAB的人脸识别算法的研究[D].内蒙古大学, 2014.[2]张伟.基于matlab的人脸识别仿真系统的设计与实现[J].硅谷, 2009(15):52+98.[3]孔令钊,唐文静.基于PCA的人脸识别系统的研究与实现[J].计算机仿真,2012,29(06):27~29+116.[4]孔安.基于PCA和LDA算法的人脸识别考勤管理系统的设计与实现[D].湖南大学,2016.[5]刘光超.基于嵌入式的人脸识别系统设计与实现[D].西安科技大学, 2016.[6]潘磊.基于人脸识别算法的门禁系统的设计与实现[D].西南石油大学,2016.[7]于洋.基于人脸识别算法的门禁系统的设计与实现[D].电子科技大学,2014.收稿日期:2018-9-20基于异质集成学习方法的房价预测何睿婷(北京市一零一实验学校)【摘要】房价预测问题属于人工智能领域中的回归问题。
对于回归问题的解决,常见的机器学习模型有Ridge Regression模型,基于集成学习方法的Random Forest模型,AdaBoost模型以及XGBoost模型。
不同的模型在不同的问题中具有不同的效果,本文依据“房价预测”这一具体问题,采用了上述几种算法模型进行预测,综合了不同模型的预测情况得出最后的预测结果。
对算法模型进行了原理分析,比较了不同的分类模型解决该问题的效果,横向对比了不同模型的优缺点,并对造成结果差异的原因进行了总结。
【关键词】房价预测;Ridge Regression;RandomForest;AdaBoost;XGBoost【中图分类号】TP181【文献标识码】A【文章编号】1006-4222(2018)10-0296-021引言在机器学习领域,对分类模型的研究具有重要的意义。
集成学习作为一种能够有效提高分类模型性能的方法也被广泛使用。
集成学习分为两种类型,包括同质集成学习与异质集成学习,目前在实际应用中,大多数采用同质集成学习,包括sklearn等主流的机器学习框架,都实现了同质集成学习。
因此,对于异质集成学习进行探索就有了重要意义。
本文依据房价预测这一具体问题,通过对不同模型的综合分析,探究异质集成学习的方法。
1.1数据集特征房价预测是进行机器学习算法研究的一个经典问题。
本研究采用kaggle公开的房屋信息数据集,其中包含1460×80的训练数据集以及1460×79的测试数据集。
所有数据都包含79个特征列,其中有35个特征是数值类型的,有44个特征是类别类型的,此外在训练数据中还含有真实房价标签。
1.2数据集预处理1.2.1缺失值处理经过对数据集的统计分析发现,在整个数据集中,19个特征存在不同程度的信息缺失。
当含缺失值的特征对预测的作用不大,或者数据缺失量高于15%时,可以进行删除,比如数据集中的Alley这一特征,可分析的数据只有6.23%,可以考虑从训练数据和测试数据中直接删去这一特征。
其他含有缺失值的特征需要根据具体数据类型进行补全,常用的补全方式有mean、median或mod等。
此外,如果某一特征只在一个样本中是缺失的,那么只删除这一样本即可。
对样本精确度要求较高的模型,还可以采取分析缺失值的缺失原因,并用一定建模方法将其补全。
1.2.2缺失值补全与变换在导入数据集之后,需要对变量类型进行处理。
①对于离散变量进行一元方差分析,获得各个离散变量对房价方差的影响。
②找出会对最终房价产生较大影响的离散变量,在它们各自的取值下,会衍生出相应的房价均值。
③给各个取值划定1、2、3、4的类别来定量描述他们对于房价的影响大小,也就将离散变量转化为了数值型的有序变量。
1.2.3特征互相关分析与特征选取采取数学方法对数据进行相关性分析,离散变量间、连续变量间、两种变量间某些变量存在互相关关系,在特征选取时,应在这些互相关的特征中n选1。
1.2.4数据变换与归一化经过上述的数据分析后,我们还需要对数据进行预处理,使数据满足机器学习模型的输入要求。
这其中最重要的便是将数据的分布调整为正态分布,根据绘出的房价直方图可知,很多实际数据并不是一般的正态分布,对于这样的数据需要将其输到特定函数中,进行一定的数据变换与归一化操作,得到一条连续平滑的曲线。
1.3数据集划分1~1460条数据是80维的训练数据,1461~2920条数据是79维的测试数据。
2构建回归模型2.1构建Ridge Regression模型2.1.1基本原理岭回归模型是以最小二乘法为基础。
针对样本得到预测值和真实值之间的误差后,所得到的平方损失函数,对应存在最小值,所以这便成为了一个求极值的问题,通过梯度下降算法,不断优化模型参数[1]。
2.1.2在房价预测数据集上应用Ridge Regression模型先用线性模型拟合房产特征,再用更直观的矩阵描述出多项式,拟合出高维空间中的一个曲线。
经样本值减去期望值论述2962018年10月得到其误差,对每个样本的误差进行平方求和,得到平方损失函数,之后通过求梯度,这样也就求得了最小误差所对应的模型参数。
在参数的最小二乘估计中加入一个小扰动λI,令原先的矩阵变为满秩矩阵,使得问题稳定,再用同样的方式求偏导、参数,得到权之间的方差。
最终找到一个方差、误差均不甚大的权衡点。
2.1.3结果分析Alpha=10-20的时候,损失函数score可以降低到0.135左右。
2.2构建集成学习模型Random Forest2.2.1基本原理Bagging基于有放回抽样的思想,从给定样本的数据集中随机抽取出一个样本,放入采样集中,然后把这个样本放回最初的数据集中,使其拥有可以再次被选中的几率。
这样,对拥有n个样本的数据集经过≤n次操作后,得到了所需的采样集,而在这个采样集中,给定数据集的数据约63.2%多次出现,约36.8%没有出现。
重复上述操作,得到K个采样集,对每个采样集都训练出来一个基学习器,再通过加和求平均、简单投票法或者进行有权重的投票等集成方法,把N个基本学习器结合起来[2]。
随机森林以决策树为基学习器,在Bagging的基础上引入了对特征的随机选择,即对采样集中n个样本的m个特征进行随机抽样,改变了每个采样集的特征选取,增大了样本的多样性。
对每个采样集建立一棵决策树,最后综合所有决策树的预测情况得到最终结果。
2.2.2在房价预测数据集上应用Random Forest模型从房价预测数据集中随机抽取出一个样本,放入采样集中,然后将其放回原本的数据集,使每一次的采样都有1460个候选项。
对数据集进行1460次操作,得到一个采样集。
重复上述操作N次,得到N个采样集,相当于对样本集进行了一定程度的扩充。
对N个采样集分别训练出各自的基学习器,经过一系列的预测后,把预测出的N个房价加和,求出平均值,作为整体的预测效果。
在此抽样过程中,63.2%的数据多次出现,而将近37%的数据没有被抽到,利用未抽到的数据来验证模型的预测能力,即作为交叉验证集检测模型泛化到未知数据的能力。
从底层开始,通过包外估计辅助剪枝,在交叉验证集上比较剪枝与否对预测效果的影响,选择最优的参数和模型,能够有效地减小过拟合。
在Bagging的基础上进行随机特征选择,对形成每棵树所用到的特征随机抽样。
从每个节点的m个属性集合中随机选择一个含有k个属性的子集,然后再从该子集中选择最优分割属性作为节点,建立决策树。
重复上述操作,建立多棵决策树,形成随机森林。
2.2.3结果分析Max Features在0.5附近的时候,损失函数score可以降低到0.137~0.138。
2.3构建集成学习模型AdaBoost2.3.1基本原理Adaboost的基本思想是针对同一个训练集训练出不同的弱分类器,基于残差的概念集合起所有的弱分类器,构成一个强分类器。
Adaboost模型不需要精确地了解样本空间的分布,只需要在每个弱学习器的基础上调整样本空间分布,更新训练样本的权重,把被正确分类的样本权重降低,把被错误分类的样本权重升高。
它自适应地调整弱学习算法,经过若干次迭代后,错误率可以减小到预期效果。
同时,它在集成弱分类器时使用了加权的投票机制,分类效果好的弱分类器具有较大的权重,而分类效果差的弱分类器具有较小的权重。
2.3.2在房价预测数据集上应用AdaBoost模型首先,通过对训练样本中的房价数据进行学习得到第一个弱分类器,根据弱分类器的分类效果调整训练样本的权重,把被正确分类的样本权重降低,把被错误分类的样本权重升高得到第二份样本。
接着在第一个弱分类器的基础上用第二份样本训练第二个弱分类器,根据第二个分类的正确率,调整样本权重,得到第二个分类器和第三份样本。
重复上述过程,经过若干次训练后,整合所有的弱分类器,对它们进行加权求和,最终得到一个错误率较低的强学习器。
2.3.3结果分析n_estimators在5附近的时候,损失函数score可以降低到0.126。
2.4构建集成学习模型XGBoost2.4.1基本原理该模型由若干CART回归树组合而成,是基于Boosting 的集成学习,是特征到结果之间的映射。
其分裂点需根据预测误差的数值来划分,例如均方误差、对数误差等。
同时,它由多个相关联的回归树进行联合决策。
基于残差的概念,下一棵回归树的输入样本与前面回归树的训练、预测相关。
2.4.2在房价预测数据集上应用XGBoost模型根据真实值和预测值之间的最小均方误差来划分回归树的属性节点,而叶子节点下各个样本实际值的均值则作为分类后节点的预测值。
以此建立k个回归树,且希望树群预测的准确率高且有较大的泛化能力。
2.4.3结果分析max_depth在5附近的时候,损失函数score可以降低到0.127。
2.5应用异质集成学习方法综合各模型的预测结果我们在测试过程中,对各个预测结果采用了求和取平均的集成方法。
对岭回归的预测模型,Alpha=10~20的时候,损失函数score可以降低到到0.135左右,集成时采用了Alpha 参数为20的岭回归。
对随机森林的预测模型,MaxFeatures在0.5附近的时候,损失函数score可以降低到0.137~0.138,集成时采用了最大特征数为50%的随机森林模型。
对Adaboost 模型,n_estimators在5附近的时候,损失函数score可以降低到0.126,集成时采用了估计器个数为5的Adaboost模型。