第二章 一元线性回归习题

第2章 一元线性回归模型一、单项选择题1、变量之间的关系可以分为两大类__________。

A 函数关系与相关关系B 线性相关关系和非线性相关关系C 正相关关系和负相关关系D 简单相关关系和复杂相关关系 2、相关关系是指__________。

A 变量间的非独立关系B 变量间的因果关系C 变量间的函数关系D 变量间不确定性的依存关系 3、进行相关分析时的两个变量__________。

A 都是随机变量B 都不是随机变量C 一个是随机变量，一个不是随机变量D 随机的或非随机都可以 4、表示x 和y 之间真实线性关系的是__________。

A 01ˆˆˆt tY X ββ=+ B 01()t t E Y X ββ=+ C 01t t t Y X u ββ=++ D 01t t Y X ββ=+5、参数β的估计量ˆβ具备有效性是指__________。

A ˆvar ()=0βB ˆvar ()β为最小C ˆ()0ββ－＝ D ˆ()ββ－为最小 6、对于01ˆˆi i i Y X e ββ=++，以σˆ表示估计标准误差，Y ˆ表示回归值，则__________。

A i i ˆˆ0Y Y 0σ∑＝时，（－）＝B 2iiˆˆ0Y Y σ∑＝时，（－）＝0 C ii ˆˆ0Y Y σ∑＝时，（－）为最小 D 2iiˆˆ0Y Yσ∑＝时，（－）为最小 7、设样本回归模型为i 01i i ˆˆY =X +e ββ+，则普通最小二乘法确定的i ˆβ的公式中，错误的是__________。

A ()()()i i 12iX X Y -Y ˆX X β--∑∑＝B()i iii122iin X Y -X Y ˆn X -X β∑∑∑∑∑＝C ii122iX Y -nXY ˆX -nXβ∑∑＝ D i i ii12xn X Y -X Y ˆβσ∑∑∑＝8、对于i 01i iˆˆY =X +e ββ+，以ˆσ表示估计标准误差，r 表示相关系数，则有__________。

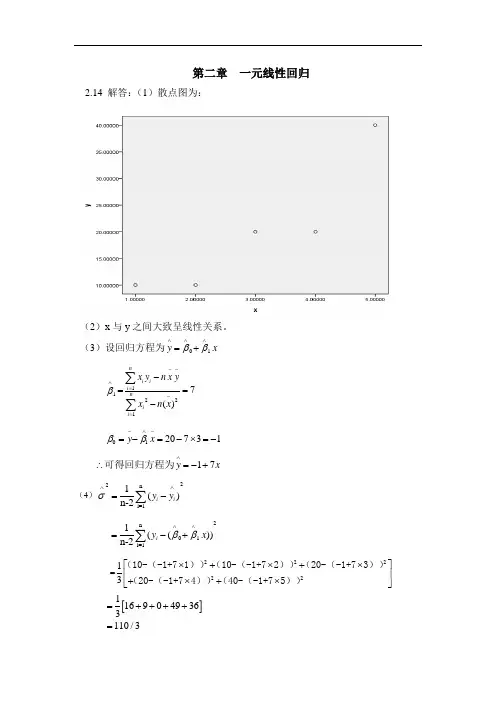
第二章 一元线性回归2.14 解答：（1）散点图为：（2）x 与y 之间大致呈线性关系。

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1169049363110/3=++++=6.1σ∧=（5）由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。

因而/2||(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即：1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为（7-2.3537+2.353 即为：（2.49，11.5）2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。

因而/2|(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为（）（6）x 与y 的决定系数22121()490/6000.817()ni i nii y y r y y ∧-=-=-==≈-∑∑（7）由于(1,3)F F α>,拒绝0H ,说明回归方程显著，x 与y 有显著的线性关系。

（8）t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈/2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0，因变量y 对自变量x 的一元线性回归成立。

第二章 一元线性回归模型典型例题分析例1、令kids 表示一名妇女生育孩子的数目，educ 表示该妇女接受过教育的年数。

生育率对教育年数的简单回归模型为μββ++=educ kids 10（1）随机扰动项μ包含什么样的因素？它们可能与教育水平相关吗？（2）上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗？请解释。

例2．已知回归模型μβα++=N E ，式中E 为某类公司一名新员工的起始薪金（元），N 为所受教育水平（年）。

随机扰动项μ的分布未知，其他所有假设都满足。

如果被解释变量新员工起始薪金的计量单位由元改为100元，估计的截距项与斜率项有无变化？如果解释变量所受教育水平的度量单位由年改为月，估计的截距项与斜率项有无变化？例3．对于人均存款与人均收入之间的关系式t t t Y S μβα++=使用美国36年的年度数据得如下估计模型，括号内为标准差：)011.0()105.151(067.0105.384ˆtt Y S +=＝0.538 023.199ˆ=σ （1）β的经济解释是什么？（2）α和β的符号是什么？为什么？实际的符号与你的直觉一致吗？如果有冲突的话，你可以给出可能的原因吗？（3）对于拟合优度你有什么看法吗？ （4）检验统计值？例4．下列方程哪些是正确的？哪些是错误的？为什么？⑴ y xt n t t=+=αβ12,,, ⑵ yx t n t tt=++=αβμ12,,, ⑶ y x t n t t t=++= ,,,αβμ12⑷ ,,,y x t n t t t =++=αβμ12 ⑸ y x t n t t =+= ,,,αβ12 ⑹ ,,,y x t n t t=+=αβ12 ⑺ y x t n t t t =++= ,,,αβμ12 ⑻ ,,,y x t n t t t=++=αβμ12 其中带“＾”者表示“估计值”。

例5．对于过原点回归模型i i i u X Y +=1β ，试证明∑=∧221)(iu X Var σβ例6、对没有截距项的一元回归模型i i i X Y μβ+=1称之为过原点回归（regression through the origin ）。

第一章绪论一、单项选择题1、变量之间的关系可以分为两大类，它们是【】A 函数关系和相关关系B 线性相关关系和非线性相关关系C 正相关关系和负相关关系D 简单相关关系和复杂相关关系2、相关关系是指【】A 变量间的依存关系B 变量间的因果关系C 变量间的函数关系D 变量间表现出来的随机数学关系3、进行相关分析时，假定相关的两个变量【】A 都是随机变量B 都不是随机变量C 一个是随机变量，一个不是随机变量D 随机或非随机都可以4、计量经济研究中的数据主要有两类：一类是时间序列数据，另一类是【】A 总量数据B 横截面数据C平均数据 D 相对数据5、横截面数据是指【】A 同一时点上不同统计单位相同统计指标组成的数据B 同一时点上相同统计单位相同统计指标组成的数据C 同一时点上相同统计单位不同统计指标组成的数据D 同一时点上不同统计单位不同统计指标组成的数据6、下面属于截面数据的是【】A 1991-2003年各年某地区20个乡镇的平均工业产值B 1991-2003年各年某地区20个乡镇的各镇工业产值C 某年某地区20个乡镇工业产值的合计数D 某年某地区20个乡镇各镇工业产值7、同一统计指标按时间顺序记录的数据列称为【】A 横截面数据B 时间序列数据C 修匀数据D原始数据8、经济计量分析的基本步骤是【】A 设定理论模型→收集样本资料→估计模型参数→检验模型B 设定模型→估计参数→检验模型→应用模型C 个体设计→总体设计→估计模型→应用模型D 确定模型导向→确定变量及方程式→估计模型→应用模型9、计量经济模型的基本应用领域有【】A 结构分析、经济预测、政策评价B 弹性分析、乘数分析、政策模拟C 消费需求分析、生产技术分析、市场均衡分析D 季度分析、年度分析、中长期分析10、计量经济模型是指【】A 投入产出模型B 数学规划模型C 包含随机方程的经济数学模型D 模糊数学模型11、设M为货币需求量，Y为收入水平，r为利率，流动性偏好函数为：M＝a＋bY＋cr＋u，b’和c’分别为b、c的估计值，根据经济理论，有【】A b’应为正值，c’应为负值B b’应为正值，c’应为正值C b’应为负值，c’应为负值D b’应为负值，c’应为正值12、回归分析中定义【】A 解释变量和被解释变量都是随机变量B 解释变量为非随机变量，被解释变量为随机变量C 解释变量和被解释变量都是非随机变量D 解释变量为随机变量，被解释变量为非随机变量13、线性模型的影响因素【】A 只能是数量因素B 只能是质量因素C 可以是数量因素，也可以是质量因素D 只能是随机因素14、下列选项中，哪一项是统计检验基础上的再检验(亦称二级检验)准则【】A. 计量经济学准则 B 经济理论准则C 统计准则D 统计准则和经济理论准则15、理论设计的工作，不包括下面哪个方面【】A 选择变量B 确定变量之间的数学关系C 收集数据D 拟定模型中待估参数的期望值16、计量经济学模型成功的三要素不包括【】A 理论B 应用C 数据D 方法17、在模型的经济意义检验中，不包括检验下面的哪一项【】A 参数估计量的符号B 参数估计量的大小C 参数估计量的相互关系D 参数估计量的显著性18、计量经济学模型用于政策评价时，不包括下面的那种方法【】A 工具变量法B 工具—目标法C 政策模拟D 最优控制方法19、在经济学的结构分析中，不包括下面那一项【】A 弹性分析B 乘数分析C 比较静力分析D 方差分析二、填空题1、计量经济学是_________的一个分支学科，是以揭示_________中的客观存在的_______ 为内容的分支学科。

第二章 一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答： 假设1、解释变量X 是确定性变量，Y 是随机变量；假设2、随机误差项ε具有零均值、同方差和不序列相关性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关： Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi （i=1,2, …,n ）仍满足基本假定。

求β1的最小二乘估计 解： 得：2.3 证明（2.27式），∑e i =0 ，∑e i X i =0 。

证明：∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中：即： ∑e i =0 ，∑e i X i =021112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=0)ˆ(2ˆ111=--=∂∂∑=ii ni i eX X Y Q ββ)()(ˆ1211∑∑===ni i ni ii X Y X β01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂2.4回归方程E （Y ）=β0+β1X 的参数β0，β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。

答：由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函数：使得Ln （L ）最大的0ˆβ，1ˆβ就是β0，β1的最大似然估计值。

同时发现使得Ln （L ）最大就是使得下式最小，∑∑+-=-=nii i n i X Y Y Y Q 121021))ˆˆ(()ˆ(ββ上式恰好就是最小二乘估计的目标函数相同。

习 题第二章 经典单方程计量经济学模型：一元线性回归模型1.假设居民户储蓄（Y ）与收入（X ）之间可建立如下形式的储蓄模型：μββ++=X Y 10 εμ21X =其中，ε为具有零均值0)(=εE 、同方差2)(εσε=Var 且与X 相互独立的随机变量。

（1） 该模型服从零均值基本假设吗？（2） 该模型服从同方差基本假设吗？（3） 如果该模型不满足同方差性，试解释随着居民户收入X 的提高，随机扰动项μ的方差是增大还是缩小？2.对于人均存款与人均收入之间的关系式t t t Y S μβα++=∧，使用美国36年的年度数据，得到如下估计模型（括号内为标准差）：t t Y S 067.0105.384+=∧（151.105） （0.011）（1）β的经济解释是什么？（2） α、β的符号是什么？为什么？实际的符号与你的直觉一致吗？如果有冲突的话，你可以给出可能的原因吗？（3） 你对于拟合优度有什么看法？（4） 检验是否每一个回归系数都与零显著不同（在1%的水平下）。

同时对零假设和备择假设，检验统计值及其分布和自由度，以及拒绝零假设的标准进行陈述。

你的结论是什么？3.对于一元线性回归模型μββ++=X Y 10，试证明OLS 估计量∧1β在所有线性无偏估计量中具有最小方差。

第三章 经典单方程计量经济学模型：多元线性回归模型1.在经典线性模型基本假定下，对含有三个自变量的多元回归模型：μββββ++++=3322110X X X Y你想检验的虚拟假设是12:210=-ββH 。

（1）用∧1β，∧2β的方差及其协方差求出)2(21∧∧-ββVar 。

（2）写出检验12:210=-ββH 的t 统计量。

（3）如果定义θββ=-212，写出一个涉及0β，θ，2β和3β的回归方程，以便能直接得到θ的估计值∧θ及其标准差。

2. 对于涉及三个变量Y ，1X ，2X 的数据做以下回归：（1）1110i i i X Y μαα++=（2）2210i i i X Y μββ++=（3）322110i i i i X X Y μγγγ+++=问在什么条件下才能有∧∧=11γα及∧∧=21γβ，即多元回归与各自的一元回归所得的参数估计值相同。

第二章 经典单方程计量经济学模型：多元线性回归模型1、下列表达式中，哪些是正确的，哪些是错误的，为什么？⑴ n t X Y tt ,,2,1 =+=βα ⑵ n t X Y tt t ,,2,1 =++=μβα ⑶ n t X Y tt t ,,2,1ˆˆ =++=μβα ⑷ n t X Y tt t ,,2,1ˆˆˆ =++=μβα ⑸ n t X Y tt ,,2,1ˆˆ =+=βα ⑹ n t X Y tt ,,2,1ˆˆˆ =+=βα ⑺ n t X Y t tt ,,2,1ˆˆˆ =++=μβα ⑻ n t X Y t t t ,,2,1ˆˆˆˆ =++=μβα2、一元线性回归模型的基本假设主要有哪些？违背基本假设的计量经济学模型是进行普通最小二乘估计吗？3、线性回归模型n i X Y ii i ,,2,1 =++=μβα 的零均值假设是否可以表示为011=∑=ni i n μ？为什么？4、假设已经得到关系式X Y 10ββ+=的最小二乘估计，试回答：（1）假设决定把变量X 的单位扩大10倍，这样做对回归模型的斜率和截距的估计会有什么样的影响？如果把变量Y 的单位扩大10倍，结果又会怎样？（2）假定给X 的每个观测值都增加2，对原回归的斜率和截距会有什么样的影响？如果给Y 的每个观测值都增加2，又会怎样？5、假使在回归模型i i i X Y μββ++=10中，用不为零的常数δ去乘每一X 值，这会不会改变Y 的拟合值及残差？如果对每个X 都加大一个非零常数δ，又会怎样？6、假设有人做了如下的回归i i i x y μββ++=10其中，i i x y ,分别为i i X Y ,关于各自均值的离差。

求1β和0β的普通最小二乘估计？7、令YX βˆ和XYβˆ分别为Y 对X 回归和X 对Y 回归中的斜率（假设X 与Y 之间互为因果关系），证明2ˆˆr XYYX =ββ，其中r 为X 与Y 之相的样本相关系数。

第2章 一元线性回归模型习 题一、单项选择题 1．最小二乘法是指（） A. 使达到最小值 B. 使达到最小值 C. 使达到最小值 D. 使达到最小值2． 在一元线性回归模型中，样本回归方程可表示为（ ） A. B.C ． D.3．线设OLS 法得到的样本回归直线为，以下说法不正确的是( )A ．B ．C ．D ．在回归直线上4．对样本的相关系数，以下结论错误的是（ ）A. 越接近0， 与之间线性相关程度高B.越接近1，与之间线性相关程度高 C.D 、，则与相互独立二、多项选择题1．最小二乘估计量的统计性质有（ ）A. 无偏性B. 线性性C. 最小方差性D. 不一致性E. 有偏性2．利用普通最小二乘法求得的样本回归直线的特点（）A. 必然通过点B. 可能通过点C. 残差的均值为常数D. 的平均值与的平均值相等E. 残差与解释变量之间有一定的相关性3．随机变量（随机误差项）中一般包括那些因素（ ）A 回归模型中省略的变量B 人们的随机行为C 建立的数学模型的形式不够完善。

()∑=-nt ttYY 1ˆˆmin i i Y Y -tt Y Y ˆmax -()21ˆ∑=-n t t t Y Y 01i i i Y X u ββ=++01ˆˆˆi i i Y X e ββ=++01ˆˆˆi i Y X ββ=+()01i iE Y X ββ=+01ˆˆi i i Y X e ββ=++0=∑i e 0),(≠i i e X COV YY =ˆ),(Y X γγX Y γX Y 11γ-≤≤0γ=X Y 01ˆˆˆi i Y X ββ=+(,)X Y (,)X Y i e ˆi Y i Y i e i X i uD经济变量之间的合并误差。

E测量误差。

三、计算题1．表1是中国1978年-1997年的财政收入Y和国内生产总值X的数据，表2为一元线性回归模型的估计结果表1 中国1978－1997年的财政收入与国内生产总值（单位：亿元）数据来源:《中国统计年鉴》表2 Eviews 软件的估计结果试根据这些数据完成下列问题；(1)建立财政收入对国内生产总值的简单线性回归模型，并解释斜率系数的经济意义；(2)对此模型进行评价；(3)若是1998年的国内生产总值为78017.8亿元，确定1998年财政收入的预测值和预测区间(,)。

第二章一元线性回归习题补充第二章一元线性回归习题补充1、微观金融学和投资学中很重要的资本资产定价模型(CAPM),需要知道值,股票的大于1的股票称为进攻型股票,小于1的股票称为防卫型股票。

观察个股的价格变化与指数的价格走势,会发现在大多数情况下,当指数上升,个股的价格也上升,反之,当指数下降时,个股的价格也下降。

如果我们用价格(指数)环比增长率来表示收益率,即: 其中是个股价格,是指数价格。

我们用武钢股份和上证综合指数为例,采用2002.8.9-2007.10.26的周收盘价数据。

根据CAPM理论,方程设定为:是武钢股份的周价格环比增长率,是上证综合指数的周价格环比增长率,作为收益率。

(1)根据提供的2002.8.9-2007.10.26的周收盘价数据,做出武钢股份的CAPM模型,此期间,武钢股份是进攻型还是防卫型股票?(2)请在股票软件中找到相关数据,并做武钢股份最新数据的CAPM模型。

(3)如果用表示收益率,请重新做CAPM模型,比较两个模型的结果。

2、上题中,如果对截距进行检验,截距与0有显著差异吗?如果不显著,请做无截距回归,并比较两个模型的回归结果。

提示:根据CAPM模型,截距预期为0。

截距为0的模型叫做过原点回归模型,其他适合于零截距的例子还有弗里德曼的永久收入假说:永久消费正比于永久收入;成本分析理论:生产的可变成本正比于产出;货币主义者的某些假说:价格变化率(即通货膨胀率)正比于货币供应变化率。

在EViews中,只要在方程设定框,删除“c”就可以了。

3、在一个运用EViews做的回归中,得到下表,但是空缺了两个数据(有问号处):回归结果Variable Coefficient Std. Error t-Statistic ProbC 282.2434 287.2649 ? 0.3340X ? 0.036928 20.54026 0.0000R-squared 0.935685 Mean dependent var 5982.476Adjusted R-squared 0.933467 S.D. dependent var 1601.762S.E. of regression 413.1593 Akaike info criterion 14.94788Sum squared resid 4950317Schwarz criterion 15.04040Log likelihood -229.6922 F-statistic 421.9023Durbin-Watson stat 1.481439 ProbF-statistic 0.000000(1)请补充这两个数据(2)如果显著性水平,请用值法进行检验。

一元线性回归模型一、单项选择题1、变量之间的关系可以分为两大类__________。

AA 函数关系与相关关系B 线性相关关系和非线性相关关系C 正相关关系和负相关关系D 简单相关关系和复杂相关关系 2、相关关系是指__________。

DA 变量间的非独立关系B 变量间的因果关系C 变量间的函数关系D 变量间不确定性的依存关系 3、进行相关分析时的两个变量__________。

AA 都是随机变量B 都不是随机变量C 一个是随机变量，一个不是随机变量D 随机的或非随机都可以 4、表示x 和y 之间真实线性关系的是__________。

CA 01ˆˆˆt tY X ββ=+ B 01()t t E Y X ββ=+ C 01t t t Y X u ββ=++ D 01t t Y X ββ=+5、参数β的估计量ˆβ具备有效性是指__________。

B A ˆvar ()=0βB ˆvar ()β为最小C ˆ()0ββ－＝ D ˆ()ββ－为最小 6、对于01ˆˆi i iY X e ββ=++，以σˆ表示估计标准误差，Y ˆ表示回归值，则__________。

BA i i ˆˆ0Y Y 0σ∑＝时，（－）＝B 2iiˆˆ0Y Y σ∑＝时，（－）＝0 C ii ˆˆ0Y Y σ∑＝时，（－）为最小 D 2iiˆˆ0Y Yσ∑＝时，（－）为最小 7、设样本回归模型为i 01i iˆˆY =X +e ββ+，则普通最小二乘法确定的i ˆβ的公式中，错误的是__________。

DA ()()()ii12i X X Y -Y ˆX X β--∑∑＝B ()i iii122iin X Y -X Y ˆn X -X β∑∑∑∑∑＝C ii 122iX Y -nXY ˆX -nX β∑∑＝ D i i ii12xn X Y -X Y ˆβσ∑∑∑＝8、对于i 01i i ˆˆY =X +e ββ+，以ˆσ表示估计标准误差，r 表示相关系数，则有__________。

第二章 一元线性回归模型一、单项选择题1、D2、B 6、C 7、D 8、C 9、C 10、B11、B 12、B 13、B 14、D一、单项选择题1、设OLS 法得到的样本回归直线为1ˆi Y β=2ˆi i X e β++，以下说法正确的是（ D ） A 、0i e ≠∑ B 、ˆ0i ieY ≠∑C 、ˆY Y ≠D 、0i ie X =∑ 2、回归分析中定义的 （ B ）A 、解释变量和被解释变量都是随机变量B 、解释变量为非随机变量，被解释变量为随机变量C 、解释变量和被解释变量都为非随机变量D 、解释变量为随机变量，被解释变量为非随机变量6、在一元线性回归模型中，样本回归方程可表示为： （ C ）A 、01tt t Y X ββμ=++ B 、(/)t t t Y E Y X μ=+C 、01ˆˆˆt t Y X ββ=+D 、01(/)t tE Y X X ββ=+ 7、最小二乘准则是指按使（ ）达到最小值的原则确定样本回归方程 （ D ）A 、1n i i e=∑ B 、1n i i e =∑ C 、max i e D 、21ni i e=∑8、设Y 表示实际观测值，ˆY 表示OLS 回归估计值，则下列哪项成立 （ C ）A 、ˆYY = B 、 ˆY Y = C 、ˆYY = D 、ˆY Y = 9、最大或然准则是按从模型中得到既得的n 组样本观测值的（ ）最大的准则确定样本回归方程。

（ C ）A 、离差平方和B 、均值C 、概率D 、方差10、一元线性回归模型01i i i Y X ββμ=++的最小二乘回归结果显示，残差平方和RSS=40.32,样本容量n=25，则回归模型的标准差σ为 （ B ）A 、1.270B 、1.324C 、1.613D 、1.75311、参数i β的估计量ˆi β具备有效性是指 （ B ） A 、ˆ()0i Var β= B 、在iβ的所有线性无偏估计中ˆ()i Var β最小C 、ˆ0i i ββ-=D 、在iβ的所有线性无偏估计中ˆ()i i ββ-最小 12、反映由模型中解释变量所解释的那部分离差大小的是 （ B ）A 、总离差平方和B 、回归平方和C 、残差平方和D 、可决系数13、总离差平方和TSS 、残差平方和RSS 与回归平方和ESS 三者的关系是 （ B ）A 、TSS>RSS+ESSB 、TSS=RSS+ESSC 、TSS<RSS+ESSD 、TSS 2=RSS 2+ESS 214、对于回归模型01i i i Y X ββμ=++，i = 1，2，…，n检验01:0H β=时，所用的统计量1ˆ11ˆβββS -服从 （ D ） A 、2(2)n χ- B 、(1)t n -C 、2(1)n χ-D 、(2)t n -二、判断题二、判断题1、×2、×3、×4、√5、×6、×7、×8、×9、√ 10、√1、满足基本假设条件下，随机误差项i μ服从正态分布，但被解释变量Y 不一定服从正态分布。

第二章 练习题1. 为什么计量经济学的理论方程中必须包含随机干扰项？2. 下列计量经济学方程哪些是正确的？哪些是错误的？为什么？(1) t t X Y βα+=， n t ，， 2,1=； (2) t t t X Y μβα++=， n t ，， 2,1=；(3) t t t X Y μβα++=ˆˆ n t ，， 2,1=； (4) tt t X Y μβα++=ˆˆˆ n t ，， 2,1=； (5) t t X Y βαˆˆ+=， n t ，， 2,1=； (6) tt X Y βαˆˆˆ+=， n t ，， 2,1=； (7) t t t X Y μβαˆˆˆ++= n t ，， 2,1=； (8) t tt X Y μβαˆˆˆˆ++= n t ，， 2,1=。

3. 一元线性回归模型的基本假设主要有哪些？违背基本假设的计量经济学模型是否就不可以估计？4. 线性回归模型i i i X Y μβα++=，n i ，，2,1=的零均值假设是否可以表示为 011=∑=ni i n μ？ 为什么？5. 假设已经得到关系式X Y 10ββ+=的最小二乘估计，试回答：(1) 假设决定把X 变量的单位扩大10倍，这样对原来回归的斜率和截距会有什么样的影响？如果把Y 变量的单位扩大10倍，又会怎样？(2) 假定给X 的每个观测值都增加2，对原来回归的斜率和截距会有什么样的影响？如果给Y 的每个观测值都增加2，又会怎样？ 6. 假使在回归模型i i i X Y μββ++=10中，用不为零的常数δ去乘每一个X 值，这会不会改变Y 的拟合值及残差？如果对每个X 都加大一个非零常数δ，又会怎样？7. 假设有人做了如下的回归：ii i e x y ++=10ˆˆββ。

其中，i y ，i x 分别为i Y ，i X 关于各自均值的离差。

问0ˆβ和1ˆβ将分别取何值？ 8. 令YX βˆ和XYβˆ分别为Y 对X 的回归和X 对Y 的回归中的斜率，证明： 2ˆˆr XY YX =ββ其中r 为X 与Y 之间的线性相关系数。

第二章 一元线性回归2.14 解答：（1）散点图为：（2）x 与y 之间大致呈线性关系。

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1169049363110/3=++++=6.1σ∧=≈ （5）由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。

因而/2|(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即：1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为（7-2.3537+2.353 即为：（2.49，11.5）2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。

因而/2(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为（）（6）x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑（7）由于(1,3)F F α>,拒绝0H ,说明回归方程显著，x 与y 有显著的线性关系。

（8）t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈ /2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0，因变量y 对自变量x 的一元线性回归成立。

第二章 一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答： 假设1、解释变量X 是确定性变量，Y 是随机变量；假设2、随机误差项ε具有零均值、同方差和不序列相关性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关： Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi （i=1,2, …,n ）仍满足基本假定。

求β1的最小二乘估计 解： 得：2.3 证明（2.27式），∑e i =0 ，∑e i X i =0 。

证明：∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中：即： ∑e i =0 ，∑e i X i =021112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=0)ˆ(2ˆ111=--=∂∂∑=ii ni i eX X Y Q ββ)()(ˆ1211∑∑===ni i ni ii X Y X β01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂2.4回归方程E （Y ）=β0+β1X 的参数β0，β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。

答：由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函数：使得Ln （L ）最大的0ˆβ，1ˆβ就是β0，β1的最大似然估计值。

同时发现使得Ln （L ）最大就是使得下式最小，∑∑+-=-=nii i n i X Y Y Y Q 121021))ˆˆ(()ˆ(ββ上式恰好就是最小二乘估计的目标函数相同。

2.10以下回归方程中存在明显错误的有哪些？（1）其中Y为贷款额，X为贷款利率（2）其中Y为消费支出，X为可支配收入（3）其中ER为差错率，T为训练时间（4）其中CPR为资本利润率，CC为资本周转次数（5）其中SR为小时工资，WLR为失业率（6）其中Q为食品消费支出，IN为消费者收入，P为食品消费价格指数【解析】（1）错误。

贷款额与贷款利率之间是负向关系，所以解释变量X贷款利率前的参数估计值应该为负。

（2）错误。

X为可支配收入，则其对应的参数估计值应该在[0,1]范围内，该回归结果参数估计值为1.2345，超出理论范围。

（3）错误。

差错率与训练时间之间是负向关系，所以T训练时间前的参数估计值应该为负。

（4）正确。

（5）错误。

一般宏观经济学理论描述的是SR小时工资变动对WLR失业率的影响关系，即应该将SR小时工资变动作为解释变量更符合经济学原理。

并且二者之间是负相关关系。

（6）正确。

2.12收集2013年中国31省、区、市农村居民人均纯收入X与人均现金消费支出Y的数据，如下表（单位：元）：地区名称纯收入X消费支出Y 地区名称纯收入X消费支出Y北京18337.513470.2湖北8867.05531.1天津15841.010088.6湖南8372.15854.2河北9101.95969.6广东11669.37881.5山西7153.55463.2广西6790.94547.0作内蒙古8595.76763.3海南8342.65090.7辽宁10522.76864.9重庆8332.05057.8吉林9621.26827.6四川7895.35406.1黑龙江9634.16542.1贵州5434.03888.3上海19595.013872.9云南6141.33953.0江苏13597.89486.9西藏6578.22661.5浙江16106.011541.1陕西6502.65420.7安徽8097.95344.9甘肃5107.84393.7福建11184.27552.5青海6196.45506.6江西8781.54910.1宁夏6931.05942.1山东10619.97184.2新疆7296.55519.9河南8475.35353.0资料来源：2014年版《中国统计年鉴》。