第三章二计量经济学-需求函数
- 格式:ppt
- 大小:596.50 KB
- 文档页数:48



需求函数公式需求函数公式是指描述需求与某个或某些因素之间关系的函数表达式。
需求函数通常用来分析和预测市场需求的变化情况,帮助企业制定合理的生产和销售策略。
需求函数一般形式为:Q = f(P, I, T, O, E),其中Q表示需求量,P表示产品价格,I表示消费者收入,T表示相关的市场和消费者特征,O表示其他相关因素,E表示误差项。
需求函数可以是线性的、非线性的、多元的等形式,具体形式取决于所研究的问题和数据。
需求函数的推导和分析是经济学中的重要内容,通过分析需求函数可以得到对需求的深入认识,为企业决策提供科学依据。
需求函数表达了需求与价格、收入和其他因素之间的关系,可以帮助企业理解市场需求的变化规律,合理确定产品价格和销售策略,以及预测市场需求的未来走势。
需求函数的推导和分析需要基于大量的市场数据和经济理论的支持。
通过对市场调查和数据分析,可以获取不同变量之间的关系以及其对需求的影响程度。
在推导需求函数时,需要考虑到各种因素的复杂性和相互作用的影响,以及可能存在的误差项。
通过需求函数的分析,企业可以了解不同因素对需求的影响程度,从而制定相应的策略。
例如,当产品价格上涨时,需求量可能会下降,企业可以考虑适当降低价格以刺激需求;当消费者收入增加时,需求量可能会增加,企业可以考虑推出高档产品以满足消费者需求。
需要注意的是,需求函数只是一种理论模型,实际情况可能存在很多复杂因素和不确定性。
因此,在应用需求函数时,需要结合实际情况进行合理的调整和预测。
同时,需求函数的分析也需要不断更新和修正,以适应市场的变化和发展。
需求函数是描述需求与价格、收入和其他因素之间关系的函数表达式。
通过分析需求函数,企业可以深入了解市场需求的变化规律,制定合理的生产和销售策略,预测市场需求的未来走势。
然而,需求函数只是一种理论模型,实际应用时需要结合实际情况进行调整和修正,以适应市场的变化和发展。

需求函数公式需求函数是描述一种现象、商品或服务对某一特定问题的需求程度的数学模型。
它通常用数学公式形式化表示,以定量的方式测量需求的程度。
需求函数的一般形式可以表示为:Q = f(P, I, A, T, O, S)其中,Q是需求的数量,P是商品或服务的价格,I是消费者的收入水平,A是替代品的价格或可用性,T是与商品或服务有关的个体偏好或市场环境的趋势因素,O是其他市场因素,S是特定的经济、社会或文化因素。
这些因素在不同的需求函数中起着不同的作用。
下面是一些常见的需求函数及其相关参考内容:1. 单变量线性需求函数:Q = a - bP这是最简单的需求函数形式之一,其中a和b是常数。
a表示需求量的最大值,b表示价格弹性。
相关参考内容可以包括市场调查、历史数据分析和价格弹性的文献研究。
2. 多变量线性需求函数:Q = a - b1P - b2I - b3A这个需求函数考虑了价格、收入和替代品的影响。
b1、b2和b3是价格弹性、收入弹性和替代品价格弹性的系数。
相关参考内容可以包括调查数据、经济统计和市场报告。
3. Cobb-Douglas需求函数:Q = a * P^b * I^c * A^d这个函数是一种经典的生产函数形式,常用于描述多个因素对需求的影响。
指数b、c和d表示价格弹性、收入弹性和替代品价格弹性的影响。
相关参考内容可以包括经济学文献、市场研究和市场调查。
4. 拉格朗日乘数法需求函数:Q = f(P, I, A, T) + λ(g(P, I, A, T) - O)这个需求函数结合了约束条件的优化问题。
拉格朗日乘数λ表示了约束条件与目标函数的关系。
相关参考内容可以包括微积分教材、最优化理论和经济学优化模型的文献。
这些需求函数形式只是其中的一部分,实际上还存在许多其他的需求函数形式,因为需求函数往往是根据具体问题和背景来选择的。
建立需求函数需要结合特定的市场、行业和产品特征,并且需要基于可靠的数据和经济理论加以推导和验证。


计量经济学讲义投资函数模型和货币需求函数模型投资函数模型和货币需求函数模型是财务管理和投资管理领域中常用的计量经济学模型。
这些模型可以帮助分析和解释投资决策和货币需求的关键因素,进而指导企业和个人进行有效的财务和投资管理。
本文将就这两个模型进行详细介绍。
一、投资函数模型投资函数模型是描述投资支出与其决定因素之间关系的经济模型。
投资支出是指企业和个人为购买和增加生产资产而进行的支出,通常包括固定资产投资和存货投资。
投资函数模型通过分析各种因素对投资支出的影响,帮助企业和个人预测和规划投资支出。
投资函数模型通常采用线性回归模型表示,基本形式为:I=α+βY+γR+δI其中,I表示投资支出,Y表示收入,R表示利率,α、β、γ、δ分别表示参数。
在这个模型中,收入是影响投资支出最重要的因素之一、通常情况下,较高的收入会促使企业和个人增加投资支出。
利率也是影响投资支出的重要因素之一,一般来说,较低的利率会鼓励更多的投资支出。
此外,企业和个人的预期收入和投资支出也会对实际投资支出产生影响。
根据这个模型,企业和个人可以根据自身情况预测和规划未来的投资支出。
同时,政府和金融机构也可以通过调控利率和提供相关政策,影响企业和个人的投资决策。
货币需求函数模型是描述货币需求与其决定因素之间关系的经济模型。
货币需求是指企业和个人为进行交易和储备而持有的货币数量。
货币需求函数模型通过分析各种因素对货币需求的影响,帮助企业和个人预测和规划货币需求。
货币需求函数模型通常采用经济学模型表示MD=f(Y,R,P)其中,MD表示货币需求,Y表示收入,R表示利率,P表示物价水平。
在这个模型中,收入是影响货币需求的最重要因素之一、一般来说,较高的收入会促使企业和个人增加货币需求。
利率也是影响货币需求的关键因素,一般情况下,较低的利率会减少货币需求。
物价水平也会对货币需求产生影响,一般来说,较高的物价水平会增加货币需求。
根据这个模型,企业和个人可以根据自身情况预测和规划未来的货币需求,例如确定适当的储蓄和投资计划。

需求函数公式需求函数是指用来描述消费者对某种商品或服务需求的数学函数。
它通常用来表示消费者的需求量如何随着价格、收入和其他相关因素的变化而变化。
需求函数的公式可以根据具体的情况和经济模型来确定,下面是一些相关参考内容。
一、线性需求函数:线性需求函数是最简单直接的一种需求函数形式,它假设需求量与价格成反比。
线性需求函数的一般形式可以表示为:Q =a - bP其中Q表示需求量,P表示价格,a和b为常数。
a表示需求函数的截距,表示当价格为0时的需求量;b表示负的斜率,表示需求量随价格变化的速度。
二、非线性需求函数:非线性需求函数是指需求量与价格的关系不是简单的线性关系,而是形成了一条曲线。
常见的非线性需求函数包括:1.常见的例子有二次函数需求函数形式:Q = a - bP + cP^2其中a、b、c为常数,P表示价格,Q表示需求量。
二次函数形式的需求函数在价格变化时呈现出一种曲线的关系。
2.指数函数需求函数形式:Q = aP^b其中a和b为常数,P表示价格,Q表示需求量。
指数函数形式的需求函数在价格变化时呈现出一种指数增长或指数衰减的关系。
三、多变量需求函数:多变量需求函数考虑了除了价格之外的其他影响因素对需求量的影响。
常见的多变量需求函数包括:1.收入影响的需求函数形式:Q = a + bP + cY其中Q表示需求量,P表示价格,Y表示收入,a、b、c为常数。
这种需求函数考虑了收入对需求量的影响,可以用来分析在不同收入水平下的需求量变化。
2.广义线性需求函数形式:Q = a + b1P + b2I + b3A + b4O +b5T其中Q表示需求量,P表示价格,I表示收入,A表示广告投入, O表示其他相关因素(如季节性因素),T表示时间,a,b1,b2,b3,b4, b5为常数。
这种需求函数考虑了多种影响因素对需求量的影响,可以用来分析需求量如何受到多种因素的共同影响。
以上是一些关于需求函数公式的参考内容。

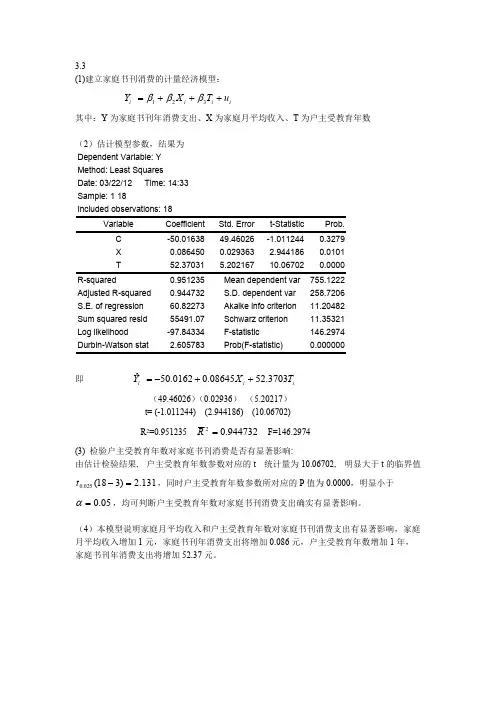
3.3(1)建立家庭书刊消费的计量经济模型:ii i i u T X Y +++=321βββ其中:Y 为家庭书刊年消费支出、X 为家庭月平均收入、T 为户主受教育年数(2)估计模型参数,结果为Dependent Variable: Y Method: Least SquaresDate: 03/22/12 Time: 14:33Sample: 1 18Included observations: 18Variable Coefficient Std. Error t-Statistic Prob. C -50.0163849.46026-1.0112440.3279X 0.0864500.029363 2.9441860.0101T52.370315.20216710.067020.0000R-squared0.951235 Mean dependent var 755.1222Adjusted R-squared 0.944732 S.D. dependent var 258.7206S.E. of regression 60.82273 Akaike info criterion 11.20482Sum squared resid 55491.07 Schwarz criterion 11.35321Log likelihood -97.84334 F-statistic146.2974Durbin-Watson stat2.605783 Prob(F-statistic)0.000000即 ii i T X Y 3703.5208645.00162.50ˆ++-=(49.46026)(0.02936) (5.20217) t= (-1.011244) (2.944186) (10.06702)R 2=0.951235 F=146.2974944732.02=R (3) 检验户主受教育年数对家庭书刊消费是否有显著影响:由估计检验结果, 户主受教育年数参数对应的t 统计量为10.06702, 明显大于t 的临界值,同时户主受教育年数参数所对应的P 值为0.0000,明显小于131.2)318(025.0=-t ,均可判断户主受教育年数对家庭书刊消费支出确实有显著影响。

总需求函数“需求(demand)”是指消费者在市场交换过程中,有意愿愿愿以某种价格购买某种商品或服务的程度。
它是市场经济体系中消费、生产、价格和收入都关键的活动因素。
需求的定量表示是一种需求函数,也称为总需求函数,它根据消费者在不同价格水平下,对该商品或服务的需求量,来表示需求函数。
需求函数通常具有以下几个重要特征:(1)需求之间存在拉锯式的关系,即当价格降低时,消费者对该商品的需求量会增加;而价格升高时,消费者对该商品的需求量则减少。
(2)需求函数的斜率表示消费者对价格的反应强度,即需求函数的斜率越大,消费者对价格的反应强度也越大。
(3)需求函数在不同价格水平下,可以描述出消费者对商品或服务的需求量。
一般来说,我们可以根据消费者的不同偏好,以及消费者在不同价格水平下对某种商品或服务的需求量,来构建总需求函数。
尽管总需求函数的每个因素都会有所不同,但它们一般有如下几种形式:(1)线性需求函数:在此类型的需求函数中,消费者对价格的反应强度是平等的,也就是说,每增加一个单位价格,消费者对该商品或服务的需求量都会减少一个单位量。
(2)指数需求函数:在此类型的需求函数中,消费者对价格的反应强度是不等的,也就是说,随着价格的上涨,消费者对该商品或服务的需求量也会成指数式的减少。
(3)双曲线需求函数:该类需求函数也被称为双台塔函数,是由三段线性函数组成的一种复杂的需求函数。
它是以拐点作为中心,一端接近线性需求函数,另一端接近指数需求函数,是两者相结合的一种需求函数。
(4)S型需求函数:S型需求函数由两条线性函数组成,其中一条描述的是消费者对商品的需求增加随着价格的减少,另一条描述的是随着价格的上涨,消费者对商品的需求量逐渐降低。
无论是哪种需求函数,其实质都是通过表明消费者对价格的反应来表示消费者对某种商品或服务的需求,这样,企业可以根据总需求函数来更有效地提升商品或服务的销量。
企业可以通过降低商品价格,并从中获得更大的利润空间,或者提高商品价格,从而提高该商品的利润率。
需求函数名词解释需求函数是指在特定的条件下,描述单个或群体所需的产品或服务数量与价格的关系的函数。
需求函数是由消费者的购买意愿、预算、个人品味以及市场竞争等因素决定的。
它可以用来衡量消费者对产品或服务的需求程度,从而为企业制定价格、决策市场战略提供依据。
需求函数通常以价格作为自变量,表示价格对需求的影响。
在典型的需求函数中,需求通常随着价格的增加而减少,即存在逆向的线性关系。
该函数可以用数学形式表示为:Q = f(P),其中Q表示需求量,P表示价格,f(P)表示价格对需求的函数关系。
需求函数还可以进一步扩展为多变量的形式,考虑其他影响需求的因素,例如收入、市场规模、广告宣传等。
多变量的需求函数通过引入其他自变量来解释需求量的波动和变化,可以更准确地预测需求的变化。
需求函数的图像通常是一个下降的曲线,即需求曲线。
需求曲线的斜率表示需求的弹性,即需求对价格变动的敏感程度。
当需求曲线陡峭时,需求的弹性较低,产品价格的变动对需求的影响较小;当需求曲线平缓时,需求的弹性较高,产品价格的变动对需求的影响较大。
通过分析需求函数,可以获得以下几点重要信息:1.需求弹性:需求函数可以定量地衡量价格变动对需求的影响,从而帮助企业了解市场需求的变化情况。
如果需求弹性较低,企业可能可以提高价格以获取更高的利润;如果需求弹性较高,企业则需要在价格上具有竞争优势。
2.市场定价:需求函数可以帮助企业确定适当的产品或服务价格,从而在市场上取得竞争优势。
通过分析需求函数,企业可以了解市场对产品或服务的需求量,并根据市场需求的变化调整价格策略。
3.市场预测:需求函数可以预测市场需求的变化趋势。
通过分析历史数据和市场环境的变化,可以建立需求函数模型,并通过模型来预测将来市场需求的变化情况。
这对企业进行生产计划、库存管理以及市场推广活动的决策非常有帮助。
总之,需求函数是一个重要的经济学概念,在市场分析和决策中扮演着重要的角色。
通过对需求函数的研究和分析,企业可以更好地了解市场需求的变化,制定合适的市场策略,并实现盈利和可持续发展。
需求函数的公式表达式需求函数是衡量消费者对其中一种商品或服务的需求量与价格、收入、替代品和补充品的关系的数学表达式。
需求函数通常以价格为自变量,以需求量为因变量。
根据不同的经济理论和模型,需求函数可以具有不同的形式和结构。
下面将介绍几种常见的需求函数的公式表达式。
1.线性需求函数:线性需求函数是最简单的需求函数形式,它假设需求量与价格之间存在线性关系。
线性需求函数的一般形式为:Q=a-bP其中Q表示需求量,P表示价格,a和b是常数。
线性需求函数的斜率为负数,表示需求量随价格的上升而下降。
2.指数需求函数:指数需求函数假设需求量与价格之间存在指数关系。
指数需求函数的一般形式为:Q=a*P^b其中Q表示需求量,P表示价格,a和b是正常数。
指数需求函数的特点是价格弹性随价格水平变化而变化。
当0<b<1时,需求量对价格的弹性小于1,表示商品的需求是价格刚性的;当b>1时,需求量对价格的弹性大于1,表示商品的需求是价格弹性的。
3.双曲线需求函数:双曲线需求函数假设需求量与价格之间存在双曲线关系。
双曲线需求函数的一般形式为:Q=a/(P+b)其中Q表示需求量,P表示价格,a和b是正常数。
双曲线需求函数的特点是价格弹性随价格水平变化而变化。
当P接近0时,需求量对价格的弹性接近无限大,表示商品的需求是价格极度弹性的;当P趋近正无穷大时,需求量对价格的弹性接近0,表示商品的需求是价格刚性的。
4. Cobb-Douglas需求函数:Cobb-Douglas需求函数假设需求量与价格之间存在指数关系,并加入了收入的影响。
Cobb-Douglas需求函数的一般形式为:Q=a*P^b*Y^c其中Q表示需求量,P表示价格,Y表示收入,a、b和c是正常数。
Cobb-Douglas需求函数考虑了价格和收入的影响,可以更好地解释商品需求的变化。
需要注意的是,以上介绍的需求函数只是常见的一些形式,实际上需求函数的具体形式取决于对商品需求关系的理论假设和具体的实证研究。
需求函数公式范文需求函数可以表示为物品数量与消费者对该物品的需求之间的关系。
它是经济学中的一个重要概念,用于描述消费者在不同价格和收入水平下对物品的需求变化。
需求函数的一般形式可以表示为:Q=f(P,Y,T,PR,E)其中,Q代表需求的数量,P代表物品的价格,Y代表消费者的收入,T代表相关的价格,PR代表广告宣传的支出,E代表外部因素对需求的影响。
需求函数的具体形式取决于物品的性质以及市场环境。
下面是几种常见的需求函数形式:线性需求函数:Q=a-bP这种需求函数假设需求与价格是线性负相关的,即价格上涨会导致需求减少。
其中,a代表需求的最大量,b代表需求对价格的敏感程度。
对数需求函数:ln(Q) = a - b ln(P)这种需求函数假设需求与价格成对数负相关,即价格上涨对需求的影响是递减的。
其中,a代表需求的最大量,b代表需求对价格的弹性。
多项式需求函数:Q=a+bP+cP^2这种需求函数假设需求与价格之间存在二次关系,即需求的变化不是线性的。
其中,a、b、c分别代表需求函数的系数,可以根据实际数据进行估计。
需求函数还可以考虑其他因素对需求的影响,比如收入、相关物品的价格、广告宣传等。
在实际分析中,可以根据研究的具体情况,选择合适的需求函数形式。
需求函数的推导和估计可以利用统计方法,比如经济计量分析和回归分析。
通过对历史数据的分析,可以估计出需求函数的参数,从而预测未来的需求变化。
需求函数对于企业和政府决策非常重要。
企业可以根据需求函数来确定最优的价格和产量,以实现最大化的利润。
而政府可以利用需求函数来制定税收政策和经济调控措施,以实现社会福利的最大化。
总而言之,需求函数是研究需求与价格、收入等因素之间关系的重要工具。
通过对需求函数的分析和建模,可以更好地理解消费者行为和市场运作规律,进而指导决策和政策制定。