北京市昌平区2016届高三第二次(5月)统一练习数学文试题 Word版含答案

北京市昌平区2007－2008学年第二学期高三第二次统练数学试卷（文科）2008.05本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至9页，共150分．考试时间120分钟．第Ⅰ卷（选择题 共40分）一、选择题(本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项，并将答案填在题后的答题表中．．．．．．．．．．．．．．) 1．不等式1202xx+>-的解集是 Ａ．12,2⎛⎫- ⎪⎝⎭ B ．()2,2- C ．1,22⎛⎫ ⎪⎝⎭ D ．1,22⎛⎫- ⎪⎝⎭2．10(1)x -的展开式中，中间一项的二项式系数是A ．510CB ．510C -C ．410CD ．410C -3．设集合A={1,2},则满足{1,2,3}A B ⋃=的集合B 的个数是A.1B.3C.4D.8 4.等比数列{}n a 中，若 1231a a a =，2348a a a =，则公比q =A ．12B ．2C ．D ．85．双曲线2213x y -=的渐近线与准线的夹角是 A ．30B ．45C ．60D ．1206．已知直线,m n 和平面α,则m ∥n 的一个必要非充分条件是 A ． m ∥α、n ∥α B ． m ⊥α、n ⊥αC ． m ∥α、n ⊂αD ． ,m n 与α成等角7．若直线x a =与函数()sin ,()cos f x x g x x ==的图像分别交于M 、N 两点，则MN 的最大值为A ．1B C D ．28．从P 点出发三条射线PA ，PB ，PC 两两成60°，且分别与球O 相切于A ，B ，C 三点，若球的体积为π34，则OP 的距离为（ ）A ．2B ．3C ．23 D ．2北京市昌平区2007－2008学年第二学期高三第二次统练数学试卷（文科）2008.05第Ⅱ卷（共110分）注意事项：1． 用钢笔或圆珠笔将答案直接写在试卷上．二、 填空题(本大题共6小题，每小题5分，共30分．请把答案填在题中横线上．) 9. 抛物线231y x -=的准线方程是 __________ . 10．已知y x z y y x y x +=⎪⎩⎪⎨⎧≥≥-≤+300632则的最大值为 .11．在△ABC 中，A=120°，AB=5，BC=7，则CBsin sin 的值为 .12.两位到北京旅游的外国游客要与2008奥运会的5名志愿者合影留念，要求排成一排，两位游客相邻且不排在两端，则不同的排法共有 ．13．在ABC ∆中，90BAC ∠=，60ABC ∠=，AD ⊥BC 于D ， 若AD AB AC λμ=⋅+⋅，则有序实数对(),λμ= ．14．奇函数()y f x =在(,)-∞+∞上单调递增，偶函数()y g x =在[0,)+∞上的图象与()y f x =的图象重合。

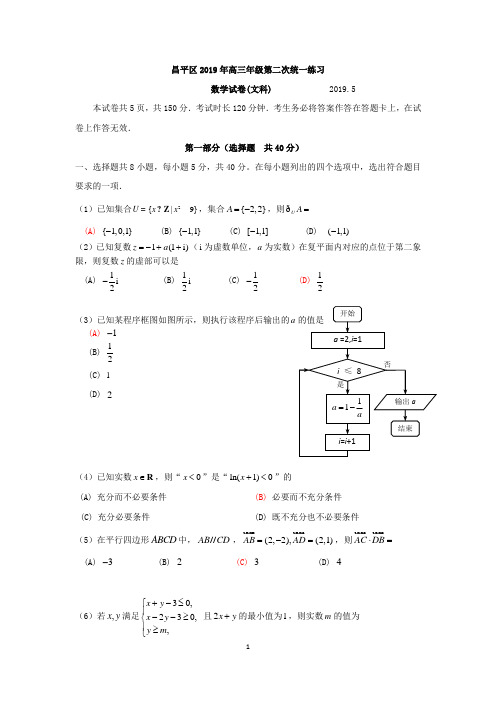
昌平区2019年高三年级第二次统一练习数学试卷(文科) 2019.5本试卷共5页，共150分．考试时长120分钟．考生务必将答案作答在答题卡上，在试卷上作答无效．第一部分（选择题 共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项．（1）已知集合2{|9}U x x Z =?，集合{2,2}A =-，则U A =ð(A) {1,0,1}- (B) {1,1}- (C) [1,1]- (D) (1,1)-（2）已知复数1(1i)z a =-++（i 为虚数单位，a 为实数）在复平面内对应的点位于第二象限，则复数z 的虚部可以是(A) 1i 2- (B) 1i 2 (C) 12- (D) 12（3）已知某程序框图如图所示，则执行该程序后输出的a 的值是 (A) 1-(B) 12(C) 1(D) 2（4）已知实数x ∈R ，则“0x <”是“ln(1)0x +<”的 (A) 充分而不必要条件 (B) 必要而不充分条件 (C) 充分必要条件(D) 既不充分也不必要条件（5）在平行四边形ABCD 中，AB CD //，(2,2),(2,1)AB AD =-=，则AC DB ⋅= (A) 3- (B) 2 (C) 3 (D) 4（6）若,x y 满足30,230,,x y x y y m +-≤⎧⎪--≥⎨⎪≥⎩且2x y +的最小值为1，则实数m 的值为开始a =2,i =1i ≤ 811a a=-i =i +1结束输出a否是俯视图侧(左)视图正(主)视图1222(A) 5- (B) 1- (C) 1 (D) 5 （7）某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为 (A) 5(B) 22(C) 23 (D) 3（8） 一次数学竞赛，共有6道选择题，规定每道题答对得5分，不答得1分，答错倒扣1分．一个由若干名学生组成的学习小组参加了这次竞赛，这个小组的人数与总得分情况为 (A) 当小组的总得分为偶数时，则小组人数一定为奇数 (B) 当小组的总得分为奇数时，则小组人数一定为偶数 (C) 小组的总得分一定为偶数，与小组人数无关 (D) 小组的总得分一定为奇数，与小组人数无关第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分．（9）已知幂函数()f x x =α（α是实数）的图象经过点(2,2)，则(4)f 的值为 . （10）为了落实“回天计划”，政府准备在回龙观、天通苑地区各建一所体育文化公园. 针对公园中的体育设施需求，某社区采用分层抽样的方法对于21岁至65岁的居民进行了调查. 已知该社区21岁至35岁的居民有840人，36岁至50岁的居民有700人，51岁至65岁的居民有560人．若从36岁至50岁的居民中随机抽取了100人，则这次抽样调查抽取的总人数是 ．(11) 能说明“设,a b 为实数，若220a b +≠，则直线10ax by +-=与圆221x y +=相切”为假命题的一组,a b 的值依次为___________.（12）等差数列{}n a 满足25968a a a a ++=+，则5a =_____;若116,a =则n =______时，{}n a 的前n 项和取得最大值．（13）已知双曲线221:13y C x -=，若抛物线22:2(0)C x py p =>的焦点到双曲线1C 的渐近线的距离为1，则抛物线2C 的方程为_________________.（14）已知函数()cos()(0,0)f x x =+><ωϕωϕ的最小正周期为π，且π()()3f x f ≥对任意6442987330550237894750238891466621873205987654高二 高一的实数x 都成立，则ω的值为_____;ϕ的最大值为__________．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． （15）（本小题13分）在等差数列{}n a 中，28a =，且3524a a a +=. （I ）求等差数列{}n a 的通项公式；（II ）设各项均为正数的等比数列{}n b 满足41b a =，64b a =，求数列{}n n b a -的前n 项和n S .（16）（本小题13分）在ABC △中，4AC =，43BC =，2π3BAC ∠=. （I ）求ABC ∠的大小；（II ）若D 为BC 边上一点，7AD =，求DC 的长度. （17）（本小题13分）某学校为了解学生的体质健康状况，对高一、高二两个年级的学生进行了体质测试 . 现从两个年级学生中各随机选取20人，将他们的测试数据，用茎叶图表示如下：《国家学生体质健康标准》的等级标准如下表. 规定：测试数据≥60，体质健康为合格. 等级 优秀 良好 及格不及格 测试数据[90,100][80,89][60,79][0,59]（I ）从该校高二年级学生中随机选取一名学生，试估计这名学生体质健康合格的概率； （II ）从两个年级等级为优秀的样本中各随机选取一名学生，求选取的两名学生的测试数据平均数大于95的概率；（III ）设该校高一学生测试数据的平均数和方差分别为112,X S ，高二学生测试数据的平均ABCDE P数和方差分别为222,X S ，试估计12X X 与、2212S S 与的大小 . （只需写出结论）（18）（本小题14分）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面 PCD ⊥平面ABCD ，2AB =，1BC =，2PC PD ==，E 为PB 中点．（I ）求证：PD //平面ACE ； （II ）求证：PD ⊥平面PBC ； （III ）求三棱锥E ABC -的体积.（19）（本小题13分）已知椭圆()2222+=1>>0x y G :a b a b的离心率为32，经过点(0,1)B .设椭圆G 的右顶点为A ，过原点O 的直线l 与椭圆G 交于,P Q 两点（点Q 在第一象限），且与线段AB 交于点M . （I ）求椭圆G 的标准方程；（II ）是否存在直线l ，使得BOP ∆的面积是ΔBMQ 的面积的3倍？若存在，求直线l 的方程；若不存在，请说明理由.（20）(本小题14分)已知函数2()[(1)1]e x f x x a x =+++.（I ） 若曲线()y f x =在点(0,(0))f 处的切线与x 轴平行，求a 的值； （II ）若()f x 在1x =-处取得极大值，求a 的取值范围；（III ） 当2a =时，若函数()()1g x mf x =-有3个零点，求m 的取值范围.（只需写出结论）。

高考衣食住用行衣：高考前这段时间，提醒同学们出门一定要看天气，否则淋雨感冒，就会影响考场发挥。

穿着自己习惯的衣服，可以让人在紧张时产生亲切感和安全感，并能有效防止不良情绪产生。

食：清淡的饮食最适合考试，切忌吃太油腻或者刺激性强的食物。

如果可能的话，每天吃一两个水果，补充维生素。

另外，进考场前一定要少喝水！住：考前休息很重要。

好好休息并不意味着很早就要上床睡觉，根据以往考生的经验，太早上床反而容易失眠。

考前按照你平时习惯的时间上床休息就可以了，但最迟不要超过十点半。

用：出门考试之前，一定要检查文具包。

看看答题的工具是否准备齐全，应该带的证件是否都在，不要到了考场才想起来有什么工具没带，或者什么工具用着不顺手。

行：看考场的时候同学们要多留心，要仔细了解自己住的地方到考场可以坐哪些路线的公交车？有几种方式可以到达？大概要花多长时间？去考场的路上有没有修路堵车的情况？考试当天，应该保证至少提前20分钟到达考场。

2016年高考新课标Ⅱ卷文数试题参考解析一、 选择题：本大题共12小题。

每小题5分，在每个小题给出的四个选项中，只有一项是符合要求的。

1. 已知集合{123}A =，，，2{|9}B x x =<，则A B =I （A ）{210123}--，，，，， （B ）{21012}--，，，， （C ）{123}，， （D ）{12}，【答案】D【解析】由29x <得，33x -<<，所以{|33}B x x =-<<，所以{1,2}A B =I ，故选D. 2. 设复数z 满足i 3i z +=-，则z =（A ）12i -+ （B ）12i - （C ）32i + （D ）32i - 【答案】C【解析】由3z i i +=-得，32z i =-，故选C. 3. 函数=sin()y A x ωϕ+ 的部分图像如图所示，则（A ）2sin(2)6y x π=-（B ）2sin(2)3y x π=-（C ）2sin(2+)6y x π=（D ）2sin(2+)3y x π=【答案】A4. 体积为8的正方体的顶点都在同一球面上，则该球面的表面积为 （A ）12π （B ）323π （C ）8π （D ）4π 【答案】A【解析】因为正方体的体积为8，所以正方体的体对角线长为233，所以球面的表面积为243)12ππ⋅=，故选A.5. 设F 为抛物线C ：y 2=4x 的焦点，曲线y =kx（k >0）与C 交于点P ，PF ⊥x 轴，则k = （A ）12 （B ）1 （C ）32（D ）2【答案】D【解析】(1,0)F ，又因为曲线(0)ky k x=>与C 交于点P ，PF x ⊥轴，所以21k =，所以2k =，选D.6. 圆x 2+y 2−2x −8y +13=0的圆心到直线ax +y −1=0的距离为1，则a =（A ）−43 （B ）−34（C ）3 （D ）2 【答案】A【解析】圆心为(1,4)，半径2r =，所以2211a =+，解得43a =-，故选A.7. 如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（A ）20π （B ）24π （C ）28π （D ）32π 【答案】C【解析】因为原几何体由同底面一个圆柱和一个圆锥构成，所以其表面积为28S π=，故选C.8. 某路口人行横道的信号灯为红灯和绿灯交替出现，红灯持续时间为40秒.若一名行人来到该路口遇到红灯 ，则至少需要等待15秒才出现绿灯的概率为 （A ）710 （B ）58 （C ）38 （D ）310【答案】B【解析】至少需要等待15秒才出现绿灯的概率为40155408-=，故选B. 9. 中国古代有计算多项式值得秦九韶算法，右图是实现该算法的程序框图．执行该程序框图，若输入的a 为2，2，5，则输出的s = （A ）7 （B ）12 （C ）17 （D ）34【答案】C【解析】第一次运算，a=2，s=2，n=2，k=1，不满足k>n; 第二次运算，a=2，s=2226⨯+=，k=2，不满足k>n; 第三次运算，a=5，s=62517⨯+=，k=3，满足k>n ， 输出s=17，故选C ．10. 下列函数中，其定义域和值域分别与函数y=10lg x的定义域和值域相同的是 （A ）y =x （B ）y =lg x （C ）y =2x（D ）y x=【答案】D 【解析】lg 10xy x ==，定义域与值域均为()0,+∞，只有D 满足，故选D ．11. 函数π()cos 26cos()2f x x x =+-的最大值为 （A ）4 （B ）5（C ）6（D ）7【答案】B【解析】因为2311()2(sin )22f x x =--+，而sin [1,1]x ∈-，所以当sin 1x =时，取最大值5，选B.12. 已知函数f (x )（x ∈R ）满足f (x )=f (2-x )，若函数 y =|x 2-2x -3| 与 y =f (x ) 图像的交点为（x 1,y 1），(x 2,y 2)，…，（x m ,y m ），则1=mi i x =∑(A)0 (B)m (C) 2m (D) 4m 【答案】B【解析】因为2(),y |23|y f x x x ==--都关于1x =对称，所以它们交点也关于1x =对称，当m 为偶数时，其和为22m m ⨯=，当m 为奇数时，其和为1212m m -⨯+=，因此选B. 二．填空题：共4小题，每小题5分.13. 已知向量a =(m ,4)，b =(3,-2)，且a ∥b ，则m =___________. 【答案】6-【解析】因为a ∥b ，所以2430m --⨯=，解得6m =-．14. 若x ，y 满足约束条件103030x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩，则z =x -2y 的最小值为__________.【答案】5-15. △ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若4cos 5A =，5cos 13C =，a =1，则b =____________. 【答案】2113【解析】因为45cos ,cos 513A C ==，且,A C 为三角形内角，所以312sin ,sin 513A C ==，13sin sin(C)sin cos cos sin 65B A AC A C =+=+=，又因为sin sin a b A B =，所以sin 21sin 13a Bb A ==.16. 有三张卡片，分别写有1和2，1和3，2和3. 甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是________________. 【答案】1和3【解析】由题意分析可知甲的卡片上数字为1和3，乙的卡片上数字为2和3，丙卡片上数字为1和2. 三、解答题：解答应写出文字说明，证明过程或演算步骤．17．(本小题满分12分)等差数列{n a }中，34574,6a a a a +=+= （I ）求{n a }的通项公式；(II)设nb =[na ]，求数列{nb }的前10项和，其中[x]表示不超过x 的最大整数，如[0.9]=0,[2.6]=2【试题分析】（I ）先设{}n a 的首项和公差，再利用已知条件可得1a 和d ，进而可得{}n a 的通项公式；（II ）根据{}n b 的通项公式的特点，采用分组求和法，即可得数列{}n b 的前10项和．18． (本小题满分12分)某险种的基本保费为a （单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：（I ）记A 为事件：“一续保人本年度的保费不高于基本保费”。

北京市东城区2015-2016学年第二学期高三综合练习（二）数学参考答案及评分标准 （文科）一、选择题（本大题共8小题，每小题5分，共40分）（1）A （2）C （3）D （4）A（5）B （6）B （7）C （8）D二、填空题（本大题共6小题，每小题5分，共30分）（9） 2i - （10）1（11）2 （12）（13）2 0 （14）B 225注：两个空的填空题第一个空填对得3分，第二个空填对得2分．三、解答题（本大题共6小题，共80分）（15）（共13分）解：（Ⅰ）由sin sin A C =，得a c =.又23a bc =，所以3c b =．由余弦定理可得222222991cos 2236b c a b b b A bc b b +-+-===⨯．……………………6分 （Ⅱ）由已知23a bc =，且3a =,所以3bc =．故△ABC 的面积11sin 3222S bc A ==⨯⨯=………………… 13分（16）（共13分）解：（Ⅰ）设等差数列{}n a 的公差为d ，由2675=+a a ，得613a =，又6336a a d -==，解得2d =．所以3(3)72(3)21n a a n d n n =+-=+-=+．所以21321222n n a a n S n n n n +++=⨯=⨯=+． ……………………6分 （Ⅱ）由1n n b S n=-，得21111(1)1n b n n n n n n ===-+++． 设{}n b 的前n 项和为n T ， 则8111111118(1)()()()1223348999T =-+-+-++-=-= ． 故数列{}n b 的前8项和为89． ………………… 13分 （17）（共14分）证明：（Ⅰ）由题意知，梯形ABCD 为等腰梯形，且2AB a =，AC =，由222AB BC AC +=，可知AC BC ⊥. 又平面ACEF ⊥平面ABCD ，且平面ACEF 平面ABCD AC =，BC ⊂平面ABCD ，所以BC ⊥平面ACEF .又AM ⊂平面ACEF ，所以BC ⊥AM . ……………………5分（Ⅱ）当AM =时，AM 平面BDE .证明如下：当AM =，可得3FM a =，故EM = 在梯形ABCD 中，设ACBD N =，连结EN ，由已知可得:1:2CN NA =，所以AN =. 所以EM AN =.又EM AN ,所以四边形ANEM 为平行四边形.所以AM NE .又NE ⊂平面BDE ，AM ⊄平面BDE ，所以AM平面BDE .当AM =时，AM 平面BDE . ………………… 11分（Ⅲ）由已知可得△ABD的面积2S =，故231133A BFD F ABD ABD V V AF S a --==⨯⨯=⨯=△. ………… 14分（18）（共13分）解：（Ⅰ）从这140辆汽车中任取一辆，则该车行驶总里程超过10万公里的概率为120202031407P ++==． ……………………3分 （Ⅱ）（ⅰ）依题意3020145140n +=⨯=． ……………………6分 （ⅱ）5辆车中已行驶总里程不超过10万公里的车有3辆，记为,,a b c ；5辆车中已行驶总里程超过10万公里的车有2辆，记为,m n ．“从5辆车中随机选取两辆车”的所有选法共10种：,,,,,,,,,ab ac am an bc bm bn cm cn mn ．“从5辆车中随机选取两辆车，恰有一辆车行驶里程超过10万公里”的选法共6种： ,,,,,am an bm bn cm cn ．则选取两辆车中恰有一辆车行驶里程超过10万公里的概率263105P ==．………………… 13分（19）（共13分）解：（Ⅰ）依题意可得22b =，且2224a b c =+=，解得1b =． 所以椭圆C 的方程是2214x y +=． ………………… 5分 （Ⅱ）由221,41x y x my ⎧+=⎪⎨⎪=+⎩消x ，得22(4)230m y my ++-=．设11(,)P x y ，22(,)Q x y ，则111(,)P x y -． 且12224m y y m +=-+，12234y y m =-+．经过点111(,)P x y -，22(,)Q x y 的直线方程为211121().y y y y x x x x ++=-- 令0y =，则21211112211211211212()().x x x x y x y y x y x y x y x y y y y y y --+++=+==+++ 又11221,1,x my x my =+=+故当0y =时，221121212121226(1)(1)2()4131424m m y y m y y m y y y y m x m y y y y m -++++++===+=+=++-+． 即直线1PQ 与x 轴交于定点(4,0)． ………………… 13分（20）（共14分）解：（Ⅰ）当1a =-时，1()f x x x=--． 221(1)(1)()1x x f x x x --+'=-=． 令()0f x '=，得1x =-或1x =． 当1[,1)2x ∈，有()0f x '>，所以()f x 在区间1[,1)2上是增函数；当(1,3]x ∈时，有()0f x '<，所以()f x 在区间(1,3]上是减函数；所以()f x 在区间1[,3]2上的最大值为(1)2f =-． ………………… 5分 （Ⅱ）设过点(,)P b b -的直线与曲线()y f x =相切于点00(,)Q x y ， 则0001y x x =--，且切线斜率为0201()1k f x x '==-． 所以000()()y b f x x b --'=-，即00200111x b x x b x --+=--． 所以 22000001()(1)()x b x x x b x --+=--，解得02b x =． 即存在唯一的切点2(,)22b b b --．所以过点(,)P b b -有且只有一条直线与曲线()y f x =相切． ………………… 9分 （Ⅲ）当1x =时，对任意a ∈R ，不等式显然成立；当1x ≠时，不等式等价于21xa x x ≤+-． 当1[,1)2x ∈时，不等式等价于21xa x x ≤+-恒成立． 令2()1xg x x x =+-， 1[,1)2x ∈， 则21()2(1)g x x x '=+-，当1[,1)2x ∈时，显然()0g x '>，所以()g x 在区间1[,1)2上单调递增，所以()g x 在区间1[,1)2上有最小值15()24g =． 所以54a ≤．当(1,2]x ∈时，不等式等价于21xa x x ≤+-恒成立． 令2()1xh x x x =+-，(1,2]x ∈，当(1,2]x ∈时，2221()=11211xh x x x x x x =+++>+>--，所以，当54a ≤时，不等式21xa x x ≤+-对(1,2]x ∈恒成立．综上，实数a 的取值范围是5(,]4-∞．………………… 14分。

北京市昌平区2015-2016高三下学期化学第二次模拟试题 2016.5 可能用到的相对原子质量：H：1C：12O：16Na：23Cl：35.5S：32 6. 下列物质性质与应用对应关系正确的是 A氨气具有还原性，可用于检查HCl泄漏 B浓硫酸具有吸水性，可用于干燥CO2 C铝具有高熔点，可用于生产耐火砖 D 7. X、Y、Z为短周期主族元素，X的最外层电子数为内层电子数的2倍，Y的最高化合价与最低化合价的代数和为4，Z与Y同周期，Z的原子半径小于Y。

下列叙述不正确的是 AZ的氢化物是同主族简单氢化物 B．非金属性：Z＞Y＞X CXY2中各原子最外层均满足8电子结构 D 8. 下列离子方程式书写正确的是 ACaCl2溶液中通入少量的CO2：Ca2++CO2+H2OCaCO3↓+2H+ B向碳酸氢铵溶液中加入过量氢氧化钠溶液：HCO3+OHCO32+H2O 粉HNO3：Cu+4H+ +2NO3==2NO2↑+2H2O D．氯化铵溶液显酸性的原因：NH4+ + OH·H2O+H+ 9. 下列说法不正确的是 A B．饱和硫酸铵和醋酸铅溶液均能使鸡蛋清溶液发生变性 油脂、二肽发生水解反应均能得到含羧基的物质 天然橡胶和杜仲胶 的单体是同种物质 根据下列操作及现象，所得结论正确的是 序号操作及现象结论A向溴水中加入少量苯，振荡静置后水层为无色苯与Br2发生了加成反应B向某无色溶液中滴加硝酸酸化的BaCl2溶液，产生白色沉淀原溶液中一定含有SO42-C向25 mL冷水和沸水中分别滴入5滴FeCl3饱和溶液，前者为黄色，后者为红褐色温度升高，Fe3+的水解程度增大D将1 mL KSCN溶液与1mL 同浓度FeCl3溶液充分混合；再继续加入KSCN溶液，溶液颜色加深证明溶液中存在平衡：Fe3++3SN-Fe(SCN)311. 硝酸生产中500℃时NH3和O2可能发生如下反应： ① 4NH3 (g) + 5O2 (g)4NO (g) + 6H2O (g) △H=-9072kJ·mol-1K=1.1×1026 ② 4NH3 (g) + 4O2 (g)2N2O (g) + 6H2O (g) △H=-1104.9kJ·mol-1K=4.4×1028 ③ 4NH3 (g) + 3O2 (g)2N2 (g) + 6H2O (g) △H=-1269.2kJ·mol-1K=7.1×1034 下列说法正确的是 A．增大压强，则反应的②K不变，反应①和③的K减小 B．500℃时NH3 (g) + 2O2 (g)N2O (g) + 3H2O (g) K=2.2×1028 C．500℃时N2 (g) + O2 (g)=2NO (g) △H=+181 kJ·mol-1 D．500℃时，2NH3与2.5 mol O2混合发生反应①， kJ 12. 常温下，向20 mL 0.01mol/LCH3COOH溶液中逐滴加入0.01mol/L的溶液，溶液c(H+)随加入NaOH溶液如图所示，下列说法正确的是 A B．a、d对应的纵坐标数值分别是：＞10-12＞10-7 b点：c(Na+)＝c(CH3COO-)＋c(CH3COOH) D10-7的点 第二部分非选择题 （14 聚芳酯（PAR）在航空航天等领域具有广泛应用。

北京市东城区2015-2016学年度第二学期高三综合练习（二）数学 （文科） 学校_____________班级_______________姓名______________考号___________本试卷共5页，共150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共40分）一、选择题（共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项）（1）已知集合，，那么（A） （B）（C） （D）（2）如图，根据样本的频率分布直方图，估计样本的中位数是（A）（B）（C）（D）（3）执行如图所示程序框图，则输出的结果是（A） （B）（C） （D）（4）已知，为圆上关于点对称的两点，则直线的方程为（A）（B）（C）（D）（5）设，为实数，则“”是“”的（A）充分而不必要条件（B）必要而不充分条件（C）充分必要条件（D）既不充分也不必要条件（6）已知函数是偶函数,且，则（A） （B）（C） （D）（7）已知向量，将向量绕坐标原点逆时针旋转角得到向量 ，则下列说法不正确的是（A）（B）（C）（D）（8）如图，在边长为的正方形组成的网格中，有椭圆，，，它们的离心率分别为，，，则（A）（B）（C）（D）第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

（9）如图所示，在复平面内，点A对应的复数为，则复数．（10）若函数在区间上有且只有一个零点，则实数．（11）已知双曲线的虚轴长是实轴长的倍，则实数 .（12）已知一个三棱锥的三视图如图所示，其中俯视图是等腰直角三角形，则该三棱锥的四个面中，最大面积为________.（13）已知数列满足,，且，，则 ；数列的前项的和为________．（14）一名顾客计划到某商场购物，他有三张商场的优惠劵，商场规定每购买一件商品只能使用一张优惠券．根据购买商品的标价，三张优惠券的优惠方式不同，具体如下：优惠劵A：若商品标价超过元，则付款时减免标价的；优惠劵B：若商品标价超过元，则付款时减免元；优惠劵C：若商品标价超过元，则付款时减免超过元部分的．某顾客想购买一件标价为元的商品，若想减免钱款最多，则应该使用优惠劵（填A,B,C）；若顾客想使用优惠券C，并希望比优惠券A和B减免的钱款都多，则他购买的商品的标价应高于________元．三、解答题共6小题，共80分。

昌平区2019年高三年级第二次统一练习数学试卷(文科)参考答案一、选择题(共8小题，每小题5分，共40分)二、填空题(共6小题，每小题5分，共30分)(9) 2 (10) 300 (11) 1,1(答案不唯一) (12) 4;6 (13) 28x y = (14) 5π2;3- 三、解答题(共6小题，共80分) (15)（共13分）解：（Ⅰ）设数列{}n a 的公差为d ，由已知11118,244()a d a d a d a d ì+=ïïíï+++=+ïî， 解得14,=4a d ì=ïïíïïî，所以*=4()n a n n N Î. ….5分 （Ⅱ）设数列{}n b 的公比为q ，由已知464,16b b ì=ïïíï=ïî，解得112=2b q ，ìïï=ïíïïïî或112=2b q ，ìïï=-ïíïï-ïî（舍）， 所以121222n n n b --=⨯=，所以224n n n b a n --=- .10121012212*(24)(28)(212)(24)(22+22)(48124)1(12)(44)112(21)22222().12222n n n n n n S n n n n n n n n n -----=-+-+-++-=+++-++++-+=-=---=---?-N L L L ….13分(16)（共13分）解： （Ⅰ）在ABC ∆中， 由正弦定理得sin sin BC ACBAC ABC=∠∠， 所以2π4sin1sin 2ABC ∠==. 因为2π3BAC ∠=，所以π(0,)3ABC ∠∈,所以π6ABC ∠=. ….6分（Ⅱ）在ABC ∆中, 2πππ=π366C ∠--=.PFEDCBA在ADC ∆中，由余弦定理2222cos AD AC DC AC DC C =+-⋅∠，得2π7168cos6DC DC =+-，即290DC -+=，解得DC =DC =经检验，都符合题意. ….13分. ….4分(II) 设等级为优秀的样本中高一年级测试数据是93,94,96的学生分别为123,,,a a a 高二年级测试数据是90,95,98的学生分别为123,,.b b b 选取的两名学生构成的基本事件空间为111213212223313233{(,),(,),(,),(,),(,),(,),(,),(,),(,)}a b a b a b a b a b a b a b a b a b ，总数为9，选取的测试数据平均数大于95的两名学生构成的基本事件空间为13233233{(,),(,),(,),(,)}a b a b a b a b ，总数为4，（III ）112222,S X X S ><. ….13分(18)（共14分）证明：（I ）连结BD 交AC 于点F ，连结EF . 因为底面ABCD 是矩形, 所以F 为BD 中点.又因为E 为PB 中点, 所以EF //PD . 因为PD ACE EF ACE ⊄⊂平面，平面, 所以PD //平面ACE . ….4分(II) 因为底面ABCD 为矩形, 所以BC CD ⊥. 又因为PCD ABCD ⊥平面平面,,BC ABCD PCD ABCD CD ⊂⋂=平面平面平面, 所以BC PCD ⊥平面.因为PD PCD ⊂平面,所以BC PD ⊥.因为2,PC PD CD AB === 所以222PC PD CD +=，即PD PC ⊥. 因为,,BCPC C BC PC =⊂平面PBC ，所以PD ⊥平面PBC . ….9分（III ）因为底面ABCD 是矩形, 所以AD BC //.因为AD ⊄平面PBC ，BC ⊂平面PBC ， 所以AD //平面PBC .由（II ）得，PD ⊥平面PBC ，所以---1111111323226E ABC A EBC D EBC PBC V V V S PD ∆===⨯⋅=⨯⨯⨯=. 所以三棱锥E ABC -的体积为16. ….14分(19)（共13分）解：（I）由题意可知：2221,b c a a b c =⎧⎪⎪=⎨⎪⎪=+⎩，解得2,1,a b c ⎧=⎪=⎨⎪=⎩. 所以椭圆G 的标准方程为2214x y +=. ….5分（Ⅱ）设()00,Q x y ，则()00,P x y --，易知002x <<，001y <<. 若使BOP ∆的面积是BMQ ∆的面积的3倍，只需使得3OQ MQ =，即00222(,)333OM OQ x y ==，即0022(,)33M x y .由()2,0A ，()0,1B ，所以直线AB 的方程为220x y +-=. 点M 在线段AB 上，所以00242033x y +-=，整理得0032x y =-，① 因为点Q 在椭圆G 上，所以220014x y +=，②把①式代入②式可得20081250y y -+=，因为判别式小于零，该方程无解.所以，不存在直线l ，使得BOP ∆的面积是BMQ ∆的面积的3倍. ….13分 (20) (共14分)解：函数()f x 的定义域为(,)-∞+∞.2'()[(3)2]e x f x x a x a =++++.（Ⅰ）因为曲线()y f x =在点(0,(0))f 处的切线与x 轴平行， 所以0'(0)(2)e 0f a =+=，解得2a =-.此时(0)10f =≠，所以a 的值为2-. ….5分 （Ⅱ）因为2'()[(3)2]e (1)[(2)]e x x f x x a x a x x a =++++=+++,① 若1a <-，(2)1a -+>-，则当(,1)x ??时，10,(2)10,x x a x +<++<+<所以'()0f x >； 当(1,(2))x a ?-+时，10,(2)0,x x a +>++<所以'()0f x <. 所以()f x 在1x =-处取得极大值. ② 若1a ?，(2)1a -+?，则当(1,0)x ?时，10,(2)10,x x a x +>++?>所以'()0f x >.所以1-不是()f x 的极大值点 .综上可知，a 的取值范围为(,1)-∞-. ….10分（Ⅲ）4e 5m >. ….14分。

昌平区2016年高三年级第二次统一练习 理科综合能力测试 2016．5本试卷分第一部分（选择题）和第二部分（非选择题）两部分，第一部分1至5页，第二部分6至16页，共300分。

考试时间150分钟。

考生务必将答案填写在答题卡上相应区域内，在试卷上作答无效。

考试结束后，将答题卡交回。

可能用到的相对原子质量： H ：1 C ：12 O ：16 Na ：23 Cl ：35.5 S ：32第一部分（选择题，每小题6分，共120分）在每小题列出的四个选项中，选出最符合题目要求的一项。

1. 下列关于人体细胞中各种有机物合成场所的叙述，正确的是A ．癌变细胞在核糖体合成核糖B ．神经元在细胞核内合成RNAC ．浆细胞在内质网合成蛋白质D ．性腺细胞在细胞膜合成激素2. 寨卡病毒的遗传物质是一条单链RNA ，可以作为模板翻译出衣壳蛋白等（如图所示）。

有关说法错误．．的是A ．物质M 的合成过程还需要其他RNAB ．①②③过程都遵循碱基互补配对原则C ．物质N 一定能降低化学反应的活化能D ．全部过程受细胞核DNA 分子的控制3. 黑带食蚜蝇的幼虫以蚜虫为食，雌性黑带食蚜蝇一般会将卵产在蚜虫的附近。

长瓣兜兰不分泌花蜜，其花粉也无法被食蚜蝇取食，但其花瓣基部长了很多黑栗色的小突起，形似大量蚜虫，吸引雌性食蚜蝇来产卵，在产卵的同时替长瓣兜兰完成了传粉。

孵化出来的食蚜蝇幼虫会因为没有食物而不明不白地饿死。

有关叙述正确的是 A ．食蚜蝇和长瓣兜兰之间存在协同进化 B ．食蚜蝇和长瓣兜兰的种间关系是互利共生 C ．食蚜蝇、蚜虫和长瓣兜兰构成生物群落 D ．长瓣兜兰和食蚜蝇间能量传递效率10～20%4. 产肠毒素大肠杆菌可分泌EtpA 蛋白介导菌体与宿主细胞的粘附，引起腹泻。

酿酒酵母是肠道中的有益菌，将控制EtpA 蛋白的基因导入酿酒酵母中，使酿酒酵母具有与产肠毒素大肠杆菌竞争粘附位点的能力。

有关说法正确的是 A ．EtpA 蛋白介导的粘附过程和受体无关 B ．EtpA 蛋白在肠道内引起机体免疫反应 C ．可通过PCR 技术扩增EtpA 基因 D ．可通过显微注射法导入EtpA 基因学校_______________________班级______________________姓名______________________考试编号_______________________密 封 线 内 不 要 答 题5. 在分离土壤中分解纤维素的细菌过程中，需要进行的是A ．用紫外线对样品进行消毒B ．用显微镜对菌落进行计数C ．用选择性培养基进行筛选D ．用刚果红对菌体进行染色6. 下列物质性质与应用对应关系正确的是A ．氨气具有还原性，可用于检查HCl 泄漏B ．浓硫酸具有吸水性，可用于干燥CO 2C ．铝具有高熔点，可用于生产耐火砖D ．硅有导电性，可用作光导纤维7. X 、Y 、Z 为短周期主族元素，X 的最外层电子数为内层电子数的2倍，Y 的最高化合价与最低化合价的代数和为4，Z 与Y 同周期，Z 的原子半径小于Y 。

绝密★启用前2016年普通高等学校招生全国考试数学（文）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本市卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合{|24},{|3>5}A x x B x x x =<<=<或，则AB =（A ）{|2<<5}x x （B ）{|<45}x x x >或 （C ）{|2<<3}x x （D ）{|<25}x x x >或 （2）复数12i=2i+- （A ）i （B ）1+i （C ）i - （D ）1i -（3）执行如图所示的程序框图，输出的s 值为 （A ）8 （B ）9 （C ）27（D ）36（4）下列函数中，在区间(1,1)- 上为减函数的是 （A ）11y x=- （B ）cos y x = （C ）ln(1)y x =+ （D ）2x y -= （5）圆（x +1）2+y 2=2的圆心到直线y =x +3的距离为（A ）1 （B ）2 （C ）2 （D ）22 （6）从甲、乙等5名学生中随机选出2人，则甲被选中的概率为（A ）15 （B ）25（C ）825 （D ）925 （7）已知A （2，5），B （4，1）.若点P （x ，y ）在线段AB 上，则2x −y 的最大值为（A ）−1 （B ）3 （C ）7 （D ）8（8）某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩，其中有三个数据模糊.学生序号12345678910立定跳远（单位：米） 1.96 1.92 1.82 1.80 1.78 1.76 1.74 1.72 1.68 1.60 30秒跳绳（单位：次） 63a7560637270a −1b65在这10名学生中，进入立定跳远决赛的有8人，同时进入立定跳远决赛和30秒跳绳决赛的有6人，则（A ）2号学生进入30秒跳绳决赛 （B ）5号学生进入30秒跳绳决赛 （C ）8号学生进入30秒跳绳决赛 （D ）9号学生进入30秒跳绳决赛第二部分（非选择题共110分）二、填空题（共6小题，每小题5分，共30分）（9）已知向量=(1,3),(3,1)=a b ，则a 与b 夹角的大小为_________. （10）函数()(2)1xf x x x =≥-的最大值为_________. （11）某四棱柱的三视图如图所示，则该四棱柱的体积为___________.(12) 已知双曲线22221x y a b-= （a ＞0，b ＞0）的一条渐近线为2x +y =0，一个焦点为（5 ,0），则a =_______；b =_____________. (13)在△ABC 中，23A π∠=，a=3c ，则bc =_________.(14)某网店统计了连续三天售出商品的种类情况：第一天售出19种商品，第二天售出13种商品，第三天售出18种商品；前两天都售出的商品有3种，后两天都售出的商品有4种，则该网店 ①第一天售出但第二天未售出的商品有______种； ②这三天售出的商品最少有_______种.三、解答题（共6题，共80分.解答应写出文字说明，演算步骤或证明过程）（15）（本小题13分）已知{a n }是等差数列，{b n }是等差数列，且b 2=3，b 3=9，a 1=b 1，a 14=b 4. （Ⅰ）求{a n }的通项公式；（Ⅱ）设c n = a n + b n ，求数列{c n }的前n 项和.（16）（本小题13分）已知函数f （x ）=2sin ωx cos ωx + cos 2ωx （ω>0）的最小正周期为π. （Ⅰ）求ω的值；（Ⅱ）求f （x ）的单调递增区间.（17）（本小题13分）某市民用水拟实行阶梯水价，每人用水量中不超过w 立方米的部分按4元/立方米收费，超出w 立方米的部分按10元/立方米收费，从该市随机调查了10000位居民，获得了他们某月的用水量数据，整理得到如下频率分布直方图：（I ）如果w 为整数，那么根据此次调查，为使80%以上居民在该月的用水价格为4元/立方米，w 至少定为多少？（II ）假设同组中的每个数据用该组区间的右端点值代替，当w=3时，估计该市居民该月的人均水费.（18）（本小题14分）如图，在四棱锥P-ABCD 中，PC ⊥平面ABCD ，,AB DC DC AC ⊥∥ （I ）求证：DC PAC ⊥平面； （II ）求证：PAB PAC ⊥平面平面；(III)设点E 为AB 的中点，在棱PB 上是否存在点F ，使得P A C E F ⊥平面?说明理由.（19）（本小题14分）已知椭圆C ：22221x y a b+=过点A （2,0），B （0,1）两点.（I ）求椭圆C 的方程及离心率；（II ）设P 为第三象限内一点且在椭圆C 上，直线PA 与y 轴交于点M ，直线PB 与x 轴交于点N ，求证：四边形ABNM 的面积为定值.（20）（本小题13分） 设函数()32.f x x ax bx c =+++（I ）求曲线().y f x =在点()()0,0f 处的切线方程；（II ）设4a b ==，若函数()f x 有三个不同零点，求c 的取值范围；（III ）求证：230a b -＞是().f x 有三个不同零点的必要而不充分条件.2016年普通高等学校招生全国统一考试数学(文)(北京卷)参考答案一、选择题（共8小题，每小题5分，共40分）（1）C （2）A （3）B （4）D （5）C （6）B （7）C （8）B 二、填空题（共6小题，每小题5分，共30分） （9）6π （10）2 （11）32（12）1 2 （13）1 （14）16 29 三、解答题（共6小题，共80分） （15）（共13分） 解：（I ）等比数列{}n b 的公比32933b q b ===， 所以211b b q==，4327b b q ==． 设等差数列{}n a 的公差为d ． 因为111a b ==，14427a b ==， 所以11327d +=，即2d =．所以21n a n =-（1n =，2，3，⋅⋅⋅）．（II ）由（I ）知，21n a n =-，13n n b -=． 因此1213n n n n c a b n -=+=-+．从而数列{}n c 的前n 项和()11321133n n S n -=++⋅⋅⋅+-+++⋅⋅⋅+()12113213n n n +--=+-2312n n -=+．（16）（共13分）解：（I ）因为()2sin cos cos2f x x x x ωωω=+sin 2cos2x x ωω=+2sin 24x πω⎛⎫=+ ⎪⎝⎭，所以()f x 的最小正周期22ππωωT ==． 依题意，ππω=，解得1ω=． （II ）由（I ）知()2sin 24f x x π⎛⎫=+ ⎪⎝⎭．函数sin y x =的单调递增区间为2,222k k ππππ⎡⎤-+⎢⎥⎣⎦（k ∈Z ）． 由222242k x k πππππ-≤+≤+，得388k x k ππππ-≤≤+． 所以()f x 的单调递增区间为3,88k k ππππ⎡⎤-+⎢⎥⎣⎦（k ∈Z ）． （17）（共14分）解：（I ）由用水量的频率分布直方图知，该市居民该月用水量在区间[]0.5,1，(]1,1.5，(]1.5,2，(]2,2.5，(]2.5,3内的频 率依次为0.1，0.15，0.2，0.25，0.15．所以该月用水量不超过3立方米的居民占85%，用水量不超过2立方米的居民占45%． 依题意，w 至少定为3．（II ）由用水量的频率分布直方图及题意，得居民该月用水费用的数据分组与频率分布表： 组号 12345678分组 []2,4(]4,6(]6,8(]8,10(]10,12(]12,17 (]17,22 (]22,27频率0.10.150.20.250.150.050.050.05根据题意，该市居民该月的人均水费估计为：40.160.1580.2100.25120.15170.05220.05270.05⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯10.5=（元）． （18）（共13分）解：（I ）因为C P ⊥平面CD AB ， 所以C DC P ⊥． 又因为DC C ⊥A ， 所以DC ⊥平面C PA ．（II ）因为//DC AB ，DC C ⊥A ， 所以C AB ⊥A ．因为C P ⊥平面CD AB ， 所以C P ⊥AB ．所以AB ⊥平面C PA ．所以平面PAB ⊥平面C PA ．（III ）棱PB 上存在点F ，使得//PA 平面C F E ．证明如下： 取PB 中点F ，连结F E ，C E ，CF ． 又因为E 为AB 的中点， 所以F//E PA ．又因为PA ⊄平面C F E ， 所以//PA 平面C F E ．（19）（共14分） 解：（I ）由题意得，2a =，1b =．所以椭圆C 的方程为2214x y +=． 又223c a b =-=， 所以离心率32c e a ==． （II ）设()00,x y P （00x <，00y <），则220044x y +=．又()2,0A ，()0,1B ，所以， 直线PA 的方程为()0022y y x x =--． 令0x =，得0022y y x M =--，从而002112y y x M BM =-=+-． 直线PB 的方程为0011y y x x -=+． 令0y =，得001x x y N =--，从而00221x x y N AN =-=+-． 所以四边形ABNM 的面积12S =AN ⋅BM 00002121212x y y x ⎛⎫⎛⎫=++ ⎪⎪--⎝⎭⎝⎭()22000000000044484222x y x y x y x y x y ++--+=--+ 00000000224422x y x y x y x y --+=--+2=．从而四边形ABNM 的面积为定值． （20）（共13分）解：（I ）由()32f x x ax bx c =+++，得()232f x x ax b '=++．因为()0f c =，()0f b '=，所以曲线()y f x =在点()()0,0f 处的切线方程为y bx c =+． （II ）当4a b ==时，()3244f x x x x c =+++，所以()2384f x x x '=++．令()0f x '=，得23840x x ++=，解得2x =-或23x =-． ()f x 与()f x '在区间(),-∞+∞上的情况如下：x(),2-∞-2-22,3⎛⎫-- ⎪⎝⎭23- 2,3⎛⎫-+∞ ⎪⎝⎭()f x ' +-+()f xc3227c -所以，当0c >且32027c -<时，存在()14,2x ∈--，222,3x ⎛⎫∈-- ⎪⎝⎭，32,03x ⎛⎫∈- ⎪⎝⎭，使得()()()1230f x f x f x ===．由()f x 的单调性知，当且仅当320,27c ⎛⎫∈ ⎪⎝⎭时，函数()3244f x x x x c =+++有三个不同零点．（III ）当24120a b ∆=-<时，()2320f x x ax b '=++>，(),x ∈-∞+∞，此时函数()f x 在区间(),-∞+∞上单调递增，所以()f x 不可能有三个不同零点．当24120a b ∆=-=时，()232f x x ax b '=++只有一个零点，记作0x ．当()0,x x ∈-∞时，()0f x '>，()f x 在区间()0,x -∞上单调递增； 当()0,x x ∈+∞时，()0f x '>，()f x 在区间()0,x +∞上单调递增． 所以()f x 不可能有三个不同零点．综上所述，若函数()f x 有三个不同零点，则必有24120a b ∆=->． 故230a b ->是()f x 有三个不同零点的必要条件．当4a b ==，0c =时，230a b ->，()()232442f x x x x x x =++=+只有两个不同 零点， 所以230a b ->不是()f x 有三个不同零点的充分条件． 因此230a b ->是()f x 有三个不同零点的必要而不充分条件．。