运筹学实验一：规划求解操作(线性规划问题)

商学院课程实验报告课程名称 运筹学 专业班级 金融工程班 姓 名 指导教师 成 绩2018年 9 月 20日学号：表2 所需营业员统计表星期一二三四五六日需要人数300 300350400480600 5503.建立线性规划模型设x j（j=1，2，…，7）为休息2天后星期一到星期日开始上班的营业员数量，则这个问题的线性规划问题模型为minZ=x1+x2+x3+x4+x5+x6+x7{x1+x4+x5+x6+x7≥300 x1+x2+x5+x6+x7≥300 x1+x2+x3+x6+x7≥350 x1+x2+x3+x4+x7≥400 x1+x2+x3+x4+x5≥480x2+x3+x4+x5+x6≥600x3+x4+x5+x6+x7≥550x≥0,j=1,2,…,7（二）操作步骤1.将WinQSB安装文件复制到本地硬盘，在WinQSB文件夹中双击setup.exe。

图1 WinQSB文件夹2.指定安装软件的目标目录，安装过程中输入用户名和单位名称（任意输入），安装完毕之后，WinQSB菜单自动生成在系统程序中，熟悉软件子菜单内容和功能，掌握操作命令。

图2 目标目录3.启动线性规划和整数规划程序。

点击开始→程序→WinQSB→Linear and Lnteger Programming，屏幕显示如图3所示的线性规划和整数规划界面。

图3 线性规划4.建立新问题或打开磁盘中已有文件。

按图3所示操作建立或打开一个LP问题，或点击File→New Problem建立新问题。

点击File→Load Problem打开磁盘中的数据文件，点击File→New Problem，出现图4所示的问题选项输入界面。

图4 建立新问题5.输入数据。

在选择数据输入格式时，选择Spreadsheet Matrix Form则以电子表格形式输入变量系统矩阵和右端常数矩阵，是固定格式，如图5所示。

选择Normal Model Form则以自由格式输入标准模型。

运筹学实验指导书-CAL-FENGHAI.-(YICAI)-Company One1实验一、线性规划综合性实验一、实验目的与要求：使学生掌握线性规划建模的方法以及至少掌握一种线性规划软件的使用，提高学生应用线性规划方法解决实际问题的实践动手能力。

通过实验，使学生更深入、直观地理解和掌握线性规划的基本概念及基本理论和方法。

要求学生能对一般的线性规划问题建立正确的线性规划数学模型，掌握运筹学软件包线性规划模块的操作方法与步骤，能对求解结果进行简单的应用分析。

二、实验内容与步骤：1.选择合适的线性规划问题学生可根据自己的建模能力，从本实验指导书提供的参考选题中或从其它途径选择合适的线性规划问题。

2.建立线性规划数学模型学生针对所选的线性规划问题，运用线性规划建模的方法，建立恰当的线性规划数学模型。

3.用运筹学软件求解线性规划数学模型学生应用运筹学软件包线性规划模块对已建好的线性规划数学模型进行求解。

4.对求解结果进行应用分析学生对求解结果进行简单的应用分析。

三、实验例题：(一)线性规划问题某集团摩托车公司产品年度生产计划的优化研究1)问题的提出某集团摩托车公司是生产各种类型摩托车的专业厂家，有30多年从事摩托车生产的丰富经验。

近年来，随着国内摩托车行业的发展，市场竞争日趋激烈，该集团原有的优势逐渐丧失，摩托车公司的生存和发展面临严峻的挑战。

为此公司决策层决心顺应市场，狠抓管理，挖潜创新，从市场调查入手，紧密结合公司实际，运用科学方法对其进行优化组合，制定出1999年度总体经济效益最优的生产计划方案。

2)市场调查与生产状况分析1998年，受东南亚金融风暴的影响，国内摩托车市场出现疲软，供给远大于需求，该集团的摩托车生产经营也出现开工不足、库存增加和资金周转困难等问题。

该集团共有三个专业厂，分别生产轻便摩托车、普通两轮车和三轮摩托车三大系列产品。

20000辆和22000辆。

为1600万元。

根据以上情况，该公司应如何制定1999年度总体经济效益最优的生产计划方案(二)线性规划建模设X j表示生产M j型摩托车的数量(j=1,2,…,9),则总利润最大的摩托车产品生产计划数学模型为：MaxZ=×+×+×+×+×+×+×+×+×=++++++++满足 X1+X2+X3≤50000 (1)X4+X5+X6≤60000 (2)X7+X8+X9≤10000 (3)++++++++≤4000×5 (4)X3≤20000 (5)X6≤22000 (6)×(X1+X2+X3)+×(X4+X5+X6)+×3(X7+X8+X9)≤3000 (7)++++++++≤1600(8)X j≥0(j=1,2,3,4…9)模型说明：约束(1)、(2)、(3)分别表示三种系列摩托车的最大生产能力限制；约束(4)表示摩托车的生产受流动资金的限制；约束(5)和(6)表示M3和M6两种车产量受发动机供应量限制；约束 (7)表示未销售的产量受库存能力的限制；约束(8)表示未销售产品占用资金的限制。

Excel中规划求解宏模块的使用Excel自带的宏模块“规划求解”可用于求解线性规划、非线性规划、整数规划的最优解。

规划求解宏模块在Excel普通运行状况下一般不会启动，当需要调用时，可以从工具菜单条中加载宏来启动，其基本步骤如下。

（1）在工具菜单中选择“加载宏”选型。

（2）在加载宏对话框中选择“规划求解”选型。

图0-1加载“规划求解”宏（3）如果成功加载，则在工具菜单条中会出现“规划求解”选型。

由此，可以运用规划求解宏模块求解任何一个线性规划问题、整数规划问题、非线性规划问题，分别举例说明如下。

例1 营养配餐问题根据生物营养学理论，一个成年人每天要维持人体正常的生理健康需求，需要从食物中获取3000卡路里热量、55g蛋白质和800mg钙。

假定市场上可供选择的食品有猪肉、鸡蛋、大米和白菜，这些食品每千克所含热量和营养成分以及市场价格如表1-1所示。

如何选购才能在满足营养的前提下，使购买食品的总费用最小？表0-1 营养配餐问题数据表解，建立该问题的线性规划模型如下：假设x j （j=1,2,3,4）分别为猪肉、鸡蛋、大米和白菜每天的购买量，则其线性规划模型为：⎪⎪⎩⎪⎪⎨⎧=≥≥+++≥+++≥++++++=)4,3,2,1(0800500300200400551020605030002009008001200..24820min 4321432143214321j x x x x x x x x x x x x x t s x x x x z j 第一步：需要在Excel 中建立该问题的电子表格模型，如图0-2所示。

图0-2 营养配餐问题的Excel 表模型其中单元格B10：E10设置为决策变量单元格，F12设置为目标单元格，F4：F6设置为三个约束条件的左边项，即表示实际获得的营养。

目标单元格和约束条件左边项的函数如图0-3所示图0-3营养配餐问题中的公式设置函数sumproduct(区域1，区域2)为Excel 的常用函数，表示将区域1中对应元素与区域2中对应元素相乘后再相加。

实验报告一、实验名称：线性规划问题二、实验目的：通过本实验，能掌握Spreadsheet方法，会熟练应用Spreedsheet建模与求解方法。

在Excel（或其他）背景下就所需解决的问题进行描述与展平，然后建立线性规划模型，并用Excel的命令与功能进行运算与分析。

三、实验设备计算机、Excel 四、实验内容1、线性规划其中，目标函数为求总利润的最大值。

B11=SUMPRODUCT(B6:C6,B9:C9)；B14=SUMPRODUCT(B3:C3,$B$9:$C$9); B15=SUMPRODUCT(B4:C4,$B$9:$C$9); B16=SUMPRODUCT(B5:C5,$B$9:$C$9); D14=D3; D15=D4; D16=D5; 用规划求解工具求解：目标单元格为B11，求最大值，可变单元格为$B$9:$C$9，约束条件为B14：B16<=D14:D16。

在【选项】菜单中选择“采用线性模型”“假定非负”。

即可进行求解得结果，即确定产品A的产量为20，产品B的产量为24，可实现最大总利润为428。

2、灵敏度分析在【可变单元格】表中：在【可变单元格】表中：“终值”表示最优解，即产品A 产量为20，产品B 产量为24。

“递减成本”表示产品的边际收入与按影子价格折算的边际成本的差，当递减成本小于0时，表示不应该安排该产品的生产，在表中的情况反映了产品A 产品、B 都进行生产，因为在产品A 与产品B 产量增加的同时利润也是在增加的。

产量增加的同时利润也是在增加的。

“目标式系数”是在目标函数中变量的系数，也是产品A 与产品B 的单位利润。

的单位利润。

“允许的增量”“允许的增量”和“允许的减量”表示在不改变最优解结构的前提下，和“允许的减量”表示在不改变最优解结构的前提下，和“允许的减量”表示在不改变最优解结构的前提下，单个目标系数可变的单个目标系数可变的上下限。

也就是说，在目标函数中，产品A 的价值系数在（3.6，9.6】内，产品B 的价值系数不变，或者产品A 的价值不变，产品B 的价值系数在【23.3，8.75】内，最有的生产方案依旧为产品A 产量为20，产品B 产量为24，以达到最大利润。

运筹学实验报告学院：安全与环境工程学院姓名：侯小洁学号：1350940109专业：物流工程班级：1301班实验时间：5月6、8日5月13、15日5月20、22日湖南工学院安全与环境工程学院2015年5月实验一线性规划一、实验目的1、理解线性规划的概念。

2、对于一个问题，能够建立基本的线性规划模型。

3、会运用Excel解决线性规划电子表格模型。

二、实验内容线性规划的一大应用适用于联邦航空公司的工作人员排程，为每年节省开支超过600万美元。

联邦航空公司正准备增加其中心机场的往来航班，因此需要雇佣更多的客户服务代理商，但是不知道到底要雇用多少数量的代理商。

管理层意识到在向公司的客户提供令人满意的服务水平的同时必须进行成本控制，因此，必须寻找成本与收益之间合意的平衡。

于是，要求管理团队研究如何规划人员才能以最小的成本提供令人满意的服务。

分析研究新的航班时间表，以确定一天之中不同时段为实现客户满意水平必须工作的代理商数目。

在表1.1最后一栏显示了这些数目，其中第一列给出对应的时段。

表中的其它数据反映了公司与客户服务代理商协会所定协议上的一项规定，这一规定要求每一代理商工作8小时为一班，各班的时间安排如下：轮班1：6:00AM～2:00PM轮班2：8:00AM～4:00PM轮班3：中午～8:00PM轮班4：4:00PM～午夜轮班5：10:00PM～6:00AM表中打勾的部分表示这段时间是有相应轮班的。

因为轮班之间的重要程度有差异，所以协议中工资也因轮班所处的时间而不同。

每一轮班对代理商的补偿（包括收益）如最低行所示。

问题就是，在最低行数据的基础上，确定将多少代理商分派到一天之中的各个轮班中去，以使得人员费用最小，同时，必须保证最后一栏中所要求的服务水平的实现表1.1联邦航空公司人员排程问题的数据轮班的时段时段 1 2 3 4 5 最少需要代理商的数量6:00AM～8:00AM √ 488:00AM～10:00AM √ √ 7910:00AM～中午√ √ 65中午～2:00PM √ √ √ 872:00PM～4:00PM √ √ 644:00PM～6:00PM √ √ 736:00PM～8:00PM √ √ 828:00PM～10:00PM √ 4310:00PM～午夜√ √ 52午夜～6:00AM √15每个代理商的每日170 160 175 180 195成本实验要求:（1）如何规划人员才能以最小的成本提供令人满意的服务？（2）根据实验内容自行设计模型，求解最优方案。

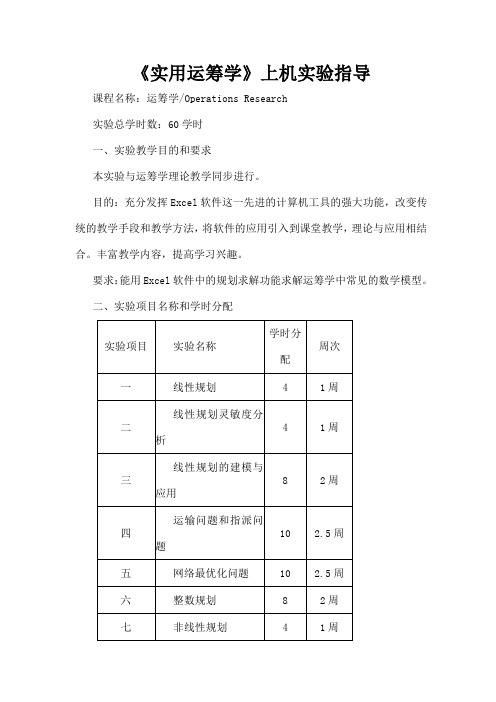
《实用运筹学》上机实验指导课程名称：运筹学/Operations Research实验总学时数：60学时一、实验教学目的和要求本实验与运筹学理论教学同步进行。

目的：充分发挥Excel软件这一先进的计算机工具的强大功能，改变传统的教学手段和教学方法，将软件的应用引入到课堂教学，理论与应用相结合。

丰富教学内容，提高学习兴趣。

要求：能用Excel软件中的规划求解功能求解运筹学中常见的数学模型。

二、实验项目名称和学时分配三、单项实验的内容和要求实验一线性规划（－）实验目的：安装Excel软件“规划求解”加载宏，用Excel软件求解线性规划问题。

（二）内容和要求：安装并启动软件，建立新问题，输入模型，求解模型，结果的简单分析。

（三）实例操作：求解习题1.1。

（1）建立电子表格模型：输入数据、给单元格命名、输入公式等；（2）使用Excel软件中的规划求解功能求解模型；（3）结果分析：如五种家具各生产多少？总利润是多少？哪些工序的时间有剩余，并对结果提出你的看法；（4）在Excel或Word文档中写实验报告，包括线性规划模型、电子表格模型和结果分析等。

案例1 生产计划优化研究某柴油机厂年度产品生产计划的优化研究。

某柴油机厂是我国生产中小功率柴油机的重点骨干企业之一。

主要产品有2105柴油机、x2105柴油机、x4105柴油机、x4110柴油机、x6105柴油机、x6110柴油机，产品市场占有率大，覆盖面广。

柴油机生产过程主要分成三大类：热处理、机加工、总装。

与产品生产有关的主要因素有单位产品的产值、生产能力、原材料供应量与生产需求情况等。

每种产品的单位产值如错误!未找到引用源。

所示。

表 C－1 各种产品的单位产值为简化问题，根据一定时期的产量与所需工时，测算了每件产品所需的热处理、机加工、总装工时，如表 C－2所示。

表 C－2 单位产品所需工时同时，全厂所能提供的总工时如表 C－3所示。

表 C－3 各工序所能提供的总工时产品原材料主要是生铁、焦碳、废钢、钢材四大类资源。

运筹学实验报告一、实验目的：通过实验熟悉单纯形法的原理，掌握matlab循环语句的应用，提高编程的能力和技巧，体会matlab在进行数学求解方面的方便快捷。

二、实验环境：Matlab2012b,计算机三、实验内容（包含参数取值情况）：构造单纯形算法解决线性规划问题Min z=cxs.t. Ax=bxj>=0,j=1,…,n函数功能如下：function[S,val]=danchun(A1,C,N)其中，S为最优值，Val为最优解，A1为标准形式LP问题的约束矩阵及最后一列为资源向量（注：资源向量要大于零），A1=[A+b]；C是目标函数的系数向量，C=c；N为初始基的下标（注：请按照顺序输入，若没有初始基则定义N=[]）。

先输入A1,C,N三个必要参数，然后调用danchun（A1,C,N）进行求解。

在此函数中，首先判断N的长度是否为空，若为空，则flag=1，进入初始解问题的迭代求值，添加辅助问题，构建单纯形表，求g所对应的RHS值，若其>0,则返回该问题无解，若其=0，则返回A1,C,N三个参数，继续构造单纯形表求解。

A1为经过变换后的系数及资源向量，C为单纯形表的第一行，N为经过辅助问题求解之后的基的下标。

否则，直接构建单纯形表，对该问题进行求解，此时flag=2,多次迭代后找到解。

另外，若在大于零的检验数所对应的系数均小于零时，会显示“此问题无界”。

若找到最优解和最优值时，会输出“val”和“S=”以及具体数值。

四、源程序（在matlab中输入edit后回车，写在.M文件中，并保存为danchun.M）function[S,val]=danchun(A1,C,N)if(length(N)==0)gN=zeros(1,length(A1(:,1)));gC=[-C,gN,0];%原文题的检验数的矩阵G=[zeros(1,length(C)),-ones(1,length(gN)),0];val=zeros(1,length(C));%val为最优解；for i=(length(C)+1):length(C)+length(A1(:,1))%生成基变量gN(i-length(C))=i;endNn=gN;%%%%%%%ll=zeros(1,length(N));%比值最小原则%生成除了最上端两行的表的矩阵gb=A1(:,length(C)+1);A1(:,length(C)+1)=[];l=zeros(length(gN),length(gN));gA=[A1,l,gb];for i=1:length(gb)gA(i,gN(i))=1;endfor i=1:length(gN)%J为基本可行基所对应的检验数J(i)=G(gN(i));endfor i=1:length(gN)%找到基本可行基的检验数，将其赋值为0 if(J(i)~=0)G=G-(J(i)/gA(i,gN(i)))*gA(i,:);endendflag=1;elseflag=2;A=A1;Z=[-C,0];%单纯形表的第一行val=zeros(1,length(C));%val为最优解；ll=zeros(1,length(N));%比值最小原则end%%初始解问题while flag==1for i=1:length(gN)%J为基本可行基所对应的G的检验数J(i)=G(gN(i));JZ(i)=Z(gN(i));%JZ为基本可行基所对应的Z的检验数endfor i=1:length(gN)%找到基本可行基的检验数，将其赋值为0 if(J(i)~=0)G=G-(J(i)/gA(i,gN(i)))*gA(i,:);Z=Z-(JZ(i)/gA(i,gN(i)))*gA(i,:);endG1=G;%G1为检验数G1(:,length(G1))=[];D=max(G1);%找到检验数的最大值if(D<=0)%检验数都小于0if(G(length(G))>=1)disp('此情况无解');flag=0;elseif(G(length(G))>=0)for i=1:length(gN)if(max(gN)<=length(A1(1,:)));flag=2;for j=1:length(Nn)a=Nn(1);gA(:,a)=[];Z(a)=[];endA=gA;N=gN;break;endendendendelse%检验数大于0for i=1:length(G)if(G(i)==D)%找到最大的那个检验数所对应的元素for j=1:length(gN)if(gA(j,i)>0)ll(j)=gA(j,length(G))/gA(j,i);%求比值elsell(j)=10000;endendd=min(ll);for k=1:length(ll)%找到进基和离基if(ll(k)==d)gN(k)=i;gA(k,:)=gA(k,:)/gA(k,i);for m=1:k-1gA(m,:)=-(gA(m,i)/gA(k,i))*gA(k,:)+gA(m,:);endfor n=k+1:length(ll)gA(n,:)=-(gA(n,i)/gA(k,i))*gA(k,:)+gA(n,:);endbreak;endendendendendendwhile(flag==2)for i=1:length(N)%J为基本可行基所对应的检验数J(i)=Z(N(i));endfor i=1:length(N)%找到基本可行基的检验数，将其赋值为0if(J(i)~=0)Z=Z-(J(i)/A(i,N(i)))*A(i,:);endendZ1=Z;%Z1为检验数Z1(:,length(Z1))=[];D=max(Z1);%找到检验数的最大值if(D<=0)%检验数都小于0disp('已找到最优解和最优值')for i=1:length(N)val(N(i))=A(i,length(Z));endS=Z(length(Z));disp('val');disp(val);flag=0;else%检验数大于0for i=1:length(Z)if(Z(i)==D)%找到最大的那个检验数所对应的元素for j=1:length(N)if(A(j,i)>0)ll(j)=A(j,length(Z))/A(j,i);%求比值elsell(j)=10000;endendd=min(ll);if(d==10000)disp('此问题无界')flag=0;break;endfor k=1:length(ll)%找到进基和离基if(ll(k)==d)N(k)=i;A(k,:)=A(k,:)/A(k,i);for m=1:k-1A(m,:)=-(A(m,i)/A(k,i))*A(k,:)+A(m,:);endfor n=k+1:length(ll)A(n,:)=-(A(n,i)/A(k,i))*A(k,:)+A(n,:);endbreakendendendendendend五、运行结果与数据测试参考例题：例1：Min z=3x1+x2+x3+x4s.t. -2x1+2x2+x3=43x1+2x+x4=6Xj>=0,j=1,2,3,4在workspace中写入，形式如下：>> A=[-2 2 1 0 43 1 0 1 6]A =-2 2 1 0 43 1 0 1 6>> C=[3 1 1 1]C =3 1 1 1>> N=[3 4]N =3 4>> danchun(A,C,N)已找到最优解和最优值val0 2 0 4ans =6例2：初始解问题Min z=5x1+21x3s.t. x1-x2+6x3-x4=2x1+x2+2x3-x5=1xj>=0,j=1,…,5在workspace中写入，形式如下：>> A=[1 -1 6 -1 0 21 12 0 -1 1]A =1 -1 6 -1 0 21 12 0 -1 1 >> C=[5 0 21 0 0]C =5 0 21 0 0>> N=[]N =[]>> danchun(A,C,N)已找到最优解和最优值val0.5000 0 0.2500 0 0ans =7.7500六、求解实际问题（即解决附件中的实验题目）实验题目列出下列问题的数学模型，并用你自己的单纯形算法程序进行计算，最后给出计算结果。

实验报告课程名称：物流运筹学学院：专业班级：姓名：学号：管理学院课程名称物流运筹学实验项目名称线性规划问题求解、灵敏度分析、运输问题求解指导教师实验软件Exsel实验地点实验时间2019.11.21一、实验目的及要求熟练使用Exsel软件求解本课程中的线性规划问题、灵敏度分析及运输问题，结合教材中的例题，完成Exsel求解。

要求在报告中体现求解过程，对每一步过程要求有截图。

二、实验内容与步骤1、运用Exsel求解线性规划问题(1)根据题干输入相应数据，如下图(2)建模，输入相关数据实际使用=(甲)单位产品消耗定额*计划生产量生产量+(乙)单位产品消耗定额*理化生产量(E5=C5*C10+D5*D10；E6=C6*C10+D6*D10；E7=C7*C10+D7*D10) 总利润=单位利润*计划生产量(G10=C5*C10+D5*D10)(4)计算结果点击“数据”–“模拟分析”–“规划求解”如上图输入。

按“选项”按钮，勾选“采用线性模型”和“假定非负”，点击“确定”，最后点击求解后可求出所需要的解。

(5)输出结果2、运用Exsel进行灵敏度分析点击敏感性报告3、运用Exsel求解运输问题(1)根据题干输入相关数据。

（2）定义名称，选中单元格右键定义名称。

（单位运价，运输量，销量等）（3）建模，输入相关数据实际产量=销地B1+销地B2+销地B3+销地B4；实际销量=产地A1+产地A2+产地A3.G9=C9+D9+E9+F9;G10=C10+D10+E10+F10;G11=C11+D11+E11+F11;C12=C9+C10+C11; D12=D9+D10+D11; E12=E9+E10+E11; F12=F9+F10+F11点击“数据”—“模拟分析”—“规划求解”--如图输入点击选项，勾选“采用线性模型”和“假定非负”，点击确定，进行求解。

输出结果如下图。

三、实验结果（结论）注：可根据内容加页。

运筹学实验报告实验课程:运筹学实验日期: 2020年4月4日任课教师:杨小康班级：数学1802 姓名：王超学号：2501180224一、实验名称: 简单线性规划模型的求解与Lingo软件的初步使用二、实验目的：了解Lingo软件的基本功能和简单线性规划模型的求解的输入和输出结果。

熟悉Lingo 软件在运筹学模型求解中的作用，增强自身的动手能力，提高实际应用能力三、实验要求:1、熟悉Lingo软件的用户环境，了解Lingo软件的一般命令2、给出Lingo中的输入，能理解Solution Report中输出的四个部分的结果。

4、能给出最优解和最优值；5、能给出实际问题的数学模型，并利用lingo求出最优解四、报告正文（文挡，数据，模型，程序，图形）:1.在Lingo中求解下面的线性规划数学模型;(1)12132412512345 max2543..28,,,,0z x xx xx xs tx x xx x x x x=++=⎧⎪+=⎪⎨++=⎪⎪≥⎩(2)12121212max2343..28,0z x xxxs tx xx x=+≤⎧⎪≤⎪⎨+≤⎪⎪≥⎩(3)12121212max243..28,0z x xxxs tx xx x=+≤⎧⎪≤⎪⎨+≤⎪⎪≥⎩(4)12121212max324 ..3,0z x xx xs t x xx x=+-≤⎧⎪-+≤⎨⎪≥⎩(5)1212121212max102401.530.50,0z x xx xx xs tx xx x=++≤⎧⎪+≤⎪⎨+≥⎪⎪≥⎩2、某工厂利用三种原料生产五种产品，其有关数据如下表。

原料可利用数（千克）每万件产品所用材料数（千克）A B C D E甲10 1 2 1 0 1 乙24 1 0 1 3 2 丙21 1 2 2 2 2 每万件产品的利润（万元）8 20 10 20 21 (l)建立该问题的运筹学模型。

（2）利用lingo 软件求出最优解，得出最优生产计划解：（1）设xi（i=1,2...,5）为所用材料生产的件数则数学模型,,,,21 2222242 3102;212010208max543215 43215431532154321≥≤++++≤+++≤+++++++ =xxxxxx xxxxt xxxx xxxxsxxxxxz （2）结果为220.3：现有15米长的钢管若干，生产某产品需4米、5米、7米长的钢管各为100、150、120根，问如何截取才能使原材料最省？（建立线性规划模型并利用lingo软件求解）解：方案4米5米7米剩余量截取长度1 3 0 0 32 2 1 0 23 2 0 1 04 1 2 0 15 0 3 0 06 0 1 1 37 0 0 2 14人力资源分配问题某昼夜服务的公交线路每天各时间段内所需司机和乘务人员人数如表1所示。

一、实验背景运筹学是一门应用数学的分支，它运用数学模型和算法来解决各种优化问题。

随着现代科技的发展，运筹学在各个领域的应用越来越广泛，如生产管理、物流运输、资源分配等。

为了提高学生运用运筹学知识解决实际问题的能力，我们开展了运筹学实训实验。

二、实验目的1. 熟悉运筹学的基本概念和常用方法；2. 掌握线性规划、整数规划、运输问题、目标规划等运筹学模型；3. 学会运用计算机软件解决实际问题；4. 培养学生的团队合作精神和创新意识。

三、实验内容本次实验主要包括以下内容：1. 线性规划：以生产计划问题为例，建立数学模型，并运用Excel规划求解器求解最优解。

2. 整数规划：以人员排班问题为例，建立数学模型，并运用Lingo软件求解最优解。

3. 运输问题：以物流配送问题为例，建立数学模型，并运用Lingo软件求解最优解。

4. 目标规划：以投资组合问题为例，建立数学模型，并运用Lingo软件求解最优解。

四、实验步骤1. 线性规划实验（1）问题分析：某企业需要生产甲、乙两种产品，已知生产甲、乙两种产品所需的原料、劳动力及设备等资源消耗量，以及产品的售价和利润。

（2）模型建立：根据问题分析，建立线性规划模型，目标函数为最大化利润，约束条件为资源消耗量不超过限制。

（3）求解：运用Excel规划求解器求解最优解。

2. 整数规划实验（1）问题分析：某公司需要安排员工值班，要求每天至少有3名员工值班，且员工值班时间不能超过一周。

（2）模型建立：根据问题分析，建立整数规划模型，目标函数为最小化员工值班成本，约束条件为员工值班时间不超过限制。

（3）求解：运用Lingo软件求解最优解。

3. 运输问题实验（1）问题分析：某物流公司需要将货物从A、B两个仓库运送到C、D两个销售点，已知各仓库的货物量、各销售点的需求量以及运输成本。

（2）模型建立：根据问题分析，建立运输问题模型，目标函数为最小化运输成本，约束条件为各仓库的货物量不超过需求量。

实验一：线性规划问题1、实验目的：①学习建立数学模型的方法，并懂得区别运筹学中不同分支的数学模型的特点。

②掌握利用计算机软件求解线性规划最优解的方法。

2、实验任务①结合已学过的理论知识，建立正确的数学模型；②应用运筹学软件求解数学模型的最优解③解读计算机运行结果，结合所学知识给出文字定性结论3、实验仪器设备：计算机4、实验步骤：（1）在主菜单中选择线性规划模型，在屏幕上就会出现线性规划页面，如图所示。

（2）在点击“新建”按钮以后，按软件的要求输入目标函数个数和约束条件个数，输入目标函数及约束条件的各变量的系数和b值，并选择好“≥”、“≤”或“=”号，如图所示。

（3）当约束条件输入完毕后，请点击“解决”按钮，屏幕上将显现线性规划问题的结果，如图所示。

例题一：例题二：例题三：例题四：例题五5、试验体会或心得运筹学是一门实用的学科，学习运筹学，结合生活实际运用运筹学，我们可以将资源最大化利用。

学习理论的目的就是为了解决实际问题。

线性规划的理论对我们的实际生活指导意义很大。

当我们遇到一个问题，需要认真考察该问题。

如果它适合线性规划的条件，那么我们就利用线性规划的理论解决该问题。

线性规划指的是在资源有限的条件下，为达到预期目标最优，而寻找资源消耗最少的方案。

其数学模型有目标函数和约束条件组成。

一个问题要满足一下条件时才能归结为线性规划的模型：⑴要求解的问题的目标能用效益指标度量大小，并能用线性函数描述目标的要求；⑵为达到这个目标存在很多种方案；⑶要到达的目标是在一定约束条件下实现的，这些条件可以用线性等式或者不等式描述。

所以，通过这次实验，不仅对运筹学的有关知识有了进一步的掌握，同时对在自己的计算机操作水准也有了很大的提高。

这次实验让我懂得了运筹学在电脑的应用，让我对运输与数学相结合的应用理解更深了。

实验二：整数规划与运输问题1、实验目的：①学习建立数学模型的方法，并懂得区别运筹学中不同分支的数学模型的特点。

实验一：线性规划注：以下四个题目任选一个来写实验报告，其他三道作为参考。

题目1：生产计划问题某企业生产3种产品甲、乙、丙，产品所需的主要原料为A、B两种，每单位原料A可生产产品甲、乙、丙的底座为别为12、18、16个；每个产品甲、乙、丙需要原料B分别为13kg、8kg、10kg，设备生产用时分别为10.5、12.5、8台时，每个产品的利润分别为1450元、1650元、1300元。

按月计划，可提供的原料A为20个单位，原料B为350kg，设备正常的月工作时间为3000台时。

建立实现总利润最高的数学模型并求解。

题目2：投资问题某公司受人委托，准备用120万元投资A和B两种基金，其中A基金的单位投资额为50元，年回报率为10%，B基金的单位投资额为100元，年回报率为4%。

委托人要求在每年的年回报金额至少达到6万元的基础上要求投资风险最小。

据测定每单位A基金的投资风险指数为8，每单位B基金的投资风险指数为3，风险指数越大表面投资风险越大。

委托人要求至少在基金B中的投资额不少于30万元。

（1）为了使总的投资风险指数最小，该公司在基金A和B中各投资多少单位？这时每年的回报金额是多少？（2）为了使总的投资回报金额最大，应该如何投资？这时投资风险指数是多少？题目3：配料问题某化工厂根据一项合同要为用户生产一种用甲、乙两种原料混合配置而成的特殊产品。

甲、乙两种原料都含有A、B、C三种化学成分，其含量（％）是：甲为12，2，3；乙为3，3，15。

按合同规定，产品中三种化学成分的含量（％）不得低于4，2，5。

甲、乙原料成本为每千克3，2元。

厂方希望总成本达到最某咨询公司，受厂商的委托，对新上市的一种新产品进行消费者反应的调查。

该公司采用了挨户调查的方法，委托他们调查的厂商以及该公司的市场研究专家对该调查提出下列几点要求：（1）至少调查2000户人家；（2）在晚上调查的户数和白天调查的户数相等；（3）至少调查700户有孩子的家庭；（4）至少调查450户无孩子的家庭。

运筹学实验报告(一)线性规划问题的计算机求解-(1)-CAL-FENGHAI.-(YICAI)-Company One1运筹学实验报告实验课程:运筹学实验日期: 任课教师:王挺第五种方案0 3 0 0第六种方案0 1 1 3第七种方案0 0 2 1设：第i种方案需要的钢管为Xi根（其中i=1，2...6）,可得:minz=X1+X2+X3+X4+X5+X6+X7解：model:min= X1+X2+X3+X4+X5+X6+X7;3*X1+2*X2+2*X3+X4>=100;X2+2*X4+3*X5+X6>=150;X3+X6+2*X7>=120;endObjective value: 135.0000Infeasibilities: 0.000000Total solver iterations: 2Variable Value Reduced CostX1 0.000000 0.2500000X2 0.000000 0.1666667X3 50.00000 0.000000X4 0.000000 0.8333333E-01X5 50.00000 0.000000X6 0.000000 0.1666667X7 35.00000 0.0000004人力资源分配问题某昼夜服务的公交线路每天各时间段内所需司机和乘务人员人数如表1所示。

班次时间所需人数班次时间所需人数1 6:00~10:00 60 4 18:00~22:00 502 10:00~14:00 70 5 22:00~2:00 203 14:00~18:00 60 6 2:00~6:00 30设司机和乘务人员分别在各时间段开始时上班，并连续工作8小时，问该公交线路应怎样安排司机和乘务人员，既能满足工作需要，又使配备司机和乘务人员的人数最少？5投资计划问题某地区在今后三年内有四种投资机会，第一种是在3年内每年年初投资，年底可获利润20%，并可将本金收回。

荆楚理工学院运筹学实训实验室实验报告 课程名称：运筹学实训 专业：数学与应用数学实验题目 利用excel 实现单纯形表计算学生姓名 李武阳赵星浩王 铖学 号 2016409010113 2016409010114 2018ZSB091107 班级 16级数学与应用数学1班 指导教师 张玲 实验日期 2018.10.10 成绩一、实验目的与要求：1、理解单纯形算法的原理和基本过程2、能利用EXCEL 实现单纯形表计算二、实验任务：利用excel 实现下列线性规划问题的单纯形算法的过程1、在excel 中输入单纯形表；2、在表格中计算检验数；3、在表格中实现换基运算；4、在表格中实现初等行变换。

用单纯形法解决下面线性规划问题（用大M 法）；⎪⎪⎩⎪⎪⎨⎧≥≥≥+≥+++-=0,,0-222-622max 3213231321321x x x x x x x x x x x x x Z三、实验步骤和结果，（给出主要过程的文字说明，包含代码、图、表）1、在excel 表格中输入题目数据；2、计算检验数，找出最大的检验数并进基X2退基X9；3、重复换基，当人工变量全部退基时候，X4的检验数为1.25理应进基，但X4所在列的系数均小于等于0，即线性规划问题有无界解。

（具体计算过程如下所示）由上面的结果可以得到：此线性方程组的可行域是无界的，所以该线性方程组无有限解。

四、实验总结(对实验过程进行分析,总结实验过程中出现的问题、体会和收获)本次实验在excel表格中完成，所以容易因为看错数字而出错，单纯形表的运算性质决定在一步错之后往往需要重新算，所以比较费时费力，我们在计算时要注意每个量及每一步的进基和出基的选择。

但是我们可以利用这个方法可以解决实际问题中比较复杂的一些线性规划问题，特别是一些手工计算难以求解的问题。

五附录Excel。