2018年中考数学复习第4单元图形的初步认识与三角形第19课时全等三角形检测湘教版
- 格式:doc
- 大小:379.50 KB
- 文档页数:6

第四章图形的认识§4.1图形的初步认识A组2015年全国中考题组一、选择题1.(2015·重庆,6,3分)如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H,若∠1=135°,则∠2的度数为()A.65°B.55°C.45°D.35°解析利用两直线平行,同旁内角互补.答案 C2.(2015·福建福州,2,3分)下列图形中,由∠1=∠2能得到AB∥CD的是()解析只有B中可以利用内错角相等,两直线平行.答案 B3.(2015·四川泸州,5,3分)如图,AB∥CD,CB平分∠ABD.若∠C=40°,则∠D的度数为()A.90°B.100°C.110°D.120°解析∵AB∥CD,∠C=40°,∴∠ABC=40°.∵CB平分∠ABD,∴∠ABD=80°,∴∠D=100°.答案 B4.(2015·山东泰安,5,3分)如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于()A.122°B.151°C.116°D.97°解析由AB∥CD得到∠EFD=∠1=58°,再由FG平分∠EFD,得到∠GFD =29°,又∵AB∥CD,∴∠FGB=180°-29°=151°.答案 B5.(2015·浙江金华,9,3分)以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是()A.如图1,展开后,测得∠1=∠2B.如图2,展开后,测得∠1=∠2,且∠3=∠4C.如图3,测得∠1=∠2D.如图4,展开后,再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD解析A中内错角相等,两直线平行;B中可得∠1=∠2=90°,且∠3=∠4=90°,从而可得两直线平行;D中有条件可知两三角形全等,可得∠CAO =∠DBO,所以a,b互相平行.答案 C6.(2015·浙江绍兴,10,4分)挑游戏棒是一种好玩的游戏,游戏规则:当一根棒条没有被其它棒条压着时,就可以把它往上拿走.如图中,按照这一规则,第1次应拿走⑨号棒,第2次应拿走⑤号棒,…….则第6次应拿走 ( )A .②号棒B .⑦号棒C .⑧号棒D .⑩号棒解析 注意题目要求:当一根棒条没有被其它棒条压着时,就可以把它往上拿走. 答案 D 二、填空题7.(2015·浙江杭州,14,4分)如图,点A ,C ,F ,B 在同一直线上,CD 平分∠ECB ,FG ∥CD .若∠ECA 为α,则∠GFB 为________(用关于α的代数式表示). 解析 ∵∠ECA =α,∴∠ECB =180°-α,由角的平分线可得∠DCB =90°-α2,再由FG ∥CD ,可得∠GFB =∠DCB =90°-α2. 答案 90°-α28.(2015·四川宜宾,10,3分)如图,AB ∥CD ,AD 与BC交于点E ,若∠B =35°,∠D =45°,则∠AEC =________.解析 ∵AB ∥CD ,∠B =35°,∴∠C =∠B =35°.∵∠AEC 可以看作是△CED 的一个外角,∴∠AEC =∠C +∠D =35°+45°=80°. 答案 80°9.(2015·浙江嘉兴,12,5分)右图是百度地图的一部分(比例尺1∶4 000 000),按图可估测杭州在嘉兴的南偏西________度方向上,到嘉兴的实际距离为________.解析以嘉兴为方位中心,画出方向标,可估计杭州在嘉兴南偏西45度;再测量出两地的图上距离,利用比例尺1∶4 000 000=图上距离∶实际距离,可得两地的实际距离.答案南偏西45 4 380 kmB组2014~2011年全国中考题组一、选择题1.(2013·浙江湖州,4,3分)如图,已知直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数为()A.30°B.60°C.120°D.150°解析法一∵a∥b,∴∠3=∠1=60°.∵∠2+∠3=180°,∴∠2=180°-∠3=120°,故选C;法二∵a∥b,∴∠6=∠1=60°.∵∠2+∠6=180°,∴∠2=180°-∠6=120°,故选C;法三∵a∥b,∴∠1+∠5=180°.∵∠1=60°,∴∠5=120°,∴∠2=∠5=120°,故选C;法四∵∠1+∠4=180°,∠1=60°,∴∠4=180°-∠1=120°.∵a∥b,∴∠2=∠4=120°,故选C.答案 C2.(2014·浙江金华,2,3分)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线.能解释这一实际应用的数学知识是()A.两点确定一条直线B.两点之间线段最短C.垂线段最短D.在同一平面内,过一点有且只有一条直线与已知直线垂直解析经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是两点确定一条直线,故选A.答案 A3.(2014·浙江杭州,5,3分)下列命题中,正确的是() A.梯形的对角线相等B.菱形的对角线不相等C.矩形的对角线不能互相垂直D.平行四边形的对角线可以互相垂直解析选项A,只有特殊的梯形——等腰梯形的对角线相等,而一般梯形的对角线不相等,错误;选项B,特殊的菱形——正方形的对角线相等,错误;选项C,特殊的矩形——正方形的对角线互相垂直,错误;选项D,特殊的平行四边形——菱形的对角线互相垂直,正确.故选D.答案 D4.(2014·浙江宁波,9,4分)已知命题“关于x的一元二次方程x2+bx+1=0,当b<0时必有实数解”,能说明这个命题是假命题的一个反例可以是() A.b=-1 B.b=2 C.b=-2 D.b=0解析命题的条件是b<0,结论是一元二次方程x2+bx+1=0有实数解,B,D不符合.当b=-2时,关于x的一元二次方程为x2-2x+1=0,方程有实数解,舍去;当b=-1时,关于x的一元二次方程为x2-x+1=0,(-1)2-4×1×1<0,方程没有实数解,符合题意,故选A.答案 A二、填空题5.(2013·浙江湖州,12,4分)把15°30′化成度的形式,则15°30′=________度.解析30′÷60=0.5°,∴15°30′=15.5°.答案15.56.(2013·浙江温州,13,5分)如图,直线a,b被直线c所截.若a∥b,∠1=40°,∠2=70°,则∠3=________度.解析如图,∵a∥b,∴∠4=∠1=40°,∴∠3=∠2+∠4=110°.答案 1107.(2013·广东佛山,15,3分)命题“对顶角相等”的条件是________. 解析 对顶角是指两条直线相交形成的四个角中,两个没有公共边的角,所以这个命题的条件是两个角是对顶角. 答案 两个角是对顶角8.(2014·浙江杭州,12,4分)已知直线a ∥b ,若∠1=40°50′,则∠2=______________. 解析 如图,∵a ∥b ,∴∠3=∠1=40°50′.∵∠2+∠3=180°,∴∠2=180°-∠3=180°-40°50′=139°10′.故答案为139°10′. 答案 139°10′ 三、解答题9.(2013·广东,19,5分)如图,已知▱ABCD .(1)作图:延长BC ,并在BC 的延长线上截取线段CE ,使得CE =BC (用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,连结AE ,交CD 于点F .求证:△AFD ≌△EFC . (1)解 如图所示,CE 即为所求.(2)证明 在▱ABCD 中, AD ∥BC ,AD =BC .由(1)中作图可知AD ∥BE ,AD =CE , ∴∠DAF =∠CEF . 在△AFD 和△EFC 中,⎩⎨⎧∠DAF =∠CEF (已证),∠DF A =∠CFE (对顶角),AD =CE (已证),∴△AFD ≌△EFC (AAS).10.(2013·甘肃兰州,22,5分)如图,两条公路OA 和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P到两条公路OA,OB的距离相等,且到两工厂C,D的距离相等,用尺规作出货站P的位置(要求:不写作法,保留作图痕迹,写出结论).解如图,作∠AOB的平分线OH,CD的垂直平分线EF,OH与EF的交点P就是货站的位置.所以点P就是所要求作的点.11.(2013·江苏宿迁,23,10分)如图,在平行四边形ABCD中,AD>AB.(1)作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);(2)若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连结EF.求证:四边形ABFE为菱形.(1)解如右图:(2)证明∵BE平分∠ABC,∴∠ABO=∠FBO.∵AF⊥BE于点O,∴∠AOB=∠FOB=∠AOE=90°.又∵BO=BO,∴△AOB≌△FOB.∴AO=FO,AB=FB.∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEO=∠FBO.∴△AOE≌△FOB.∴AE=BF.又∵AE∥BF,∴四边形ABFE是平行四边形.又∵AB=FB,∴平行四边形ABFE是菱形.。

云南省曲靖市师宗县2018届中考数学横向复习第四单元图形的初步认识与三角形第19讲相似三角形考点测试题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(云南省曲靖市师宗县2018届中考数学横向复习第四单元图形的初步认识与三角形第19讲相似三角形考点测试题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为云南省曲靖市师宗县2018届中考数学横向复习第四单元图形的初步认识与三角形第19讲相似三角形考点测试题的全部内容。
第19讲 相似三角形1.(2017·兰州)已知2x =3y(y≠0),则下面结论成立的是(A )A .错误!=错误!B .错误!=错误!C .xy=错误! D 。
错误!=错误! 2.(2017·杭州)如图,在△ABC 中,点D,E 分别在边AB,AC 上,DE ∥BC 。
若BD =2AD,则(B )A 。
ADAB=错误! B 。
错误!=错误! C .错误!=错误! D 。
错误!=错误!3.(2017·楚雄州永仁县一模)如图,在△ABC 中,AD ,BE 是两条中线,则S △EDC ∶S △ABC =(B )A .1∶2B .1∶4C .1∶3D .2∶34.(2017·昆明五华区一模)如图,△ABC 中,∠A =78°,AB =4,AC =6.将△ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(C )A .B 。
C 。
D 。
5.(2017·云南考试说明)如图,AC是矩形ABCD的对角线,E是边BC延长线上一点,AE与CD 相交于点F,则图中的相似三角形(含全等)共有(C)A.2对B.3对C.4对D.5对6.(2017·罗平县模拟)如图,在△ABC中,点D,E分别在边AB,AC上,请添加一个条件:∠AED =∠B(答案不唯一),使△ABC∽△AED.7.(2017·天水)如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A 处,则小明的影子AM长为5米.8.(2017·昆明市官渡区二模)如图,AB,CD相交于点O,OC=4,OD=6,AC∥BD,EF是△ODB的中位线,且EF=4,则AC的长为错误!.9.将正方形与直角三角形纸片按如图所示方式叠放在一起,已知正方形的边长为20 cm,点O为正方形的中心,AB=5 cm,则CD的长为20cm.10.(2017·江西)如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG。
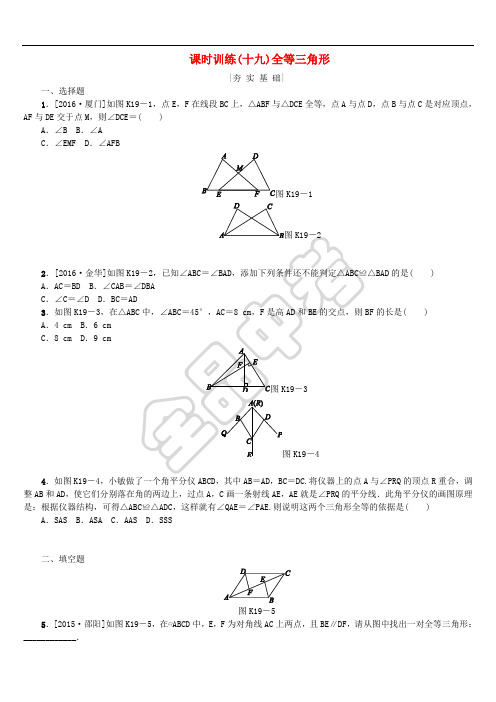
课时训练(十九)全等三角形|夯实基础|一、选择题1.[2016·厦门]如图K19-1,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )A.∠B B.∠AC.∠EMF D.∠AFBK19-12.[2016·金华]如图的是( )A.AC=BD BC.∠C=∠D D.BC=3.如图K19-3的长是( )A.4 cm B.6 cmC.8 cm D.9 cm4.如图K19-4,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( ) A.SAS B.ASA C.AAS D.SSS二、填空题图K19-55.[2015·邵阳]如图K19-5,在▱ABCD中,E,F为对角线AC上两点,且BE∥DF,请从图中找出一对全等三角形:____________.图K19-66.[2017·怀化]如图K19-6,AC=DC,BC=EC,请你添加一个适当的条件:________,使得△ABC≌△DEC.7.[2017·黔东南州]如图K19-7,点B,F,C,E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件________,使得△ABC≌△DEF.K19-78.[2016·贺州]如图BCE,连接AE,BD交于点O,则∠AOB三、解答题9.[2017·吉林]如图求证:∠A=∠D.10.[2017·南充]如图求证:AC∥BD.图K19-1011.[2017·温州]如图K19-11,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.(1)求证:△ABC≌△AED;(2)当∠B=140°时,求∠BAE的度数.图K19-1112.[2016·泰安](1)已知△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是直线BC上一点,且∠DEC =∠DCE,若∠A=60°(如图K19-12①),求证:EB=AD;(2)若将(1)中的“点D在线段AB上”改为“点D在线段AB的延长线上”,其他条件不变(如图②),(1)中的结论是否成立,并说明理由.图K19-12|拓展提升|图K19-1313.[2017·陕西]如图K19-13,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为________.14.[2017·重庆A]在△ABM中,∠ABM=45°,AM⊥BM,垂足为M.点C是BM延长线上一点,连接AC.(1)如图①,若AB=3 2,BC=5,求AC的长;(2)如图②,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F 是线段BC的中点,求证:∠BDF=∠CEF.图K19-14参考答案1.A2.A [解析] 两边与其中一边的对角对应相等的两个三角形不一定全等.3.C [解析] ∵高AD和BE相交于F点,∴∠ADC=∠ADB=∠AEF=90°,∴∠CAD+∠AFE=90°,∠DBF+∠BFD=90°,∵∠AFE =∠BFD,∴∠CAD =∠FBD,∵∠ADB =90°,∠ABC =45°,∴∠BAD =45°=∠ABD,∴AD =BD.在△DBF 和△DAC 中,⎩⎪⎨⎪⎧∠FBD=∠CAD,DB =AD ,∠FDB =∠CDA,∴△DBF ≌△DAC(ASA),∴BF =AC =8 cm.4.D [解析] 在△ADC 和△ABC 中,∵⎩⎪⎨⎪⎧AD =AB ,DC =BC ,AC =AC ,∴△ADC ≌△ABC(SSS),∴∠DAC =∠BAC,即∠QAE=∠PAE.5.答案不唯一,如△ADF≌△CBE [解析] ∵四边形ABCD 是平行四边形, ∴AD =BC ,AD ∥BC ,∴∠DAC =∠BCA. ∵BE ∥DF ,∴∠DFC =∠BEA,∴∠AFD =∠BEC.在△ADF 和△CBE 中,⎩⎪⎨⎪⎧∠DAC=∠BCA,∠AFD =∠BEC,AD =CB ,∴△ADF ≌△CBE(AAS).故答案为△ADF≌△CBE(答案不唯一).6.答案不唯一,如AB =DE(或∠ACD=∠BCE,∠ACB =∠DCE 等) 7.答案不唯一,如AC =FD ,∠B =∠E 等.8.120° [解析] 根据△ACD,△BCE 都是等边三角形,不难证明△DCB≌△ACE(SAS), ∴∠CAE =∠CDB,又∠DCH+∠CHD+∠BDC=180°,∠AOH +∠AHO+∠CAE=180°,∠DHC =∠OHA, ∴∠AOH =∠DCH=60°,∴∠AOB =180°-∠AOH=120°.9.证明:∵BE=CF ,∴BE +EF =CF +EF ,即BF =CE ,在△ABF 和△DCE 中,∵AB =DC ,∠B =∠C,BF =CE ,∴△ABF ≌△DCE ,∴∠A =∠D. 10.证明:∵AE=BF ,∴AE +EF =BF +EF ,即AF =BE.∵DE ⊥AB ,CF ⊥AB ,∴∠AFC =∠BED=90°.在△AFC 和△BED 中,⎩⎪⎨⎪⎧AF =BE ,∠AFC =∠BED,CF =DE ,∴△AFC ≌△BED(SAS).∴∠A =∠B.∴AC∥BD.11.解:(1)证明:∵AC=AD ,∴∠ACD =∠ADC, 又∵∠BCD=∠EDC=90°,∴∠BCD -∠ACD=∠EDC-∠ADC , 即∠BCA=∠ADE.在△ABC 和△AED 中,⎩⎪⎨⎪⎧BC =ED ,∠BCA =∠ADE,AC =AD ,∴△ABC ≌△AED(SAS).(2)由△ABC≌△AED 得∠B=∠E=140°, 五边形内角和为(5-2)×180°=540°, ∴∠BAE =540°-2×140°-2×90°=80°.12.解:(1)证明:过点D 作DF∥BC 交AC 于F(如图①),则∠ADF=∠ABC,∠AFD =∠ACB,∠FDC =∠DCE. ∵在等腰三角形ABC 中,∠A =60°,∴△ABC 是正三角形,∴∠ABC =∠ACB=60°, ∴∠DBE =120°,∠ADF =∠AFD=60°=∠A, ∴△ADF 是正三角形,则∠DFC=120°,AD =DF. ∵∠DEC =∠DCE,∴∠FDC =∠DEC,ED =CD , 在△DBE 和△CFD 中, ⎩⎪⎨⎪⎧∠DEC=∠FDC,∠DBE =∠DFC=120°,ED =CD ,∴△DBE ≌△CFD(AAS), ∴EB =DF ,∴EB =AD.(2)EB =AD 依然成立.理由如下:过点D 作DF∥BC 交AC 的延长线于F(如图②). 类似(1)有:AD =DF ,∠FDC =∠DEC,ED =CD , 又∵∠DBE=∠DFC=60°,∴在△DBE 和△CFD 中,⎩⎪⎨⎪⎧∠DEC=∠FDC,∠DBE =∠DFC,ED =CD ,∴△DBE≌△CFD(AAS),∴EB =DF ,∴EB =AD.13.18 [解析] 过点A 作AE⊥AC 交CD 的延长线于点E ,由题意易证△AED≌△ACB,故AE =AC =6,四边形ABCD的面积等于△ACE 的面积,即四边形ABCD 的面积=12AC×AE=12×6×6=18.14.解:(1)∵AM⊥BM,∴∠AMB =∠AMC=90∵∠ABM =45°,∴∠ABM =∠BAM=45°, ∴AM =BM ,∵AB =3 2,∴AM =BM =3, ∵BC =5,∴MC =2,∴AC =22+32=13.(2)证明:延长EF 到点G ,使得FG =EF ,连接BG. ∵DM =MC ,∠BMD =∠AMC=90°,BM =AM , ∴△BMD ≌△AMC ,故AC =BD ; 又CE =AC ,因此BD =CE ,∵点F 是线段BC 的中点,∴BF =FC , 由BF =FC ,∠BFG =∠EFC,FG =FE , ∴△BFG ≌△CFE ,故BG =CE ,∠G =∠E, ∴BD =CE =BG ,∴∠BDG =∠G, ∴∠BDG =∠E.。



课时训练(十九)全等三角形|夯实基础|一、选择题1.[2016·厦门]如图K19-1,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )A.∠B B.∠AC.∠EMF D.∠AFBK19-1K19-22.[2016·金华]如图K19-2,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )A.AC=BD B.∠CAB=∠DBAC.∠C=∠D D.BC=AD3.如图K19-3,在△ABC中,∠ABC=45°,AC=8 cm,F是高AD和BE的交点,则BF的长是( )A.4 cm B.6 cmC.8 cm D.9 cmK19-3K19-44.如图K19-4,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( ) A.SAS B.ASA C.AAS D.SSS二、填空题图K19-55.[2015·邵阳]如图K19-5,在▱ABCD中,E,F为对角线AC上两点,且BE∥DF,请从图中找出一对全等三角形:____________.6.[2017·怀化]如图K19-6,AC=DC,BC=EC,请你添加一个适当的条件:________,使得△ABC≌△DEC.7.[2017·黔东南州]如图K19-7,点B,F,C,E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件________,使得△ABC≌△DEF.K19-7K19-88.[2016·贺州]如图K19-8,在△ABC中,分别以AC,BC为边作等边三角形ACD和等边三角形BCE,连接AE,BD交于点O,则∠AOB的度数为________.三、解答题9.[2017·吉林]如图K19-9,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.图K19-910.[2017·南充]如图K19-10,DE⊥AB,CF⊥AB,垂足分别是E,F,DE=CF,AE=BF.求证:AC∥BD.图K19-1011.[2017·温州]如图K19-11,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.(1)求证:△ABC≌△AED;(2)当∠B=140°时,求∠BAE的度数.图K19-1112.[2016·泰安](1)已知△ABC 是等腰三角形,其底边是BC ,点D 在线段AB 上,E 是直线BC 上一点,且∠DEC =∠DCE,若∠A=60°(如图K19-12①),求证:EB =AD ;(2)若将(1)中的“点D 在线段AB 上”改为“点D 在线段AB 的延长线上”,其他条件不变(如图②),(1)中的结论是否成立,并说明理由.图K19-12|拓 展 提 升|图K19-1313.[2017·陕西]如图K19-13,四边形ABCD 中,AB =AD ,∠BAD =∠BCD=90°,连接AC.若AC =6,则四边形ABCD 的面积为________.14.[2017·重庆A]在△ABM 中,∠ABM =45°,AM ⊥BM ,垂足为M.点C 是BM 延长线上一点,连接AC. (1)如图①,若AB =3 2,BC =5,求AC 的长;(2)如图②,点D 是线段AM 上一点,MD =MC ,点E 是△ABC 外一点,EC =AC ,连接ED 并延长交BC 于点F ,且点F 是线段BC 的中点,求证:∠BDF=∠CEF.图K 19-14参考答案1.A2.A [解析] 两边与其中一边的对角对应相等的两个三角形不一定全等. 3.C [解析] ∵高AD 和BE 相交于F 点,∴∠ADC =∠ADB=∠AEF=90°, ∴∠CAD +∠AFE=90°,∠DBF +∠BFD=90°, ∵∠AFE =∠BFD,∴∠CAD =∠FBD,∵∠ADB =90°,∠ABC =45°,∴∠BAD =45°=∠ABD,∴AD =BD.在△DBF 和△DAC 中,⎩⎪⎨⎪⎧∠FBD=∠CAD,DB =AD ,∠FDB =∠CDA,∴△DBF ≌△DAC(ASA),∴BF =AC =8 cm.4.D [解析] 在△ADC 和△ABC 中,∵⎩⎪⎨⎪⎧AD =AB ,DC =BC ,AC =AC ,∴△ADC ≌△ABC(SSS),∴∠DAC =∠BAC,即∠QAE=∠PAE.5.答案不唯一,如△ADF≌△CBE [解析] ∵四边形ABCD 是平行四边形, ∴AD =BC ,AD ∥BC ,∴∠DAC =∠BCA. ∵BE ∥DF ,∴∠DFC =∠BEA,∴∠AFD =∠BEC.在△ADF 和△CBE 中,⎩⎪⎨⎪⎧∠DAC=∠BCA,∠AFD =∠BEC,AD =CB ,∴△ADF ≌△CBE(AAS).故答案为△ADF≌△CBE(答案不唯一).6.答案不唯一,如AB =DE(或∠ACD=∠BCE,∠ACB =∠DCE 等) 7.答案不唯一,如AC =FD ,∠B =∠E 等.8.120° [解析] 根据△ACD,△BCE 都是等边三角形,不难证明△DCB≌△ACE(SAS), ∴∠CAE =∠CDB,又∠DCH+∠CHD+∠BDC=180°,∠AOH +∠AHO+∠CAE=180°,∠DHC =∠OHA, ∴∠AOH =∠DCH=60°,∴∠AOB =180°-∠AOH=120°.9.证明:∵BE=CF ,∴BE +EF =CF +EF ,即BF =CE ,在△ABF 和△DCE 中,∵AB =DC ,∠B =∠C,BF =CE ,∴△ABF ≌△DCE ,∴∠A =∠D. 10.证明:∵AE=BF ,∴AE +EF =BF +EF ,即AF =BE.∵DE ⊥AB ,CF ⊥AB ,∴∠AFC =∠BED=90°.在△AFC 和△BED 中,⎩⎪⎨⎪⎧AF =BE ,∠AFC =∠BED,CF =DE ,∴△AFC ≌△BED(SAS).∴∠A =∠B.∴AC∥BD.11.解:(1)证明:∵AC=AD ,∴∠ACD =∠ADC, 又∵∠BCD=∠EDC=90°,∴∠BCD -∠ACD=∠EDC-∠ADC , 即∠BCA=∠ADE.在△ABC 和△AED 中,⎩⎪⎨⎪⎧BC =ED ,∠BCA =∠ADE,AC =AD ,∴△ABC ≌△AED(SAS).(2)由△ABC≌△AED 得∠B=∠E=140°, 五边形内角和为(5-2)×180°=540°, ∴∠BAE =540°-2×140°-2×90°=80°.12.解:(1)证明:过点D 作DF∥BC 交AC 于F(如图①),则∠ADF=∠ABC,∠AFD =∠ACB,∠FDC =∠DCE. ∵在等腰三角形ABC 中,∠A =60°,∴△ABC 是正三角形,∴∠ABC =∠ACB=60°, ∴∠DBE =120°,∠ADF =∠AFD=60°=∠A, ∴△ADF 是正三角形,则∠DFC=120°,AD =DF. ∵∠DEC =∠DCE,∴∠FDC =∠DEC,ED =CD , 在△DBE 和△CFD 中,⎩⎪⎨⎪⎧∠DEC=∠FDC,∠DBE =∠DFC=120°,ED =CD ,∴△DBE ≌△CFD(AAS), ∴EB =DF ,∴EB =AD.(2)EB =AD 依然成立.理由如下:过点D 作DF∥BC 交AC 的延长线于F(如图②). 类似(1)有:AD =DF ,∠FDC =∠DEC,ED =CD , 又∵∠DBE=∠DFC=60°,∴在△DBE 和△CFD 中,⎩⎪⎨⎪⎧∠DEC=∠FDC,∠DBE =∠DFC,ED =CD ,∴△DBE≌△CFD(AAS),∴EB =DF ,∴EB =AD.13.18 [解析] 过点A 作AE⊥AC 交CD 的延长线于点E ,由题意易证△AED≌△ACB,故AE =AC =6,四边形ABCD的面积等于△ACE 的面积,即四边形ABCD 的面积=12AC×AE=12×6×6=18.14.解:(1)∵AM⊥BM,∴∠AMB =∠AMC=90∵∠ABM =45°,∴∠ABM =∠BAM=45°, ∴AM =BM ,∵AB =3 2,∴AM =BM =3, ∵BC =5,∴MC =2,∴AC =22+32=13.(2)证明:延长EF 到点G ,使得FG =EF ,连接BG. ∵DM =MC ,∠BMD =∠AMC=90°,BM =AM , ∴△BMD ≌△AMC ,故AC =BD ; 又CE =AC ,因此BD =CE ,∵点F 是线段BC 的中点,∴BF =FC , 由BF =FC ,∠BFG =∠EFC,FG =FE , ∴△BFG ≌△CFE ,故BG =CE ,∠G =∠E, ∴BD =CE =BG ,∴∠BDG =∠G, ∴∠BDG =∠E.。