顺义区2013届初三一模数学试卷_(word版)

西城区24．在Rt △ABC 中，∠ACB =90°，∠ABC =α，点P 在△ABC 的内部．(1) 如图1，AB =2AC ，PB =3，点M 、N 分别在AB 、BC 边上，则cos α=_______， △PMN 周长的最小值为_______；(2) 如图2，若条件AB =2AC 不变，而P A =2，PB =10，PC =1，求△ABC 的面积； (3) 若P A =m ，PB =n ，PC =k ，且cos sin k m n αα==，直接写出∠APB 的度数．24．解：（1）cos αPMN 周长的最小值为 3 ； ………………………2分 （2）分别将△P AB 、△PBC 、△P AC 沿直线AB 、BC 、AC 翻折，点P 的对称点分别是点D 、E 、F ，连接DE 、DF ，（如图6）则△P AB ≌△DAB ，△PCB ≌△ECB ，△P AC ≌△FAC .∴AD =AP =AF ， BD =BP =BE ，CE =CP =CF .∵由（1）知∠ABC =30°，∠BAC =60°，∠ACB =90°， ∴∠DBE =2∠ABC =60°，∠DAF =2∠BAC =120°， ∠FCE =2∠ACB =180°. ∴△DBE 是等边三角形，点F 、C 、E 共线. ∴DE =BD =BP EF =CE +CF =2CP =2. ∵△ADF 中，AD =AF ∠DAF =120°， ∴∠ADF =∠AFD =30°.∴DF .∴22210EF DF DE +==. ∴∠DFE =90°. ………………………………………………………4分 ∵2ABC DBE DFE DAF BDAFE S S S S S ∆∆∆∆==++多边形，∴21122222ABC S ∆=++=PBACD E F图6∴ABC S ∆=. ……………………………………………5分 （3）∠APB =150°. ………………………………………………………… 7分 说明：作BM ⊥DE 于M ，AN ⊥DF 于N .（如图7） 由（2）知∠DBE =2α，∠DAF =1802α-o . ∵BD =BE=n ，AD =AF=m ， ∴∠DBM =α，∠DAN =90α-o . ∴∠1=90α-o，∠3=α. ∴DM =sin n α，DN =cos m α. ∴DE =DF =EF . ∴∠2=60°.∴∠APB =∠BDA =∠1+∠2+∠3=150°.昌平区24．在△ABC 中，AB =4，BC =6，∠ACB =30°，将△ABC 绕点B 按逆时针方向旋转，得到△A 1BC 1．（1）如图1，当点C 1在线段CA 的延长线上时，求∠CC 1A 1的度数； （2）如图2，连接AA 1，CC 1．若△CBC 1的面积为3，求△ABA 1的面积；（3）如图3，点E 为线段AB 中点，点P 是线段AC 上的动点，在△ABC 绕点B 按逆时针方向旋转的过程中，点P 的对应点是点P 1，直接写出线段EP 1长度的最大值与最小值．C 1C BA 1A图2A 1C 1ABC图1图3A24．解：（1）如图1，依题意得：△A 1C 1B ≌△ACB .……… 1分∴BC 1=BC ，∠A 1C 1B =∠C =30°. ∴∠BC 1C = ∠C =30°.321NMP ACD EB图7A 1C 1ABC图1∴∠CC 1A 1 = 60°.…………………………… 2分 （2）如图2，由（1）知：△A 1C 1B ≌△ACB .∴A 1B = AB ，BC 1 = BC ，∠A 1BC 1 =∠ABC . ∴∠1 = ∠2，114263A B AB C B BC === ∴ △A 1BA ∽△C 1BC ………………… 3分 ∴112ΔΔ2439A BA C BCS S ⎛⎫== ⎪⎝⎭. ……………………4分∵1Δ3C BC S =， ∴1Δ43A BA S =. ……………………………5分 （3）线段EP 1长度的最大值为8，EP 1长度的最小值1. ………… 7分房山区24（1）如图1，△ABC 和△CDE 都是等边三角形，且B 、C 、D 三点共线，联结AD 、BE 相交于点P ，求证： BE = AD .（2）如图2，在△BCD 中，∠BCD ＜120°，分别以BC 、CD 和BD 为边在△BCD 外部作等边三角形ABC 、等边三角形CDE 和等边三角形BDF ，联结AD 、BE 和CF 交于点P ，下列结论中正确的是 （只填序号即可）①AD=BE=CF ；②∠BEC=∠ADC ；③∠DPE=∠EPC=∠CP A =60°； （3）如图2，在（2）的条件下，求证：PB+PC+PD=BE .24.(1)证明：∵△ABC 和△CDE 都是等边三角形∴BC=AC ，CE=CD ，∠ACB=∠DCE=60° ∴∠BCE=∠ACD∴△BCE ≌△ACD （SAS ）21C 1CBA 1A图2AB 第24题图1第24题图2ADACB∴BE=AD --------------1分 （2）①②③都正确 --------------4分 （3）证明：在PE 上截取PM=PC ，联结CM由（1）可知，△BCE ≌△ACD （SAS ） ∴∠1=∠2设CD 与BE 交于点G ,,在△CGE 和△PGD 中 ∵∠1=∠2，∠CGE=∠PGD∴∠DPG=∠ECG=60°同理∠CPE=60° ∴△CPM 是等边三角形--------------5分 ∴CP=CM ，∠PMC=60° ∴∠CPD=∠CME=120°∵∠1=∠2,∴△CPD ≌△CME （AAS ）---6分 ∴PD=ME∴BE=PB+PM+ME=PB+PC+PD. -------7分 即PB+PC+PD=BE .怀柔区24. 如图，△ABC 中，∠ACB=90°，AD=AC,AB=AN,连结CD 、BN,CD 的延长线交BN 于点F ．（1）当∠ADN 等于多少度时，∠ACE=∠EBF,并说明理由； （2）在（1）的条件下，设∠ABC=α，∠CAD =β，试探索α、β满足什么关系时，△ACE ≌△FBE ，并说明理由．24. （1）解：当∠ADN 等于90度时，∠ACE=∠EBF. ……………………………1分 理由如下：∵∠ACB=∠ADN =90°，∴△ABC 和△AND 均为直角三角形又∵AC=AD ，AB=AN∴△ABC ≌△AND ……………………………2分∴∠CAB=∠DAN∴∠CAD=∠BAN又∠ACD=∠ADC, ∠ABN=∠ANB∴∠ACD= ∠ABN 即∠ACE=∠EBF……………………………3分（2）解：当2βα=时，△ACE ≌△FBE ． ……………………………4分在△ACD 中，∵AC=AD ，∴αβ-=-=∠-=∠οοο9021802180CAD ACD ……………………………5分 21GM PDECAB在Rt △ABC 中， ∠ACD+∠BCE=90°，即9090BCE α︒-+∠=︒，∴∠BCE=α．∵∠ABC=α，∴∠ABC=∠BCE ……………………6分 ∴CE=BE由（1）知：∠ACE=∠EBF,又∠AEC=∠BEF∴△ACE ≌△FBE ．………………………7分密云县24．如图1，在等腰梯形ABCD 中，AD BC ∥，E 是AB 的中点，过点E 作EF BC ∥交CD 于点F ．46AB BC ==，， 60B =︒∠.（1）点E 到BC 的距离为 ；（2）点P 为线段EF 上的一个动点，过P 作PM EF ⊥交BC 于点M ，过M 作MN AB ∥交折线ADC 于点N ，连结PN ，设EP x =.①点N 在线段AD 上时（如图2），PMN △的形状是否发生改变？若不变，求出PMN △的周长；若改变，请说明理由；②当点N 在线段DC 上时（如图3），是否存在点P ，使PMN △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由.A D EBF C（备用）A D E BF C（备用）A D E BF C图1图2A DE BF CP N M图3A DE BF CP N24．（1）如图1，过点E 作EG ⊥BC 于点G ．∵E 为AB 的中点， ∴BE=21AB=2 在Rt △EBG 中，∠B=60°，∴∠BEG=30度． ∴BG=21BE=1，EG=31222=- 即点E 到BC 的距离为3……………………………………1分（2）①当点N 在线段AD 上运动时，周长不变．∵PM ⊥EF ，EG ⊥EF ， ∴PM ∥EG ． ∵EF ∥BC ，∴EP=GM ，PM=EG= 3同理MN=AB=4．如图2，过点P 作PH ⊥MN 于H ， ∵MN ∥AB ，∴∠NMC=∠B=60°，∠PMH=30度．∴PH=21PM=23∴MH=3/2.则NH=MN-MH=4- 3/2=5/2.在Rt △PNH 中，PN=.723252222=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+PH NH ∴△PMN 的周长=PM+PN+MN=37 4.................................3++分②当点N 在线段DC 上运动时，存在．当PM=PN 时，如图3，作PR ⊥MN 于R ，则MR=NR ． 类似①，MR= 3/2. ∴MN=2MR=3．∵△MNC 是等边三角形， ∴MC=MN=3．此时，x=EP=GM=BC-BG-MC=6-1-3=2．…………………………………5分朝阳区24．在Rt △ABC 中，∠A =90°，D 、E 分别为AB 、AC 上的点．（1）如图1，CE =AB ，BD =AE ，过点C 作CF ∥EB ，且CF =EB ，连接DF 交EB 于点G ，连接BF ，请你直接写出EBDC的值； （2）如图2，CE =kAB ，BD =kAE ，12EB DC =，求k 的值．24. 解：(1)EB DC =………………………………………………………………………2分(2)过点C 作CF ∥EB 且CF =EB ，连接DF 交EB 于点G , 连接BF .∴四边形EBFC 是平行四边形. …………………………………………………3分 ∴CE ∥BF 且CE =BF . ∴∠ABF =∠A =90°.∵BF =CE =kAB .∴BFk AB=. 图2B 图1FB∵BD=kAE，∴BDkAE=.………………………………………………………………………4分∴BF BDAB AE=.∴DBF∆∽EAB∆.……………………………………………………………5分∴DFkBE=,∠GDB=∠AEB.∴∠DGB=∠A=90°.∴∠GFC=∠BGF=90°.∵12CF EBDC DC==.∴3DF DFEB CF==.∴k=3.…………………………………………………………………………7分大兴区24. 如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A、点D重合）将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH．（1）求证：∠APB=∠BPH；（2）当点P在边AD上移动时，△PDH的周长是否发生变化？并证明你的结论；（3）设AP为x，四边形EFGP的面积为S，请直接写．．．出．S与x的函数关系式，并求出．．S的最小值．24．（1）证明：∵PE=BE ，∴∠EBP=∠EPB .又∵∠EPH=∠EBC=90°,∴∠EPH-∠EPB=∠EBC-∠EBP .即∠PBC=∠BPH .又∵AD∥BC ,GFDECBA∴∠APB=∠PBC .∴∠APB=∠BPH . ………………………………………2分 （2）△PHD 的周长不变，为定值 8 ………………………3分证明：过B 作BQ ⊥PH ，垂足为Q由（1）知∠APB=∠BPH 又∵ ∠A=∠BQP=90°，BP=BP∴ △ABP ≌△QBP ∴ AP=QP , AB=BQ 又∵ AB=BC ∴ BC = BQ 又∵ ∠C=∠BQH=90°，BH=BH ∴ △BCH ≌△BQH ∴ CH=QH∴ △PHD 的周长为：PD+DH+PH =AP+PD+DH+HC =AD+CD =8………………5分（3）21282S x x =-+ 配方得，21(2)62S x =-+，∴当x =2时，S 有最小值6 …………………………………7分东城区24. 问题1：如图1，在等腰梯形ABCD 中，AD ∥BC ，AB =BC =CD ，点M ，N 分别在AD ，CD 上，若∠MBN =12∠ABC ，试探究线段MN ，AM ，CN 有怎样的数量关系？请直接写出你的猜想，不用证明；问题2：如图2，在四边形ABCD 中，AB =BC ，∠ABC +∠ADC =180°，点M ，N 分别在DA ，CD 的延长线上，若∠MBN =12∠ABC 仍然成立，请你进一步探究线段MN ，AM ，CN 又有怎样的数量关系？写出你的猜想，并给予证明.A B CDEF G H PQ24. （本小题满分7分）解：（1）猜想的结论：MN=AM+CN．……………1分（2）猜想的结论：MN=CN-AM．……………3分证明:在NC截取CF= AM，连接BF．∵∠ABC+∠ADC=180°，∴∠DAB+∠C=180°．又∵∠DAB+∠MAB=180°，∴∠MAB=∠C．∵AB=BC AM=CF，∴△AMB≌△CFB ．∴∠ABM=∠CBF，BM=BF．∴∠ABM +∠ABF =∠CBF+∠ABF．即∠MBF =∠ABC．∵∠MBN=12∠ABC，∴∠MBN=12∠MBF．即∠MBN=∠NBF．又∵BN=BN BM=BF，∴△MBN≌△FBN．∴MN=NF．∵NF=CN-CF，∴MN=CN-AM．…………………7分丰台区 24．在ABC △中，∠ACB =90°，AC ＞BC ，D 是AC 边上的动点，E 是BC 边上的动点，AD =BC ，CD =BE ．（1） 如图1，若点E 与点C 重合，连结BD ，请写出∠BDE 的度数；（2）若点E 与点B 、C 不重合，连结AE 、BD 交于点F ，请在图2中补全图形，并求出∠BFE 的度数．24.海淀区24．在△ABC 中，∠ACB ＝90︒．经过点B 的直线l （l 不与直线AB 重合）与直线BC 的夹角等于ABC ∠，分别过点C 、点A 作直线l 的垂线，垂足分别为点D 、点E ．（1）若45ABC ∠=︒，CD =1（如图），则AE 的长为 ；（2）写出线段AE 、CD 之间的数量关系，并加以证明； （3）若直线CE 、AB 交于点F ， 56CF EF =，CD =4，求BD 的长．24．（1）2AE =.………………………1分（2）线段AE 、CD 之间的数量关系为2AE CD =.………………………2分 证明：如图1，延长AC 与直线l 交于点G ． 依题意，可得∠1＝∠2． ∵∠ACB ＝90︒，D BC （E ）A图1图2CABFEDCAB∴∠3=∠4. ∴BA BG =.∴CA ＝CG ．………………………3分 ∵AE ⊥l ，CD ⊥l ， ∴CD ∥AE ． ∴△GCD ∽△GAE ． ∴12CD GC AE GA =＝． ∴2AE CD =．………………………4分 （3）解：当点F 在线段AB 上时，如图2， 过点C 作CG ∥l 交AB 于点H ，交AE 于点G ． ∴∠2＝∠HCB ． ∵∠1=∠2， ∴∠1＝∠HCB ． ∴CH BH =． ∵∠ACB ＝90︒，∴∠3+∠1＝∠HCB +∠4 =90︒． ∴∠3＝∠4． ∴CH AH BH ==． ∵CG ∥l ，∴△FCH ∽△FEB ． ∴56CF CH EF EB =＝． 设5,6CH x BE x ==，则10AB x =．∴在△AEB 中，∠AEB ＝90︒，8AE x =． 由（2）得，2AE CD =． ∵4CD =, ∴8AE =. ∴1x =.∴10,6,5AB BE CH ===． ∵CG ∥l ，∴△AGH ∽△AEB ． ∴12HG AH BE AB ==． ∴3HG =．………………………5分 ∴8CG CH HG =+=．图3图2∵CG ∥l ，CD ∥AE , ∴四边形CDEG 为平行四边形. ∴8DE CG ==.∴2BD DE BE =-=．……………………6分 当点F 在线段BA 的延长线上时，如图3， 同理可得5CH =,3GH =,6BE =. ∴DE =2CG CH HG =-=． ∴ 8BD DE BE =+=．∴2BD =或8．……………………7分门头沟区24．已知：在△ABC 中，AB ＝AC ，点D 为BC 边的中点，点F 是AB 边上一点，点E 在线段DF 的延长线上，点M 在线段DF 上，且∠BAE ＝∠BDF ，∠ABE ＝∠DBM ． （1） 如图1，当∠ABC ＝45°时，线段 DM 与AE 之间的数量关系是 ； （2） 如图2，当∠ABC ＝60°时，线段 DM 与AE 之间的数量关系是 ；（3）① 如图3，当ABC α∠=（0<<90α︒︒）时，线段 DM 与AE 之间的数量关系是 ；② 在（2）的条件下延长BM 到P ，使MP ＝BM ，连结CP ，若AB ＝7，AE＝求sin ∠ACP 的值．24．解：（1）DM AE ．………………………………………………………………2分 （2）12DM AE =． ……………………………………………………………3分（3）① cos DM AE =α． ………………………………………………………4分② 如图，连结AD 、EP ． ∵AB =AC ，∠ABC =60°， ∴△ABC 为等边三角形．又∵D 为BC 的中点，∴AD ⊥BC ，∠DAC =30°，BD =DC =12BC =72． ∵∠BAE =∠BDM ，∠ABE =∠DBM ，∴△ABE ∽△DBM ．A B CD EFMMFED CA ACD EF M 图1图2图3∴12BM DB BE AB ==．∴EB =2BM ． 又∵PB =2BM ，∴EB =PB ．∵60EBP ABE ABP PBC ABP ABC ∠=∠+∠=∠+∠=∠=︒, ∴△BEP 为等边三角形． ∴EM ⊥BP ．∴∠BMD =90°． ∵D 为BC 的中点，M 为BP 的中点，∴DM ∥PC ．∴∠BPC =∠BMD = 90°． ∵AB CB =，BE BP =，∠ABE ＝∠DBM ， ∴△ABE ≌△CBP ．∴BCP BAE ∠=∠，∠BPC =∠BEA = 90°．在Rt △AEB 中，∵∠BEA =90°，AE =AB =7， ∴cos EAB ∠．∴cos cos PCB BAE ∠=∠5分 在Rt △ABD 中，sin AD AB ABD =⋅∠ 在Rt △NDC 中，cos DC CN NCD =∠∴ND =． ∴NA AD ND =-=． 过点N 作NH ⊥AC 于H ． ∴12NH AN ==．…………………………………………………6分 ∴sin NH ACP CN ∠=．……………………………………………7分平谷区 24．（1）如图(1)，△ABC 是等边三角形，D 、E 分别是 AB 、BC 上的点，且BD CE =，连接AE 、CD 相交于点P . 请你补全图形，并直接写出∠APD 的度数；= （2）如图（2）,Rt △ABC 中，∠B =90°，M 、N 分别是 AB 、BC 上的点，且,AM BC =BM CN =，连接AN 、CM 相 交于点P . 请你猜想∠APM = °，并写出你的推理过程. 24．解：（1）60°HP ACEF M N 图2（2）45° ………………………………..2分 证明：作AE ⊥AB 且AE CN BM ==.可证EAM MBC ∆≅∆. ……………………………..3分 ∴ ,.ME MC AME BCM =∠=∠∵ 90,CMB MCB ∠+∠=︒∴ 90.CMB AME ∠+∠=︒ ∴ 90.EMC ∠=︒∴ EMC ∆是等腰直角三角形,45.MCE ∠=︒ ……………….5分又△AEC ≌△CAN （s ， a ， s ）…………………………………………………………..6分 ∴ .ECA NAC ∠=∠ ∴ EC ∥AN.∴ 45.APM ECM ∠=∠=︒…………………………………………………………………..7分顺义区24．如图1，将三角板放在正方形ABCD 上，使三角板的直角顶点E 与正方形ABCD 的顶点A 重合．三角板的一边交CD 于点F ，另一边交CB 的延长线于点.G （1）求证：EF EG =； （2）如图2，移动三角板，使顶点E 始终在正方形ABCD 的对角线AC 上，其他条件不变， （1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由； （3）如图3，将（2）中的“正方形ABCD ”改为“矩形ABCD ”，且使三角板的一边经过点B ，其他条件不变，若AB a =，BC b =，求EFEG的值．24．（1）证明：∵9090GEB BEF DEF BEF ∠+∠=∠+∠=°，°，∴.DEF GEB ∠=∠又∵ED BE =，∴Rt Rt FED GEB △≌△.∴.EF EG = ………………………………………………………2分（2）成立.证明：如图，过点E 分别作BC CD 、的垂线，垂足分别为H I 、，则90EH EI HEI =∠=，°. ∵9090GEH HEF IEF HEF ∠+∠=∠+∠=°，°，∴.IEF GEH ∠=∠∴Rt Rt FEI GEH △≌△.图2∴.EF EG = …………………………………4分（3）解：如图，过点E 分别作BC CD 、的垂线，垂足分别为M N 、，则90MEN ∠=°，.EM AB EN AD ∥，∥∴.EM CE ENAB CA AD == ∴.EM AD a EN AB b ==…………………………………5分 ∴9090GME MEF FEN MEF ∠+∠=∠+∠=°，°， ∴.MEN GEM ∠=∠∴Rt Rt FEN GEM △∽△. ∴.EF EN b EG EM a ==…………………………………7分通州区24．已知：2AD =，4BD =，以AB 为一边作等边三角形ABC .使C 、D 两点落在直线AB 的两侧.（1）如图，当∠ADB=60°时，求AB 及CD 的长； （2）当∠ADB 变化，且其它条件不变时，求CD 的 最大值，及相应∠ADB 的大小.24． 解：（1）过点A 作AG BC ⊥于点G . ∵∠ADB=60°，2AD =， ∴1DG =，3AG =， ∴ 3GB =，∴ tan 33AG ABG BG ∠==， ∴30ABG ∠=o，23AB =， ……………… 1分；∵ △ABC 是等边三角形，∴ 90DBC ∠=o，23BC =， ……………… 2分；由勾股定理得：()222242327CD DB BC =+=+=. …… 3分；（2）作60EAD ∠=o，且使AE AD =，连接ED 、EB . ………… 4分；第24题图ADBCG第24题图D CBA∴△AED 是等边三角形， ∴AE AD =，60EAD ∠=o，∵ △ABC 是等边三角形， ∴AB AC =，60BAC ∠=o ，∴EAD DAB BAC DAB ∠+∠=∠+∠， 即EAB DAC ∠=∠，∴△EAB ≌△DAC . ……………… 5分； ∴EB =DC .当点E 、D 、B 在同一直线上时，EB 最大，∴246EB =+=， ……………… 6分； ∴ CD 的最大值为6，此时120ADB ∠=o. …………… 7分.另解：作60DBF ∠=o，且使BF BD =，连接DF 、AF . 参照上面解法给分第24题图ECBA FA BC D第24题图。

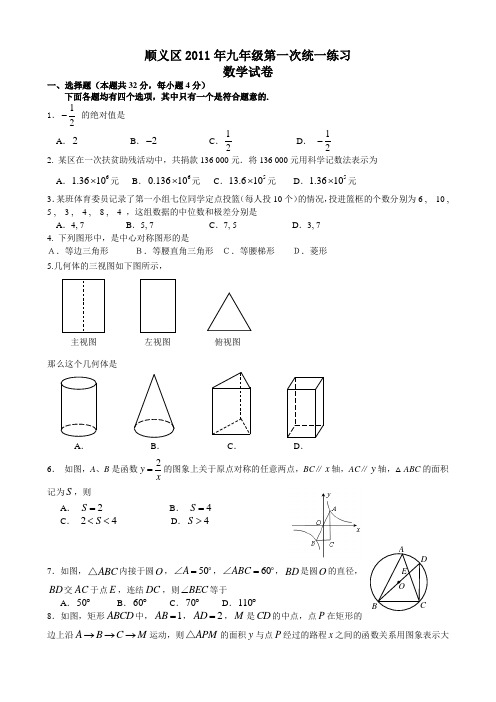
顺义区2011年九年级第一次统一练习数学试卷一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个是符合题意的. 1．12-的绝对值是 A ．2B ．2-C ．12D ． 12-2. 某区在一次扶贫助残活动中，共捐款136 000元．将136 000元用科学记数法表示为 A ．61.3610⨯元 B ．60.13610⨯元 C ．513.610⨯元 D ．51.3610⨯元3．某班体育委员记录了第一小组七位同学定点投篮（每人投10个）的情况，投进篮框的个数分别为6 , 10 , 5 , 3 , 4 , 8 , 4 ，这组数据的中位数和极差分别是 A ．4, 7 B ．5, 7 C ．7, 5 D ．3, 7 4. 下列图形中，是中心对称图形的是 Ａ．等边三角形 Ｂ．等腰直角三角形 Ｃ．等腰梯形 Ｄ．菱形 5.几何体的三视图如下图所示，那么这个几何体是6． 如图，A 、B 是函数2y x=的图象上关于原点对称的任意两点，BC ∥x 轴，AC ∥y 轴，△ABC 的面积记为S ，则A ． 2S =B ． 4S =C ． 24S <<D ．4S >7．如图，ABC △内接于圆O ，50A =o∠，60ABC =o∠，BD 是圆O 的直径，BD 交AC 于点E ，连结DC ，则BEC ∠等于 A ．50︒ B ．60︒ C ．70︒ D ．110︒ 8．如图，矩形ABCD 中，1AB =，2AD =，M 是CD 的中点，点P 在矩形的边上沿A B C M →→→运动，则APM △的面积y 与点P 经过的路程x 之间的函数关系用图象表示大E AB CDOA ．B ．C ．D ．主视图左视图俯视图致是下图中的二、填空题（本题共16分, 每小题4分）9.若分式223xx--有意义,则x的取值范围是.10．分解因式: 322ab ab ab++= .11. 从下面的4张牌中，任意抽取两张．其点数和是奇数的概率是．12. 将除去零以外的自然数按以下规律排列，根据第一列的奇数行的数的规律，写出第一列第9行的数为，再结合第一行的偶数列的数的规律，判断2011所在的位置是第行第列.三、解答题(本题共30分，每小题5分)13．计算: 0212124sin60(13)()2--︒--+14. 解不等式2151132x x-+-≥,并把它的解集在数轴上表示出来.15.已知a是一元二次方程2320x x+-=的实数根，求代数式2352362aaa a a-⎛⎫÷+-⎪--⎝⎭的值.16 已知：如图，ABC△中，45ABC∠=°，CD AB⊥于D，BE AC⊥于E，BE与CD相交于点F．求证：BF AC=；C．D．11 2 3 3.5xyA．11 2 3 3.5xyB．11 2 3 3.5xy11 2 3 3.5xyD CBAPM17. 列方程或方程组解应用题:我区教委要求各学校师生开展“彩虹读书活动”. 某校九年级一班和九年级二班的学生向学校图书馆借课外读物共196本，一班为每位学生借3本，二班为每位学生借2本，一班借的课外读物数量比二班借的课外读物数量多44本，求九年级一班和二班各有学生多少人？18． 已知：如图，在平面直角坐标系xOy 中，一次函数24y x =-+的图象分别与x y 、轴交于点A 、 B ，点P 在x 轴上，若6ABP S ∆=,求直线PB 的函数解析式．四、解答题（本题共20分，每小题5分）19．已知：如图，梯形ABCD 中，AD ∥BC ，90B ∠=︒，4AD AB ==，7BC =，点E 在BC 边上，将△CDE 沿DE 折叠，点C 恰好落在AB 边上的点'C 处． （1）求'C DE ∠的度数；（2）求△'C DE 的面积．20. 已知：如图，AB 是O e 的直径，BC 切O e 于B ，AC 交O e 于P ，D 为BC 边的中点，连结DP ． (1) DP 是O e 的切线；(2) 若3cos 5A =， O e 的半径为5， 求DP 的长.21. 学校为了学生的身体健康，每天开展体育活动一小时，开设排球、篮球、羽毛球、体操课．学生可根据自己的爱好任选其中一项，老师根据学生报名情况进行了统计，并绘制了右边尚未完成的扇形统计图和频数分布直方图，请你结合图中的信息，解答下列问题：（1）该校学生报名总人数有多少人？（2）从表中可知选羽毛球的学生有多少人？选排球和篮球的人数分别占报名总人数的百分之几？ （3）将两个统计图补充完整．C'E D C B AOPB22． 如图，将正方形沿图中虚线（其x y <）剪成① ② ③ ④ 四块图形，用这四块图形恰好能拼成一个矩形（非正方形）．（1）画出拼成的矩形的简图； （2）求xy的值．五、解答题（本题共22分，第23题8分，第24题7分，第25题7分）23． 已知：关于x 的一元二次方程23(1)230mx m x m --+-= ()m 为实数(1) 若方程有两个不相等的实数根，求m 的取值范围； （2）求证：无论m 为何值，方程总有一个固定的根；（3）若m 为整数，且方程的两个根均为正整数，求m 的值.24． 已知：如图，等边△ABC 中，点D 为BC 边的中点，点F 是AB 边上一点，点E 在线段DF 的延长线上，∠BAE ＝∠BDF ，点M 在线段DF 上，∠ABE ＝∠DBM ． （1）猜想：线段AE 、MD 之间有怎样的数量关系，并加以证明； （2）在（1）的条件下延长BM 到P ，使MP ＝BM ，连接CP ，若AB ＝7，AE ＝72，求tan ∠BCP 的值．25． 已知：如图，抛物线22(0)y ax ax c a =-+≠与y 轴交于点(0,3)C ，与x 轴交于A 、B 两点，点A 的坐标为(1,0)-．（1）求抛物线的解析式及顶点D 的坐标； （2）设点P 是在第一象限内抛物线上的一个动点，求使与四边形ACDB 面积相等的四边形ACPB 的点P 的坐标；（3）求APD ∆的面积．yy x y x y x x④③②①羽毛球25%体操40%顺义区2011年九年级第一次统一练习数学试题参考答案及评分参考题号 1 2 3 4 5 6 7 8 答案CDBDCBCA二、填空题 9. 32x ≠; 10. 2(1)ab b + ; 11. 12; 12. 81 ; 第45行第15列 ． 三、解答题13.解：原式=32234142⨯-⨯-+ ----------------------------4分 =233+ ---------------------------------------------5分14. 解：去分母，得 2(21)3(51)6x x --+≥ -------------------------1分 去括号，得 421536x x ---≥ ----------------------------2分移项合并同类项，得 1111x -≥ ----------------------------3分系数化为1，得 1x ≤- --------------------------------4分 所以，此不等式的解集为1x ≤- ，在数轴上表示如图所示-----------------------------5分15. 解： 原式=3(2)(2)53(2)22a a a a a a a -+-⎡⎤÷-⎢⎥---⎣⎦------------2分 =2393(2)2a a a a a --÷--=323(2)(3)(3)a a a a a a --⨯-+- --------------------3分=13(3)a a +=2139a a+ ------------------------4分∵ a 是方程2320x x +-=的实数根，∴ 232a a += ∴ 原式=21113(3)326a a ==+⨯ ------------------------------5分16. 证明： ∵ CD AB ⊥∴ 90BDC CDA ∠=∠=︒ --------1分 ∵ 45ABC ∠=︒∴ 45DCB ABC ∠=∠=︒∴ DB DC = ----------------------2分 ∵ BE AC ⊥ ∴ 90AEB ∠=︒∴ 90A ABE ∠+∠=︒ ∵ 90CDA ∠=︒∴ 90A ACD ∠+∠=︒∴ ABE ACD ∠=∠ ----------------3分 在BDF ∆和CDA ∆中BDC CDA DB DCABE ACD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BDF ∆≌CDA ∆ ------------------4分 ∴BF AC = --------------------------5分17. 解：设九年级一班有x 名学生，二班有y 名学生. ----------------------1分 根据题意列方程组，得321963244x y x y +=⎧⎨-=⎩--------------------------------3分解此方程组，得 4038x y =⎧⎨=⎩答：九年级一班有40名学生，二班有38名学生. -----------------------5分18. 解：令0y =，得 2x = ∴ A 点坐标为（2 ，0） 令0x =， 得 4y =∴ B 点坐标为（0 ，4）---------------------------------1分 ∵ 6ABP S ∆= ∴1462AP ⨯⨯= 即3AP = ∴ P 点的坐标分别为1(1,0)P -或2(5,0)P -----------2分 设直线PB 的函数解析式为y kx b =+∴ 04k b b -+=⎧⎨=⎩ 或504k b b +=⎧⎨=⎩ ------------------4分∴ 44k b =⎧⎨=⎩或454k b ⎧=-⎪⎨⎪=⎩ ∴ 直线PB 的函数解析式为44y x =+或445y x =-+ ------------------------------5分19. 解：(1) 过点D 作DF BC ⊥于F . ∵ AD BC P , 90B ∠=︒, AD AB =, ∴ 四边形ABFD 是正方形.∴4DF BF AB === , 3FC = --------1分 在Rt DFC ∆中，2222435CD DF FC =+=+=∴ '5C D =∵ AD FD =,90A DFC ∠=∠=︒, 'C D CD =∴ 'AC D FCD ∆≅∆∴ 'ADC FDC ∠=∠ , '3AC FC == ----------------------------------2分 ∴ ''''90ADF ADC C DF FDC C DF C DC ∠=∠+∠=∠+∠=∠=︒ ∵ 'C DE CDE ∠=∠∴ '45C DE ∠=︒ -----------------------------------------------------------3分(2) 设 EC x = ， 则7BE x =- ，'C E x = ∵'3AC = ∴'1BC =在Rt 'BEC ∆中22(7)1x x -+= 解方程，得 257x =∴ '11255014722777C DE CDES S EC DF ∆∆==⋅=⨯⨯== ---------------5分20.（1） 证明：连结OP 和BP∵AB 是O e 的直径，BC 切O e 于B ，∴ 90APB ∠=︒ , AB BC ⊥ ,∴ 90ABC ABP PBC ∠=∠+∠=︒ ------1分在Rt BPC ∆中，D 为BC 边的中点 ∴ BD PD =∴ BPD PBD ∠=∠∵ OB OP =∴OPB OBP ∠=∠--------------------------------2分∴ 90OPD OPB BPD OBP PBD ABC ∠=∠+∠=∠+∠=∠=︒ 即 PD OP ⊥∴DP 是O e 的切线 -----------------------------3分OPB(2) 连结OD 在Rt ABC ∆中∵ 3cos 5A =， O e 的半径为5 ∴ 50cos 3AB AC A ==∵ OA OB =, DC DB =∴ 12523OD AC ==在Rt OPD ∆中222225202()56333PD OD OP =-=-== --------5分 21. 解：（1）由两个统计图可知该校报名总人数是16016040040%0.4==（人）．-----1分 （2）选羽毛球的人数是40025%100⨯=（人）． --------------------------------------2分因为选排球的人数是100人，所以10025%400=， 因为选篮球的人数是40人，所以4010%400=，即选排球、篮球的人数占报名的总人数分别是25%和10%．---------------------------3分 （3）如图（每补充完整一个图得1分，共2分）．22．（1）如图-----------------------------2分 （2）面积可得 2()(2)x y x y y +=+ ----------------------3分 22222x xy y xy y ++=+ 220x xy y +-= 2()10x xyy+-= ----------------------------------------4分 BD CPO④③②①51x y --=(舍去) 51x y -= ------------5分 23. （1）解： []22243(1)4(23)(3)b ac m m m m ∆=-=----=--------1分 ∵方程有两个不相等的实数根，∴ 2(3)0m -> 且 0m ≠------------------------------------------------2分∴ 3m ≠且 0m ≠∴m 的取值范围是3m ≠且 0m ≠ ------------------------------------3分（2）证明：由求根公式243(1)(3)2b b ac m m x m-±--±-== -----------------------4分∴ 133323322m m m x m m m -+--===-233312m m x m--+==∴无论m 为何值，方程总有一个固定的根是1 ----------------5分（3）∵m 为整数，且方程的两个根均为正整数∴132x m=-必为整数∴ 1m =± 或 3m =±当1m =时 ，11x =- ；当1m =-时，15x =； 当3m =时， 11x = ； 当3m =-时，13x =.∴ 1m =- 或3m =± --------------------------------------------8分24．（1）猜想：2AE MD = ------------------------------------------1分证明：∵ △ABC 是等边三角形，点D 为BC 边的中点，∴ 2AB BC BD ==∵ ∠BAE ＝∠BDF , ∠ABE ＝∠DBM∴ ABE ∆∽DBM ∆ ----------------------2分 ∴2AE ABDM DB== 即 2AE MD = -------------3分（2）解：如图， 连接EP 由（1）ABE ∆∽DBM ∆∴2BE ABBM DB == ∴2BE BM =∵MP BM = ∴ 2BP BM =∴ BE BP =∵ 60EBP ABE ABP PBC ABP ABC ∠=∠+∠=∠+∠=∠=︒ ∴EBP ∆为等边三角形 ----------------------4分∴ EM BP ⊥∴ 90BMD ∠=︒∴90AEB ∠=︒ -----------------------5分 在Rt △AEB 中，AB ＝7，AE ＝72∴ BE =21=22AE -AB∴ 3tan 2BAE ∠=-------------------6分 ∵ AB CB = ，BE BP = ，∠ABE ＝∠DBM ∴ ABE CBP ∆≅∆ ∴ BCP BAE ∠=∠∴ tan BCP ∠=3tan BAE ∠= ---------7分25.解：（1）∵抛物线22(0)y ax ax c a =-+≠与y 轴交于点(0,3)C ，与x 轴交于A (1,0)-∴203a a c c ++=⎧⎨=⎩ 解得13a c =-⎧⎨=⎩∴ 抛物线的解析式为223y x x =-++ ----------------1分 ∵222(2)3(211)3(1)4y x x x x x =--+=--+-+=--+ ∴顶点D 的坐标为（ 1 ，4） -----------------2分（2）连结BC ,过点D 作DE x ⊥轴于点E . 令0y = 则2230x x -++= ∴ 11x =- ，23x = ∴ 点B 的坐标为（3 ，0）∴AOC EBD ACDB OEDC S S S S ∆∆=++四边形梯形11113(34)1249222=⨯⨯+⨯+⨯+⨯⨯=--------3分 ∵14362ABC S ∆=⨯⨯= ∴3BCD S ∆=∵点P 是在第一象限内抛物线上的一个动点， ACDB ACPB S S =四边形四边形∴3BCP BCD S S ∆∆==∴ 点P 是过 D 且与直线BC 平行的直线和抛物线的交点 而直线BC 的函数解析式为3y x =-+--------------------4分 ∴设直线DP 的函数解析式为y x b =-+ ， 过点D （1，4） ∴14b -+= ， 5b =∴直线DP 的函数解析式为5y x =-+ ----------------------5分把5y x =-+代入223y x x =-++中，解得11x =，22x =∴点P 的坐标为（2，3） ---------------------------------6分（3）∵点P 与点C 关于DE 对称，点B 与点A 关于 DE 对称 ∴APD BCD ∆≅∆∴3APD BCD S S ∆∆==．---------------7分。

西城区19．如图，平行四边形ABCD 的对角线AC 、BD 交于点OAC ⊥AB ，AB =2，且AC ︰BD =2︰3． (1) 求AC 的长； (2) 求△AOD 的面积．19．解：（1）如图2.∵平行四边形ABCD 的对角线AC 、BD 交于点 ∴OA = 12AC ，OB = 12BD . …………… 1分∵AC ︰BD =2︰3， ∴OA ︰OB =2︰3 .设OA =2x (x >0)，则OB =3x .∵AC ⊥AB ，∴∠BAC =90°.在Rt △OAB 中，OA 2+AB 2=OB 2. …………………………………… 2分 ∵AB =2， ∴(2x )2+22=(3x )2 . 解得x =±255(舍负).∴AC =2OA =855. …………………………………………………… 3分 （2）∵平行四边形ABCD 的对角线AC 、BD 交于点O ，∴OB =OD .∴S △AOD = S △AOB = 12 AO ²AB = 12×455×2= 455. ……………………… 5分昌平区19. 如图，四边形ABCD 是⊙O 的内接正方形，延长AB 到E ，使BE =AB ，连接CE . （1）求证：直线CE 是⊙O 的切线；（2）连接OE 交BC 于点F ，若OF =2 , 求EF 的长.E19．（1）证明：连接OC∵四边形ABCD 是O 的内接正方形，∴AB=BC ，CO 平分∠DCB ，∠DCB =∠ABC =90°. ∴∠1=45°，∠EBC =90°. ∵AB=BE ， ∴BC=BE . ∴∠2=45°.∴∠OCE =∠1+∠2 = 90°. ∵点C 在O 上，∴直线CE 是O 的切线. …………………………………… 2分（2）解：过点O 作OM ⊥AB 于M ,∴11=22AM BM AB BE ==.∴23BE ME =. ………………………………………………………3分 ∵FB ⊥AE , ∴FB ∥OM .∴△EFB ∽△EOM . …………………………………………………………4分∴EF EB EO EM =. ∴223EF EF =+. ∴EF=4. …………………………………………………………5分房山区19.一副直角三角板如图放置，点C 在FD 的延长线上，AB ∥CF ，∠F =∠ACB =90°,∠E =45°,∠A =60°,A C=10,试求CD 的长．19.解：过点B 作BM ⊥FD 于点M ． ----------------------------------------1分第19题图DA CB在△ACB 中，∠ACB =90°, ∠A =60°,AC =10,∴∠ABC =30°,BC =AC -----------------------------2分 ∵AB ∥CF ，∴∠BCM =30°．∴1sin 302BM BC =⋅︒==-----------------------------3分cos3015CM BC =⋅︒==-------4分 在△EFD 中，∠F =90°, ∠E =45°,∴∠EDF =45°, ∴MD BM ==∴15CD CM MD =-=-． --------------------------------------------5分怀柔区19. 将一副三角板如图拼接：含30°角的三角板（△ABC ）的长直角边与含45°角的三角板（△ACD ）的斜边恰好重合．已知AB ＝23，P 是AC 上的一个动点，连接DP ．（1）当点P 运动到∠ABC 的平分线上时，求DP 的长；（2）当点P 在运动过程中出现PD ＝BC 时，求此时∠PDA 的度数；19. 解：（1）在Rt △ABC 中，AB ＝23，∠BAC ＝30°∴BC ＝3，AC ＝3． 如图（1），作DF ⊥AC∵Rt △ACD 中，AD ＝CD ∴DF ＝AF ＝CF ＝23………………………………………… 1分 ∵BP 平分∠ABC ∴∠PBC ＝30° ∴CP ＝BC·tan30°＝1 ∴PF ＝21∴DP ＝22DF PF +＝210． ………………………………………… 2分（2）当P 点位置如图（2）所示时，根据（1）中结论，DF ＝23，∠ADF ＝45° 又PD ＝BC ＝3∴cos ∠PDF ＝PDDF ＝23∴∠PDF ＝30°………………………………………… 3分∴∠PDA ＝∠ADF －∠PDF ＝15°………………………………………… 4分 当P 点位置如图（3）所示时，同（2）可得∠PDF ＝30°． ∴∠PDA ＝∠ADF ＋∠PDF ＝75°………………………………………… 5分密云县19．如图，已知菱形ABCD，AB=AC，E、F分别是BC、AD的中点，连接AE、CF（1）证明：四边形AECF是矩形； （2）若AB=8，求菱形的面积。

北京市顺义区2013年中考数学一模试卷一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个是符合题意的．B，的相反数是．2．（4分）（2013•顺义区一模）据2013年4月1日《CCTV﹣10讲述》栏目报道，2012年7月11日，一位26岁的北京小伙樊蒙，推着坐在轮椅上的母亲，开始从北京到西双版纳的公里．请把3 359用科学记数法表示徒步旅行，圆了母亲的旅游梦，历时93天，行程3 359B6．（4分）（2013•顺义区一模）如图，AB∥CD，点E在BC上，∠BED=68°，∠D=38°，则∠B的度数为（）7．（4分）（2013•顺义区一模）若x，y为实数，且，则的解：根据题意得：8．（4分）（2013•顺义区一模）如图，AB为半圆的直径，点P为AB上一动点，动点P从点A出发，沿AB匀速运动到点B，运动时间为t，分别以AP与PB为直径做半圆，则图中阴影部分的面积S与时间t之间的函数图象大致为（）B=t二、填空题（本题共16分，每小题4分）9．（4分）（2013•顺义区一模）分解因式：3ab2﹣12ab+12a=3a（b﹣2）2．10．（4分）（2013•顺义区一模）一个袋子中装有6个黑球3个白球，这些球除颜色外，形状、大小、质地等完全相同，在看不到球的条件下，随机地从这个袋子中摸出一个球，摸到白球的概率为．所以随机地从这个袋子中摸出一个球，摸到白球的概率为．11．（4分）（2013•顺义区一模）如图，扇形的半径为6，圆心角θ为120°，用这个扇形围成一个圆锥的侧面，所得圆锥的底面半径为2．=12．（4分）（2013•顺义区一模）如图，边长为1的菱形ABCD中，∠DAB=60度．连接对角线AC，以AC为边作第二个菱形ACC1D1，使∠D1AC=60°；连接AC1，再以AC1为边作第三个菱形AC1C2D2，使∠D2AC1=60°；…，按此规律所作的第n个菱形的边长为（）n﹣1．BM=AM=，AC=AC=个菱形的边长为（故答案为（三、解答题（本题共30分，每小题5分）13．（5分）（2013•顺义区一模）计算：+4sin60°﹣（π﹣3.14）0﹣．×﹣214．（5分）（2013•顺义区一模）解不等式组，并把其解集在数轴上表示出来．，15．（5分）（2013•顺义区一模）已知：如图，CA平分∠BCD，点E在AC上，BC=EC，AC=DC．求证：∠A=∠D．16．（5分）（2013•顺义区一模）已知a2+3a﹣2=0，求代数式÷的值．+•=17．（5分）（2013•顺义区一模）如图，已知A （4，a），B （﹣2，﹣4）是一次函数y=kx+b的图象和反比例函数y=的图象的交点．（1）求反比例函数和一次函数的解祈式；（2）求△A0B的面积．y=的图象上，则由y=中，得，y=×18．（5分）（2013•顺义区一模）某商店销售一种旅游纪念品，3月份的营业额为2000元，4月份该商店对这种纪念品打8折销售，结果销售量增加30件，营业额增加800元，求该种纪念品3月份每件的销售价格是多少？=×，=50四、解答题（本题共20分，每小题5分）19．（5分）（2013•顺义区一模）已知：如图，四边形ABCD中，对角线AC、BD相交于点E，BD⊥DC，∠ABD=45°，∠ACD=30°，AD=CD=2，求AC和BD的长．AD=CD=2×，×=×，BBM+ME+DE=+1+2=3+20．（5分）（2013•顺义区一模）如图，已知△ABC，以AC为直径的⊙O交AB于点D，点E为的中点，连结CE交AB于点F，且BF=BC．（1）判断直线BC与⊙O的位置关系，并证明你的结论；（2）若⊙O的半径为2，cosB=，求CE的长．cosB=求出cosB=，==CE=21．（5分）（2013•顺义区一模）某课外实践小组的同学们为了解2012年某小区家庭月均用（1）表中m=12，n=0.08；（2）把频数分布直方图补充完整；（3）求该小区用水量不超过15t的家庭占被调查家庭总数的百分比；（4）若该小区有1500户家庭，根据调查数据估计，该小区月均用水量超过20t的家庭大约有多少户？n==0.0822．（5分）（2013•顺义区一模）如图1，在四边形ABCD中，AB=CD，E，F分别是BC，AD的中点，连结EF并延长，分别与BA，CD的延长线交于点M，N，则∠BME=∠CNE （不需证明）．小明的思路是：在图1中，连结BD，取BD的中点H，连结HE，HF，根据三角形中位线定理和平行线性质，可证得∠BME=∠CNE．问题：如图2，在△ABC中，AC＞AB，D点在AC上，AB=CD，E，F分别是BC，AD的中点，连结EF并延长，与BA的延长线交于点G，若∠EFC=60°，连结GD，判断△AGD 的形状并证明．HF=CD五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23．（7分）（2013•顺义区一模）已知关于x的方程mx2﹣（3m+2）x+2m+2=0（1）求证：无论m取任何实数时，方程恒有实数根．（2）若关于x的二次函数y=mx2﹣（3m+2）x+2m+2的图象与x轴两个交点的横坐标均为正整数，且m为整数，求抛物线的解析式．，24．（7分）（2013•顺义区一模）如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F．另一边交CB的延长线于点G．（1）求证：EF=EG；（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：（3）如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB=a、BC=b，求的值．，，即=25．（8分）（2013•顺义区一模）如图，已知抛物线y=ax2+bx+3与y轴交于点A，且经过B （1，0），C（5，8）两点，点D是抛物线顶点，E是对称轴与直线AC的交点，F与E关于点D对称．（1）求抛物线的解析式；（2）求证：∠AFE=∠CFE；（3）在抛物线的对称轴上是否存在点P，使△AFP与△FDC相似？若有，请求出所有符合条件的点P的坐标；若没有，请说明理由．，=== =（点之间）或=。

新世纪教育网精选资料 版权全部 @新世纪教育网九年级综合水平质量调研数学试卷2013.3学校 ___________________ 班级 _______________姓名 ________________ 学号 _____________考1． 本试卷共 8 页，共五道大题， 25 道小题，满分 120 分，考试时间 120 分钟 .生 2． 在试卷和答题卡上正确填写学校．班级．姓名．学号.须3． 试题答案一律填涂或书写在 答题卡 上，在试卷上作答无效 .知4． 考试结束，请将本试卷和答题卡一并交回.注 意 1 ． 考生要按规定的要求在机读答题卡上作答，题号要对应，填涂要规范.事项 2 ． 考试结束后，试卷和机读答题卡由监考人一并回收.第一卷（机读卷 32 分）一 1.4 的算术平方根是选 A ． 2B ．± 2C ． 16D ．± 16择2. 如图，已知 △ ABC 为直角三角形， ∠ C=90°，若 C题 沿图中虚线剪去∠ C ， 则∠ 1+∠ 2 等于D本 A.90°B. 135 °E12题C. 150 °D. 270 °BA32第 2分题图，3.布袋中装有 1 个红球， 2 个白球， 3 个黑球，它们除颜色外完好同样，从袋中任每 小 意摸出一个球，摸出的球是白球．．的概率是题 A ．1B ．1C ． 1D ．543626分4.某班的 9 名同学的体重分别是（单位：千克）： 61，59， 70，59， 65，67，59，63，57，这组数据的众数和中位数分别是A ． 59，61B ．59，63C ． 59， 65D ． 57，61 5.全世界可被人类利用的淡水总量仅占地球上总水量的 0.00003 ，所以珍惜水、保护 水，是我们每一位公民当仁不让的责任．此中数字 0.00003 用科学记数法表示为A ．3 10 4B ．3 10 5C ．0.310 4D ．0.3 10 56.如图，模块①－⑤均由 4 个棱长为 1 的小正方体构成，模块⑥由 15 个棱长为 1的小正方体构成 .现从模块①－⑤中选出三个放到模块⑥上，使得模块⑥成为一个棱长为 3 的大正方体 . 则以下选择方案中，能够达成任务的为新世纪教育网精选资料版权全部@新世纪教育网一选择题本题32分，每小题4分A．模块②，④，⑤B．模块①，③，⑤C．模块①，②，⑤D．模块③，④，⑤7.如图，两个齐心圆，大圆的弦 AB与小圆相切于点 P，大圆的弦CD经过点 P，且 CD=13， PC=4，则两圆构成的圆环的面积是A．16πB．36πC．52πD．81π第 7题图8. 矩形 ABCD 中，AD8cm， AB 6cm ．动点E从点C开始沿边 CB 向点B以 2cm/s 的速度运动至点 B 停止，动点 F从点 C 同时出发沿边CD 向点 D 以 1cm/s 的速度运动至点D停止．如图可获得矩形CFHE ，设运动时间为 x（单位： s），此时矩形 ABCD 去掉矩形 CFHE 后节余部分的面积为y(单位： cm2) ，则 y 与 x 之间的函数关系用图象表示大概是以下图第 8题图中的注 1．第Ⅱ卷包含 4 道填空和 13 道解答，共 8 . 答前要真，看清目意要求，按要求真作答.事2．答笔迹要工整，画要清楚，卷面要整.3．考生除画能够用笔外，答必用色或黑色笔、珠笔.二填空本共16分，每小4分三解答本第二卷（非机读卷88 分）9.若分式 x 24的 0， x 的．x210.如，点 A、 B 、C是半径6的⊙O上的点，BB 30,AC 的_____________.AOC第 10如，在△ ABC 中， D、 E 分 AB、 AC 上的点， DE∥A 11.BC．若 AD ＝3， DB＝ 5，DE ＝ 1.2， BC＝．D EB C第 1112. 如，在ABC 中，A，ABC 的平分与ACD 的均分交于点A，得 A，11A1=． A1 BC 的均分与A1CD 的均分交于点A2，得A2，⋯⋯，A2009 BC 的均分与A2009CD的均分第 12交于点 A2010，得 A2010，A2010=．13.（本小 5 分）( 3 1)04sin6027题14. （本小题 5 分）共3x1430解不等式组x，并把它的解集表示在数轴上．2x2分，每小题5分15. （本小题 5 分）A D如图， E、F 是平行四边形ABCD 对角线 AC E上两点， BE ∥ DF ，求证：AF CE 。

顺义区2013届初三第一次统一练习物 理 试 卷 2013.04学校__________________姓名________________准考证号________________ 考 生 须 知1．本试卷共8页，共五道大题、41道小题，满分100分。

考试时间120分钟。

2．在试卷和答题卡上准确填写学校名称、姓名和准考证号。

3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4．在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答。

5．考试结束，将本试卷、答题卡和草稿纸一并交回。

一、单项选择题（下列各小题均有四个选项，其中只有一个选项符合题意。

共28分，每小题2分）1．以下用品中，在通常情况下属于导体的是A ．塑料刻度尺B ．橡胶轮胎C ．细铁丝D ．绘画橡皮2．下列物理量中，用科学家焦耳的名字作为单位的是A ．功B ．力C ．压强D ．速度 3．下列用电器中，利用电流热效应工作的是A ．微波炉B ．电炉子C ．电风扇D ．电脑 4. 下列现象中，属于光的直线传播的是A ．墙壁上装面大镜子，有增大空间的感觉B ．清澈的河底，看起来变浅了C ．清晨，太阳还在地平线以下时，就看到它D ．人在路灯下行走，出现人影相随 5．在图1所示的实例中，目的是为了减小摩擦的是6．在图2所示的四种剪刀中，正常使用时属于费力杠杆的是7．用水平风吹如图3所示的四个模型中，表示空气对模型下表面的压强小于上表面的压强的是图1B.钳子手柄上套有橡胶套 D.拖鞋的底部压有花纹C.电暖气下装有轮子 A.车把上刻有花纹 图2 A B C D8．下列估测值最接近实际的是A ．一张课桌的高度约为20cmB ．一支粉笔的长度约为60cmC ．一个鸡蛋的质量约为500gD ．一名初中学生的质量约为60kg 9．下列关于物态变化以及吸、放热的说法中，正确的是A ．冰箱里冷冻食物的表面结霜是凝华现象，凝华需要放热B ．地球变暖，导致冰川消融是液化现象，液化需要放热C ．冬季河水结冰是凝固现象，凝固需要吸热D ．夏天装有冷饮的杯子“出汗”是熔化现象，熔化需要吸热10．在图4所示的三幅图中，能形象地描述气态物质分子运动特点的是A ．甲图B ．乙图C ．丙图D ．甲图和乙图11．如图5所示，直杆OA 可O 绕点转动，直杆下端挂一重物G 。

顺义区2013届初三第一次练习数学试卷学校 姓名 准考证号 道小题，满分一、选择题（本题共32分，每小题4分） 下面各题均有四个选项，其中只有一个．．是符合题意的． 1．3-的倒数是A ．13- B ． 13C ． 3-D ．32．据2013年4月1日《CCTV —10讲述》栏目报道，2012年7月11日，一位26岁的北京小伙樊蒙，推着坐在轮椅上的母亲，开始从北京到西双版纳的徒步旅行，圆了母亲的旅游梦，历时93天，行程3 359公里．请把3 359用科学记数法表示应为A ．233.5910⨯ B ．43.35910⨯ C ．33.35910⨯ D ．433.5910⨯3．下面四个几何体中，俯视图为四边形的是则这组数据的中位数与众数分别是（ ）A ．17，17B ． 17，18C ．18，17D ．18，185．下列计算正确的是 A ．235a a a += B ．236a a a ⋅= C. 235()a a = D. 532a a a ÷=D6．如图，AB ∥CD ，点E 在BC 上，68BED ∠=︒，38D ∠=︒，则B ∠的度数为A ． 30︒B ． 34︒C ． 38︒D ．68︒7．若x y ，为实数，且30x +=，则2013y x ⎛⎫⎪⎝⎭的值为A ．1B ． 1-C ． 2D ． 2- 8．如图，AB 为半圆的直径， 点P 为AB 上一动点，动点P 从点A 出发，沿AB 匀速运动到点B ，运动时间为t ，分别以AP 和PB 为直径作半圆，则图中阴影部分的面积S 与时间t 之间的函数图象大致为A ．B ．C ．D ．二、填空题（本题共16分，每小题4分）9．分解因式：231212ab ab a -+= ．10．袋子中装有3个红球和4个黄球，这些球除颜色外均相同．在看不到球的条件下，随机从袋中摸出一个球，则摸出红球的概率是_____________．11．如图，扇形的半径为6，圆心角θ为120︒，用这个扇形围成一个圆锥的侧面，所得圆锥的底面半径为 ．12．如图，边长为1的菱形ABCD 中，60DAB ∠=°，则菱形ABCD 的面积是 ，连结对角线AC ，以AC 为边作第二个菱形11ACC D ，使160D AC ∠=°；连结1AC ，再以1AC 为边作第三个菱形122ACC D ，使2160D AC ∠=°；……，按此规律所作的第n 个菱形的面积为___________．C 1D 1D 2C 2D A B图EDCBA三、解答题（本题共30分，每小题5分）13．计算：101()4sin60( 3.14)3π-+︒--14．解不等式组312(1)312x x x -<+⎧⎪⎨+⎪⎩，≥， 并把解集在数轴上表示出来．15．已知：如图，CA 平分BCD ∠, 点E 在AC 上，BC EC =，AC DC =．求证：A D ∠=∠ ．16．已知2320a a +-=，求代数式2231()933a a a a +÷-+-的值．17．如图，已知(2,2)A --，(,4)B n 是一次函数y kx b =+的图象和反比例函数m y x=的图象的两个交点．（1）求反比例函数和一次函数的解析式； （2）求AOB ∆的面积.18．某商店销售一种旅游纪念品，3月份的营业额为2000元，4月份该商店对这种纪念品打8折销售，结果销售量增加30件，营业额增加800元，求该种纪念品3月份每件的销售价格是多少？四、解答题（本题共20分，每小题5分）19．已知：如图，四边形ABCD 中，对角线AC 、BD 相交于点E ，BD DC ⊥，45ABD ∠=︒，30ACD ∠=︒，AD CD ==AC 和BD 的长.DCBAEED CBA20．如图，已知ABC △，以AC 为直径的O 交AB 于点D ，点E 为AD 的中点，连结CE 交AB 于点F ，且BF BC =.（1）判断直线BC 与⊙O 的位置关系，并证明你的结论； （2）若O 的半为2,3cos 5B =,求CE 的长.21．某课外实践小组的同学们为了解2012年某小区家庭月均用水情况，随机调查了该小区请解答以下问题：（1）表中m = ，n = ； （2）把频数分布直方图补充完整；（3）求该小区用水量不超过15t 的家庭占被调查家庭总数的百分比；（4）若该小区有1500户家庭，根据调查数据估计，该小区月均用水量超过20t 的家庭大约有多少户？22． 如图1，在四边形ABCD中，AB CD =，E F 、分别是BC AD 、的中点，连结EF并延长，分别与BA CD 、的延长线交于点M N 、，则BME CNE ∠=∠（不需证明）．小明的思路是：在图1中，连结BD ，取BD 的中点H ，连结HE HF 、，根据三角形中位线定理和平行线性质，可证得BME CNE ∠=∠．问题：如图2，在ABC △中，AC AB >，D 点在AC 上，AB CD =，E F 、分别是BC AD 、的中点，连结EF 并延长，与BA 的延长线交于点G ，若60EFC ∠=°，连结GD ，判断AGD △的形状并证明．五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）C月用水量频数（户）124252015105083023．已知关于x 的方程2(32)220mx m x m -+++= （1）求证：无论m 取任何实数时，方程恒有实数根.（2）若关于x 的二次函数2(32)22y mx m x m =-+++的图象与x 轴两个交点的横坐标均为正整数，且m 为整数，求抛物线的解析式.24．如图1，将三角板放在正方形ABCD 上，使三角板的直角顶点E 与正方形ABCD 的顶点A 重合．三角板的一边交CD 于点F ，另一边交CB 的延长线于点.G （1）求证：EF EG =； （2）如图2，移动三角板，使顶点E 始终在正方形ABCD 的对角线AC 上，其他条件不变， （1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由； （3）如图3，将（2）中的“正方形ABCD ”改为“矩形ABCD ”，且使三角板的一边经过点B ，其他条件不变，若AB a =，BC b =，求EFEG的值．25．如图，已知抛物线23y ax bx =++与y 轴交于点A ，且经过(1,0)(5,8)B C 、两点，点D 是抛物线顶点，E 是对称轴与直线AC 的交点，F 与E 关于点D 对称．（1）求抛物线的解析式；（2）求证：AFE CFE ∠=∠；（3）在抛物线的对称轴上是否存在点P ，使AFP ∆与FDC ∆相似．若有，请求出所有符合条件的点P 的坐标；若没有，请说明理由．顺义区2013届初三第一次统一练习数学试题参考答案及评分参考13．解：原式=341+- …………………………………………4分 =2 ……………………………………………… 5分 14． 解：解不等式312(1)x x -<+，得3x <． ………………………………… 1分解不等式312x +≥，得1x -≥． ………………………………… 2分 ∴不等式组的解集为13x -<≤． ………………………………… 4分在数轴上表示其解集为如图所示…………………………………5分15．证明：∵CA 平分BCD ∠∴ ACB DCE ∠=∠ ……………………………………………1分在ABC ∆和DEC ∆中∵BC EC ACB DCE AC DC =⎧⎪∠=∠⎨⎪=⎩……………………………………………3分 ∴ABC ∆≌DEC ∆ …………………………………………… 4分 ∴A D ∠=∠ ……………………………………………5分16．解：原式=333()(3)(3)(3)(3)a a a a a a a--+⨯+-+- ………………………2分=23(3)(3)a a a a a-⨯+-………………………………………… 3分=1(3)a a +=213a a+ ……………………………………………… 4分∵2320a a +-= ∴232a a +=∴原式=12………………………………………………5分 17．解：（1）将(2,2)A --代入my x=中，得4m =． ∴4y x=． …………………………………………………………………1分 将(,4)B n 代入4y x=中，得．1n = ………………………………2分将(2,2)A --，(1,4)B 代入y kx b=+中22,4.k b k b -+=-⎧⎨+=⎩………3分 解得2,2.k b =⎧⎨=⎩∴22y x =+． ……………………………………………4分 （2）设直线AB 与y 轴交于点C 当0x =时，2y =． ∴2O C =．∴112221322AOBAOC BOC S S S ∆∆∆=+=⨯⨯+⨯⨯= ………………………5分18．解：设该种纪念品3月份每件的销售价格为x 元， ……………………………1分根据题意，列方程得20002000800300.8x x+=- ………………………………………………3分 解之得50x =． …………………………………………………………4分 经检验50x =是所得方程的解．答：该种纪念品3月份每件的销售价格是50元． …………………………5分 解法二：设3月份销售这种纪念品x 件，则4月份销售（x +30）件 …………1分根据题意，列方程得420002000800530x x +⨯=+ ……………………………………………3分 解之得40x =． ………………………………………………4分 经检验40x =是所得方程的解答：该种纪念品3月份每件的销售价格是20005040=（元）…………5分19解：∵ BD DC ⊥∴ 90BDC ∠=︒∵30ACD ∠=︒，AD CD ==∴60,30,DEC DAC ACD ∠=︒∠=∠=︒tan3023DE CD =⋅︒== ∴ 24EC DE == ，30ADE ∠=︒ …………………………………………1分∴ 2AE DE == ……………………………………………………… 2分- ∴ 246AC AE EC =+=+= ………………………………………………3分过点A 作AM BD ⊥,垂足为M ∵ 60AEB DEC ∠=∠=︒∴sin6022AM AE =⋅︒= 1c o s 60212M E A E =︒=⨯= ………………………………………………4分∵45ABD ∠=︒∴BM AM ==∴123BD BM ME DE =+++= …………………………5分20．⑴ BC 与⊙O 相切 证明：连接AE ，∵AC 是O 的直径∴90E ∠=∴90EAD AFE ∠+∠=︒ ∵BF BC =∴BCE BFC ∠=∠又 ∵E 为AD 的中点 ∴EAD ACE ∠=∠ …………………………1分∴ 90BCE ACE ∠+∠=︒ 即AC BC ⊥ 又∵AC 是直径∴BC 是O 的切线 …………………………2分 （2）∵O 的半为2∴4AC =, ∵3cos 5B =由（1）知，90ACB ∠=，∴5AB = ,3BC =∴3BF = ,2AF = ………………………… 3分 ∵EAD ACE ∠=∠, E E ∠=∠C∴AEF ∆∽CEA ∆，∴12EA AF EC CA == ∴2EC EA =， …………………………4分设,2EA x EC x ==由勾股定理22416x x +=，x = （舍负） ∴CE …………………………5分 21． 解：（1）表中填12m =；0.08n =. …………………………2分(2）补全的图形如下图.- …………………………3分（3）0.120.240.320.68++=.即月均用水量不超过15t 的家庭占被调查的家庭总数的68%.…………………………4分 （4）(0.080.04)1500180+⨯=.所以，该小区月均用水量超过20t 的家庭大约有180户. ………………5分22．判断AGD ∆是直角三角形证明：如图连结BD ，取BD 的中点H ，连结HF HE 、，……………………1分F 是AD 的中点，∴HF AB ∥，12HFAB =，………………… 2分 ∴13∠=∠． 同理，12HE CD HE CD =∥，， ∴2EFC ∠=∠． AB CD = ， ∴H F H E =， ∴12∠=∠． …………………………………………3分 60EFC ∠= °，3080510152025412频数（户）月用水量A BCD FGH E1 2 3∴360EFC AFG ∠=∠=∠=°，∴AGF ∆是等边三角形．………………………………4分 AF FD = ， ∴GF FD =，∴30FGD FDG ∠=∠=° ∴90AGD ∠=°即AGD △是直角三角形．…………………………… 5分23．（1）证明：①当0m =时，方程为220x -+=，所以 1x =，方程有实数根.…… 1分②当0m ≠时,[]2(32)4(22)m m m ∆=-+-+=22912488m m m m ++--=244mm ++=2(2)0m +≥ ………………………………2分所以,方程有实数根综①②所述，无论m 取任何实数时，方程恒有实数根 …………3分（2）令0y =，则2(32)220mx m x m -+++=解关于x 的一元二次方程，得11x = ，222x m=+……………………5分 二次函数的图象与x 轴两个交点的横坐标均为正整数，且m 为整数， 所以m 只能取1，2所以抛物线的解析式为254y x x =-+或2286y x x =-+………………7分 24．（1）证明：∵9090GEB BEF DEF BEF ∠+∠=∠+∠=°，°，∴.DEF GEB ∠=∠又∵ED BE =，∴Rt Rt FED GEB △≌△.∴.EF EG = ………………………………………………………2分（2）成立.证明：如图，过点E 分别作BC CD 、的垂线，垂足分别为H I 、，则90EH EI HEI =∠=，°.∵9090GEH HEF IEF HEF ∠+∠=∠+∠=°，°，∴.IEF GEH ∠=∠∴Rt Rt FEI GEH △≌△. ∴.EF EG = …………………………………4分（3）解：如图，过点E 分别作BC CD 、的垂线，垂足分别为M N 、，则90MEN ∠=°，.EM AB EN AD ∥，∥∴.EM CE EN AB CA AD == ∴.EM AD a EN AB b == …………………………………5分 ∴9090GME MEF FEN MEF ∠+∠=∠+∠=°，°，∴.MEN GEM ∠=∠∴Rt Rt FEN GEM △∽△. ∴.EF EN b EG EM a == …………………………………7分25．解：（1）将点(1,0)(5,8)B C 、代入2y ax bx =+3025538a b a b ++=⎧⎨++=⎩ ……………………1解之得14a b =⎧⎨=-⎩， 所以抛物线的解析式为243y x x =-+ ……………………2分（2）由（1）可得抛物线顶点(2,1)D -……………………3分直线AC 的解析式为3y x =+由E 是对称轴与直线AC 的交点，则E 由F 与E 关于点D 对称 ，则(2,7)F - ……………………4分证法一：从点,A C 分别向对称轴作垂线,AM CN ，交对称轴于,M N在Rt FAM ∆和Rt FCN ∆中090AMF CNF ∠=∠=，21310515AM CN MF NF==== 所以Rt FAM ∆∽Rt FCN ∆所以AFE CFE ∠=∠ …………………………………5分证法二：直线AF 的解析式为53y x =-+点 (5,8)C 关于对称轴的对称点是(1,8)Q -将点(1,8)Q -代入53y x =-+可知点Q 在直线AF所以AFE CFE ∠=∠（3）在FDC ∆中，三内角不等，且CDF ∠为钝角10 若点P 在点F 下方时，在AFP ∆中，AFP ∠为钝角因为AFE CFE ∠=∠，00180,180AFE AFP CFE CDF ∠+∠=∠+∠< 所以AFP ∠和CDF ∠不相等所以，点P 在点F 下方时，两三角形不能相似 …………………… 6分 20 若点P 在点F 上方时，由AFE CFE ∠=∠，要使AFP ∆与FDC ∆相似 只需AF PF CF DF =（点P 在DF 之间）或AF PF DF CF=（点P 在FD 的延长线上） 解得点P 的坐标为(2,3)-或(2,19)………………………………………8分。

顺义区2013届初三第一次统一练习 数学试题参考答案及评分参考二、填空题三、解答题13．解：原式=3412+⨯-- …………………………………………4分 =2 ……………………………………………… 5分 14． 解：解不等式312(1)x x -<+，得3x <． ………………………………… 1分解不等式312x +≥，得1x -≥． ………………………………… 2分 ∴不等式组的解集为13x -<≤． ………………………………… 4分在数轴上表示其解集为如图所示…………………………………5分15．证明：∵CA 平分BCD ∠∴ ACB DCE ∠=∠ ……………………………………………1分在ABC ∆和DEC ∆中∵BC EC ACB DCE AC DC =⎧⎪∠=∠⎨⎪=⎩……………………………………………3分 ∴ABC ∆≌DEC ∆ …………………………………………… 4分 ∴A D ∠=∠ ……………………………………………5分16．解：原式=2333()(3)(3)(3)(3)a a a a a a a--+⨯+-+-………………………2分=23(3)(3)a a a a a-⨯+- ………………………………………… 3分=1(3)a a +=213a a+ ……………………………………………… 4分∵ 2320a a +-=∴ 232a a += ∴原式=12………………………………………………5分 17．解：（1）将(2,2)A --代入my x=中，得4m =． ∴4y x=． …………………………………………………………………1分 将(,4)B n 代入4y x=中，得．1n = ………………………………2分 将(2,2)A --，(1,4)B 代入y kx b=+中22,4.k b k b -+=-⎧⎨+=⎩………3分 解得2,2.k b =⎧⎨=⎩ ∴22y x =+． ……………………………………………4分 （2）设直线AB 与y 轴交于点C 当0x =时，2y =． ∴2OC =．∴112221322AOB AOC BOC S S S ∆∆∆=+=⨯⨯+⨯⨯= ………………………5分 18．解：设该种纪念品3月份每件的销售价格为x 元， ……………………………1分根据题意，列方程得20002000800300.8x x+=- ………………………………………………3分 解之得50x =． …………………………………………………………4分 经检验50x =是所得方程的解．答：该种纪念品3月份每件的销售价格是50元． …………………………5分 解法二：设3月份销售这种纪念品x 件，则4月份销售（x +30）件 …………1分根据题意，列方程得420002000800530x x +⨯=+ ……………………………………………3分 解之得40x =． ………………………………………………4分 经检验40x =是所得方程的解答：该种纪念品3月份每件的销售价格是20005040=（元）…………5分19解：∵ BD DC ⊥∴ 90BDC ∠=︒∵ 30ACD ∠=︒，AD CD ==， ∴ 60,30,DEC DAC ACD ∠=︒∠=∠=︒tan 302DE CD =⋅︒== ∴ 24EC DE == ，30ADE ∠=︒ …………………………………………1分∴ 2AE DE == ……………………………………………………… 2分- ∴ 246AC AE EC =+=+= ………………………………………………3分过点A 作AM BD ⊥,垂足为M ∵ 60AEB DEC ∠=∠=︒∴sin 602AM AE =⋅︒== 1c o s 60212M E A E=︒=⨯= ………………………………………………4分∵45ABD ∠=︒∴BM AM ==∴123BD BM ME DE =+++= …………………………5分20．⑴ BC 与⊙O 相切 证明：连接AE ，∵AC 是O 的直径∴90E ∠=∴90EAD AFE ∠+∠=︒ ∵BF BC =∴BCE BFC ∠=∠ 又 ∵E 为 AD 的中点∴EAD ACE ∠=∠ …………………………1分 ∴ 90BCE ACE ∠+∠=︒ 即AC BC ⊥ 又∵AC 是直径∴BC 是O 的切线 …………………………2分 （2）∵O 的半为2∴4AC =, ∵3cos 5B =由（1）知，90ACB ∠=， ∴5AB = ,3BC =C∴3BF = ,2AF = ………………………… 3分 ∵EAD ACE ∠=∠, E E ∠=∠ ∴AEF ∆∽CEA ∆，∴12EA AF EC CA == ∴2EC EA =， …………………………4分设 ,2EA x EC x ==由勾股定理 22416x x +=，5x =±（舍负） ∴CE =…………………………5分 21． 解：（1）表中填12m =；0.08n =. …………………………2分(2）补全的图形如下图.- …………………………3分（3）0.120.240.320.68++=.即月均用水量不超过15t 的家庭占被调查的家庭总数的68%.…………………………4分 （4）(0.080.04)1500180+⨯=.所以，该小区月均用水量超过20t 的家庭大约有180户. ………………5分22．判断AGD ∆是直角三角形证明：如图连结BD ，取BD 的中点H ，连结HF HE 、，……………………1分F 是AD 的中点，∴HF AB ∥，12HF AB =，………………… 2分 ∴13∠=∠．同理，12HE CD HE CD =∥，， ∴2EFC ∠=∠． AB CD = ， ∴HF HE =，3080510152025412频数（户）月用水量A BCD FG H E1 2 3∴12∠=∠． …………………………………………3分60EFC ∠= °，∴360EFC AFG ∠=∠=∠=°，∴AGF ∆是等边三角形．………………………………4分AF FD = ，∴GF FD =，∴30FGD FDG ∠=∠=° ∴90AGD ∠=°即AGD △是直角三角形．…………………………… 5分23．（1）证明：①当0m =时，方程为220x -+=，所以 1x =，方程有实数根.…… 1分 ②当0m ≠时, []2(32)4(22)m m m ∆=-+-+ =22912488m m m m ++-- =244m m ++=2(2)0m +≥ ………………………………2分 所以,方程有实数根综①②所述，无论m 取任何实数时，方程恒有实数根 …………3分（2）令0y =，则2(32)220mx m x m -+++= 解关于x 的一元二次方程，得11x = ，222x m=+……………………5分 二次函数的图象与x 轴两个交点的横坐标均为正整数，且m 为整数， 所以m 只能取1，2所以抛物线的解析式为254y x x =-+或2286y x x =-+………………7分 24．（1）证明：∵9090GEB BEF DEF BEF ∠+∠=∠+∠=°，°，∴.DEF GEB ∠=∠又∵ED BE =，∴Rt Rt FED GEB △≌△.∴.EF EG = ………………………………………………………2分（2）成立.证明：如图，过点E 分别作BC CD 、的垂线，垂足分别为H I 、，则90EH EI HEI =∠=，°.∵9090GEH HEF IEF HEF ∠+∠=∠+∠=°，°，∴.IEF GEH ∠=∠∴Rt Rt FEI GEH △≌△.∴.EF EG = …………………………………4分（3）解：如图，过点E 分别作BC CD 、的垂线，垂足分别为M N 、，则90MEN ∠=°，.EM AB EN AD ∥，∥ ∴.EM CE ENAB CA AD == ∴.EM AD aEN AB b ==…………………………………5分 ∴9090GME MEF FEN MEF ∠+∠=∠+∠=°，°，∴.MEN GEM ∠=∠∴Rt Rt FEN GEM △∽△. ∴.EF EN bEG EM a ==…………………………………7分25．解：（1）将点(1,0)(5,8)B C 、代入2y ax bx =+3025538a b a b ++=⎧⎨++=⎩ ……………………1解之得14a b =⎧⎨=-⎩，所以抛物线的解析式为243y x x =-+……………………2分（2）由（1）可得抛物线顶点(2,1)D -……………………3分直线AC 的解析式为3y x =+由E 是对称轴与直线AC 的交点，则E 由F 与E 关于点D 对称 ，则(2,7)F - ……………………4分证法一：从点,A C 分别向对称轴作垂线,AM CN ，交对称轴于,M N 在Rt FAM ∆和Rt FCN ∆中090AMF CNF ∠=∠=，21310515AM CNMF NF==== 所以Rt FAM ∆∽Rt FCN ∆所以AFE CFE ∠=∠…………………………………5分证法二：直线AF 的解析式为53y x =-+ 点 (5,8)C 关于对称轴的对称点是(1,8)Q -将点(1,8)Q -代入53y x =-+可知点Q 在直线AF 所以AFE CFE ∠=∠（3）在FDC ∆中，三内角不等，且CDF ∠为钝角10 若点P 在点F 下方时，在AFP ∆中，AFP ∠为钝角因为AFE CFE ∠=∠，00180,180AFE AFP CFE CDF ∠+∠=∠+∠< 所以AFP ∠和CDF ∠不相等所以，点P 在点F 下方时，两三角形不能相似 …………………… 6分 20 若点P 在点F 上方时，由AFE CFE ∠=∠，要使AFP ∆与FDC ∆相似 只需AF PF CF DF =（点P 在DF 之间）或AF PFDF CF=（点P 在FD 的延长线上） 解得点P 的坐标为(2,3)-或(2,19)………………………………………8分。