激光雷达方程的三种解

偏振激光雷达
偏振激光雷达是通过探测非球形粒子后 向散射光的退偏振比来研究它们的形态的, 是一种研究卷云和沙尘气溶胶等大气非球 形粒子形态的有效工具。 同时,偏振激光雷达还具有一般米散射激光 雷达的功能,仍然可以利用探测的大气后向 散射光的平行分量来反演卷云和大气气溶 胶消光系数的垂直廓线以及大气气溶胶光收 到的大气后向散射回波功率的平行分量和 垂直分量的激光雷达方程分别用下式表示
• 退偏振比D(z)定义为：
•
对于随机取向的卷云和大气气溶胶粒 子,Ap(z) =As(z),若令K=kp/ks,则(3)式可以 写成:

激光雷达方程推导1. 引言激光雷达（Lidar）是一种通过测量激光脉冲的传播时间和反射强度来获取目标物体位置和形状信息的主动光学遥感技术。

在自动驾驶、环境感知、地质勘探等领域有着广泛的应用。

激光雷达方程是描述激光雷达测距原理的数学模型，本文将对激光雷达方程进行推导。

2. 激光雷达工作原理激光雷达发射器发出一个短脉冲的激光束，该束经过大气层并与目标物体相互作用后被接收器接收。

通过测量激光脉冲从发射到接收所需的时间以及反射回来时的强度，可以确定目标物体与激光雷达之间的距离和位置。

3. 推导过程为了推导激光雷达方程，我们需要考虑以下几个因素：•激光束在空气中传播时会发生衰减；•目标物体会反射一部分入射到其表面的激光束；•接收器只能接收到反射激光束的一部分。

3.1 衰减因素激光束在空气中传播时会发生衰减，主要有两个原因：吸收和散射。

我们可以用以下公式表示激光束的衰减：I=I0e−αd其中，I是接收到的激光强度，I0是初始激光强度，α是吸收系数，d是激光传播距离。

3.2 反射因素目标物体会反射一部分入射到其表面的激光束。

我们可以用以下公式表示反射激光强度：I r=ρI其中，I r是反射激光强度，ρ是反射系数。

3.3 接收因素接收器只能接收到反射激光束的一部分。

我们可以用以下公式表示接收到的激光强度：I recv=A⋅I r其中，A是接收器探测效率。

3.4 测距原理根据测距原理，我们可以得到以下公式：d=c⋅t 2其中，d是目标物体与激光雷达之间的距离，c是光速，t是激光脉冲从发射到接收所需的时间。

3.5 激光雷达方程推导将上述公式整合起来，我们可以得到激光雷达方程：I recv=A⋅ρI0e−αd将测距公式代入上式中，可以得到：I recv=A⋅ρI0e−αct 24. 总结本文对激光雷达方程进行了推导。

通过考虑衰减因素、反射因素和接收因素，并结合测距原理，我们得到了描述激光雷达测距原理的数学模型。

这个模型可以帮助我们理解激光雷达的工作原理，并为相关应用提供基础支持。

Klett 反演算法大气激光雷达接收到的距离R 处大气后向散射回波信号功率P (R )可以由激光雷达方程确定：()()()2102r C P A R T R P R R β=………………………………（A.1）式中：C 1——激光雷达校正常数，与几何因子、透过率、系统效率、距离分辨率等参数有关； P 0——发射的激光脉冲的功率； A r ——接收望远镜的有效接收面积； β(R ) ——距离R 处大气后向散射系数； T (R ) ——大气透过率。

大气透过率与大气消光系数α有关，可表示为：()()()exp RT R r dr α=-⎰………………………………（A.2）将公式（A.2）代入激光雷达方程中，经过变形可得：()()()()2100exp 2Rr R R R C P A R r dr βα=-⎰……………………（A.3）公式（A.3）两边取自然对数后求导后可得：()()()()12dS R d R R dR R dRβαβ=-………………………（A.4）式中：S (R )——距离平方校正信号P (R )R 2取自然对数。

在Klett 反演算法中，首先假设大气消光系数α与后向散射系数β之间存在如下关系：2C k βα=…………………………………………（A.5）式中： C 2——常数；k ——与激光探测波长和气溶胶性质有关，范围一般在0.67~1之间。

将公式（A.5）代入到公式（A.4）中，可得：()()()()=2dS R d R k R dR R dRααα-…………………………（A.6） 对公式（A.6）求解，可得大气消光系数。

()()()()()()()()()()1exp =2exp m m R m mR S R S R kR R S r S R k dr k αα--⎛⎫+- ⎪⎝⎭⎰………………（A.6）式中：R m——参考距离，一般选探测区域的最远距离。

附 录 B （资料性附录） Fernald 反演算法在Fernald 反演方法中将大气看作两部分：大气分子与气溶胶。

机动车颗粒物的激光雷达监测张春光;张玉钧;韩道文;刘文清;陈臻懿【摘要】为了用激光雷达遥测机动车排放颗粒物的浓度分布,从理论上分析了颗粒物后向散射系数和质量浓度之间的关系;利用激光雷达测量的后向散射系数以及黑碳仪测量的黑碳气溶胶质量浓度数据,采用最小二乘法对颗粒物后向散射系数与浓度以及后向散射系数与车流量之间进行了相关性分析.结果表明,激光雷达测量的后向散射系数能够很好地反演机动车颗粒物质量浓度,它们之间存在正比关系.激光雷达探测的气溶胶颗粒物浓度和车流量具有很好的一致性,可以用来研究机动车排放颗粒物的水平分布和扩散特性;这对于机动车的管理以及大气污染控制具有重要意义.【期刊名称】《激光技术》【年(卷),期】2009(033)002【总页数】4页(P130-133)【关键词】激光技术;激光雷达;最小二乘法;后向散射系数;气溶胶质量浓度;车流量【作者】张春光;张玉钧;韩道文;刘文清;陈臻懿【作者单位】中国科学院,安徽光学精密机械研究所,环境光学与技术重点实验室,合肥,230031;中国科学院,安徽光学精密机械研究所,环境光学与技术重点实验室,合肥,230031;中国科学院,安徽光学精密机械研究所,环境光学与技术重点实验室,合肥,230031;中国科学院,安徽光学精密机械研究所,环境光学与技术重点实验室,合肥,230031;中国科学院,安徽光学精密机械研究所,环境光学与技术重点实验室,合肥,230031【正文语种】中文【中图分类】X831引言大气气溶胶是指液体或固体微粒均匀散布在气体中形成的相对稳定的悬浮体系，其粒径范围一般为0.001μm～100μm。

大气气溶胶是观测城市对流层空气质量的天然载体[1]，是衡量大气环境质量的一个重要指标。

悬浮在大气中的气溶胶粒子还会直接影响到地-气系统的能量收支[2],进而影响气候变化,而且会污染人类的生存环境,进而直接危害人体健康。

因此，探测城市大气中污染源的时间、空间分布特征[3-4]，以及风速风向、温度、湿度和湍流场的规律，更深入地了解气溶胶的扩散、沉降、稀释等大气物理、化学过程具有重要的意义。

雷达方程公式雷达是一个常用的电子设备，它能够使用无线电波来探测周围环境中的物体。

雷达技术在军事、航空、天气预报等领域有着广泛的应用。

雷达的核心是雷达方程公式，它是雷达技术的基础，本文将详细介绍雷达方程公式的含义、推导过程和应用。

一、雷达方程公式的含义雷达方程公式是描述雷达探测能力的数学公式，它可以计算雷达的最大探测距离、最小探测目标尺寸等参数。

雷达方程公式的一般形式为：P_r=frac{P_tG_tG_rlambda^2sigma}{(4pi)^3R^4L} 其中，P_r是接收功率，P_t是发射功率，G_t是发射天线增益，G_r是接收天线增益，λ是雷达的工作波长，σ是目标的雷达截面积，R是雷达与目标之间的距离，L是系统的损耗因子。

从公式中可以看出，雷达方程公式包含了雷达探测能力的各种因素，如发射功率、天线增益、波长、目标雷达截面积、距离和系统的损耗因子。

这些因素综合影响着雷达的探测能力。

因此，通过雷达方程公式的计算，可以评估雷达的探测性能，对雷达的设计和使用具有重要意义。

二、雷达方程公式的推导过程雷达方程公式是基于电磁学原理推导出来的。

雷达是通过发射电磁波并接收反射回来的信号来探测目标的，因此，雷达方程公式的推导需要考虑电磁波在空间中的传播和反射。

首先，考虑雷达发射天线向外发射电磁波的情况。

发射天线的功率可以表示为：P_t=frac{E^2}{2Z_0}其中，E是电场强度，Z_0是自由空间的特征阻抗。

根据电磁波的传播原理，电场强度与距离的平方成反比，即：E=frac{E_0}{R}其中，E_0是发射天线上的电场强度，R是雷达与目标之间的距离。

将上式代入发射功率公式中，得到：P_t=frac{E_0^2}{2Z_0R^2}接下来，考虑雷达接收天线接收到的信号功率。

根据电磁波的反射原理，当电磁波照射到目标表面时，会发生反射，反射回来的信号功率可以表示为：P_r=frac{E_r^2}{2Z_0}其中，E_r是接收天线上的电场强度。

雷达原理笔记之雷达方程推导参数符号雷达发射机的发射功率为P t 目标距离R目标的雷达截面积发射天线增益G t 接收天线增益G r 天线的有效接受面积A e 电磁波波长接收机最小可检测功率S imin 雷达原理笔记之雷达方程的推导H1雷达作用距离跟雷达方程的各个参数关系紧密。

雷达作用距离的改善往往需要利用雷达方程的各项影响参数进行改善。

1，基本方程H2参数列表：公式推导：首先假设，发射天线为无方向性天线，即各向同性。

那么空间中任何一点的电磁波功率密度为：然后加上天线增益系数G t ：空间中，被目标截获并产生二次辐射的电磁波功率：被目标二次辐射到空间的电磁波功率密度：目标二次辐射的电磁波功率，被雷达接收天线截获得到的功率：雷达接收机能检测的回波信号最小功率为S min ，因此应满足的不等式：解不等式得到：进而，最大作用距离R max ：参数符号玻尔兹曼常数k 接收机噪声带宽B n /B s 环境温度（噪声温度）T 0接收机噪声系数F 0检测因子(未相参积累)D 0信号处理增益G sp 损耗衰减因子L 相参积累脉冲个数N脉冲宽度脉冲雷达发射期间的平均功率P t 信号积累有效总时宽T s 对于脉冲体制雷达，常用收发共用天线，则G t =R r ,可得R max 的其他两种形式：2，雷达方程的其他形式H22.1考虑相参积累增益H3将S imin =kT 0B n F 0D 0代入雷达基本方程，得到：s信号处理后：D 0=D 0/G sp ,信号处理后：2.2考虑各种损耗H32.3用信号能量表示的形式H3根据,得到：,式14可化简为：,最终得到能量形式的R max表达式：2.4脉冲体制雷达的雷达方程H33，雷达方程对设计的指导意义H2根据不同情况下对应的雷达方程的具体形式，可以对雷达的设计提供指导性的方案。

1. 提高接收机灵敏度2. 降低损耗3. 增大信号能量4. 降低噪声系数5. 提高天线增益6. …………。

Klett 反演算法大气激光雷达接收到的距离R 处大气后向散射回波信号功率P (R )可以由激光雷达方程确定：()()()2102r C P A R T R P R R β=………………………………（A.1）式中：C 1——激光雷达校正常数，与几何因子、透过率、系统效率、距离分辨率等参数有关； P 0——发射的激光脉冲的功率； A r ——接收望远镜的有效接收面积； β(R ) ——距离R 处大气后向散射系数； T (R ) ——大气透过率。

大气透过率与大气消光系数α有关，可表示为：()()()exp RT R r dr α=-⎰………………………………（A.2）将公式（A.2）代入激光雷达方程中，经过变形可得：()()()()2100exp 2Rr R R R C P A R r dr βα=-⎰……………………（A.3）公式（A.3）两边取自然对数后求导后可得：()()()()12dS R d R R dR R dRβαβ=-………………………（A.4）式中：S (R )——距离平方校正信号P (R )R 2取自然对数。

在Klett 反演算法中，首先假设大气消光系数α与后向散射系数β之间存在如下关系：2C k βα=…………………………………………（A.5）式中： C 2——常数；k ——与激光探测波长和气溶胶性质有关，范围一般在0.67~1之间。

将公式（A.5）代入到公式（A.4）中，可得：()()()()=2dS R d R k R dR R dRααα-…………………………（A.6） 对公式（A.6）求解，可得大气消光系数。

()()()()()()()()()()1exp =2exp m m R m mR S R S R kR R S r S R k dr k αα--⎛⎫+- ⎪⎝⎭⎰………………（A.6）式中：R m——参考距离，一般选探测区域的最远距离。

附 录 B （资料性附录） Fernald 反演算法在Fernald 反演方法中将大气看作两部分：大气分子与气溶胶。

SLAM（Simultaneous Localization and Mapping）即同时定位与地图构建，它是指在未知环境中，通过移动机器人进行感知和运动控制，实现机器人自身位置的估计和地图的构建。

SLAM问题可以用一组运动方程和观测方程来描述。

下面是常见的基于激光雷达的2D SLAM的运动方程和观测方程：
1. 运动方程：
- 里程计运动模型：通常使用简化的运动模型（如平移运动模型或增量式旋转运动模型），将机器人的运动表示为里程计度量值。

具体形式如下：
x_t = x_{t-1} + delta_x
y_t = y_{t-1} + delta_y
theta_t = theta_{t-1} + delta_theta
2. 观测方程：
- 激光雷达观测模型：通过激光雷达测量环境中的障碍物，可以获得一系列距离和角度观测值。

观测模型将这些观测值映射到机器人坐标系或世界坐标系中，以获得障碍物在地图中的位置信息。

具体形式如下：
z_t = h(x_t) + epsilon
在上述方程中，x_t、y_t和theta_t分别表示机器人在时间t的位置和姿态（方向），delta_x、delta_y和delta_theta表示机器人的增量运动，z_t表示激光雷达的观测值，
h(x_t)表示观测模型将机器人位置映射到地图坐标系中的函数，epsilon表示观测误差。

需要注意的是，SLAM问题是一个非线性的问题，通常需要使用滤波器（如扩展卡尔曼滤波器或粒子滤波器）来进行状态估计和地图构建。

在实际应用中，还可能根据具体情况引入其他传感器数据和环境模型，以提高定位和地图构建的精度与鲁棒性。

激光雷达原理------读书笔记99121-佃邓洪川一•概念:雷达"(Radio Detection and Range,Radar)是一种利用电磁波探测目标位置的电子设备.电磁波其功能包括搜索目标和发现目标；测量其距离，速度，角位置等运动参数；测量目标反射率，散射截面和形状等特征参数。

传统的雷达是微波和毫米波波段的电磁波为载波的雷达。

激光雷达以激光作为载波.可以用振幅、频率、相位和振幅来搭载信息，作为信息载体。

激光雷达利用激光光波来完成上述任务。

可以采用非相干的能量接收方式，这主要是一脉冲计数为基础的测距雷达。

还可以采用相干接收方式接收信号，通过后置信号处理实现探测。

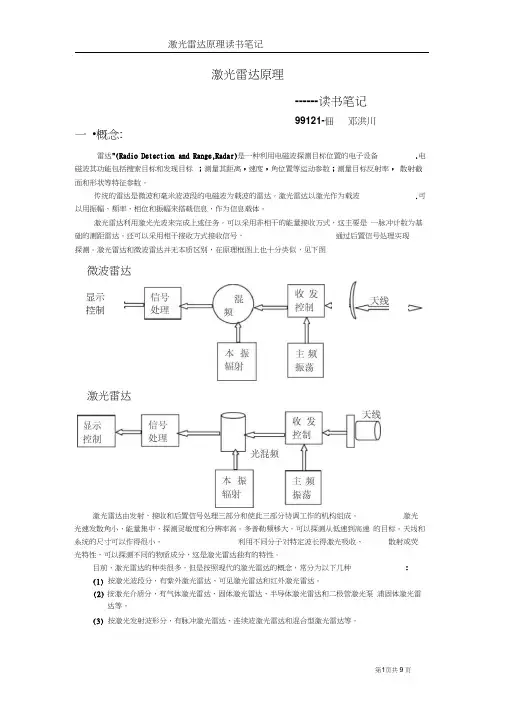
激光雷达和微波雷达并无本质区别，在原理框图上也十分类似，见下图微波雷达显示控制激光雷达激光雷达由发射，接收和后置信号处理三部分和使此三部分协调工作的机构组成。

激光光速发散角小，能量集中，探测灵敏度和分辨率高。

多普勒频移大，可以探测从低速到高速的目标。

天线和系统的尺寸可以作得很小。

利用不同分子对特定波长得激光吸收、散射或荧光特性，可以探测不同的物质成分，这是激光雷达独有的特性。

目前，激光雷达的种类很多，但是按照现代的激光雷达的概念，常分为以下几种：(1)按激光波段分，有紫外激光雷达、可见激光雷达和红外激光雷达。

(2)按激光介质分，有气体激光雷达、固体激光雷达、半导体激光雷达和二极管激光泵浦固体激光雷达等。

(3)按激光发射波形分，有脉冲激光雷达、连续波激光雷达和混合型激光雷达等。

（4）按显示方式分，有模拟或数字显示激光雷达和成像激光雷达。

（5）按运载平台分，有地基固定式激光雷达、车载激光雷达、机载激光雷达、船载激光雷达、星载激光雷达、弹载激光雷达和手持式激光雷达等。

（6）按功能分，有激光测距雷达、激光测速雷达、激光测角雷达和跟踪雷达、激光成像雷达，激光目标指示器和生物激光雷达等。

（7）按用途分，有激光测距仪、靶场激光雷达、火控激光雷达、跟踪识别激光雷达、多功能战术激光雷达、侦毒激光雷达、导航激光雷达、气象激光雷达、侦毒和大气监测激光雷达等。

雷达方程及其推导过程雷达方程是雷达工程中的重要概念，用来描述雷达系统中的回波信号强度与目标之间的关系。

通过雷达方程，可以计算出目标的反射截面积、目标与雷达之间的距离以及目标的速度等重要信息。

雷达方程的推导过程首先从麦克斯韦方程组出发，利用电磁波的传播特性和目标的散射特性，最终得到雷达方程。

下面我们来逐步推导雷达方程。

根据电磁波的传播特性，可以得到电磁波在自由空间中的传播方程：∇²E - με∂²E/∂t² = 0其中，E表示电场强度，μ和ε分别表示自由空间的磁导率和电容率。

这个方程描述了电磁波在自由空间中的传播行为。

接下来，考虑雷达系统中的目标，假设目标是一个小球体，其直径远小于入射波的波长。

目标的散射特性可以用散射截面积σ描述，σ表示目标对电磁波的散射能力。

当电磁波照射到目标上时，一部分能量将被目标散射，形成回波信号。

假设入射波的电场强度为Ei，目标产生的散射场为Es，回波场为Er。

根据叠加原理，总场强可以表示为：E = Ei + Es + Er其中，入射场和散射场可以看作是波源，它们的传播方程可以写为：∇²Ei - με∂²Ei/∂t² = 0∇²Es - με∂²Es/∂t² = 0而回波场是由目标散射场产生的，可以表示为：Er = αEs其中，α为雷达截面积的比例因子。

将上述三个场强代入电磁波的传播方程中，可以得到：∇²E - με∂²E/∂t² = 0将总场强E展开，可以得到：∇²(Ei + Es + Er) - με∂²(Ei + Es + Er)/∂t² = 0进一步展开并整理，可以得到：∇²Es - με∂²Es/∂t² - αμε∂²Es/∂t² = -(∇²Ei + με∂²Ei/∂t²)根据散射场的传播方程，可以得到：∇²Es - με∂²Es/∂t² - αμε∂²Es/∂t² = 0将上述方程进一步化简，可以得到：(1 + α)∇²Es - (1 + α)με∂²Es/∂t² = 0继续化简，可以得到雷达方程：∇²Es - με∂²Es/∂t² = 0其中，Es表示目标产生的散射场，也就是回波场。

激光雷达在大气环境监测中的应用鲁岸立sc12002044摘要：本文介绍了RAMAN激光雷达、多普勒激光雷达、MIE激光雷达的工作原理。

并讨论了它们在气象和环境监测中的应用。

1.RAMAN激光雷达RAMAN散射是激光与大气中各种分子之间的一种非弹性相互作用过程，散射光的波长和入射光不同，产生了向长波或短波方向的移动。

散射光频率的改变v~因入r射光和受作用的分子不同而异。

分析该散射光的频率和强度的光谱图可以得到大气分子的相关信息,所以Raman 散射激光雷达可以用来测量环境中某种污染气体的浓度分布,接收系统用的是光谱分析仪,以便接收污染分子散射的不同Raman 散射波长的回波信号。

图1 RAMAN激光雷达结构原理图图2 典型的污染物分子相对于激光频率的振动-转动拉曼散射频率变化在实验中用RAMAN激光雷达测量了羽油烟和机动车尾气的组成成分。

RAMAN激光雷达使用的是波长337.1nm的激光作为探测光。

首先给出正常大气气体的拉曼后向散射及频率不变成分包括瑞利及米散射成分的光谱图。

图3 正常大气气体的拉曼后向散射及频率不变成分包括瑞利及米散射成分的光谱图图3中每个箭头对应一特定分子的拉曼散射线的中心波长。

正常大气中的主要成分包括N2,O2,水汽分子，CO2在光谱图中可以方便的检测出来。

在得到正常大气气体的光谱图之后，用激光雷达337.1nm波长激光分析羽油烟气体和机动车尾气中各种成分的拉曼频移，从而得出羽油烟气体具体组成。

图4 羽油烟气体中各组分分子的拉曼光谱图图5 机动车尾气中各组分分子的拉曼光谱图由探测结果可以看出，羽油烟气体和机动车尾气中除了包括N2,O2,水汽分子，CO2还探测到了SO2,CO,H2S等有害气体。

RAMAN激光雷达不仅可以检测分析污染气体成分，还可以进行气溶胶探测。

中科院安徽光机所在原有的一台Mie散射激光雷达的基础上，增加了一个Raman 通道，从而可以接受空气分子（如N 2分子）的RAMAN 散射回波信号。

（3）激光外差探测具有良好的窄带滤波性能。在直接探测中， 光探测器除接收信号光以外，杂散背景光也可同时入射到光探 测器上。为了抑制杂散背景光的干扰，提高信噪比，一般都要 在光探测器上加窄带滤光片。在外差探测中，只有落在中频带 宽以内的杂散背景光才能进入探测系统。而且，杂散背景光不 会在原来信号光和本振光所产生的相干项上产生附加的相干项。 因此，对激光外差探测来讲，杂散背景光的影响可以忽略不计， 由此可见激光外差探测方法具有良好的滤波性能。
激 光 束 的 物 理 描 述
I A (r)
U A (r)
2
I
0
2
J
1(
)
2
-光波波长； F-光学天线的有效焦距； D-光学天线的有效孔径； F-光学天线系统的“F”数, F=(f/d)； J1()-第一类贝塞尔函数, =(r/F)； UA(r)-爱里斑振幅分布函数；
I P (r) U P (r) 2 I00
P
1
Re(
E
A2
E
)dA
1 2
S
Us
2 dS
若光探测器的负载电阻RL，则光探测器输出的电功率为：
i e P e
U
(r ,
t
)
2
dS
h 2h S
式中：S为光探测器光敏面积。光探测器输出的光电流为：
PS
i 2 RL
(
e h
)
2
P
2
RL
光探测器输出的电功率正比于入射光功率的平方
直 接 探 测 理 论
考虑到信号和噪声的独立性，则有： S p (e / h )2 RL Ps2
N p (e / h )2 RL (2Ps Pn Pn2 )
根据信噪比的定义，则输出功率比为：

简析偏振米散射微脉冲激光雷达的原理与应用作者：谷金峰来源：《价值工程》2016年第09期摘要：随着人类活动和工业排放的增加，气溶胶数量在不断增加。

研究气溶胶与云形成和发展的关系、交互模式，特别是垂直分布关系、间接效应、辐射关系等，对大气降水、气象预报、气象灾害研究等有重要的科学意义，近些年来大气气溶胶对全球天气和气候的影响已经被大量的研究，激光雷达为气溶胶的垂直结构，成分和动力探测提供了有力的工具。

Abstract： With the increase of human activities and industrial emissions， the amount of aerosol is increasing. It has important scientific significance to study the relationship between aerosol and cloud formation and development， interaction patterns， especially the vertical distribution relationship， indirect effect， radiation relationship for studying the atmospheric precipitation，weather forecasting， meteorological disasters. In recent years the impact of atmospheric aerosol on the global weather and climate has been researched. Laser radar provides a powerful tool for aerosol vertical structure， composition and dynamic detection.关键词：激光雷达；气溶胶；光散射Key words： laser radar；aerosol；light scattering中图分类号：TN958.98 文献标识码：A 文章编号：1006-4311（2016）09-0219-020 引言气溶胶在大气中的含量虽然不很高，但却对大气质量有着很大的影响。

激光雷达测距测速原理1. 激光雷达通用方程激光雷达方程用来表示一定条件下，激光雷达回波信号的功率，其形式如下： r P 为回波信号功率，t P 为激光雷达发射功率，K 是发射光束的分布函数，12a a T T 分别是激光雷达发射系统到目标和目标到接收系统的大气透过率，t r ηη分别是发射系统和接收系统的透过率，t θ为发射激光的发散角，12R R 分别是发射系统到目标和目标到接收系统的距离，Γ为目标的雷达截面，r D 为接收孔径。

方程作用：激光雷达方程可以在研发激光雷达初期确定激光雷达的性能。

其次，激光雷达方程提供了回波信号与被探测物的光学性质之间的函数关系，因此可以通过激光雷达探测的回波信号，通过求解激光雷达方程获得有关大气性质的信息。

2. 激光雷达测距基本原理2.1 脉冲法脉冲激光雷达测距的基本原理是，在测距点向被测目标发射一束短而强的激光脉冲，激光脉冲到达目标后会反射回一部分被光功能接收器接收。

假设目标距离为L ，激光脉冲往返的时间间隔是t ，光速为c ，那么测距公式为L=tc/2。

时间间隔t 的确定是测距的关键，实际的脉冲激光雷达利用时钟晶体振荡器和脉冲计数器来确定时间t ，时钟晶体振荡器用于产生固定频率的电脉冲震荡∆T=1/f ，脉冲计数器的作用就是对晶体振荡器产生的电脉冲计数N 。

如图所示，信息脉冲为发射脉冲，整形脉冲为回波脉冲，从发射脉冲开始，晶振产生脉冲与计数器开始计数时间上是同步触发的。

因此时间间隔t=N ∆T 。

由此可得出L=NC/2f 。

图1 脉冲激光测距原理图2.2 相位法相位测距法也称光束调制遥测法，激光雷达相位法测距是利用发射的调制光和被目标反射的接受光之间光强的相位差包含的距离信息来实现被测距离的测量。

回波的延迟产生了相位的延迟，测出相位差就得到了目标距离。

假设发射处与目标的距离为D ，激光速度为c ，往返的间隔时间为t ，则有：图2 相位法测距原理图假设f 为调制频率，N 为光波往返过程的整数周期，∆ϕ为总的相位差。

1.3.3激光雷达的基本原理激光雷达最基本的工作原理与普通雷达类似，即由发射系统发送一个信号，与目标作 用产生的返回信号被接收系统收集并处理，以获得所需信息。

不同的是激光雷达的发射信 号为激光束，与普通无线电雷达发送的毫米波相比，波长要短得多。

无线电雷达由于波长 长，无法探测小型或微粒型目标，而用于激光雷达系统的激光波长一般在微米量级，因而 能用于探测极细小的微粒和分子。

图1-3激光雷达原理 Figl-3 Principle of lidar激光雷达的基本原理如图1-3所示，由激光器发出一束波长为λ0，宽度为t P 的脉冲,经准直扩束后垂直射入大气，光脉冲在通过大气时受到散射和衰减，其后向散射光被接收面积为Ar 的望远镜系统接收，高度z 处的后向散射信号功率可用雷达方程表示[36]：()()()()z T z zAr2t c z Y P z P 22p 0，，，λλβλ⋅⋅⋅⋅⋅⋅= （1.1） 式中，λ为接收到的散射信号的波长，P 0为发射的激光脉冲的峰值功率，Y(z)为发送 器与接收器光路的几何重叠系数，c 为光速，()z ，λβ为大气体积后向散射系数，()z T ，λ 为大气的透过率，由朗伯定律可知:()()⎥⎦⎤⎢⎣⎡=⎰’’’，，z 0dz z -exp z T λαλ （1.2）式中，()z ，λα为大气的消光系数。

从理论上，()z ，λβ为大气数密度N (z)与散射截面Ωd d σ的乘积，即 ()()Ω⋅=d d z N σλβz ， (1.3) 如前所述，大气中与激光雷达脉冲相互作用产生的后向散射信号成分包括了大气气体分子和气溶胶粒子，由于分子尺寸小，所产生的散射光相对较弱，瑞利散射截面与激发波长的四次方成反比，大气气溶胶粒子对激光的散射光为米散射。

对某一激光雷达的特定波长，分子散射直接随着大气分子的浓度而发生变化，但气溶胶散射却很复杂，取决于粒径分布以及气溶胶粒子的折射率。

这些气溶胶粒子随地域、时间变化明显，所以无法对其准确估算与预测。

激光雷达原理-------读书笔记99121-19 邓洪川一.概念:“雷达”(Radio Detection and Range,Radar)是一种利用电磁波探测目标位置的电子设备.电磁波其功能包括搜索目标和发现目标;测量其距离,速度,角位置等运动参数;测量目标反射率,散射截面和形状等特征参数。

传统的雷达是微波和毫米波波段的电磁波为载波的雷达。

激光雷达以激光作为载波.可以用振幅、频率、相位和振幅来搭载信息，作为信息载体。

激光雷达利用激光光波来完成上述任务。

可以采用非相干的能量接收方式，这主要是一脉冲计数为基础的测距雷达。

还可以采用相干接收方式接收信号，通过后置信号处理实现探测。

激光雷达和微波雷达并无本质区别，在原理框图上也十分类似，见下图微波雷达激光雷达激光雷达由发射，接收和后置信号处理三部分和使此三部分协调工作的机构组成。

激光光速发散角小，能量集中，探测灵敏度和分辨率高。

多普勒频移大，可以探测从低速到高速的目标。

天线和系统的尺寸可以作得很小。

利用不同分子对特定波长得激光吸收、散射或荧光特性，可以探测不同的物质成分，这是激光雷达独有的特性。

目前，激光雷达的种类很多，但是按照现代的激光雷达的概念，常分为以下几种:(1)按激光波段分，有紫外激光雷达、可见激光雷达和红外激光雷达。

(2)按激光介质分，有气体激光雷达、固体激光雷达、半导体激光雷达和二极管激光泵浦固体激光雷达等。

(3)按激光发射波形分，有脉冲激光雷达、连续波激光雷达和混合型激光雷达等。

(4) 按显示方式分，有模拟或数字显示激光雷达和成像激光雷达。

(5) 按运载平台分，有地基固定式激光雷达、车载激光雷达、机载激光雷达、船载激光雷达、星载激光雷达、弹载激光雷达和手持式激光雷达等。

(6) 按功能分，有激光测距雷达、激光测速雷达、激光测角雷达和跟踪雷达、激光成像雷达，激光目标指示器和生物激光雷达等。

(7) 按用途分，有激光测距仪、靶场激光雷达、火控激光雷达、跟踪识别激光雷达、多功能战术激光雷达、侦毒激光雷达、导航激光雷达、气象激光雷达、侦毒和大气监测激光雷达等。

激光雷达物理参数的反演及其应用[摘要]目前，激光雷达是一种非常先进的大气和气象环境监测的仪器。

它在大气的垂直结构和成分构成观测方面提供了非常可靠的依据。

通过对激光雷达信号的物理参数的反演，可以得到一系列我们需要的物理量。

在气象方面，可以应用在气溶胶，大气边界层，云物理学等学科的深入研究中。

[关键词]激光雷达后向散射气溶胶大气边界层0前言激光雷达是一种主动遥感技术，是传统雷达技术与现代激光技术相结合的产物。

50多年来，激光雷达技术从最简单的激光测距技术，逐步发展了激光跟踪、测速、扫描成像、多普勒成像等技术，陆续开发出不同用途的激光雷达，使激光雷达成为一类具有多种功能的系统。

激光雷达之所以受到关注，是因为其具有一系列独特的优点：具有极高的角分辨率、具有极高的距离分辨率、速度分辨率高、测速范围广、能获得目标的多种图像、抗干扰能力强、比微波雷达的体积和重量小等。

随着技术的不断成熟，成本的下降，其他领域陆续引进了激光雷达，并发挥着非常重要的作用。

1激光雷达的结构和原理一般情况下，激光雷达主要由三部分组成，激光发射单元，信号探测控制单元和光学接受单元。

激光发射单元发射出激光脉冲，在传输过程中遇到粒子会产生一个向后的反射信号，光学接受单元接受到这个信号并进行处理，把光信号放大转化成电子信号输出。

根据反馈信号的强度可以确定所研究粒子的浓度，粒子所处的高度可以由从发射到接受之间的时间间隔来确定。

激光雷达的方程为：P（Z）为激光雷达接收到的高度Z处的大气后向散射回波信号的能量，E 为激光雷达的发射能量，C是激光雷达常数，和发射频率，接收灵敏度等有关；Z是到激光雷达到目标粒子的距离；βtotal是总的后向散射系数，βmol是空气后向散射系数，βpart是气溶胶后向散射系数；ζtotal是总的消光系数，是激光脉冲在传输过程中衰减产生的，ζsmol是空气散射系数，ζspart是气溶胶散射系数，ζAmol是空气气吸收系数，ζApart是气溶胶吸收系数。