高等数学(同济大学数学系-第七版)上册第五章课后答案[001]
- 格式:docx
- 大小:2.15 MB
- 文档页数:38

高等数学同济大学第七版上册答案题型:选择题1. 下列哪个函数是奇函数?A. y=x^2B. y=2x-1C. y=|x|D. y=\sin x答案:C2. 已知函数f(x)在区间[a,b]内单调递增,那么在以下哪个区间内f^{-1}(x)单调递减?A. [f(a),f(b)]B. [a,b]C. [f(b),f(a)]D. (-\infty,+\infty)答案:A3. 设\alpha为第二象限的角,则\cos\alpha等于A. -√2/2B. √2/2C. -√3/2D. -√6/2答案:B4. 若y=\log_3{(x+√1+x^2)},则(1/y)等于A. 3√1+x^2B. \dfrac{3x}{√1+x^2}C. \dfrac{x}{√1+x^2}D. \dfrac{√1+x^2}{x}答案:B5. 函数f(x)=(1/2)(2x-1)\ln{(x+1)}在(0,+\infty)有单峰。
对于f(x)的单峰值点x_0,下列说法正确的是?A. f'(x_0)>0,且f''(x_0)>0B. f'(x_0)<0,且f''(x_0)<0C. f'(x_0)>0,且f''(x_0)<0D. f'(x_0)<0,且f''(x_0)>0答案:C题型:填空题6. 已知f(x)=x^3-3x^2+bx+c在x=1处取极小值-2,则b=____},c=____}。
答案:b=-3,c=0。
7. 设a,b均为正数,若a\ln{3}+b\ln{5}=0,则\log_{15}{√a}+\log_{45}{√b}=____}。
答案:0。
8. 设函数f(x)具有二阶导数,f(0)=0,f'(0)=1,f''(0)=-2,则f(x)+f(-x)的极小值为____}。




第二章 导数与微分2.2 课后习题详解习题2-1 导数概念1.设物体绕定轴旋转,在时间间隔[0,t]上转过角度θ,从而转角θ是t的函数:θ=θ(t).如果旋转是匀速的,那么称为该物体旋转的角速度.如果旋转是非匀速的,应怎样确定该物体在时刻t 0的角速度?解:物体在时间间隔上的平均角速度在时刻t 0的角速度2.当物体的温度高于周围介质的温度时,物体就不断冷却.若物体的温度T 与时间t 的函数关系为T =T(t),应怎样确定该物体在时刻t 的冷却速度?解:物体在时间间隔上平均冷却速度[,]t t t +∆在时刻t 的冷却速度3.设某工厂生产x件产品的成本为函数C(x)称为成本函数,成本函数C(x)的导数在经济学中称为边际成本.试求(1)当生产100件产品时的边际成本;(2)生产第101件产品的成本,并与(1)中求得的边际成本作比较,说明边际成本的实际意义.即生产第101件产品的成本为79.9元,与(1)中求得的边际成本比较,可以看出边际成本的实际意义是近似表达产量达到x单位时再增加一个单位产品所需的成本.4.设f(x)=10x2,试按定义求.解:5.证明证:6.下列各题中均假定存在,按照导数定义观察下列极限,指出A表示什么:以下两题中给出了四个结论,从中选出一个正确的结论:7.设则f(x)在x=1处的( ).A.左、右导数都存在B.左导数存在,右导数不存在C.左导数不存在,右导数存在D.左、右导数都不存在【答案】B【解析】 故该函数左导数存在,右导数不存在.8.设f(x)可导,,则f(0)=0是F(x)在x=0处可导的( ).A.充分必要条件B .充分条件但非必要条件C .必要条件但非充分条件D .既非充分条件又非必要条件【答案】A 【解析】 当f(0)=0时,,反之当时,f(0)=0,为充分必要条件.9.求下列函数的导数:10.已知物体的运动规律为s =t 3m ,求这物体在t =2s 时的速度.解:11.如果f(x)为偶函数,且f '(0)存在,证明f '(0)=0.证:f(x)为偶函数,得.因为所以f '(0)=0.。


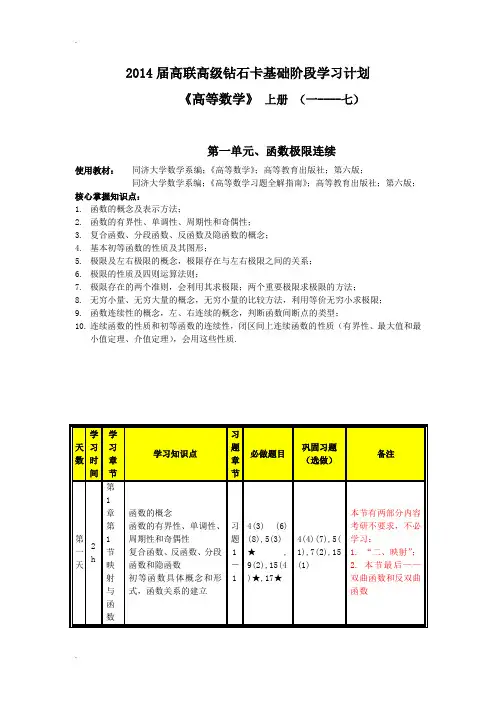
2014届高联高级钻石卡基础阶段学习计划《高等数学》上册(一----七)第一单元、函数极限连续使用教材:同济大学数学系编;《高等数学》;高等教育出版社;第六版;同济大学数学系编;《高等数学习题全解指南》;高等教育出版社;第六版;核心掌握知识点:1.函数的概念及表示方法;2.函数的有界性、单调性、周期性和奇偶性;3.复合函数、分段函数、反函数及隐函数的概念;4.基本初等函数的性质及其图形;5.极限及左右极限的概念,极限存在与左右极限之间的关系;6.极限的性质及四则运算法则;7.极限存在的两个准则,会利用其求极限;两个重要极限求极限的方法;8.无穷小量、无穷大量的概念,无穷小量的比较方法,利用等价无穷小求极限;9.函数连续性的概念,左、右连续的概念,判断函数间断点的类型;10.连续函数的性质和初等函数的连续性,闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),会用这些性质.天数学习时间学习章节学习知识点习题章节必做题目巩固习题(选做)备注第一天2h第1章第1节映射与函数函数的概念函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数初等函数具体概念和形式,函数关系的建立习题1-14(3) (6)(8),5(3)★,9(2),15(4)★,17★4(4)(7),5(1),7(2),15(1)本节有两部分内容考研不要求,不必学习:1. “二、映射”;2. 本节最后——双曲函数和反双曲函数第二天3h1章第2节数列的极限数列极限的定义数列极限的性质(唯一性、有界性、保号性)习题1-21(2) (5)(8)★3(1)1. 大家要理解数列极限的定义中各个符号的含义与数列极限的几何意义;2. 对于用数列极限的定义证明,看懂即可。
第1章第3节函数的极限函数极限的概念函数的左极限、右极限与极限的存在性函数极限的基本性质(唯一性、局部有界性、局部保号性、不等式性质,函数极限与数列极限的关系等)习题1-32,4★3,1. 大家要理解函数极限的定义中各个符号的含义与函数极限的几何意义;2. 对于用函数极限的定义证明,看懂即可。

5.2 课后习题详解习题5-1 定积分的概念与性质1.利用定积分定义计算由抛物线y =x 2+1,两直线x =a 、x =b (b >a )及x 轴所围成的图形的面积.解:因为函数f(x)=x 2+1在区间[a ,b]上连续,所以函数可积,为计算方便,不妨把[a ,b]分成n 等份,则分点为每个小区间长度为取ξi 为小区间的右端点x i ,则当n→∞时,上式极限为即为所求图形的面积.2.利用定积分定义计算下列积分:解:因为被积函数在积分区间上连续,所以把积分区间分成n等份,并取ξi为小区间的右端点,得到(1)(2)3.利用定积分的几何意义,证明下列等式:证:(1)根据定积分的几何意义,定积分表示由直线y=2x、x=1及x轴围成的图形的面积,该图形是底边长为1、高为2的三角形,因此面积为1,即(2)根据定积分的几何意义,定积分表示的是由曲线以及x轴、y轴围成的在第I象限内的图形面积,即单位圆的四分之一的图形,因此有(3)因为函数y=sinx在区间[0,π]上非负,在区间[-π,0]上非正.根据定积分的几何意义,定积分表示曲线y=sinx(x∈[0,π])与x轴所围成的图形D1的面积减去曲线y=sinx(x∈[-π,0])与x轴所围成的图形D2的面积,显然图形D1与D2的面积是相等的,所以有(4)因为函数y=cosx在区间上非负.根据定积分的几何意义,定积分表示曲线与x轴和y轴所围成的图形D1的面积加上曲线与x轴和y轴所围成的图形D2的面积,而图形D1的面积和图形D2的面积显然相等,所以有4.利用定积分的几何意义,求下列积分:解:(1)根据定积分的几何意义,表示的是由直线y=x,x=t以及x轴所围成的直角三角形面积,该直角三角形的两条直角边的长均为t,因此面积为因此有(2)根据定积分的几何意义,表示的是由直线x=-2,x=4以及x轴所围成的梯形的面积,该梯形的两底长分别为梯形的高为4-(-2)=6,因此面积为21.因此有(3)根据定积分的几何意义,表示的是由折线y=|x|和直线x=-1,x=2以及x轴所围成的图形的面积.该图形由两个等腰直角三角形组成,一个由直线y=-x,x=-1和x轴所围成,其直角边长为1,面积为另一个由直线y=x,x=2和x轴所围成,其直角边长为2,面积为2.因此(4)根据定积分的几何意义,表示的是由上半圆周以及x轴所围成的半圆的面积,因此有5.设a<b,问a、b取什么值时,积分取得最大值?解:根据定积分几何意义,表示的是由y=x-x2,x=a,x=b,以及x轴所围成的图形在x轴上方部分的面积减去x轴下方部分面积.因此如果下方部分面积为0,上方部分面积为最大时,的值最大,即当a=0,b=1时,积分取得最大值.6.已知试用抛物线法公式求出ln2的近似值(取n=10,计算时取4位小数).解:计算y i并列表表5-2-1按抛物线法公式,求得7.设求解:(1)(2)(3)(4)8.水利工程中要计算拦水闸门所受的水压力.已知闸门上水的压强p与水深h存在函数关系,且有p=9.8h(kN/m2).若闸门高H=3m,宽L=2m,求水面与闸门顶相齐时闸门所受的水压力P.解:在区间[0,3]上插入n-1个分点,取ξi∈[h i-1,h i],并记Δh i=h i-h i-1,得到闸门所受水压力的近似值为根据定积分的定义可知闸门所受的水压力为因为被积函数连续,而连续函数是可积的,因此积分值与积分区间的分法和ξi的取法无关.为方便计算,对区间[0,3]进行n等分,并取ξi为小区间的端点所以。

习题1-11.求下列函数的自然定义域:(1)1(3)(5)sin (7)arcsin(3);(9)ln(1);y y x y y x y x ====-=+211(2);1(4);(6)tan(1);1(8)arctan ;(10).xe y xy y x y xy e =-==+=+=解:2(1)3203x x +≥⇒≥-,即定义域为2,3⎡⎫-+∞⎪⎢⎣⎭2(2)101,x x -≠⇒≠±即定义域为(,1)(1,1)(1,)-∞-⋃-⋃+∞(3)0x ≠且2100x x -≥⇒≠且1x ≤即定义域为[)(]1,00,1-⋃2(4)402x x ->⇒<即定义域为(2,2)-(5)0,x ≥即定义域为[)0,+∞(6)1(),2x k k Z ππ+≠+∈即定义域为1(1,2x x R x k k Z π⎧⎫∈≠+-∈⎨⎬⎩⎭且(7)3124,x x -≤⇒≤≤即定义域为[]2,4(8)30x -≥且0x ≠,即定义域为(](,0)0,3-∞⋃(9)101x x +>⇒>-即定义域为(1,)-+∞(10)0,x ≠即定义域为(,0)(0,)-∞⋃+∞2.下列各题中,函数()f x 和()g x是否相同?为什么?222(1)()lg ,()2lg (2)(),()(3)()()(4)()1,()sec tan f x x g x x f x x g x f x g x f x g x x x========-解:(1)不同,因为定义域不同(2)不同,因为对应法则不同,,0(),0x x g x x x ≥⎧==⎨-<⎩(3)相同,因为定义域,对应法则均相同(4)不同,因为定义域不同3.设sin ,3()0,3x x x x πϕπ⎧<⎪⎪=⎨⎪≥⎪⎩求(),((),(2),644πππϕϕϕϕ--并指出函数()y x ϕ=的图形解:1()sin ,()sin 66244()sin(),(2)0,44ππππϕϕππϕϕ====-=-=-=()y x ϕ=的图形如图11-所示4.试证下列函数在指定区间内的单调性:(1);1(2)ln ,(0,)xy xy x x =-=++∞证明:1(1)()1,(,1)11x y f x x x===-+-∞--设121x x <<,因为212112()()0(1)(1)x x f x f x x x --=>--所以21()(),f x f x >即()f x 在(,1)-∞内单调增加(2)()ln ,(0,)y f x x x ==++∞设120x x <<,因为221211()()ln 0x f x f x x x x -=-+>所以21()()f x f x >即()f x 在(0,)+∞内单调增加5.设()f x 为定义在(,)l l -内的奇函数,若()f x 在(0,)l 内单调增加,证明()f x 在(,0)l -内也单调增加证明:设120l x x -<<<,则210x x l<-<-<由()f x 是奇函数,得2121()()()()f x f x f x f x -=-+-因为()f x 在(0,)l 内单调增加,所以12()()0f x f x --->即()f x 在(,0)l -内也单调增加6.设下面所考虑的函数都是定义在区间(,)l l -上的。

余弦级数ðɕn=1cosπnkn的敛散性杜先云1㊀任秋道2(1.四川省成都信息工程学院数学学院㊀610225ꎻ2.四川省绵阳师范学院数理学院㊀621000)摘㊀要:本文给出一种任意项级数收敛判定方法:如果级数ðɕn=1an的项添加括号后所成的级数收敛ꎬ且limnңɕan=0ꎬ则该级数收敛.由此获得:级数ðɕn=1cosπnkn收敛ꎬ其中kɪN+.关键词:数列ꎻ数列收敛ꎻ级数收敛ꎻ三角函数中图分类号:G632㊀㊀㊀㊀㊀㊀文献标识码:A㊀㊀㊀㊀㊀㊀文章编号:1008-0333(2020)33-0002-02收稿日期:2020-08-25作者简介:杜先云(1964-)ꎬ男ꎬ四川省三台人ꎬ博士ꎬ教授ꎬ从事应用数学方面的研究.任秋道(1965-)ꎬ男ꎬ四川省盐亭人ꎬ硕士ꎬ教授ꎬ从事应用数学方面的研究.基金项目:四川省教育厅基金资助(16ZB0314).㊀㊀一㊁引入目前«高等数学»与«数学分析»教材中ꎬ对任意项级数收敛的内容涉及少ꎬ而大量级数的敛散需要确定.我们通过数列收敛方法来判定级数收敛.从新的角度去认识收敛数列的渐进性:当n无限增大时ꎬ可以认为收敛数列yn{}相邻两项的差所构成的数列{yn-yn-1}(n>2)ꎬ无限接近一个公差为0的等差数列ꎬ从而给出了利用yn-yn-1趋于0来判断数列收敛的方法.这说明了收敛数列各项变化的微小性.本文给出了任意项级数收敛的一个判定定理ꎬ讨论了一些余弦级数的敛散性.㊀㊀二㊁任意项级数收敛的判定引理㊀设yn{}为一个有界数列.∀ε>0ꎬ∃NɪZ+ꎬ当n>N时ꎬ不等式|yn-yn-1|<ε恒成立ꎬ则数列yn{}收敛.推论㊀若级数ðɕn=1an有界ꎬ且limnңɕan=0ꎬ则该级数收敛.一个收敛级数任意加括号后所成级数仍然收敛ꎬ其逆命题不成立.但是有下面的定理:定理1㊀若级数ðɕn=1an的项添加括号后所成的级数收敛ꎬ且limnңɕan=0ꎬ则该级数收敛.证明㊀在级数ðɕn=1an的项添加括号过程中ꎬ如果存在一个括号里面有无穷多项ꎬ显然它是级数添加的最后一个括号ꎬ根据级数的性质ꎬ去掉该括号前面所有的项ꎬ它的敛散性不改变ꎬ从而结论成立.现在假设添加的每一个括号里面只有有限项.设ðɕn=1an的项添加括号后所成的级数为:(a1+a2+ +an)+(an+1+an+2+ +an)+ +(an+1+an+2+ +an)+ ꎬ其和为tꎬ记作ðɕk=1bn=t.从而∃KɪZ+ꎬ其余项满足ðɕk=Kbn|<1.令M=max{nk+1-nk|k=1ꎬ2ꎬ3ꎬ }<ɕ.又因为limnңɕan=0ꎬ对于ε=1Mꎬ∃N1ɪZ+ꎬ使得当n>N1时ꎬ有|an|<1M.取N=max{nKꎬN1}.对于充分大的自然数nꎬ∃k0ɪZ+ꎬ使得N<nkɤnɤnk+1ꎬ则ðɕn=1an的部分和Sn=ðni=1ai满足|Sn|=|bn+bn+ +bn+(an+1+an+2+ +an)|ɤ|ðɕk=1bn-ðɕk=k+1bn|+|an+1|+|an+2|+ +|an|ɤ|ðɕk=1bn|+|ðɕk=k+1bn|+|an+1|+|an+2|+ +|an|ɤ|t|+1+n-nkMɤ|t|+2.从而该级数有界.利用引理的推论可得结论.证毕.这个定理推广了交错级数收敛的莱布尼兹定理ꎬ可以说给出了判定级数的一个简便方法.定理2㊀余弦级数ðɕn=1cosπnkn收敛ꎬ其中kɪZ+.证明㊀当k=1时ꎬ容易知道结论成立.设Z[0]={2i|iɪZ}ꎬZ[1]={2i+1|iɪZ}.当k=2sꎬsȡ1时ꎬ根据二项式定理可得(n+1)2s=n2s+C12s(n2s-1+n)+C22s(n2s-2+n2)+ +Cs-12s(ns+1+ns-1)+Cs2sns+1=n2s+2sn(n2s-2+1)+12(2s)(2s-1)n2(n2s-4+1)+ +1(s-1)!(2s)(2s-1)2(s+2)ns-1(n2+1)+1s!(2s)(2s-1) (s+1)ns+1.对于n2s-r+1利用二项式定理可得Cr2snr(n2s-r+1)ɪZ[0]ꎬ1ɤrɤs-1ꎻ由Cs2sɪZ[0]得Cs2snsɪZ[0].由此可得ꎬ㊀(n+1)2s-n2s-1ɪZ[0]ꎬ[nk+(n+1)k]ɪZ[1].同理可得[nk-(n+1)k]ɪZ[1].当k=2s+1ꎬsȡ1时ꎬ有同样的结论.因此ꎬcosπnkn+cosπ(n+1)kn+1=cosπnkn(n+1)+cosπnk+cosπ(n+1)kn+1=cosπnkn(n+1)+cosπ2[nk+(n+1)k]cosπ2[nk-(n+1)k]n+1=cosπnkn(n+1).从而ðɕm=1cosπ(2m-1)k2m-1+cosπ(2m)k2mæèçöø÷=ðɕm=1cosπ(2m-1)k2m(2m-1).该级数绝对收敛.且limnңɕcosπnkn=0ꎬ根据定理1ꎬ级数ðɕn=1cosπnkn收敛.证毕.利用定理2可得ꎬ级数ðɕn=1cosaπnkn收敛ꎬ其中a=2r+1ꎬrɪZꎬkɪZ+.㊀㊀参考文献:[1]同济大学数学系.高等数学(第七版)[M].北京:高等教育出版社ꎬ2016.[2]华东师范大学数学科学学院.数学分析[M].北京:高等教育版社ꎬ2004.[3]杜先云ꎬ任秋道ꎬ王敏.单调有界准则的推广与级数ðɕn=1sinmnnα的敛散性[J].四川理工学院学报(自然科学版)ꎬ2017ꎬ6(32):126-130.[4]杜先云ꎬ任秋道.如何利用构造法培养学生的创新思维[J].绵阳师范学院学报(自然科学版)ꎬ2015ꎬ11(34):126-130.[责任编辑:李㊀璟]转化思想在高中数学函数解题中的应用李玉珊(安徽省宣城中学㊀242000)摘㊀要:本文将重点探讨转化思想在函数解题中的应用ꎬ以供参考.关键词:转化思想ꎻ换元ꎻ结合ꎻ构造中图分类号:G632㊀㊀㊀㊀㊀㊀文献标识码:A㊀㊀㊀㊀㊀㊀文章编号:1008-0333(2020)33-0003-02收稿日期:2020-08-25作者简介:李玉珊(1993.1-)ꎬ女ꎬ安徽省黄山市祁门人ꎬ本科ꎬ中学二级教师ꎬ从事高中数学教学研究.㊀㊀一㊁通过换元进行转化通过换元对要求解的问题进行转化ꎬ可使得一些参数之间的关系直观地呈现出来ꎬ从而找到解题思路.为使学生掌握这一转化方法ꎬ平时就要注重为学生讲解相关的理论ꎬ使学生把握进行换元转化的一些细节.同时ꎬ为使学生感受换元转化在解题中的妙用ꎬ应注重为学生讲解相关的例题ꎬ要求学生认真听讲ꎬ仔细揣摩解题过程ꎬ把握换元转化的精髓ꎬ以实现灵活应用.例1㊀已知函数f(x)为R上的单调函数ꎬ且对任意实数xꎬ均有f[f(x)+22x+1]=13ꎬ则f(log23)的值为(㊀㊀).A.-1㊀㊀㊀B.1㊀㊀㊀C.12㊀㊀㊀D.-12该道题目以复合函数为背景出题ꎬ难度较大ꎬ很多学生看到题目后不知如何打开解题思路.课堂上应注重要求学生认真观察给出的等式ꎬ并与学生一起分析ꎬ通过转化思想化陌生为熟悉.由已知可设f(x)+22x+1=tꎬ则f(x)=t-22x+1.又ȵf[f(x)+22x+1]=13ꎬ则f(t)=13ꎬʑt-22t+1=13.令g(x)=x-22x+1ꎬȵg(x)在R上单调递增ꎬ且g(1)=1-22+1=13ꎬʑt=1ꎬ则f(x)=1-22x+1ꎬʑf(log23)=1-3。
第四章不定积分习题4-1不定积分的概念与性质1.利用导数验证下列等式:解:2.求下列不定积分:(g是常数);解:3.含有未知函数的导数的方程称为微分方程,例如方程,其中为未知函数的导数,f(x)为已知函数.如果将函数y=φ(x)代入微分方程,使微分方程成为恒等式,那么函数y=φ(x)就称为这个微分方程的解.求下列微分方程满足所给条件的解:解:(1)因为,得C=0,所以所求的解为,因为,得C1=2,因此因为,得C2=-2,所以所求的解为4.汽车以20m/s的速度行驶,刹车后匀减速行驶了50m停住,求刹车加速度.可执行下列步骤:(1)求微分方程满足条件及的解;(2)求使的t值;(3)求使s=50的k值.解:(1),因为,得C1=20,因此因为,得C2=0,所以所求的解为(2)令,解得(3)根据题意,当时,s=50,即解得k=4,即得刹车加速度为-4m/s2.5.一曲线通过点(e2,3),且在任一点处的切线的斜率等于该点横坐标的倒数,求该曲线的方程.解:设曲线方程为y=f(x),则点(x,y)处的切线斜率为f'(x),由条件得因此f(x)为的一个原函数,得又根据条件曲线过点(e2,3),有f(e2)=3解得C=1,即得所求曲线方程为y=lnx+16.一物体因为静止开始运动,经t秒后的速度是3t2(m/s),问(1)在3秒后物体离开出发点的距离是多少?(2)物体走完360m需要多少时间?解:(1)设此物体自原点沿横轴正向由静止开始运动,位移函数为s=s(t),则由假设可知s(0)=0,因此s(t)=t3,所以所求距离为s(3)=27(m).(2)因为t3=360,得7.证明函数arcsin(2x-1),arccos(1-2x)和都是的原函数.证:因此结论成立.习题4-2换元积分法1.在下列各式等号右端的空白处填入适当的系数,使等式成立(例如:。
第四章 不定积分4.1 复习笔记一、不定积分的概念与性质1.原函数与不定积分的概念(1)原函数①定义如果在区间I 上,可导函数的导函数为,即对任意一,都有,则函数就称为在区间I 上的一个原函数.②原函数存在定理如果函数在区间I 上连续,则在区间I 上存在可导函数使对任一都有即连续函数一定有原函数.③注意两点a .如果有一个原函数,则就有无限多个原函数.b .若和都是的原函数,则()Fx ()x φ()f x(C 0为某个常数)(2)不定积分在区间I 上,函数的带有任意常数项的原函数称为(或)在区间I上的不定积分,记作,其中称为积分号,称为被积函数,称为被积表达式,x称为积分变量.2.基本积分表3.不定积分的性质(1)性质1设函数的原函数存在,则注:性质1对于有限个函数都是成立的.(2)性质2设函数的原函数存在,k为非零常数,则二、换元积分法1.第一类换元法设具有原函数,可导,则有换元公式()[()]()[()]u x f x x dx f u du ϕϕϕ='=⎰⎰2.第二类换元法设是单调的可导函数,并且又设具有原函数,则有换元公式1()()[[()]()]t x f x dx f t t dtψψψ-='=⎰⎰其中的反函数.三、分部积分法1.分部积分法设函数具有连续导数,则两个函数乘积的导数公式为移项,得对这个等式两边求不定积分,得称为分部积分公式.注:2.运用分部积分法需注意(1)v 要容易求得;(2)要比容易积出;(3)遵循“反对幂指三”原则.①“反对幂指三”定义“反对幂指三”分别指反三角函数、对数函数、幂函数、指数函数和三角函数.②“反对幂指三”原则“反对幂指三”原则是指在用分部积分法计算积分时,若出现上面相关函数,把被积表达式按照“反对幂指三”的积分次序,排在前面的看成“u”,排在后面的看成“dv”.【例】3.常见函数的不定积分四、有理函数的积分1.有理函数的积分(1)相关概念①有理函数 两个多项式的商称为有理函数.②有理分式 有理函数又称有理分式.③真分式 当P(x)的次数小于Q(x)的次数时,称这有理函数为真分式.④假分式 当P(x)的次数大于Q(x)的次数时,称这有理函数为假分式.(2)真分式的分解对于真分式,如果分母可分解为两个多项式的乘积且Q 1(x)与Q 2(x)没有公因式,则它可分拆成两个真分式之和。