动力总成悬置系统频率和解耦率的稳健优化方法
- 格式:pdf
- 大小:485.49 KB
- 文档页数:7

动力总成悬置系统优化及稳健性分析动力总成悬置系统是指汽车中发动机、变速器和驱动轴等汽车动力总成部件的组成系统,它对车辆的性能和安全性具有重要的影响。
因此,优化动力总成悬置系统的设计和提高其稳健性是汽车设计和生产中的一个重要课题。
在动力总成悬置系统设计中,需要考虑多个方面,包括系统整体重量、系统刚度、支撑件材料选用、降低噪音、减少振动等。
为了实现这些要求,通常需要结合数值分析和实验方法进行优化设计。
在系统整体重量的优化方面,设计师可以采用新型材料或优化零部件设计等措施来减轻体重。
例如,使用降低密度但强度较高的铝合金,或采用轻量化的减震器等。
在系统刚度方面,可以通过各种方式提高系统刚度,例如增加材料厚度、设计增加支撑件数量和位置等方案,同时还可以结合实验技术和数值分析方法,优化系统的刚度。
在支撑件材料选用方面,需要考虑动力总成悬置系统所处环境的特殊性质,如温度、湿度、腐蚀等,并且应该考虑到材料成本、加工工艺性、可靠性等因素。
这些要素均需在材料选用过程中进行综合考虑。
在噪音和振动方面的优化,需要采用减震、减振等措施,例如在发动机与车身之间设计隔振器,利用减振器改善驾驶稳定性并降低噪音。
同时,还可以采用模拟试验和理论模拟等方法,以确定系统的不同工况下的振动和噪声水平,并加以适当的改善。
此外,动力总成悬置系统的稳健性分析也是一个非常关键的方面。
系统的稳健性指的是系统能够在各种不确定情况下保持良好的性能和稳定性。
在系统的稳健性分析中,需要考虑到各种可能的负载情况、失效情况和故障情况,并结合设计要求和汽车行驶情况,确定系统的最佳稳健性设计方案。
这一过程需要采用可靠性分析方法,综合评估系统的稳健性。
总之,动力总成悬置系统的优化和稳健性设计是汽车工程设计中的一个重要环节。
通过采用先进的设计方法和技术手段,可以不断提高汽车的性能和安全性,满足消费者不断增长的需求和期望。
此外,为了实现动力总成悬置系统的优化和稳健性设计,需要充分了解系统的工作原理和特性。

《汽车动力总成悬置系统振动分析及优化设计》篇一一、引言随着汽车工业的快速发展,汽车动力总成悬置系统的性能逐渐成为影响汽车乘坐舒适性和驾驶稳定性的关键因素。
本文旨在通过对汽车动力总成悬置系统的振动进行分析,提出有效的优化设计方案,以提高汽车的整体性能。
二、汽车动力总成悬置系统概述汽车动力总成悬置系统是连接发动机、变速器等动力总成部件与车身的重要装置,其作用是减少动力总成振动对车身的影响,保证汽车行驶的平稳性和舒适性。
该系统主要由橡胶悬置、金属部件以及相应的控制系统组成。
三、振动分析1. 振动来源汽车动力总成悬置系统的振动主要来源于发动机的燃烧振动、曲轴转动引起的惯性力振动以及路面不平引起的整车振动等。
这些振动通过动力总成传递到悬置系统,进而影响汽车的乘坐舒适性和驾驶稳定性。
2. 振动传递路径振动在动力总成悬置系统中的传递路径主要包括:发动机振动通过橡胶悬置传递到金属部件,再通过金属部件传递到车身。
此外,控制系统也会对振动传递产生影响。
3. 振动影响过大的振动会导致车身抖动、噪音增大,影响乘坐舒适性;同时,也会对动力总成部件产生损伤,降低汽车的使用寿命。
因此,对动力总成悬置系统的振动进行分析至关重要。
四、优化设计1. 设计原则针对汽车动力总成悬置系统的振动问题,优化设计应遵循以下原则:减小振动传递、提高系统刚度、优化控制系统等。
同时,还需考虑系统的轻量化、可靠性以及制造成本等因素。
2. 优化方案(1)材料选择:选用高弹性模量、高阻尼性能的橡胶材料,提高悬置系统的减振性能。
(2)结构优化:通过有限元分析等方法,对悬置系统的结构进行优化设计,减小振动传递,提高系统刚度。
例如,可以调整橡胶悬置的形状、尺寸以及布置位置等。
(3)控制系统优化:通过引入先进的控制算法和传感器技术,实现动力总成悬置系统的智能控制,提高系统的响应速度和减振效果。
(4)多场耦合分析:综合考虑发动机、变速器等动力总成部件的振动特性以及车身的动态响应,进行多场耦合分析,为优化设计提供依据。

图1动力总成悬置系统力学模型动力总成悬置系统有x、y、z3个方向的平动和绕、z3个方向的转动,多自由度振动系统的振动微分方程式为[1]:(其中:;M———系统质量矩阵;C———系统阻尼矩阵;K———系统刚度矩阵;F(t)———系统所受激励向量。
固有频率和模态方程为由式(2)可得系统的主振型方程:2动力总成悬置系统的优化设计动力总成6自由度运动通常相互耦合,其中:m kl ———M 的第k 行l 列元素;Øi ———系统的第i 阶主阵型。
动力总成6自由度中沿z 轴的平动(Bounce 轴的转动(动力总成横置为Pitch ,动力总成纵置为本文以某车型为例,其输入质量参数如表中质量单位为kg ,惯量参数单位为kg.m 2。
由表1参数,采用MATLAB 及ISIGHT 对悬置系统进行优化,由于悬置类型及受整车布置的限制,本实例仅优化悬置刚度,悬置安装位置及安装角度不做优化。
联合优化后的悬置刚度如表2所示,系统各阶频率及解耦率如表所示。
该车型为三点悬置,其中左悬置为变速器侧悬置,置为衬套式悬置,其压剪比为3.7满足压剪比3~8图2ISIGHT 与MATLAB 联合优化框图表1输入质量参数Jxx Jyy Jzz Jxy Jyz 10.715.6210.28-0.921.15图3能量解耦率分布[2]阎红玉,徐石安.发动机—悬置系统的能量法解耦及优化设计[J].汽车工程,1993,15(6):321-328.[3]赵彤航.CA1261汽车发动机悬置系统隔振的研究[D].吉林大学硕士学位论文,2002.[4]庞剑,谌刚,何华.汽车噪声与振动—理论与应用[M].北京:北京理工大学出版社,2006.[5]周明,等.遗传算法原理及应用[M].北京:国防工业出版社,1999.[6]上官文斌,徐驰,黄振磊,李岐,李涛.汽车动力总成悬置系统位移控制设计计算方法[J].汽车工程,2006,28(8):738-742.左悬置隔振率右悬置隔振率后悬置隔振率图5三档全油门悬置隔振率图4悬置怠速隔振率。


动力总成悬置系统优化及稳健性分析童东红;郝志勇【摘要】To improve the vibration insulation performance of the powertrain mounting system, we use a mounting system as research object and construct a DOF vibration analysis mathematical model in the torque axis coordinate system, and analyze energy decoupling method. The mounting system is optimized with genetic algorithm with vibration decoupling ratios and natural frequencies as design objectives, and dynamic stiffness of individual mount as design variables. Finally, the design robustness is analyzed by using Monte Carlo simulation method. The results illustrate that the decoupling ratios and frequencies meet the design requirements after optimization, and the design robustness is also satisfactory.%为改善动力总成悬置系统的隔振性能,以某车辆的悬置系统为研究对象,在扭矩轴坐标系下建立6自由度振动分析数学模型,阐述能量解耦的计算方法。
以悬置系统振动解耦率和固有频率分布为设计目标,以悬置刚度为设计变量,采用遗传算法对该悬置系统进行优化设计,并且用蒙特卡罗模拟方法对优化结果进行稳健性分析。
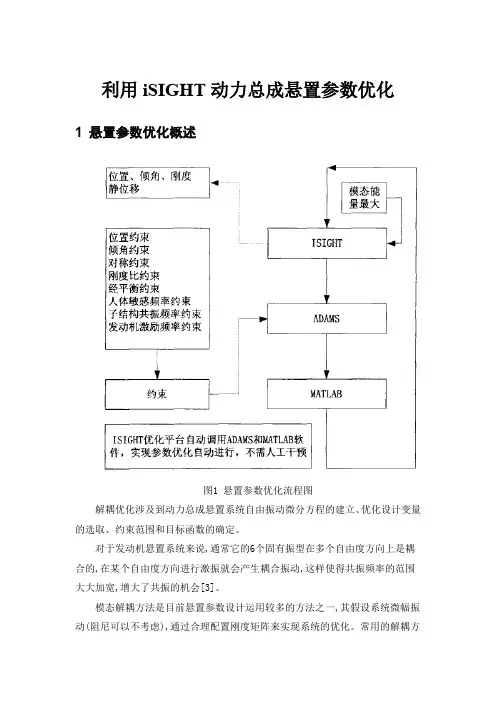
利用iSIGHT动力总成悬置参数优化1 悬置参数优化概述图1 悬置参数优化流程图解耦优化涉及到动力总成悬置系统自由振动微分方程的建立、优化设计变量的选取、约束范围和目标函数的确定。
对于发动机悬置系统来说,通常它的6个固有振型在多个自由度方向上是耦合的,在某个自由度方向进行激振就会产生耦合振动,这样使得共振频率的范围大大加宽,增大了共振的机会[3]。
模态解耦方法是目前悬置参数设计运用较多的方法之一,其假设系统微幅振动(阻尼可以不考虑),通过合理配置刚度矩阵来实现系统的优化。
常用的解耦方法有弹性中心法、刚度矩阵解耦法、能量解耦法等。
弹性中心法受到悬置布置位置的限制,而刚度矩阵法对于缺少对称面的动力总成结构应用不便,能量解耦方法则可以在原坐标系中进行解耦设计,基本脱离发动机类型和布置形式,解耦总指标在(0, 1)范围内变化,使优化计算保持较好的稳定性。
1.1 动力总成悬置设计的总体原则对于动力总成悬置系统的设计而言,总体的设计思路是:对于存在较大激振力的自由度而言,在避免出现共振的基础上应使动力总成悬置在该方向的刚度小,以利于减振;对于没有激振力或激振力小的自由度而言,应使动力总成悬置在该方向的刚度大,以利于支撑。
按照振动理论,动力总成悬置通用的隔振原则是:1、悬置的布置应尽可能满足非耦合条件,力图使各自由度的振动互相分离。
在此基础上,力图使外部激励频率和系统固有频率之比大于2,使共振点处于实用频率之外,提高隔振效果;2、考虑到动力总成及其支撑车架都是弹性体,应力争将动力总成的悬置支撑在其弯曲振动的节点上,极力降低传递给车体的振动,改善高速行驶时的驾驶室室内噪声水平;3、动力总成的主要运动自由度是侧倾,悬置必须确保能够支撑动力总成的重量,并降低侧倾方向的刚度。
在此前提下考虑悬置布置的倾斜角度,使垂直和剪切方向的刚度得到优化;4、为了防止抖动(轮胎一阶振动模式引起的10~30 Hz车体振动),提高舒适性,必须将悬置系统垂向固有频率设计得较簧下质量振动系统固有频率略高;5、悬置的静变形应在4mm左右,静变形过大将影响悬置元件的寿命,静变形过小意味悬置的刚度过大,不利于减振的需要;6、对于半阶和一阶激振频率都很大的发动机而言,侧倾模态应该在半阶频率和一阶频率之间;7、动力总成的刚体模态应尽量避开人体的最敏感范围;8、动力总成的横向刚度大,利于整车的操纵稳定性。


《汽车动力总成悬置系统振动分析及优化设计》篇一一、引言汽车动力总成悬置系统作为车辆动力传递与振动控制的关键部分,其性能的优劣直接关系到整车的驾驶舒适性和行驶稳定性。
因此,对汽车动力总成悬置系统的振动进行分析,并进行相应的优化设计,是汽车工程领域研究的重要课题。
本文将深入探讨汽车动力总成悬置系统的振动问题,分析其成因,并针对现有问题提出优化设计方案。
二、汽车动力总成悬置系统概述汽车动力总成悬置系统主要由发动机、变速器、离合器等组成,通过悬置装置与车架相连。
其作用是支撑和固定动力总成,同时减少振动和噪声的传递,保证驾驶的舒适性和行驶的稳定性。
三、汽车动力总成悬置系统振动分析1. 振动产生原因汽车动力总成悬置系统振动的主要原因是发动机运转时产生的激励力,包括燃烧力、惯性力和摩擦力等。
此外,道路不平、车辆行驶中的颠簸等也会对悬置系统产生振动。
2. 振动影响分析振动不仅会影响驾驶的舒适性,还会对车辆的行驶稳定性、零部件的寿命和车辆的噪音产生影响。
长期受到振动的零部件容易出现松动、磨损等问题,影响车辆的正常运行。
四、汽车动力总成悬置系统优化设计针对汽车动力总成悬置系统的振动问题,本文提出以下优化设计方案:1. 材料选择优化选用高强度、轻量化的材料,如铝合金、高强度塑料等,以降低系统质量,提高其刚度和减振性能。
同时,采用阻尼材料,如橡胶等,以吸收振动能量,减少振动传递。
2. 结构优化设计对悬置系统的结构进行优化设计,如增加支撑点、改变支撑方式等,以提高系统的稳定性和减振性能。
同时,采用多级减振设计,使系统在不同频率下的减振效果更加明显。
3. 控制系统优化通过引入先进的控制系统,如液压控制系统、电子控制系统等,对悬置系统的振动进行实时监测和控制。
通过调整控制参数,使系统在不同工况下都能保持良好的减振性能。
五、结论通过对汽车动力总成悬置系统的振动分析,我们发现其产生的主要原因包括发动机运转产生的激励力和道路、行驶中的颠簸等外部因素。

动力总成悬置系统振动耦合及解耦理论详解动力总成悬置系统作为汽车振动系统的一个重要子系统,其振动的传递特性对汽车的NVH性能有很大影响。
多自由度振动中的耦合振动扩大了引起共振的频率范围,增加了振动的响应方向,不利于控制系统的振动,因此谈到悬置系统设计都绕不过解耦的问题,这篇文章就来详细介绍一下这两个概念。
耦合是指两个振动模态在某一振动模态下(或在某一广义坐标方向上)的振动输入,导致另一振动模态下(或另一广义坐标方向上)的响应。
使耦合分离称为解耦。
解耦的目的是使各个自由度上(即各振动模态)的振动相对独立或分离,这样可对隔振效果不佳的自由度独立采取措施而不影响其他自由度方向上的有关性能。
当各自由度独立后,可能产生共振的频率比存在耦合时要小,特别在激振能量大的方向上要保证解耦。
振动耦合不利于隔振,因为两个耦合振动的模态可能产生相互激励,导致振动放大,并使某些自由度的振动频带变宽,从而使隔振性能下降。
例如四缸发动机在怠速工况下产生的扭矩波动可能同时激起动力总成俯仰(Pitch)和垂向(Z)振动,这将导致车身振动增加,并且俯仰(Pitch)运动(Pitch)又可能和其它刚体运动模态相互耦合,从而引发车身振动变形,造成整车噪声增大、舒适性变差、零部件早期损坏等现象。
对于动力总成悬置系统来说,耦合振动可以在多个自由度之间发生,如果在合理的位置和方向上布置动力总成悬置以及设计合适的悬置系统的刚度可以减小或消除耦合振动。
悬置系统能量法解耦分析理论1、动力总成悬置系统坐标系统如图1所示,把发动机动力总成视为一个具有六自由度的刚体,它通过悬置支撑在车架上,悬置被视为具有三向刚度的弹性阻尼组件。
图1 动力总成悬置系统动力学模型图2为悬置件简化模型,一般可将悬置件简化为三个沿主轴方向的弹簧-阻尼系统,并且每一主轴与动坐标轴之间存在图中所列的夹角关系。
图2 悬置动力学模型2、动力总成悬置系统动力学方程根据自由振动的Lagrange方程:(1)式中T为系统动能;V为系统势能;qj为系统的广义坐标。

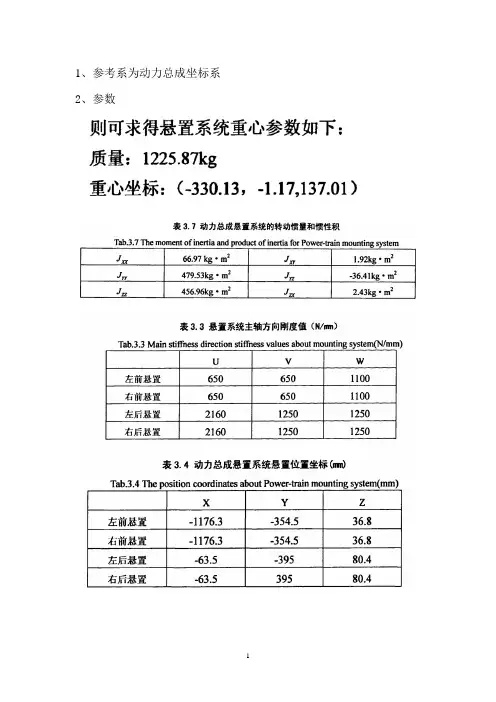
1、参考系为动力总成坐标系2、参数前两个悬置的安装角度为45°,后两个悬置的安装角度为90°。
怠速工况(600r/min)、额定转速工况(2200r /min)和最大扭矩工况(1400r /min)2、悬置频率范围(6缸4冲程)发动机激振频率f =τ60ni,n:发动机转数,i:发动机汽缸数,τ:冲程系数,两冲程为1,四冲程为2。
怠速600r/min,则最小频率为30Hz 。
怠速激振频率60/2n f ==21Hz.2222)2()1()2(1ξλλξλβ+-+=;其中β为振动传递率,λ为频率比(激振频率与系统固有频率比值ω/0ω),ξ为阻尼比。
当λ>2时,系统传递率小于1,系统起到隔振作用,此时ωω>2,即固有频率小于2/1倍的激振频率,则悬置系统的最大固有频率应小于14.14Hz 。
为了保证悬置系统的使用寿命,悬置系统的最小固有频率应大于5Hz 。
3、时域分析3.1、动力总成激振力矩在ADAMS view中使用周期性正弦载荷作用,其正弦函数表达式分别为:怠速工况:760000.0*sin*(30*2*pi*time)额定转速工况:1050000.0*sin*110*2*pi*time)最大扭矩工况:1250000.0*sin*(70*2*pi*time)在动力总成悬置系统质心处作用激振力矩,绕曲轴方向,如下图示。
3.2、置支撑处响应力测量在怠速工况下,对动力总成悬置系统进行仿真,选择测量对象busing 元件,选择measure选项,特征选项选择force,方向选择Z向,测量悬置支撑处Z向响应力。
(end time:15,step:8000 )分别对4个悬置支撑响应力进行测试得图3.2-1左前悬置软垫支撑处的响应力图3.2-2右前悬置软垫支撑处的响应力图3.2-3左后悬置软垫支撑处的响应力图3.2-4右后悬置软垫支撑处的响应力从四个悬置支撑点响应力曲线可以看出,后两个悬置支撑点响应力明显比前悬置支撑点响应力要大。
机械设计与制造工程Machine Design and Manufacturing Enginee/ng 2021年4月第50卷第4期Apr. 2021Vol. 50 No. 4DOI : 10. 3969/j. issn. 2095 - 509X. 2021.04. 019汽车动力总成悬置系统的多目标优化方法姜立标,罗健(华南理工大学机械与汽车工程学院,广东广州510641)摘要:对汽车动力总成悬置系统的多目标优化问题进行了研究,明确了优化方向。
基于算法融合理论,提出了结合多目标粒子群优化(MOPSO )算法和非支配排序遗传算法'% NSGA -')的混合算法,并运用经典测试函数分别对MOPSO 算法、NSGA -'及混合算法进行测试,验证了混合算法的可行性和高效性。
运用混合算法解决了动力总成悬置系统的解耦问题,得 了多组满足的解集。
实例优化结果证明,该 合算法对解决复杂动力总成多目标优化问题是有效的。
关键词:动力总成悬置系统;多目标粒子群优化;非支配排序遗传算法';混合算法;多目标优化中图分类号:U464. 13 文献标识码:A 文章编号:2095 -509X ( 2021)04 -0087 -05车作为交通工具,其各项性能越来越受到人们的关注,其中整车NVH (noise 、vibration 、harshnes )性能是目前人们的一项。
影响车NVH 性能的因素,动力总成的振动是中一个重要的因素。
动力总成的振动 复杂的多自由度振动。
为使复杂的振动:简单化,在设计悬置系统时,应对系统的解耦,对动力总成的模态频率%陈剑等'1(提出了基于Chebyshev 区间的动力总成悬置,获得的率;毕凤荣等'2(提出了基于K/ging 模型的动力总成悬置系统目 ,通过 得的 !率。
目,对于动力总成悬置系统多目用单一的, 率 。
为提高动力总成悬置的多目标优化效率,本文首先建立动力总成悬置 ,确向,基融合理论,提出 目标粒优化"multi - objective particle swam optimization ,MOPSO )算法和非 排序'(non -dominated sorting genetic algorithm ',NSGA -')的混合算法;然后 测试, 混合算法的 率更高度高;最后运用混 对具体的悬置, 得的 , 为悬置提供 组合理的参数。
电动汽车动力总成悬置系统的多目标稳健优化设计随着全球节能减排与环保意识的不断提高,人们对电动汽车的需求越来越大。
但是相对于燃油汽车,电动汽车还存在着许多问题,如续航里程不足、充电时间长、电池寿命不佳等,而电动汽车的关键在于动力总成悬置系统,因为它关系到汽车的动力输出、悬挂舒适性和操控稳定性,因此优化设计是必不可少的。
多目标稳健优化设计是一种考虑不确定因素的优化方法,能够有效地提高系统的稳健性和可靠性。
因此,本文将探讨电动汽车动力总成悬置系统的多目标稳健优化设计方案。
首先,为了提高汽车的动力输出,我们需要考虑选择合适的电机和逆变器,以及传动系统的优化设计。
同时,为了保证车辆的悬挂舒适性,我们需要采用有效的悬挂系统,如空气悬挂、自适应悬挂等。
此外,为了保证汽车的操控稳定性,我们需要对转向系统、制动系统以及轮胎进行优化设计。
在进行设计时,我们需要考虑优化目标和优化限制条件。
优化目标可以包括动力性能、燃料消耗、车辆稳定性等多个方面,优化限制条件可以包括安全性、舒适性、成本等多个方面。
为了解决这个多目标问题,我们可以采用多目标优化算法,如NSGA-II、MOEA/D等,将不同的目标权重进行设定,得到一系列的最优解。
在考虑不确定因素时,我们需要将这些因素纳入到设计过程中去,例如电机参数的波动、制动系统的故障、路面状况的不确定性等。
一般情况下,我们可以采用确定性建模和随机建模相结合的方式进行多目标稳健优化设计。
最后,值得注意的是,设计迭代过程中需要注意对各个参数的监控和调整,以便在不断优化的过程中及时发现和解决问题,确保设计的实际性和合理性。
综上所述,电动汽车动力总成悬置系统的多目标稳健优化设计是目前研究的热点,它可以充分考虑到多个方面的优化目标和限制条件,来达到尽可能优秀的汽车性能。
未来,我们可以采用更加先进的优化算法和技术手段,来进一步提高电动汽车的整体性能和市场竞争力。
除此之外,电动汽车动力总成悬置系统的优化设计还需要考虑材料的选择和汽车结构的优化。
汽车动力总成悬置优化设计分析作者:佘振成张露来源:《科学导报·学术》2019年第25期摘 ;要:合理的汽车动力总成悬置系统可以降低汽车动力总成和车体的振动。
从系统固有频率配置及振动解耦角度分析悬置系统的振动特性;根据实际条件,以提高系统振动解耦率为目标,对动力总成悬置系统隔振性能进行优化设计,有效提高系统固有频率配置合理性和系统振动解耦率,使系统的隔振特性有了较大提升,从而改善了系统的稳定性。
关键词:动力总成;悬置系统一、汽车动力总成悬置系统的作用1、隔离振动在发动机所有工作转速范围内,发动机产生的振动必须通过悬置系统加以隔离,尽可能降低传给汽车底盘和车身的振动。
同时,悬置系统还必须隔离由道路不平引起的车轮、悬挂系统的振动,防止这一振动向发动机传递,避免发动机振动加剧,以满足车辆运行时的平稳性和舒适性,并保证怠速和停机时发动机的稳定性。
2、发动机支承和定位在发动机本身振动和外界作用力驱动下,发动机和底盘之间必然存在着相对运动。
所以悬置系统必须具有控制发动机相对运动和位移的功能。
3、保护发动机车辆在行驶过程中承载着动态负荷和冲击负荷,悬置系统应具有保护发动机的能力,防止发动机个别部位因承受过大的冲击载荷而损坏。
4、发动机与底盘之间的连接零件必须要有足够的柔性如:排气管、进气管、燃油管、冷却水管、油门操纵机构及变速箱操纵机构等。
如果他们的刚度较大,发动机的振动容易损坏这些零件,尤其在怠速停机、出现共振时。
5、悬置系统的零件必须具有足够的强度和可靠性,在严重的冲击负荷下应保证不发生损坏。
二、动力总成悬置系统的优化设计方法1、动力总成悬置系统的解耦设计通常动力总成悬置系统的六个自由度的振动是耦合的,这样会导致动力总成悬置系统的振幅加大、振动频带过宽。
因此在设计时悬置应尽量采用解耦形式布置。
从理论上讲,当前后悬置的弹性中心与动力总成的质心完全重合时,则悬置系统在六个方向的振动完全解耦。
但由于受到整车布置等各种条件的制约,完全解耦难以实现,因此通常的做法是将与激振力有关的几个主要振动方向的振动模态解耦,即部分解耦。